Simple correction factor for laser speckle imaging of flow dynamics

Abstract

One of the major constraints facing laser speckle imaging for blood-flow measurement is reliable measurement of the correlation time (τ_C) of the back-scattered light and, hence, the blood’s speed in blood vessels. In this Letter, we present a new model expression for integrated speckle contrast, which accounts not only for temporal integration but spatial integration, too, due to the finite size of the pixel of the CCD camera; as a result, we find that a correction factor should be introduced to the measured speckle contrast to properly determine τ_C; otherwise, the measured blood’s speed is overestimated. Experimental results support our theoretical model.

Light propagation in scattering media produces speckle patterns. If the media contain moving scatterers, the scattered intensity field will fluctuate in proportion to the speed of scattering centers. Typically, CCD cameras are used to image the ensuing pattern. If the camera exposure time is large compared to the speckle correlation time, then the speckle visibility is reduced. Using this fact, Fercher and Briers [1] employed speckle imaging of tissue to determine blood flow. Due in part to the simplicity and low cost of this approach, researchers have rapidly integrated laser speckle imaging (LSI) in their studies, which cover a wide range of applications, including ophthalmology [2], dermatology [3,4], dentistry [5,6], and neurobiology [7,8], among others.

The methods to extract blood-flow information from the imaged speckle patterns have been refined over the years [9,10]. For example, Parthasarathy et al. [11] recently derived a new relationship between speckle contrast and speckle correlation time that takes into account contributions from stationary and dynamic scattering centers.

In this Letter, we demonstrate that the size of the camera pixel plays an important role in blood flow measurements. We use principles first introduced by Goodman [12] to derive a new model expression that accounts for the finite size of camera pixels. We demonstrate that, if the finite size is not taken into account, the correlation time of the backscattered light is underestimated, and hence blood flow is overestimated. We present experimental data that support our new model.

The electric field re-emitted from a scattering object depends on the superposition of fields associated with the spatiotemporal distribution of optical scattering centers within the object. The Siegert relation [10] describes the relationship between the electric field and intensity autocorrelation functions (g₁ and g₂, respectively):

$$g_2\left(\tau \right)=1+{\mid g_1\left(\tau \right)\mid }^2.$$ (1)

Starting with this equation, Bandyopadhyay et al. [10] derived a second-generation relationship between speckle contrast K and correlation time τ_c, which takes into account the finite size of the optical detector:

$$K^2=\beta \frac{e^{-2x}-1+2x}{2x^2},$$ (2)

where β is a correction factor [13], x = T/τ_c, and T is the camera’s exposure time.

Recently, research groups [10,11,13,14] demonstrated the need to further modify the model to account for the presence of light scattered from stationary optical scatterers. The scattered electric field is the superposition of a fluctuating (E_f) plus a static (E_s) component [11]:

$$E\left(t\right)=E_f\left(t\right)e^{-iwt}+E_s{e}^{-iwt},$$ (3)

where ω is the optical frequency of the excitation source. Using the Siegert relation, Parthasarathy et al. [11] derived the following third-generation relationship between K and τ_c:

$$K={\beta }^{1∕2}{\left[{\rho }^2\frac{e^{-2x}-1+2x}{2x^2}+4\rho (1-\rho )\frac{e^{-x}-1+x}{x^2}+{(1-\rho )}^2\right]}^{1∕2}+C_n,$$ (4)

where ρ = I_f/(I_f + I_s) is the fraction of total light that interacts with moving scatterers, $I_f=\langle E_f{E}_f^{\ast }\rangle$ is the intensity of light interacting with moving scatterers, $I_s=\langle E_s{E}_s^{\ast }\rangle$ is the intensity of light interacting with stationary scatterers, and C_n is a term that accounts for noise contributions to the measurement. We propose a related approach to study the effects of stationary and moving scatterers on the remitted speckle pattern. We model the re-emitted electric field as a superposition of a stationary but spatially dependent component [E_s(x′,y′)] and a fluctuating component [E_f(x′,y′,t)], which has scattered at least once from a moving scatterer. Similar to Eq. (3), the resultant electric field is

$$E(x^{\prime },y^{\prime },t)=E_f(x^{\prime },y^{\prime },t)e^{-iwt}+E_s(x^{\prime },y^{\prime })e^{-iwt}.$$ (5)

Following the approach of Boas [14], we substituted Eq. (5) into Eq. (1) to arrive at the following equation:

$$\begin{array}{cc}\hfill g_2(\Delta x^{\prime },\Delta y^{\prime },\tau )& =1+{\mid g_1(\Delta x^{\prime },\Delta y^{\prime },\tau )\mid }^2\hfill \\ \hfill & =1+\alpha {\mid \frac{\langle E(x_1^{\prime },y_1^{\prime },t)E^{\ast }(x_1^{\prime }+\Delta x^{\prime },y_1^{\prime }+\Delta y^{\prime },t+\tau )\rangle }{\langle E(x_1^{\prime },y_1^{\prime },t)E^{\ast }(x_1^{\prime },y_1^{\prime },t)\rangle }\mid }^2\hfill \\ \hfill & =1+a{p}^2{\mid g_{1,f}(\Delta x^{\prime },\Delta y^{\prime },\tau )\mid }^2+2\alpha \rho (1-\rho )\mid g_{1,f}(\Delta x^{\prime },\Delta y^{\prime },\tau )\mid \mid g_{1,s}(\Delta x^{\prime },\Delta y^{\prime })\mid +\alpha {(1-\rho )}^2{\mid g_{1,s}(\Delta x^{\prime },\Delta y^{\prime })\mid }^2+C_n^2,\hfill \end{array}$$ (6)

where α is a normalization parameter that accounts for effects (e.g., polarization) that reduce speckle contrast and that differ from spatial sampling of the speckle pattern; g_1,f and g_1,s are the normalized correlation functions of the fluctuating and static electric fields, respectively; and Δx′ and Δy′ are the distances between two arbitrary points ($x_1^{\prime }$, $y_1^{\prime }$) and ($x_2^{\prime }$, $y_2^{\prime }$) on the detector surface. The constant term ($C_n^2$) was introduced to account for contributions of noise [15]. g_1,f and g_1,s are given as

$$\begin{array}{cc}\hfill g_{1,f}(\Delta x^{\prime },\Delta y^{\prime },\tau )& =\frac{\langle E_f(x_1^{\prime },y_1^{\prime },t)E_f^{\ast }(x_1^{\prime }+\Delta x^{\prime },y_1^{\prime }+\Delta y^{\prime },t+\tau )\rangle }{\langle E_f(x_1^{\prime },y_1^{\prime },t)E_f^{\ast }(x_1^{\prime },y_1^{\prime },t)\rangle }\hfill \\ \hfill g_{1,s}(\Delta x^{\prime },\Delta y^{\prime })& =\frac{\langle E_s(x_1^{\prime },y_1^{\prime })E_s^{\ast }(x_1^{\prime }+\Delta x^{\prime },y_1^{\prime }+\Delta y^{\prime })\rangle }{\langle E_f(x_1^{\prime },y_1^{\prime })E_s^{\ast }(x_1^{\prime },y_1^{\prime })\rangle }.\hfill \end{array}$$ (7)

The intensity correlation function [Eq. (6)] is a general form of the function derived by Parthasarathy et al. [11]. It represents a new expression for the Siegert relation, taking into account not only temporal variations but also spatial variations in the speckle pattern resulting from a mixture of moving and stationary scatterers. Note that for constant values of Δx′ and Δy′, Eq. (6) reduces to the Siegert relation derived by Boas and Dunn [15]:

$$g_2\left(\tau \right)=1+{\rho }^2{\mid g_{1,f}\left(\tau \right)\mid }^2\beta +2\rho (1-\rho )\mid g_{1,f}\left(\tau \right)\mid \beta +{(1-\rho )}^2\beta +C_n^2.$$ (8)

We now use Eq. (6) to derive a new expression relating K and τ_c. Based on Goodman [12], the second moment of measured intensity depends on the spatial intensity correlation function [Eq. (6)] and a map of the spatial detector photosensitivity:

$$\begin{array}{cc}\hfill \langle I^2\rangle & =\frac{1}{A_D^2{T}^2}\int {\int }_0^T\int {\int }_{-\infty }^{\infty }\int {\int }_{-\infty }^{\infty }D(x_1^{\prime },y_1^{\prime })D(x_2^{\prime },y_2^{\prime })\times \langle I(x_1^{\prime },y_1^{\prime },t_1)I(x_2^{\prime },y_2^{\prime },t_2)\rangle \mathrm{d}{x}_1^{\prime }\mathrm{d}{y}_1^{\prime }\mathrm{d}{x}_2^{\prime }\mathrm{d}{y}_2^{\prime }\mathrm{d}{t}_1\mathrm{d}{t}_2\hfill \\ \hfill & =\frac{1}{A_D^2{T}^2}\int {\int }_0^T\int {\int }_{-\infty }^{\infty }\int {\int }_{-\infty }^{\infty }D(x_1^{\prime },y_1^{\prime })D(x_2^{\prime },y_2^{\prime })\times {\langle I\rangle }^2{g}_2(\Delta x^{\prime },\Delta y^{\prime },\tau )\mathrm{d}{x}_1^{\prime }\mathrm{d}{y}_1^{\prime }\mathrm{d}{x}_2^{\prime }\mathrm{d}{y}_2^{\prime }\mathrm{d}{t}_1\mathrm{d}{t}_2,\hfill \end{array}$$ (9)

where D(x′,y′) is a real and positive weighting function that represents the spatial distribution of detector photosensitivity. For a uniformly sensitive photodetector:

$$D(x^{\prime },y^{\prime })=\{\begin{array}{cc}1\hfill & \text{in the sensitive area}\hfill \\ 0\hfill & \text{outside of the sensitive area}\hfill \end{array}\phantom{\}}.$$ (10)

The sensitive area of the photodetector A_D is

$$A_D=\int {\int }_{-\infty }^{\infty }D(x^{\prime },y^{\prime })\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }.$$ (11)

Substituting Eq. (6) into (9), we obtain

$$K^2\equiv \frac{\langle I^2\rangle -{\langle I\rangle }^2}{{\langle I\rangle }^2}=\frac{{\rho }^2\alpha }{A_D^2{T}^2}\int {\int }_0^T\int {\int }_{-\infty }^{\infty }{K}_D(\Delta x^{\prime },\Delta y^{\prime }){\mid g_{1,f}(\Delta x^{\prime },\Delta y^{\prime },t_2-t_1)\mid }^2\times \mathrm{d}\left(\Delta x^{\prime }\right)\mathrm{d}\left(\Delta y^{\prime }\right)\mathrm{d}{t}_1\mathrm{d}{t}_2+\frac{2\alpha \rho (1-\rho )}{A_D^2{T}^2}\int {\int }_0^T\int {\int }_{-\infty }^{\infty }{K}_D(\Delta x^{\prime },\Delta y^{\prime })\mid g_{1,s}(\Delta x^{\prime },\Delta y^{\prime })\mid \times \mid g_{1,f}(\Delta x^{\prime },\Delta y^{\prime },t_2-t_1)\mid \mathrm{d}\left(\Delta x^{\prime }\right)\mathrm{d}\left(\Delta y^{\prime }\right)\mathrm{d}{t}_1\mathrm{d}{t}_2+\frac{\alpha {(1-\rho )}^2}{A_D^2{T}^2}\int {\int }_0^T\int {\int }_{-\infty }^{\infty }{K}_D(\Delta x^{\prime },\Delta y^{\prime }){\mid g_{1,s}(\Delta x^{\prime },\Delta y^{\prime })\mid }^2\times \mathrm{d}\left(\Delta x^{\prime }\right)\mathrm{d}\left(\Delta y^{\prime }\right)\mathrm{d}{t}_1\mathrm{d}{t}_2,$$ (12)

where

$$K_D(\Delta x^{\prime },\Delta y^{\prime })=\int {\int }_{-\infty }^{\infty }D(x_1^{\prime },y_1^{\prime })D(x_1^{\prime }-\Delta x^{\prime },y_1^{\prime }-\Delta y^{\prime })\mathrm{d}{x}_1^{\prime }\mathrm{d}{y}_1^{\prime }.$$ (13)

For a spatially incoherent source model that represents many scattering systems, the electric-field correlation function can be separated into terms describing the stationary and moving scatterers [16]:

$$\mid g_{1,f}(\Delta x^{\prime },\Delta y^{\prime },t_2-t_1)\mid =\mid g_{1,s}(\Delta x^{\prime },\Delta y^{\prime })\mid \mid g_f(t_2-t_1)\mid .$$ (14)

We use Eq. (14) to rewrite Eq. (12) as

$$K^2=\alpha \left\{\frac{1}{A_D^2}\int {\int }_{-\infty }^{\infty }{K}_D(\Delta x^{\prime },\Delta y^{\prime }){\mid g_{1,s}(\Delta x^{\prime },\Delta y^{\prime })\mid }^2\times \mathrm{d}\left(\Delta x^{\prime }\right)\mathrm{d}\left(\Delta y^{\prime }\right)\right\}\times \left\{\frac{1}{T^2}\int {\int }_0^T[{\rho }^2\mid g_f(t_2-t_1)\mid +\rho (1-\rho )\mid g_f(t_2-t_1)\mid +{(1-\rho )}^2]\mathrm{d}{t}_1\mathrm{d}{t}_2\right\}.$$ (15)

For a square detector with uniform photosensitivity and a Gaussian-shaped intensity pattern, the first term of Eq. (15) is simplified to [12]

$$\frac{1}{A_D^2}\int {\int }_{-\infty }^{\infty }{K}_D(\Delta x^{\prime },\Delta y^{\prime }){\mid g_s(\Delta x^{\prime },\Delta y^{\prime }\mid }^2\mathrm{d}\left(\Delta x^{\prime }\right)\mathrm{d}\left(\Delta y^{\prime }\right)={\left\{\sqrt{\frac{1}{M}}\mathrm{erf}\left(\sqrt{\pi M}\right)-\left(\frac{1}{\pi M}\right)(1-e^{-\pi M})\right\}}^2\equiv \beta \left(M\right),$$ (16)

where M = A_D/A_C, and A_C is the correlation area of the intensity (effectively, the speckle size) on the detector:

$$A_C=\int {\int }_{-\infty }^{\infty }{\mid g_s(\Delta x^{\prime },\Delta y^{\prime })\mid }^2\mathrm{d}\left(\Delta x^{\prime }\right)\mathrm{d}\left(\Delta y^{\prime }\right).$$ (17)

The second factor of Eq. (15) is rewritten as [11,15]

$$\frac{1}{T^2}\int {\int }_0^T[{\rho }^2\mid g_f(t_2-t_1)\mid +\rho (1-\rho )\mid g_f(t_2-t_1)\mid +{(1-\rho )}^2]\mathrm{d}{t}_1\mathrm{d}{t}_2={\rho }^2\frac{e^{-2x}-1+2x}{2x^2}+4\rho (1-\rho )\frac{e^{-x}-1+x}{x^2}+{(1-\rho )}^2\equiv K_t\left(x\right).$$ (18)

Substituting Eqs. (16) and (18) into Eq. (15) and adding a noise term K_n, we obtain

$$\begin{array}{cc}\hfill K& ={\alpha }^{1∕2}\left[\sqrt{\frac{1}{M}}\mathrm{erf}\left(\sqrt{\pi M}\right)-\left(\frac{1}{\pi M}\right)(1-e^{-\pi M})\right]\times {\left[{\rho }^2\frac{e^{-2x}-1+2x}{2x^2}+4\rho (1-\rho )\frac{e^{-x}-1+x}{x^2}+{(1-\rho )}^2\right]}^{1∕2}+K_n\hfill \\ \hfill & ={\alpha }^{1∕2}{\beta }^{1∕2}\left(M\right)K_t^{1∕2}\left(x\right)+K_n.\hfill \end{array}$$ (19)

Equation (19) represents a new equation for speckle contrast that accounts for electric-field contributions from moving and stationary optical scatterers, and the finite dimensions of each pixel. The expression for β^1/2 M takes into account the spatial integration of the speckle pattern by a finite-size detector pixel and modulates the term K_t(x), which accounts for the temporal integration of the speckle pattern [15].

To assess the accuracy of the new speckle contrast model [Eq. (19)], we designed an experimental study involving an in vitro flow phantom. The phantom consisted of a microchannel (inner diameter of 300 μm) placed at the surface of a rigid polymer resin that contained TiO₂ particles (particle size <25 nm, 0.3 g/100 ml). We used a syringe-based infusion pump to inject Intralipid (1% concentration) into the microchannel via Tygon tubing. We collected data with flow rates of up to 20 mm/s.

We used a conventional LSI device [17] and published analysis methods [17,18] to capture and convert raw speckle images to speckle contrast images. We used a Retiga CCD camera (7.4 μm × 7.4 μm pixel size) equipped with a lens with variable aperture size and a 532 nm laser (Verdi, Coherent Inc.) to illuminate uniformly the flow phantom. To mitigate specular reflectance from the phantom, we placed a polarizer in front of the camera lens whose transmission axis was perpendicular to polarization of the incident light.

For a given flow rate, we obtained 30 images of speckle, which were processed using the spatial [17] and temporal [18] algorithms to calculate the contrast. Spatial analysis involved use of a sliding structuring element (7 × 7 window size) to calculate the corresponding local contrast [17]. We reduced the contrast image to a mean value calculated from a region of interest (30 × 100 pixels) within the microchannel of the contrast image. The same images were processed using the temporal LSI algorithm [18] and analyzed the same region of interest.

To evaluate the new speckle contrast model, Eq. (19), a set of experiments, which enabled the study of the effects of the finite detector pixel size on speckle contrast, were performed. In order to achieve specific values of M = A_D/A_C, the lens f-stop was changed and, thus, the speckle’s size (A_C). The parameter A_C is related to the f-stop by [19]

$$A_C\propto {\left[1.22\right(1+\mathrm{Mag}\left)\lambda \#f\right]}^2,$$ (20)

where λ is the excitation wavelength, Mag is the optical magnification, and #f is the f-stop of the lens. We adjusted the laser irradiance to achieve a set exposure time T of 10 ms each time we ran the auto-exposure function in the acquisition software.

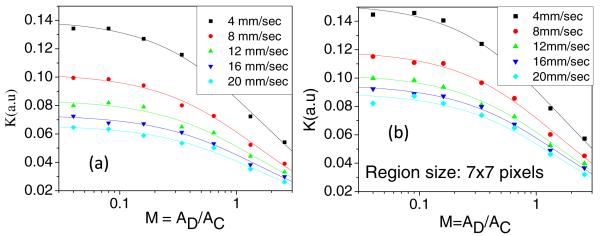
Speckle contrast determined with the new model [Eq. (19)] for a range of flow speeds (4–20 mm/s) agrees quite well with measured values, as shown in Fig. 1. In this figure, each symbol corresponds to a measurement, and the solid lines represent fits of Eq. (19) to the measured data with (αK_t)^1/2 and K_n as the fitting parameters. The R² value associated with each fit was greater than 0.97. A similar trend was observed for an exposure time T = 5 ms.

Fig. 1.

Experimental measurements of speckle contrast as a function of M obtained with the (a) temporal and (b) spatial analysis methods. The continuous lines represent the corresponding fit of the data to Eq. (19).

Our data and model collectively demonstrate that speckle contrast is reduced even when the Nyquist sampling criterion is satisfied. In the 1990s and early 2000s, published studies on LSI consisted of experimental designs in which the speckle size was matched to the pixel size (i.e., M = 1). In 2008, Kirkpatrick et al. [9] published data suggesting instead that M < 0.5 is required for proper sampling of the speckle pattern. However, simulated data from Thompson et al. [20] and Ramirez-San-Juan et al. [21] suggested that even the use of M = 0.5 results in a reduction in the maximum achievable speckle contrast.

Our data (Fig. 1) and new speckle imaging model [Eq. (19)] support the findings of Kirkpatrick et al., Thompson et al., and Ramirez-San-Juan et al. Hence, speckle contrast measurements depend on interactions of the incident electric field with static and dynamic scatterers [12] and on spatial sampling of the pattern. To account for the reduction in speckle contrast due to the finite pixel size of the CCD detector, we propose use of a correction factor to calculate a more accurate value of speckle contrast from experimental measurements.

We propose that a simple algebraic expression β^1/2 is sufficient to account for the finite pixel size of the camera and, hence, correct speckle contrast measurements. Thompson et al. [20] suggested use of data extracted from speckle images collected at multiple T and empirical determination of a maximum speckle contrast value achieved at short T. In turn, this value is used as a normalization factor (this technique could be useful when the parameter M is unknown).

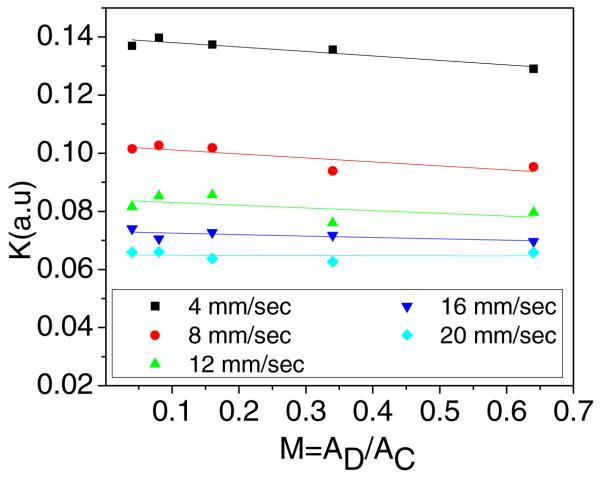
We instead derived an expression [Eq. (16)] for a normalization factor β^½, which depends only on the camera pixel size and speckle size. With use of this term, we observe that the corrected speckle contrast value is nearly independent of M for our evaluated range of values for M (Fig. 2).

Fig. 2.

Corrected speckle contrast obtained after applying the correction factor to the data shown in Fig. 1(a), similar results are obtained for Fig. 1(b).

In conclusion, we presented a new speckle contrast model [Eq. (19)] that accounts for (1) electric-field contributions from moving and stationary scatterers and (2) effects of spatial integration due to the finite pixel size of the camera pixels. With this model, we can explain the reduction in speckle contrast that results despite satisfying the Nyquist sampling criterion. The model agrees well with data collected in in vitro experiments. We expect that use of Eq. (19) will improve on the accuracy of flow estimates using either single- or multi-exposure LSI methods.