A variational Bayes discrete mixture test for rare variant association

Abstract

Recently, many statistical methods have been proposed to test for associations between rare genetic variants and complex traits. Most of these methods test for association by aggregating genetic variations within a predefined region, such as a gene. Although there is evidence that “aggregate” tests are more powerful than the single marker test, these tests generally ignore neutral variants and therefore are unable to identify specific variants driving the association with phenotype. We propose a novel aggregate rare-variant test that explicitly models a fraction of variants as neutral, tests associations at the gene-level, and infers the rare-variants driving the association. Simulations show that in the practical scenario where there are many variants within a given region of the genome with only a fraction causal our approach has greater power compared to other popular tests such as the Sequence Kernel Association Test (SKAT), the Weighted Sum Statistic (WSS), and the collapsing method of Morris and Zeggini (MZ). Our algorithm leverages a fast variational Bayes approximate inference methodology to scale to exome-wide analyses, a significant computational advantage over exact inference model selection methodologies. To demonstrate the efficacy of our methodology we test for associations between von Willebrand Factor (VWF) levels and VWF missense rare-variants imputed from the National Heart, Lung, and Blood Institute’s Exome Sequencing project into 2,487 African Americans within the VWF gene. Our method suggests that a relatively small fraction (~10%) of the imputed rare missense variants within VWF are strongly associated with lower VWF levels in African Americans.

Introduction

Genome-wide association studies (GWAS) have discovered thousands of common single nucleotide polymorphisms (SNPs) associated with complex phenotypes [1, 2], yet these common variants generally explain a small fraction (<10%) of trait heritability [3, 2]. Rare coding polymorphisms, those with minor allele frequency (MAF) less than 1–5%, may in part explain this missing heritability [3, 4]. With advances in sequencing technologies, it has become affordable to assay genome-wide rare variation in large studies and identify novel rare variant associations[5, 6].

While rare variants may have larger effects than common variants [7], detecting such variants by a single variant test is typically underpowered due to the low frequencies of the variants and the large number of rare variants in the human genome [5]. The standard approach has been to aggregate rare variant associations across a gene or region of the genome [8, 9, 10, 11, 12, 13, 14]. Many different aggregate rare variant tests have been proposed, largely grouped into three classes.

The first class tests whether or not the (weighted) sum of all rare variants in a gene or region of the genome is associated with a shift in the mean of a trait, so-called “burden tests”. Popular examples include the weighted sum statistic (WSS) [9], the Morris-Zeggini (MZ) test [13], and the combined multivariate and collapsing test (CMC) [8]. These tests are well powered if the proportion of variants with non-zero effect is high and each variant’s effect is in the same direction. However, these assumptions may be violated, e.g. if most variants have little or no effect or some variants are protective and other variants are deleterious.

To address these potential limitations, tests in the second class model heterogeneity in the effect distribution of rare variants. Essentially these methods test for a non-zero variance component in a normal random effect model. Popular examples include the c-alpha test [11] and the more general Sequence Kernel Association Test (SKAT) [14]. These tests are advantageous when the effects of rare variants are either in the opposite direction, or a mixture of neutral and non-neutral effects [14]. Under diverse genetic architectures, neither of the two aforementioned classes of tests is uniformly most powerful. This drives development of the third class of tests, that combine the mean shift test with the test for heterogeneity of effect (e.g., SKAT-O [15], aSum [12] and others [16]), aiming to achieve greater power over a range of genetic architectures.

Previous authors have noted that even among nonsynonymous variants only approximately 20% are likely functional [17, 18]. This implies that aggregate tests may lose power because the inclusion of a substantial number of neutral variants increases the “noise” in the aggregate test. In particular, both SKAT and SKAT-O assume that the effects of rare variants follow a normal distribution, yet in published simulations for demonstrating power, only a portion of variants were set to be causal [14, 15]. Model misspecification may lead to power loss.

Other authors have explored variant level model selection methods, including a step-wise selection model [19] and Bayesian hierarchical models with different variant level priors [20, 21]. In this article we propose a test based on a simple discrete mixture model for rare variant effects. Rather than lumping all SNPs together, every variant has a latent variable determining whether it has an effect on the phenotype. Unlike the random effect tests such as SKAT and SKAT-O, we assume that the variant level effects are distributed as a mixture of a point mass at zero and a point mass away from zero. The separation of neutral and causal variants is thus directly modeled, thereby improving power. This is similar in vein to rare variant model selection methods proposed by Quintana et al. [22, 23]. The two major differences of our method compared to the method of Quintana et al. [22] are 1) we propose a computationally efficient variational Bayes approximate inference algorithm that is scalable to whole-genome analysis, and 2) we propose a likelihood ratio test that can be used to prioritize genes or regions of the genome for further investigation that has an approximately ${\chi }_1^2$ asymptotic distribution. Similar to Quintana et al. [22, 23], another feature of our method is that a variant-level posterior probability of association is generated, which can be used to prioritize variants for follow-up.

Through extensive simulations, we demonstrate our proposed method has proper type I error rates and superior power performance over existing methods in a wide range of parameter settings. As an example to illustrate the test statistic and the posterior probability of association, we present results from applying our method to data on quantitative von Willebrand Factor levels and rare missense variants in the VWF gene from the National Heart, Lung, and Blood Institute (NHLBI)-Exome Sequencing Project (ESP), and the NHLBI Candidate Gene Association Resource (CARe) consortium.

Materials and Methods

Variational Bayes discrete mixture model

Suppose n subjects are sequenced at a region with J variants observed. For the i^th subject, i = 1, ..., n, observed data contain (Y_i, X_i, G_i), where Y_i denote the disease trait, X_i = (X_i1 , ..., X_iK ) denote K covariates (that may include eigenvectors used for controlling for population stratification), and G_i = (G_i1 , . . ., G_iJ ) denote the vector of 0, 1, or 2 at J loci for an additive genetic model. Our goal is to test for genetic association in the region.

For a quantitative trait, we propose the following probabilistic discrete mixture model

$$Y_i={\gamma }_0+\sum _k^K{X}_{ik}{\gamma }_k+\theta \sum _j^J{Z}_j{G}_{ij}+e_i,$$

where Z_j is a latent indicator variable that determines whether the j^th variant is truly causal (Z_j = 1) or neutral (Z_j = 0), θ is the “average” effect among causal variants, γ_k is the k^th covariate effect, and e_i is the error distributed as 0, σ² . We assume that Z_j is distributed as Bernoulli(p_fun ) for all j, so that p_fun denotes the proportion of causal variants in the region.

Compared to the burden tests and the tests for heterogeneity [8, 9, 13, 14, 15], our model adds a probabilistic assessment of whether a variant is causal and should be lumped with other causal variants, thereby filtering out neutral variants based on their evidence of association. One could extend the model to allow causal variants that have different effects by assigning a normal prior distribution to θ. However for testing genetic association in the region as a whole, a simple model with a single average effect θ, after teasing out the neutral variants, offers computational simplicity and good power. Similar arguments have been made for why burden tests are more powerful than SKAT when a majority of variants are causal [24].

The null hypothesis of no genetic association can be expressed as

$$\theta =0\text{or}{p}_{\mathit{fun}}=0.$$

The two parameters θ and p_fun are identifiable under the alternative hypothesis, but not under the null. This causes irregular large-sample behavior of the usual likelihood ratio test (LRT) statistic. For a simple finite mixture model, the asymptotic distribution of the likelihood ratio test of the mixing parameter has a complex distribution based on an autoregressive Gaussian process [25]. To remedy this problem, we take a Bayesian view and apply an informative prior distribution Beta (2, 2) for p_fun . The density function of Beta (2, 2) is between 0 and 1, peaking at 0.5. Use of the Beta prior discourages p_fun from being near 0 or 1, the boundary of the parameter space, essentially adding a penalty to the log likelihood, in a frequentist version of the model, similar to Chen et al. [25]. Such a penalty can simplify the asymptotic distribution of the LRT to a more tractable distribution.

To fit this discrete mixture model using a standard expectation-maximization algorithm [26], we would have to sum over all possible assignments of Z_j for each variant within a gene in the likelihood, which can be prohibitive for genes with many variants. Alternatively, we could derive a Bayesian Markov chain Monte Carlo solution with a Gibbs sampler [27], but this is also computationally intensive because of the number of iterations necessary for the Markov chain to converge to the posterior distribution. To overcome these computational difficulties in genome-wide analysis, we use a variational Bayes approximate inference method [28].

The variational Bayes method was first developed for problems in statistical mechanics as mean-field theory [29], and recently has found popular applications in fitting complex statistical models for high dimensional data in genomics [30, 31, 32, 33]. In particular, when the covariates under model selection are independent, the variational Bayes approximation is nearly the same as the exact likelihood calculation [34], suggesting that the method should work well for rare variant association due to typically low correlation between rare variants.

For a quantitative trait, a variational Bayes algorithm approximates the true posterior distribution p(Z₁, ... , Z_J, p_fun | G, X, y, γ, θ, σ²) by estimating a factorized posterior distribution Q (Z, p_fun ) = q_pfun (p_fun) Π_j q_j (Z_j ) by minimizing the Kullback-Leibler divergence

$$D_{KL}(Q(Z,p_{\mathit{fun}})\Vert p(Z,p_{\mathit{fun}}\mid G,X,Y,\gamma ,\theta ,{\sigma }^2))=\sum _Z\int Q(Z,p_{\mathit{fun}})log\left(\frac{Q(Z,p_{\mathit{fun}})}{p(Z,p_{\mathit{fun}}\mid G,X,Y,\gamma ,\theta ,{\sigma }^2)}\right){dp}_{\mathit{fun}},$$

where Σ_Z indicates ${\sum }_{Z_1=0}^1\cdots {\sum }_{Z_J=0}^1$. Because of the factorization approximation, there exist efficient closed form coordinate updates for all q_j (Z_j ) and q_pfun (p_fun ) to find a local solution to the optimization problem

$$\widehat{Q}(Z,p_{\mathit{fun}})={\text{argmin}}_{Q(Z,p_{\mathit{fun}})}{D}_{KL}(Q(Z,p_{\mathit{fun}})\Vert p(Z,p_{\mathit{fun}}\mid G,X,Y,\gamma ,\theta ,{\sigma }^2)).$$

Further details of the derivations of these approximate posterior distributions are provided in the Supplementary Information. Fitting this model produces a lower bound

$$\mathcal{L}(Y\mid G,X,\gamma ,\theta ,{\sigma }^2)=\sum _Z\int \widehat{Q}(Z,p_{\mathit{fun}})log\left(\frac{p(Z,p_{\mathit{fun}},Y\mid G,X,\gamma ,\theta ,{\sigma }^2)}{\widehat{Q}(Z,p_{\mathit{fun}})}\right){dp}_{\mathit{fun}}$$

for the marginal log-posterior probability of the data log (p (Y | G, X, γ θ , σ²)). The parameters γ , θ, and σ² are estimated as

$$\left(\widehat{\gamma },\widehat{{\sigma }^2},\widehat{\theta }\right)={\text{argmax}}_{\gamma ,{\sigma }^2,\theta }\mathcal{L}(Y\mid G,X,\gamma ,\theta ,{\sigma }^2).$$

Based on the Beta prior distribution for p_fun , we propose the following test statistic

$${\chi }_{dm}^2=-2{\mathcal{L}}_0\left(Y\mid G,X,\widehat{\gamma },\widehat{\theta }=0,\widehat{{\sigma }^2}\right)+2\mathcal{L}\left(Y\mid G,X,\widehat{\gamma },\widehat{\theta },\widehat{{\sigma }^2}\right),$$

where ${\mathcal{L}}_0\left(Y\mid G,X,\widehat{\gamma },\widehat{\theta }=0,\widehat{{\sigma }^2}\right)$ is the lower bound of the data when fitting the null model (θ = 0). Our simulation results suggest that the asymptotic approximation of this test statistic as a ${\chi }_1^2$ holds fairly well for realistic data-sets. We found that different parameters in the Beta prior on p_fun had very little effect on the model inference (results not shown), and that fitting this model with θ = 0 produces the expected approximate posterior densities for q_Zj (Z_j = 1) = 0.5, and q_pfun (p_fun ) = Beta(J/2+2, J/2+2). It would be possible to incorporate different types of priors based on evidence of functionality in each individual variant, for example from information obtained from PolyPhen-2 [35].

In addition to the gene level test statistic ${\chi }_{dm}^2$, the unique feature of our method compared to competing aggregate rare variant tests is a per-variant measure of association based on the estimated probability q_j (Z_j ). This is the approximate posterior probability that a given variant is associated with the phenotype. This posterior probability estimate can be used to assess which variants in a gene are driving the association with phenotype, and to rank these variants for functional follow-up or replication.

Simulation Design

Genotypes were simulated based upon the observed minor allele frequency spectrum from all imputed exonic variants from the NHLBI-ESP project with imputation R² > 0.5 and 0.001 < MAF < 0.05 (Figure S1). As other authors have noted, based on the recent hyper exponential population growth of the last 2,000 years, there is a severe shift in the site frequency spectrum for variants with very low minor allele frequencies [5]. Because of the possible biological relevance of this excess of very rare variation we accounted for it in our simulations. We simulated genes with 10, 20, or 40 independent rare variants, with minor allele frequencies sampled from this empirical frequency spectrum. Rare variants are often effectively independent because they lie on different haplotype backgrounds [36].

Phenotypes were simulated under multiple models. We first simulated phenotypes based on the null model with 10⁶ replicates. Phenotype data were simulated under the alternative hypothesis for two distinct cases for a range of genetic architectures. The first case focused on simulated genotype data and genetic architectures where the effect sizes were independent of allele frequency (i.e. the unweighted model). We simulated data with θ = 1, the proportion of functional variants within a gene was either 0.1, or 0.2, the total heritability associated with a gene was between 0.005 and 0.02, the sample size was 2,000 and 1, 000 replicate simulations were run. Next, we simulated a model where θ ~ 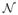μ = 1, σ² = 1/4 to model a deviation from the assumption that each functional variant has the same effect. The significance level α for all tests was 10⁻³.

For the second case we used the 30 imputed missense variants from VWF with 0.001< MAF < 0.05 and imputation R² > 0.5 as the genotype data, and simulated models where the variant effect magnitudes were dependent on allele frequency. We simulated phenotype data with $\theta =1/\sqrt{(f_j(1-f_j))}$, the proportion of functional variants within a gene was either 0.1, or 0.2, the total heritability associated with a gene was between 0.005 and 0.02, and 1, 000 replicate simulations were run. Next, we simulated a model where $\theta ~\mathcal{N}\left(\mu =1/\sqrt{(f_j(1-f_j))},{\sigma }^2=1/(4f_j(1-f_j))\right)$ to model a deviation from the assumption that each functional variant has the same effect. Age, sex, sub-study and their corresponding estimated effects were also included in all of these simulations. As before, the significance level α for all tests was 10⁻³. Finally, for the imputed VWF genotypes, we also considered simulations where the proportion of non-null variants was either 0.5 or 1.0, with effect distributions as before.

NHLBI ESP, WHI SHARe, and CARe data

The NHLBI’s ESP was designed to identify novel rare variant associations with common heart, lung, and blood traits in 6,823 individuals from 20 studies. Genotype data were collected at both the University of Washington and the Broad Institute via deep whole-exome sequencing on Illumina GAII or Illumina HiSeq platforms using one of four capture targets (CCDS 2008 (~26 Mb), Roche/Nimblegen SeqCap EZ Human Exome Library v1.0 (~32 Mb; Roche Nimblegen EZ Cap v1) or EZ Cap v2 (~34 Mb), and Agilent Ref-Seq2010V2, (~36 Mb)). Single nucleotide variants were called using the UMAKE pipeline at the University of Michigan, which allowed all samples to be analyzed simultaneously, both for variant calling and filtering [5]. Samples were filtered based on call-rate, heterozygosity, concordance with GWAS data, concordance between self-reported race and genetic ancestry as determined through principal component analysis, and concordance between self-reported sex and depth of coverage on the X and Y chromosomes. Duplicate and related samples were identified using PLINK [37], for each duplicate/related pair, we retained the sample with the higher call-rate. Variants were filtered based on a support vector machine classifier [5], depth of coverage, and Hardy-Weinberg equilibrium. After filtering, there were 1,904,903 variants available for analysis. The final data-set contained > 111 fold coverage of coding sequence in the majority of samples. Further details on study design, sequencing, and variant calling are provided in Tennessen et al. [5]. Next, we briefly describe the primary studies which contain the African American samples used in this study.

Data from Womens Health Initiative (WHI) SNP Health Association Resource (WHI-SHARe) and the NHLBI Candidate Gene Association Resource (CARe) consortium (Atherosclerosis Risk in Communities (ARIC), Cardiovascular Risk in Communities (CARDIA), Jackson Heart Study (JHS), Multiethnic Study of Atherosclerosis (MESA)) were used to impute variants identified in ESP into over 13,000 African Americans. Genome-wide genotyping was performed in all participants using the Affymetrix 6.0 platform, either at Affymetrix (for the WHI-SHARe project) or at the Broad Institute (for the CARe consortium). DNA samples with a genome-wide genotyping success rate < 97%, duplicate discordance or sex mismatch, genetic ancestry outliers (as determined by cluster analysis performed using principal components), SNPs with genotyping success rate < 98%, monomorphic SNPs, SNPs with minor allele frequency (MAF) < 1%, and SNPs with a p-value testing Hardy-Weinberg equilibrium < 10⁻⁴ were removed from the analyses. Data from 7,563 WHI AAs on 816,361 SNPs and 6,205 CARe AAs on 712,556 SNPs remained after QC. We took the intersection of SNPs passing QC in SHARe and CARe for a total of 702,205 GWA markers. The 6,205 CARe and 7,563 SHARe samples were combined into a single target set of 13,768 samples for phasing. Phasing was performed using BEAGLE v3.3.1 [38]. An imputation reference panel of 2,163 samples was constructed using individuals with both ESP and Affymetrix 6.0 data. These samples did not overlap with the 13,768 in the target set. Prior to imputation, the imputation reference panel was pre-phased across all 2,163 samples using BEAGLE v3.3.1. Using the 4,326 statistically phased haplotypes in the reference panel we imputed 375,024 bi-allelic autosomal markers into the SHARe and CARe target panels using minimac [39], similar to Auer et al. [40].

We tested for association of imputed rare variants with natural log transformed von Willebrand Factor levels in the CARe (n=2,487) study. Von Willebrand factor antigen levels were measured in ARIC, CARDIA, and MESA participants using stored EDTA plasma samples, as previously described [41]. Only exonic missense variants with an imputation R² > 0.5 and 0.001 < MAF < 0.05 were considered in our model. Because of the sensitivity of the aggregate rare variant tests for genes with many very rare variants, we also Winsorized the log(VWF) data at the 0.005 and 0.995 percentiles; this improved the quality of the test statistic for all tests considered. The imputed dosages are used in all statistical tests (though the dosages are rounded for visualization purposes). All analyses were run with covariates of the first two principal components from the GWAS data to correct for possible population structure, age, sex, and sub-study.

Ethics Statement

Informed consent for collection of genetic and phenotypic data was received from all participants within each of the studies that contributed to the Exome Sequencing Project, the NHLBI Candidate Gene Association Resource, and the Womens Health Initiative SNP Health Association Resource, where each individual study received approval from all respective institutional review boards. In our analyses all data was analyzed anonymously.

Results

Simulations

First we demonstrate that the asymptotic VBDM test statistic has appropriate type-I error control. As described in the methods, we performed 10⁶ replicate null simulations of genes with either 10 or 20 independent variants with allele frequencies sampled from the empirical allele frequency distribution of imputed exome variants in the WHI-SHARe and CARe studies (as shown in Figure S1). In Table 1 we show the type-I error rates for both the weighted and unweighted version of the VBDM test statistic for different sig-nificance thresholds. The weighted statistic assumes the effect of a variant is proportional to its minor allele frequency, while the unweighted version does not make that assumption. The type-I error is well controlled for moderate significance cutoffs, and becomes slightly inflated for more stringent cutoffs, e.g. α < 10⁻³. We therefore recommend running permutations on any result that is significant based on this likelihood ratio test, to ensure that the type-I error rate is exactly controlled. The inflation of the test statistic in the tails likely arises because the χ² reference distribution for our test statistic only holds approximately.

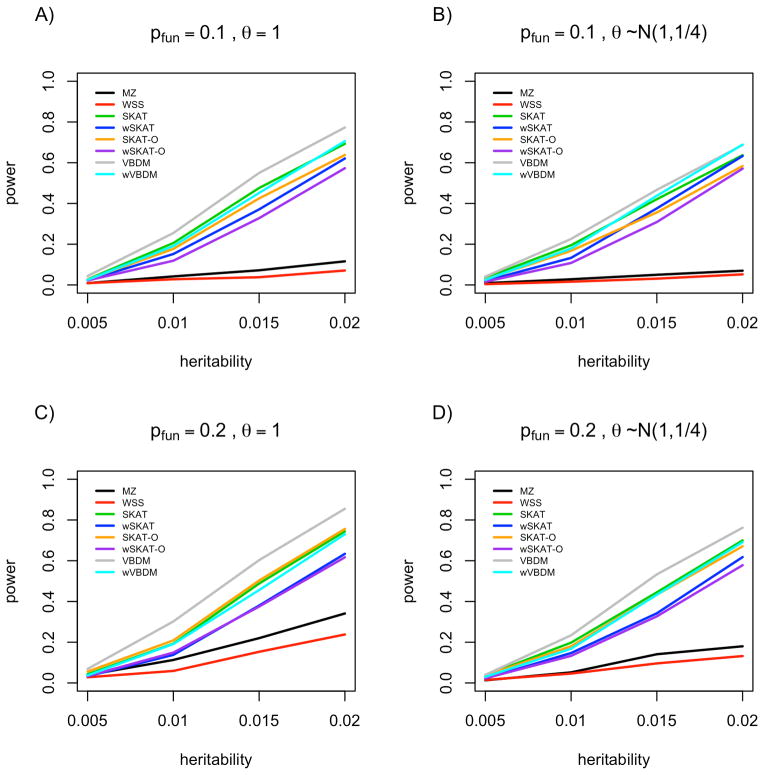
For the power simulations we compared our approach to other popular aggregate rare variant tests including WSS, MZ, SKAT, and SKAT-O (the “w” in front of names of methods refers to the variation on the method where each variant is re-weighted based upon the standard deviation of each locus, WSS is essentially a weighted version of MZ). As shown in Figure 1, we see that VBDM has greater power when compared to the other methods when there are 40 variants within the simulated gene. Because the variant effects were simulated independently of allele frequency for the simulations shown in Figure 1, we see that the unweighted versions of each statistic tend to do better than their weighted counterparts (e.g. SKAT vs. wSKAT). The performance gain for VBDM is present across a range of simulations, including varying sparsity, heritability, and effect distributions at a significance cutoff of α = 10⁻³. For genes with 10 and 20 variants a similar pattern is observed (Figures S2 and S3), though the performance gain is attenuated. Adaptive permutations were performed to ensure the type-I error rate of VBDM was exactly controlled. Specifically, our approach has much greater power than the naive collapsing methods of WSS and MZ when the true distribution of effects is sparse because our mixture model is directly accounting for neutral variants in the effect distribution.

Figure 1.

Power results from simulations of genes with 40 rare variants. A) 10% of variants within a gene have an effect on phenotype, with a fixed effect size. B) 10% of variants have an effect on phenotype, with effects sampled from a N(1,1/4) distribution. C) 20% of variants within a gene have an effect on phenotype, with a fixed effect size. D) 20% of variants within a gene have an effect on phenotype, with effects sampled from a N(1,1/4) distribution.

We also compared our approach to another model selection approach, the ‘step-up’ approach of Hoffmann et al. [19], for a smaller set of simulations (simulated genes with 10 variants, 20% of variants as causal, and effects sampled from a N(1,1/4) distribution). The results of the simulations are shown in Figure S4, where the ‘step-up’ method performed worse than both our method as well as the simple collapsing methods. We used the implementation of the ‘step-up’ method available in the ‘thgenetics’ R package. We also found that the ‘step-up’ method was more computationally intensive than our approach, where on average our algorithm took 1.0 seconds to fit a single model (with 1000 permutations), whereas it took the method of Hoffmann et al. 3.0 seconds to fit a single model (with 1000 permutations). We didn’t include the method of Hoffmann et al. in all of the simulations studies because it became computationally infeasible for genes with greater numbers of variants.

In addition, for the simulations shown in Figure 1C where the proportion of causal variants is 20% and the effect size is fixed, we also inspected the behavior of the per variant posterior probability p_j = q_j (Z_j ). The densities of the empirical p_j statistics for these simulations are shown in Figure S5. For the low heritability simulations in Figure S5A (h² = 0.005), there is not enough signal in the data to over-come the weak prior that each variant has a probability of 0.5 of being associated with outcome. As the heritability increases (Figure S5B-5D), the p_j statistics for casual variants shift to the right, and the p_j statistics for neutral variants shift to the left as the p_j statistics become more informative with respect to which variants are driving the association. For the highest heritability simulations (h² = 0.02, Figure S5D) any effect of the weak prior distribution on the posterior probabilities p_j has disappeared and the p_j statistics are highly informative of which variants are neutral and which variants are causal.

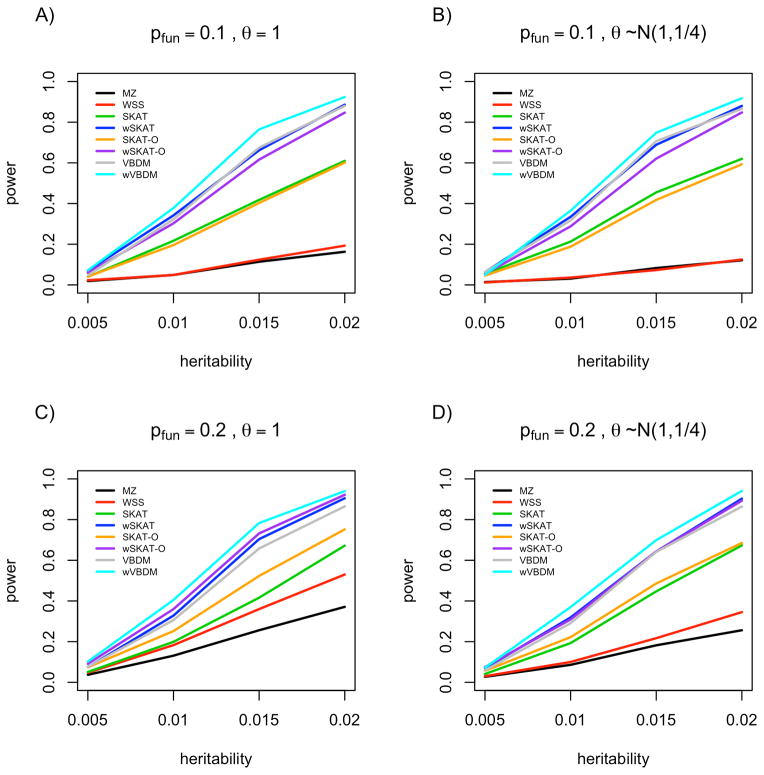
Next we considered simulations using the 30 imputed rare missense variants within VWF with MAF < 5%. In this case the effects were sampled in a way that was dependent on allele frequency, and hence the weighted versions of all the test statistics tend to do better. We see in Figure 2 that now wVBDM outperforms the alternative methods when only 10–20% of variants are functional within the gene. In contrast when 50%–100% of variants are functional our method is still competitive, but is not the most powerful (as shown in Figure S6). Our method outperforms both SKAT approaches when the number of variants in a gene is large and the signal is sparse, and has similar performance for genes with fewer variants. The SKAT tests have more power than the naive collapsing methods for the sparse models because of the heterogeneity in the simulated effect distribution, even though the assumed normal effect distribution is misspecified. The SKAT model performs better when the simulated model is sparse, whereas SKAT-O performs better when the true distribution of effects is not sparse. Yet neither SKAT approach has the additional advantage of ranking variants within a gene for follow-up based on each variant’s estimated posterior probability of association.

Figure 2.

Power results from phenotypic simulations based on 30 imputed VWF missense variants with MAF < 5%. A) 10% of missense variants within VWF have an effect on phenotype, with a fixed effect size. B) 10% of variants have an effect on phenotype, with effects sampled from a N(1,1/4) distribution. C) 20% of variants within VWF have an effect on phenotype, with a fixed effect size. D) 20% of variants within a gene have an effect on phenotype, with effects sampled from a N(1,1/4) distribution.

Analyses of von Willebrand Factor Levels in African Americans

Von Willebrand Factor (VWF) is a multimeric plasma glycoprotein that plays an important role in hemostasis and thrombosis [42]. VWF binds to platelets at sites of vascular injury, stabilizes coagulation factor VIII (FVIII). High levels of VWF are associated with increased risk of various cardiovascular outcomes [43, 44]. Decreased VWF levels are associated with the common bleeding disorder von Willebrand Disease (VWD) [45]. The VWF gene on chromosome 12 contains a large number of non-synonymous coding variants, some of which have been identified in patients with VWD. Using data from ESP AA participants, Johnsen et al., recently showed that common and lower frequency variants (including Ser1486Leu and Arg2287Trp) VWF missense variants are associated with VWF levels within the African American population [41]. Therefore, we performed a gene-wide association analysis of plasma VWF levels using imputed genotype data on low-frequency VWF missense variants from the ESP AA to demonstrate the efficacy our approach.

We analyzed log transformed von Willebrand factor levels of 2,487 AA participants from the CARe consortium and 30 imputed missense VWF variants derived from exome sequencing. The 30 imputed missense variants, their allele frequencies, and imputation quality scores are shown in Table S1. The results of the aggregate rare variant analyses for each method are shown in Figure 3, with significance cutoffs of 0.05 and 5×10⁻⁷ shown in black and red respectively. Our wVBDM approach found a significant association between rare-variants in the VWF gene and lower VWF levels, with an approximate likelihood ratio test p-value of 1.59×10⁻⁹, and a permutation p-value of < 1×10⁻⁷. Both SKAT and SKAT-O appear to detect some signal, but neither are as significant as wVBDM. Moreover, SKAT is unable to localize which variants are driving the association. Interestingly, the unweighted version of our method is unable to detect the association signal. We speculate that by not weighting variants based on allele frequency, our model was dominated by weak positive effects from the slightly more common imputed variants. This suggests that even in cases when the rare variant signal is strong, it can be hidden if there is additional weak signal in the opposite direction. Under these circumstances models that allow for effects in both directions may be advantageous. Our results support this assertion, where we see in Figure 3 that the SKAT methods have increased power to detect the VWF association as compared to the simple burden tests methods (MZ and WSS). Luckily, in this particular case the weighted VBDM test prioritized the rarer variants, and was then able to identify the small subset that were driving this strong negative VWF association.

Figure 3.

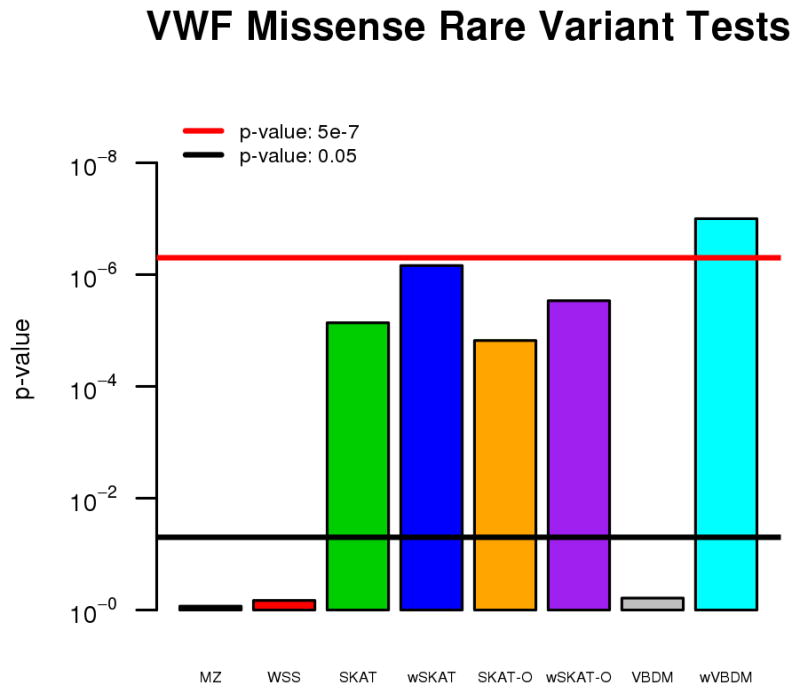
Aggregate rare variant test results for the association of imputed missense variants within VWF with VWF levels in African Americans in the CARe consortium.

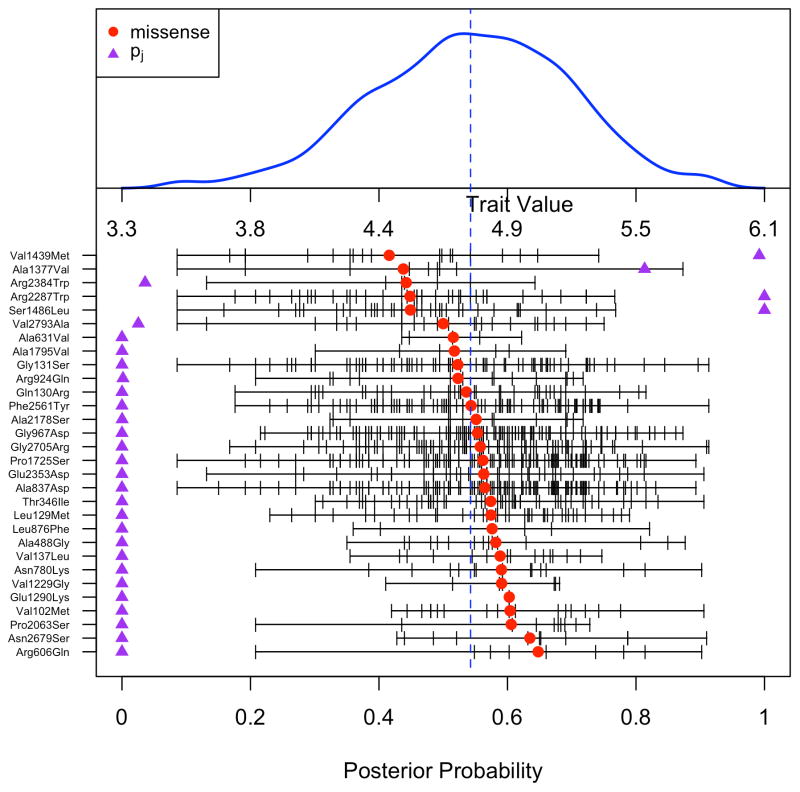
Figure 4 shows the burden plot for this association. The burden plot depicts the distribution of the log VWF levels, the distribution of alleles for each variant as a function of phenotype, and the mean effect of each variant on phenotype. The posterior probabilities from the VBDM algorithm are depicted to indicate which variants contribute the most to the association. It appears that the four low-frequency variants driving the strong association with phenotype are rs61750625 (Arg2287Trp), rs149424724 (Ser1486Leu), rs150077670 (Val1439Met), and rs141211612 (Ala1377Val). Based on the VBDM analysis, the estimated additive effect of the burden of rare variants is −39.1 IU/dL lower VWF levels.

Figure 4.

Burden plot of VWF levels for the VWF gene from the CARe consortium. Histogram of Winsorized log transformed VWF levels is shown on top. The thirty imputed missense variants are shown on bottom, ordered by mean log VWF levels of the imputed non reference allele. Each tick mark for a given variant represents the phenotypic value of an individual estimated to have the non-reference allele for that variant based on the imputation. The solid circles indicate the mean of all individuals with imputed non-reference alleles. The dotted line indicates the overall mean of VWF levels. The purple triangles indicate the posterior probability of association of a given variant with VWF levels.

Discussion

We have demonstrated several advantages of our discrete mixture test. Compared to other popular rare variant aggregate tests such as the SKAT-O test, our VBDM test had greater power, particularly as the number of variants increases (e.g., for testing large genes or multiple genes within a pathway). In addition, the exact inference implementation of this model proposed in Quintana et al. [22, 23] relies on computationally inefficient MCMC methodologies that can take multiple hours to run for a single gene with 134 variants [23]. In contrast, our method takes a fraction of a second to fit a single gene, and can therefore be used efficiently for genome-wide analyses. As the size of sequencing studies grows, the number of rare variants in any given region of the genome will also increase dramatically, while the likelihood that any given variant in that region will be functional for a given phenotype will be low. Having a test that performs well for this circumstance will be invaluable to association mapping practitioners. Not only is this test well powered to detect rare variant associations when there is significant heterogeneity in the effect distribution (e.g., the association is driven by a small proportion of the overall number of variants tested), it can also provide a variant level measure of association with phenotype. The variant level association works by determining the level of evidence that a particular variant has an effect θ on the phenotype. In cases where there is weak or no association (θ = 0) the Beta(2,2) prior on the p_fun parameter will cause p_j to have a null expectation of 0.5 (Figure S5A). Alternatively, in cases where there is ample evidence of θ ≠ 0, the p_j statistics are highly informative with respect to which variants have an effect θ (Figure S5D).

We showed an example of the utility of the wVBDM statistic in identifying rare variant associations with lower von Willebrand Factor levels. Our test statistic captures a more realistic effect distribution of a mixture of null and non-null variants as compared to the popular SKAT random effect test. It can also detect both heterogeneity in the effects distribution and a mean shift, making it competitive with the SKAT-O type tests. Extensions of the VBDM statistic that allow different effects for some variants in one direction and for other variants in other directions will be considered in future work. These extensions will hopefully allow for a more natural accommodation of the phenomena we observed for VWF, where there appeared to be many slightly more common variants with positive effects, and only a few rare variants with large negative effects. An additional extension would be to apply VBDM to dichotomous outcomes. The variational algorithm applied to the logistic regression models is non-trivial [34], therefore we also plan to extend the VBDM framework to logistic models in future work. Finally, another extension of the VBDM model would be to apply it to testing for associations genome-wide. This would require a very careful selection of the hyperparameters α and β to prevent model over-fitting, since the number of variants would exceed the observed sample size. Of course one could also apply VBDM to each gene across the genome in a genome-wide search.

In our data set of >2,400 African Americans, the association of the 30 VWF imputed variants reached an exome-wide significance level (5×10⁻⁷) with our wVBDM test. To the authors knowledge, the application of aggregate rare-variant tests to imputed rare variants is novel, and could be used to identify sparse aggregate associations in general GWAS studies where imputation has been performed for rare variation. The association of VWF with VWF levels was completely undetectable by the naive collapsing methods (WSS and MZ) that don’t take into account sparsity or heterogeneity in the effect distribution. Notably, our wVBDM model provides additional insight into the possible genetic architecture underlying VWF’s putative association with VWF levels. Specifically, four rare variants with MAF < 1% appeared to be driving this strong association with lower VWF levels.

Our results from the aggregate VDBM test are consistent with a prior single-variant variant analysis [41], in which 3 of these four variants (Arg2287Trp,Ser1486Leu, and Val1439Met) were significantly associated with lower plasma VWF levels in ESP AA. The fourth variant (Ala1377Val) had an effect size of similar magnitude in the single-variant analysis [41], but did not reach statistical significance (perhaps due to power/sample size limitations). Additional evidence supports the functional importance of these 4 VWF missense variants. Arg2287Trp has been reported in a patient with VWD and low VWF levels [46, 47]. Arg2287Trp has also been shown to be associated with abnormal expression in multiple studies [48, 47] Arg2287Trp and Ala1377Val are predicted to be functionally deleterious based on sequence conservation analyses [41], while Ser1486Leu disrupts a highly conserved O-linked glycosylation site that modulates VWF function [49]. As mentioned previously, another natural extension of the model would be to incorporate these functional predictions into the prior distribution over individual variants. This generalization would provide a test of association that integrates multiple sources of prior belief about variant effect distributions and probability of functionality.

Studies of the distribution of genetic variation within human populations have observed a severe excess of very rare genetic polymorphism [5, 50] because of recent hyper exponential population growth. Being able to account for this severe excess of rare variation in association models will be necessary to identify the source of missing heritability for complex disease and complex phenotypes. Our method provides a novel approach, that exploits a biologically plausible assumption of the effect distribution, is well powered to identify genes or regions of the genome with an aggregation of rare variation associated with phenotype, and classifies which variants in that region are most likely to be contributing to phenotype. Software for the VBDM algorithm is freely available in the “vbdm” package from CRAN (http://cran.r-project.org).