Single-Molecule Fluorescence Resonance Energy Transfer Studies of the Human Telomerase RNA Pseudoknot: Temperature-/Urea-Dependent Folding Kinetics and Thermodynamics

Abstract

The ribonucleoprotein telomerase is an RNA-dependent DNA polymerase that catalyzes the repetitive addition of a short, species-specific, DNA sequence to the ends of linear eukaryotic chromosomes. The single RNA component of telomerase contains both the template sequence for DNA synthesis and a functionally critical pseudoknot motif, which can also exist as a less stable hairpin. Here we use a minimal version of the human telomerase RNA pseudoknot to study this hairpin–pseudoknot structural equilibrium using temperature-controlled single-molecule fluorescence resonance energy transfer (smFRET) experiments. The urea dependence of these experiments aids in determination of the folding kinetics and thermodynamics. The wild-type pseudoknot behavior is compared and contrasted to a mutant pseudoknot sequence implicated in a genetic disorder–dyskeratosis congenita. These findings clearly identify that this 2nt noncomplementary mutation destabilizes the folding of the wild-type pseudoknot by substantially reducing the folding rate constant (≈ 400-fold) while only nominally increasing the unfolding rate constant (≈ 5-fold). Furthermore, the urea dependence of the equilibrium and rate constants is used to develop a free energy landscape for this unimolecular equilibrium and propose details about the structure of the transition state. Finally, the urea-dependent folding experiments provide valuable physical insights into the mechanism for destabilization of RNA pseudoknots by such chemical denaturants.

1. Introduction

Conventional DNA replication presents a serious problem for the ends of linear chromosomes. Each successive replication event results in the loss of genetic material at the ends of these long DNA duplexes, which has come to be known as the end replication problem.¹ One of nature’s solution to this problem is a ribonucleoprotein (RNP) complex, telomerase, that functions to maintain the long term fidelity of eukaryotic chromosomes.^2,3 This task is accomplished by processively adding multiple replicates of a species-specific DNA sequence to the ends of the chromosomes, which results in the formation of telomeres.⁴ Not only does repetitive elongation of telomeres buffer the natural shortening of chromosomes that occurs during DNA replication, but the presence of the telomeres allows for recruitment of a number of specific DNA binding proteins that are capable of protecting the chromosome ends from other potentially damaging cellular processes.

Proper telomere maintenance is essential for highly proliferative cells (e.g., stem cells) and is partially responsible for cellar immortality. Unfortunately, the marvels of telomerase are also beneficial for the highly proliferative constituents of cancerous tumors, with up-regulation of telomerase activity observed in > 85% of oncogenic cells.⁵ Indeed, the ability to repress telomerase activity offers a broadly applicable target for cancer therapeutics, while the ability to enhance telomerase activity has applications in stem-cell-based regenerative medicine. In order for medicinal applications to target telomerase activity more precisely, a deeper understanding of the complete RNP is essential. Until recently, mechanistic information about telomerase holoenzyme activity has proven quite challenging to obtain, though single-molecule studies of model systems have recently started to elucidate some key structural and mechanistic aspects of telomerase function.⁶⁻¹⁰ Specifically, these efforts have started to unveil details associated with the functional importance of the pseudoknot domain and the global conformation of the RNA in catalytically active enzymes; however, much of the detailed biophysics of telomerase activity still remains poorly understood.

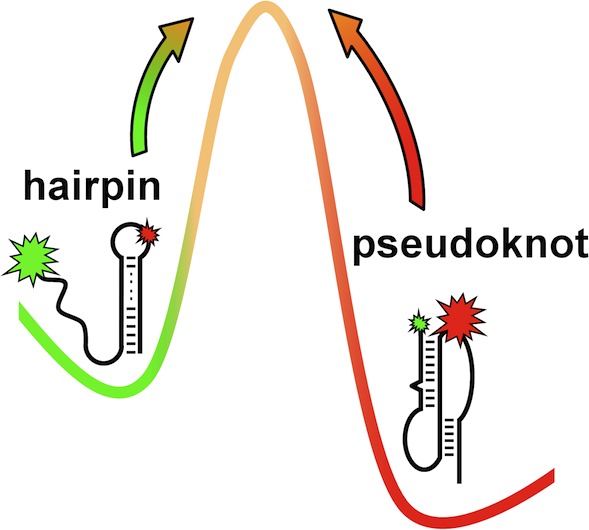
What is known about telomerase is that the RNP consists primarily of two crucial structural components, though additional species-specific components have been shown to be required in various systems.¹¹ The first is a protein subunit, telomerase reverse transcriptase (TERT), which is responsible for catalyzing the addition of telomeric repeats to the ends of eukaryotic chromosomes.¹² The second component is telomerase RNA (TR), which, among other things, provides the template for this RNA-dependent DNA synthesis.¹² One of the few highly conserved domains within TR is the core domain, which is essential for both RNP assembly and activity.¹³⁻¹⁹ It has been shown that within this domain there is a functionally critical region that forms a pseudoknot motif. In general, a pseudoknot is formed when the nucleotides in the loop of an RNA hairpin make stable, typically canonical, base pairing interactions with the free nucleotides of a single-stranded region elsewhere in the RNA. The pseudoknot base pairing interactions (P3) found in human TR (hTR) are formed, in part, between the nucleotides in the loop of the P2 hairpin and the single-stranded nucleotides of J2a/3 (Figure 1a). A number of NMR experiments have determined the molecular structure of a minimal wild-type (WT) hTR pseudoknot (Figure 1b) and various mutants.²⁰⁻²⁴ These structural experiments, together with recent single-molecule experiments^25,26 and computational folding models,^27,28 indicate that the WT pseudoknot exists in equilibrium between a partially unfolded hairpin and a folded pseudoknot (PK) with a stable and conserved triple helix (Figure 1c). Such detailed investigations of the pseudoknot region of hTR have been used in conjunction with existing mutational studies to develop several models for the functional importance of this structural motif. To date, however, substantial accumulation of evidence in support of (or against) any of these model predictions has remained elusive, which therefore represents substantial motivation for the present work.

Figure 1.

Details of the human telomerase RNA pseudoknot. (a) Secondary structure diagrams of the minimal pseudoknot motif in a partially unfolded (hairpin) conformation and a folded (pseudoknot) conformation. The GC→AG mutation at the orange nucleotides in the pseudoknot region corresponds to the genetic disorder dyskeratosis congenita. Green (Cy3) and red (Cy5) stars indicate the location of two fluorophores, where the sizes of the stars reflect fluorescence resonance energy transfer (FRET) efficiency between the two dyes and the black vertical bar represents the ligation site. (b) Model solution structure of the minimal pseudoknot motif, with the same color scheme as the secondary structure diagram. (c) Schematic equilibrium between the pseudoknot and hairpin conformations.

In this study, single-molecule fluorescence resonance energy transfer (smFRET) techniques^29,30 are used to further characterize the kinetics and thermodynamics of two minimal hTR PK constructs: (i) the wild-type (WT hTR PK) and (ii) a mutant thereof that is associated with the genetic disorder dyskeratosis congenita (DKC hTR PK). These smFRET experiments provide a remarkably quantitative methodology for observing molecular dynamics of biomolecules. Single-molecule techniques are extremely advantageous for kinetic studies of RNA folding in that they are able to resolve conformational dynamics unobservable in more traditional ensemble measurements. The ability to measure the kinetics of RNA folding at equilibrium and in real time significantly increases the amount of information attainable from the experimental system.³¹⁻³³ Furthermore, the temperature dependence of these smFRET studies can be exploited to extract the enthalpic and entropic components associated with free energies.³⁴⁻³⁷ Lastly, experiments that utilize urea as a chemical denaturant provide important quantitative information about the free energy stability of the pseudoknot motif.^36,38 The results of this study and the associated implications are discussed with regard to the following: (i) the folding pathway of the minimal RNA pseudoknot motif, (ii) the use of urea as a general tool for probing the single-molecule kinetics and thermodynamics of RNA folding, and (iii) the molecular function and various disease states of telomerase.

2. Experimental Methods

2.1. Construct Design

To generate suitable FRET labeled wild-type (WT hTR PK) and mutant (DKC hTR PK) pseudoknot constructs for single-molecule studies, we exploit the powerful and increasingly common technique of RNA ligation.³⁹⁻⁴² For the wild-type construct, two synthetically modified oligonucleotides—strands 1 and 2—are purchased commercially (Integrated DNA Technologies, Inc.). Strand 1 contains both a 5′ biotin moiety for surface immobilization as well as a internal amino-modified dT (dT*) at position 106 (numbering from full length hTR¹³) for fluorescent labeling: (5′-biotin-AAA GGG CUG UUU UUC U[dT*]G CUG ACU UUC AGC CCC AAA-3′). This rC→dT* substitution was chosen to be the site of internal fluorophore labeling for three reasons: (i) this nucleotide is one of the least conserved positions in this region of the human TR pseudoknot motif,²⁰ (ii) functional studies of the hTR PK have shown that a complementary mutation of C106 did not affect in vitro activity of telomerase,^13,43 and (iii) structural models of the minimal WT hTR PK depict this nucleotide as being completely solvent exposed and devoid of hydrogen-bonding interactions with any of the surrounding functional groups.²⁰ The amino-modified nucleotide within strand 1 is reacted with NHS-ester functionalized Cy5 dye (GE Healthcare) following the manufacturer’s suggested protocol. Removal of unreacted Cy5 dyes is accomplished via microcentrifuge spin columns (Thermo Fisher Scientific, Inc.). The second oligonucleotide, strand 2, contains a terminal 3′ Cy3 attached via phosphoramidite chemistry: (5′-phosphate-CAA AAA AUG UCA GCA A-Cy3-3′). Based on modifications to existing RNA ligation techniques,^42,44 strands 1 and 2 are annealed together by heating to 85 °C at a 1:3 molar ratio in 50 mM hemisodium HEPES, 100 mM NaCl, pH 7.5, and allowed to slowly cool to 37 °C. T4 RNA ligase I (New England BioLabs, Inc.) is then added to the mixture following the manufacturer’s recommended procedures, with the reaction held at 37 °C for 2 h to allow for maximal ligation of the two strands (Figure 1). The product is purified via HPLC using a reverse-phase column (Agilent Technologies) resulting in completely ligated RNA constructs containing Cy3, Cy5, and the biotin functional group.

The mutant DKC hTR PK construct is created in a similar fashion, with the only exception being that strand 1 for the DKC hTR PK contains the GC→AG mutation at positions 108–109 associated with the genetic disorder dyskeratosis congenita. A second wild-type construct with alternative labeling locations (WT^alt hTR PK) serves as a control to demonstrate that the observed conformational transitions are due to disruption and formation of the P3, rather than P2, region of the pseudoknot (see Supporting Information Figure S1). This WT^alt hTR PK construct is synthesized using the same procedures described above with two different oligonucleotides: strand 1^alt, 5′-Cy3-GGG CUG UUU UUC-3′, and strand 2^alt, 5′-phosphate-UCG CUG ACU UUC AGC CC[dT*] AAA CAA AAA AUG UCA GCA AAA-biotin-3′. These alternate oligonucleotides shift the Cy3 and Cy5 labeling sites from nucleotides 50 and 17 in the WT hTR PK to nucleotides 1 and 30 in the WT^alt hTR PK (numbering from 5′-end of the smFRET constructs used within this study).

2.2. Single-Molecule Microscope

All single-molecule experiments are performed with an inverted confocal fluorescence microscope (Olympus Corp.) outfitted with a 1.2 NA water-immersion objective (Olympus; Figure 2). Direct excitation of the Cy3 (donor) fluorophore is accomplished via a pulsed (20 MHz) 532 nm laser (Time Bandwidth Products Inc.). As needed, direct excitation of the Cy5 fluorophore (acceptor) can also be acomplished with a pulsed 635 nm laser diode (PicoQuant GmbH) triggered with a fixed 25 ns delay with respect to the 532 nm donor excitation pulse. The light from both excitation sources is coaxially aligned and directed into the back aperture of the objective, resulting in spatially overlapped laser foci and the ability for alternating laser excitation methods (ALEX)⁴⁵⁻⁴⁷ to verify the presence of both donor and acceptor dyes on any given single-molecule construct.

Figure 2.

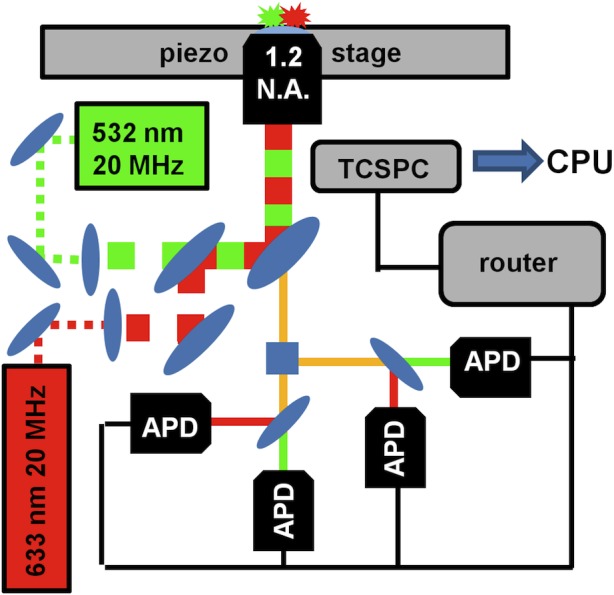
Single-molecule fluorescence microscope. Diagram of the experimental setup and data collection (see Experimental Methods for details).

Photons are collected by the same objective in epifluorescence and focused through a spatial pinhole (50 μm) aligned for optimal fluorescence collection from the laser excitation volume. After passing through the pinhole, the light is spatially separated by polarization (i.e., perpendicular, parallel) and color (i.e., donor, acceptor) before being refocused onto one of four single-photon avalanche photodiodes (APD, PerkinElmer Inc.) coupled to a time-correlated single-photon counting (TCSPC) module (Becker & Hickl GmbH; Figure 2). The arrival of each fluorescence photon is recorded with respect the exciting laser pulse (microtime) and start of the experiment (macrotime). The stream of photon macrotimes is used to construct a donor–acceptor fluorescence time trajectory, which is a visual representation of the raw data collected in both the freely diffusing and surface-immobilized smFRET experiments (see below). Conversely, the photon microtimes are used to construct fluorescence lifetime profiles of the two dyes, which, among other things, can be used to ensure isotropic rotational diffusion of the donor and acceptor fluorophores and thus the absence of any dye–RNA interactions.

2.3. Freely Diffusing smFRET Experiments

Freely diffusing experiments, similar to two-color coincidence detection one-color excitation experiments,^8,48 are performed at relatively high average laser powers (≈ 75 μW) with low RNA concentrations (≈ 125 pM). At these concentrations there is, on average, significantly fewer than one RNA molecule in the confocal excitation volume at any time (Figure 3a). As an individual RNA in solution stochastically passes through the excitation volume of the focused laser beams, a short (<1 ms) burst of fluorescence is emitted that corresponds to the resonance time of the RNA in the confocal volume (Figure 3b). Sorting photon arrival times via ALEX methods provides the crucial ability to restrict analysis only to constructs containing both non-photobleached donor and acceptor fluorophores. This is accomplished by assigning a threshold of 20 kHz on the minimum photon count rate for a given fluorescent burst to ensure sufficient determination of E_FRET, with the reported values insensitive within quoted uncertainties to changes in such a choice of threshold.

Figure 3.

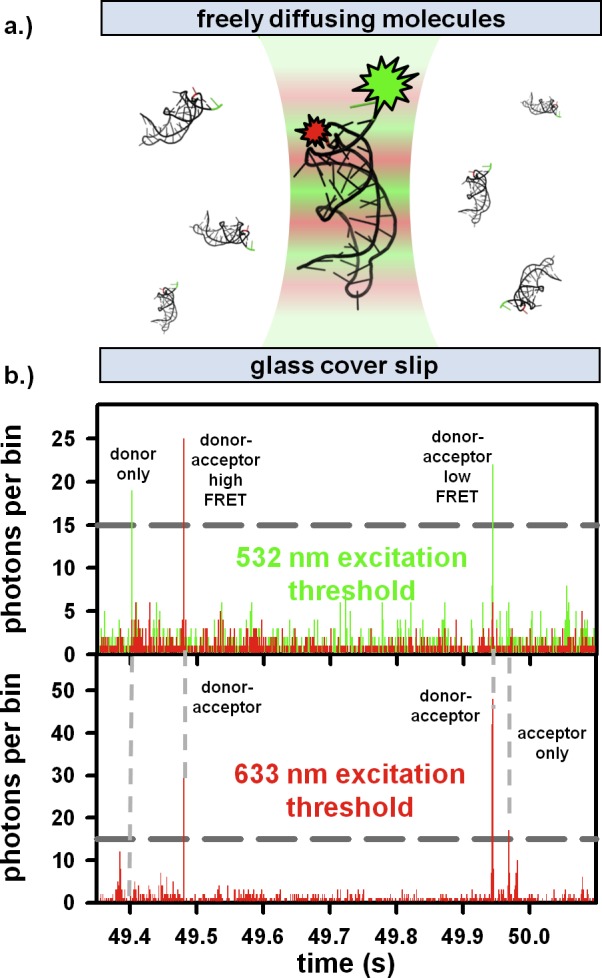
Freely diffusing experiments. (a) Schematic representation of single molecules freely diffusing in and around the overlapping excitation volumes of the red and green lasers (see Experimental Methods for details). (b) Freely diffusing data of the human telomerase RNA pseudoknot obtained using ALEX methods, with the four possible outcomes for the fluorescent molecules. ALEX filtering permits events from dually labeled donor–acceptor molecules to be selectively considered for data analysis.⁴⁷

Data analysis is accomplished by calculating E_FRET values for all ALEX sorted bursts with both the donor and acceptor dyes present, which are then used to construct a histogram representing an equilibrium distribution of E_FRET for the hTR PK molecules under a given set of experimental conditions.⁴⁹ From the minimum (E_FRET ≈ 0.55) in such a bimodal distribution (see Figure 4), it is easy to determine which fluorescent bursts arise from molecules in the hairpin (unfolded, E_FRET < 0.55) or pseudoknot (folded, E_FRET > 0.55) conformation. Due to sample purity and the use of ALEX methods, the number of high- and low-E_FRET bursts is directly proportional to the concentration of each of the conformers at equilibrium; thus the ratio of high- and low-E_FRET burst frequencies provides direct experimental access to the equilibrium constant (Figure 1c).

Figure 4.

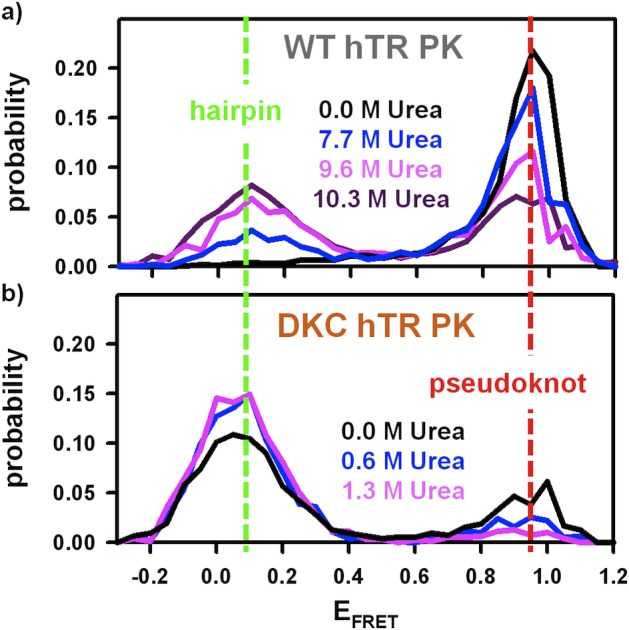
Freely diffusing FRET histograms of (a) the wild-type human telomerase RNA pseudoknot and (b) the dyskeratosis congenita mutant of the human telomerase RNA pseudoknot. The urea titrations demonstrate strong shifts in the pseudoknot–hairpin equilibrium behavior for both constructs.

2.4. Surface-Immobilized smFRET Experiments

For surface-immobilized experiments, molecules are noncovalently attached to the surface via biotin–streptavidin chemistry, with a typical surface coverage of <1 molecule/μm². To generate an image of the surface-immobilized molecules, a piezoelectric stage raster scans a 10 × 10 μm² region of the sample with respect to the microscope objective to generate a 256 × 256 pixel image. Each diffraction-limited feature in the image corresponds to the fluorescence from a single surface-immobilized molecule. The stage is then used to position the sample so that the laser light is focused at the center of an individual fluorescence spot, from which the fluorescence can be continuously observed in real time. Again, the use of ALEX-filtered surface images ensures that only dually labeled molecules are considered for data analysis. As mentioned previously, the collected donor and acceptor photon streams are used to construct both fluorescence and E_FRET time trajectories, which for surface-immobilized experiments depict individual molecules actively switching between conformations with distinct FRET efficiencies. Rate constants for these conformational transitions are calculated by constructing cumulative distribution plots of the dwell times for the pseudoknot (E_FRET > 0.55) and hairpin (E_FRET < 0.55) conformations.

2.5. smFRET Temperature Control

For all of the temperature-dependent smFRET experiments, a heated objective collar (Bioptechs, Inc.) and Peltier-base stage heater (Instec, Inc.) are used to provide thermal control of the sample with temperature gradients < 0.1 °C/cm. The absolute sample temperature is determined from measurements at the focus of the excitation source using a micro-thermocouple. All other experiments are performed at room temperature (20–22 °C).

2.6. smFRET Buffer Conditions

Experiments are performed in a standard fluorescence-imaging buffer (50 mM HEPES, 25 mM KOH, 10 mM NaOH, 95 mM KCl, and 2 mM TROLOX, pH 7.7), which consists of the well-characterized protocatechuic acid/protocatechuate-3,4-dioxygenase oxygen scavenging system (100 nM PCD and 5 mM PCA).⁵⁰ For all experiments, the molar concentrations of each of the buffer components are held constant by accounting for changes in solution volume and density due to the added solute.

3. Results

3.1. Freely Diffusing Burst Measurements

In the standard fluorescence-imaging buffer (see Experimental Methods), the wild-type (WT) human telomerase RNA pseudoknot (hTR PK) appears to exist in a single high-FRET conformation (E_FRET = 0.95(1); full width at half-maximum (FWHM) =0.11(1); Figure 4a, black). This E_FRET corresponds to a length of R ≈ 32(1) Å which, when one considers the flexible carbon linkers (≈ 5 Å) connecting each of the two fluorescent dyes to the RNA, is consistent with the modeled distance (≈22 Å; see ref²⁰) between the two nucleotides nearest to the fluorophores. Therefore, the observed high-FRET state is the result of a stably folded pseudoknot.

This is in stark contrast to the equilibrium distributions of FRET states associated with the DKC hTR PK (Figure 4b, black). Under the same experimental conditions, the dyskeratosis congenita (DKC) hTR PK adopts two conformations: (i) a high-FRET conformation (E_FRET = 0.94(2); FWHM = 0.14(2)), indistinguishable from the pseudoknot structure for WT hTR PK; and (ii) a low-FRET conformation (E_FRET = 0.07(1); FWHM = 0.19(1)), indicative of a substantial increase in donor–acceptor distance. From the 1/R⁶ dependence of FRET efficiency on distance, this low-FRET value corresponds to ≈ 80(2) Å of separation between the two dyes and is indeed consistent with the hairpin conformation.

To better assess the stability of the WT hTR PK and to explore other partially folded or unfolded conformations, freely diffusing experiments have been performed as a function of urea concentration (Figure 4a). Upon addition of 7.7 M urea, a second conformation with low FRET (E_FRET = 0.11(1); FWHM = 0.20(1)) begins to appear, which is essentially indistinguishable from the low-FRET conformation of the DKC hTR PK under nondenaturing conditions (Figure 4a, blue and Figure 4b, black). This suggests that the low-FRET state for WT hTR PK in the presence of high urea concentrations is almost identical to the extended hairpin structure that the DKC hTR PK occupies under nondenaturing conditions. For the WT hTR PK, the relative population of molecules in the hairpin conformation continues to increase with increasing denaturant concentration up to the solubility limit of urea (≈10.3 M). This same trend is apparent for the DKC hTR PK; however, it occurs over a much more dilute range of urea concentrations (Figure 4b). Both smFRET constructs are able to reversibly and completely redistribute between the low- and high-FRET states depending upon urea and monovalent cation concentration. Such behavior is consistent with a simple, two-state, unimolecular equilibrium between the pseudoknot and hairpin conformations.

An alternatively labeled RNA construct (WT^alt hTR PK) has been designed to further validate that the WT hTR PK exists in a hairpin–pseudoknot equilibrium under all urea concentrations (Supporting Information Figure S1a). For this construct, the fluorophore labeling specifically probes disruption and formation of the P2 region of the pseudoknot, rather than the P3 region sampled with the conventional labeling scheme. The WT^alt hTR PK exists solely in a high-FRET conformation at both 0 M urea (E_FRET = 0.95(1); FWHM = 0.09(1)) and 10.3 M urea (E_FRET = 0.95(1); FWHM = 0.13(1)), which confirms that the observed dynamics in the conventional construct are indeed the result of disruption and formation of the P3 region of the WT hTR PK (Supporting Information Figure S1b).

Given that a unimolecular equilibrium can be used to accurately describe the hairpin–pseudoknot transition of both the WT and DKC hTR PK constructs used in this study, the ratio of the relative population of the pseudoknot and hairpin conformations yields the equilibrium constant (K_eq = [pseudoknot]/[hairpin]) for the two species (Figure 1c). The equilibrium constant can easily be converted to the standard-state Gibb’s free energy change associated with transitioning between the two conformations (i.e., ΔG° = −RT ln[K_eq]). As previously observed in other RNA systems,^36,38,51 the free energy change depends linearly on the urea concentration (Figure 5). Although the slopes (m-values) for the two constructs are not identical (see Discussion), the pronounced linearity of both plots at high and low urea concentrations makes it reasonable to assume linear behavior across all urea concentrations. As a result, a simple linear extrapolation to 0 M urea should yield the ΔG°(295K) values associated with hairpin-to-pseudoknot transitions under nondenaturing conditions (ΔG°_DKC = 0.26(4) kcal/mol; ΔG°_WT = −4.2(2) kcal/mol).

Figure 5.

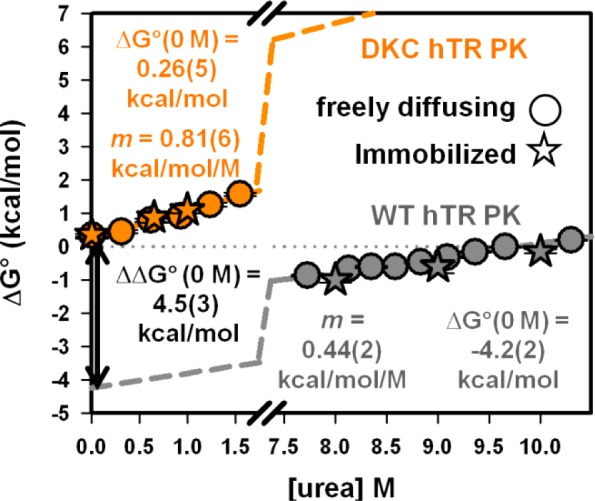
Urea dependence of the free energy change for forming the pseudoknot from the hairpin conformation for the wild-type human telomerase RNA pseudoknot (gray) and the dyskeratosis congenita mutant (orange) of the human telomerase RNA pseudoknot. Linear extrapolation to 0 M urea yields the 4.5(3) kcal/mol differential folding free energy between the WT and mutant pseudoknot under nondenaturing conditions.

3.2. Surface-Immobilized Images

ALEX-filtered, raster-scanned surface images of immobilized molecules qualitatively recapitulate the results of the freely diffusing experiments (Figure 6). Under nondenaturing conditions, the WT hTR PK molecules exist entirely in the high-FRET (pseudoknot) conformation (Figure 6a), while the DKC hTR PK molecules are distributed between the two conformations, with the low-FRET (hairpin) state being slightly more populated (Figure 6c). Upon closer inspection, however, the surface-immobilized images provide partial information on the lifetime associated with the pseudoknot and hairpin conformations. Specifically, the uniformity of color for each diffraction-limited spot (Figure 6a,c,d) suggests that dwell times for the pseudoknot and hairpin conformations are, on average, longer than the ≈ 10 s time scale sampled in rastering across each of the ≈ 10 horizontal rows of pixels that comprise a single fluorescent spot. This contrasts subtly but quite significantly with images for WT hTR PK at 10.3 M urea (Figure 6b), where individual fluorescent spots exhibit both red and green contributions but only with complete rows of either fully red or green pixels. Such color continuity in the horizontal but not necessarily vertical dimension suggests that switching must take place on a time scale that is (i) clearly faster than 10 s overall scan time but apparently also (ii) slower than the ≈10 ms it takes to scan across ≈10 horizontal pixels within a single row for a given fluorescence spot.

Figure 6.

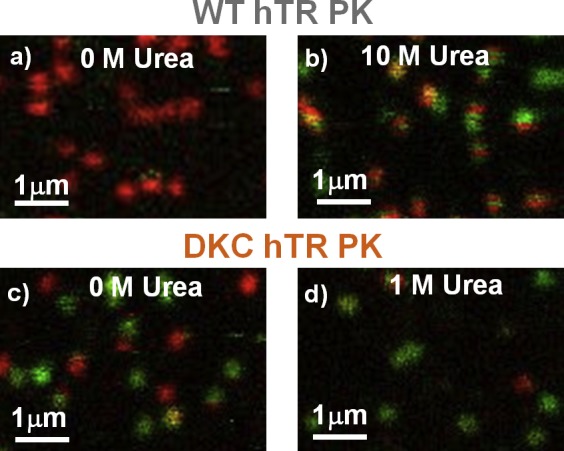
Images of surface-immobilized molecules for the wild-type (a, b) and dyskeratosis congenita (c, d) pseudoknots. Each diffraction-limited fluorescence spot represents the location of an individual dually labeled RNA molecule. The urea dependence of the images yields kinetic information about the two different pseudoknot constructs (see text for details).

3.3. Surface-Immobilized Time Trajectories

To obtain more quantitative kinetic information about the rate constants for transitioning between the pseudoknot and hairpin conformations, donor–acceptor fluorescence time trajectories are acquired for individual surface-immobilized molecules (Figure 7a,c). The fluorescence trajectories can easily be converted to FRET trajectories that cleanly demonstrate the two-state behavior for both RNAs, with FRET values consistent with the previously discussed freely diffusing experiments. For such a two-state equilibrium system, the dwell times associated the pseudoknot and hairpin states should be distributed exponentially, with characteristic time constants corresponding to rate constants for unfolding (k_unfold, pseudoknot → hairpin) or folding (k_fold, pseudoknot ← hairpin) (Figure 1c). This expectation is nicely confirmed for both WT (Figure 7b) and DKC (Figure 7d) RNAs under denaturing and nondenaturing conditions, respectively. Clearly, both pseudoknot and hairpin dwell times are distributed exponentially with well-defined single-exponential rate constants.

Figure 7.

Surface-immobilized folding and unfolding kinetics for the (a) wild-type pseudoknot and (c) the mutant human telomerase RNA pseudoknots under denaturing and nondenaturing conditions, respectively. Rate constants are determined from exponential fits to cumulative distribution plots of dwell times for the (b) wild-type and (d) dyskeratosis congenita pseudoknots.

The FRET time trajectories for the WT hTR PK under nondenaturing conditions are overwhelmingly dominated by the high-FRET state. Given the finite observation window of fluorescent molecules prior to photobleaching (≈ 100 s), only a few conformational transitions have been observed under nondenaturing conditions. This prevents quantitative determination of dwell times and therefore rate constants associated with the WT construct under nondenaturing conditions. However, the fact that very few time trajectories exhibit even a single unfolding event during a 100 s photobleaching lifetime suggests an upper limit for the unfolding rate constant of ≈ 0.01 s^–1.

To achieve a better understanding of the WT hTR PK folding kinetics, surface-immobilized time trajectories have been acquired under denaturing conditions (Figure 7a). Interestingly, high urea concentrations strongly increase the unfolding rates without substantially influencing the folding rates (Table 1a, Figure 8a). From the kinetics experiments, it is also possible to readily extract equilibrium constants for the pseudoknot–hairpin system (K_eq = k_fold/k_unfold), based on the assumption of a two-state system. As expected, the surface-immobilized equilibrium constant data, derived from folding/unfolding kinetics, are in excellent agreement with the freely diffusing experiments (Figure 5). Such agreement between surface-immobilized and freely diffusing data sets provides additional evidence to support the claim that surface immobilization does not perturb the conformation dynamics for either the WT or DKC constructs.

Table 1. Rate and Equilibrium Constants for the (a) Wild-Type and (b) Mutant Forms of the Human Telomerase RNA Pseudoknot under Varying Urea Concentrations^a.

[urea], M	kfold, s-1	kunfold, s-1	Keq
(a) WT hTR PK
8.0	10(1)	1.8(3)	5.7(6)
9.0	9.8(3)	3(1)	3(1)
10.0	9.4(8)	7.2(6)	1.3(2)
0.0	10b	0.009b	1100b
(b) DKC hTR PK
0.0	0.023(5)	0.043(3)	0.5(1)
0.8	0.038(5)	0.13(1)	0.29(4)
1.0	0.05(1)	0.3(1)	0.15(5)

^aFor both RNA pseudoknot constructs, the rate constant for forming the pseudoknot from the hairpin conformation is largely insensitive to urea concentration.

^bEstimated values based on the urea-insensitive folding rate constant and the extrapolated free energy at 0 M urea (see text for details).

Figure 8.

Log-linear plot of the urea-dependent folding and unfolding kinetics for the (a) wild-type and (b) dyskeratosis congenita pseudoknots. For both constructs, the unfolding rate constant is substantially more sensitive to addition of urea than the folding rate constant, which suggests that most of the change in base solvent accessible surface area (SASA) occurs after formation of the transition state. Lines indicate trends and are not actual fits to the data.

The linear dependence of the folding free energy change on urea concentration (Figure 5) can be used to develop a more quantitative understanding for the folding kinetics of the WT hTR PK under nondenaturing conditions. Specifically, the extrapolation of ΔG° to 0 M urea in Figure 5 yields ΔG°_WT(295K) = −4.2(2) kcal/mol, which would imply K_eq = k_fold/k_unfold ≈ 1100 and thus a highly stable WT pseudoknot. Experimentally, the folding rate constant is observed to be mostly insensitive to urea concentration, which would imply any urea dependence of ΔG° is due primarily to changes in the unfolding rate constant. Therefore, a urea-independent folding rate constant of ≈ 10 s^–1 from Figure 8a would suggest an unfolding rate constant of ≈ 0.009 s^–1 at 0 M urea (Table 1a), which is certainly consistent with the ≈ 0.01 s^–1 upper limit established by photostability of the present donor–acceptor FRET pair.

In contrast with the WT construct, each trajectory for the DKC hTR PK construct under nondenaturing conditions undergoes multiple conformational transitions between the two FRET states (Figure 7c), which permits accurate determination of dwell times and rate constants (Figure 7d). As was the case for the WT hTR PK, addition of urea has only a small effect on k_fold while substantially increasing k_unfold (Table 1, Figure 8b). It is worth noting that the above kinetic measurements for the DKC hTR PK under nondenaturing conditions serve as a valuable benchmark for the corresponding rate constants for WT hTR PK extrapolated to 0 M urea. Interestingly, such a comparison reveals that the net 4.5(3) kcal/mol destabilization of the mutant DKC pseudoknot is achieved by a combination of much slower folding (≈ 400-fold) and only slightly faster (≈ 5-fold) unfolding rate constants (Table 1).

3.4. van’t Hoff Thermodynamics

Via direct measurement of the equilibrium constant, these single-molecule studies have thus far focused on standard Gibbs free energy change (ΔG°) as the primary, experimentally determined, thermodynamic parameter. However, temperature-dependent information about the equilibrium constant can be used to deconstruct Gibbs free energy changes into enthalpic (ΔH°) and entropic (ΔS°) components. Furthermore, the observation that ΔG° is linearly dependent on urea concentration makes it reasonable to assume that the two additive components of ΔG° = ΔH° – TΔS° might also be linearly dependent on urea, which facilitates additional thermodynamic comparisons between the wild-type and mutant RNA constructs.

In freely diffusing experiments, the equilibrium constant for the WT hTR PK has been measured at temperatures ranging from 20.0(1) to 33.0(1) °C for three different urea concentrations (7.7, 8.4, and 9.1 M). At all urea concentrations, increasing the temperature results in unfolding of the pseudoknot, thus reducing the equilibrium constant. As shown in Figure 9a, a van’t Hoff plot (ln[K_eq] vs 1/T) of the data is used to infer the entropy (ΔS° = intercept × R) and enthalpy (−ΔH° = slope × R) changes associated with pseudoknot formation. It is interesting to note the nearly identical slopes for each of the plots, i.e., enthalpy changes (ΔH°), associated with pseudoknot formation are largely insensitive to urea. Along with more quantitative results from a nonlinear least-squares fit (Table 2a), these data sets provide clear evidence that the addition of urea primarily decreases the folding entropy (ΔΔS° < 0), with a negligible effect on the folding enthalpy (ΔΔH° ≈ 0). To further break parameter correlation and thereby more precisely examine the dependence of ΔS° on urea, these van’t Hoff data sets have been refitted with a common enthalpic slope. As shown in Figure 9b, the resulting entropy changes are linearly dependent on urea concentrations and predict ΔS° = −250.2(6) cal/(mol K) at 0 M urea. In conjunction with the urea-independent ΔH° = −78.2(6) kcal/mol, this limiting ΔS° value corresponds to ΔG°(295K) = −4.4(6) kcal/mol under nondenaturing conditions. It is worth noting that this is experimentally indistinguishable from the ΔG°(295K) = −4.2(2) kcal/mol value obtained from extrapolation of the freely diffusing data (Figure 5a), which provides additional support for analyses of this conformational transition based on a linear dependence of free energy and entropy on urea.

Figure 9.

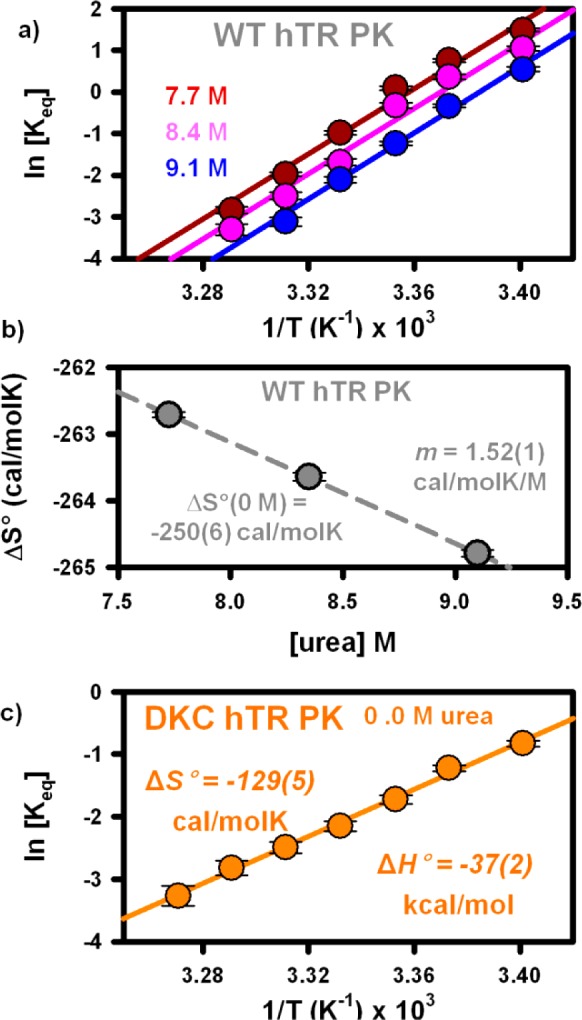
Single-molecule van’t Hoff analyses. (a) Plot of the temperature dependence of the equilibrium constant of the wild-type human telomerase RNA pseudoknot at three urea concentrations. Identical slopes indicate a urea-independent folding enthalpy, while the constant vertical offset indicates a urea-dependent entropy. (b) Plot of the urea-dependent entropy suggesting a linear dependence of folding entropy on urea concentration. (c) van’t Hoff analysis of the mutant pseudoknot under nondenaturing conditions. All entropy and enthalpy changes can be found in Table 2

Table 2. Thermodynamic Parameters from Single-Molecule van't Hoff Analysis.

[urea], M	ΔH°, kcal/mol	ΔS°, cal/(mol K)
(a) WT hTR PK
9.1	–79(2)	–267(4)
8.4	–78(2)	–262(6)
7.7	–78(1)	–261(4)
0.0	–78.2(6)b	–250(6)c
(b) DKC hTR PK
0.0	–37(2)	–129(5)

^aTogether they predict folding thermodynamics under non-denaturing conditions.

^bValues from common slope analysis (see text for details).

^cExtrapolated values from the linear dependence of the entropy change on urea concentration (see text for details).

To enable thermodynamic comparison between the two RNA pseudoknot constructs under nondenaturing conditions, temperature-dependent equilibrium constants for DKC hTR PK have also been measured. The resulting van’t Hoff plot (Figure 8c) predicts ΔS° = −129(5) cal/(mol K) and ΔH° = −37(2) kcal/mol at 0 M Urea (Table 2b). Such a van’t Hoff analysis of the DKC hTR PK data predicts ΔG°(295K) = 1(2) kcal/mol at 0 M Urea, which is also consistent with the ΔG°(295K) = 0.26(5) kcal/mol value obtained from the freely diffusing data (Figure 5b). Lastly, comparison of the WT and DKC constructs reveals that pseudoknot formation in the mutant is both half (≈ 47%) as exothermic and half (≈ 51%) as entropically costly, which makes formation of the WT pseudoknot more favorable thermodynamically.

4. Discussion

The above studies demonstrate the well-behaved, two-state nature of both the wild-type and dyskeratosis congenita variants of the minimal hTR PK, which is consistent with recent smFRET findings.²⁶ As a function of experimental conditions, both constructs are able to switch completely and reversibly between readily distinguishable low- and high-FRET states. This observation supports the existence of a two-state pseudoknot–hairpin unimolecular equilibrium for both the WT and DKC constructs.²³ Implications of the kinetic and thermodynamic parameters associated with this equilibrium are discussed in detail as follows.

4.1. Folding Free Energies

For solution conditions used throughout these studies, which appropriately mimic physiological concentrations of free monovalent ions, the two RNA constructs exhibit vastly different ΔG°(295K) values for pseudoknot formation. The free energy of folding for the WT hTR PK is −4.2(2) kcal/mol, as determined by a linear extrapolation to 0 M urea (Figure 5a), which should be compared to 0.26(5) kcal/mol for the DKC variant. Such a substantial stability difference between the WT and DKC constructs (ΔΔG°(295K) = 4.5(3) kcal/mol) is qualitatively consistent with existing thermal denaturation studies (6.6 kcal/mol) and theoretical calculations (6 kcal/mol),²³ especially accounting for differences in solution conditions (e.g., salt, pH, and temperature) associated with each value. Furthermore, the overall sign of this shift is in the expected direction, with the 2 nt noncomplementary substitution resulting in less favorable formation of the pseudoknot.

It is instructive to explore how ΔΔG°(295K) between the WT and DKC constructs (4.5(3) kcal/mol) manifests itself in the kinetics of the hairpin–pseudoknot unimolecular equilibrium. As noted previously, the presence of the DKC mutation results in a large reduction (≈ 400-fold) and yet only a modest increase (≈ 5-fold) in the folding and unfolding rate constants, respectively. In conjunction with the overall ΔΔG°, such kinetic information can be used to build a simple free energy reaction coordinate for the hairpin–pseudoknot folding transition (Figure 10). Specifically, the measured rate constants data are used to estimate the free energy barrier for folding from transition-state theory (eq 1), which would be consistent with a 15–20 kcal/mol transition-state barrier along the reaction coordinate for a typical attempt frequency of ν ≈ 10¹³ s^–1.

1

It is worth noting, however, that ΔG^⧧ depends only logarithmically on ν; thus, any differential changes in free energy barriers predicted from eq 2 should specifically remain completely independent of any such ad hoc and/or estimated choices for the prefactor, ν.

2

From this expression, the changes associated with the folding and unfolding rate constants for the DKC mutant correspond to a 3.6 kcal/mol increase and a 0.9 kcal/mol decrease in the folding and unfolding free energy barriers, respectively.

Figure 10.

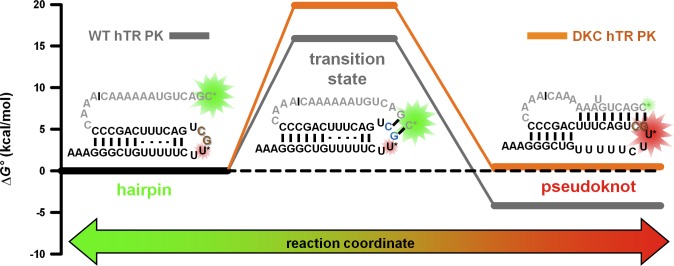
Free energy landscape for formation of the pseudoknot from the hairpin conformation. Secondary structure diagrams for the wild-type human telomerase RNA pseudoknot are shown, including the predicted structure of the transition state where only a few nucleotides from the P3 region of the pseudoknot have formed (see Discussion for details).

Furthermore, we can extract additional physical insights into these changes in barrier height from a Φ-analysis.^36,52 Specifically, for a given pair of modifications (e.g., DKC and WT), Φ represents the fraction of the free energy barrier change for folding (ΔΔG^⧧_fold) that results per unit change in the overall equilibrium stability (ΔΔG°).

3

Φ-analysis for the DCK and WT hTR pseudoknots demonstrates that 80% of the ΔΔG°(295K) comes from decreasing the DKC folding rate constant. This implies that the WT nucleotides at the positions associated with the DKC mutation (i.e., G108 and C109) play an important role in lowering the free energy transition-state barrier for folding. Furthermore, the results of the Φ-analysis can be used to provide insights into the structure of the transition state for this conformational transition. Specifically, this strongly suggests that the WT hTR PK constructs at the transition state already have well-formed stabilizing contacts (e.g., base stacking and hydrogen bonding) at nucleotides G108 and C109.

4.2. Urea-Dependent Free Energies and Rate Constants

Denaturation of nucleic acids is thought to occur because of favorable interactions between urea and the base “solvent accessible surface area” (SASA).⁵³ For RNA in a conformational equilibrium, the presence of urea preferentially stabilizes the structure with the most base SASA—typically unfolded and/or less compact. This manifests itself as a linear dependence of the folding free energy change on urea concentration (∂ΔG°/∂[urea]), which is often referred to as the m-value.^38,54 Consequently, one would expect the m-value for RNA folding to be positively correlated with the amount of base SASA buried due to a folding transition, as has been shown in several studies.^38,51 It is therefore interesting to note that the m-values for the WT and DKC constructs differ in a counterintuitive direction. Specifically, due to two fewer base pairing interactions in the P3 region, pseudoknot formation might be anticipated to lead to less base SASA burial in DKC vs WT hTR PK. As a result, one would expect WT hTR PK folding to be more sensitive to urea, when in fact it is nearly half as sensitive (WT, m = 0.44(2) (kcal/mol)/M; DKC, m = 0.81(6) (kcal/mol)/M). The precise origin of this difference is not well understood. However, these results certainly indicate unexpected differences in base SASA burial, which could potentially result from structural differences between (i) the WT and DKC hairpin conformations and (ii) the WT and DKC pseudoknot conformations that may be related to the formation of base triples in the WT hTR PK. Together these structural differences could give rise to larger base SASA burial in the DKC hTR PK, which would be consistent with the experimentally observed m-values.

This m-value analysis can be similarly applied to the folding kinetics, by assuming that the urea dependence of the rate constants is also related to the amount of base SASA burial associated with formation of the transition state that separates the two conformations.³⁶ For both of the hTR PK constructs, the very modest urea dependence of the folding rate constant suggests that there is little base SASA burial associated with forming the transition state from the hairpin conformation. In conjunction with the observation that nucleotides 108 and 109 are important for fast folding, the urea-independent folding rate constant for the hTR PK implies a transition state where only the last two base pairs in P3 (e.g., G108 and C109) are formed, leaving the remainder of the bases in J2a/3 solvent exposed (Figure 10). Minimal burial of base SASA resulting from formation of the transition state from the hairpin conformation provides the rational for a largely urea-insensitive folding rate constant, as observed experimentally. Accordingly, most of the total base SASA burial takes place after the transition state during formation of the remainder of the P3 pseudoknot, which gives rise to a substantial dependence of the unfolding rate constant on urea concentration. Interestingly, similar conclusions have been made in quite different RNA constructs,^36,55 which (i) suggest that urea may generally destabilize all RNA tertiary folding transitions by selectively accelerating the unfolding rate constant and (ii) support the notion that many transition states for RNA tertiary folding may be conformationally aligned, yet still devoid of significant base SASA burial (e.g., minimal hydrogen-bonding and base-stacking).

4.3. Urea-Dependent Entropies and Enthalpies

The measured urea-independent enthalpy for WT pseoduknot formation (ΔH° = −78.2(6) kcal/mol) is remarkably close to both theoretical calculations (−78.9 kcal/mol⁵⁶) and previous experimental observations using ensemble techniques (−72.7 kcal/mol^22,23). Such quantitative agreement serves as strong support for the use of urea as a valuable tool to study highly stable RNAs at the single-molecule level under denaturing conditions. Additionally, van’t Hoff analysis as a function of urea yields new insights into the thermodynamic origin of urea-induced denaturation of the hTR PK. For example, the near complete insensitivity of ΔH° to urea provides experimental evidence that destabilization associated with urea is predominantly due to changes in ΔS°. This entropic origin of urea destabilization, together with the observation that urea has little effect on the folding rate constant, suggests that the majority of the denaturing power of urea results from increasing the entropic reward associated with forming the transition state from the pseudoknot conformation. Simply stated, urea destabilizes the WT hTR PK by making unfolding more entropically beneficial. This is a surprising observation, given that the proposed mechanism for urea denaturation of nucleic acids results from favorable hydrogen bonding between urea and the base SASA of RNA. The lack of any substantial enthalpic component to urea denaturation therefore must imply nearly perfect cancellation of any differential exothermicity between the competing urea–base and base–base interactions. Additionally, the determination of a urea-independent enthalpy change and a linear urea-dependent entropy change makes it feasible to compare the folding thermodynamics between the WT and DKC hTR PK constructs used throughout this work (Figures 9a,c and Table 2).

One additional surprising observation is that the increase in folding free energy (ΔΔG° = 4.5(3) kcal/mol) associated with the WT vs DKC mutant results from a fortuitous near cancellation between much larger changes of both the folding enthalpy (ΔΔH° ≈ 41 kcal/mol) and entropy (ΔΔS° ≈ 121 kcal/(mol K), TΔΔS° ≈ 37 kcal/mol). An approximately 50% reduction in the enthalpic and entropic components of pseudoknot formation is certainly unexpected but clearly indicates that substantial thermodynamics differences exist between the WT and the DKC hTR PK. These large entropic and enthalpic differences may be related to the vastly different m-values associated with the two constructs. As mentioned previously, it is likely that the WT and DKC constructs have different pseudoknot conformations. Specifically, the DKC hTR PK may not be able to form the well-defined triple-helical structure of the WT sequence. If this were the case, then pseudoknot formation in the DKC construct would lack the additional exothermicity as well as the entropic cost associated with forming the five base triples within the WT triple helix, resulting in the large ΔΔH° and ΔΔS° values that are observed experimentally. Differentiation between these two types of folding conformations (i.e., pseudoknot vs triple-helix) is not possible with the current FRET constructs but clearly identifies an interesting direction for future structural efforts.

5. Conclusion

Single-molecule FRET experiments have been used to cleanly observe folding transitions in a minimal RNA pseudoknot (PK) designed to mimic the wild-type motif within the human telomerase RNA. These experiments are compared and contrasted with experiments conducted on a second minimal human telomerase RNA pseudoknot that contains a 2 nt noncomplementary substitution mutation implicated in the telomerase-associated genetic disorder—dyskeratosis congenital (DKC). These experiments have demonstrated that the wild-type pseudoknot is substantially more stable (ΔΔG = 4.5(3) kcal/mol) than the mutant. Single-molecule kinetic studies of these constructs have identified the kinetic origin of this differential stability as being the result of (i) a substantially reduced folding rate constant and (ii) a moderately increased unfolding rate constant, both of which contribute to destabilization of the fully folded mutant pseudoknot conformation. With the help of urea-induced denaturation, smFRET experiments have been used to elucidate the free energy landscape and various structural aspects of the folding reaction coordinate. Lastly, single-molecule van’t Hoff analyses highlight a potential folding pathway wherein the mutant pseudoknot is unable to form the functionally important triple-helix structure known to exist in the wild-type RNA. Together, these results suggest that the disease mechanism associated with this particular genetic mutation is related to a combination of (i) differential stabilities of the wild-type and mutant pseudoknot conformations, (ii) differential folding/unfolding kinetics associated with the pseudoknot–hairpin unimolecular equilibrium for the wild-type and mutant RNAs, and (iii) the potential lack of the a RNA triple helix in the mutant pseudoknot. Precise determination of the detailed mechanism of telomerase and the associated disease states would benefit substantially from extensions of these single-molecule experiments on minimal hTR pseudoknots to more holoenzyme-like systems that more closely recapitulate telomerase activity and function.

Supporting Information Available

Figure depicting the results of smFRET experiments conducted on an alternatively labeled RNA construct (WT^alt hTR PK). This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interests.

Funding Statement

National Institutes of Health, United States