Abstract
Humans map number onto space. However, the origins of this association, and particularly the degree to which it depends upon cultural experience, are not fully understood. Here we provide the first demonstration of a number-space mapping in a non-human primate. We trained four adult male rhesus macaques (Macaca mulatta) to select the fourth position from the bottom of a five-element vertical array. Monkeys maintained a preference to choose the fourth position through changes in the appearance, location, and spacing of the vertical array. We next asked whether monkeys show a spatially-oriented number mapping by testing their responses to the same five-element stimulus array rotated ninety degrees into a horizontal line. In these horizontal probe trials, monkeys preferentially selected the fourth position from the left, but not the fourth position from the right. Our results indicate that rhesus macaques map number onto space, suggesting that the association between number and space in human cognition is not purely a result of cultural experience and instead has deep evolutionary roots.
Keywords: Numbers, Space, SNARC, effect, Ordinal representation, Monkeys
1. Introduction
Number and space are integrally linked in the human mind (Bueti & Walsh, 2009; Fias & Fischer, 2005; Hubbard, Piazza, Pinel, & Dehaene, 2005). A prominent behavioral manifestation of this interaction is the SNARC (Spatial-Numerical Association of Response Codes) effect, whereby smaller numbers are associated with one side of space and larger numbers with the other. In the original demonstration of the SNARC effect, subjects making parity judgments (i.e. odd or even) were faster to respond to smaller numbers with a left-side response key and larger numbers with a right-side response key (Dehaene, Bossini, & Giraux, 1993). This pattern has been replicated in a variety of experimental paradigms and populations (reviewed in Fias & Fischer, 2005), including in the auditory modality among both blind and sighted subjects (Castronovo & Seron, 2007), indicating that the number-space mapping is amodal. Interestingly, in cultures that read from right to left the SNARC effect can be attenuated or even reversed, suggesting that experience may drive the mapping of number onto space (Shaki & Fischer, 2008; Shaki, Fischer, & Petrusic, 2009; Zebian, 2005).
Although the specific orientation of the SNARC effect varies with cultural conventions for reading direction, its presence across cultures suggests that the spatial mapping of numbers may be a universal cognitive strategy (Gobel, Shaki, & Fischer, 2011). In fact, preschool children, who have not begun learning to read, are quicker and more accurate at finding an object hidden in a numbered compartment when compartment numbers increase from left to right rather than right to left, indicating they expect numbers to increase from left to right (Opfer, Thompson, & Furlong, 2010; Opfer & Furlong, 2011). These results suggest that spatial-numerical associations are not a product of extensive formal education or reading experience. Moreover, even preverbal infants, who have not yet learned to count or use measurement tools like rulers, are sensitive to the relationship between number and space (de Hevia & Spelke, 2010). When habituated to dot arrays (i.e. non-symbolic numbers) presented in either increasing or decreasing order, eight-month-old infants looked longer (indicating a novelty response) to line lengths presented in the opposite, but not the same, order. Furthermore, when infants were shown several exemplars of dot arrays paired with lines such that the line length either increased (positive pairing) or decreased (inverse pairing) with number of dots, infants extracted the rule from the positive but not the inverse pairing. Infants also showed a preference for positive pairings between numbers and line lengths over inverse pairings. These findings indicate that human infants have a predisposition to relate number to space and that our privileged number-space mapping does not depend upon language. An important question then is whether number is mapped onto space in any nonhuman species.
Rugani and colleagues found evidence for a left-to-right mental number line in baby chickens. First, they showed that 5-day-old domestic chicks (Gallus gallus) could learn to identify the third, fourth, or sixth hole in a series of ten identical holes sagittal to the chicks’ starting point, even when distance between holes was varied (Rugani, Regolin, & Vallortigara, 2007). Critically, when the line of holes was rotated 90° so that it was horizontal to the chicks’ starting point, chicks that had learned to select the fourth hole preferentially approached the fourth hole from the left, and rarely the fourth hole from the right. This finding was investigated further in newborn chicks and adult nutcrackers (Nucifraga columbiana). When trained to select the fourth (or sixth) item in a sagitally-oriented line of sixteen identical items, both species preferentially chose the fourth (or sixth, respectively) item from the left – but not the right – in a horizontally-oriented line (Rugani et al., 2010). However, when inter-element distances were varied during training or test, chicks were equally likely to choose the correct position from the left or the right (Rugani et al., 2011). The authors interpret their results as evidence for asymmetric processing of number and space. They posit that the purely ordinal aspect of the array is bilaterally represented in the left and right cerebral hemispheres, whereas the purely spatial aspect is unilaterally represented in the right hemisphere, biasing attention to the left side of space only when spatial cues (such as constant inter-element distance) could be used to complete the task. This explanation seems viable in birds, who have lateralized visual fields and a complete crossing of nerves at the optic chiasm, coupled with minimal interhemispheric connections (lack of corpus callosum), which results in visual information from one side of space being represented almost entirely in the opposite hemisphere (Larsson, 2013; Rogers et al., 2013). This strong lateralization likely underlies the numerous behavioral asymmetries observed in birds (Rogers et al., 2013). Primates, on the other hand, receive visual information from both sides of space in each cerebral hemisphere, due to frontally placed eyes, only partial crossing of nerves at the optic chiasm, and communication between the hemispheres (Larsson, 2013). Thus although Rugani and colleagues found a SNARC-like effect in a non-human species, the mechanism driving this effect could be different from that driving the effect in humans. Exploring whether monkeys orient numerical representations spatially might yield more information about the evolutionary precursors of the spatial mapping of number in humans.
The SNARC effect depends upon the ordinality inherent in number representation. The ability to identify a particular ordinal position in a sequence is crucial for many everyday activities, such as following directions (i.e. take the third right) or locating a car in a parking lot (i.e. in the eighth spot of the fifth row). Using numbers to denote rank or ordinality is theoretically distinguished from using numbers to denote quantity or cardinality. Indeed, behavioral (Franklin et al., 2009; Rubinsten & Sury, 2011; Turconi, et al., 2006), neurological (Butterworth, 1997; Turconi & Seron, 2002), and neuroimaging (Tang et al., 2008; Turconi et al., 2004; Zorzi et al., 2011) evidence indicates that distinct cognitive processes are engaged when accessing the ordinal rather than the cardinal meaning of numbers. A broad range of animal species can compare sets to choose the greater or lesser numerical value: birds (e.g. Aïn et al., 2008; Bogale et al., 2011; Roberts, 2010), fish (e.g. Agrillo et al., 2010; Gómez-Laplaza & Gerlai, 2012; Piffer et al., 2011; Stancher et al., 2013), amphibians (e.g. Krusche et al., 2010; Uller et al., 2003), non-human primates (e.g. Beran, 2008; Brannon & Terrace, 1998; Hanus & Call, 2007), and other mammals (e.g. Jaakkola et al., 2005; Uller & Lewis, 2009; Vonk & Beran, 2012; Ward & Smuts, 2007).
Other research shows that animals can learn to respond to arbitrary stimuli in prescribed ordinal sequences and represent the abstract ordinal position of each item (e.g. monkeys: Chen et al., 1997; Terrace, 2005; Terrace et al., 2003; domestic chicks: Rugani et al., 2007). Pigeons show more limited ability to encode ordinal positions of arbitrary items in a sequence ( Scarf & Colombo, 2010; Terrace, 1993; Terrace et al., 1996). Rats (Davis & Bradford, 1986; Suzuki & Kobayashi, 2000), bees (Dacke, 2008), and chicks (Rugani et al., 2007) moving through space can learn to select a target landmark based on how many identical landmarks they have already passed. Only one previous study tested the ability of a non-human primate to respond selectively to a particular ordinal position in a sequence. Using the Wisconsin General Test Apparatus, Ruby trained a single rhesus monkey to select the third block from the left in a formboard from three, four, five, six, or seven identical blocks in a row (Ruby, 1984). However, in that study the food reward was always placed in the hole under the correct block, leaving open the possibility that the monkey used odor cues. Spacing between the blocks was also held constant throughout the experiment, so the monkey may have relied on spatial position rather than ordinal position.
We developed a set of touch-screen tasks for rhesus macaques that parallel the experiments Rugani and colleagues conducted with birds (Rugani et al., 2007; 2010; 2011). By using a touch-screen, we avoided experimenter cuing and odor cuing, and gained precise control over the appearance and spatial placement of stimuli. First we trained monkeys to select the fourth item from the bottom in a vertical array of five identical items presented on a touch-screen. We then tested their ability to identify the fourth position over changes in the appearance, location, and spacing of the stimuli. Next we rotated the array ninety degrees into a horizontal line to assess whether monkeys map number to space in a preferred direction. If monkeys do not have a spatially oriented mental number line, they should respond to the fourth position from the left and fourth position from the right with equal likelihood. If macaques do have a spatially oriented mental number line, they should preferentially select the fourth position from the left, suggesting a left-to-right orientation, or the fourth position from the right, suggesting a right-to-left orientation, but not both.
2. Methods
2.1 Subjects
Four adult male rhesus macaques served as subjects (Macaca mulatta, mean age = 9.8 years, range = 7-15 years). Monkeys were housed singly (n=3) or in pairs (n=1) in a vivarium, and those housed in pairs were separated for testing. All animals had participated in previous touch-screen tasks unrelated to the present study. Fresh fruit and Purina monkey chow were provided daily. The monkeys’ water consumption was restricted for unrelated experiments.
2.2 Apparatus
A 15-inch touch-sensitive computer monitor (Elo TouchSystems, Menlo Park, CA) and a food pellet reward delivery system (Med Associates, St. Albans, VT) were attached to the front of each macaque's home cage. Stimulus presentation, reward delivery, data collection, and data analysis were performed via custom-written programs in MATLAB (MathWorks, Natick, MA).
2.3 Training
Training sessions consisted of 50 trials and were designed to train the monkeys to respond to the fourth oval from the bottom of a five-oval array presented along the vertical midline of the screen (Figure 1a). Each oval measured 2.4cm wide and 1.4cm high. The bottom-most point of the bottom-most oval was 7cm above the bottom of the screen, and there were 2.2cm between oval centers. Each trial required initiation by touching a red rectangle presented in the bottom-center of the screen. The placement of this “start” stimulus was chosen to anchor monkeys to the bottom of the screen so that they would likely perceive the target oval as the fourth from bottom rather than second from top.
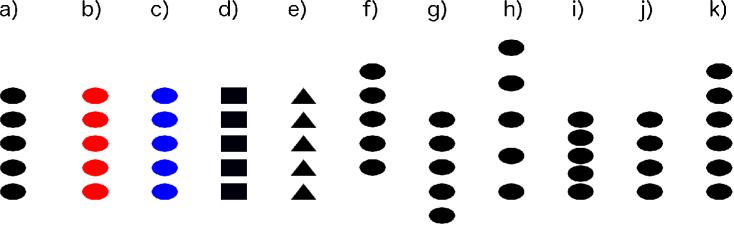
Figure 1.
Stimuli presented during ordinal position testing. a) Final phase of training, and standard trials during testing. Subjects were rewarded for selecting the fourth position from the bottom (second from the top). b) Red, c) Blue, d) Rectangle, e) Triangle, f) Up, g)Down, h) Sparse, i) Dense, j) Four, and k) Six probe trials, in which subjects were nondifferentially rewarded.
In the first phase the target oval (fourth from bottom) was bright green with three horizontal white stripes and in subsequent phases it became increasingly darker until it was solid black and matched the other ovals. In the first phase of training incorrect responses to other targets were recorded but did not end the trial and each trial continued until the monkey touched the target oval. In subsequent phases incorrect responses ended the trial. A touch was registered for a particular shape if it fell within the (invisible) rectangle bounding the top, bottom, left, and right border of that shape. Correct responses elicited a 1-2 second green screen, a pleasant auditory signal, and the delivery of a miniature M&M or Reese's Pieces candy. Incorrect responses elicited a blue screen presented for 2-4 seconds, an unpleasant auditory stimulus, and no food reward.
A performance criterion of 80% was required to advance from the first to the second phase of training. The performance criterion for advancement was then decreased because as training phases progressed, the target oval became less distinguishable from the surrounding ovals and trials became more difficult. The criterion for advancing from the second and third phases was 70%, and from the fourth and fifth phases 60%, accuracy in a single complete session. Once monkeys reached the final (sixth) training phase all five shapes were solid black ovals (Figure 1a). The criterion for advancing to testing was attainment of 50% accuracy during each of two consecutive sessions. Note that throughout all phases chance performance was 20%.
2.4 Ordinal Position Testing
Five test conditions were designed to assess the generality of the ordinal rule that the monkeys had learned. In each condition, two types of probe trials were intermixed with standard trials. The standard trials were identical to phase 6 training trials and were differentially reinforced (Figure 1a). The probe trials were nondifferentially positively reinforced: that is, whichever ordinal position the subject selected, the screen turned green, a pleasant sound was played, and a candy was delivered. Each test session began with a string of at least three standard trials; otherwise the standard and probe trials were randomly intermixed. Sessions consisted of 80 trials total: 48 standard trials, 16 of one probe type, and 16 of another probe type.
Two of the five conditions were designed to assess whether the rule the monkeys learned would transfer to physically distinct elements. In the ‘Color’ condition all of the stimuli were either red (‘red’ probe trials, Figure 1b) or blue (‘blue’ probe trials, Figure 1c), but remained oval-shaped and in the same location and size as standard trials. In the ‘Shape’ condition all of the stimuli were either rectangles (‘rectangle’ probe trials, Figure 1d) or triangles (‘triangle’ probe trials, Figure 1e), but remained black and in the same location and size as standard trials.
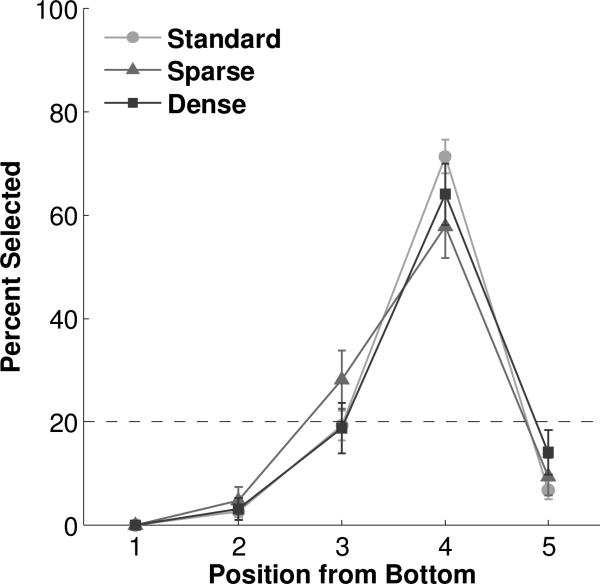
Two of the five conditions were designed to distinguish whether the monkeys had learned the ordinal or physical position of the target oval. In the ‘Shift’ condition the array of five black ovals was shifted up (‘up’ probe trials, Figure 1f) or down (‘down’ probe trials, Figure 1g) on the screen by 2.2cm with respect to standard trials such that the third or fifth oval, respectively, was in the same physical position as the target (fourth) oval on standard trials. The size, shape, color, and spacing of the elements within the array were identical to standard trials. In the ‘Spaced’ condition the first oval at the bottom of the array was in the same position as in standard trials, but spacing among the five ovals was increased to 3.3cm (‘sparse’ probe trials, Figure 1h) or decreased to 1.65cm (‘dense’ probe trials, Figure 1i) between centers of adjacent stimuli such that the third or fifth oval was in the same physical position as the target fourth oval on standard trials, where distance between centers of adjacent stimuli was 2.2cm. The size, shape, and color of stimuli within the array were identical to standard trials.
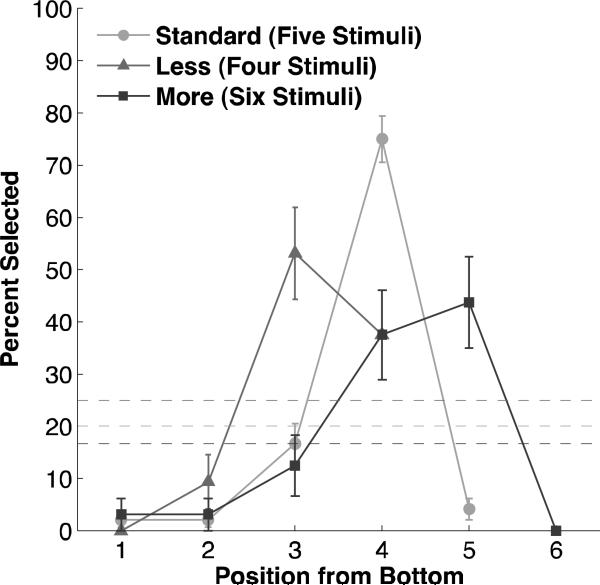
A final condition tested whether the monkeys were anchoring to the bottom or top of the array. In the ‘Length’ condition the stimulus array consisted of four (‘four’ probe trials, Figure 1j) or six (‘six’ probe trials, Figure 1k) ovals rather than five, but the size, shape, color, and spacing of stimuli within the array, as well as the distance from the bottom of the screen to the bottom of the array, were identical to standard trials.
Two of the monkeys were tested with four sessions on each of the first four conditions in a blocked fashion (they were not tested on the Length condition because that condition was added after they had completed the study). Given that we were most interested in performance during the first session of each condition, and performance had remained stable in each condition over the four sessions, the remaining two monkeys were tested with a single session on each of the five conditions. The order of conditions was randomized and different for each monkey.
2.5 Number-Space Mapping Testing
Each trial was initiated when the subject touched a red rectangle at the bottom- center of the screen. Standard trials were identical to the standard trials in ordinal position testing except that elements were circles rather than ovals so that they would appear the same whether the array was horizontal or vertical (Figure 2). Subjects received retraining sessions between the two test phases to familiarize them with the circle stimuli. Each retraining session consisted of 50 trials in which five black circles (1.75cm diameter, 3.0cm between adjacent centers) were presented along the screen's vertical midline (the bottom of the bottom-most circle was 4cm above the lower screen edge; Figure 2a). Subjects received at least two sessions of retraining and proceeded from retraining to testing when they completed either one session with at least 80% correct (n=3), or five consecutive sessions with over 60% correct (n=1).
Figure 2.
Stimuli presented during Number-Space Mapping Testing. a) Standard and retraining trials, in which subjects were rewarded for selecting the fourth position from the bottom (second from the top). b) Horizontal probe trials, in which subjects were nondifferentially rewarded. If subjects chose the fourth position from the left (second from the right), this would suggest a left-to-right spatial mapping of number; if they chose the fourth position from the right (second from the left), this would suggest a right-to-left spatial mapping of number.
As in ordinal testing, during Number-Space Mapping testing positively reinforced probe trials were randomly intermixed with differentially reinforced standard trials. Standard trials were identical to retraining trials: five circles appeared along the vertical midline, and subjects were rewarded for touching the fourth from the bottom (Figure 4a). In probe trials, the array was rotated 90° around its center, to display a horizontal line of five circles with size and spacing identical to standard trials (Figure 4b). Each session consisted of 48 vertical standard trials and 24 horizontal probe trials. Because we were interested in monkeys’ spontaneous behavior in the horizontal probes before they began building up a reinforcement history (i.e. before they discovered that touching any position in these trials would yield the same reward), only the first half of trials in each subject's first Number-Space Mapping testing session were included for analysis.
Figure 4.
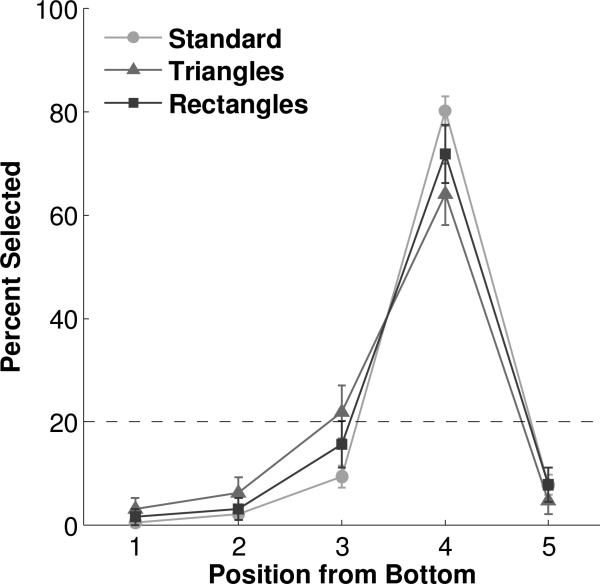
Performance in the Shape condition. Dashed line represents chance expectation. Error bars represent standard error of the mean.
2.6 Hand Preference Assessment
It is essential to rule out an alternative explanation for the monkeys’ preference to choose the circle second from the right. Monkeys may have had a side-bias in responding to the touch screen, perhaps due to preferential use of one hand or the other. Such a scenario is unlikely, since rhesus macaques as a population do not exhibit “handedness,” though they and other Old World monkeys may have a slight left-hand preference (McGrew & Marchant, 1997; Papademetriou et al., 2005). Nonetheless the possibility of a hand or side preference was tested in these subjects in the following three ways: 1) ‘Hand Used’: The hand each subject used for touching the screen during the experiments described above was recorded on one training session and subsequently observed throughout the study to monitor for changes. 2) ‘Basic Touch Screen Response Speed’: Monkeys B, C, and O participated in an additional touch screen task, where each trial consisted of a single black circle varying in size (1.5- 3.5cm radius) and appearing at a random location on a white background. Monkey Y was no longer available for testing at the time of this assay. The subject had to touch the circle to earn a candy reward and move on to the next trial. Subjects completed 50 trials each, and their response latencies (time from black circle appearing to the subject touching it) were recorded. Trials were coded as to whether the stimulus fell on the left or right half of the screen. For each of the two categories we coded whether the left or right hand was used to respond and mean response time. 3) ‘Fruit-in-Cup Test’: Monkeys B, C, and O participated in a cup- and fruit-grabbing task, in which chunks of dried fruit were placed at the bottom of a small paper cup. Monkey Y was no longer available for testing at the time of this assay. The inside of the cup was shown to each monkey while he was in one part of his enclosure, and then the cup was placed in another part of the monkey's enclosure. The monkey was given access to this second area of his enclosure, and the hand he used to grab the cup as well as the hand he used to reach inside the cup, remove the fruit and eat the fruit were recorded. Each subject completed five trials (i.e. five cups).
3. Results
3.1 Ordinal Position Testing
On average subjects required 16 training sessions (range = 13 to 19) before moving to the test sessions. During training and every testing condition, subjects always completed the full number of trials constituting each session. One-tailed exact binomial tests were used to determine whether each position was selected above the 20% chance expectation. Here we report data on all subjects together; individual subjects’ accuracy and binomial test p-values are shown in Supplementary Tables S1-S14. Subjects selected the correct position on standard trials more than expected by chance from the first day of testing (70.31%, binomial p<0.0001). This performance was maintained throughout testing (73.50%, binomial p<0.0001). No other position was selected with frequencies above chance expectations (first: 0.81%, second: 2.66%, third: 12.85%, fifth: 9.49%; all binomial p’s>0.9). Chi-square tests with one degree of freedom confirmed that the fourth position was chosen with a different frequency than any other position (first: χ2=977.5, p<0.0001; second: χ2=919.3, p<0.0001; third: χ2=647.7, p<0.0001; fifth: χ2=729.0, p<0.0001).
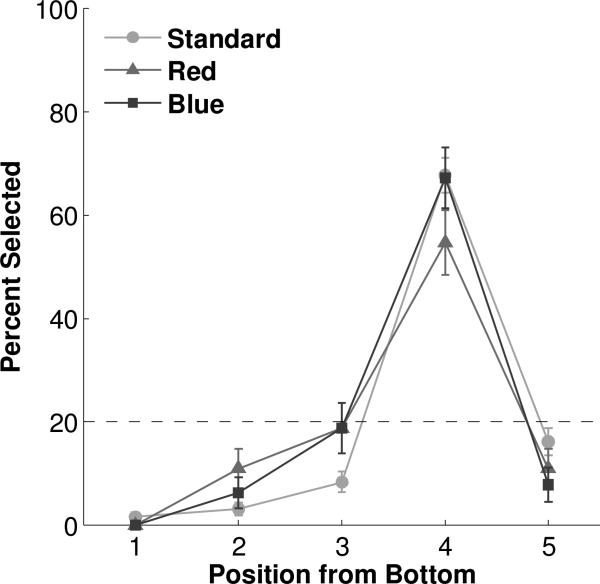
Responding to the fourth ordinal position from the bottom was robust to changes in the appearance of the elements in the array. During nondifferentially reinforced probe trials, subjects continued to choose the fourth position from the bottom in both the Color (Figure 3, Tables S3 & S4) and Shape (Figure 4, Tables S5 & S6) conditions, when the arrays were composed of red ovals (54.69%, binomial p<0.0001), blue ovals (67.19%, binomial p<0.0001), black rectangles (71.88%, binomial p<0.0001), or black triangles (64.06%, binomial p<0.0001). None of the other positions exceeded chance level in any of the Color or Shape probe conditions (all binomial p's>0.2). Chi-square tests with one degree of freedom confirmed that the fourth position was chosen at a significantly different level than any other position in each probe condition (all χ2’s>23.2, all p's<0.0001). All individual monkeys followed this pattern, except for Monkey B who selected the third non-significantly more than the fourth position in triangle probes of the Shape condition (χ2=0.533, p=0.47).
Figure 3.
Performance in the Color condition. Dashed line represents chance expectation. Error bars represent standard error of the mean.
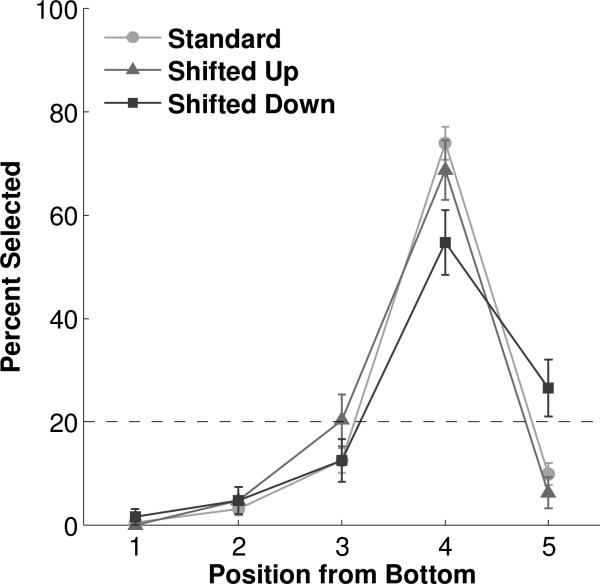
Additional transfer conditions revealed that subjects based their decisions upon the ordinal, rather than physical, position of the elements in the array. In the Shift (Figure 5, Tables S7 & S8) and Spaced (Figure 6, Tables S9 & S10) conditions, the fourth oval moved to a different location on the screen and a different ordinal position occupied the physical location where the fourth oval appeared in standard trials. Subjects continued to select the fourth position, whether stimuli were shifted up (68.75%, binomial p<0.0001) or down (54.69%, binomial p<0.0001), or spaced more sparsely (57.81%, binomial p<0.0001) or densely (64.06%, binomial p<0.0001) as compared with standard trials. The only other positions to approach statistical significance in any of the Shift or Spaced probe conditions were the fifth position in Shifted Down trials (26.56%, binomial p=0.075) and the third position in Sparse trials (28.12%, binomial p=0.042). Even so, in these and all other Shift and Spaced probe conditions, chi-square tests with one degree of freedom confirmed that the fourth position was chosen at a significantly different level than any other position (all χ 2’s>10.4, all p's<0.01).
Figure 5.
Performance in the Shift condition. Dashed line represents chance expectation. Error bars represent standard error of the mean.
Figure 6.
Performance in the Spaced condition. Dashed line represents chance expectation. Error bars represent standard error of the mean.
All individual monkeys followed this pattern, except that Monkey B chose the fifth (75.00%, binomial p<0.0001) and not fourth (18.75%, binomial p=0.402) position above chance level in Shifted Down trials. A few individual monkeys selected the third position above chance expectation, but not more than the fourth position, in certain conditions: during Dense trials for Monkey Y (50.00%, binomial p=0.0015; compared to the fourth position, χ2= 0.126, p=0.723); Sparse (50.00%, binomial p=0.0015; compared to the fourth position, χ2= 0.126, p=0.723), Shifted Up (37.50%, binomial p=0.0267; compared to the fourth position, χ2= 0.130, p=0.719), and Shifted Down (37.50%, binomial p = 0.0267; compared to the fourth position, χ2= 0.508, p=0.476) trials for Monkey C; and Sparse trials for Monkey O (37.500%, binomial p = 0.0267; compared to the fourth position, χ2=1.129, p=0.288). The tendency to select the third position above chance level in the Dense and Shifted Down trials, as well as in the Triangle trials described for Monkey B above, may have resulted from the monkey accidentally touching the screen too early as his hand traveled up from the “Start” response. In other conditions, subjects’ behavior could have resulted from spatial coding. Monkey B chose the fifth position in Shifted Down trials, Monkeys C and O chose the third (but not as much as the fourth) position in Sparse trials, and Monkey C chose the third (but not as much as the fourth) position in Shifted Up trials. These aberrations suggest that subjects may have encoded the precise physical location of the target oval during Standard trials, but that this geometric representation weakly conflicted with the ordinal numeric representation only in certain conditions for certain monkeys.
To examine whether monkeys anchored their responses from the bottom or the top of the array, we conducted the Length condition probe trials, where the total number of ovals in the array was reduced to four or increased to six. Results indicated that subjects chose both the fourth position from the bottom and the second position from the top more than would be expected by chance (Figure 7, Tables S11 & S12). When there were four ovals (chance = 25%), subjects chose the second position from the top on 53.12% of trials (binomial p<0.0001) and the fourth position from the bottom on 37.50% of trials (binomial p=0.038). A chi-square test indicated that preference for the fourth from the bottom and the second from the top did not differ significantly (χ2=1.58, p=0.21). When there were six total ovals (chance = 16.67%), subjects chose the second position from the top on 43.75% of trials (binomial p=0.0001) and the fourth position from the bottom on 37.50% of trials (binomial p=0.0011). A chi-square test again indicated that preference for the fourth from the bottom and the second from the top did not differ significantly (χ2=0.26, p=0.61). Thus in both Length probe conditions subjects were equally likely to choose the fourth from the bottom and the second from the top.
Figure 7.
Performance in the Length condition. Dashed lines represent chance expectation for each trial type. Error bars represent standard error of the mean.
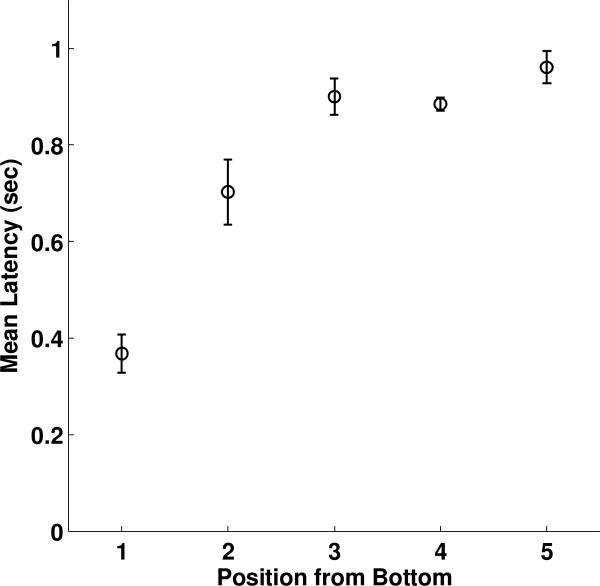
An examination of response latencies on standard trials, however, suggests that subjects typically anchored their standard trial decisions from the bottom of the array. Latency was measured as the elapsed time between the stimuli appearing (following the subject touching the “start” rectangle) and the subject touching one of the stimuli in the array. Mean latencies increased with position selected as follows (standard error in parentheses): selected position one, 0.37 sec (0.04); two, 0.70 sec (0.07); three, 0.90sec (0.04); four, 0.88 sec (0.01); five, 0.96sec (0.03) (Figure 8). A one-way ANOVA revealed a significant effect of stimulus position on latency (F(4) = 6.82, p<0.0001). A linear regression on latency by stimulus position revealed a positive linear trend (β = 0.071, p<0.001). The location of the “start” rectangle at the bottom-center of the screen was selected specifically to anchor subjects to this position, and the pattern of response times confirms that this anchoring was successful. Although this anchoring was physical and we cannot rule out the possibility that monkeys may have encoded the sequence from top to bottom while simultaneously moving through space from bottom to top, it seems likely that subjects visually scanned the array from bottom to top and thus ordered items from bottom to top. Importantly, our main finding does not hinge on which interpretation is correct.
Figure 8.
Mean response latency to each position during Standard trials of ordinal position testing.
3.2 Number-Space Mapping Testing
Subjects required 2.75 sessions on average to meet retraining criterion (range = 2-5 sessions). During testing, all subjects maintained their high performance on standard vertical trials, selecting the fourth position from the bottom on 81.25% of trials (Table S13), which was well above the 20% chance expectation (binomial p<0.0001). No other position was selected with above chance levels (all binomial p's>0.99).
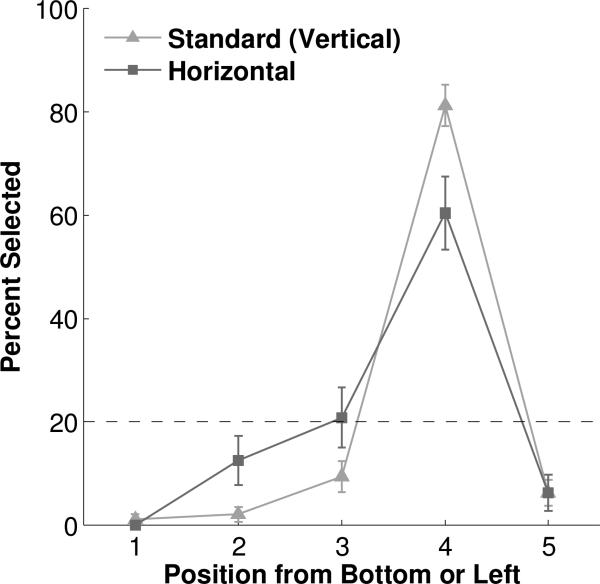
On average subjects selected the fourth position from the left (i.e. second from the right) on 60.42% of horizontal probe trials, substantially above the 20% chance expectation (binomial p<0.0001) (Figure 9, Table S14). No other position was chosen above chance expectation (all binomial p's>0.3). Notably, the fourth position from the right (i.e. second from the left) was only selected on 12.50% of trials. The monkeys’ preference for the fourth position from the left suggests that macaques map number onto space in a left-to-right orientation.
Figure 9.
Performance in Number-Space Mapping Testing. Dashed line represents chance expectation. Error bars represent standard error of the mean.
Individually, three of the four subjects followed this pattern of choosing the fourth position from the left – and no other position – above chance level. The remaining subject, Monkey C, chose the third from the left as well as the fourth from the left above chance (third: 50.00%, binomial p<0.01; fourth: 50.00%, binomial p<0.01). Although this subject deviated somewhat from the common pattern, he did not behave in a manner consistent with a right-to-left oriented mental number line, as he never chose the fourth position from the right. Instead it seems that rotating the array more generally disoriented him and resulted in less precise responding.
One alternative explanation for our finding that monkeys chose the fourth position from the left is that the monkeys may have an inherent side bias. That is, perhaps some aspect of the experimental set-up or the monkeys’ predispositions influenced them to touch stimuli closer to the right-hand side of the screen. We believe that this is unlikely because this would have resulted in a preference for the spot furthest to the right (i.e., the fifth from the left); however, subjects selected that position on only 15.62% of trials on average, which did not differ from chance expectations (binomial p>0.8). Nonetheless we assessed monkeys’ hand and side preferences in three different ways, described in Methods Section 2.6.
Half of the subjects (n=2, Monkeys B & C) exclusively used their right hands and half (n=2, Monkeys O & Y) exclusively used their left hands during both the training and testing phases of the experiment. When tested with the basic touch-screen response assessment we found that all three monkeys that we were able to test were equally fast at responding to the left and right halves of the screen (two-tailed t-test, t145 = 0.791, p = 0.430 for all monkeys together; Monkey B: t47 = 0.356, p = 0.723; Monkey C: t47 = 0.949, p = 0.348; Monkey O: t47 = 0.652, p = 0.518). Finally we used a fruit cup test modeled after prior studies (e.g. the TUBE task: Hopkins et al., 2003; Hopkins, 2013). Such a task can tease out whether one hand is specialized for gross support (picking up the cup) while the other is specialized for fine manipulations like extracting the treat and moving it toward the mouth. The three subjects tested here each showed a different pattern of behavior in this task. Across the five trials, one subject (Monkey B) typically held the cup with his left hand and reached in with his right; another (Monkey O) typically held the cup with his right hand and reached in with his left; while the other (Monkey C) held the cup with his right hand on half the trials but his left on the other half, switching between the two during one trial, and used the opposite hand to reach into the cup. Thus as a population, our subjects did not show a preference to use a particular hand for gross support or fine manipulation.
Together these three assessments indicate that monkeys in this study did not have an overall hand preference or a predisposition to respond to stimuli on the right side of the screen. These results concord with previous findings that while individual animals may prefer to use the left or right hand for particular tasks, at the population level rhesus macaques do not exhibit a strong hand preference (McGrew & Marchant, 1997; Papademetriou et al., 2005). Hence our findings in Number-Space Mapping testing do not reflect a simple side bias.
4. Discussion
We investigated whether rhesus monkeys, like humans, map number to space. To test this question, we first trained monkeys to select a specific ordinal position in a vertical array of homogeneous items. All four monkeys rapidly learned to identify the fourth oval from the bottom of a five-oval vertical array. They maintained high performance when the color or shape of the stimuli was altered, indicating that their responses did not depend upon the particular appearance of the array elements. Moreover, they continued to select the fourth item even when its physical location was changed. Their performance was robust to variations in inter-element spacing and to position of the array on the screen, showing that they were not relying upon distance from the end of the array or from the edge of the screen as a cue.
Our main finding was that on probe trials when the stimulus array was rotated ninety degrees to a horizontal line, monkeys preferentially selected the fourth position from the left. Such a result could emerge from three possible interpretations: 1) monkeys learned to respond to the fourth position from the bottom, and number is mapped onto space in such a way that biases them to orient from the left rather than the right; 2) monkeys learned to respond to the second position from the top, and number is mapped onto space in such a way that biases them to orient from the right rather than the left; 3) some monkeys follow the first pattern and others follow the second pattern. All three of these interpretations suggest a SNARC-like effect is present in monkeys. The experiment was designed to anchor monkeys’ responses to the bottom of the screen, so the first interpretation seems most likely, but the second interpretation remains possible. The third interpretation seems least parsimonious, as it would require that certain subjects anchored to the bottom of the array during training, and then precisely those subjects exhibited a left-to-right spatial mapping of number, while other subjects anchored to the top of the array during training, and then precisely those subjects exhibited a right-to-left spatial mapping of number. However, even in this unlikely scenario, rhesus macaques could be said to exhibit a SNARC-like effect with individual differences regarding the orientation of the number line. Thus the finding that monkeys consistently selected the same ordinal position in the rotated five-element array – whether this position is considered the fourth from the left or second from the right – indicates that monkeys map number to space.
We ruled out an alternative explanation of a more general side bias in our participants. Monkeys in general do not exhibit a strong hand preference at the population level (McGrew & Marchant, 1997; Papademetriou et al., 2005). Moreover, we found no evidence for a consistent handedness preference or side bias in our monkeys (see Results Section 2.3). There are unfortunately few prior studies of visual scene scanning preferences in monkeys, but those that exist have not revealed any consistent left-to-right or right-to-left viewing tendency (Fitch & Braccini, 2013). Thus it is unlikely that our results stem from simple side biases. Additionally, the prior task experience of the monkeys in this study could not have set up the spatial-numerical association observed here. All four subjects had participated in several previous experiments, but only two of these involved numerical judgments. In one study, Monkeys B and Y were presented with two stimulus arrays at the left and right of the screen, and were rewarded for touching the array with a greater number of dots (Jones et al., in press). In another unpublished study, Monkey B was presented with two stimulus arrays at the left and right or top and bottom of the screen, and was rewarded for making an eye movement toward the array with a greater number of dots. In both of these experiments, the location of the larger array was perfectly counterbalanced, so this task should not have caused subjects to associate either side with lesser or greater numerosities or with a higher reward probability. The rewarded location was similarly counterbalanced in all other non-numerical eye movement, joystick, and touch-screen experiments in which these four monkeys were previously tested. Therefore our results cannot be explained by subjects’ task history.
Our results complement those of Rugani et al. (2007, 2010, 2011) in birds. Nutcrackers and domestic chicks approached the fourth (or sixth, respectively) item from the left in a horizontally-oriented row of sixteen items following training to select the fourth (or sixth, respectively) item from the starting point in a sagitally-oriented line of sixteen items (Rugani et al., 2010). It is notable that we found a similar pattern in monkeys despite differences in the experimental paradigm: our subjects selected shapes on a touch screen while sitting in their home cages, whereas the birds walked through space; and for our subjects, the fourth item from the left actually fell on the right half of the screen, whereas the fourth (or sixth) item from the left was in the left half of space for the birds. The presence of the space-number mapping in all three species even with these experimental differences raises the question of whether similar neural mechanisms may underlie the effect in birds and monkeys – and, in turn, humans. Although birds’ visual systems and brains are generally far more lateralized than those of primates (Larsson, 2013; Rogers et al., 2013), it may be that some of the hemispheric specialization for representing numeric and spatial information posited to produce the effect in chicks (Rugani et al., 2011) persists in primates. Future studies in monkeys could investigate this possibility.
Several explanations have been proposed for the SNARC effect in humans, some of which emphasize specific cultural experiences. The verbal-spatial account proposes that particular words are associated with each other - “small” with “left” and “large” with “right” – and so the concept of “small” activates the concept of “left” and facilitates leftward responses for small values (Gevers et al., 2010). Such a mechanism requires use of language, which our monkeys do not possess. Similarly, reading or writing direction (Shaki et al., 2009; Shaki & Fischer, 2008; Zebian, 2005) cannot contribute to a space-number mapping in monkeys. Another theory is that finger counting gives rise to spatial-numerical associations: individuals who begin counting on their left hand come to associate smaller numbers with the left side of space (Fischer & Brugger, 2011). However, our monkeys have never been taught to count on their hands and more generally monkeys have not shown evidence of spontaneous finger enumeration. While verbal associations and finger counting or reading habits appear to modulate the SNARC effect in humans, our finding in monkeys suggests that none of these is the primary driver. Instead explanations that do not require specific lifetime experiences are more likely, including the original idea of a spatial coding of number that exists in long-term memory (Dehaene et al., 1993), and the more recent working memory account which holds that a given ordinal position in working memory is associated with a particular region of space (van Dijck & Fias, 2011). Additional investigations are needed to determine which of these latter mechanisms underlies the SNARC-like effect in monkeys.
In conclusion, our novel demonstration of a space-number mapping in a non-human primate suggests that the interplay between these two types of magnitudes in human cognition has a biological basis. Evidence that cultural factors can mediate the SNARC effect (Fischer & Brugger, 2011; Gevers et al., 2010; Shaki et al., 2009; Shaki & Fischer, 2008; Zebian, 2005) has raised the possibility that the interaction between number and space could be entirely learned. However, we have shown that monkeys – who do not read, write, or count on their hands and have no experience with items like rulers – also seem to associate number with space. Our results, along with those of de Hevia and Spelke (2010) in human infants and Rugani et al. (2007, 2010, 2011) in birds, support the view that the predisposition to map number onto space is not a cultural invention. Instead this tendency has deep developmental and evolutionary roots.
Supplementary Material
Highlights.
Monkeys represent ordinal information about identical objects.
Monkeys map number onto space.
The space-number mapping has evolutionary, rather than purely cultural, roots.
Acknowledgements
We thank Monica Carlson and all members of Elizabeth Brannon's and Michael Platt’s labs for assistance with data collection and helpful discussions of this study. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. 1106401 to CBD, and NIH Grant 5R01-EY-019303-03 and the James McDonnell Scholar Award to EMB.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Agrillo C, Piffer L, Bisazza A. Chapouthier G, editor. Large Number Discrimination by Mosquitofish. PLoS One. 2010;5(12):e15232. doi: 10.1371/journal.pone.0015232. doi:10.1371/journal.pone.0015232.g006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aïn SA, Giret N, Grand M, Kreutzer M, Bovet D. The discrimination of discrete and continuous amounts in African grey parrots (Psittacus erithacus). Animal Cognition. 2008;12(1):145–154. doi: 10.1007/s10071-008-0178-8. doi:10.1007/s10071-008-0178-8. [DOI] [PubMed] [Google Scholar]
- Beran MJ. Monkeys (Macaca mulatta and Cebus apella) track, enumerate, and compare multiple sets of moving items. Journal of Experimental Psychology: Animal Behavior Processes. 2008;34(1):63–74. doi: 10.1037/0097-7403.34.1.63. doi:10.1037/0097-7403.34.1.63. [DOI] [PubMed] [Google Scholar]
- Bogale BA, Kamata N, Mioko K, Sugita S. Quantity discrimination in jungle crows, Corvus macrorhynchos. Animal Behaviour. 2011;82(4):635–641. doi:10.1016/j.anbehav.2011.05.025. [Google Scholar]
- Brannon E, Terrace H. Ordering of the numerosities 1 to 9 by monkeys. Science. 1998;282(5389):746. doi: 10.1126/science.282.5389.746. [DOI] [PubMed] [Google Scholar]
- Bueti D, Walsh V. The parietal cortex and the representation of time, space, number and other magnitudes. Philosophical Transactions of the Royal Society B: Biological Sciences. 2009;364(1525):1831–1840. doi: 10.1098/rstb.2009.0028. doi:10.1098/rstb.2009.0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butterworth MDB. A Dissociation of Number Meanings. Cognitive Neuropsychology. 1997;14(4):613–636. doi:10.1080/026432997381501. [Google Scholar]
- Castronovo J, Seron X. Semantic numerical representation in blind subjects: The role of vision in the spatial format of the mental number line. The Quarterly Journal of Experimental Psychology. 2007;60(1):101–119. doi: 10.1080/17470210600598635. doi:10.1080/17470210600598635. [DOI] [PubMed] [Google Scholar]
- Chen S, Swartz KB, Terrace HS. Knowledge of the ordinal position of list items in rhesus monkeys. Psychological Science. 1997;8(2):80–86. [Google Scholar]
- Dacke M. Evidence for counting in insects. Animal Cognition. 2008 doi: 10.1007/s10071-008-0159-y. [DOI] [PubMed] [Google Scholar]
- Davis H, Bradford SA. Counting behavior by rats in a simulated natural environment. Ethology. 1986;73(4):265–280. [Google Scholar]
- de Hevia MD, Spelke ES. Number-Space Mapping in Human Infants. Psychological Science. 2010;21(5):653–660. doi: 10.1177/0956797610366091. doi:10.1177/0956797610366091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S, Bossini S, Giraux P. The mental representation of parity and number magnitude. Journal of Experimental Psychology General. 1993;122(3):371. [Google Scholar]
- Fias W, Fischer MH. Spatial representation of number. In: Campbell J, editor. Handbook of mathematical cognition. Pschology Press; 2005. pp. 43–54. [Google Scholar]
- Fitch WT, Braccini SN. Primate laterality and the biology and evolution of human handedness: a review and synthesis. Annals of the New York Academy of Sciences. 2013;1288:70–85. doi: 10.1111/nyas.12071. [DOI] [PubMed] [Google Scholar]
- Fischer MH, Brugger P. When digits help digits: Spatial-numerical associations point to finger counting as prime example of embodied cognition. Frontiers in Psychology. 2010;2:1–7. doi: 10.3389/fpsyg.2011.00260. article 260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin MS, Jonides J, Smith EE. Processing of order information for numbers and months. Memory & Cognition. 2009;37(5):644–654. doi: 10.3758/MC.37.5.644. doi:10.3758/MC.37.5.644. [DOI] [PubMed] [Google Scholar]
- Gevers W, Santens S, Dhooge E, Chen Q, Van den Bossche L, Fias W, Verguts T. Verbal-spatial and visuospatial coding of number-space interactions. Journal of Experimental Psychology: General. 2010;139(1):180–190. doi: 10.1037/a0017688. [DOI] [PubMed] [Google Scholar]
- Gobel SM, Shaki S, Fischer MH. The Cultural Number Line: A Review of Cultural and Linguistic Influences on the Development of Number Processing. Journal of Cross-Cultural Psychology. 2011;42(4):543–565. doi:10.1177/0022022111406251. [Google Scholar]
- Gómez-Laplaza LM, Gerlai R. Quantification abilities in angelfish (Pterophyllum scalare): the influence of continuous variables. Animal Cognition. 2012 doi: 10.1007/s10071-012-0578-7. doi:10.1007/s10071-012-0578-7. [DOI] [PubMed] [Google Scholar]
- Hanus D, Call J. Discrete quantity judgments in the great apes (Pan paniscus, Pan troglodytes, Gorilla gorilla, Pongo pygmaeus): The effect of presenting whole sets versus item-by-item. Journal of Comparative Psychology. 2007;121(3):241–249. doi: 10.1037/0735-7036.121.3.241. doi:10.1037/0735-7036.121.3.241. [DOI] [PubMed] [Google Scholar]
- Hopkins WD. Comparing human and nonhuman primate handedness: Challenges and a modest proposal for consensus. Developmental Psychobiology. 2013;55(6):621–636. doi: 10.1002/dev.21139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopkins WD, Stoinski TS, Lukas KE, Ross SR, Wesley MJ. Comparative assessment of handedness for a coordinated bimanual task in chimpanzees (Pan troglodytes), gorillas (Gorilla gorilla), and orangutans (Pongo pygmaeus). Journal of Comparative Psychology. 2003;117(3):302–308. doi: 10.1037/0735-7036.117.3.302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubbard E, Piazza M, Pinel P, Dehaene S. Interactions between number and space in parietal cortex. Nature Reviews Neuroscience. 2005;6(6):435–448. doi: 10.1038/nrn1684. [DOI] [PubMed] [Google Scholar]
- Jaakkola K, Fellner W, Erb L, Rodriguez M, Guarino E. Understanding of the concept of numerically “less” by bottlenose dolphins (Tursiops truncatus). Journal of Comparative Psychology. 2005;119(3):296–303. doi: 10.1037/0735-7036.119.3.296. doi:10.1037/0735-7036.119.3.296. [DOI] [PubMed] [Google Scholar]
- Jones SM, Pearson J, DeWind NK, Paulsen D, Tenekedjieva AM, Brannon EM. Lemurs and macaques share similar numerical sensitivity. Animal Cognition. doi: 10.1007/s10071-013-0682-3. (in press) doi: 10.1007/s10071-013-0682-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krusche P, Uller C, Dicke U. Quantity discrimination in salamanders. Journal of Experimental Biology. 2010;213(11):1822–1828. doi: 10.1242/jeb.039297. doi:10.1242/jeb.039297. [DOI] [PubMed] [Google Scholar]
- Larsson M. The optic chiasm: a turning point in the evolution of eye/hand coordination. Frontiers in Zoology. 2013;10(41) doi: 10.1186/1742-9994-10-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGrew WC, Marchant LF. On the other hand: Current issues in and meta-analysis of the behavioral laterality of hand function in nonhuman primates. Yearbook of Physical Anthropology. 1997;40:201–232. [Google Scholar]
- Opfer JE, Furlong EE. How numbers bias preschoolers' spatial search. Journal of Cross-Cultural Psychology. 2011;42(4):682–695. [Google Scholar]
- Opfer JE, Thompson CA, Furlong EE. Early development of spatial-numerica associations: evidence from spatial and quantitative performance of preschoolers. Developmental Science. 2010;13(5):761–771. doi: 10.1111/j.1467-7687.2009.00934.x. [DOI] [PubMed] [Google Scholar]
- Papademetriou E, Sheu CF, Michel GF. A meta-analysis of primate hand preferences, particularly for reaching. Journal of Comparative Psychology. 2005;119(1):33–48. doi: 10.1037/0735-7036.119.1.33. [DOI] [PubMed] [Google Scholar]
- Piffer L, Agrillo C, Hyde DC. Small and large number discrimination in guppies. Animal Cognition. 2011;15(2):215–221. doi: 10.1007/s10071-011-0447-9. doi:10.1007/s10071-011-0447-9. [DOI] [PubMed] [Google Scholar]
- Roberts WA. Distance and magnitude effects in sequential number discrimination by pigeons. Journal of Experimental Psychology: Animal Behavior Processes. 2010;36(2):206–216. doi: 10.1037/a0017226. doi:10.1037/a0017226. [DOI] [PubMed] [Google Scholar]
- Rogers LJ, Vallortigara G, Andrews RJ. Divided Brains: The Biology and Behaviour of Brain Asymmetries. Cambridge University Press; 2013. [Google Scholar]
- Rubinsten O, Sury D. Processing Ordinality and Quantity: The Case of Developmental Dyscalculia. PLoS One. 2011;6(9):e24079. doi: 10.1371/journal.pone.0024079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruby LM. An Investigation of Number-concept Appreciation in a Rhesus Monkey. Primates. 1984;25(2):236–242. [Google Scholar]
- Rugani R, Kelly D, Szelest I, Regolin L, Vallortigara G. Is it only humans that count from left to right? Biology Letters. 2010;6:290–292. doi: 10.1098/rsbl.2009.0960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rugani R, Regolin L, Vallortigara G. Rudimental numerical competence in 5-day-old domestic chicks (Gallus gallus): Identification of ordinal position. Journal of Experimental Psychology: Animal Behavior Processes. 2007;33(1):21–31. doi: 10.1037/0097-7403.33.1.21. doi:10.1037/0097-7403.33.1.21. [DOI] [PubMed] [Google Scholar]
- Rugani R, Vallortigara G, Vallini B, Regolin L. Asymmetrical number-space mapping in the avian brain. Neurobiology Of Learning And Memory. 2011;95(3):231–238. doi: 10.1016/j.nlm.2010.11.012. doi:10.1016/j.nlm.2010.11.012. [DOI] [PubMed] [Google Scholar]
- Scarf D, Colombo M. Representation of serial order in pigeons (Columba livia). Journal of Experimental Psychology: Animal Behavior Processes. 2010;36(4):423–429. doi: 10.1037/a0020926. doi:10.1037/a0020926. [DOI] [PubMed] [Google Scholar]
- Shaki S, Fischer M. Reading space into numbers-a cross-linguistic comparison of the SNARC effect. Cognition. 2008;108(2):590–599. doi: 10.1016/j.cognition.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Shaki S, Fischer MH, Petrusic WM. Reading habits for both words and numbers contribute to the SNARC effect. Psychonomic Bulletin & Review. 2009;16(2):328–331. doi: 10.3758/PBR.16.2.328. doi:10.3758/PBR.16.2.328. [DOI] [PubMed] [Google Scholar]
- Stancher G, Sovrano VA, Potrich D, Vallortigara G. Discrimination of small quantities by fish (redtail splitfin, Xenotoca eiseni). Animal Cognition. 2013;16(2):307–312. doi: 10.1007/s10071-012-0590-y. [DOI] [PubMed] [Google Scholar]
- Suzuki K, Kobayashi T. Numerical competence in rats (Rattus norvegicus): Davis and Bradford (1986) extended. Journal of Comparative Psychology. 2000;114(1):73–85. doi: 10.1037/0735-7036.114.1.73. doi:10.1037//0735-7036.114.1.73. [DOI] [PubMed] [Google Scholar]
- Tang J, Ward J, Butterworth B. Number forms in the brain. Journal of Cognitive Neuroscience. 2008;20(9):1547–1556. doi: 10.1162/jocn.2008.20120. doi:10.1162/jocn.2008.20120. [DOI] [PubMed] [Google Scholar]
- Terrace H. The simultaneous chain: A new approach to serial learning. Trends in Cognitive Sciences. 2005;9(4):202–210. doi: 10.1016/j.tics.2005.02.003. [DOI] [PubMed] [Google Scholar]
- Terrace HS. The phylogeny and ontogeny of serial memory: List learning by pigeons and monkeys. Psychological Science. 1993;4(3):162–169. [Google Scholar]
- Terrace HS, Chen S, Jaswal V. Recall of three-item sequences by pigeons. Learning & Behavior. 1996;24(2):193–205. [Google Scholar]
- Terrace H, Son L, Brannon E. Serial expertise of rhesus macaques. Psychological Science. 2003;14(1):66. doi: 10.1111/1467-9280.01420. [DOI] [PubMed] [Google Scholar]
- Turconi E, Seron X. Dissociation Between Order and Quantity Meanings in a Patient with Gerstmann Syndrome. Cortex. 2002;38(5):911–914. doi:10.1016/S0010-9452 (08)70069-8. [Google Scholar]
- Turconi E, Campbell J, Seron X. Numerical order and quantity processing in number comparison. Cognition. 2006;98(3):273–285. doi: 10.1016/j.cognition.2004.12.002. [DOI] [PubMed] [Google Scholar]
- Turconi E, Jemel B, Rossion B, Seron X. Electrophysiological evidence for differential processing of numerical quantity and order in humans. Cognitive Brain Research. 2004;21(1):22–38. doi: 10.1016/j.cogbrainres.2004.05.003. [DOI] [PubMed] [Google Scholar]
- Uller C, Lewis J. Horses (Equus caballus) select the greater of two quantities in small numerical contrasts. Animal Cognition. 2009;12(5):733–738. doi: 10.1007/s10071-009-0225-0. doi:10.1007/s10071-009-0225-0. [DOI] [PubMed] [Google Scholar]
- Uller C, Jaeger R, Guidry G. Salamanders (Plethodon cinereus) go for more: rudiments of number in an amphibian. Animal Cognition. 2003 doi: 10.1007/s10071-003-0167-x. [DOI] [PubMed] [Google Scholar]
- van Dijck J-P, Fias W. A working memory account for spatial-numerical associations. Cognition. 2011;119(1):114–119. doi: 10.1016/j.cognition.2010.12.013. [DOI] [PubMed] [Google Scholar]
- Vonk J, Beran MJ. Bears ‘count’ too: quantity estimation and comparison in black bears, Ursus americanus. Animal Behaviour. 2012:1–8. doi: 10.1016/j.anbehav.2012.05.001. doi:10.1016/j.anbehav.2012.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward C, Smuts BB. Quantity-based judgments in the domestic dog (Canis lupus familiaris). Animal Cognition. 2007;10(1):71–80. doi: 10.1007/s10071-006-0042-7. doi:10.1007/s10071-006-0042-7. [DOI] [PubMed] [Google Scholar]
- Zebian S. Linkages between number concepts, spatial thinking, and directionality of writing: The SNARC effect and the reverse SNARC effect in English and Arabic monoliterates, biliterates, and illiterate Arabic speakers. Journal of Cognition and Culture. 2005;51(2):165–190. [Google Scholar]
- Zorzi M, Di Bono MG, Fias W. Distinct representations of numerical and non numerical order in the human intraparietal sulcus revealed by multivariate pattern recognition. NeuroImage. 2011;56(2):674–680. doi: 10.1016/j.neuroimage.2010.06.035. doi:10.1016/j.neuroimage.2010.06.035. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.