Rigidity sensing and adaptation through regulation of integrin types

Abstract

Tissue rigidity regulates processes in development, cancer and wound healing. However, how cells detect rigidity, and thereby modulate their behaviour, remains unknown. Here, we show that sensing and adaptation to matrix rigidity in breast myoepithelial cells is determined by the bond dynamics of different integrin types. Cell binding to fibronectin through either α5β1 integrins (constitutively expressed) or αvβ6 integrins (selectively expressed in cancer and development) adapts force generation, actin flow, and integrin recruitment to rigidities associated with healthy or malignant tissue, respectively. In vitro experiments and theoretical modelling further demonstrate that this behaviour is explained by the different binding and unbinding rates of both integrin types to fibronectin. Moreover, rigidity sensing through differences in integrin bond dynamics applies both when integrins bind separately and when they compete for binding to fibronectin.

The rigidity of the extracellular matrix (ECM) determines cell proliferation¹, drives differentiation into different lineages², and can induce malignant phenotypes if increased above a certain threshold³. To detect rigidity, cells must first mechanically probe the ECM. Different contractile structures that apply forces to the ECM have been proposed to serve that purpose^{4, 5, 6, 7}, and to mediate the complex signalling pathways that depend on substrate rigidity^{6, 8}. However, the molecular mechanism by which cell-substrate forces detect rigidity and trigger any downstream signalling remains unknown. An appealing hypothesis is that this mechanism could be mediated by the unbinding rates of molecular bonds, which have long been described to be determined by force⁹. Such an effect has indeed been proposed to directly mediate rigidity sensing⁷, but the hypothesis remains unproven as the relevant molecular bonds have not been identified. Among the different bonds involved in cell-substrate adhesion, those between integrins and the ECM are particularly promising candidates. Indeed, they provide the main molecular mechanical link between cells and their substrate, and they are affected by substrate rigidity¹⁰. We thus conjectured that integrins provide a rigidity sensing mechanism through their binding and unbinding rates. Further, given the variety of integrin types and their redundancy in binding partners¹¹, regulation of integrin types with different binding rates to the same ECM component could provide a simple mechanism of rigidity adaptation.

To test this hypothesis, we focused on two receptors to the ECM protein fibronectin (FN): α5β1 integrin, the main FN receptor, with a very well characterized interaction¹², and αvβ6, expressed selectively in developmental, cancer, and wound healing processes and thus potentially providing an adaptation mechanism¹³. As a cell model we used two immortalized lines of human breast myoepithelial cells¹⁴: myo β6 cells, overexpressing β6 integrins (as occurs in ductal carcinoma in situ), and control cells without β6 overexpression (myo ctrl). Both lines constitutively express α5β1. Those lines were ideally suited to study FN-integrin interactions, since adhesion to FN-coated substrates required only α5β1 in myo ctrl cells, but was mediated by both α5β1 and αvβ6 in myo β6 cells (Supplementary Figure 1).

Mechanical response to rigidity

We first used traction force microscopy^{15, 16} to measure the forces exerted by both cell types on FN-coated polyacrylamide gels of different rigidities calibrated with Atomic Force Microscopy (AFM). Cells on all rigidities deformed the gels above noise levels, allowing the measurement of forces (Supplementary Figure 2). Force generation in Myo ctrl cells showed a peak at the stiffness corresponding to healthy breast tissue (~1 kPa, as measured also with AFM¹⁷), decreased for higher stiffness characteristic of malignant tissue¹⁷, and then increased again for stiffness values above 5 kPa (Figure 1a-b). That behaviour was lost in myo β6 cells, which showed a monotonic increase in force with stiffness (Figure 1a-b).

Figure 1. Expression of αvβ6 integrins alters response to substrate stiffness.

(a) Colour maps showing the traction forces applied by individual myo ctrl or myo β6 cells on FN-coated polyacrylamide gels of increasing rigidity. (b) Average forces as a function of rigidity for myo ctrl cells (red) and myo β6 cells (blue). (c) Average forces for both cell types after blocking αvβ6 with an inhibitory antibody. Differences between cell types were significant without antibodies (p<0.05) but not with antibodies, and the effect of stiffness was significant in all cases (p<0.05). n≥11 cells per condition. Scale bar is 20 μm.

We then carried out several experiments to further explore this mechanical behaviour. First, we checked that the differences between cell lines were caused specifically by αvβ6. Indeed, differences were abolished by an αvβ6 blocking antibody (Figure 1c) but unaffected by an isotype control antibody (Supplementary Figure 3b-c). The other FN receptor known to play a mechanical role, αvβ3¹⁸, did not significantly affect force generation (Supplementary Figure 3d-e). Second, we confirmed that the effect of αvβ6 was mediated by the bond to FN and not by other possible interactions, since plating cells on substrates coated with collagen (which does not bind to αvβ6) eliminated the force differences between cell types (Supplementary Figure 3f-g). Confirming the specific role of FN, overall forces decreased for both cell types when cells were plated on substrates coated with a lower FN density (Supplementary Figure 3h-i). However, the relative differences and the rigidity trends were maintained for both cell types. Additionally, performing experiments using culture medium without foetal bovine serum (FBS) did not affect measurements (Supplementary Figure 3j-k), thereby discarding possible effects of ECM components other than FN present in FBS. Other effects due to cell geometry or substrate coating were also ruled out (see Supplementary Note 1). Finally, we used primary human breast myoepithelial cells to check that our results were not an artefact of the immortalized myo ctrl and myo β6 cell lines. Primary cells featured the same behaviour as myo ctrl cells, and the same behaviour as myo β6 cells after transfecting β6 integrin (Supplementary Figure 3l-m). Thus, rigidity sensing by myo β6 cells was altered by the FN-αvβ6 bond, which abolished the local force peak at healthy stiffness present in control cells.

Next, we evaluated whether the different forces exerted by myo ctrl and myo β6 cells could be due to altered myosin activity. Before plating on the gels, the levels of total myosin light chain (MLC) and active phosphorylated MLC (pMLC) were the same between cell types (Supplementary Figure 4ab). The levels of Rho and Rac, known regulators of contractility and cytoskeletal organization, and of α5β1 integrins, were also the same (Supplementary Figure 4a-b). Once attached to the gels, myosin phosphorylation moderately decreased for both cell types as rigidity increased, and was slightly higher for myo β6 cells than myo ctrl cells (Supplementary Figure 4c-d). The activation of Rho and Rac also exhibited some differences (Supplementary Figure 4e-h). However, the variations induced by rigidity and cell type in either myosin phosphorylation or Rho/Rac activation did not globally match the corresponding variations measured in forces. Thus, the measured force/rigidity curves could not be explained by biochemical regulation of myosin activity.

Binding dynamics of α5β1 and αvβ6 integrins

Since regulation of myosin activity could not explain the effect of the FN-αvβ6 bond, we then evaluated whether bond dynamics could provide a mechanism. To this end, we first measured the true binding rate (k_ont) and unbinding rate (k_off) to FN of both purified α5β1 and αvβ6 integrins using surface plasmon resonance (Figure 2a). αvβ6 integrins had a slightly reduced k_ont and strongly increased k_off with respect to α5β1 integrins. However, for a given FN molecule on the substrate, actual binding rates to integrins will depend not only on the true binding rate (which defines the probability of binding between two individual molecules) but also on the number of integrins available for binding on the cell membrane. This can be captured by defining an effective binding rate k_on as k_on=k_ont·d_int, where d_int is the density of integrins on the cell membrane¹⁹. We thus measured integrin densities, which were 5-fold higher for αvβ6 than for α5β1 (Figure 2b and Supplementary Figure 5). As k_ont only decreased by half, k_on in myo β6 cells was thus predicted to be higher for αvβ6 than for α5β1. To test whether that increase in both k_on and k_off of αvβ6 was observed in cells, we used magnetic tweezers to pull with a constant force on FN-coated beads attached to cells. Consistently with an increase in k_off, beads bound to FN through αvβ6 (because α5β1 had been blocked) detached faster than beads bound through α5β1 (Figure 2c and Supplementary Note 2). Those bead detachment times were not affected by the stiffness of the substrate that cells were on, discarding that downstream processes triggered by rigidity could affect k_off (Supplementary Note 2). Further, the expression of αvβ6 reduced the recruitment of α5β1 to FN-coated beads bound to the cell membrane (Figure 2d-e), but the inverse did not take place (Figure 2f-g). This shows that αvβ6 had a higher affinity for FN than α5β1, indicating that k_on had to increase even more than k_off to compensate for the increased unbinding (see Supplementary Note 2). Thus, in myo β6 cells and with respect to α5β1, αvβ6 had an increased k_off, and an even more increased k_on.

Figure 2. Both binding and unbinding rates to FN are higher for αvβ6 than for α5β1.

(a) Surface Plasmon Resonance curves showing attachment and subsequent detachment of solutions of purified α5β1 integrins and αvβ6 integrins to a FN-coated substrate. Lines of increasing height represent increasing integrin concentrations (9-264 nM for α5β1 and 67-527 nM for αvβ6). Data for 264 nM is marked in bold in both cases. Fitted k_ont and k_off values are shown below graph (n ≥3 experiments). (b) Integrin densities on the membrane for both cell types (n≥46 cells per condition, see also Supplementary Figure 5). (c) Top: The tip of a magnetic tweezers device was approached to cells with attached FN-coated magnetic beads, and used to apply a force of 0.5 nN to beads for 2 minutes. Scale bar is 20 μm. Bottom: time required to detach beads from myo ctrl or myo β6 cells (with or without blocking antibodies) after force application (n≥64 beads from ≥47 cells per condition). (d) DIC images and β1 integrin staining images of myo ctrl or myo β6 cells (with or without blocking αvβ6 integrins) showing β1 integrin recruitment to FN-coated beads. Insets show beads marked with a red square. (e) Corresponding quantification of integrin recruitment to beads (n≥20 beads from ≥10 cells per condition). (f-g) Same as d-e, but staining for β6 integrins and blocking α5β1 integrins instead of the reverse (n≥ 23 beads from ≥ 15 cells per condition). Scale bar is 20 μm. *: p<0.05.

Rigidity sensing through integrin binding dynamics

We next evaluated how integrin-FN bond dynamics could determine rigidity sensing. As proposed in a computational model by Chan and Odde^{7, 20}, substrate rigidity regulates the loading rate of cell-substrate forces, which in turn determine molecular unbinding rates. This model considers myosin motors pulling on actin filaments, generating the characteristic rearward flow of actin towards the cell centre²¹. Actin flow then connects to a substrate of given rigidity through “clutch” molecules with defined k_on and k_off. In the filopodia of embryonic chick forebrain neurons, this model successfully predicted traction force dynamics, as well as the effect of substrate rigidity to increase actin speeds and decrease traction forces. However, the model did not relate the clutches to specific molecular bonds, and did not include reinforcement, i.e., the strengthening and growth of cell-ECM adhesions commonly observed after force application in several cell types^{18, 22}. To address this, we developed a model expanding on that proposed by Chan and Odde (see Figure 3 and methods for details).

Figure 3. Integrin-FN clutch model of force transmission.

(a) Myosin motors pull on actin filaments, which move with rearward speed v_a. Integrins of two different types connect to the actin flow through adaptor proteins, and compete for binding to FN with effective binding rates k_on1 and k_on2 given by true binding rates (k_ont1, k_ont2) multiplied by integrin densities on the membrane (d_int1, d_int2). FN molecules are in turn connected to a compliant substrate, represented as a linear elastic spring of varying rigidity. (b) Flow of events (from top to bottom). (i) The model considers a given number of FN molecules (triangles) attached to the substrate, to which integrins can bind. (ii) Orange integrins, with higher k_on, will bind faster. (iii) Once they bind, actin rearward movement applies a force on all integrins and the substrate. Because orange integrins also have a higher k_off, they will detach sooner. (iv) Eventually, blue integrins will detach as well, and if before detaching the force transmitted through them reaches a threshold value, a reinforcement mechanosensing event will result in increased integrin density. (v) Once all integrins detach, force on the substrate is released and the cycle begins again. (c-e) Cell traction forces (c), integrin densities (d), and actin speeds (e) predicted by the model, the three regimes (1-3) are discussed in the main text and in Supplementary Note 4.

First, we specifically modelled the clutches as FN molecules on the substrate, and the binding and unbinding rates as those between each FN molecule and integrins (see Supplementary Note 3). For binding, we considered the effective rate k_on, determined by multiplying the true binding rate k_ont by the density of integrins d_int available for binding to each FN molecule. We also allowed different integrin types (characterized by different k_on values) to compete for FN binding (Figure 3a). For unbinding, we used k_off values determined experimentally for the FN-α5β1 single molecule bond as a function of the applied force¹². This measured k_off depends on force as a catch bond, presenting a maximum stability (minimum k_off) at a force of about 30 pN. To allow for possible differences in integrin activation between cell types, we multiplied the k_off vs force curve by an adjustable scaling factor. By contrast, no experimental data exist for the k_off/force curve of single FN-αvβ6 bonds. For simplicity and since αvβ6 binds to the same RGD motif in fibronectin, unbinding in FN-αvβ6 bonds was thus modelled simply by changing the scaling factor of the FN-α5β1 k_off/force curve. We note however that the catch bond assumption is not essential for model output, and that the same qualitative results can be obtained using slip bonds^{7, 20}. This could be because under collective loading catch bond features may only be observable under uniform bond loading^{23, 24}, which is not the case in a system driven by rearward flow. Finally, since reinforcement was observed in our cells (Supplementary Figure 6), we included that aspect by increasing integrin density d_int by a given amount each time the force in any integrin-FN bond surpassed a certain threshold before breakage (Figure 3b). This force sensing event could correspond to force-induced conformational changes in proteins linking integrins to actin²⁵, exposing binding sites to other molecules and providing a mechanotransduction signal to increase integrin concentration.

In essence, substrate rigidity affected the outcome of our model by regulating the rate of force loading experienced by integrin-FN bonds pulled by actin rearward flow. Indeed, the rate at which rearward flow deforms the substrate translates into a small or large rate of force loading depending on whether the substrate is soft or stiff, respectively. Integrin-FN bonds respond to this loading rate, resulting in three regimes as rigidity increases (Figure 3c): (1) At very low rigidities, force builds so slowly that bonds (which have a non-zero k_off even at zero force) detach spontaneously before significant forces can be loaded. In this first regime, increasing loading rates thereby improve force transmission. (2) However, above a certain rigidity loading rates become so high that bonds quickly reach forces where k_off increases enough to dominate over k_on. In catch bonds, this increase in k_off takes place after the force of maximum stability, but the crossover between unbinding and binding dynamics would also happen in a slip bond featuring a monotonic increase of k_off with force. Bonds then unbind before allowing time for others to form, decreasing force transmission by reducing the amount of bonds engaged simultaneously. (3) As loading rates increase further, unbinding forces in individual bonds (which increase with loading rate) start surpassing the threshold reinforcement force. That increases integrin density and k_on (Figure 3d), leading to faster bond formation and improved force transmission. In all cases, transmitted forces pull on and slow actin filaments, leading to an inverse relationship between force and actin rearward flow as previously reported²⁶ (Figure 3e, see Supplementary Note 4 for details on model predictions).

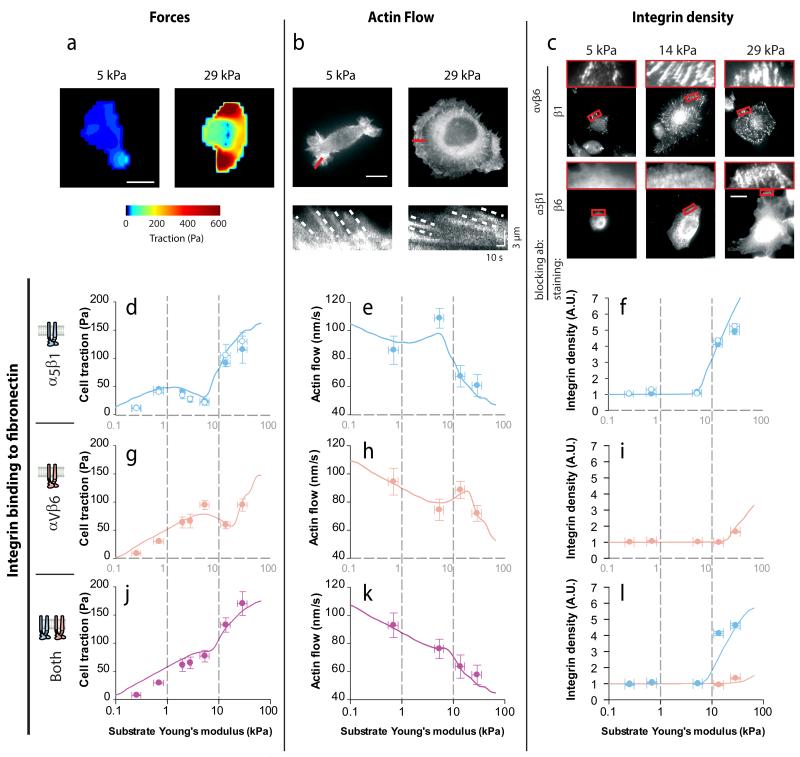
To test our model, we first considered the case in which cell-substrate adhesion is mediated by a single integrin type. Using parameters in the range of measured experimental values and a single population of α5β1 integrins (Supplementary Table 1 and Supplementary Note 5), we were able to capture force generation by cells bound to FN through α5β1 (both myo ctrl cells and myo β6 cells with αvβ6 blocked, Figure 4d). By contrast, when the same myo β6 cells bound to FN substrates through αvβ6 (because α5β1 had been blocked), the traction peak moved to malignant rigidities (5 kPa, Figure 4g), and the onset of the third reinforcement regime was delayed. This behaviour was captured by the model after leaving all other parameters constant and increasing only k_on (5-fold) and k_off (3-fold), matching thus the trends in bond dynamics between α5β1 and αvβ6 measured in Figure 2. Thus, simply by binding to fibronectin through integrins with different binding and unbinding rates, cells are able to tune the position of the traction peak. When both integrin types were included (using again the same parameters), the model predicted the monotonic increase in traction force with rigidity that was observed in myo β6 cells when no integrins were blocked (Figure 4j and Supplementary Note 4).

Figure 4. Integrin-fibronectin binding dynamics predict force generation, actin flow, and integrin recruitment in response to substrate stiffness.

(a) Examples of traction maps exerted by myo ctrl cells plated on substrates of 5 or 29 kPa. (b) Top: examples of myo ctrl cells transfected with lifeact-GFP plated on substrates of 5 or 29 kPa. Bottom: kymographs showing the movement of actin features along the lines marked in red in the top image. The slope of the traces created by the features (marked with dotted lines) was used to calculate actin speed. (c) Staining of β1 integrins in myo β6 cells where αvβ6 was blocked, and of β6 integrins in cells where α5β1 was blocked. Zoomed regions on top of images correspond to rectangles marked in red in the main image. Scale bars are 20 μm. (d-l) For cells on FN-coated gels of varying stiffness, quantifications of average cell traction forces (d,g,j, n≥14 cells per condition), actin rearward flows (e,h,k, n≥19 traces from ≥7 cells per condition), and integrin densities in adhesions (f,I,l, n≥52 adhesions from ≥10 cells per condition). Results are shown for cells with adhesion mediated by α5β1 integrins (d-f; ●: myo ctrl, ○: myo β6 + αvβ6 ab), αvβ6 integrins (g-i, myo β6+ α5β1 ab), and both integrins (j-l, myo β6 cells without any ab). Lines indicate model predictions. In panel l, blue and orange symbols correspond respectively to β1 and β6 integrin densities. Statistical analyses are detailed in methods.

We next tested whether our model was able to predict actin flow velocities. To this end, we measured the speed of actin movement in lifeact-GFP transfected cells, which was higher in cells generating low forces (Figure 4a,b). When we quantified rearward flow for all conditions, forces and actin speeds were inversely correlated in all cases, with local maxima in forces becoming local minima in speeds and vice versa (Figure 4e,h,k and Supplementary Videos 1-3). Further, our model quantitatively predicted actin speeds with the same parameters used to predict forces (Figure 4e,h,k). The model also predicted that the onset of the third regime was associated with an increase in integrin density (Figure 3d). Indeed, α5β1 and αvβ6 integrin densities increased sharply at the points predicted by the model: 14 kPa for α5β1, and 29 kPa for αvβ6 (Figure 4c and Supplementary Figure 7). A quantitative analysis of integrin densities in adhesions was also in agreement with model predictions in all cases (Figure 4f,i,l). Thus, bond dynamics to FN were sufficient to explain how α5β1 and αvβ6 integrins regulate force generation, actin flow, and integrin recruitment in response to substrate rigidity.

Outlook

Different theoretical approaches have been used to propose how the binding dynamics of clustered catch bonds^{23, 24} could mediate rigidity sensing. Recently, a computational analysis²⁰ detailed how different parameters, including binding and unbinding rates, could modulate rigidity sensing by molecular clutches driven by rearward flow. However, how this could be achieved experimentally, and what molecules were involved, remained unknown. Our results demonstrate that, by regulating the expression on the membrane of different integrin types, cells can tune their force generation to be optimal at healthy breast tissue stiffness (with α5β1), malignant stiffness (with αvβ6), or to increase monotonically (with both integrins). This rigidity sensing and adaptation emerges naturally from integrin-ECM bond dynamics. Interestingly, integrin bond dynamics also predict the onset of integrin recruitment and subsequent increase in force generation that takes place at high rigidities (regime 3). In the model, this feature emerges simply after assuming a threshold for force sensing in single mechanosensing molecules, suggesting a mechanism by which cells could couple integrins to mechanosensors sensible to one mechanical parameter (force) to detect a different mechanical parameter (substrate rigidity). Potentially, such mechanism could also explain how integrin binding affects a downstream process like differentiation²⁷ in a stiffness-dependent manner¹⁰. Of note, the only effect of force sensing events that we considered was an increase in integrin recruitment, which was sufficient to predict our results. However, additional reported events associated with adhesion formation, such as activation of the FAK-paxillin-vinculin pathway⁶ could play synergistic effects by further reinforcing the clutch.

Since biological tissues stiffen with force application²⁸, local force generation maxima provide a homeostatic mechanism: in healthy tissue, a small perturbation tending to increase stiffness would reduce force generation by cells, decreasing tissue stiffness back to the healthy range. In tissue remodelling scenarios (given by developmental processes, wound healing, or cancer), αvβ6 recruitment to the membrane would break homeostasis by shifting or eliminating the force peak. Further, since integrin recruitment is triggered by a mechanosensing event after a given stiffness threshold, any process causing a large increase in tissue stiffness beyond this threshold could provide the signal required to break homeostasis.

Methods

Traction force measurements

For traction force measurements, cells seeded on gels were placed on an inverted microscope (Nikon Eclipse Ti). Single cells were tracked for 12 h, while we acquired phase contrast images of the cells and fluorescence images of the embedded nanobeads using a 40x objective. Then, cells were trypsinized and an image of bead position in the relaxed state of the gel was acquired. By comparing bead positions with and without cells, a map of gel deformations caused by cells was first obtained using custom particle imaging velocimetry software¹⁵. Then, after assuming that gel displacements were caused by forces exerted by cells in the cell-gel contact area, the corresponding map of cell forces was calculated using a previously described Fourier transform algorithm^{16, 29}. The average forces per unit area exerted by each cell were then calculated. Force measurements for each cell were taken each hour during the measurement, and the average value for all time measurements was used. Total strain energy exerted by the cells was calculated by performing a scalar product between gel displacement and force for each pixel in the force map, and then adding the result for the entire traction map. Phase contrast images were also used to calculate average cell spreading areas as a function of substrate stiffness.

Surface Plasmon Resonance experiments

True binding rates (k_ont) and unbinding rates (k_off) were measured using a Biacore T-100 system. First, 82 RU of monomeric biotinylated FN7-10 molecules and biotinylated bovine serum albumin (BSA) molecules were immobilized to flow cells of avidinated sensorchips (Xantec bioanalytics). FN7-10 is a segment of FN responsible for cell binding and containing the integrin-binding motifs RGD and PHSRN³⁰. Then, different concentrations of purified recombinant human α5β1 and αvβ6 integrins were diluted in Tris-Buffered Saline (25 nM Tris, 150 mM NaCl, pH 7.4) with 1 mM of CaCl₂, MgCl₂, and MnCl₂ to ensure that integrins were in their activated ligand-binding state³¹. Integrin dilutions were then injected at a constant rate of 30 μl/min for 60 seconds, followed by an injection of buffer for 60 seconds. All measurements were taken as the difference between the sensorgrams obtained in the flow cell with FN7-10 molecules and the reference sensorgrams obtained in the flow cell with biotinylated BSA. The same Tris-buffered saline containing 20 mM EDTA instead of Ca, Mg, and Mn ions was used to remove bound integrins and regenerate the surface between measurements. Data were analysed using Scrubber (BioLogic Software) software and k_ont and k_off values were obtained after fitting a 1:1 Langmuir binding model.

Magnetic tweezers and bead recruitment experiments

Magnetic tweezers experiments were carried out as previously described^{18, 32}. Briefly, carboxylated 3μm magnetic beads (Invitrogen) were coated with a mixture of biotinylated pentameric FN7-10 and biotinylated BSA (either 1:5 or 1:30). For measurements, cells were first plated on coverslips coated with 40 μg/ml laminin (Sigma), to ensure that blocking antibodies used to disrupt adhesion to FN affected only cell-bead and not cell-substrate interactions. FN-coated beads were then deposited on the coverslips, and attached to cells. The tip of the magnetic tweezers device was then used to apply a force of 0.5 nN for 2 min on beads attached to cell lamellipodia. Then, the percentage of beads still attached to cells after force application was calculated. For beads that detached, the time of force application required for detachment was also calculated. To quantify integrin recruitment to beads, cells attached to FN7-10-coated beads were fixed and stained for β1 and β6 integrins as described in the immunostaining section. 3 μm carboxylated silica beads (Kisker Biotech) were used to avoid the high autofluorescence of magnetic beads. The average fluorescence intensity on the beads and on surrounding areas was then measured, and the difference between both values was taken as a measure of integrin recruitment.

Rearward flow measurements

To measure actin rearward flow, cells were transfected with lifeact-GFP, lifeact-mRuby, or α5 integrin (courtesy of Rick Horwitz³³, addgene plasmid 15238) using jetPRIME transfection kit (Polyplus transfection) 2 days before measurements. Cells were then plated on gels of varying rigidity, and imaged every second for 2 minutes with an oil immersion 100× objective with spinning disk confocal microscopy (Andor). For each cell, kymographs were obtained at the cell periphery, and actin speed was measured from the slope of actin features observed in the kymographs. In cells plated on 0.25 kPa gels, actin features were so diffuse that no reliable slopes could be measured in kymographs.

Immunostaining

For fluorescence staining of integrins, cells were fixed with 4% paraformaldehyde, permeabilized with 0.1% Triton X-100, and labelled first with primary antibodies (1 h, room temperature), and then with Alexa-conjugated secondary antibodies (Invitrogen) (1 h, room temperature). Fluorescence images were then acquired with a 60x oil immersion objective (NA 1.40) using a Nikon Eclipse Ti microscope.

Supplementary methods

Cells and reagents, preparation of polyacrylamide gels, measurement of polyacrylamide gel stiffness, adhesion reinforcement measurements, western blotting and Rac/Rho activation measurements, statistical analysis, and the stochastic modelling of traction force generation are described in supplementary methods.