DISCRIMINANT VALUE OF CUSTOM OCULAR RESPONSE ANALYZER WAVEFORM DERIVATIVES IN KERATOCONUS

Abstract

Purpose

To evaluate the performance of corneal hysteresis (CH), corneal resistance factor (CRF), and 16 investigator-derived Ocular Response Analyzer (ORA) variables in distinguishing keratoconus (KC) from the non-diseased state.

Design

Retrospective case series.

Participants

Fifty-four eyes of 27 unaffected patients and 49 eyes of 25 KC patients from the Instituto de Olhos, Rio de Janeiro, Brazil.

Methods

Sixteen candidate variables were derived from exported ORA signals to characterize putative indicators of biomechanical behavior. Area under the receiver operating characteristic curve (AUROC) and the Z-statistic were used to compare diagnostic performance.

Main Outcome Measures

Discriminant value of standard and derived ORA variables as measured by AUROC.

Results

Fifteen of 16 candidate variables performed significantly better than chance (AUROC > 0.5) at discriminating KC. Diagnostic performance was greatest for a custom variable related to the depth of deformation (ConcavityMin (0.985±0.002, mean AUROC±standard error) and a new measure incorporating the pressure-deformation relationship of the entire response cycle (Hysteresis Loop Area (HLA) 0.967 ± 0.002). Z statistics assessing the discriminative value of each of the top 5 variables demonstrated superiority to CH (AUROC 0.862 ± 0.002). ConcavityMin had the best overall predictive accuracy (cutoff value 50.37, 94.9% sensitivity, 91.7% specificity and 93.2% test accuracy), and the top 4 variables demonstrated the most consistent relationships to KC severity.

Conclusions

Investigator-derived ORA variables related to the depth of deformation and the pressure-deformation relationship demonstrated very high test accuracy for detecting presence of keratoconus. Beyond their diagnostic value, the candidate variables described in this report provide mechanistic insight into the nature of the ORA signal and the characteristic changes in corneal dynamics associated with keratoconus.

Keratoconus (KC) is an ectatic disease that has a significant impact on quality of life¹ and often requires specialty contact lens wear or corneal transplantation for visual rehabilitation. Though characteristic corneal topographic signs and slit lamp microscopy criteria have been established for confirming the diagnosis of KC, ² diagnosis of early disease or disease propensity on the basis of topography alone can be difficult in the absence of additional disease indicators. ^{3, 4, 5}

Early detection of KC is especially important in the setting of refractive surgery screening to identify those patients at risk for post-LASIK ectasia. KC is a contraindication for LASIK, and while serious complications such as post-LASIK ectasia are rare, they are significant considering LASIK is an elective procedure.⁶ The risk factors for post-LASIK ectasia remain a matter of significant debate and speak to the complexity of the condition and the lack of adequate screening tools. ^{7, 8, 9} An ongoing need exists for more effective approaches to preoperative screening for ectasia susceptibility ^{2, 6, 7} and identification of patients with early KC so that early disease-stabilizing interventions such as UV/riboflavin corneal crosslinking can be offered prior to the onset of significant visual loss.¹⁰

The Ocular Response Analyzer (ORA, Reichert Ophthalmic Instruments, Buffalo, NY) is a modified non-contact pneuomotonometer that measures aspects of the corneal biomechanical response during an air puff perturbation. It reports two biomechanical variables—Corneal Hysteresis (CH) and Corneal Resistance Factor (CRF)—which are described as measures of the viscoelastic damping capabilities and overall elastic resistance of the cornea and associated structures. ¹¹ Low CH and CRF have been associated with ectatic disease ^{5, 12, 13, 14}, but the utility of CH and CRF for differentiating low-grade KC from the normal state is unclear. ¹⁴ While Schweitzer et al demonstrated significantly lower values of CH and CRF in forme fruste KC compared to normal eyes,¹⁵ Kirwan found no significant difference. ⁵ Moreover, CH and CRF did not significantly differ when comparing stages of KC severity.¹² In all published studies, the variables have a high degree of overlap between study groups that limits diagnostic utility. ^{5, 12, 13, 15}

The ORA applanation and pressure signals contain more information than the pressure differences described by CH and CRF. A comprehensive mechanical approach to describing the material behavior of the cornea in the context of the ORA measurement regime would include analysis of signal features that describe the time course and magnitude of perturbation by the ORA air puff and the magnitude and temporal response of the cornea throughout the loading and unloading cycle.¹⁶ Kerautret et al presented the first published report qualitatively demonstrating the potential utility of more comprehensive signal analysis in assessing ectatic predisposition.⁹

In 2007, our group developed a panel of candidate diagnostic variables using exported ORA data to characterize the temporal, applanation signal intensity, and pressure features of the corneal response (Hallahan et al, ARVO e-abstract 2008). In this study, we investigate the behavior of these variables in normal and KC eyes of differing grades, and evaluate their ability to differentiate normal corneas from KC corneas relative to standard ORA-derived biomechanical variables.

Subjects and Methods

This retrospective case series followed the tenets of the Declaration of Helsinki for retrospective research and was HIPAA-compliant. The research was approved by the ethics committee of the Federal University of Sao Paulo (Protocol 0123/06). Patients were sequentially evaluated from October 2005 to December 2008.

Fifty-four normal eyes of 27 patients and 49 keratoconic eyes from 25 patients underwent examinations that included Placido disk-based corneal topography (Humphrey ATLAS; Carl Zeiss Meditec, Dublin, CA), rotating Scheimpflug tomography (Pentacam; Oculus, Wetzlar, Germany), and ORA evaluation (software v.1.01) (Table 1). KC was diagnosed by a corneal specialist (RA) on the basis of slit lamp microscopy signs of stromal thinning, conical protrusion, Fleischer’s ring, Vogt’s striae, scissoring of the red reflex or an abnormal retinoscopy reflex, and topographic evidence of focally increased corneal curvature, inferior-superior curvature asymmetry, and/or skewing of the steepest radial axes above and below the horizontal meridian.^{3, 17, 18} No subjects had glaucoma, a history of previous eye surgery, or current topical eye medication use. KC eyes were grouped by severity according to the Amsler-Krumeich keratoconus classification. ¹⁹

Table 1.

Comparison of characteristics of normal and keratoconus groups (mean ± SD).

	Normal	Keratoconus	P value
Number of eyes	54	49
Age, mean ± SD	44.8 ± 20.0	36.4 ± 17.2	0.03
Gender, n (%)
Male	15 (56%)	14 (56%)
Female	12 (44%)	11 (44%)
Max K (Diopter)	43.8 ± 1.9	49.0 ± 6.2	0.0001
CCT (micron)	547.7 ± 45.2	477.1 ± 47.4	0.0001
IOPg (mmHg)	15.4 ± 2.3	11.2 ± 3.1	0.0001
IOPcc (mmHg)	15.8 ± 2.1	14.4 ± 3.2	0.02

P values calculated with unpaired t-test; SD = Standard deviation; Max K = maximum corneal curvature; CCT = central corneal thickness; IOPg = Goldmann-equivalent intraocular pressure; IOPcc = cornea-compensated intraocular pressure

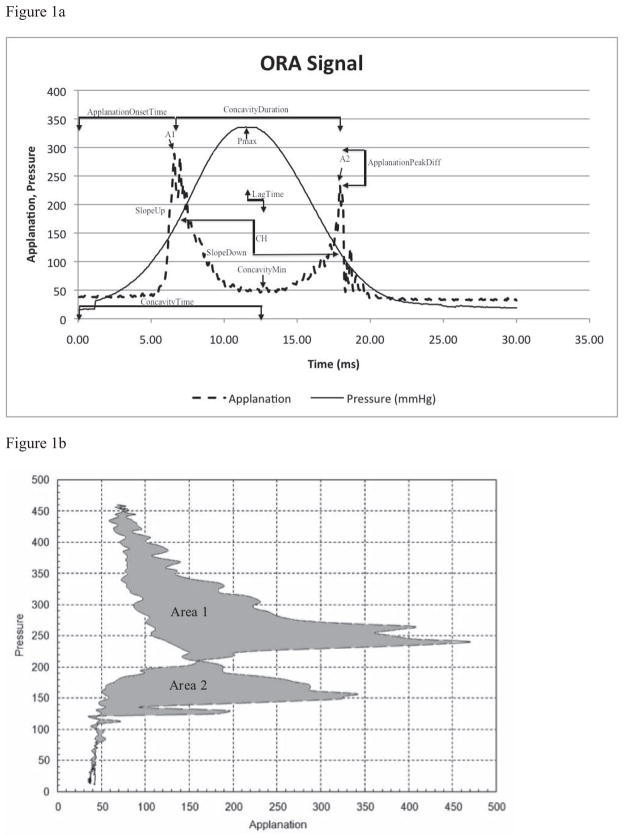
The ORA method of operation has been previously described in detail. ¹¹ Briefly, an air jet generates a force directed at the central cornea that causes deformation of the cornea into a slight concavity followed by a return to its pre-perturbation convex shape. During this sequence of events, which takes place over 20–30 milliseconds, the plenum pressure of the air jet chamber is measured and an infrared detector system monitors the number of photons reflected from the corneal center. The intensity of the infrared signal is a function of specular reflection from the anterior corneal surface, and it reaches a local maximum when the cornea is most planar (applanated or near-applanated).²⁰ Maximum planarity occurs at two points in the cycle: 1) during the inward phase of the response just before concavity and 2) during the outward phase of the response after concavity. Figure 1a provides a sample of the ORA pressure and infrared intensity waveforms, which are both recorded by the device in dimensionless units. Two ORA measurements of acceptable quality as defined by the manufacturer’s user manual were obtained for each eye and averaged results were used for analysis.

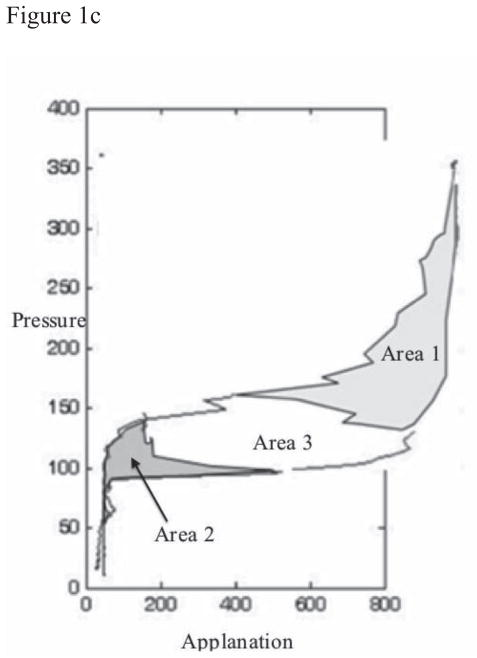
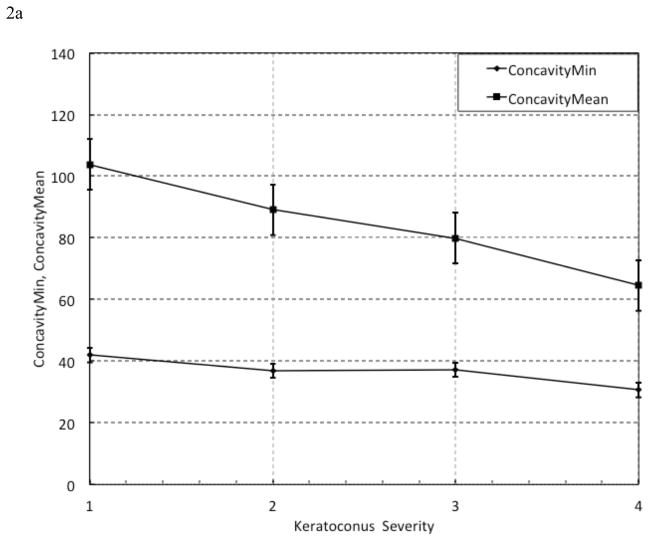
Figure 1. Representation of Selected Variables.

(a) Ocular Response Analyzer Signal Output with selected variables. A1 = first applanation state; A2 = second applanation state; Pmax = maximum achieved pressure; CH = corneal hysteresis.

(b) Calculation of Hysteresis Loop Area (HLA). From a single measurement of the Ocular Response Analyzer, Pressure values of the signal output were plotted against Applanation values at each time point. HLA was calculated as the sum of Area 1 and Area 2 within the closed loop.

(c) Construction of Hysteresis Loop Area complete (HLAc). To calculate HLAc, Area 1 of the HLA plot in Figure 1b is inverted and yields Area 3. HLAc is the summation of Area 1, Area 2, and Area 3.

Standard ORA variables

FDA-approved versions of the ORA software provide two similar measurements of biomechanical behavior based on the pressures obtained at the two applanation events. CH is calculated as the difference between the pressure values at the ingoing (P1) and outgoing (P2) corneal applanation events. ^{8, 11} CRF is based on the same pressure values but is a linear combination of the applanation pressure values, P1 − (k * P2), ²⁰ that biases CRF toward the pressure associated with the ingoing applanation event. The coefficient, k, has been empirically set to 0.7 by the manufacturer to maximize the dependence of CRF on central corneal thickness.

Candidate ORA variables

ORA infrared intensity and pressure time series data were exported using ORA software and analyzed in Matlab (v.7.0, MathWorks, Natick, MA). Sixteen variables were derived from aspects of the ORA signal suspected of being of biomechanical relevance (Figure 1a).

All variables and their classifications are described in Tables 2–5. Because the ORA records pressure and applanation versus time, the 16 custom variables can be classified based on their relationship to one or a combination of these features. Group 1 variables are based on applanation signal intensity. Group 2 includes variables derived from the applied pressure, and Group 3 includes variables related to temporal aspects of the infrared signal. Group 4 takes into account the applanation signal intensity as a function of response time. Group 5 consists of two variables characterizing pressure and applanation signal intensity relationships, and Group 6 variables relate pressure to time. A smoothing function was applied to the applanation signal by averaging every ten data points and reconstructing the signal for variables that required defining the minimum applanation signal intensity during corneal concavity (ConcavityMin and ConcavityTime).

Table 2.

Definition and comparison of Ocular Response Analyzer variables (mean ± SD) based on Applanation Signal Intensity for normal and keratoconus groups.

Group	Variable	Operational Definition	Related to:	Normal	Keratoconus	P value
1: Applanation Signal Intensity	A1	Peak intensity of 1st applanation event	Maximum surface area achieving planarity during inward deformation	681 ± 153	433 ± 148	<0.0001
	A2	Peak intensity of2nd applanation event	Maximum surface area achieving planarity during recovery	564 ± 172	371 ± 169	<0.0001
	ApplanationPeakDiff	A2 – A1	Difference in maximum planarity between inward and recovery phases	−117 ± 197	−62 ± 148	0.02
	ConcavityMin	Minimum applanation intensity between A1 and A2	Depth and irregularity (non-planarity) of deformation	61 ± 11	39 ± 8	<0.0001
	ConcavityMean	Mean applanation intensity between A1 and A2	Depth and irregularity of deformation, averaged	150 ± 28	93 ± 26	<0.0001

SD = standard deviation

Table 5.

Definition and comparison of Ocular Response Analyzer variables (mean ± SD) based on combinations of signal characteristics for normal and keratoconus groups.

Group	Variable	Operational Definition	Related to:	Normal	Keratoconus	P value
4: Applanation Intensity and Response Time (msec−1)	SlopeUp	Positive slope of the first applanation peak, from inflection point to peak	Rate of achieving peak planarity	35 ± 12	23 ± 10	<0.0001
	SlopeDown	Negative slope of the first applanation peak, from peak to inflection point	Rate of loss of peak planarity	44 ± 31	25 ± 36	<0.0001
5: Pressure and Applanation Intensity	Hysteresis Loop Area (HLA)	Area enclosed by pressure vs. applanation function (Figure 1B)	Hysteresis aggregated over entire deformation cycle except concavity	11.8 ± 2.1 (×104)	6.7 ± 2.0 (×104)	<0.0001
	Hysteresis Loop Area Closed Form (HLAc)	HLA plus interpolated region between applanation events (Figure 1C)	Hysteresis of complete corneal deformation cycle (including concavity)	16.9 ± 3.2 (×104)	9.6 ± 3.1 (×104)	<0.0001
6: Pressure and Time	Impulse	Area under pressure vs. time curve	Air pressure intensity	4691 ± 275	4225 ± 501	<0.0001
	P_rate	Slope of pressure vs. time from onset to peak pressure	Rate of pressure rise leading to first applanation event (A1)	1.87 ± 0.02	1.87 ± 0.02	0.25

SD = standard deviation

Group 5 variables include Hysteresis Loop Area (HLA, Figure 1b) and closed-form Hysteresis Loop Area (HLAc, Figure 1c). To calculate these variables, pressure was plotted against applanation signal intensity values, and the areas created by the closed loops were calculated using the trapezoidal rule of integration which uses linear interpolation to estimate the area enclosed by two successive data points. ²¹ Area 1 and Area 2 were summed to compute HLA (Figure 1b), which reflects hysteresis aggregated over the entire corneal deformation cycle excluding concavity. HLA does not represent the complete closed-form stress-strain relationship obtained during traditional ex vivo testing because, while the cornea continues to deform in the same axial direction, the applanation signal values reverse when the first applanation event is reached. To capture the inter-applanation component of hysteresis during corneal concavity, the HLAc variable was designed. To arrive at HLAc, Area 1 (Figure 1b) is inverted to yield another closed loop, Area 3, (Figure 1c); then, Areas 1, 2, and 3 are summed.

Statistical Analysis

All variables were checked for normality using the Kolmogorov-Smirnov test. A nonparametric analysis of clustered receiver operating characteristic (ROC) curve data was performed for each variable to account for intracluster correlation since normal distribution of data was not assumed and independent samples could not be assumed due to the use of both eyes in some subjects. ²² ROC curves were constructed using Fortran codes provided by Obuchowski. ^{22, 23} Area under the ROC curve (AUROC) was calculated for each variable. The Z statistic was calculated for CH and the five variables with highest AUROC including CRF in order to compare their performance independent of prevalence in the sample or arbitrarily chosen decision thresholds.²²

These selected variables were also plotted against KC severity as classified by the Amsler-Krumeich keratoconus severity scoring system. The potential dependence of standard and custom variables on cornea-compensated intraocular pressure (IOPcc), central corneal thickness (CCT) from Scheimpflug tomography, and maximum corneal curvature (Max K) from Scheimpflug topography was explored through univariate linear regression analyses. A two-tailed p-value <0.05 was considered statistically significant for all tests. Statistical analyses and plots were performed using MedCalc software (v.9.5.2.0) and Microsoft Excel (Microsoft Corporation, Redmond, WA).

Results

Table 1 summarizes the normal and KC populations. One eye in the KC group was excluded from the analyses due to a Max K observation of over 80 D. The value was suspected to be related to measurement artifact and was formally determined to be an influential point by the Cook statistic. Comparing the normal and KC groups, Max K, intraocular pressure (IOP) as measured by IOPg and IOPcc, and CCT were significantly different, and their mean ± SD values are reported in Table 1.

Values for existing and custom ORA variables are reported in Tables 2–5 for KC and normal groups. All but ConcavityTime, Lagtime, and P_rate were significantly different between the two diagnostic groups. Originally defined by our group as a variable for normalizing other candidate variables to the rate of pressure application, P_rate was found to be essentially constant regardless of the presence or absence of KC. While the ORA turns off the air jet when the first applanation event occurs such that peak pressure can vary from eye to eye (Pmax), the rate of pressure rise appears to remain constant independent of disease state or Pmax.

AUROC ± SE values for all variables are reported in Table 6. All except LagTime were statistically significant when compared to an AUROC of 0.5, indicating no better diagnostic capability compared to chance. The five best-performing variables as determined by the highest AUROC values were ConcavityMin, HLA, ConcavityMean, HLAc, and CRF (Table 6). Additional analyses were conducted only for these variables and CH.

Table 6.

Comparison of area under the receiver operator characteristic curve (AUROC ± standard error (SE)), Selected Parameter Cutoff, Sensitivity, Specificity, and Test Accuracy for CH, CRF and custom Ocular Response Analyzer variables.

Variable	AUROC ± SE	P value (Area = 0.5)	Cutoff, Sensitivity, Specificity, Test Accuracy
ConcavityMin	0.985 ± 0.002	0.0001	50.37, 94.9%, 91.7%, 93.2%
HLA	0.967 ± 0.002	0.0001	92629, 88.8%, 88.9%, 88.8%
ConcavityMean	0.966 ± 0.002	0.0001	118.6, 83.7%, 88.9%, 86.4%
HLAc	0.959 ± 0.002	0.0001	146689, 98.0%, 79.6%, 88.4%
CRF	0.921 ± 0.004	0.0001	8.60, 77.6%, 86.0%, 82.0%
A1	0.918 ± 0.004	0.0001
SlopeUp	0.872 ± 0.005	0.0001
Impulse	0.865 ± 0.005	0.0001
CH	0.862 ± 0.002	0.0001	8.50, 52.0%, 95.4%, 74.8%
Pmax	0.862 ± 0.005	0.0001
ApplanationOnsetTime	0.858 ± 0.006	0.0001
P1P2Avg	0.843 ± 0.007	0.0001
A2	0.835 ± 0.006	0.0001
SlopeDown	0.834 ± 0.007	0.0001
ConcavityTime	0.797 ± 0.008	0.0001
ConcavityDuration	0.731 ± 0.009	0.0001
ConcavityDuration_IOPcc	0.670 ± 0.009	0.008
ApplanationPeakDiff	0.676 ± 0.008	0.002
LagTime	0.541 ± 0.010	0.557

Results of ROC analysis showed ConcavityMin to have the highest test accuracy (cutoff, 50.37; sensitivity, 94.9%; specificity, 91.7%; test accuracy, 93.2%). CH was the poorest predictor of KC (cutoff, 8.50; sensitivity, 52.0%; specificity, 95.4%; test accuracy 74.8%) (Table 6). Z statistic results showed that ConcavityMin, HLA, ConcavityMean, HLAc, and CRF statistically outperformed CH. All other comparisons between selected variables showed no statistical difference in test performance (Table 7).

Table 7.

Z-statistic for parameters with the highest area under the receiver operator characteristic curve values, CRF, and CH. Reported as: Z-statistic; CI [upper limit, lower limit]; p-value.

	HLA	ConcavityMean	HLAc	CRF	CH
ConcavityMin	0.891; [−0.022, 0.058] (p=0.373)	0.964; [−0.020, 0.058] (p=0.335)	1.240; [−0.015, 0.067] (p=0.215)	1.872; [−0.003, 0.131] (p=0.061)	2.811*; [0.037, 0.208] (p=0.005)
HLA		0.103; [−0.018, 0.020] (p=0.918)	0.900; [−0.009, 0.025] (p=0.368)	1.762; [−0.005, 0] (p=0.078)	2.660*; [0.028, 0.182] (p=0.008)
ConcavityMean			0.666; [−0.014, 0.028] (p=0.506)	1.414; [−0.017, 0.107] (p=0.157)	2.420*; [0.020, 0.188] (p=0.016)
HLAc				1.378; [−0.016, 0.092] (p=0.168)	2.538*; [0.022, 0.172] (p=0.011)
CRF					2.111*; [0.004, 0.114] (p=0.035)

CI = 95% confidence interval of the difference between parameters.

^*denotes statistically significant, p<0.05 for two-tailed test.

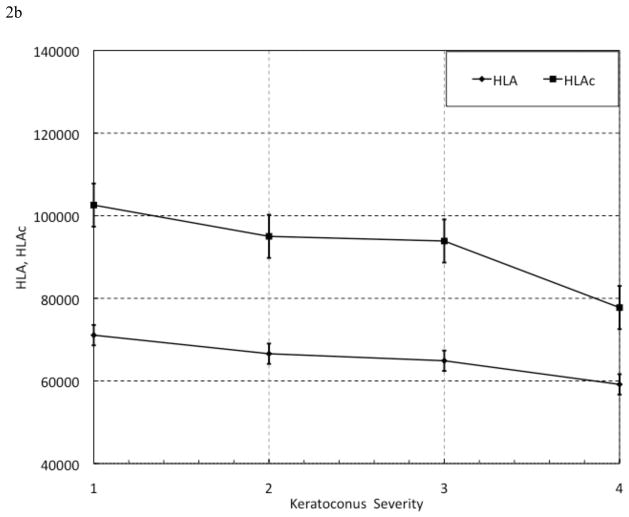
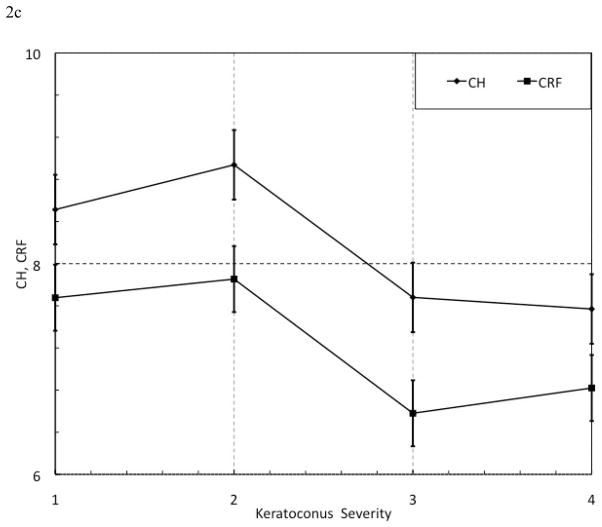
When plotted against KC severity, ConcavityMin and ConcavityMean (Figure 2a) and HLA and HLAc (Figure 2b) exhibited an overall inverse relationship with increasing KC severity that was not seen with CH and CRF (Figure 2c). The results of regression analyses assessing relationships between standard and custom variables and IOPcc, CCT and Max K are presented in Table 8.

Figure 2. Selected Parameter Trends with Keratoconus (KC) Severity. KC patients were grouped by severity using the Amsler-Krumeich scoring system. All showed a general inverse relationship with disease severity. Sample sizes for each group, however, were not large enough to statistically analyze these trends. n(KC severity 1) = 26 eyes; n(KC severity 2) = 14 eyes; n(KC severity 3) = 5 eyes; n(KC severity 4) = 5 eyes.

(a) MinATrough and MeanTrough versus KC Severity score.

(b) HLA and HLAc versus KC Severity score. HLA = Hysteresis Loop Area; HLAc = Hysteresis Loop Area complete;

(c) CH and CRF versus KC Severity score. CH = Corneal Hysteresis (mmHg); CRF = Corneal Resistance Factor (mmHg).

Table 8.

Linear regression analysis results of Ocular Response Analyzer variables as a function of cornea-compensated intraocular pressure (IOPcc), central corneal thickness (CCT) and maximum corneal curvature (Kmax).

	IOPcc		CCT		MaxK
Variable	R2 (+/−)*	p value	R2(+/−)	p value	R2 (+/−)	p value
A1	0.12(+)	0.0004	0.25(+)	<0.0001	0.15(−)	<0.0001
A2	0.05(+)	0.02	0.1(+)	0.001	0.11(−)	0.0004
ApplanationPeakDiff	0.01(+)	0.3	0.13(+)	0.0001	0.05(−)	0.028
ConcavityMin	0.08 (+)	0.003	0.42(+)	<0.0001	0.24(−)	<0.0001
ConcavityMean	0.13 (+)	0.0002	0.37(+)	<0.0001	0.22(−)	<0.0001
P1P2Avg	0.44(+)	<0.0001	0.35(+)	<0.0001	0.26(−)	<0.0001
Pmax	0.11 (+)	0.0007	0.3(+)	<0.0001	0.26(−)	<0.0001
ConcavityDuration	0.43(−)	<0.0001	0.12(−)	0.0003	0.09(+)	0.002
ConcavityTime	0.02(−)	0.2	0.03(+)	0.08	0.05(−)	0.03
LagTime	0.11(−)	0.0007	0.002(−)	0.7	0.00008(−)	0.928
ApplanationOnsetTime	0.31(+)	<0.0001	0.38(+)	<0.0001	0.29(−)	<0.0001
SlopeUp	0.05(+)	0.02	0.11(+)	0.0004	0.11(−)	0.0006
SlopeDown	0.004(+)	0.5	0.02(+)	0.2	0.09(−)	0.002
Impulse	0.09(+)	0.002	0.28(+)	<0.0001	0.25(−)	<0.0001
CH	0.003(−)	0.6	0.26(+)	<0.0001	0.1(−)	0.001
CRF	0.05(+)	0.03	0.39(+)	<0.0001	0.25(−)	<0.0001
HLA	0.16(+)	<0.0001	0.45(+)	<0.0001	0.35(−)	<0.0001
HLAc	0.09(+)	0.002	0.43(+)	<0.0001	0.35(−)	<0.0001

P values < 0.05 indicate a slope term significantly different than zero.

^*”+/−“ indicates directionality of the linear relationship.

Discussion

The ORA is the first commercially available clinical device to measure biomechanical properties of the cornea in vivo. Although the device was introduced as a tool for measuring intraocular pressure in eyes with altered corneal material properties, its potential role in detecting any biomechanical propensity toward KC before the manifestation of topographic signs has garnered significant interest. ^{5, 9, 11, 12, 13,} CH and CRF have been shown to decrease with increasing severity of KC but have not demonstrated much sensitivity for detecting mild forms of ectatic disease. ^{5, 11, 12, 13, 14} For instance, Kirwan’s study showed a high degree of overlap in CH and CRF between normal, forme fruste KC, and KC groups. ⁵ Likewise, in a study of 207 normal and 93 KC eyes, the variability of CH was too large to differentiate between normal eyes and mild KC, between mild and moderate KC, and between moderate and severe KC. ¹² CH and CRF are also insensitive to the effects of corneal collagen crosslinking,^{4, 24} a procedure that has been shown to increase corneal stiffness in vitro. ^{25, 26} Several investigators have observed that ORA signal morphology displays characteristic differences between ectatic and normal corneas, but these features have been investigated and quantified only to a limited extent. ^{11, 15, 20}

This study provides insight into differences in the dynamic behavior of keratoconic and normal eyes through analysis of novel waveform-derived candidate variables related to pressure, applanation signal intensity, response time or combinations of these variables. In interpreting the behavior of these variables, it is important to note that the infrared signal intensity is determined by the number of photons reflected from the corneal surface and entering the detector, which is in turn influenced by the quality of specular reflection and the total area of planar surface in the 3mm sampling zone. Lower values can occur when the cornea deforms irregularly with less planarity, both of which are likely in keratoconic corneas with irregular curvature or inhomogenous mechanical properties across the corneal width. Temporal variables describe aspects of latency and recovery time that relate to initial resistance to deformation and viscoelastic determinants of recovery. Tables 2–5 show that keratoconic eyes overall demonstrated 1) lower infrared signal peaks, 2) evidence of greater maximal deformation, 3) lower mean applanation pressures, 4) lower pressure requirements for deformation, 5) longer duration of concavity (delayed deformation recovery), 6) earlier applanation and concavity, and marked reductions in a more comprehensive hysteresis analog. The directionality of these changes is consistent with the anticipated mechanical behavior of keratoconic corneas with pathologically low material strength.²⁷ These discriminant factors are dynamic metrics that cannot be derived from the static features that are currently used to describe the keratoconus phenotype. Accordingly, they offer novel insight into the biomechanical behavior of the keratoconic eye and potentially independent predictors of disease that may be of additive value in diagnostic models that consider both static and biomechanical features of the disease. Although the current study does not explicitly study the diagnostic value of these variables in “suspect” cases with weaker topographic evidence of disease, the introduction of novel variables with more discriminative value than CH and CRF for manifest disease is a critical step toward resolving early or marginal cases of KC.

Our findings confirmed prior results showing that CH and CRF are lower in eyes with KC (Tables 2–5), ^{5, 11, 12, 13, 20} then compared the custom variables to CH and CRF in their ability to distinguish KC from normal corneas. The AUROC of all variables except LagTime were statistically significant, and 8 variables, including CRF, had higher AUROC values than CH. The test accuracies of ConcavityMin, HLA, ConcavityMean, and HLAc were also superior to those of CRF and CH (Table 6). Fontes et al previously showed that CRF and CH had test accuracies of 77.0% and 74.8%, respectively, again demonstrating the limitations of CRF and CH in discriminating between mild KC and normal corneas. ¹⁴ The high test accuracy of the custom variables described in the current report suggests their potential superiority to standard ORA variables in distinguishing ectatic disease.

Other studies have also investigated the potential of the ORA, beyond CRF and CH, to detect early KC. Avetisov et al developed an elasticity coefficient from the ORA applanation curve that describes velocity change occurring at the end of applanation. ²⁸ Touboul et al proposed a variable (CH-CRF) expressing the difference between CH and CRF that was greater in KC and post-LASIK corneas while rare in normal and glaucoma study groups. ²⁰ Schweitzer et al investigated some aspects of the infrared signal (peak amplitude 1, peak amplitude 2, width of peak 1 at half the maximum value, and width of peak 2 at half the maximum value) and air pressure curve (P1, P2, Pmax and time at these points) and found that all but the width of peak 2 at half the maximum value were significantly lower in KC when compared to CCT-matched healthy corneas; however, significant overlap existed for the variables. ¹⁵ Reichert has released a new software version for the ORA (v.3.01), not yet approved for clinical use in the United States, that introduces 37 additional variables based on a generalized morphological approach to the infrared signal waveform. Mikielewicz et al tested these and found that CRF and p2area (the area under the second peak of the signal curve) had the highest AUROC, and 14 parameters significantly correlated with KC severity.²⁹ Another study correlated dive (the speed of corneal concave deformation past applanation) with KC severity. ³⁰ Our study included an analog of dive (slope down), but several other variables demonstrated greater discriminative value.

Touboul et al also compared time-based variables between KC and normal pre-operative LASIK patients who did not develop ectasia within 24 months of the post-LASIK follow-up period.³¹ Their “time1” and “peak interval time” represent the same waveform features as our “ApplanationOnsetTime” and “ConcavityDuration,” respectively. Likewise, these equate to “time1” and “deltatime” derived by Mikielewicz et al who made comparisons between normal patients and stage I or stage II KC.³⁰ In all three studies, AUROC was measured for these two variables, with ApplanationOnsetTime equivalents out-performing ConcavityDuration equivalents. Of the equivalent variables described in these studies, none outperformed the standard ORA variable CRF.^{30, 31} In the current study, the novel variables HLA, HLAc and Concavity Min demonstrated greater sensitivity and specificity than any of the aforementioned variables and CRF.

HLA and HLAc may provide closer approximations to the classical concept of hysteresis compared to CH. ²⁰ Hysteresis is classically calculated as the area within the loading and unloading stress-strain loop of a viscoelastic material and represents the energy dissipated by the material. ^{32, 33} The ORA’s applied pressure is analogous to stress, and the applanation signal intensity is a function of displacement of the cornea from a pre-deformation configuration and thus is analogous to strain. As described in the Methods, HLA and HLAc are calculated from the construction of a pressure versus applanation signal plot that also captures temporal data (Figure 1b and 1c). This is significant since viscoelasticity prescribes that for a given stress, the corneal resultant strain is time dependent, where immediate deformation is likely due to fiber properties and the following slow deformation can be attributed to collagen matrix properties. ¹² Whereas CH provides a measure of corneal absorption capacity at a single point in the deformation history, HLA and HLAc reflect information about the cornea’s memory of form throughout much greater portions of the loading-unloading cycle.

For the 5 top predictors of disease state, the portion of the variance explained by IOPcc was no greater than 16% for any one variable and only 8% for the most predictive variable, ConcavityMin. The two variables with the strongest IOP association were, not surprisingly, a pressure-based variable, P1P2Avg (R² = 0.44), and a temporal variable, ConcavityDuration (R² = 0.43 with shorter inter-applanation durations being associated with higher IOP). A weaker relationship between the time from initiation of the air pulse to the first applanation event, ApplanationOnsetTime, was observed (R² = 0.31 with longer times associated with higher IOP). R² values for all remaining variables were 0.16 or lower. To further explore the question of whether or not IOP differences between the diagnostic groups could confound the predictive value of a custom variable with a stronger relationship to IOP, an IOPcc-normalized version of ConcavityDuration was defined (Table 4). Normalization by IOPcc resulted in no meaningful change in the performance of ConcavityDuration relative to other variables (Table 6), and it remained a statistically significant predictor of disease. Overall, only minor covariance was observed between most ORA variables and IOP, and differences in the measured IOP between the KC and normal groups did not appear to have a significant impact on discriminative value.

Table 4.

Definition and comparison of Ocular Response Analyzer variables (mean ± SD) based on Response Time for normal and keratoconus groups.

Group	Variable	Operational Definition	Related to:	Normal	Keratoconus	P value
3: Response Time (msec)	ConcavityDuration	Time lapse between A1 and A2	Temporal delay of deformation recovery between applanation events	10.7 ± 0.3	11.2 ± 0.9	<0.0001
	ConcavityDuration_IOPcc	Time lapse between A1 and A2, normalized by IOPcc	Temporal delay of deformation recovery between applanation events, normalized by IOPcc	0.87±0.46	0.69±0.11	0.01
	ConcavityTime	Time from onset of applied pressure to ConcavityMin	Time required to achieve maximum deformation from onset of impulse	13.34 ± 0.46	13.06 ± 1.82	0.14
	LagTime	Time between Pmax and ConcavityMin	Delay between peak applied pressure and maximal deformation	0.69 ± 0.43	0.96 ± 1.5	0.09
	ApplanationOnsetTime (AOT)	Time from onset of applied pressure to A1	Time required to achieve first aplanation from onset of impulse	7.97 ± 0.37	7.32 ± 0.50	<0.0001

SD = standard deviation; IOPcc = cornea-compensated intraocular pressure

Unlike the observed differences in IOP between the KC and normal groups (Table 1), abnormalities in CCT and Kmax are established morphological features of KC and primary clinical markers of disease severity. Accordingly, some co-variance between these “static” shape variables and some dynamic ORA variables can be expected even if they account for distinct physical aspects of the KC phenotype. Larger sample sizes would be needed to determine the degree of statistical orthogonality of the numerous ORA candidate variables described here and CCT and Max K in a multivariable regression model, but univariate analyses (Table 8) suggested that no more than 45% of the variance of any ORA variable was explained by CCT and no more than 35% by Max K.

In summary, ORA variables related to the degree of deformation, more comprehensive hysteresis analogues, and response time demonstrated high predictive value for KC. The most sensitive and specific variable, the minimum infrared signal during corneal concavity, is an indirect measure of maximum deformation amplitude and a more explicit indicator of corneal bending resistance than the standard ORA variables. Emerging devices such as the CorvisST³⁴ (Oculus) and OCT-based deformation analysis techniques^{35, 36} may provide more direct measures of this behavior, but this custom analysis adds immediate utility to a widely implemented clinical device and allows for future comparative studies of deformation behavior on different devices. Further studies are needed to determine the value of these variables in discriminating subclinical KC cases, but their higher discriminative value is likely to yield benefits in this challenging diagnostic group.

Table 3.

Definition and comparison of Ocular Response Analyzer variables (mean ± SD) based on Pressure for normal and keratoconus groups.

Group	Variable	Operational Definition	Related to:	Normal	Keratoconus	P value
2: Pressure	Corneal Resistance Factor (CRF), mmHg	P1 - 0.7P2	Difference in applanation pressures, weighted toward pressure required to produce the first applanation, maximizes correlation to central corneal thickness	10.4 ± 1.5	7.4 ± 1.6	<0.0001
	Corneal Hysteresis (CH), mmHg	P2 − P1	Difference in pressures between the two applanation events (a single cross-section of the pressure-deformation relationship)	11.4 ± 6.6	8.4 ± 1.4	<0.0001
	P1P2Avg	(P1+P2)/2	Average of the pressures at the two applanation events	188 ± 18	158 ± 24	<0.0001
	Pmax	Peak value of pressure signal	Force and time required to reach first applanation event	438 ± 29	387 ± 50	<0.0001

SD = standard deviation