Propensity Score Methods for Confounding Control in Non-Experimental Research

Background

Non-experimental studies are increasingly used to investigate the safety and effectiveness of medical products as they are used in routine care. One of the primary challenges of such studies is confounding, systematic differences in prognosis between patients exposed to an intervention of interest and the selected comparator group. In the presence of uncontrolled confounding, any observed difference in outcome risk between the groups cannot be attributed solely to a causal effect of the exposure on the outcome.

Confounding in studies of medical products can arise from a variety of different socio-medical processes.¹ The most common form of confounding arises from good medical practice, physicians prescribing medications and performing procedures on patients who are most likely to benefit from them. This leads to a bias known as “confounding by indication,” which can cause medical interventions appear to cause events that they prevent.^{2, 3} Conversely, patients who are perceived by a physician to be near the end of life may be less likely to receive preventive medications leading to confounding by frailty or comorbidity.^4-6 Additional sources of confounding bias can result from patient health-related behaviors. For example, patients who initiate a preventive medication may be more likely than other patients to engage in other healthy, prevention-oriented behaviors leading to bias known as the healthy user/adherer effect.^7-9

Many statistical approaches can be used to remove the confounding effects of such factors if they are captured in the data. The most common statistical approaches for confounding control are based on multivariable regression models of the outcome. To yield unbiased estimates of treatment effects, these approaches require that the researcher correctly model the effect of the treatment and covariates on the outcome. However, correct specification of an outcome model can be challenging, particularly in studies involving many confounders, rare outcomes, or strong treatment effect heterogeneity that must be correctly modeled.¹⁰ Propensity score (PS) models are an approach for estimating treatment effects that do not rely on modeling the outcome.¹¹ Rather, PS methods rely on a model of the treatment given confounders. In many cases, these models may be easier to specify.

In this paper we outline the steps involved in the implementation of a PS analysis, including a description of the various ways that a PS can be used. We focus on the practical application of these methods in the area of non-experimental studies of medical interventions. Using a large insurance claims database, we illustrate the discussed concepts using a substantive example involving the comparison of angiotensin converting enzyme inhibitors (ACEi) and angiotensin receptor blockers (ARBs) on the risk of angioedema, a well-established adverse event of ACEi initiation.^12-15

The Propensity Score

A PS is defined as the conditional probability of treatment or exposure given all confounders.¹¹ Rosenbaum and Rubin formalized PS methods and showed that all confounding can be controlled through the use of the PS.¹¹ They demonstrated that among patients with the same PS, treatment is unrelated to confounders. Therefore, the treated and untreated tend to have the same distribution of measured confounders, something that we would also achieve using randomization. Robins extended the application of PSs through the development of inverse probability of treatment weighted (IPTW) estimation¹⁶ and other weighting approaches have been proposed.¹⁷

Given a propensity score, treatment effects are usually estimated by matching, weighting, stratification, or adjustment for the PS in a multivariable regression model. In the presence of treatment effect heterogeneity, these different approaches may result in different estimates of the treatment effect.¹⁸ In PS matching each treated subject is matched to one or more control subjects depending on the matching algorithm used. The effect estimate obtained from PS matching is generalizable only to populations similar to the matched patients. In many applications, one is matching a small group of treated patients to a larger population of untreated patients. When all treated patients can be matched, this results in the average treatment effect in the treated (ATT). In some cases we cannot find untreated matches for each treated patient and therefore the estimate is not completely generalizable to the entire treated population (the ATT). In some situations, PS methods based on matching can result in a substantial reduction in sample size. See Guo and Fraser for an overview of different approaches to matching.¹⁹

PSs can also be used to generate weights that can be used to control confounding. This approach, unlike matching, does not result in a reduction of the original sample size. The purpose of PS weighting is to reweight the individuals within the original treated and control samples to create a so-called “pseudo-population” in which there is no longer an association between the confounders and treatment. Two types of weighting are commonly used: inverse probability treatment weighting (IPTW) and standardized mortality ratio weighting (SMRW).¹⁷

Inverse probability treatment weights are defined as the inverse of the estimated PS for treated patients and the inverse of one minus the estimated PS for control patients. Patients who receive an unexpected treatment are weighted up to account for the many patients like them who did receive treatment. Patients who receive a typical treatment are weighted down since they are essentially overrepresented in the data. These weights create a pseudo-population where the weighted treatment and control groups are representative of the patient characteristics in the overall population. Therefore, IPTW results in estimates that are generalizable to the entire population from which the observed sample was taken. The treatment effect obtained after applying IPTW is referred to as the population average treatment effect (ATE).^{18, 20}

Precision of estimated effects from an IPTW analysis can be improved by stabilizing the weights. This is done by multiplying the previously defined weights by the marginal probability of receiving treatment for those treated, and the marginal probability of not receiving treatment for those not treated.²¹ Stabilized weights do not increase or decrease bias, but can increase precision in the estimated treatment effects by reducing the variance of the weights.^{16, 21, 22}

For SMR weighting, treated patients are given a weight of one while weights for control patients are defined as the ratio of the estimated PS to one minus the estimated PS.^{18, 20} SMR weighting reweights the control patients to be representative of the treated population. SMR weighting results in an estimate of ATT.²⁰ Unlike PS matching, which also often estimates the ATT, no treated individuals are excluded from this analysis. Both IPTW and SMRW require the use of a robust variance estimator, similar to the variance estimator used in the generalized estimating equation methodology. This approach results in confidence intervals that are conservative, i.e., have a slightly greater than nominal coverage.

Researchers also commonly estimate treatment effects by conducting an analysis stratified across the PS. Often the strata are taken to be quintiles or deciles of the PS. Treatment effects are estimated within these strata and a summary effect is generated by taking the weighted average of the stratum-specific estimates using weights that are proportional to the number of outcomes in each stratum, optimizing statistical efficiency of estimation. Assuming uniform treatment effects, this approach results in an estimate of the average treatment effect in the population. In the presence of heterogeneous treatment effects, however, this approach may no longer result in an estimate of the average treatment effect.

Finally, it is possible to combine PS and regression methods in various ways. For example, researchers often include the PS in a regression model along with other covariates or use regression adjustment in cohorts that have already been matched on the PS. These approaches are not unreasonable and may help to remove some residual confounding. However, they may not result in estimates of a parameter of interest, such as ATE or ATT (although these could be obtained from the fitted model using marginalization). One principled approach to combining regression and PS weighting is through the use of the augmented inverse probability of treatment weighted (AIPTW) estimator.^{23, 24} This estimator depends on both a PS and multivariable outcome model and results in an estimate of the ATE. The estimator is often more efficient than an IPTW estimator. The AIPTW estimator also posses an appealing “doubly robust” property, meaning that to be consistent (asymptotically unbiased), it needs only one of the two models to be correctly specified.²⁵

Estimating the Propensity Score

In practice, the true probability of treatment is unknown and therefore must be estimated from the available data. The ability of estimated PSs to control for measured confounding is contingent on both correctly selecting variables for the PS model and specifying the functional form of the relation between selected covariates and treatment.^{11, 26, 27} Logistic regression is the most widely used method to estimate PSs.²⁸ Models that are more flexible than logistic regression are increasingly used for PS estimation and have been found to perform well in specific settings.^29-31

Once a model has been chosen, the analyst must select which variables to include in the model. Ideally, this process is guided by subject-matter knowledge. In practice, however, treatment assignment is usually determined by a complex interaction of patient, physician, and healthcare system factors that are often incompletely understood.

Various model building and variable selection strategies have been proposed to help researchers select variables for inclusion in a PS. Variable selection strategies range from simply selecting covariates a priori based on expert and substantive knowledge to approaches that are more empirical, or data-driven where very large PS models are constructed that control for large numbers of covariates.^32-34

The choice of variables that one includes in a PS model can influence both the validity and efficiency of effect estimates. Simulation studies have demonstrated that the best predictive models of exposure do not necessarily result in optimal propensity score models.²⁶ For example, the inclusion of variables in a PS model that affect the outcome but not treatment are beneficial as they decrease the variance of the estimated treatment effect.²⁶ Conversely, including variables that affect only treatment can be harmful.²⁶ These variables can increase the variability of effect estimates and, in the presence of unmeasured confounding, can increase bias.^{1, 35, 36} Studies of variable selection for PS suggest that optimal PS models, in terms of bias and precision, include all variables that affect the outcome of interest, regardless of whether they are important determinants of treatment.²⁶ Ideally, this should be determined from subject-matter knowledge, for example, as coded in causal graphs.³⁷

In the common setting of rare outcomes but common treatments, it is possible to build much larger models of treatment than of the outcome. This allows one to control for many more covariates in a PS analysis. This has led to researchers to use algorithms that result in very large PS models, including the so-called high-dimensional propensity score algorithm.^{33, 34} These methods have performed well in several empirical examples; however, theoretically, in some situations they could result in a more biased estimate than more parsimonious propensity score models.

Regardless of the particular approach that is adopted, one helpful feature of PS methods is the ability to explicitly evaluate the performance of an estimated PS model by assessing the balance of covariates after matching or weighting on the estimated PSs. Residual imbalances in the covariates indicate a possible problem with PS model specification. This process allows the researcher to evaluate and modify the PS model before attempting to estimate the treatment effect. Various strategies for PS variable and model selection based on the evaluation of covariate balance have been proposed.²⁹

Once the PS model is fit and the estimated propensity scores are generated, it is common to plot the frequency distribution (or estimated density function) of the PS within each treatment group. These plots allow the researcher to identify regions of the PS distributions with little or no overlap where treatment effects cannot be reliably estimated. It is reasonable to consider removing patients from these regions from the analysis, an approach referred to as PS trimming. Matching will automatically remove most of the patients from this region since they cannot be matched, and IPT and SMR weighted methods will reduce their influence by giving them small weights.

IPTW methods can be particularly sensitive to the influence of patients who receive unexpected treatments. Because IPTW estimates the average treatment effect in the population, it must up-weight individuals in the population who are given an apparently unusual treatment.³⁸ If treatment effects differ in these patients or there is an unmeasured reason for the unexpected treatment which affects the risk for the outcome,⁴³ IPTW estimates can be unlike estimates from other approaches. This has been observed in several empirical examples.^{20, 39}

In situations where a small number of patients influence analysis results because of their large weights, one should carefully investigate potential causes of this issue and rule out problems such as data errors. It may be reasonable to consider removal of these patients from the analysis through PS trimming. However, this changes the target population for inference, and the benefits of estimating causal effects on a well-defined population are lost. If the cause of the large weights is unmeasured confounding, however, trimming may decrease bias.⁴³ In this case, the disadvantage of losing the causal interpretation would be moot since generalizability is no longer relevant in the setting of a biased estimator.

It is worth noting that both PS methods and multivariable outcome models can identify treatment effects in patients in the non-overlapping regions of the PS by model extrapolation, i.e., assuming that the effect of treatment in the patients who are always treated or never treated is similar to the treatment effect in other patients. This assumption is often unknowingly made and can lead to misleading results. Therefore, an advantage of PS methods is the ability to identify patients whose treatment effects cannot be reliably estimated.

Exploring Effect Modification by the Propensity Score

Differences between the various approaches to using the PS occur when there is substantial treatment effect heterogeneity.¹⁸ If the treatment effect varies with the PS, different PS methods will give different results.^22,39 It can be informative to report estimated effects by strata of the PS distribution. For example, in a study of thrombolytic therapy for ischemic stroke, the IPTW approach suggested thrombolytic therapy was associated with a large risk of in-hospital mortality.²⁰ However, based on PS matching the authors found little evidence of a substantially increased mortality attributable to the treatment.

By examining treatment effects across PS strata, the authors discovered that treatment in patients with a very low probability of receiving treatment was associated with a greatly increased risk of mortality. This suggested the possibility that these patients may have possessed an unmeasured contraindication for treatment. If so, the treatment effect estimate generated by IPTW generalized to many patients who should not have received thrombolytic therapy and therefore may not be of great clinical interest. Note that the ATT estimate based on PS matching or SMRW reduces the potential for estimating the treatment effect in patients with contraindications. Examining treatment effects across strata of the PS is an effective way of identifying treatment effect heterogeneity. However, further analysis would be required to identify the true source of the heterogeneity.

Propensity Score Methods for Multi-Categorical Treatments

In the setting of a treatment that has multiple levels, the PS becomes a vector, i.e., the predicted probability of each treatment category. These can be estimated using a model for a categorical outcome, such as multinomial logistic regression. IPTW methods can be used directly in this setting. As in the case of a dichotomous treatment, each patient receives a weight equal to the inverse of the probability that they would receive their actual treatment. Stratification and matching on a multivariate PS are possible, but not preferred in this setting since the PS is no longer single dimensional.

EXAMPLE: Angioedema risk among new users of angiotensin converting enzyme inhibitors versus angiotensin receptor blockers

We identified a cohort of new users of ACE inhibitors or ARBs in a large, US employer-based insurance claims database—the MarketScan Commercial Claims and Encounters and Medicare Supplementary and Coordination of Benefit (Truven Healthcare, Inc.). The database contains patient billing information for in- and outpatient procedures and diagnoses, pharmacy medication dispensing, and enrollment information for enrolled employees, spouses, dependents, and retirees.

New ACEi or ARB use was defined as a pharmacy dispensing of an ACEi or ARB to individuals who had been free of anti-hypertensive use (beta blockers, calcium channel blockers, alpha blockers, thiazide diuretics, ACEi or ARB medications) for 6 months. To restrict to ACEi or ARB monotherapy, we also excluded individuals who initiated another antihypertensive within one day of the index ACEi or ARB prescription. Patients were followed for one year after initiation. The outcome was an occurrence of angioedema, defined as an International Classification of Diseases, Ninth Revision, Clinical Modification code of 995.1 associated with an in- or out-patient encounter. Patients with angioedema occurring during the washout period were excluded. This is a setting that may be particularly well suited to PS methods since angioedema is a relatively rare outcome and the database provides a very large collection of candidate covariates that one may wish to include in a model as potential confounders.¹⁰ Furthermore, the risk of angioedema is known to vary across race and may be heterogeneous across other subgroups.⁴⁰ The PS approach allows us to estimate a population treatment effect without the need to explicitly specify these interactions.

Estimating the Probability of ACEi versus ARB use

For the example considered in this paper, we identified covariates a priori based on the literature, substantive knowledge, and the availability of covariates within the data. Covariates were defined from diagnoses and procedures occurring during the 6-month baseline period. Considered covariates included: markers of cardiovascular risk and CVD management; recent acute events; other cardiovascular medication use and co-administration (diuretics, statins and other anti-cholesterol drugs, and anti-coagulants); and patient characteristics. A list of these covariates along with a description of their distributions stratified by exposure status is shown in Table 1.

Table 1.

Covariate distribution by treatment groups in the overall population, PS matched population, and SMR and inverse-probability of treatment weighted populations

	Overall		Propensity Score Matched		SMRW Weighted		IPTW weighted
	ARB N=289,167	ACEi N=947,004	ARB N=288,401	ACEi N=288,401	ARB N=950,218*	ACEi N=947,004*	ARB N=289,919*	ACEi N=946,946*
Patient characteristics
Mean age (SD)	55.6 (13.3)	55.3 (13.9)	55.6 (13.3)	55.7 (13.3)	55.8 (25.3)	55.3 (13.9)	55.8 (13.8)	55.4 (13.8)
Male (%)	48.0	52.5	48.0	47.7	52.2	52.5	51.2	51.5
Medicare (%)	22.3	22.5	22.3	22.4	24.0	22.5	23.6	22.5
CVD management (%)
Angiography	0.1	0.3	0.1	0.2	0.4	0.3	0.3	0.3
Cardiac stress test	7.2	6.1	7.2	7.2	6.1	6.1	6.4	6.4
Echocardiograph	9.6	9.4	9.6	9.7	9.6	9.4	9.6	9.5
Mean lipid tests (SD)	0.59 (0.90)	0.61 (0.93)	0.59 (0.90)	0.59 (0.90)	0.61 (0.93)	0.61 (0.93)	0.59 (0.91)	0.60 (0.93)
Angioplasty	0.1	0.1	0.1	0.1	0.2	0.1	0.1	0.1
Coronary stent placement	0.3	0.7	0.3	0.3	0.7	0.7	0.6	0.6
CABG	0.1	0.2	0.1	0.1	0.3	0.2	0.2	0.1
Comorbidities and acute events (%)
MI	0.2	0.6	0.2	0.2	0.8	0.6	0.7	0.5
MI in past 3 weeks	0.1	0.4	0.1	0.1	0.6	0.4	0.5	0.3
Former MI	0.3	0.4	0.3	0.3	0.4	0.4	0.4	0.3
Unstable angina	0.4	0.4	0.4	0.4	0.4	0.4	0.4	0.4
Unstable angina in past 3 weeks	0.2	0.6	0.2	0.3	0.7	0.6	0.6	0.5
Ischemic heart disease	6.2	6.7	6.2	6.1	7.2	6.7	7.0	6.6
Stroke	3.6	3.9	3.6	3.5	4.1	3.9	4.0	3.9
Diabetes	22.3	31.2	22.2	22.2	31.3	31.2	29.2	29.1
CKD	2.2	1.6	2.2	2.1	1.8	1.6	1.9	1.8
ESRD	0.7	0.5	0.7	0.6	0.5	0.5	0.6	0.5
Hypertension	55.2	44.3	55.2	54.7	44.4	44.3	46.9	46.9
Hyperlipidemia	27.6	26.7	27.6	27.7	26.3	26.7	26.6	26.9
Atrial fibrillation	1.6	1.8	1.6	1.6	2.0	1.8	1.9	1.8
Heart failure	2.0	2.8	2.0	1.9	3.1	2.8	2.9	2.6
Prevalent medication use (%)
Statins	25.7	27.3	25.7	25.9	25.8	27.3	25.8	26.9
Anti-platelets	3.3	3.1	3.2	3.2	3.2	3.1	3.2	3.2
Potassium-sparing diuretics	0.9	0.8	0.9	0.9	0.8	0.8	0.8	0.8
Loop diuretics	5.2	4.9	5.2	5.1	4.9	4.9	5.0	4.9
Niacin	1.3	1.2	1.3	1.3	1.2	1.2	1.2	1.3
Fibrates	3.4	3.5	3.3	3.3	3.3	3.5	3.3	3.4
Ezetimibe	4.2	3.5	4.2	4.2	3.4	3.5	3.6	3.7
Anti-coagulants	2.6	2.7	2.5	2.5	2.7	2.7	2.7	2.7
Concurrent medication initiation (%)
Statins	5.8	11.4	5.8	5.8	11.5	11.4	10.2	10.1
Anti-platelets	0.5	1.3	0.5	0.6	1.5	1.3	1.3	1.1
Potassium-sparing diuretics	0.2	0.3	0.2	0.2	0.4	0.3	0.3	0.3
Loop diuretics	0.8	1.6	0.8	0.9	1.9	1.6	1.7	1.5
Niacin	0.3	0.4	0.3	0.3	0.5	0.4	0.4	0.4
Fibrates	0.7	1.2	0.7	0.7	1.3	1.2	1.1	1.1
Ezetimibe	1.1	1.1	1.1	1.1	1.3	1.1	1.3	1.1
Anti-coagulants	0.2	0.6	0.2	0.3	0.7	0.6	0.6	0.5

^*Synthetic N's derived from weights

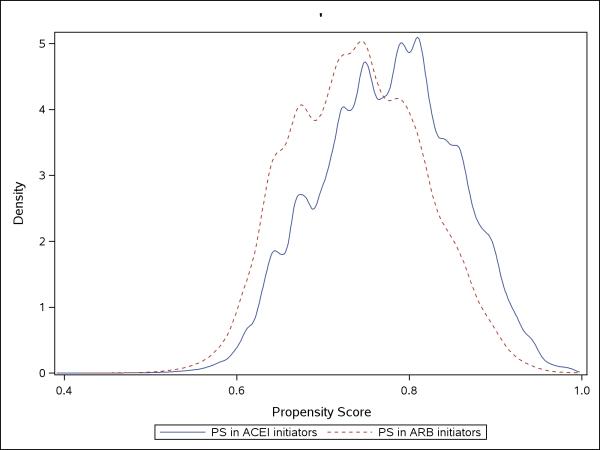
Using logistic regression, we estimated the PSs by modeling the main effects of the covariates listed in Table 1. To assess the comparability of the covariate distributions between the ACEi and ARB groups, we plotted the distributions of the estimated PSs stratified by exposure status (Figure 1). Treated (ACEi initiators) and control (ARB initiators) patients with similar PS values will, on average, have similar covariate distributions. Therefore, the overlapping region of the PS distributions identifies the subset of the observed population where the patient populations are comparable.

Figure 1.

Estimated density of the propensity scores among new users of ACE inhibitors and ARBs.

Propensity Score Implementation and Causal Effect Estimation

In each of the example analyses in this paper, we compared rates of angioedema in ACEi versus ARB users with Cox proportional hazard models in which the outcome was censored by plan disenrollment or administratively by one year after the index date. We present hazard ratios (HR) and 95% confidence intervals (CI).

We matched ACE inhibitor initiators to ARB initiators 1-to-1, without replacement, using a varying-width caliper matching algorithm (five to one digit matching). Because there were many more ACEi users and substantial overlap in the PS distributions between ACEi and ARB users, almost all of the ARB users could be matched but many ACEi users were discarded. From the matched set of observations, the treatment effect was then estimated using an unadjusted Cox proportional hazards model.

We next estimated the treatment effect using PS weighting, including IPTW and SMR weighted approaches. For IPTW, stabilized weights were used to reduce variance of the estimated treatment effect. The estimated weights were incorporated into a Cox regression model that only included the treatment variable.

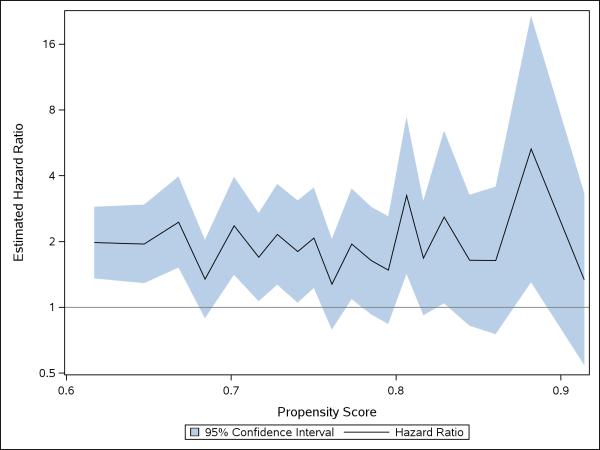
Finally, we conducted an analysis that was stratified across deciles of the PS. We plotted the strata-specific estimates in an effort to identity the existence of systematic trends in the strength and direction of the estimated effects as a function of the estimated PS (Figure 2). A stratified summary estimate was calculated using unadjusted Cox regression with an indicator variable for each PS strata.

Figure 2.

Estimated treatment effects and 95% CIs within deciles of the estimated propensity scores

For comparison, we also estimated the unadjusted treatment effect using the crude outcome model and the multivariable-adjusted treatment effect by controlling for all covariates explicitly in an outcome model. These two outcome models do not implement any PS analysis and are, therefore, not of primary interest but serve for comparison with the performance of the PS methods. All analyses were conducted in SAS. Example code that can be used to conduct these analyses is provided in the appendix.

Results

We identified 947,004 patients initiating ACEi and 289,167 patients initiating ARBs. Table 1 shows the relative similarities between ACEi and ARB groups prior to PS adjustment. Comparability of a large proportion of the observed sample is also demonstrated by a large amount of overlap in the estimated PS distributions (Figure 1).

Despite the similarities in the characteristics between ACEi and ARB groups, adjusting for the covariates in Table 1 through PS matching and weighting improved balance of the observed characteristics. For example, prior to PS adjustment, diabetes was strongly associated with receiving an ACEi vs. an ARB. Among patients with diabetes, 31% received an ACEi and 22% received an ARB. After PS weighting or matching, the proportion with diabetes is approximately equal between the two groups with 22% of patients having diabetes among the ACEi and ARB groups after PS matching, 29% after IPTW, and 31% after SMR weighting (Table 1).

As discussed, different methods of PS implementation result in estimates that generalize to different populations. The characteristics of these different populations are evident in the difference in the means and frequencies of patient characteristics reported in Table 1. Using the example of diabetes, PS matching changes the proportion of patients with diabetes in the ACEi group to match that in the ARB group (Table 1). This pattern is expected because most ARB users could be matched to an ACEI user. SMR weighting adapted the proportion of individuals with diabetes in the ARB group to reflect of the proportion in the unadjusted treatment (ACEi) population. IPTW resulted in a proportion that reflects the proportion of patients with diabetes in the overall population. Similar patterns are found for all covariates (Table 1).

Results of the estimated treatment effects are presented in Table 2. The unadjusted effect estimate resulted in an estimated hazard ratio of 1.77 (95% CI: 1.57-2.00). After adjustment for potential confounding factors, PS matching, IPTW, and SMR weighting all resulted in elevated hazard ratios compared to the unadjusted estimate, as shown in Table 2 (matching: HR=1.91 (95% CI: 1.67-2.19); IPTW: HR=1.87 (95% CI: 1.64-2.13); SMR weighting: HR=1.86 (95% CI: 1.62-2.14)). The similarity among the estimates obtained from the different methods of PS implementation suggests that there is an absence of strong treatment effect heterogeneity. In other words, the risk of angioedema associated with ACEi use appears to be constant over various sub-groups.

Table 2.

Estimated treatment effects comparing new-users of ACEi to new-users of ARBs on risk of angioedema after PS adjustment.

Model	Treatment	N	Events (%)	HR	95% CI
	ARBs	289,167	310 (0.1)	--	--
Crude (unadjusted)	ACEi	947,004	1,713 (0.2)	1.77	1.57, 2.00
Multivariable Adjusted				1.87	1.65, 2.11
	ARBs	288,401	309 (0.1)	--	--
PS-matched	ACEi	288,401	601 (0.1)	1.91	1.67, 2.19
	ARBs	950,218	938 (0.1)	--	--
SMRW	ACEi	947,004	1,713 (0.2)	1.86	1.62, 2.14
	ARBs	289,919	292 (0.1)	--	--
IPTW	ACEi	946,946	1,751 (0.2)	1.87	1.64, 2.13
	ARBs	289,167	310 (0.1)	--	--
Summary Stratified	ACEi	947,004	1,713 (0.2)	1.87	1.66, 2.12

To further explore the impact of potential effect heterogeneity, we calculated treatment effect estimates within each of the 10 PS strata. The estimates are graphically depicted in Figure 2. The estimated hazard ratios appear to fluctuate randomly around their mean suggesting that no strong systematic treatment effect heterogeneity exists across values of the PS (Figure 2).

Conclusions

Propensity score methods have become widely used tools for confounding control in non-experimental studies of medical products and procedures. Regardless of the approach that one adopts to control for confounding in non-experimental research, it is important that the researcher understand the underlying assumptions inherent in the chosen statistical method, as well as the interpretation of the results and the population(s) to which they are generalizable. We have described the assumptions necessary for valid PS analysis, the different treatment effects obtained by the various PS methods, and the populations to which these treatment effects are generalizable.

The validity of PS and multivariable outcome models require the strong assumption that all confounders are accurately measured and the exposure or outcome model is properly specified. However, PS methods provide several advantages over multivariable outcome models. First they allow the researcher to identify patients who are never treated or untreated. These patients provide no information about treatment effects without making model assumptions that, if incorrect, could bias estimates of treatment effectiveness. Second, PS models require that analysts correctly model the effect of covariates on treatment, rather than the effect of covariates and treatment on the outcome. It may be difficult to correctly specify multivariable outcomes, particularly when treatment effects are heterogeneous across patient subgroups. In the setting of strong treatment effect heterogeneity, PS methods allow the researcher to estimate average effects of treatments in different populations without needing to explicitly specifying the interactions in the model. Finally, in the usual setting of a common exposure and a rare outcome, researchers can construct much larger models of the PS. This is advantageous in studies utilizing healthcare databases that provide a large number of weak confounders.³⁴

As we have described, in the presence of treatment effect heterogeneity, different approaches to using the PS result in estimates of different treatment effects (contrasts). When deciding which particular PS approach to use, one should consider which treatment effect is of greatest interest and also whether the parameter can be reasonably estimated with the available data. For example, when comparing treated with untreated, it may be difficult to estimate ATE because there may be many untreated patients in the population who do not have an indication for treatment and therefore who would be rarely treated. In such situations, the ATT may be both more clinically relevant and also more reliably estimated. In studies comparing two candidate treatments (i.e., comparative effectiveness research), ATE may be both easily estimated and the most useful to both clinicians and policy makers.

Despite the usefulness of PS methods in non-experimental research, it should be noted that PS methods alone do not correct for errors introduced in the design or measurement of variables. For example, bias can be introduced by immortal person time (i.e., a period of time in which exposed patients cannot experience the event because of the exposure definition),⁴¹ selection bias,⁴² control of causal intermediates,⁴³ and measurement error of the exposure or outcome. Many design issues can be addressed through the use of incident user designs and active comparators.⁴⁴ However, even with careful design and appropriate statistical adjustment, it is unlikely that all biases within healthcare database research can be completely addressed. Given the complexity of the underlying medical, sociological, and behavioral processes that determine exposure to medical products and interventions as well as the limitations of typical healthcare databases, there will often exist substantial uncertainty about how one should specify PS models to control confounding.¹

Because of the inherent challenges in non-experimental research, we suggest that researchers explore and report the sensitivity of results to changes in the epidemiologic design and specifications of the statistical models. If the results are robust to such changes, the study more strongly supports the possibility that the estimates are indeed reflecting true causal relations.