Skip to main content
PMC home page
Molecular Biology and Evolution logoLink to Molecular Biology and Evolution
. 2014 Apr 9;31(6):1568–1580. doi: 10.1093/molbev/msu131

The Genotype–Phenotype Map of Yeast Complex Traits: Basic Parameters and the Role of Natural Selection

Wei-Chin Ho 1, Jianzhi Zhang 1,*
PMCID: PMC4032135  PMID: 24723420

Abstract

Most phenotypic traits are controlled by many genes, but a global picture of the genotype–phenotype map (GPM) is lacking. For example, in no species do we know generally how many genes affect a trait and how large these effects are. It is also unclear to what extent GPMs are shaped by natural selection. Here we address these fundamental questions using the reverse genetic data of 220 morphological traits in 4,718 budding yeast strains, each of which lacks a nonessential gene. We show that 1) the proportion of genes affecting a trait varies from <1% to >30%, averaging 6%, 2) most traits are impacted by many more small-effect genes than large-effect genes, and 3) the mean effect of all nonessential genes on a trait decreases precipitously as the estimated importance of the trait to fitness increases. An analysis of 3,116 yeast gene expression traits in 754 gene-deletion strains reveals a similar pattern. These findings illustrate the power of genome-wide reverse genetics in genotype–phenotype mapping, uncover an enormous range of genetic complexity of phenotypic traits, and suggest that the GPM of cellular organisms has been shaped by natural selection for mutational robustness.

Keywords: canalization, genetic robustness, environmental robustness, morphological traits, gene expression, evolution

Introduction

Describing, understanding, and utilizing the relationship between genotypes and phenotypes, or the genotype–phenotype map (GPM), are major goals of genetics (Wagner and Zhang 2011). Because most phenotypic traits, including those relevant to human diseases, are controlled by multiple genes (Falconer and Mackay 1996) and because most genes affect more than one trait (Wang et al. 2010), the GPM is a dense bipartite network of genes and traits, where an edge between a gene and a trait indicates that the gene affects the trait, with the width of the edge representing the effect size (Wang et al. 2010). Traditionally, the GPM is constructed by forward genetics, which uses linkage or association studies to identify the genetic variants underlying particular phenotypic variations among individuals of the same species (Mackay et al. 2009). Due to the limited power and efficiency of such analyses, the GPMs of human and most model organisms remain highly incomplete and uninformative (Mackay et al. 2009; Manolio et al. 2009). For example, a recent large-scale linkage analysis estimated the number of genes affecting each of 18 yeast traits (Ehrenreich et al. 2010). However, because only two strains were compared in the study, only those genetic variants that cause the phenotypic differences between these two strains were revealed. Consequently, neither the distribution of the number of genes that could affect a trait nor the distribution of the effect sizes of these genes on a trait is known. Estimating these fundamental parameters of the GPM is of vital importance, because they impact how variable a particular trait is in a population, determine the best strategy to identify the underlying genetic variants of phenotypic variations, and predict how robust and adaptable a population is to environmental challenges.

In contrast to forward genetics, reverse genetics identifies phenotypic differences among individuals of known genetic differences. If empowered by high-throughput phenotyping of systematically generated mutants, reverse genetics can be an effective approach to the GPM. For example, the fraction of genes that affect each of the 12 physiological and behavioral traits in the mouse Mus musculus has been estimated using 250 gene-knockout lines (Flint and Mackay 2009) (fig. 1a). Similar estimates have been made for eight morphological, physiological, and behavioral traits in the fruit fly Drosophila melanogaster based on P-element insertion mutagenesis (Mackay 2010) (fig. 1b). These and a few other studies (Winzeler et al. 1999; Ramani et al. 2012) showed that the proportion of genes impacting a trait can reach 10–40% of all genes in a genome. But how general these results are is unclear because the numbers of traits and species examined are small. Regarding the size distribution of the genic effects on a trait, two competing hypotheses exist. Mather’s infinitesimal model (Mather 1941; Mackay 2001) asserts that numerous loci have small and similar effects, while Robertson (1967) posits that the distribution is approximately exponential, with a few large-effect and many small-effect loci. The effect size distributions of P-element insertions on the abdominal and sternopleural bristle numbers in Drosophila support Robertson’s model (Lyman et al. 1996), but the generality of this conclusion is unknown. Although forward genetic studies from several species also support Robertson’s model, definitive conclusions are hindered by the inherent biases and limitations of the method (Mackay 2001).

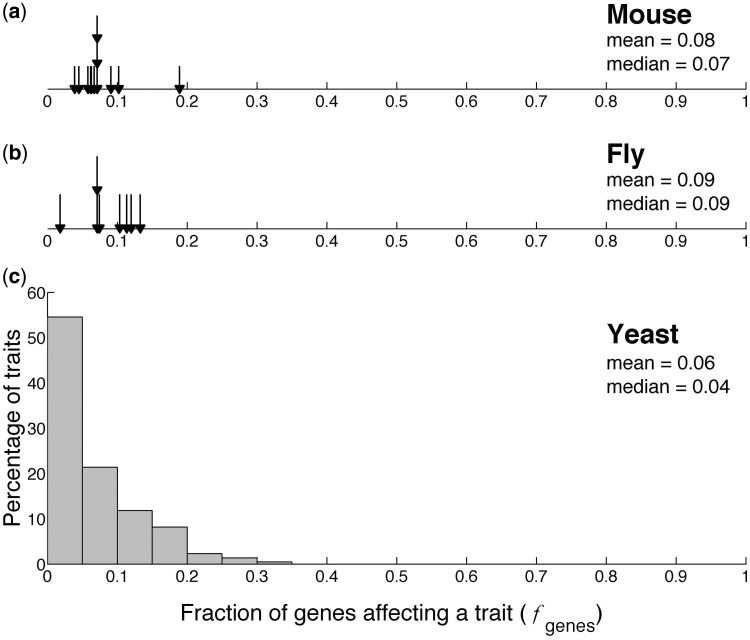
Fig. 1.

Fig. 1.

Open in a new tab

Fraction of genes affecting a trait, with the mean and median values indicated. (a) Patterns emerging from 12 traits examined in 250 lines of knockout mice. (b) Patterns emerging from eight traits examined in various P-element insertion lines of fruit flies. In (a) and (b), each arrow represents one trait. (c) Frequency distribution of the fraction of genes affecting a trait, derived from 220 morphological traits examined in 4,718 nonessential gene deletion lines of yeast.

A deeper question about the GPM is why it looks the way it does. In principle, the GPM can evolve under mutation, drift, and selection, but the relative contributions of these forces are elusive. Waddington and others proposed that the GPM has been shaped by natural selection for mutational robustness, resulting in genetic canalization (Waddington 1942; de Visser et al. 2003). Similarly, natural selection may have led to organismal robustness to environmental perturbations, or environmental canalization. These two forms of canalization, if true, would explain the surprising tolerance of living organisms to genetic and environmental disturbances, which are quite common in nature (Scharloo 1991; Flatt 2005; Wagner 2005b; Alon 2007). They also impact how adaptable and evolvable a population is in the face of mutations and environmental changes (Gibson and Wagner 2000; de Visser et al. 2003; Wagner 2005b; Draghi et al. 2010). Although selection for environmental robustness is commonly agreed upon (Gibson and Wagner 2000), direct selection for genetic robustness is controversial (Gibson and Wagner 2000; de Visser et al. 2003), except when the deleterious mutation rate is exceedingly high and/or population size is huge (e.g., in viruses) (Wilke et al. 2001; Ciliberti et al. 2007; Sanjuan et al. 2007), because for cellular organisms such selection is expected to be weak (Wagner et al. 1997; Gibson and Wagner 2000), and previous tests with relatively small data yielded ambiguous results (Stearns and Kawecki 1994; Stearns et al. 1995; Houle 1998; Gibson and Wagner 2000; de Visser et al. 2003; Proulx et al. 2007). Apparently, larger and better data are needed to evaluate it critically.

To address these fundamental questions on the basic parameters of the GPM and the role of natural selection in shaping the GPM, we use the budding yeast Saccharomyces cerevisiae, in which 220 morphological traits have been quantitatively measured by analyzing fluorescent microscopic images of triple-stained cells of the wild-type strain and 4,718 mutant strains that each of which lacks a nonessential gene (Ohya et al. 2005). The generality of the findings from the morphological traits is then verified by analyzing 3,116 gene expression traits in the wild-type and 754 gene-deletion strains of S. cerevisiae.

Results

Fraction of Genes Affecting a Morphological Trait

In the yeast phenotyping experiment, 220 morphological traits were measured in multiple wild-type cells from each of 123 replicate populations (Ohya et al. 2005). In addition, for each of the 4,718 mutant strains, multiple isogenic cells from one population were measured for the 220 traits (Ohya et al. 2005). To determine whether deleting a gene affects a trait, we used the Mann–Whitney U test to compare the trait values of multiple cells of the gene-deletion strain and those of the wild type from an arbitrary replicate population. A gene deletion is tentatively considered to affect the trait if the P value is lower than 0.05. The distribution of the fraction of genes affecting a trait (fmt) is shown in supplementary figure S1a, Supplementary Material online. The mean and median of fmt are 0.37 and 0.38, respectively. To remove the confounding factor of potential environmental differences between the mutant and wild-type strains in the experiment and to control for multiple testing, for each trait, we estimated the fraction (fwt) of the other 122 wild-type populations in which the trait value differs significantly from that of the arbitrary wild-type population used. We found fwt to be substantial (supplementary fig. S1b, Supplementary Material online). Subtracting fwt from fmt, we obtained fgenes, the true fraction of genes that, when deleted, significantly impact the trait. We found that fgenes varies greatly among traits (fig. 1c) and that this variation significantly exceeds the random expectation under homogenous fgenes (P < 0.01; permutation test). Specifically, 37.7%, 39.6%, 20.0%, and 2.7% of traits are each affected by <1%, 1–10%, 10–30%, and >30% of all nonessential genes in the yeast genome, respectively. The mean and median of fgenes are 0.06 and 0.04, respectively (fig. 1c). These results remain similar regardless of the P-value cutoff used (supplementary fig. S1c–d, Supplementary Material online). Use of another arbitrary replicate population of the wild-type strain yielded similar results. For each trait, we also estimated fgenes by examining whether the mean trait value of a mutant would be an outlier in the distribution of the 123 means of the wild-type replicate populations, but the results were similar (supplementary fig. S1e, Supplementary Material online). Because some of the 220 traits are highly correlated, we removed those traits whose genetic correlation coefficients exceed 0.7, resulting in a data set with 54 traits. But, the mean and median values of fgenes are virtually unchanged (supplementary fig. S2, Supplementary Material online).

Whether a genic effect is detectable depends on the statistical power of the experiment, which is determined by the precision of the phenotypic measurement, the sample size, and the constancy of the environment in which different strains are phenotyped. In the present case, the number of cells measured varied among traits and strains. On average, 91 and 95 cells were measured in the wild-type (per replicate population) and deletion strains, respectively. The effect of environmental variation is clearly seen in the 123 wild-type populations, because the standard deviation of the mean phenotypic value among the 123 populations is on average 2.48 times the mean strand error calculated from individual populations (supplementary fig. S3, Supplementary Material online). This observation suggests that environmental fluctuation rather than sample size or measurement error is the dominant factor limiting the detection of genic effects in the present study.

Mean Effect Size of Gene Deletion on a Morphological Trait

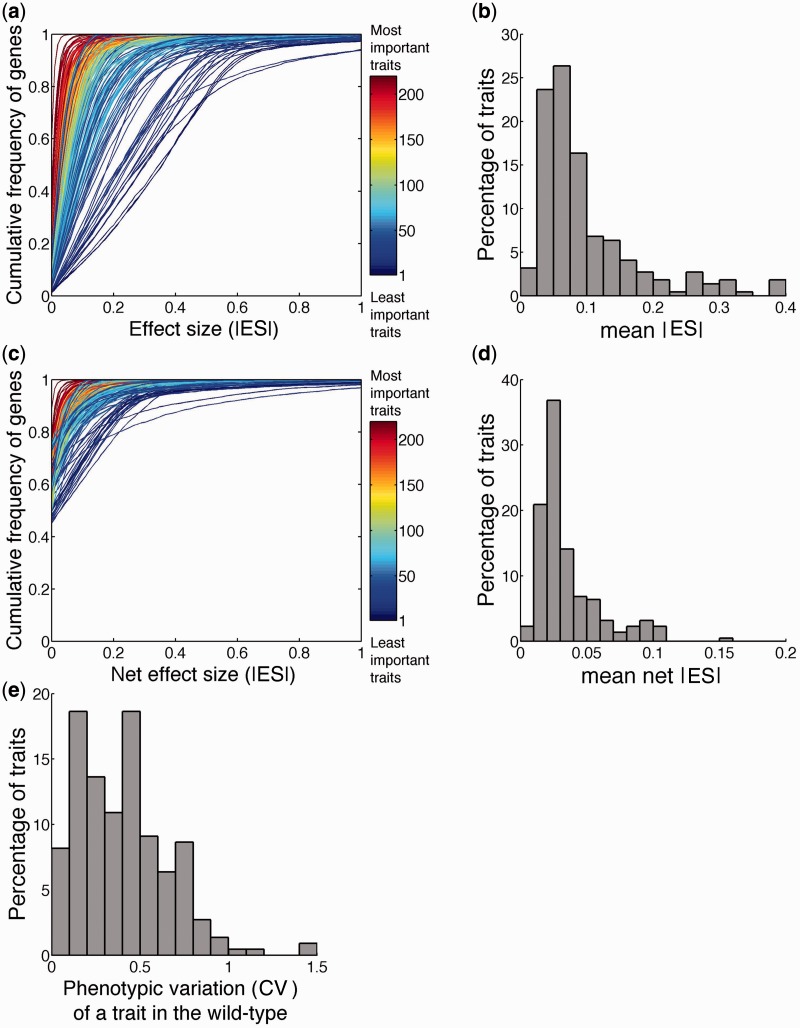
We define the raw effect size (ES) of deleting a gene on a trait as the difference between the mean trait value of the deletion strain and the average of the mean trait values of the 123 replicate populations of the wild-type strain, divided by the average of the mean trait values of the 123 populations of the wild type. The cumulative probability distribution of |ES|, or the absolute value of ES, of 4,718 genes on each of the 220 traits is depicted by a curve in figure 2a. This distribution shows that, in most cases, a trait is affected by more genes of small effects than those of large effects, as proposed by Robertson (1967). Considering only statistically significant genic effects does not alter this conclusion. The mean |ES| of all nonessential genes on a trait varies substantially among traits, with an average value of 0.098 (fig. 2b).

Fig. 2.

Fig. 2.

Open in a new tab

Distributions of the absolute values of the raw and net effect sizes (|ES|) of 4,718 nonessential gene deletions on 220 morphological traits in yeast. (a) Cumulative probability distributions of raw |ES| of 4,718 gene deletions on 220 traits. Each curve represents a trait and is colored according to trait importance (TI). The distributions are shown only in the range of 0 < |ES| < 1 to better distinguish among different curves. (b) Distribution of the mean raw |ES| among the 220 traits. (c) Cumulative probability distributions of net |ES| of 4,718 gene deletions on 220 traits. (d) Distribution of the mean net |ES| among the 220 traits. (e) Distribution of the wild-type phenotypic variation (CV) among the 220 traits.

Due to inevitable environmental fluctuations among populations of cells that were phenotyped, we computed net |ES| by subtracting from raw |ES| a term called pseudo |ES|, which is the absolute ES expected from environmental variation and sampling error arising from a limited sample size (see Materials and Methods). The cumulative probability distribution of net |ES| of 4,718 genes on each of the 220 traits is depicted by a curve in figure 2c. Again, this distribution supports Robertson’s model (1967). The mean net |ES| of all nonessential genes on a trait also varies substantially among traits, with an average value of 0.035 (fig. 2d).

For each trait, the phenotypic variation among isogenic cells includes variations originating from stochastic noise of the trait, random measurement error, and environmental variation. We quantified the phenotypic variation among isogenic wild-type cells by the coefficient of variation (CV = standard deviation/mean), including both the variation among cells in a population and the variation among replicate populations (see Materials and Methods). The mean CV of the 220 traits examined is 0.41 (fig. 2e).

More Important Morphological Traits Are More Robust to Various Perturbations

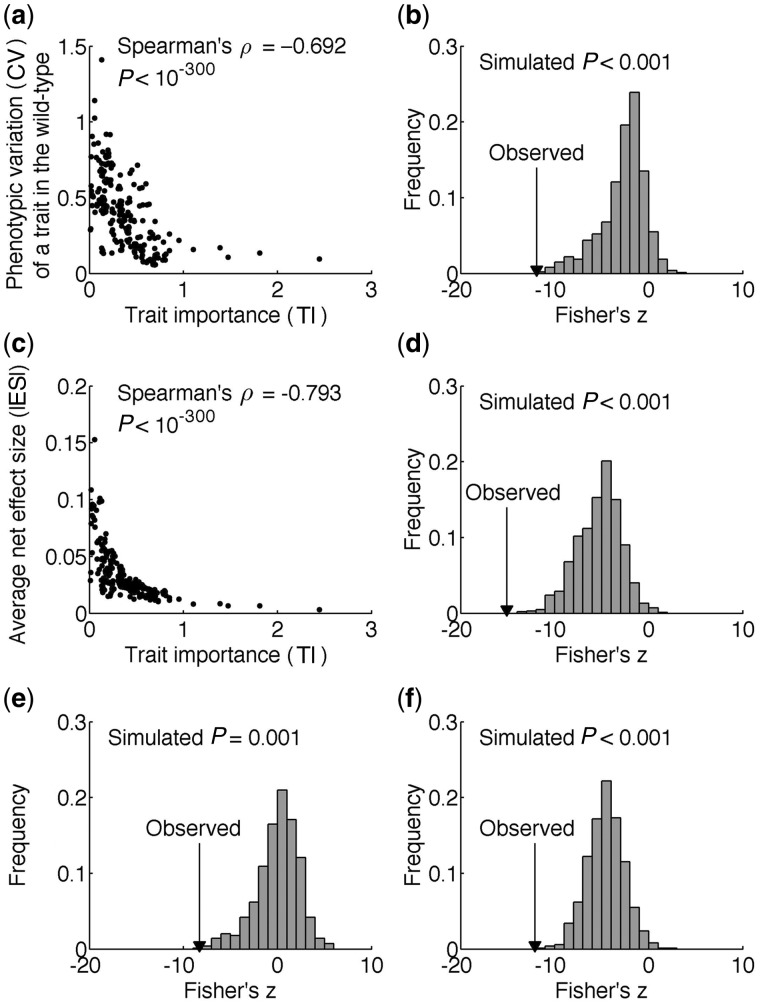
After describing the basic parameters of the GPM for yeast morphologies, we explore the potential role of natural selection in shaping the GPM. The hypothesis of natural selection for environmental robustness predicts that traits that are more important to organismal survival and reproduction have smaller CV, because natural selection for the environmental robustness of a trait intensifies with the importance of the trait. Similarly, the hypothesis of natural selection for genetic robustness predicts that, under certain conditions, traits that are more important to organismal survival and reproduction have smaller net |ES|, because such a GPM minimizes the deleterious effects of random mutations (Wagner et al. 1997) (see Materials and Methods). To test these hypotheses, we define trait importance (TI) by 100 times the reduction in fitness caused by 1% change in the phenotypic value of the trait concerned, and estimated it using the net |ES| estimates and the fitness values of the gene deletion strains in the medium where the morphological data were collected (Qian et al. 2012) (see Materials and Methods). When estimating TI, we used 2,779 gene deletion strains whose fitness values relative to the wild type are smaller than 1 (see Materials and Methods). As a result, 210 traits (out of 220) have TI > 0, 197 of which significantly exceed 0 (nominal P < 0.05). These 210 traits were subject to further analysis.

We found the CV of a trait to decrease with the rise of TI (ρ = −0.692, P < 10−300; fig. 3a). Because the phenotypic measurements of the wild type and mutants were used in estimating TI, the correlation between CV and TI could be artifactual. To exclude this possibility, we estimated 1,000 sets of pseudo TI values by randomly shuffling the fitness values among the gene deletion strains. In each set, negative TI values are ignored because they are biologically meaningless. We calculated the 1,000 rank correlations between CV and the 1,000 sets of positive pseudo TI. Because these rank correlations are not directly comparable due to different sample sizes, we converted the correlations (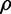Inline graphic) to Fisher’s z scores by 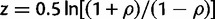Inline graphic. We found the true z score (converted from ρ = −0.692) to be more negative than all 1,000 pseudo z scores (P < 0.001; fig. 3b), suggesting that the negative correlation between CV and TI is genuine. Because the same phenotypic data were used in calculating the true z and the pseudo z scores, their disparity cannot be caused by measurement errors in phenotyping. Rather, it reveals smaller stochastic noise and environmental variation for more important traits, consistent with the hypothesis that natural selection has increased the phenotypic robustness of organisms to stochastic noise (Batada and Hurst 2007; Lehner 2008; Wang and Zhang 2011) and environmental perturbation (Gibson and Wagner 2000).

Fig. 3.

Fig. 3.

Open in a new tab

Environmental/stochastic robustness and genetic robustness of yeast morphological traits. (a) The CV of a trait among isogenic wild-type cells decreases with the rise of TI. Each dot is a trait. (b) Distribution of Fisher’s z derived from the rank correlation between CV and pseudo TI. (c) The mean net |ES| of gene deletion on a trait decreases with the rise of TI, demonstrating genetic robustness. Each dot is a trait. (d) Distribution of Fisher’s z derived from the rank correlation between mean net |ES| and pseudo TI. (e) Distribution of Fisher’s z derived from the partial rank correlation between CV and pseudo TI, after the control of mean net |ES|. (f) Distribution of Fisher’s z derived from the partial rank correlation between mean net |ES| and pseudo TI, after the control of CV. In (b), (d), (e), and (f), the real z observed from the actual data is indicated by an arrowhead, and the P value is the probability that a randomly picked pseudo z is more negative than the real z.

We also observed a negative correlation between mean net |ES| across all deletion lines and TI (ρ = −0.793, P < 10−300; fig. 3c), indicating that the mean effect size of all nonessential genes on a trait decreases as the trait becomes more important, supporting the hypothesis of natural selection for mutational robustness. This result was verified by comparing the observed z (converted from ρ = −0.793) with 1,000 pseudo z scores converted from the correlations between mean net |ES| and the 1,000 sets of positive pseudo TI (P < 0.001; fig. 3d).

Interestingly, we found no significant correlation between the TI of a trait and the number of genes affecting the trait (fgenes) (simulated P = 0.07; supplementary fig. S4, Supplementary Material online). Hence, the lower mean net |ES| of important traits is not because there are fewer genes impacting important traits but because the individual impacts are smaller.

Because genetic robustness may be a byproduct of natural selection for environmental/stochastic robustness or vice versa (the congruence hypothesis) (Gibson and Wagner 2000; de Visser et al. 2003), it is important to examine whether the two types of robustness have independent origins. We found that the partial correlation between CV and TI after the control of mean net |ES| is ρ = −0.532 (P = 1.1 × 10−16), while the partial correlation between mean net |ES| and TI after the control of CV is ρ = −0.700 (P = 4.7 × 10−32). Hence, the environmental/stochastic robustness and genetic robustness are not entirely attributable to each other and must have their separate origins. These results were further confirmed by comparing with the random expectations from the 1,000 sets of pseudo TI (fig. 3e and f). Due to the potential difference in the fitness effects of positive and negative genic effects on a trait, we also reanalyzed the data using positive (or negative) effects only, but found the results to be qualitatively unaltered (supplementary table S1, Supplementary Material online; see Materials and Methods).

To confirm that the significant correlations among CV, mean net |ES|, and TI are not due to high genetic correlations among some traits, we used two approaches to generate less correlated traits. First, we removed highly correlated traits as was done for supplementary figure S2, but the negative correlation between CV and TI and that between mean net |ES| and TI still exist, so do the partial correlations (supplementary fig. S5, Supplementary Material online). Second, we performed a principal component analysis using the net |ES| matrix (see Materials and Methods). Using the principal component traits, we confirmed the negative correlation between mean net |ES| and TI (supplementary fig. S6, Supplementary Material online).

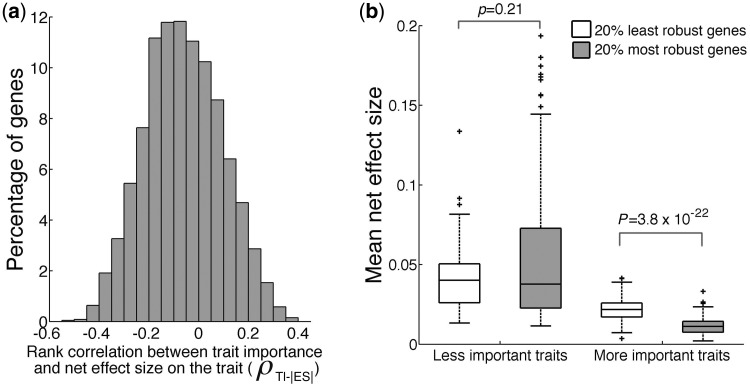
The negative correlation between mean net |ES| and TI could mean a decrease in net |ES| for important traits or an increase in net |ES| for unimportant traits; only the former supports natural selection for genetic robustness. To distinguish between these two possibilities, we analyzed the 4,718 genes separately. For each gene, we estimated the rank correlation (ρTI-|ES|) between the importance of a trait and the net |ES| of the gene on the trait among the 210 traits with estimated TI. We found ρTI-|ES| to vary greatly among genes, although most (64.8%) genes have negative ρTI-|ES| values (fig. 4a). We halved the 210 traits into a group of less important and a group of more important traits. We then, respectively, calculated the mean net |ES| of the 20% most robust genes (i.e., with the most negative ρTI-|ES| values) and 20% least robust genes (i.e., with the smallest |ρTI-|ES|| values) on each group of traits. Natural selection for mutational robustness should intensify at more important traits. Thus, for the group of less important traits, we expect net |ES| to be similar between the least robust and most robust genes; but for the group of more important traits, net |ES| should be smaller for the most robust genes than for the least robust genes. An opposite pattern would be inconsistent with selection for mutational robustness. We found that, for the less important traits, the mean net |ES| is similar between the most robust and least robust genes (P = 0.21, Wilcoxon signed-rank test; fig. 4b). But, for the more important traits, the mean net |ES| of the most robust genes becomes significantly smaller than that of the least robust genes (P = 3.8 × 10−22, Wilcoxon signed-rank test; fig. 4b). These findings demonstrate that the negative correlation between TI and mean net |ES| is caused by the reduction of mean net |ES| of a large fraction of genes on important traits, supporting natural selection for genetic robustness.

Fig. 4.

Fig. 4.

Open in a new tab

Among-gene variation in contribution to genetic robustness. (a) Frequency distribution of a gene’s rank correlation (ρ) between its absolute net effect size (|ES|) on a trait and the TI. Most genes show negative correlations. (b) Effect size differences between the 20% most robust (having the most negative ρ values in a) and 20% least robust (having the smallest |ρ| values) genes on traits of different importance. Traits are divided into two equal-size bins based on TI: less-important traits and more important traits. In the box plot (see the scale marked on the y-axis), the lower edge and upper edge of a box represent the 25% quartile (q1) and 75% quartile (q3), respectively. The horizontal line inside a box indicates the median (md). The whiskers extend to the most extreme values inside inner fences, md ± 1.5(q3 − q1). The values outside the inner fences (outliers) are plotted by plus signs.

Fitness Advantage of Genetic Robustness

One primary reason why natural selection for genetic robustness is controversial for cellular organisms is that its selection coefficient is expected to be small (Gibson and Wagner 2000). Below, we show that the selection coefficient in the present case is large enough for the effect of natural selection to surpass that of genetic drift.

If we consider only null mutations but not other deleterious mutations, the fitness advantage (g) of a robustness modifier equals ∑(μiΔsi/si), where μi is the null mutation rate at gene i and is on average 2.15 × 10−6 per gene per generation in yeast (see Materials and Methods), si and si − Δsi are the selection coefficients against the null mutation of gene i in the absence and presence of the modifier, respectively, and ∑ indicates summation over all genes considered (see Materials and Methods). The modifier is strongly selected, for when S = 2Neg = 2 × 107 × 2.15 × 10−6 × ∑(Δsi/si) = 43∑ (Δsi/si) greatly exceeds 1, where Ne is the effective population size and equals ∼107 in yeast (Wagner 2005a). For example, g = 2.15 × 10−5 and S = 430 if the modifier buffers the null mutations of 20 genes with a mean Δsi/si = 0.5.

With the above consideration, let us estimate the fitness advantage to yeast conferred by the observed genetic robustness. This advantage can be partitioned into two parts: 1) a reduction of the averaged mean effect size of all genes on all traits and 2) a greater reduction of mean effect sizes on more important traits. Ideally, we should compare the organismal fitness resulting from the real GPM in the presence of mutation and the fitness resulting from the ancestral GPM in which the effect sizes had not been reduced by selection. This comparison, however, is infeasible, because of the difficulty in inferring ancestral effect sizes. Instead, we estimated the fitness resulting from a hypothetical GPM in which the effect sizes of a gene on various traits are randomly sampled (without replacement) from the observed net effect sizes of the gene on these traits. This procedure yields a conservative estimate of the fitness advantage of genetic robustness, because only part 2) is estimated. Employing this approach, we created 1,000 hypothetical GPMs.

We built a multivariate linear model in which the fitness values of 2,779 gene deletion strains that are less fit than the wild type are explained by the phenotypes of the 220 traits (see Materials and Methods). This model explains 45% of fitness variance among the deletion strains used. Using this model and a GPM, we can predict the fitness upon the deletion of a gene. For example, the predicted expected fitness upon the deletion of one of the 2,779 nonessential genes from the real GPM is 0.9443, which is essentially identical to the experimentally determined mean fitness (differs by 4 × 10−16) of the 2,779 nonessential gene deletion strains. For the 1,000 hypothetical GPMs, the fitness is predicted to drop to 0.8956, with a standard deviation of 0.0091, when a randomly picked nonessential gene is deleted. Thus, the deleterious effect of deleting an average nonessential gene from the real GPM has been reduced by an impressive fraction of Δs/s = (0.9443 − 0.8956)/(1 − 0.8956) = 46.6%, compared with the GPMs with randomized effect sizes. Consequently, the yeast fitness upon a gene deletion has risen by (0.9443 − 0.8956)/0.8956 = 5.4%. The total fitness improvement conferred by robustness to null mutations is G = ∑(μiΔsi/si) = 2,779 × 2.15 × 10−6 × 46.6% = 2.8 × 10−3. Here we use G instead of g to denote the combined effect of multiple modifiers. Because deleterious mutations that do not completely abolish the function of a gene were not considered in the above calculation, the total fitness gain from mutational robustness should be greater than 2.8 × 10−3. Of course, as deleterious mutations become less severe after the canalization, their equilibrium frequencies in the population will increase. Consequently, the mean fitness of the population will return to the previous value (Wagner et al. 1997).

Genetic Robustness of Gene Expression Traits

To examine whether the genetic robustness observed from the morphological traits can be generalized to other traits, we turn to another large set of traits where the expression level of each of 3,116 yeast genes is considered a trait. The genetic robustness of yeast expression traits was previously assessed by calculating how much the expression of each gene varies among gene deletion lines and testing if the degree of variation is correlated with the importance of the gene, but the results were mixed (Proulx et al. 2007). We expanded the analysis from considering the effects of 276 gene deletions (Proulx et al. 2007) to 754 by combining several microarray experiments performed in rich media (see Materials and Methods). We define the raw ES of deleting gene 1 on the expression level of gene 2 by the difference in the expression level of gene 2 between the deletion strain and the wild-type strain, divided by the expression level of gene 2 in the wild type. Because the expression levels were measured in several different microarray experiments, it is difficult to assess whether an effect is statistically significant. But if we use raw |ES| of 0.2, 0.3, 0.4, and 0.5 as potential cutoffs, the average proportion of gene deletions that affect the expression level of a gene is 20%, 10%, 5.5%, and 3.3%, respectively. Thus, the expression traits are of comparable complexity as the 220 morphological traits.

In principle, we should estimate the importance of gene expression traits by the approach used for estimating the TI of morphological traits. However, this would require direct comparison of gene expression levels across different microarray data, which is unlikely to be reliable. Instead, we followed a previous study (Proulx et al. 2007) to use the fitness effect of deleting a gene as a proxy for the TI of the expression trait of the gene. That is, the expression of a gene is more important if the fitness effect of deleting the gene is larger. This proxy for TI is reasonable because the fitness effect caused by a small expression change of a gene is highly correlated with that caused by deleting the gene (Wang and Zhang 2011). We found that, regardless of whether TI is measured by gene essentiality (i.e., categorical) or the fitness effect of gene deletion (i.e., continuous), there is a significant negative correlation between the importance of a trait (TI) and the mean absolute ES of gene deletion on the trait (|ESG|, the subscript G indicates genetic perturbation) (table 1). Here, ESG is defined in the same way as ES for morphological traits. We also found a negative correlation between TI and the mean absolute ES of environmental changes (|ESE|, the subscript E indicates environmental perturbation; see Materials and Methods). Similar to the results for the morphological traits, the correlation between TI and |ESG| remains significant after the control of |ESE|, and the correlation between TI and |ESE| remains significant after the control of |ESG| (table 1), suggesting that neither the genetic nor environmental robustness of gene expression is entirely caused by the other. Similar results were obtained when the wild-type gene expression level is controlled (supplementary table S2, Supplementary Material online). We also analyzed an expanded set of environmental perturbations, and the results were similar (supplementary table S3, Supplementary Material online). After removing highly correlated expression traits (see Materials and Methods), we still observed qualitatively similar results for the 54 remaining traits (supplementary table S4, Supplementary Material online).

Table 1.

Spearman’s Rank Correlation between the Importance of a Gene Expression Trait to Fitness and the Mean Effect Size of Gene Deletion (|ESG|) or Environmental Perturbation (|ESE|).

Variables Correlated Variables Controlled Spearman’s ρ P Value
Fitness effecta, |ESE| −0.146 2.1e−16
Fitness effecta, |ESG| −0.180 3.7e−24
Fitness effecta, |ESE| |ESG| −0.094 1.3e−07
Fitness effecta, |ESG| |ESE| −0.141 1.9e−15
Essentialityb, |ESE| −0.088 8.1e−07
Essentialityb, |ESG| −0.125 2.2e−12
Essentialityb, |ESE| |ESG| −0.051 4.8e−03
Essentialityb, |ESG| |ESE| −0.103 9.6e−09
Open in a new tab

aTrait importance is measured by the fitness defect caused by deleting the gene.

bEssentiality = 0 for nonessential traits and 1 for essential traits.

Because essential genes tend not to have a canonical TATA box in their promoters (Han et al. 2013) and because the expression levels of TATA-less genes are less noisy, less sensitive to environmental changes, and more conserved among species than those of TATA-containing genes (Newman et al. 2006; Tirosh et al. 2006), one wonders whether the above findings are artifacts caused by covariations of both gene essentiality and expression insensitivity with the absence of TATA boxes. In other words, we may observe a negative correlation between TI and |ESE| and/or that between TI and |ESG| if certain genes must use TATA-less promoters for reasons other than environmental/genetic robustness. To exclude this possibility, we analyzed TATA-containing and TATA-less genes (Rhee and Pugh 2012) separately. We found that the hypothesis of adaptive origin of genetic robustness is supported for both TATA-containing and TATA-less genes (supplementary table S5, Supplementary Material online). The evidence for an independent adaptive origin of environmental robustness is weakened for TATA-containing genes, but remains strong for TATA-less genes (supplementary table S5, Supplementary Material online). Taken together, these analyses support that the signals for adaptive genetic and environmental robustness of gene expression traits are genuine.

Discussion

Using genome-wide reverse genetics, we estimated the fraction of nonessential genes affecting a trait for a large number of traits for the first time in any organism. We discovered that this fraction is on average 6% for the 220 yeast morphological traits examined. An analysis of 3,116 yeast gene expression traits revealed a comparable degree of genetic complexity. It is interesting to note that the fraction of genes affecting a trait is similar among yeast, fly, and mouse (P > 0.05 in all pairwise comparisons; Mann–Whitney U test; fig. 1), despite the rather small data from the latter two species and multiple differences in phenotyping, sample size, and type of traits examined. It is tempting to suggest that our observation from yeast, a unicellular eukaryote, may be widely applicable to other organisms, including mammals. More studies, however, are needed to verify this observation.

Although the fraction of genes affecting a yeast trait appears intermediate on average (6% or ∼300 nonessential genes), the among-trait variation of this quantity is huge. Nearly two-fifths of traits are relatively simple, each affected by <1% of genes (i.e., ∼50 genes). Two-fifths of traits are of medium complexity, each affected by 1–10% of genes (i.e., 50–500 genes). Over one-fifth of traits are highly complex, each affected by >10% of genes (i.e., >500 genes), including those impacted by >30% of genes (i.e., >1,500 genes). A systems approach (Mackay et al. 2009) is not only preferred but also necessary for understanding why and how so many genes affect each of these highly complex traits. Theoretical studies are needed to understand how the discovered distribution of genetic complexity of phenotypic traits impacts phenotypic variation and evolution.

Our findings partially explain why forward genetics is inefficient in genotype–phenotype mapping. Among the large number of genes that potentially affect a complex trait, typically only a few are variable in the mapping population of each linkage analysis. In association studies, although the number of variable causal genes may be high when the mapping population is large, the statistical power is generally low because most causal genes are not highly polymorphic. If one is interested in the actual mutations causing a particular trait variation in a population, using forward genetics seems necessary. But if one is interested in the molecular genetic network responsible for and potentially impacting a trait, reverse genetics offers a more complete and unbiased view. Although only gene deletions are considered here, genome-wide reverse genetics is applicable to other types of mutants when they become available, including gain-of-function mutants.

A common approach to verifying a candidate causal gene identified by forward genetics is to examine the phenotypic effect of deleting the gene from a wild-type strain. However, the validation can only prove that the gene affects the trait but cannot vindicate that the gene causes the trait variation seen in the mapping population. This is especially so for highly complex traits, where a randomly picked gene has a >10% chance to affect the trait. Additional tests, such as allelic replacement, will be necessary to reduce the false-positive rate.

We showed that the phenotypic variation (CV) of a trait among isogenic wild-type individuals decreases with the rise of TI, consistent with the hypothesis of natural selection for environmental/stochastic robustness. We also showed that the mean effect size of gene deletion decreases as the trait becomes more important, consistent with the hypothesis of natural selection for genetic robustness. We found that the environmental/stochastic robustness and the genetic robustness cannot fully explain each other, rejecting the congruence hypothesis (de Visser et al. 2003) and suggesting separate origins of the two types of robustness. One rationale of the congruence hypothesis is that some genes underlying environmental robustness are also used for genetic robustness (Lehner 2010). An often-cited example is the heat shock protein Hsp90 in Drosophila (Meiklejohn and Hartl 2002). But more recent work found that Hsp90 buffering of genetic perturbation is independent of environmental/stochastic robustness (Milton et al. 2003). Furthermore, mapping data from mouse, Arabidopsis, and yeast suggested that genetic robustness and environmental robustness are often controlled by different loci (Fraser and Schadt 2010). Although genetic robustness may also originate from some intrinsic properties of the gene interaction networks without direct selection for robustness (Siegal and Bergman 2002; Hermisson and Wagner 2004), this hypothesis cannot explain why the observed genetic robustness is greater for more important traits. Taken together, our results provide strong evidence for the action of natural selection in shaping the GPM and in improving the mutational robustness of relatively important traits in yeast.

Three reasons may explain why several earlier studies did not find clear evidence of natural selection for genetic robustness. First, natural selection for genetic robustness is expected to be weak unless the population size is large and the deleterious mutation rate is high (Wagner et al. 1997). The previous ambiguous results in fly (Stearns and Kawecki 1994; Stearns et al. 1995; Houle 1998) may reflect weaker selection for genetic robustness in fly than in yeast due to their difference in effective population size. In the light of this comparison, it is interesting to ask if genetic robustness potentially exists in humans, which have an effective population size of 104 and a null mutation rate of 1.5 × 10−5 per gene per generation (see Materials and Methods). We calculated that S = 2Ne∑(µiΔsi/si) = 0.3∑(Δsi/si) for a modifier buffering deleterious mutations in humans. Assuming an average Δsi/si of 0.5, S will exceed 1 if a modifier simultaneously affects >6 genes. Because the total number of genes in humans is about four times that in yeast, if fgenes in human is not lower than that in yeast, it is possible that a modifier affects much more than six genes. Nonetheless, it is clear from this calculation that selection for genetic robustness is ∼100-fold weaker in humans than in yeast. Second, TI is quantitatively estimated in our analysis but not in many previous studies, rendering our analysis more powerful and objective than those earlier analyses. But, it should be noted that we estimated morphological TI by the slope in the correlation between trait values and fitness values among 2,779 gene deletion strains. As such, our estimates may not accurately reflect causal relationships between the variation of a trait and fitness. However, it is virtually impossible to establish causal relationships between traits and fitness, because no trait is independent of all other traits such that one can manipulate a trait without affecting all other traits. The fact that our use of the inaccurate TI estimates still yields significant evidence supporting natural selection for genetic robustness suggests that the true signal is even stronger. In other words, our results are likely to be conservative. Note that in some earlier studies, TI was named or defined differently. For example, some researchers used the term “sensitivity,” defined by the percentage of fitness change associated with a 1% or 10% phenotypic change (Stearns and Kawecki 1994; Stearns et al. 1995; Houle 1998), while Proulx et al. (2007) measured the “importance” of a gene expression trait by the growth defect caused by deleting the gene. Finally and probably most importantly, our data are much larger than those used in all previous studies, allowing detecting selection for genetic robustness and excluding the congruence hypothesis.

Our analysis has three caveats. First, the morphological variations of the wild-type yeast cells were measured in the same gross environment, which may underestimate CV, which in turn may lead to an overestimation of genetic robustness unexplainable by environmental robustness. But this criticism does not apply to the gene expression data analyzed here, because they include gross environmental variations. Although these environments do not resemble the historical natural environments of yeast, they include important environmental variables that yeast faces in nature, such as temperature, osmotic pressure, and amino acid concentrations. The overall similar findings of genetic robustness between the morphological and expression traits suggest that the lack of gross environmental variation has a minimal impact on the result of morphological traits, but this conclusion requires further confirmation.

Second, our measurement of effect size is limited to null mutations, while in nature there are also abundant mutations that impact the function of a gene only slightly or moderately; their effect size would be smaller. If the effects of a genic mutation on various traits are proportionally smaller when the mutation reduces but not abolishes the gene function, all of our empirical results should still hold. Our calculation of the fitness advantage of genetic robustness is conservative, because considering additional deleterious (but not null) mutations will increase the benefit of genetic robustness. For obvious reasons, our analysis is limited to the deletions of ∼80% of yeast genes that are nonessential. Although we do not expect essential genes to behavior qualitatively differently from nonessential genes, future studies are required to validate this expectation.

Third, our study focused on lab strains of yeast because the deletion lines were all constructed in the genetic background of a lab strain. Whether our results apply to natural strains of yeast requires future research. Recent studies have revealed substantial genomic (Bergstrom et al. 2014) and morphological (Yvert et al. 2013) variations among yeast strains. Our analysis can be applied to strains of different genetic backgrounds when gene deletion lines in these backgrounds as well as their morphological data become available.

It is unknown what molecular genetic mechanisms are responsible for the observed reductions in the effect sizes of environmental and genetic perturbations on important traits. Previous yeast studies identified so-called capacitor genes, which could buffer phenotypic variations upon environmental perturbations. For example, it was found that genes with larger fitness effects upon deletion are more likely to be expression capacitors (Bergman and Siegal 2003) and genes with more genetic interactions are likely to be morphology capacitors (Levy and Siegal 2008). However, these studies did not examine whether the buffering effects on a trait varies depending on TI. Consequently, the roles of these capacitors in the adaptive genetic and environmental robustness revealed here is unclear.

The observed mutational robustness of the GPM is a double-edged sword. On the one hand, it reduces the deleterious effects of mutations on important traits such that the severity of the associated defects is lessened. On the other hand, because of the reduction in effect size, the defects are less harmful and hence tend to spread more widely in a population. The full ramifications of a GPM that is robust to mutation await further study, so do the molecular mechanisms conferring the robustness.

Materials and Methods

Morphological and Fitness Data

The phenotypic data of 501 morphological traits measured in the wild-type (123 replicate populations) and 4,718 nonessential gene deletion yeast strains (each with one population) in the rich medium YPD (yeast extract, peptone, and dextrose) were generated by Ohya et al. (2005). We focused on 220 of the 501 traits, because these 220 traits were measured in individual cells whereas the other traits were measured for populations of cells. Using single-cell measurements is necessary for our analysis. Supplementary data set S1, Supplementary Material online, lists these 220 traits as well as their CV, fgenes, mean |ES|, mean net |ES|, and TI values. The YPD fitness values of the deletion strains, relative to the wild type, were recently measured by Qian et al. (2012).

Fraction of Genes Affecting a Trait

The mouse results (fig. 1a) were from a summary of gene knockout studies (Flint and Mackay 2009). The fruit fly results (fig. 1b) were based on previously published data of P-element insertion lines (Mackay 2010). Because each line typically contains multiple P-element insertions, we calculated the fraction of single P-element insertions that affect a trait using the mean number of insertions per line (Mackay et al. 1992) under the assumption of no epistasis.

In the statistical analysis of yeast data, a gene is said to affect a trait when the gene deletion strain and the wild-type strain have a significant difference in the median trait value. We first calculated the P value by comparing multiple cells of each deletion line and those of an arbitrarily selected wild-type replicate population (04his3-1) by the Mann–Whitney U test. A P value of <5% was used to establish statistical significance. We thus obtained the faction of mutants in which the trait is affected (fmt). To control for false positives, we similarly performed the Mann–Whitney U test between 04his3-1 and each of the other 122 wild-type populations and calculated the fraction (fwt) of the 122 wild-type populations in which the trait deviates significantly from 04his3-1. The estimate of the fraction of genes affecting a trait (fgenes) equals fmt − fwt if fmt > fwt; otherwise, we set fgenes = 0.

Less Correlated Morphological Traits

To examine whether some of our results were generated by highly correlated traits, we attempted to remove genetically highly correlated traits. We measured the genetic correlation between a pair of traits by correlating their trait values across the 4,718 gene deletion strains. We then removed traits one by one from those with the highest absolute correlations until no two traits have a Pearson correlation whose absolute value is greater than 0.7. The final data set has 54 traits, and the distribution of fgenes is shown in supplementary figure S2, Supplementary Material online. Because morphological traits are naturally correlated to some extent, it remains to be determined whether the original 220 traits or the 54 less correlated traits better represent randomly sampled traits. The 54 less correlated traits were also used in supplementary figure S5, Supplementary Material online.

Raw ES and Net ES

The raw ES (ESij) of deleting gene i on trait j is defined as (xij − wj)/wj, where xij is the mean phenotypic value of trait j in the deletion strain i, and wj is the corresponding value in the wild type (averaged across all replicate populations). Conventionally, ESij is defined by (xij − wj)/SDj, where SDj is the standard deviation of the trait in the wild type (Mackay et al. 2009). We avoided using the conventional definition because the expected value of SDj is in a large part determined by the precision of the trait measurement, rendering the comparison of mean |ES| among traits primarily a comparison of the measurement quality rather than the biology of the traits. By contrast, the expected value of wj is not affected by the imprecision of the measurement.

To estimate the net |ES| of gene deletion on a trait, we generated 1,000 pseudo phenotypic data sets. To generate a pseudo data set, we randomly chose one wild-type replicate population and pick (with replacement) from this population the same number of cells as in the actual gene-deletion data. We then calculated pseudo |ES| for each of these pseudo data sets and computed its mean value. Because 1,000 pseudo data sets were generated, effectively all 123 wild-type populations were used. Net |ES| equals raw |ES| minus mean pseudo |ES| if raw |ES| > mean pseudo |ES|; otherwise, net |ES| = 0.

Phenotypic Variation

The phenotypic variation in the wild type was measured by CV. We calculated the variance among cells within each replicate population and averaged it across the 123 populations (Vwithin). We then calculated the variance among the mean phenotypic values of the 123 populations (Vbetween). Inline graphic, where m is the average of the mean phenotypic values of the 123 populations.

Relative TI

For trait j, we conducted a linear regression Fi = aj − bj (net |ESij|) for all i, where net |ESij| is the absolute value of the net ES of deleting gene i on trait j and Fi is the YPD fitness of the strain lacking gene i relative to the wild type (Qian et al. 2012). The intercept aj is the expected fitness when net |ESij| = 0, whereas the slope bj > 0 is 100 times the reduction in fitness caused by 1% change in the phenotypic value of trait j. Thus, bj is a measure of the relative importance of trait j to fitness, or TI. Because we focused on deleterious mutations in this model, we used only those genes that decrease fitness when deleted. We also tried the log model logFi = aj − bj (net |ESij|) and found the results to be similar (supplementary fig. S7, Supplementary Material online).

In the above estimation of TI, we assumed that, to a trait, a positive effect and a negative effect of the same size have the same fitness effect, which may not be true to all traits. Because positive and negative effects are arbitrarily defined, we also considered only positive (or only negative) raw effects in subsequent analysis (supplementary table S1, Supplementary Material online).

Principal Component Analysis of the Net |ES| Matrix

To examine whether the nonindependence among traits affects our results, we followed a previous study (Wang et al. 2010) to perform a principal component analysis to transform the net |ES| matrix M (4,718 genes × 220 traits). The principal component analysis was done by the “princomp” function in MATLAB. After this function returned a coefficient matrix C (220 × 220), we calculated M′ = MC (4718 transformed effects × 220 principal traits), which provides the net effect size of each gene on each of the 220 orthogonal principal component traits. We then used M′ to estimate TI.

Predicting the Fitness of a Mutant Strain Given the GPM

We built a multivariate linear model of yeast fitness that includes all 220 traits and 2,779 gene deletion strains that are less fit than the wild type: 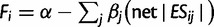Inline graphic, where α is a constant. We estimated α and βj for all 220 traits using the “glmfit” function in MATLAB. Based on the above formula and the estimated α and βj values, we predicted Fi upon the deletion of gene i when either the original or randomly shuffled net |ESij| values were used.

Null Mutation Rate Per Gene Per Generation

Based on the genome sequences of mutation accumulation yeast strains (Lynch et al. 2008), the point mutation rate in yeast is 3.3 × 10 − 10 per site per generation; the small (1–3 bp) indel mutation rate is 2 × 10−11 per site per generation; and the gene loss mutation rate is 2.1 × 10−6 per gene per generation. Taken together, we estimated the null mutation rate per gene per generation to be approximately [3.3 × 10−10 × (3/63) + 2 × 10−11× 0.83] × 1,419 + 2.1 × 10−6 = 2.146 × 10−6. Here, 3/63 is the average probability that a random point mutation in a coding region is nonsense, 0.83 is the fraction of small indels that are not multiples of three nucleotides (Zhang and Webb 2003), and 1,419 is the mean number of coding nucleotides per yeast protein-coding gene (Zhang 2000).

In humans, the point mutation rate is 1.25 × 10−9 per site per year and the indel mutation rate is 1 × 10−10 per site per year (Zhang and Webb 2003). Based on copy number variations in humans, it has been estimated that the gene loss rate is ∼10−5 per gene per generation (Zhang et al. 2009). Thus, the total null mutation rate per gene per generation is [1.25 × 10−9 × (3/63) + 1 × 10−10 × 0.83] × 1,341 × 25 + 1 × 10−5 = 1.48 × 10−5. Here, 1,341 is the mean number of coding nucleotides per human protein-coding gene (Zhang 2000) and 25 is the approximate number of years per human generation.

Fitness Advantages of Robustness Modifiers

In a diploid population, let A be the wild-type allele at gene i and a represent all null alleles, which are assumed to be completely recessive to A. The fitness values of AA, Aa, and aa are 1, 1, and 1 − si, respectively, where si > 0. Let the mutation rate from A to a be μi and the back mutation rate be 0. Under the mutation-selection balance (Hartl and Clark 1997), the equilibrium frequency of aa individuals is μi/si and the expected fitness of a randomly picked individual in the population is 1 × (1 − μi/si) + (1 − si) × (μi/si) = 1 − μi. Let us consider a robustness modifier that masks the deleterious effect of a such that aa individuals now have a fitness of 1 − si + Δsi (0 < Δsi < si). The expected fitness of an individual with the modifier is 1 × (1 − μi/si) + (1 − si + Δsi) × (μi/si) = 1 − μi + μiΔsi/si. Thus, the mean fitness advantage of the robustness modifier is g = μiΔsi/si. If gene i affects multiple traits, Δsi/si is determined by the fractional change in its combined fitness effect on these traits. Because reducing the genic effect on a trait of large fitness contribution is expected to contribute more to Δsi than reducing the same amount of effect on a trait of small fitness contribution, modifiers that preferentially reduce the mutational effects on important traits are more advantageous than those that have no such preference. As a result, natural selection is expected to preferentially enhance the mutational robustness of important traits. If the modifier buffers the null mutations of multiple genes, its fitness advantage is ∑(μiΔsi/si), where ∑ indicates summation over the multiple buffered genes. The above formula also works for deleterious mutations in general when ui is the total deleterious mutation rate at gene i, as long as all the mutations considered are completely recessive to the wild-type allele.

When a is not completely recessive to A, the fitness is 1, 1 − hisi, and 1 − si for AA, Aa, and aa, respectively, where 0 < h < 1 is the dominance of a, relative to A. Under mutation-selection balance (Hartl and Clark 1997), the equilibrium frequency of the a allele is μi/(sihi) and the expected fitness of a randomly picked individual in the population is approximately 1 − 2μi. Let us consider a robustness modifier that masks the deleterious effect of a such that Aa individuals now have a fitness of 1 − hisi + hiΔsi (0 < Δsi < si) and aa individuals have a fitness of 1 − si + Δsi. The expected fitness of an individual with the modifier will be 1 − 2μi + 2μiΔsi/si. Thus, the mean fitness advantage of the robustness modifier equals 2μiΔsi/si. If the modifier buffers the deleterious mutations of multiple genes, its fitness advantage is 2∑(μiΔsi/si), where ∑ indicates summation over the multiple buffered genes.

Gene Expression Data and Analysis

The genome-wide gene expression data of yeast single-gene deletion lines were compiled from four studies (Hughes et al. 2000; Hu et al. 2007; van Wageningen et al. 2010; Lenstra et al. 2011). In each study, the wild-type and gene-deletion strains were grown in YPD or synthetic complete (SC) medium. The microarray expression level of gene j in the strain lacking gene i was compared with that in the wild type under the same medium to measure the effect of deleting gene i on the expression level of gene j. Strains lacking more than one gene were not considered. If a deletion line was analyzed in multiple studies, we used the data from the most recent study. In the end, the data contained expression changes of 4,399 genes in 754 gene deletion lines (supplementary data set S2, Supplementary Material online). We then limited our analysis to the expression levels of 3,116 (out of 4,399) genes because these genes reduce fitness when deleted (i.e., fitness ≤ 1 regardless of statistical significance) (Qian et al. 2012).

The effect size of deleting gene i on the expression level of gene j was defined by (xij − wj)/wj = xij/wj − 1, where xij is the expression level of gene j in the strain lacking gene i and wj is the expression level of gene j in the wild type. The xij/wj value used was available from each data set. Because the expression data were obtained for populations of cells rather than individual cells, net |ES| cannot be estimated. The measurement error of the expression level of a gene in microarray is mainly determined by the expression level of the gene. Thus, controlling the expression level (supplementary tables S2–S5, Supplementary Material online) largely controls the measurement error. For these analyses, the expression levels from the wild-type strain in YPD (Nagalakshmi et al. 2008) were used. We quantified the effect sizes of 35 highly different environmental changes on the wild-type gene expression levels (Proulx et al. 2007) using the same formula, where xij/wj is the fold change in the expression of gene j induced by the ith environmental change. These 35 environments were previously chosen from a total of 162 environments to represent the least correlated environmental challenges (Proulx et al. 2007). We performed a similar analysis using all 162 environmental challenges under which the wild-type gene expression changes were previously measured (Gasch et al. 2000) (supplementary table S3, Supplementary Material online).

When examining the potential impact of highly correlated traits, we measured the genetic correlation between a pair of expression traits by correlating their expression levels across mutant strains. We then removed expression traits one by one from those with the highest correlations until no two traits have a Pearson correlation greater than 0.7. The final data set included 2,223 expression traits (supplementary table S4, Supplementary Material online).

Supplementary Material

Supplementary figures S1–S7, data sets S1, S2, and tables S1–S5 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).

Supplementary Data
supp_31_6_1568__index.html (1.1KB, html)

Acknowledgments

We thank Dr Yoshikazu Ohya for sharing the yeast morphological data and Dr Calum Maclean and Dr Jian-Rong Yang for valuable comments. This work was supported in part by the research grant R01GM103232 from the U.S. National Institutes of Health to J.Z.

References

  1. Alon U. An introduction to systems biology: design principles of biological circuits. London: Chapman & Hall; 2007. [Google Scholar]
  2. Batada NN, Hurst LD. Evolution of chromosome organization driven by selection for reduced gene expression noise. Nat Genet. 2007;39:945–949. doi: 10.1038/ng2071. [DOI] [PubMed] [Google Scholar]
  3. Bergman A, Siegal ML. Evolutionary capacitance as a general feature of complex gene networks. Nature. 2003;424:549–552. doi: 10.1038/nature01765. [DOI] [PubMed] [Google Scholar]
  4. Bergstrom A, Simpson JT, Salinas F, Barre B, Parts L, Zia A, Nguyen Ba AN, Moses AM, Louis EJ, Mustonen V, et al. A high-definition view of functional genetic variation from natural yeast genomes. Mol Biol Evol. 2014;31:872–888. doi: 10.1093/molbev/msu037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ciliberti S, Martin OC, Wagner A. Innovation and robustness in complex regulatory gene networks. Proc Natl Acad Sci U S A. 2007;104:13591–13596. doi: 10.1073/pnas.0705396104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. de Visser JA, Hermisson J, Wagner GP, Ancel Meyers L, Bagheri-Chaichian H, Blanchard JL, Chao L, Cheverud JM, Elena SF, Fontana W, et al. Perspective: evolution and detection of genetic robustness. Evolution. 2003;57:1959–1972. doi: 10.1111/j.0014-3820.2003.tb00377.x. [DOI] [PubMed] [Google Scholar]
  7. Draghi JA, Parsons TL, Wagner GP, Plotkin JB. Mutational robustness can facilitate adaptation. Nature. 2010;463:353–355. doi: 10.1038/nature08694. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ehrenreich IM, Torabi N, Jia Y, Kent J, Martis S, Shapiro JA, Gresham D, Caudy AA, Kruglyak L. Dissection of genetically complex traits with extremely large pools of yeast segregants. Nature. 2010;464:1039–1042. doi: 10.1038/nature08923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Falconer DS, Mackay TFC. Introduction to quantitative genetics. London: Pearson; 1996. [Google Scholar]
  10. Flatt T. The evolutionary genetics of canalization. Q Rev Biol. 2005;80:287–316. doi: 10.1086/432265. [DOI] [PubMed] [Google Scholar]
  11. Flint J, Mackay TF. Genetic architecture of quantitative traits in mice, flies, and humans. Genome Res. 2009;19:723–733. doi: 10.1101/gr.086660.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fraser HB, Schadt EE. The quantitative genetics of phenotypic robustness. PLOS One. 2010;5:e8635. doi: 10.1371/journal.pone.0008635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gasch AP, Spellman PT, Kao CM, Carmel-Harel O, Eisen MB, Storz G, Botstein D, Brown PO. Genomic expression programs in the response of yeast cells to environmental changes. Mol Biol Cell. 2000;11:4241–4257. doi: 10.1091/mbc.11.12.4241. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gibson G, Wagner G. Canalization in evolutionary genetics: a stabilizing theory? BioEssays. 2000;22:372–380. doi: 10.1002/(SICI)1521-1878(200004)22:4<372::AID-BIES7>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
  15. Han HW, Bae SH, Jung YH, Kim JH, Moon J. Genome-wide characterization of the relationship between essential and TATA-containing genes. FEBS Lett. 2013;587:444–451. doi: 10.1016/j.febslet.2012.12.030. [DOI] [PubMed] [Google Scholar]
  16. Hartl DL, Clark AG. Principles of population genetics. Sunderland (MA): Sinauer Associates; 1997. [Google Scholar]
  17. Hermisson J, Wagner GP. The population genetic theory of hidden variation and genetic robustness. Genetics. 2004;168:2271–2284. doi: 10.1534/genetics.104.029173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Houle D. How should we explain variation in the genetic variance of traits? Genetica. 1998;102-103:241–253. [PubMed] [Google Scholar]
  19. Hu Z, Killion PJ, Iyer VR. Genetic reconstruction of a functional transcriptional regulatory network. Nat Genet. 2007;39:683–687. doi: 10.1038/ng2012. [DOI] [PubMed] [Google Scholar]
  20. Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armour CD, Bennett HA, Coffey E, Dai H, He YD, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
  21. Lehner B. Selection to minimise noise in living systems and its implications for the evolution of gene expression. Mol Syst Biol. 2008;4:170. doi: 10.1038/msb.2008.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lehner B. Genes confer similar robustness to environmental, stochastic, and genetic perturbations in yeast. PLOS One. 2010;5:e9035. doi: 10.1371/journal.pone.0009035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lenstra TL, Benschop JJ, Kim T, Schulze JM, Brabers NA, Margaritis T, van de Pasch LA, van Heesch SA, Brok MO, Groot Koerkamp MJ, et al. The specificity and topology of chromatin interaction pathways in yeast. Mol Cell. 2011;42:536–549. doi: 10.1016/j.molcel.2011.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Levy SF, Siegal ML. Network hubs buffer environmental variation in Saccharomyces cerevisiae. PLOS Biol. 2008;6:2588–2604. doi: 10.1371/journal.pbio.0060264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lyman RF, Lawrence F, Nuzhdin SV, Mackay TF. Effects of single P-element insertions on bristle number and viability in Drosophila melanogaster. Genetics. 1996;143:277–292. doi: 10.1093/genetics/143.1.277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lynch M, Sung W, Morris K, Coffey N, Landry CR, Dopman EB, Dickinson WJ, Okamoto K, Kulkarni S, Hartl DL, et al. A genome-wide view of the spectrum of spontaneous mutations in yeast. Proc Natl Acad Sci U S A. 2008;105:9272–9277. doi: 10.1073/pnas.0803466105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Mackay TF. Mutations and quantitative genetic variation: lessons from Drosophila. Phil Trans R Soc B. 2010;365:1229–1239. doi: 10.1098/rstb.2009.0315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Mackay TF, Lyman RF, Jackson MS. Effects of P element insertions on quantitative traits in Drosophila melanogaster. Genetics. 1992;130:315–332. doi: 10.1093/genetics/130.2.315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Mackay TF, Stone EA, Ayroles JF. The genetics of quantitative traits: challenges and prospects. Nat Rev Genet. 2009;10:565–577. doi: 10.1038/nrg2612. [DOI] [PubMed] [Google Scholar]
  30. Mackay TFC. The genetic architecture of quantitative traits. Annu Rev Genet. 2001;35:303–339. doi: 10.1146/annurev.genet.35.102401.090633. [DOI] [PubMed] [Google Scholar]
  31. Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mather K. Variation and selection of polygenic characters. J Genet. 1941;41:159–193. [Google Scholar]
  33. Meiklejohn CD, Hartl DL. A single mode of canalization. Trends Ecol Evol. 2002;17:468–473. [Google Scholar]
  34. Milton CC, Huynh B, Batterham P, Rutherford SL, Hoffmann AA. Quantitative trait symmetry independent of Hsp90 buffering: distinct modes of genetic canalization and developmental stability. Proc Natl Acad Sci U S A. 2003;100:13396–13401. doi: 10.1073/pnas.1835613100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Nagalakshmi U, Wang Z, Waern K, Shou C, Raha D, Gerstein M, Snyder M. The transcriptional landscape of the yeast genome defined by RNA sequencing. Science. 2008;320:1344–1349. doi: 10.1126/science.1158441. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Newman JR, Ghaemmaghami S, Ihmels J, Breslow DK, Noble M, DeRisi JL, Weissman JS. Single-cell proteomic analysis of S. cerevisiae reveals the architecture of biological noise. Nature. 2006;441:840–846. doi: 10.1038/nature04785. [DOI] [PubMed] [Google Scholar]
  37. Ohya Y, Sese J, Yukawa M, Sano F, Nakatani Y, Saito TL, Saka A, Fukuda T, Ishihara S, Oka S, et al. High-dimensional and large-scale phenotyping of yeast mutants. Proc Natl Acad Sci U S A. 2005;102:19015–19020. doi: 10.1073/pnas.0509436102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Proulx SR, Nuzhdin S, Promislow DE. Direct selection on genetic robustness revealed in the yeast transcriptome. PLOS One. 2007;2:e911. doi: 10.1371/journal.pone.0000911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Qian W, Ma D, Xiao C, Wang Z, Zhang J. The genomic landscape and evolutionary resolution of antagonistic pleiotropy in yeast. Cell Rep. 2012;2:1399–1410. doi: 10.1016/j.celrep.2012.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Ramani AK, Chuluunbaatar T, Verster AJ, Na H, Vu V, Pelte N, Wannissorn N, Jiao A, Fraser AG. The majority of animal genes are required for wild-type fitness. Cell. 2012;148:792–802. doi: 10.1016/j.cell.2012.01.019. [DOI] [PubMed] [Google Scholar]
  41. Rhee HS, Pugh BF. Genome-wide structure and organization of eukaryotic pre-initiation complexes. Nature. 2012;483:295–301. doi: 10.1038/nature10799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Robertson A. The nature of quantitative genetic variation. In: Brink A, editor. Heritage from Mendel. Madison (WI): The Univeristy of Wisconsin Press; 1967. p. 265–280. [Google Scholar]
  43. Sanjuan R, Cuevas JM, Furio V, Holmes EC, Moya A. Selection for robustness in mutagenized RNA viruses. PLOS Genet. 2007;3:e93. doi: 10.1371/journal.pgen.0030093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Scharloo W. Canalization: genetic and developmental aspects. Annu Rev Ecol Syst. 1991;22:65–93. [Google Scholar]
  45. Siegal ML, Bergman A. Waddington's canalization revisited: developmental stability and evolution. Proc Natl Acad Sci U S A. 2002;99:10528–10532. doi: 10.1073/pnas.102303999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Stearns SC, Kaiser M, Kawecki TJ. The differential genetic and environmental canalization of fitness components in Drosophila melanogaster. J Evol Biol. 1995;8:539–557. [Google Scholar]
  47. Stearns SC, Kawecki TJ. Fitness sensitivity and the canalization of life-history traits. Evolution. 1994;48:1438–1450. doi: 10.1111/j.1558-5646.1994.tb02186.x. [DOI] [PubMed] [Google Scholar]
  48. Tirosh I, Weinberger A, Carmi M, Barkai N. A genetic signature of interspecies variations in gene expression. Nat Genet. 2006;38:830–834. doi: 10.1038/ng1819. [DOI] [PubMed] [Google Scholar]
  49. van Wageningen S, Kemmeren P, Lijnzaad P, Margaritis T, Benschop JJ, de Castro IJ, van Leenen D, Groot Koerkamp MJ, Ko CW, Miles AJ, et al. Functional overlap and regulatory links shape genetic interactions between signaling pathways. Cell. 2010;143:991–1004. doi: 10.1016/j.cell.2010.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Waddington CH. Canalization of development and the inheritance of acquired characters. Nature. 1942;150:563–565. doi: 10.1038/1831654a0. [DOI] [PubMed] [Google Scholar]
  51. Wagner A. Energy constraints on the evolution of gene expression. Mol Biol Evol. 2005a;22:1365–1374. doi: 10.1093/molbev/msi126. [DOI] [PubMed] [Google Scholar]
  52. Wagner A. Robustness and evolvability in living systems. Princeton (NJ): Princeton University Press; 2005b. [Google Scholar]
  53. Wagner G, Booth G, Bagheri-Chaichian H. A population genetic theory of canalization. Evolution. 1997;51:329–347. doi: 10.1111/j.1558-5646.1997.tb02420.x. [DOI] [PubMed] [Google Scholar]
  54. Wagner GP, Zhang J. The pleiotropic structure of the genotype–phenotype map: the evolvability of complex organisms. Nat Rev Genet. 2011;12:204–213. doi: 10.1038/nrg2949. [DOI] [PubMed] [Google Scholar]
  55. Wang Z, Liao BY, Zhang J. Genomic patterns of pleiotropy and the evolution of complexity. Proc Natl Acad Sci U S A. 2010;107:18034–18039. doi: 10.1073/pnas.1004666107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Wang Z, Zhang J. Impact of gene expression noise on organismal fitness and the efficacy of natural selection. Proc Natl Acad Sci U S A. 2011;108:E67–E76. doi: 10.1073/pnas.1100059108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Wilke CO, Wang JL, Ofria C, Lenski RE, Adami C. Evolution of digital organisms at high mutation rates leads to survival of the flattest. Nature. 2001;412:331–333. doi: 10.1038/35085569. [DOI] [PubMed] [Google Scholar]
  58. Winzeler EA, Shoemaker DD, Astromoff A, Liang H, Anderson K, Andre B, Bangham R, Benito R, Boeke JD, Bussey H, et al. Functional characterization of the S. cerevisiae genome by gene deletion and parallel analysis. Science. 1999;285:901–906. doi: 10.1126/science.285.5429.901. [DOI] [PubMed] [Google Scholar]
  59. Yvert G, Ohnuki S, Nogami S, Imanaga Y, Fehrmann S, Schacherer J, Ohya Y. Single-cell phenomics reveals intra-species variation of phenotypic noise in yeast. BMC Syst Biol. 2013;7:54. doi: 10.1186/1752-0509-7-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Zhang F, Gu W, Hurles ME, Lupski JR. Copy number variation in human health, disease, and evolution. Annu Rev Genomics Hum Genet. 2009;10:451–481. doi: 10.1146/annurev.genom.9.081307.164217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Zhang J. Protein-length distributions for the three domains of life. Trends Genet. 2000;16:107–109. doi: 10.1016/s0168-9525(99)01922-8. [DOI] [PubMed] [Google Scholar]
  62. Zhang J, Webb DM. Evolutionary deterioration of the vomeronasal pheromone transduction pathway in catarrhine primates. Proc Natl Acad Sci U S A. 2003;100:8337–8341. doi: 10.1073/pnas.1331721100. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_31_6_1568__index.html (1.1KB, html)
supp_msu131_supplementary_figures_msu131.pdf (2MB, pdf)
supp_msu131_supplementary_tables.pdf (47.6KB, pdf)
supp_msu131_dataset1.xlsx (34.1KB, xlsx)
supp_msu131_dataset2.xlsx (192.2KB, xlsx)

Articles from Molecular Biology and Evolution are provided here courtesy of Oxford University Press

RESOURCES