The Psychometric Development and Initial Validation of the DCI-A Short Form for Adolescent Therapeutic Community Treatment Process

Abstract

The 5-factor client-report Dimensions of Change in Therapeutic Communities Treatment Instrument-Adolescent (DCI-A) was developed to assess adolescent substance abuse treatment process in the therapeutic community (TC). The goal of this study was to use bifactor modeling to derive a unidimensional DCI-A short-form (DCI-A-SF) that would represent content from the original DCI-A factors. Data are from 442 adolescents receiving treatment at one of seven residential TC programs. Bifactor analyses suggested selection of seven DCI-A items to comprise the short form. Three items are from the Treatment Motivation factor, and one item was selected from each of the remaining four factors. Confirmatory factor analysis suggested that the 7-item DCI-A-SF is strongly unidimensional, and unidimensional IRT analysis of the items indicated good internal consistency. A structural equation model that demonstrates the mediating relationship of DCI-A-SF with other measures, including demographic and pre-treatment characteristics, and subsequent treatment completion, provides preliminary evidence of internal validity.

Introduction

This article discusses the development and initial validation of a short form version of an assessment of the treatment process in Therapeutic Communities (TC): the Dimensions of Change Instrument – Adolescent (DCI-A-SF). The DCI-A-SF is a brief assessment built on our previous efforts through the refinement of the DCI-A (Edelen, Tucker, Stucky, Butler, and Muehlbach, in press). While there are other measures of treatment process specific to adults in the TC (e.g., Kressel et al, 2000; Orlando et al, 2006), as well as adolescent-specific general process measures not designed for therapeutic communities (i.e., the TCU scales (Knight, Holcom, and Simpson, 1994)), to our knowledge the 5-factor client-report DCI-A is the only measure uniquely developed to assess treatment process in the TC among adolescents. The DCI-A consists of five subscales (Treatment Motivation, Personal Development, Problem Recognition, Family Relations, and Social Network). Previous research on the DCI-A has indicated that these five scales generate scores demonstrating good to excellent levels of reliability (alpha range from 0.72 to 0.91); further, the five scales of the DCI-A have also been found to be predictive of time in treatment (Edelen et al., in press).

In busy treatment settings, finding time for lengthy client assessments can be difficult, thus it is often of practical interest to have a brief assessment tool available for use. Though useful in independently assessing various aspects of the TC treatment process, the full length DCI-A requires a relatively long administration period. However, because all five factors in the DCI-A represent distinct yet related aspects of the TC treatment process, it is reasonable to expect that a much shorter, unidimensional set of items may exist that represents the content from all five factors of the parent instrument. The remainder of this brief report discusses the scale development process used to create the DCI-A-SF, which greatly reduces scale length while maintaining the instrument’s content, validity, and reliability.

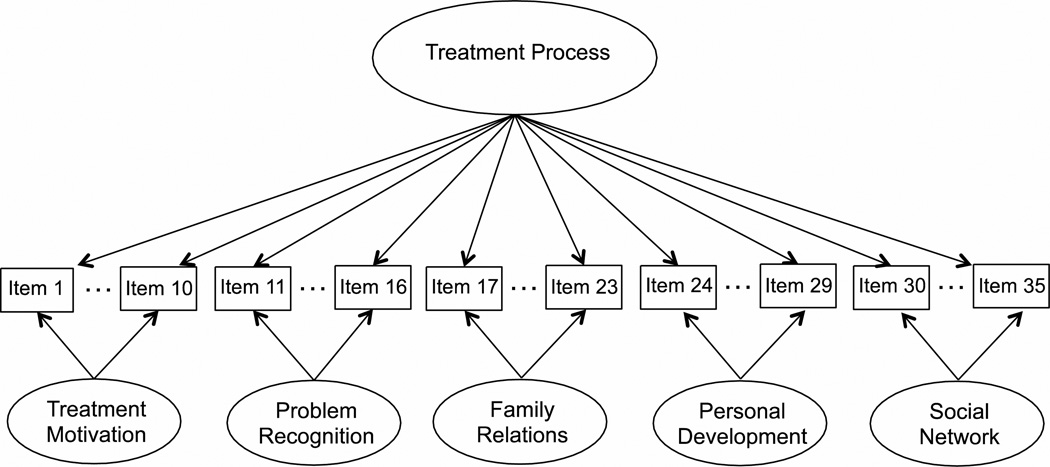
The challenge in creating the DCI-A-SF was to develop a short, one-dimensional scale based on the original five-dimensional DCI-A. While each of the DCI-A subscales represents unique content, the correlations among the factors in the original 5-factor confirmatory factor analysis (CFA) were relatively large in magnitude (ranging from 0.54 to 0.69; Edelen, et al., in press), suggesting the potential for a single general factor (Treatment Process) that may underlie all the items. In situations like this, where item responses are best represented by multidimensional models, yet whose dimensions are moderately inter-related¹, bifactor models (Gibbons and Hedeker, 1992) are particularly useful for evaluating the strength of a general factor (i.e., Treatment Process) relative to the unique strength of each subfactor (i.e., the five subscales of the DCI-A) (for examples of bifactor models see Stucky, Gottfredson, and Panter, 2012; Reise, 2012). Specifically, for each item, the bifactor model estimates a non-zero loading on the general factor and a non-zero loading on the appropriate specific factor. The relative strength of the general and specific factor loadings can then be interpreted to identify an optimal unidimensional solution. Thus, a bifactor model, following the structure of the DCI-A five-factor CFA, was used as the basis for the creation of the DCI-A-SF (see Figure 1 for a graphical representation of the DCI-A bifactor model).

Figure 1.

Bifactor representation of the DCI-A

Based on comparisons of factor loadings from the bifactor structure, a subset of items from the DCI-A specific factors can be selected to comprise a unidimensional DCI-A-SF. To aid in the selection of these items, the item level expected common variance (I-ECV) index provides a useful measure of item-level unidimensionality (see Stucky, Thissen, and Edelen, 2013). Specifically, for each item the I-ECV provides an indication of the strength of the bifactor loadings on the general factor (Treatment Process) relative to the strength of the specific factor. Thus, it is desirable to identify items with high I-ECV values, which provides initial evidence of item-level unidimensionality.

To summarize, the goal of this study was to use bifactor modeling and I-ECV values to derive a unidimensional DCI-A-SF that would represent content from all five factors in the original instrument (Treatment Motivation, Personal Development, Problem Recognition, Family Relations, Social Network) and to conduct a preliminary evaluation of the validity of the DCI-A-SF by examining its associations with demographic and pre-treatment characteristics as well as program completion status.

Methods

Sample

The study sample consists of 442 adolescents in residential treatment at one of seven TC treatment programs in the US run by the Phoenix House organization and Daytop Village². All residents who were in treatment at one of the seven participating sites during data collection were eligible for study participation. The sample of 442 respondents represents 74% of the 600 youths eligible to participate. Reasons for non-participation of the 158 residents included lack of parental consent (n=79; 50%), adolescent refusal (n=39; 25%), and unavailability at time of survey administration (n=40; 25%). The survey administration protocol is described in more detail elsewhere (Edelen et al, in press).

Participants ranged in age from 13–21 (M=17.1, SD=1.5), and were predominantly male (77%), with 40.7% Hispanic, 27.2% White, 27.2% African American, and 5% of some other race. The majority of participants were referred to treatment by the criminal justice system (62%). Other referral reasons included self/family (18%), social services (9%), transfer (6%) and referral by a medical professional (2%). At the time of the survey administration, 21.7% of respondents had been in treatment for 30 days or less, 19.2% for 31–60 days, 14.5% for 61–90 days, 29.9% for 91–180 days, and 14.7% for more than 180 days. Finally, 47.5% of respondents ultimately completed the treatment program, whereas the remainder left the program either through administrative discharge (18.6%), against clinical advice (16.1%) or were transferred or removed for some reason beyond their control (e.g., based on family’s wishes; 13.8%)

DCI-A items and descriptive measures

All participants completed the pilot version of the DCI-A, which is described in more detail elsewhere (Edelen et al, in press). The full DCI-A consists of 35 positively valenced items that comprise the 5 factors and 5 negatively valenced (filler) items that are included to avoid response bias. Thus the analyses reported here utilize the 35-item DCI-A scale. All items are assessed with a 5-point Likert-type scale indicating respondents’ extent of agreement with each statement (0=not at all, 4=completely). Higher scores indicate positive perceptions of the treatment process. We used administrative records to gather demographic information (i.e., gender, age, and race/ethnicity), and treatment information including referral source (1=criminal justice/probation, 0=other source) and the time spent in the treatment program. We also recorded participants’ disposition at discharge from treatment as they exited the program (i.e., 1 = graduated, 0 = failed to graduate (e.g., transferred, left against clinical advice, etc.)).

Analytic approach

The 35 items were fitted with a bifactor model that specified a general factor (treatment process) and five specific factors corresponding to the 5 factors of the DCI-A. The model was implemented with the Mplus version 6 software package (Muthen & Muthen, 1998–2010). Item responses were treated as categorical, using the weighted least squares, mean- and variance-adjusted (WLSMV) estimator in Mplus.

The items comprising the short form were selected from the bifactor model based on the I-ECV for each item. Each item’s explained common variance (ECV) indicates the percentage of variance that is accounted for by the general factor (Treatment Process). In order to control for local dependence, ensure unidimensionality, and identify items most representative of the general dimension, the item within each secondary factor with the highest I-ECV is selected to comprise the DCI-A-SF (5 items). In addition to these five items we also selected other items with large I-ECV values. Selecting additional items in this manner allows for the development of a undimensional scale that is strongly associated with the general factor without being overly influenced by other specific factors. Technically, retaining more than a single item from any specific factor of the bifactor model violates a strict assumption of local independence. However, this violation may be negligible (e.g., “essential unidimensionality”, Stout, 1990) when items with relatively high I-ECVs are selected (e.g., I-ECV > .85).

We next used CFA, also with the Mplus version 6 software, to evaluate the unidimensionality of the DCI-A-SF derived from the bifactor and I-ECV analysis. Fit of this model to the data was evaluated based on four indices: the root mean square error of approximation (RMSEA; Steiger & Lind, 1980); the Tucker-Lewis index (TLI; Tucker & Lewis, 1973); the comparative fit index (CFI; Bentler, 1988); and the scale-level ECV (ten Berge and Socan, 2004; Reise, Moore, and Haviland, 2010).

Following evidence of unidimensionality based on the CFA, we next evaluated the score precision of the DCI-A-SF using an item response theory (IRT) Graded Response Model (GRM) in the software program IRTPRO (Cai, du Toit, and Thissen, 2011). Because it is known that ignoring violations of undimensionality results in biased score estimates suggesting more score precision than is present (Thissen, Steinberg, and Mooney, 1989), we conducted an additional check on the dimensionality by comparing the IRT-based marginal DCI-A-SF score reliability estimates from a bifactor IRT model (accounting for multidimensionality) to the reliability estimates based on a unidimensional IRT model (ignoring multidimensionality) (Stucky et al., 2013). The magnitude of the violation of the local independence assumption corresponds to the difference in the reliability estimates, such that relatively small differences in the reliability estimates is evidence of essential undimensionality.

In IRT contexts, score reliability is a function of the latent variable and is evaluated based on the degree of information the scale’s items provide. Reliability is one less the inverse of information. So, when information is 5, reliability is 0.80 (1–1/5 = 0.80). While scores generated from IRT analyses are typically in the metric of the normal distribution with mean = 0 and standard deviation = 1, we present rescaled validity results in the T-score metric with mean = 50 and standard deviation = 10. We additionally provide a score translation table that converts the raw summed item scores of the DCI-A-SF into the IRT T-score metric (see Thissen, Pommerich, Billeaud, and Williams, 1995), which provides users the benefits of the IRT model without having to conduct an IRT analysis (for examples see Irwin et al., 2012; DeWitt et al., 2011).

Finally, to obtain a preliminary evaluation of the DCI-A-SF’s validity as a measure of treatment process, a mediation analysis was conducted in a structural equation modeling (SEM) context using Mplus version 6. The model treats the DCI-A-SF as a single latent variable that mediates the relationship between demographic and treatment information, and program completion status. To correct for biased parameter standard errors, the analysis stratified across the Daytop and Phoenix House subpopulations and accounted for the clustering of the various treatment programs nested within each subpopulation (Asparouhov, 2005).

Results and Discussion

Bifactor model and selection of unidimensional items

The complete bifactor model was found to closely fit the data (χ² = 1,371, df = 525, p < .001; RMSEA = .060, CFI = .926, TLI = .917). The 35 items were moderately multidimensional; the general factor, Treatment Process, accounted for only 62% of the total variance extracted, indicating the presence of strong content-specific factors. The factor loadings on the general factor reflect this variability, with loadings ranging from 0.25 to 0.81 (see Table 1).

Table 1.

DCI-A Bifactor loadings and I-ECV values.

Item ID	General	Treatment Motivation	Problem Recognition	Family Relations	Personal Development	Social Network	I-ECV
I am actively involved in my treatment plan	0.81	0.11					0.98
I try to help my peers in this program make better choices	0.75	0.17					0.95
I am developing new interests	0.75	0.19					0.94
It is important to follow a schedule of daily activities	0.53	0.26					0.81
Knowing my schedule of activities each day helps me feel comfortable here	0.59	0.34					0.75
I am getting something out of the time I spend doing my job function or daily task	0.61	0.37					0.73
My life will be better if I complete this program	0.53	0.44					0.59
This program can really help me	0.61	0.66					0.46
Staying in treatment can help me achieve my goals	0.56	0.74					0.36
Staying in treatment can help solve my problems	0.53	0.77					0.32
It is important for me to see my part in the problems I have	0.76		0.27				0.89
I am tired of the problems caused by drugs and alcohol	0.62		0.42				0.69
My attitudes or behaviors can cause problems with the people around me	0.41		0.41				0.50
My drug or alcohol use is related to the problems I have today	0.30		0.55				0.23
The people I choose to hang out with can add to my problems	0.29		0.59				0.19
My actions can make my problems worse	0.25		0.55				0.17
The people I care about expect me to make positive changes in my life	0.53			0.23			0.84
My family members listen to me when I tell them things	0.65			0.44			0.69
My family supports my recovery	0.57			0.44			0.63
I feel good about my ability to deal with my family issues	0.66			0.53			0.61
My family members and I are discovering some things we can agree on	0.51			0.53			0.48
My family cares about me	0.48			0.61			0.38
My family members and I can work together to solve problems	0.47			0.64			0.35
I can have fun without using drugs or alcohol	0.65				0.29		0.83
I pay attention to what I am feeling	0.50				0.24		0.81
I don't need to use drugs or alcohol to relax and hang out with my friends	0.52				0.25		0.81
I don't need drugs or alcohol to handle my emotions	0.42				0.33		0.62
I can control myself in situations that make me angry	0.48				0.61		0.38
I can deal with frustration and stress without acting out	0.48				0.61		0.38
I notice that people here can support each other despite conflict	0.60					0.17	0.93
I have friends who help me make good choices	0.58					0.27	0.82
I can rely on other people to show up for me when it really counts	0.50					0.25	0.80
I have someone close to me who helps me develop confidence in myself	0.66					0.36	0.77
There is someone I can go to when I want to talk about personal things	0.69					0.49	0.66
When I have a problem there are people I can turn to for help	0.73					0.55	0.64

Seven items were selected from the bifactor model to comprise the DCI-A-SF. Five of the items were drawn from the five secondary factors (one item from each factor), and two additional items were drawn from the Treatment Motivation factor (each with I-ECV values greater than 0.90). Evaluation of the fit the 7-item DCI-A-SF with a unidimensional CFA model and the scale-level ECV yielded excellent fit (χ² = 31, df = 14, p = .006; RMSEA = .052, CFI = .991, TLI = .986, ECV = 0.92); thus the DCI-A-SF may be considered unidimensional. Notably, among the reduced 7-item set the general factor (from the initial bifactor model) accounted for 92% of the total variance, providing additional evidence of unidimensionality. As a final indication that the selection of the three items with high I-ECV values within the Treatment Motivation factor did not sufficiently violate the IRT assumption of local independence we note that the reliability of IRT scores computed from a bifactor representation of the 7-item DCI-A-SF (reliability = 0.813) is nearly identical to the reliability from unidimensional representation of the DCI-A-SF (reliability = 0.815)³. Next, Table 2 provides the DCI-A-SF item slopes and thresholds based on the GRM along with the equivalent factor analytic item loadings (ranging from 0.52 to 0.84).

Table 2.

IRT parameters and factor loadings of the 7-item DCI-A-SF.

Item Stem	λ	a	b1	b2	b3	b4
I am actively involved in my treatment plan	.84	2.61	−1.94	−1.28	−0.46	0.34
I am developing new interests	.77	2.08	−1.73	−1.14	−0.33	0.82
I try to help my peers in this program make better choices	.76	2.01	−1.91	−1.10	−0.25	0.71
It is important for me to see my part in the problems I have	.75	1.92	−2.41	−1.57	−0.69	0.23
I can have fun without using drugs or alcohol	.62	1.34	−2.67	−1.81	−0.78	0.17
I notice that people here can support each other despite conflict	.58	1.20	−1.65	−0.53	0.78	1.97
The people I care about expect me to make positive changes in my life	.52	1.04	−5.01	−3.49	−2.75	−1.03

Reliability

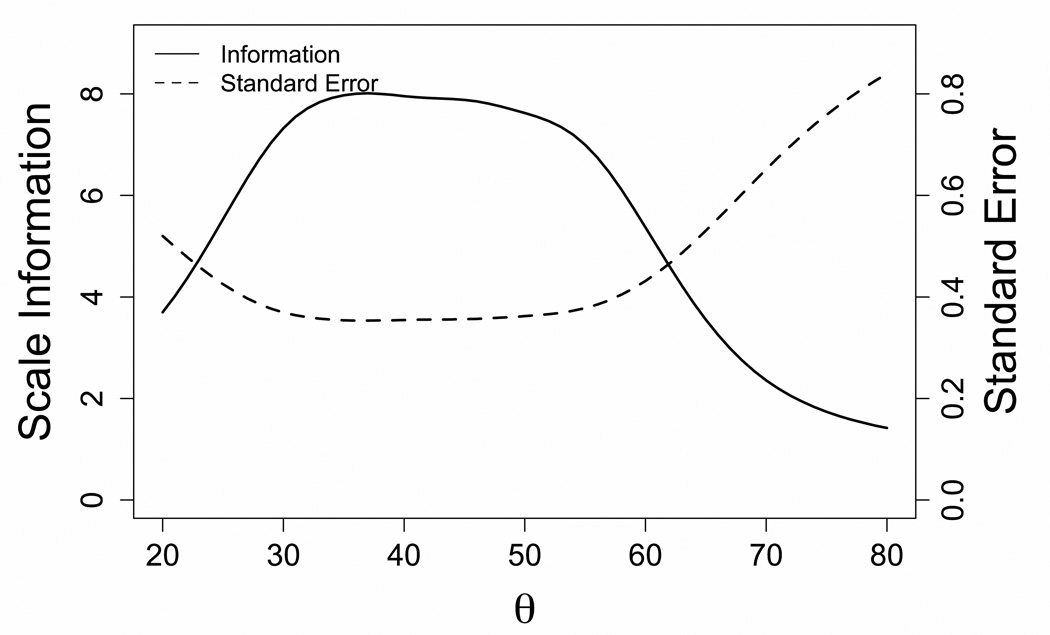
Based on the unidimensional IRT model, score precision is illustrated graphically (Figure 2). Results indicate score reliability values for the overall sample greater than 0.80 from approximately two and one-half standard deviations below the mean to one standard deviation above the mean (Response pattern marginal reliability = 0.84). Initial evidence suggests the reliabilities of the DCI-A-SF and mean values are similar across gender and race/ethnicity. Specifically, there were no significant differences in the scale’s mean values across gender (Male: mean = 49.8, SD = 8.8, alpha = .80; Female: mean = 50.9, SD = 9.4, alpha = .84) or race/ethnicity (White: mean = 50.3, SD = 7.2, alpha = .73; Black: mean = 48.6, SD = 8.8, alpha = .79; Hispanic: mean = 51.0, SD = 9.7, alpha = .84), with the exception between Black and Hispanic groups (t = 2.10, df = 296, p = .036).

Figure 2.

Test information and score standard error for the DCI-A-SF

Finally, Table 3 provides a manual translation from the raw DCI-A-SF summed score (i.e., the sum of the item scores) to a standardized IRT score and associated standard error.

Table 3.

Sum score to IRT score translation table for the 7-item DCI-A-SF

Sum Score	T-Score	Standard Error
0	20.1	5.4
1	22.1	5.1
2	24.3	4.8
3	25.7	4.7
4	27.4	4.5
5	29.1	4.3
6	30.6	4.2
7	32.2	4.1
8	33.6	4.0
9	35.0	3.9
10	36.4	3.9
11	37.7	3.9
12	39.0	3.8
13	40.3	3.8
14	41.6	3.8
15	42.9	3.8
16	44.2	3.9
17	45.5	3.9
18	46.9	3.9
19	48.3	4.0
20	49.8	4.0
21	51.3	4.1
22	53.0	4.2
23	54.8	4.3
24	56.8	4.5
25	58.9	4.7
26	61.4	5.0
27	64.1	5.3
28	68.0	6.0

DCI-A-SF mediation

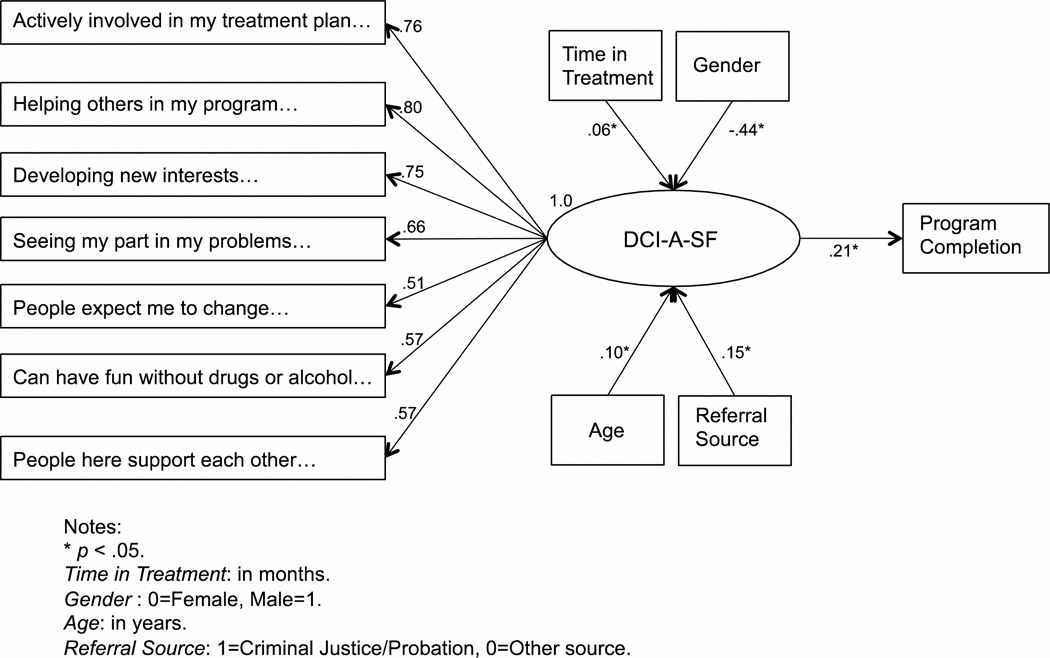
Initial validity evidence was provided via an SEM model where the DCI-A-SF mediates the relationship between various treatment and demographic variables, and program completion (Figure 3). Preliminary evidence indicates the model closely fits the data (χ² = 72, df = 48, p = .015; RMSEA = .034, CFI = .970, TLI = .963). Age (older adolescents have higher scores than younger adolescents), gender (females have higher scores than males), time in treatment (longer time in treatment is associated with higher scores), and referral source (criminal justice/probation referrals lead to higher scores) all significantly predicted DCI-A-SF treatment process, and the DCI-A-SF in turn significantly predicted successful program completion. Subsequently, a full mediation model was tested that specified direct effects of all pre-treatment independent variables on program completion in addition to effects mediated by treatment process. For this model, the direct effects for all independent variables, except time in treatment, were non-significant (i.e., indicating full mediation) while the indirect (mediated) effects through the DCI-A-SF maintained a significant relationship for all variables.

Figure 3.

DCI-A-SF path analysis

The x-axis (θ) represents the underlying latent variable for the therapeutic treatment process and is in the T-score metric, a normal distribution with mean=50 and standard deviation=10.

More simply, a bivariate analysis indicates that T-scores on the DCI-A-SF were significantly higher for those who completed the treatment program successfully (51.6, SD = 8.0) than those who did not complete the program successfully (Mean = 48.7; SD = 9.4), t = 3.37, df = 434, p < .001.

Conclusions

The goal of this study was to derive a short-form version of the DCI-A to be used in TC treatment settings for brief assessment of the adolescent treatment process. We anticipate that this brief measure can be completed in less than 5 minutes. Developed using recent psychometric advances, the 7-item DCI-A-SF contains items and content representing all five DCI-A factors yet is well characterized by a unidimensional model. Item selection for the DCI-A-SF was based on substantive knowledge of the items and the magnitude of the I-ECV values. While the present work serves as a useful demonstration of the utility of this technique for selecting unidimensional items from multidimensional data, future research is needed to develop general guidelines regarding the magnitude of the I-ECV values that are appropriate for unidimensional item selection.

Initial evidence suggests sound psychometric properties of the DCI-A-SF. Scores on the DCI-A-SF are comparable across gender and race/ethnic subgroups, and reliability estimates suggest similar levels of score precision. Importantly, preliminary evidence suggests the DCI-A-SF is a useful measure of the mediating role of treatment process in the relationship between demographic and treatment status information, and the probability of successfully completing the treatment program. In this regard researchers and practitioners may find the DCI-A-SF a useful tool in following the progress of in-treatment clients as a means of identifying those at risk for treatment dropout or failure. To facilitate its use among researchers and practitioners a score translation table is provided (Table 3) that allows users to easily obtain a standardized IRT score simply by taking the (non-missing) sum of the item scores from the 7-item DCI-A-SF⁴.

Finally, while preliminary validity evidence suggests the potential practical benefits of the DCI-A-SF in treatment settings, more research is clearly needed. In addition to the need for replication of results in an independent sample, the presentation reported here of the role of the DCI-A-SF (as a representation of the treatment process) in predicting successful treatment completion is perhaps a simplification of the complex nature of the TC process and should be viewed accordingly. For example, a more nuanced picture of the treatment process role could be garnered from repeated measures of the DCI-SF-A at prescribed time points (e.g., treatment entry, 30 days, 3 months etc.). In addition, while the DCI-A and DCI-A-SF were developed to assess the adolescent TC treatment process, the phrasing of the items is not specific to TC settings, and future research may establish the utility of the DCI-A-SF in residential and non-residential adolescent treatment settings outside of the TC. Though these findings offer an exciting insight into understanding the TC treatment process, to gain a more complete depiction of the utility of the DCI-A-SF, future research should explore the utility of the DCI-SF-A in assessing treatment process at various stages of treatment as well as within varying treatment settings.