Abstract
Purpose: Respiratory motion modeling of both tumor and surrounding tissues is a key element in minimizing errors and uncertainties in radiation therapy. Different continuous motion models have been previously developed. However, most of these models are based on the use of parameters such as amplitude and phase extracted from 1D external respiratory signal. A potentially reduced correlation between the internal structures (tumor and healthy organs) and the corresponding external surrogates obtained from such 1D respiratory signal is a limitation of these models. The objective of this work is to describe a continuous patient specific respiratory motion model, accounting for the irregular nature of respiratory signals, using patient external surface information as surrogate measures rather than a 1D respiratory signal.
Methods: Ten patients were used in this study having each one 4D CT series, a synchronized RPM signal and patient surfaces extracted from the 4D CT volumes using a threshold based segmentation algorithm. A patient specific model based on the use of principal component analysis was subsequently constructed. This model relates the internal motion described by deformation matrices and the external motion characterized by the amplitude and the phase of the respiratory signal in the case of the RPM or using specific regions of interest (ROI) in the case of the patients’ external surface utilization. The capability of the different models considered to handle the irregular nature of respiration was assessed using two repeated 4D CT acquisitions (in two patients) and static CT images acquired at extreme respiration conditions (end of inspiration and expiration) for one patient.
Results: Both quantitative and qualitative parameters covering local and global measures, including an expert observer study, were used to assess and compare the performance of the different motion estimation models considered. Results indicate that using surface information [correlation coefficient (CC): 0.998 ± 0.0006 and model error (ME): 1.35 ± 0.21 mm] is superior to the use of both motion phase and amplitude extracted from a 1D respiratory signal (CC and ME of 0.971 ± 0.02 and 1.64 ± 0.28 mm). The difference in performance was more substantial compared to the use of only one parameter (phase or amplitude) used in the motion model construction. Similarly, the patient surface based model was better in estimating the motion in the repeated 4D CT acquisitions and those CT images acquired at the full inspiration (FI) and the full expiration (FE). Once more, within this context the use of both amplitude and phase in the model building was substantially more robust than the use of phase or amplitude only.
Conclusions: The present study demonstrates the potential of using external patient surfaces for the construction of patient specific respiratory motion models. Such information can be obtained using different devices currently available. The use of external surface information led to the best performance in estimating internal structure motion. On the other hand, the use of both amplitude and phase parameters derived from an 1D respiration signal led to largely superior model performance relative to the use of only one of these two parameters in the model building process.
Keywords: respiratory motion, motion modeling, patient external surface, 4D CT, principal component analysis (PCA)
INTRODUCTION
Radiotherapy (RT) represents an important modality in the treatment of cancer. Its goal is to apply radiation to eradicate a tumor while sparing surrounding healthy tissues. This goal is not always fulfilled due to different types of errors introduced throughout the course of external beam radiotherapy. These errors include inaccurate patient setup,1 anatomical motion and deformation,2 and target volume definition inaccuracies due to the imaging modality used and the associated image quality, uncertainty about tumor extent, and/or interobserver delineation variation.3 Among these sources of uncertainty originating from the tumor delineation process to the beam delivery stage, patient physiological motion is the primary focus of this paper.
Motion management is important in the RT of thoracic and abdominal regions since respiratory-induced organ and tumor motion contribute significantly to errors in patient anatomy and tumor localization during both the radiotherapy planning (including the CT acquisition) and delivery process.4 A potential solution is the introduction of the temporal dimension in both the planning acquisition and treatment processes leading to what is known as 4D RT.5 4D RT consists of characterizing the respiratory motion of each or both tumor and anatomical structures of interest, creating a treatment plan that takes into account this motion and finally delivering this plan to the moving tumor and surrounding healthy tissues.
Within the context of 4D RT, modeling of the respiratory motion represents an important task. For example in the case of the CyberKnife Synchrony™ system, used in radiotherapy, a set of three optical fiducial markers are attached to a snugly fitting vest the patient wears, to provide a breathing signal. In order to ensure continuous correspondence between the external and internal motion,6 small gold markers are also implanted prior to treatment in the vicinity of the target organ or lesion, allowing a model to be defined between the motion of the external and internal markers. This model is updated based on frequent x-ray snapshots of the position of both marker sets simultaneously.6 Another example is the Calypso system (Calypso Medical Technologies, Seattle, US) that uses a technology that can potentially eliminate the need for an internal–external motion model by using implanted transponders with an associated wireless tracking with a frequency of up to 10 Hz.7 However, as with the CyberKnife Synchrony™ system the issue remains the use of implanted markers which involves an invasive procedure, in addition to tracking a few well localized internal markers which does not allow comprehensively accounting for non local deformations and the motion of normal surrounding to the tumor structures. The last example is the Xsight® Lung Tracking (XLT) system8 which is an evolution of the CyberKnife Synchrony™ system, capable of a real-time tracking of respiratory motion of lung tumors without the need of implanted markers, although external fiducials are still necessary. One of the issues associated with this system is the fact that it does not take into account tumor free form deformations (only transitional motion is considered).
To resolve these issues, different deformation field respiratory based models have been previously proposed in the literature. All of these models relate the motion of the tumor and the adjacent anatomy to an external surrogate such as the real time position management system (RPM).9 McClelland10, 11 proposed the generation of such a patient specific model providing displacement fields for any point in the CT volume and continuous over the respiratory cycle. However, this model is limited to the description of an average respiratory cycle. In this case, the predictability of the model is therefore limited to the information provided by that average respiratory cycle and not the acquired and potentially irregular respiratory signal. In addition, this motion model takes into account one respiratory parameter which is the phase but ignores all other respiratory parameters such as the amplitude. A model proposed more recently9, 12 relates the displacement fields to both the amplitude as well as the phase of the respiratory cycle using a 2D B-spline model. Although this model takes into account respiratory signal irregularities and describes efficiently respiration-induced organ motion, it requires a good correlation between the 1D respiratory signal (in terms of phase and amplitude), provided, for example, by the RPM or pressure belt, and the internal organ and tumor motion. A number of studies have shown a variable level of correlation between such 1D respiratory surrogates and the internal respiratory motion.13, 14, 15, 16, 17, 18 On the other hand, a recent study19 has suggested that the knowledge of a patient’s entire external surface motion allows a better correlation with the motion of internal structures. In addition, different recent studies have proposed the use of external patient surface information for respiratory motion synchronization in 4D CT imaging.20, 21, 22
Therefore, the main objective of this study was to demonstrate the interest of using the motion of a patient’s entire surface in comparison with the use of 1D respiratory signals for the construction of a patient’s specific respiratory motion model. The 3D surfaces used here are extracted by segmenting 4D CT series for each patient, although in practical terms 3D patient surface measurements can be also provided by systems such as, for example, a time of flight (ToF) camera23 which actively illuminates a patient with an incoherent light signal. Finally, the use of surface maps for the construction of a respiratory motion model based on B-spline functions would require the use of multidimensional B-splines which are time consuming and as such a compromise for real time applications. Therefore, in this work, a new approach based on the use of principal component analysis (PCA)24 has been used in order to build the patient specific respiratory motion model.
MATERIALS AND METHODS
Patient datasets
The clinical data used in this study were acquired on a GE Lightspeed multislice CT MSCT scanner with a cine CT scan capability.25 Each cine CT scan covered 2 cm (8 × 2.5 mm) with 19–23 images acquired per slice location. The total axial length covered in the cine CT acquisition for each patient was 28 cm. The real-time position management (RPM, Varian Medical Systems) system was used to obtain the patient’s respiration signal. CT scans were retrospectively binned to obtain a 4D CT series composed of ten phases (0%, 10%,… 90% of a mean respiratory cycle). These phases where sorted using an improved phase binning approach by rejecting parts of the respiratory cycle and corresponding CT images associated with irregular respiration as described by Pan et al.25 Each binned thoracic CT volume had 512 × 512 × 112 voxels, with dimensions 0.97 × 0.97 × 2.5 mm3 corresponding to the x, y, and z directions, respectively. The obtained CT volume corresponding to the full expiration was used as the “reference volume”. Ten patient datasets were used in this study, all of them having a 4D CT acquisition. Amongst these ten patients, two of them had also one repeated 4D CT acquisition within a two week period from the first 4D CT acquisition, while the last of the patients had also two additional CT acquisitions [one at full inspiration (FI) and another at full expiration (FE)].
Motion model reconstruction
In the previous work,9, 12 a respiratory motion model was proposed using a 2D B-spline based on a deformation field as a function of the amplitude (defined as the value of the signal at a given time point) and the phase of an 1D respiratory signal. This model was constructed through a 2D fitting of the x, y, and z displacements obtained for every control point of a B-spline based elastic registration approach26 applied on the 4D CT images of each patient. The registration approach uses a local spatial parametric model for the deformation based on B-splines and reformulates the registration task as a global optimization problem. The obtained transformation Ut(x) between the frame f(x,t) at time t and the reference frame f(x,0) was defined as a linear combination of B-spline basis functions, located in a rectangular grid
| (1) |
where βr is a tensor product of centered B-splines of degree, r and j are the indices of the grid location. The spacing between the grid h determines the number of parameter cj to be optimized and the final rigidity of the solution. The registration is then formulated as an optimization procedure that minimizes the sum of squared differences metric to find the best transformation parameter cj. Finally, to improve speed and robustness, a multiresolution approach is used in both the image and the transformation space.26 The performance of this algorithm has been previously evaluated on five healthy volunteers 4D MRI datasets comparing the estimated trajectories with the manual tracking provided by an expert.27 Quantitative results of motion estimations using this approach resulted in a mean error of less than 1 mm for all the analyzed 4D sequences.27
The value of every displacement was effectively plotted against the amplitude and the phase of the corresponding respiratory signal. Finally, a B-spline was fitted to the data
| (2) |
where i = floor(x) − 1, j = floor(y) − 1, s = x − floor(x), t = y − floor(y), ϕ is the value of the (i + k) and (j + l) control points and βk, βl are uniform cubic b-spline basis function9 defined as
| (3) |
where, 0 ≤ t < 1. They serve to weight the contribution of each control point to f (x,y) based on its distance to (x,y). This model cannot be easily extended to take into account the availability of patient surface information which requires a higher than 2D B-spline (amplitude + phase) function order, making it extremely complex while significantly increasing the model building computational time (∼9 min for a 2D B-spline model construction versus ∼340 min to build a 3D B-spline model). Thus, an approach based on PCA was privileged in this study for the construction of the patient specific respiratory motion model. The obtained model will relate the internal motion described by the deformation matrices and the external motion characterized by the amplitude and the phase of the respiratory signal in the case of the RPM or using regions of interest (ROI) in the case of the patients’ surface utilization.
PCA is a method used to identify data patterns and express this data in order to emphasize their distinctness and similarities. PCA can be used to compress these data by reducing dimensionality without much loss of information. In this study, PCA was applied on the internal motion described precisely by the displacement vectors and the corresponding external motion described by surrogates such as the RPM or the external surfaces. The displacement vectors are vectors obtained from registering all 4D CT frames on the reference frame (full expiration CT). The registration algorithm used is based on B-splines.26
The set of displacement vectors are placed in a vector in the following manner:24
| (4) |
where, um,i,j is the ith component of displacement for the voxel m at time point j (0 < j < J, where J is the number of phase specific frames, 10 in this study), i = 1,2,3 for the x, y, z displacement direction, respectively, M is the total number of voxels, and sn,j is the displacement of the nth surrogate at time point j, where n = 1,2,…, N (N is the total number of surrogates per deformation field) and j = 1, 2, …, J.
In the case of the 1D respiratory signals, the two motion description surrogates used are the phase (N = 1), the amplitude (N = 1), or both the phase and the amplitude (N = 2) of the respiratory signal. In the case of using patient surface information, these were extracted from the 4D CT volumes using a threshold based segmentation algorithm.28 Each extracted surface corresponds to a binary 3D volume, with the voxels constituting the patient’s surface set to 1 and all other voxels set to 0. In addition, a z-map of the 3D volume representing the distance of the patient skin from a given plane was calculated. This latter map corresponds to the distance map that can be acquired by a Time of Flight camera,23 capable of yielding 3D surface maps (acquisition rate >30Hz) in which each point corresponds to the measured Euclidean distance between the camera and the object. Such a device could be used in the clinical setup for dynamically measuring a patient’s external surface. Ten square ROIs (5 × 5 pixel each) were subsequently placed, according to the literature recommendation,5, 19 between the xyphoid process and the umbilicus on the calculated z-map (N = 10). The size, shape, and placement of these ROIs have been optimized in our previous work19 that studied the correlation between different patient surface ROI parameters (size, shape, and position) and the tumor as well as normal structures’ motion based on experts’ identification of internal anatomical landmarks.
In order for the PCA to work properly the mean is subtracted from each data dimension and a matrix D is constructed:
| (5) |
where, are centered vectors and is the mean vector representing the average motion, given by
| (6) |
The next step in the PCA procedure is to calculate the eigenvalues and eigenvectors of the covariance matrix DDT. The matrix D is a (3M + N)*J (3M + N has a typical value of about 7 × 106), and therefore the size of DDT is (3M + N)×(3M + N). So calculating the eigenvectors of this covariance matrix is computationally expensive. Let X be an eigenvector of the matrix DTD with eigenvalue λ, multiplying DDT by DX leads to
| (7) |
So DX is an eigenvector of the covariance matrix DDT and λ its corresponding eigenvalue. λ is an eigenvalue of both DDT and DTD. As a result, all eigenvalues of DDT are zero except those with non zero eigenvalues for DTD. Therefore, we can calculate eigenvalues and eigenvectors for DTD (J*J), obtaining the corresponding non zero eigenvalues and eigenvectors E = DX of DDT. Since , we have only J − 1 independent measurements and therefore J − 1 eigenvectors of DTD (and consequently of DDT) having nonzero eigenvalues. Finally, a good approximation of each possible motion state d(t) at an arbitrary time point t can be expressed as a weighted sum of the K eigenvectors ek with the largest eigenvalues
| (8) |
Using the centered vectors extracted from Eq. 8 and using the matrix notation
| (9) |
where E = [e1, …, ek] consists of the first K eigenvectors and W = […, wk, …] are corresponding weights. Given that , Eq. 6 can be split into two separate components
| (10) |
where Eu and Es are constructed from the upper 3M rows and lower N rows of E, respectively. W can be eliminated by assuming that Es is invertible, leading to
| (11) |
where is the internal motion described by the deformation fields and is the external motion described in the case of the RPM respiratory signal by the amplitude alone, the phase alone, or both amplitude and phase of the respiratory signal, and by the ten regions in the case of using patient external surfaces. B is the matrix representing the patient motion characteristics. Considering the question of computational cost the complete model building step is ∼30 min on an AMD Athlon™ 64 X2 Dual Core Processor which is almost equivalent to the time necessary for completing the first 4D CT image registration step (∼28 min on the same processor). On the other hand, the use of the model for the estimation of the 4D CT images is almost instantaneous (<1 s).
Motion model evaluation
The evaluation of the proposed patient specific motion model described by Eq. 11 has been assessed by deriving CT images using on one hand the developed model based on the respiratory signal phase “PhModel”, amplitude “AmpModel” or both of them “AmpPhModel”, and on the other using the developed model based on the surface maps extracted from the 4D CT series “SurfaceMapModel”. The leave-one-out approach was used for the comparison of these different estimation models, where at each estimation step, the acquired CT image to be predicted was excluded from the motion construction step.
The second part of the evaluation was concentrated on the capability of the models based on the different surrogate measures in terms of reproducibility within the context of the irregular nature of respiratory motion. Subsequently, the accuracy of the proposed models was tested on two repeated 4D CT scans acquired on the same patient within a two week period. This was done by creating the model using the first 4D CT series for each of the two patients and evaluating it by generating both of the two 4D CT acquired datasets (that of week 1 and week 3). In addition, to further evaluate the ability of the proposed models to deal with extreme respiratory irregularities the model created using the 4D CT series of one of the patients was used to generate, and compared to the corresponding acquired, static CT images for the same patient at full inspiration and full expiration.
The CT volumes predicted by each model have been subsequently compared with their corresponding acquired CT volumes. First, profiles were used to perform local image comparisons between the model derived and corresponding acquired CT volumes. Second, the correlation coefficient (CC) was used for global comparison purposes. It measures a linear affine relation between the intensity of the compared images. The CC between two images A and B is given by
| (12) |
where i and j are the voxel intensities of the two images to be compared, m is the mean of the image intensities, σ is the standard deviation, and pij is the joint probability. In addition to the correlation coefficients, image differences were used to provide global CT image comparisons.
Finally, a clinical expert was asked to select the same easily identifiable anatomical landmarks in both the acquired and modeled generated CT images.29 The error between each landmark in the reference and the corresponding model generated CT volumes was subsequently calculated, leading to a model error (ME) given by
| (13) |
where are the x, y, and z coordinates, respectively, of the kth landmark in the acquired CT, and are the x, y, and z coordinates, respectively, of the kth landmark in the model generated CT. The ME is in mm and n is the number of anatomical landmarks (13 used in this study). These landmarks19 were identified throughout the thoracic field covered by the 4D CT images including both regions of large and small respiratory motion.30, 31, 32, 33, 34 Examples of the landmarks used include the right apex, left apex, carina, highest left, and right diaphragm position and the high, low, left, and right boundaries of the tumor. A statistical comparison between the results of the different estimation models for each of the evaluation parameters considered was assessed using a paired t-test (p values < 0.05 were considered statistically significant).
RESULTS
At each estimation step, five different CT volumes were compared; namely, the acquired CT (original data) and predicted CT volumes using the PhModel, AmpModel, AmpPhModel, and the SurfaceMapModel. Figure 1a shows an example of the same slice for each of these CT volumes for one of the ten patient datasets used in this study. The corresponding left diaphragm profile results are shown in Fig. 1b demonstrating, in the comparison with the original CT image, a small advantage of the SurfaceMapModel over the AmpPhModel, and a clear advantage of the two previously mentioned models over the PhModel and the AmpModel.
Figure 1.
(a) Patient 1 original, CT generated using the surfaceMapModel, CT generated using the AmpPhModel, CT generated using the AmpModel and the CT generated using the PhModel. (b) Corresponding left diaphragm profile comparison.
Two global comparisons were also considered. Figure 2a shows a slice of an original acquired CT image normalized to a scale of 0–255 in order to compare with the magnitude of the subsequent difference images. The difference image between the original acquired CT [Fig. 2a] and the corresponding model predicted CT using the SurfaceMapModel, AmpPhModel, AmpModel and PhModel is shown in Figs. 2b, 2c, 2d, 2e, respectively. The larger differences were observed in the case of the use of the AmpModel and PhModel (−12 to 9 and −7 to 7, respectively). In contrast smaller differences were measured for the use of the AmpPhModel (−5 to +5) and the SurfaceMapModel (−4 to +4).
Figure 2.
(a) A Normalized CT image. Axial view of the difference image between the original acquired CT and the predicted image using the (b) SurfaceMapModel, (c) AmpPhModel, (d) AmpModel, and the (e) PhModel.
The correlation coefficient results for all ten patients between the original and the corresponding model derived CT volumes demonstrated a better correlation between the acquired and the SurfaceMapModel estimated CT volumes (0.998 ± 0.0006). On the other hand, the use of the AmpPhModel using both the amplitude and phase of the respiratory signal in the estimation model leads to superior correlation results (0.971 ± 0.02) relative to the use of either of the two parameters alone for the derivation of the 4D CT volumes (0.85 ± 0.077 and 0.81 ± 0.082 for the AmpModel and PhModel, respectively). The differences in the correlation coefficients between all of the four considered motion models were statistically significant (p-value < 0.0005).
Figure 3a shows a comparison of the ME results for the ten patient datasets considered based on the expert study using the anatomical landmarks for all of the different estimation models. These errors are >20% for four patients and <5% for only one patient. As can be seen in Fig. 3b, the proposed SurfaceMapModel resulted in the smaller mean model error of 1.35 ± 0.21 mm, better than the AmpPhModel with a larger mean error of 1.64 ± 0.28 mm. Finally, the two single parameter models led to the larger errors with 3.63 ± 0.42 and 5.08 ± 0.77 mm for the AmpModel and the PhModel, respectively. The differences in the model error between all of the four considered motion models were also statistically significant (p-value < 0.0008).
Figure 3.
(a) Comparison between the ME (mm) of the SurfaceMapModel, AmpPhModel, AmpModel, and the PhModel of all ten patients used in this study. (b) Mean and standard deviation of this ME.
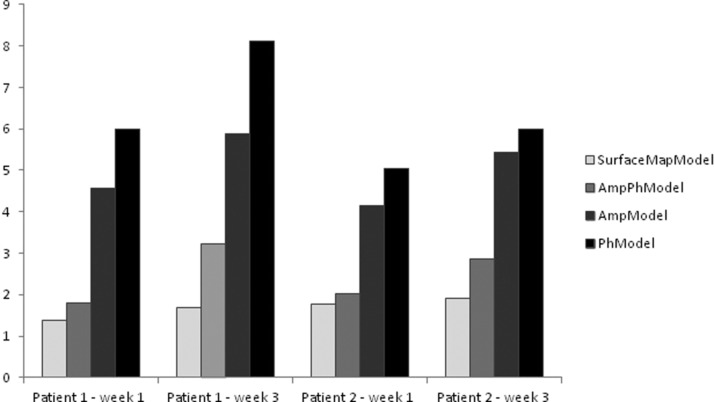
Figure 4 shows a comparison between the ME (mm) of the SurfaceMapModel, AmpPhModel, AmpModel, and the PhModel of the two patients with the two 4D CT acquisitions. The proposed SurfaceMapModel resulted in the smaller mean model error of 1.57 ± 0.21 mm (1.8 ± 0.17 mm) for the estimation of the first (and second) 4D CT image series, which was better than the AmpPhModel with a larger mean error of 1.9 ± 0.16 mm (3.04 ± 0.27 mm). Finally and within the same context, larger errors were observed when considering one of the two single parameter models with 4.36 ± 0.29 mm (5.66 ± 0.33 mm) and 5.51 ± 0.67 mm (7.05 ± 1.51 mm) for the AmpModel and the PhModel, respectively. By calculating the mean model error percentage increase between the estimation of the first (used in the model creation) and the second 4D CT series for every model considered, the SurfaceMapModel demonstrated the best robustness with 12.7% increase compared to the AmpPhModel, AmpModel, and the PhModel with a mean error percentage increase of 37.5%, 22.9%, and 21.8%, respectively.
Figure 4.
Comparison between the ME (mm) of the SurfaceMapModel, AmpPhModel, AmpModel, and the PhModel for the estimation of two different 4D CT series acquired on two patients. All models considered were constructed using the first of the two 4D CT acquisitions and subsequently evaluated for the estimation of both 4D CT series.
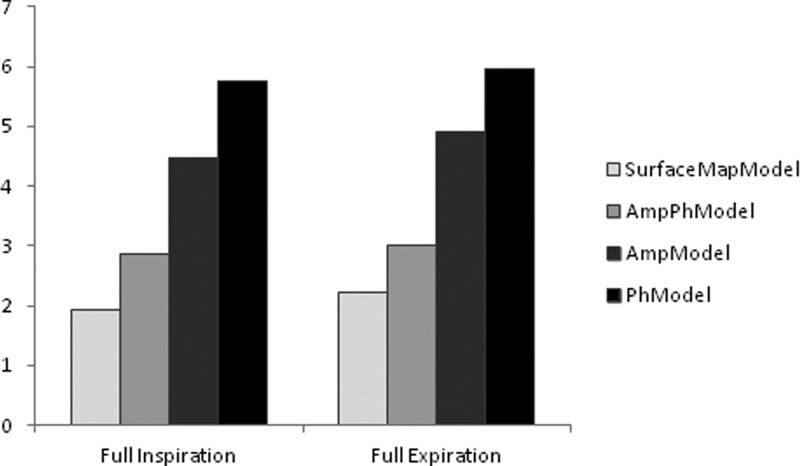
Finally, results considering the ability of the model to handle extreme irregular respiration signal positions indicate that the proposed SurfaceMapModel can generate these extreme irregular positions with an error of 1.92 and 2.21 for the FI CT and the FE CT acquisitions, respectively. Larger errors of 2.85 and 3.01 were measured for the generation of the FI CT and the FE CT images using the AmpPhModel. As shown in Fig. 5, within the same context the use of the single parameter models AmpModel and PhModel led to even larger model errors.
Figure 5.
Comparison between the ME (mm) of the SurfaceMapModel, AmpPhModel, AmpModel, and the PhModel constructed using a 4D CT acquisition in generating acquired full inspiration (FI) and full expiration (FE) CT images of the same patient.
DISCUSSION AND CONCLUSIONS
Modeling of respiratory induced motion is an essential part of accounting for one of the most important parameters compromising the accuracy of both planning and delivering radiation therapy. As such it has a direct impact on the dose received by tumors but also organs at risk during high precision radiotherapy. Different models have been previously proposed for the description of patient specific respiratory motion. Intra patient and interpatient variability in respiratory signals limits the accuracy of such proposed models, especially those parameterized by the characteristics extracted from a 1D respiratory cycle.
The development and use of alternative technology, such as, for example, a ToF camera,35 may allow real-time monitoring of the complete patient surface making available substantially more information. This enhanced information may subsequently lead to better correlation between the external and the internal normal tissues’ and tumor motion.18 As shown in the current study, the use of such 3D external surfaces for the creation of a patient specific motion model allows a higher accuracy than using the combination of amplitude and phase from a patient’s 1D respiratory signal. This difference and advantage are much larger if one considers only one of the two parameters extracted from the 1D respiratory signal. For all ten patients included in this study, the advantage of using the surface was systematic over the phase and the amplitude of the 1D RPM respiratory signal.
In order to allow the creation of such a patient specific motion model based on external 3D patient surfaces a PCA approach was implemented. This is in contrast with the use of B-splines which have been proposed up to now for patient specific motion model construction considering the use of an 1D respiratory signal amplitude, phase or a combination of the two parameters. The PCA approach was privileged in this work for its simplicity relative to the use of higher order B-spline functions which would have been necessary in taking into account the availability of surface maps.
The patient specific model developed in this work can be used to generate a 3D CT image corresponding to any patient surface requiring only one CT reference volume. The proposed model was shown to be efficient, including its ability to deal with respiratory signal irregularities. This capability was assessed on a couple of patients by using the respiratory motion models developed based on a 4D CT acquisition, in estimating a second 4D CT image series of the same patient acquired within a couple of weeks of the first 4D CT acquisition. In addition, for another patient, the different respiratory motion models derived by using the 4D CT images were used in the estimation of the CT images acquired at extreme points in the respiratory cycle (end of inspiration and expiration) well outside the limits of the respiratory signal amplitude registered during the initial 4D CT acquisition. In both cases the surface derived respiratory motion model led to the smaller average errors with <2.2 mm in comparison to 3–8 mm for the models derived using the amplitude, phase or a combination of the two parameters. Within this context, no assumption is required concerning the similarity between the respiratory signal variations during the data acquisition for the model creation and that recorded throughout the course of treatment delivery during the radiation therapy process.
However, previous day to day variation studies using repeat 4D CT scans36, 37 have shown considerable variation in the respiratory motion of individual patients. The majority of the variation can be approximated as baseline shifts.38 In these cases, the underlying anatomy and the motion trajectories are relatively stable, but the baseline position of the tumor relative to other structures varies. As shown in this study our model was able, through the use of the external patient surface variation, to efficiently manage such issues. However, this may be more complicated in cases where, relative to the initial 4D CT scan used in the motion model construction, severe respiratory (for example a change from thoracic to abdominal movement) or patient anatomy (as a result of treatment) changes occur. Future studies will concentrate on testing the model on larger number of patient datasets in order to allow the evaluation of the model under such conditions. Solutions to potential issues that may arise will include, a more frequent model update during treatment, a model update strategy based on the acquisition of two static CT images (one at FI and one at FE), or patient respiration coaching.
The accuracy of the proposed model depends on the accuracy of the deformable registration algorithm as well as on the correlation between the respiratory signal and the internal deformation. The accuracy of the registration algorithm used in this work has been previously assessed.39, 40 On the other hand although some studies have indicated a high correlation between external markers and internal motion, in almost all of these studies the observed correlation is characterized by a high inter and intrapatient variability as well as being dependent on the position of the external markers or monitoring devices. Our results demonstrate a better correlation between the internal structure motion and the patient surface than the correlation with the 1D RPM respiratory signal.
Finally, the accuracy of a respiratory motion model may also depend on the 4D CT sorting method used. In this study, we have used an improved phase binning approach25 accounting for the irregular nature of respiration. An alternative for the 4D CT binning step may be the use of a combination of respiratory phase, displacement, and velocity.41 Such alternative binning approaches may further improve the accuracy and robustness of the different respiratory motion models considered in this work.
One limitation of the current study is that the external patient surfaces used in the patient specific motion model creation were obtained though the segmentation of the patient skin from corresponding 4D CT images. As such the errors in terms of accuracy with which an external device, such a ToF camera, can determine in a real-time fashion the motion amplitude due to respiration throughout a patient surface, have not been considered in this work. Experimental studies have suggested that this accuracy may be between 1 mm and 2 mm, with a minimum variability throughout the camera’s field of view.23, 42 These experimental accuracy estimations, and their potential impact on the accuracy of the subsequent derived respiratory motion model, have to be verified by building models using datasets comprising simultaneous patient 4D CT acquisitions and external surface measurements using such devices.
A second limitation, which is also linked with the lack of real time surface measurements associated with the patient 4D CT studies used in this work, is that the 4D CT binning is done prior to the patient’s surface extraction based on the CT respiratory frames themselves. Considering the capabilities of the camera ToF systems, the patient surface can in principle be monitored during the 4D CT acquisition at a maximum rate of 30 Hz. Therefore, the multiplicity of surfaces for a corresponding CT frame has not been considered in this work. Studies allowing an optimization of the patient external surface acquisition rates to be used in clinical practice will need to be carried out in the future with monitoring systems, such as for example camera ToF technology capable of monitoring the entire patient surface at sufficiently high frequency. This optimization step will need to consider the potential impact of the patient surface acquisition rates in terms of the accuracy in characterizing the patient surface motion but also its subsequent impact in the proposed motion model accuracy. One solution to cope with this issue will be to calculate a mean surface corresponding with each CT respiratory frame, which may in turn help to decrease the potential ToF camera surface acquisition error. However, one has to ensure that such averaging will not compromise the accuracy of characterizing the patient surface motion and associated internal structure motion, particularly within the context of irregular breathing patterns.
Finally, the present study demonstrates the potential of using external patient surfaces for the construction and application of a patient specific respiratory motion model. The validation of these results on ten patients proves that the use of surfaces for the construction of patient specific motion models is more accurate than simply using the 1D respiratory signal amplitude, phase or a combination of the two. Our results suggest that the proposed method is a potentially useful tool for predicting respiration-induced motion in a patient’s 4D images during simulation and treatment, including variability in breathing patterns. Such a tool may be applicable to treatment planning and evaluation of treatment delivery.
ACKNOWLEDGMENT
This work was partly funded by the ITEA2 MEDIATE project.
References
- Gordon J. J., Crimaldi A. J., Hagan M., Moore J., and Siebers J. V., “Evaluation of clinical margins via simulation of patient setup errors in prostate IMRT treatment plans,” Med. Phys. 34, 202–214 (2007). 10.1118/1.2400842 [DOI] [PubMed] [Google Scholar]
- Webb S., “Motion effects in (intensity modulated) radiation therapy: A review,” Phys. Med. Biol. 51, R403–R425 (2006). 10.1088/0031-9155/51/13/R23 [DOI] [PubMed] [Google Scholar]
- van Herk M. et al. , “Biologic and physical fractionation effects of random geometric errors,” Int. J. Radiat. Oncol., Biol., Phys. 57, 1460–1471 (2003). 10.1016/j.ijrobp.2003.08.026 [DOI] [PubMed] [Google Scholar]
- Ozhasoglu C. and Murphy M. J., “Issues in respiratory motion compensation during external-beam radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 52, 1389–1399 (2002). 10.1016/S0360-3016(01)02789-4 [DOI] [PubMed] [Google Scholar]
- Keall P. J., Mageras G. S., Balter J. M., Emery R. S., Forster K. M., Jiang S. B., Kapatoes J. M., Low D. A., Murphy M. J., Murray B. R., Ramsey C. R., van Herk M. B., Vedam S. S., Wong J. W., and Yorke E., “The management of respiratory motion in radiation oncology report of AAPM Task Group No. 76,” Med. Phys. 33, 3874–900 (2006). 10.1118/1.2349696 [DOI] [PubMed] [Google Scholar]
- Schweikard A., Shiomi H., and Adler J., “Respiration tracking in radiosurgery,” Med. Phys. 31, 2738–2741 (2006). 10.1118/1.1774132 [DOI] [PubMed] [Google Scholar]
- Santanam L., Malinowski K., Hubenshmidt J., Dimmer S., Mayse M., Bradley J., Chaudhari A., Lechleiter K., Esthappan J., Mutic S., Low D., and Parikh P., “Fiducial-based translational localization accuracy of electromagnetic tracking system and on-board kilovoltage imaging system,” Int. J. Radiat. Oncol., Biol., Phys. 70(3), 892–899 (2008). 10.1016/j.ijrobp.2007.10.005 [DOI] [PubMed] [Google Scholar]
- Bibault J. E. et al. , “Stereotactic radiotherapy for lung cancer: Non-invasive real-time tumor tracking,” Cancer Radiother. 14(8), 690–697 (2010). 10.1016/j.canrad.2010.03.010 [DOI] [PubMed] [Google Scholar]
- Fayad H., Pan T., Roux C., Cheze Le Rest C., Pradier O., and Visvikis D., “A 2D-spline patient specific model for use in radiation therapy,” IEEE ISBI Conference Proceedings (IEEE International Symposium, Boston, MA, 2009), pp. 590–593.
- McClelland J. R., Blackall J. M., Tarte S., Chandler A. C., Hughes S., Ahmad S., Landau D. B., and Hawkes D. J., “A continuous 4D motion model from multiple respiratory cycles for use in lung radiotherapy,” Med. Phys. 33, 3348–3358 (2006). 10.1118/1.2222079 [DOI] [PubMed] [Google Scholar]
- McClelland J., Gao G., Tarte S., Blackall J., Hughes S., Ahmad S., Landau D., and Hawkes D., “Removing artifacts from 4DCT volumes acquired in Cine mode using B-spline non-rigid registrations,” 50th Annual Meeting AAPM, Houston, TX [Med. Phys. 35, 2992, (2008)].
- McClelland J. R., Hughes S., Modat M., Qureshi A., Ahmad S., Landau D. B., Ourselin S., and Hawkes D. J., “Inter-fraction variations in respiratory motion models,” Phys. Med. Biol. 56, 251–272 (2011). 10.1088/0031-9155/56/1/015 [DOI] [PubMed] [Google Scholar]
- Vedam S. et al. , “Quantifying the predictability of diaphragm motion during respiration with a noninvasive external marker,” Med. Phys. 30, 505–513 (2003). 10.1118/1.1558675 [DOI] [PubMed] [Google Scholar]
- Mageras G. S. et al. , “Measurement of lung tumor motion using respiration-correlated CT,” Int. J. Radiat. Oncol., Biol., Phys. 60, 933–941 (2004). 10.1016/j.ijrobp.2004.06.021 [DOI] [PubMed] [Google Scholar]
- Tsunashima Y. et al. , “Correlation between the respiratory waveform measured using A respiratory sensor and 3D tumor motion in gated radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 60(3), 951–958 (2004). 10.1016/j.ijrobp.2004.06.026 [DOI] [PubMed] [Google Scholar]
- Gierga D. et al. , “The correlation between external and internal markers for abdominal tumors: Implications for respiratory gating,” Int. J. Radiat. Oncol., Biol., Phys. 61(5), 1551–1558 (2005). 10.1016/j.ijrobp.2004.12.013 [DOI] [PubMed] [Google Scholar]
- Beddar A. et al. , “Correlation between internal fiducial tumor motion and external marker motion for liver tumors imaged with 4D-CT,” Int. J. Radiat. Oncol., Biol., Phys. 67(2), 630–638 (2007). 10.1016/j.ijrobp.2006.10.007 [DOI] [PubMed] [Google Scholar]
- Kanoulas E. et al. , “Derivation of the tumor position from external respiratory surrogates with periodical updating of the internal/external correlation,” Phys. Med. Biol. 52, 5443–5456 (2007). 10.1088/0031-9155/52/17/023 [DOI] [PubMed] [Google Scholar]
- Fayad H., Tinsu Pan, Clement J. F., and Visvikis D., “Technical note: Correlation of respiratory motion between external patient surface and internal anatomical landmarks,” Med. Phys. 38(6), 3157–3165 (2011). 10.1118/1.3589131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehrhardt J., Werner R., Säring D., Frenzel T., Lu W., Low D., and Handels H., “An optical flow based method for improved reconstruction of 4D CT data sets acquired during free breathing,” Med. Phys. 34(2), 711–721 (2007). 10.1118/1.2431245 [DOI] [PubMed] [Google Scholar]
- Spadea M. F., Baroni G., Gierga D. P., Turcotte J. C., Chen G. T., and Sharp G. C., “Evaluation and commissioning of a surface based system for respiratory sensing in 4D CT,” J. Appl. Clin. Med. Phys. 12(1), 3288 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gianoli C., Riboldi M., Spadea M. F., Travaini L. L., Ferrari M., Mei R., Orecchia R., and Baroni G. A., “A multiple points method for 4D CT image sorting,” Med. Phys. 38(2), 656–667 (2011). 10.1118/1.3538921 [DOI] [PubMed] [Google Scholar]
- Clement J. F., Fayad H., Lamard M., Pradier O., Cheze Le Rest C., and Visvikis D., “Time of flight camera (TOF) for contact-less and marker-less 3D respiratory motion detection,” J. Nucl. Med. 50(Suppl. 2), 1541 (2009). 10.2967/jnumed.108.056721 [DOI] [PubMed] [Google Scholar]
- Zhang Q., Pevsner A., Hertanto A., HU Y. C., Rosenzweig K. E., Ling C. C., and Mageras G. S., “A patient-specific respiratory model of anatomical motion for radiation treatment planning,” Med. Phys. 34, 4772–4781 (2007). 10.1118/1.2804576 [DOI] [PubMed] [Google Scholar]
- Pan T., Sun X., and Luo D., “Improvement of the cine-ct based 4d-ct imaging,” Med. Phys. 34(11), 4499–4503 (2007). 10.1118/1.2794225 [DOI] [PubMed] [Google Scholar]
- Ledesma-Carbayo M. J., Kybic J., Desco M., Santos A., Suhling M., Hunziker P., and Unser M., “Spatio-temporal nonrigid registration for ultrasound cardiac motion estimation,” IEEE Trans. Med. Imaging, 24(9), 1113–1126 (2005). 10.1109/TMI.2005.852050 [DOI] [PubMed] [Google Scholar]
- Ledesma-Carbayo M. J., Bajo A., Santa Marta C., Perez-David E., Garcia-Fernandez M. A., Desco M., and Santos A., “Fully automatic cardiac motion estimation from tagged MRI using non-rigid registration techniques,” Comput. Cardiol. 33, 305–308 (2006). [Google Scholar]
- Zhou X. et al. , “Automated segmentations of skin, soft-tissue and skeleton from torso CT images,” Proc. SPIE 5370, 1634–1639 (2004). 10.1117/12.534843 [DOI] [Google Scholar]
- Sarrut D., Boldea V., Miguet S., and Ginestet C., “Simulation of 4D CT images from deformable registration between inhale and exhale breath-hold CT scans,” Med. Phys. 33(3), 605–617 (2006). 10.1118/1.2161409 [DOI] [PubMed] [Google Scholar]
- Murphy M. J., Martin D., Whyte R., Hai J., Ozhasoglu C., and Le Q. T., “The effectiveness of breath-holding to stabilize lung and pancreas tumors during radiosurgery,” Int. J. Radiat. Oncol., Biol., Phys. 53(2), 475–482 (2002). 10.1016/S0360-3016(01)02822-X [DOI] [PubMed] [Google Scholar]
- Giraud P., Reboul F., Clippe S., Garcia R., Carrie C., Campana F., Dubray B., Rosenwald J. C., and Cosset J. M., “Respiration-gated radiotherapy: Current techniques and potential benefits,” cancer radiothérapie, ELSEVIER, 7(1), 15s–25s (2003). [PubMed] [Google Scholar]
- Van Sörnsen de Koste J. R., Lagerwaard F. J., Nijssen-Visser M. R., Graveland W. J., and Senan S., “Tumor location cannot predict the mobility of lung tumors: A 3D analysis of data generated from multiple CT scans,” Int. J. Radiat. Oncol., Biol., Phys. 56(2), 348–354 (2003). 10.1016/S0360-3016(02)04467-X [DOI] [PubMed] [Google Scholar]
- Wagman R., Yorke E., Ford E., Giraud P., Mageras G., Minsky B., and Rosenzweig K., “Respiratory gating for liver tumors: Use in dose escalation,” Int. J. Radiat. Oncol., Biol., Phys. 55(3), 659–668 (2003). 10.1016/S0360-3016(02)03941-X [DOI] [PubMed] [Google Scholar]
- Ionascu D., Jiang S. B., Nishioka S., Shirato H., and Berbeco R. I., “Internal-external correlation investigations of respiratory induced motion of lung tumors,” Med. Phys. 34(10), 3893–903 (2007). 10.1118/1.2779941 [DOI] [PubMed] [Google Scholar]
- Schaller C., Penne J., and Hornegger J., “Time-of-flight sensor for respiratory motion gating,” Med. Phys. 35(7), 3090–3093 (2008). 10.1118/1.2938521 [DOI] [PubMed] [Google Scholar]
- Britton K. R., Starkschall G., Tucker S. L., Pan T., Nelson C., Chang J. Y., Cox J. D., Mohan R., and Komaki R., “Assessment of gross tumour volume regression and motion changes during radiotherapy for non-small-cell lung cancer as measured by four-dimensional computed tomography,” Int. J. Radiat. Oncol., Biol., Phys. 68, 1036–1046 (2007). 10.1016/j.ijrobp.2007.01.021 [DOI] [PubMed] [Google Scholar]
- Redmond K. J., Song D. Y., Fox J. L., Zhou J., Rosenzweig C. N., and Ford E., “Respiratory motion changes of lung tumours over the course of radiation therapy based on respiratory correlated four-dimensional computed tomography scans,” Int. J. Radiat. Oncol., Biol., Phys. 75, 1605–1612 (2009). 10.1016/j.ijrobp.2009.05.024 [DOI] [PubMed] [Google Scholar]
- Sonke J.-J., Rossi M., Wolthaus J., van Herk M., Damen E., and Belderbos J., “Frameless stereotactic body radiotherapy for lung cancer using four-dimensional cone beam CT guidance,” Int. J. Radiat. Oncol., Biol., Phys. 74, 567–574 (2009). 10.1016/j.ijrobp.2008.08.004 [DOI] [PubMed] [Google Scholar]
- Ledesma-Carbayo M. J., Mahia-Casado P., Santos A., Perez-David E., Garcia-Fernandez M. A., and Desco M., “Cardiac motion analysis from ultrasound sequences using nonrigid registration: Validation against Doppler tissue velocity,” Ultrasound Med. Biol. 32, 483–490 (2006). 10.1016/j.ultrasmedbio.2005.12.006 [DOI] [PubMed] [Google Scholar]
- Lamare F., Cresson T., Savean J., Cheze Le Rest C., Reader A. J., and Visvikis D., “Respiratory motion correction for PET oncology applications using affine transformation of list mode data,” Phys. Med. Biol. 52, 121–140 (2007). 10.1088/0031-9155/52/1/009 [DOI] [PubMed] [Google Scholar]
- Langner U. W. and Keall P. J., “Accuracy in the localization of thoracic and abdominal tumors using respiratory displacement, velocity, and phase,” Med. Phys. 36(2), 386–393 (2009). 10.1118/1.3049595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wentz T., Fayad H., Clement J. F., Savéan J., Hatt M., and Visvikis D., “Extraction and evaluation of anatomical patient surface and associated respiratory motion with a time-of-flight (ToF) camera, J. Nucl. Med. 52(1), 215 (2011). [Google Scholar]