Speech recognition against harmonic and inharmonic complexes: Spectral dips and periodicity

Abstract

Speech recognition in a complex masker usually benefits from masker harmonicity, but there are several factors at work. The present study focused on two of them, glimpsing spectrally in between masker partials and periodicity within individual frequency channels. Using both a theoretical and an experimental approach, it is demonstrated that when inharmonic complexes are generated by jittering partials from their harmonic positions, there are better opportunities for spectral glimpsing in inharmonic than in harmonic maskers, and this difference is enhanced as fundamental frequency (F0) increases. As a result, measurements of masking level difference between the two maskers can be reduced, particularly at higher F0s. Using inharmonic maskers that offer similar glimpsing opportunity to harmonic maskers, it was found that the masking level difference between the two maskers varied little with F0, was influenced by periodicity of the first four partials, and could occur in low-, mid-, or high-frequency regions. Overall, the present results suggested that both spectral glimpsing and periodicity contribute to speech recognition under masking by harmonic complexes, and these effects seem independent from one another.

INTRODUCTION

Identification of a target vowel, presented against a masking vowel, is much less affected by its own harmonicity, than by the harmonicity of the masking vowel (de Cheveigné et al., 1995, 1997a). Deroche and Culling (2011a) demonstrated a similar effect for the intelligibility of connected speech using the combination of modulation of fundamental frequency (F0) and reverberation to introduce inharmonicity to a target voice or to a speech-shaped complex masker. Speech reception thresholds (SRTs) were particularly elevated when the masker's harmonicity was disrupted in this way. It therefore appears that listeners can better understand a speech source when the sounds they are ignoring are harmonic. Why is this so? A harmonic complex is distinct in a number of ways from an inharmonic sound. We will first review four associated forms of masking release described in the literature and discuss the theoretical accounts that have been put forward for them.

First, a harmonic complex may have partials that are resolved in the auditory periphery (Shackleton and Carlyon, 1994). In between resolved partials, there are spectral dips that allow listeners a better target-to-masker ratio (TMR) at those center frequencies. The term “spectral dips” refers here to dips in the blurred internal auditory spectrum of the complex tone, as seen from an excitation pattern. The term “spectral glimpsing” refers to the listeners’ ability to extract some target information at these spectral dips, without specifying whether listeners actively select specific frequency channels or simply benefit from a better overall TMR across frequency. Spectral glimpsing has, in the past, been examined with spectral dips introduced into noise. For instance, Peters et al. (1998) showed that for young normal-hearing listeners, SRT decreased by 8.7 dB when the noise was filtered to have an alternating pattern of 2 equivalent-rectangular-bandwidths (ERBs) present and 2 ERBs removed, decreased by a further 3.6 dB when the alternating pattern was 3-ERB wide, and by a further 2.6 dB when the alternating pattern was 4-ERB wide. The removal of entire spectral bands resulted in large spectral dips. It is less clear how much listeners can take advantage of the smaller spectral dips occurring between harmonic partials. Deroche et al. (2013) found that SRT for a voice against random-phase harmonic complexes at fixed F0 improved by about 3 dB for each doubling of the masker F0 (while the level per partial compensated for the reduction in spectral density). They interpreted this effect as spectral glimpsing, because there are wider and deeper spectral dips when adjacent partials are more separated, but this interpretation raised a number of interesting questions. For what range of F0s does spectral glimpsing play a role in speech recognition against harmonic complexes? How much does it account for the effect of difference in fundamental frequency between competing voices? Is it easier to glimpse in a masker with spectral dips regularly spaced in frequency, or regularly spaced in ERB, or does the regularity of the dips not matter at all? It may be that listeners can glimpse very well in any complex with discrete resolved components.

Second, harmonic complexes have temporal envelopes that can be strongly modulated in high-frequency channels, depending on the phase relationships between unresolved partials. Listeners may benefit from a better TMR within the dips of the temporal envelopes, and this effect can be facilitated by cochlear compression (Kohlrausch and Sander, 1995; Carlyon and Datta, 1997). In contrast, partials jittered in inharmonic relations (even when in phase with each other) do not offer such envelope modulations because adjacent partials are separated by different amounts, and consequently result in different modulation rates. However, this potential account has been examined by several studies with vowels (Summerfield and Assmann, 1991; de Cheveigné et al., 1997b; de Cheveigné, 1999) and with speech (Deroche and Culling, 2011a; Deroche et al., 2013; Green and Rosen, 2013) and does not seem to play a major role for F0s in the human voice range at moderate sound levels.

Third, a harmonic complex has periodicity in each within-channel waveform. Deroche and Culling (2011b) measured masked detection threshold (MDT) for a narrow band of noise (100-Hz wide) masked by harmonic or inharmonic complexes with equal-amplitude partials. The random phase relationships between partials were sufficient to exclude a role for the second mechanism mentioned above. To exclude a role for spectral glimpsing, the masker partial centered on the target noise-band was fixed for both harmonic and inharmonic maskers, such that the excitation level of the maskers was the same at the target center frequency. Even in these conditions, they found that detection of the noise band was better with the harmonic than with the inharmonic masker. This masking-level difference due to harmonicity (HMLD) occurred for center frequencies between 0.5 and 2.5 kHz. Furthermore, the HMLD was influenced by the harmonicity of partials located in spectral regions remote from the target center frequency. Thus, there may be a mechanism that integrates information about the masker periodicity across channels in order to suppress it, a mechanism known as harmonic cancellation (de Cheveigné, 1993; de Cheveigné et al., 1995, 1997a).

Fourth, a harmonic complex (provided it is stationary) produces little modulation masking because its within-channel temporal envelopes fluctuate at the rate of the F0, and consequently interfere little with the slow modulations of speech (less than 10 Hz), essential to articulation (Houtgast and Steeneken, 1985). In contrast, noise maskers have random envelope fluctuations at very slow rates and produce a substantial amount of modulation masking (Bacon and Grantham, 1989; Dau et al., 1997a,b). The extent to which modulation masking may be involved with inharmonic complexes is less clear and depends on whether some inharmonic partials, very close to each other in frequency, may produce sufficiently slow envelope modulations. Although this was not the focus of the present study, the last experiment briefly examined the role of modulation masking for harmonic, inharmonic, and noise maskers.

The present study focused primarily on the first and the third of these mechanisms in speech recognition. Complexes with partials in random phase were used throughout the study to exclude the second mechanism. A theoretical analysis first examined the size of spectral dips for harmonic and inharmonic complexes, depending on their F0. Spectral dips were more prominent in inharmonic than in harmonic complexes, and this difference increased with F0. It followed that spectral glimpsing should differentially lower thresholds in inharmonic maskers relative to harmonic maskers, reducing the apparent size of the HMLD for speech intelligibility (SI-HMLD). Consistent with these observations, experiment 1 confirmed that the SI-HMLD appears to decrease with increasing F0. Controlling for equal glimpsing opportunities between harmonic and inharmonic complexes, experiment 2 measured the “true” magnitude of SI-HMLDs for different F0s and experiment 3 measured SI-HMLD for speech filtered into different spectral regions.

THEORETICAL ANALYSIS

Harmonic complexes

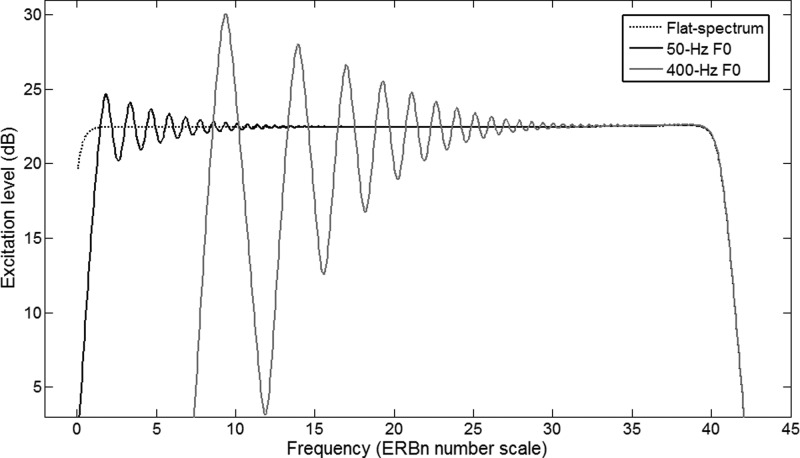
Let us first consider the case of harmonic complexes. Depending on the F0 of the complex, a certain number of partials are resolved in the auditory periphery (Shackleton and Carlyon, 1994). The excitation level is elevated in auditory filters located close to a resolved partial and relatively lowered in auditory filters located in between resolved partials, resulting in peaks and dips in the excitation pattern of the complex. Figure 1 illustrates this point for two harmonic complexes based on F0s of 50 and 400 Hz, with equal-amplitude partials, set at equal RMS level. The excitation patterns were computed from rounded-exponential filters equally spaced on an ERB-scale with level dependency (Glasberg and Moore, 1990). In the excitation patterns presented here, the energy within a given auditory filter was divided by its bandwidth to normalize excitation. To compare the relative sizes of peaks and dips as a function of F0, a flat-spectrum signal was also created from a 10-s long random-phase harmonic complex based on 1-Hz F0 gated by 30-ms onset and offset ramps. This construction ensured a much flatter excitation pattern than using white noise. At low F0, such as 50 Hz, the peaks are roughly as pronounced as the dips. At high F0, such as 400 Hz, the peaks are higher because the reduction in spectral density has been compensated by an increase in partial level; but the dips are now much more pronounced than the peaks. This effect is due to the logarithmic (decibel) scale on which we measure sound pressure levels and excitation patterns, as well as the quasi-logarithmic scale of frequency in the cochlea. The increment in partial level as F0 increases does not produce a large increase in excitation level (e.g., 3 dB in the case of doubling F0) whereas the reduction in spectral density as F0 increases produces a much larger decrease in excitation level between two partials. As a consequence, the higher the F0, the larger the difference between the size of peaks and dips: Dips deepen more than peaks grow.

Figure 1.

Excitation patterns of harmonic complexes based on F0s of 50 and 400 Hz.

Inharmonic complexes

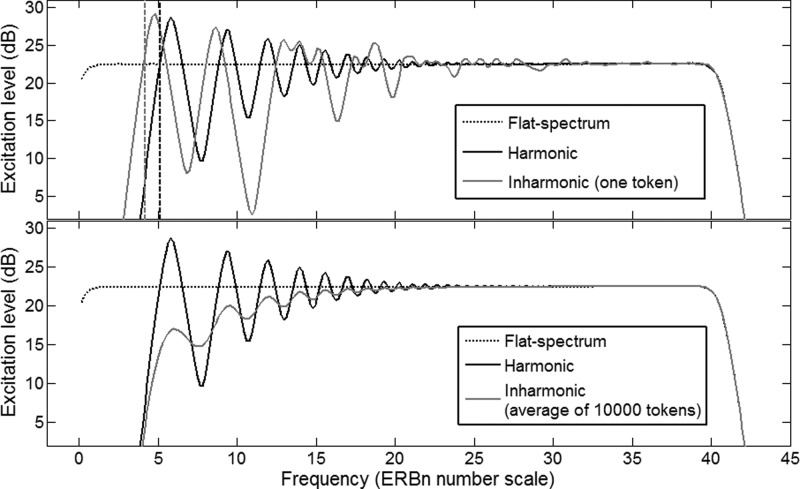
Inharmonicity may be generated in many different ways. For the scope of the present study, we only considered complexes that were generated by jittering partials from their harmonic positions (Chalikia and Bregman, 1993). The size of each jitter was taken randomly from a rectangular distribution between −F0/2 and F0/2 to preserve the order of partials. When two equal-amplitude partials get closer to each other, the excitation level in an auditory filter centered around these partials can only increase by 3 dB at most, whereas when two partials get distant from each other by the same amount, the excitation level in an auditory filter centered in between the two partials decreases potentially by much more than 3 dB. As an example, in the top panel of Fig. 2, for a nominal F0 of 200 Hz, a large spectral dip results from partials 2 and 3 being pushed apart; this dip is much larger than the dip between the respective harmonic partials. In contrast, a modest increase in excitation level results from partials 3 and 4 being closer to each other. Averaging the excitation patterns over many different tokens of inharmonic complexes illustrates the issue: As shown in the bottom panel of Fig. 2, the excitation level is equated in unresolved regions but not in resolved regions, where the averaged excitation level is lower than the flat-spectrum baseline and displays modulations characteristic of the averaged peaks and dips located at and between the masker partials. Thus, for a given nominal F0, spectral dips in the resolved region of an excitation pattern are always more prominent in an inharmonic than in a harmonic complex.

Figure 2.

Excitation patterns of harmonic and inharmonic complexes based on a nominal F0 of 200 Hz. (Top) Peaks resulting from two inharmonic partials close to each other are not as pronounced as dips resulting from two inharmonic partials distant from each other. (Bottom) Averaging the patterns over 10 000 inharmonic tokens reflects this predominance of spectral dips over spectral peaks in the resolved region.

Modeling spectral glimpsing

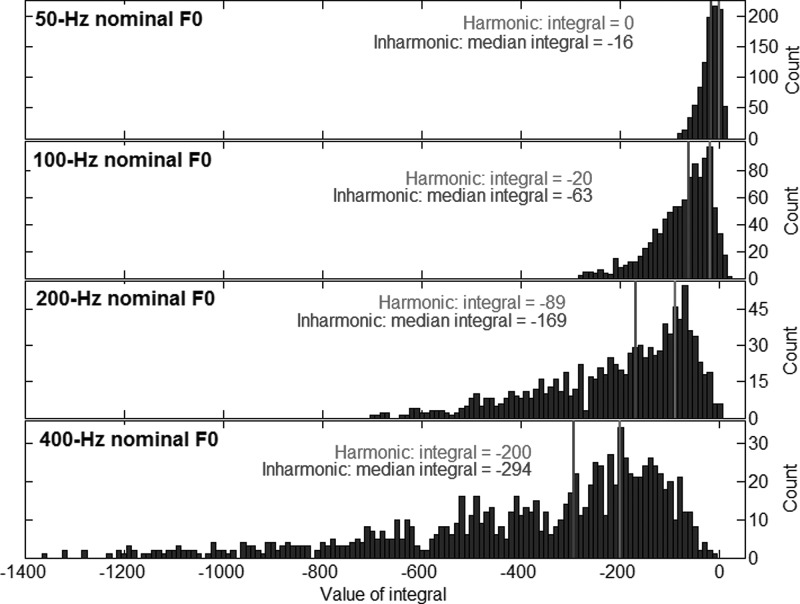
When a voice is presented against a complex masker, listeners may take advantage of substantial spectral dips in the masker's excitation pattern to glimpse some energy belonging to the target voice. Note that this ability assumes a way to distinguish what belongs to each source, which involves mechanisms of grouping by harmonic relations, which in the present study, used instantaneous differences in F0 (ΔF0s) between target and masker. On the other hand, spectral peaks are also important to consider because they result in more masking the larger the peaks. In Fig. 1 for instance, for the harmonic masker at 400-Hz F0, energy of a target voice would be largely available in auditory filters centered at 600, 1000, and 1400 Hz but would hardly be available in auditory filters centered at 400, 800, 1200 Hz. To provide a fair comparison between maskers at different F0s and between harmonic or inharmonic, it is necessary to offset the potential benefit of spectral dips with the potential detriment of spectral peaks. One simple approach was to integrate the difference between the excitation pattern of the complex and that of the flat-spectrum baseline, starting from the first peak. The frequency scale was the logarithmic ERBn scale, which has the most psychophysical relevance for masking. The starting cut-off, represented by the vertical dashed lines in the top panel of Fig. 2, was found by picking the lowest center frequency at which the excitation level in the complex exceeded the baseline; a cut-off that could be different for harmonic and inharmonic complexes. At a given F0, different tokens of inharmonic complexes result in very different integrals, so there is a distribution of integrals. Figure 3 represents this distribution for inharmonic complexes based on nominal F0s of 50, 100, 200, and 400 Hz. It can be seen that as the nominal F0 increases, the distribution of integrals is progressively more negative and also more negatively skewed. This means that at high nominal F0s, some tokens of inharmonic complexes present dramatically large spectral dips relative to the size of their spectral peaks. In such cases, the mean of the distribution does not offer a fair representation of the population of inharmonic complexes since it is pulled toward the extreme negative values. For example, at 400-Hz nominal F0 (bottom panel), the mean of the distribution is −382, whereas the median is considerably higher at −294. The pull induced by the skewness of a distribution does not occur to the same extent in a run of SRT measurement because each sentence contributes with equal weight in the final SRT. One inharmonic masker with particularly large spectral dips would only make one sentence very intelligible, but it would not pull the final SRT more than any other sentences in the run. For this reason, the median integral offered a better representation of the population of inharmonic complexes at a given nominal F0 since each token had equal weight. In the experiments, stimuli were nonetheless controlled to sample the full distribution.

Figure 3.

(Color online) Distribution of integrals computed for a population of 1000 inharmonic complexes based on nominal F0s of 50, 100, 200, and 400 Hz, as used in experiment 1.

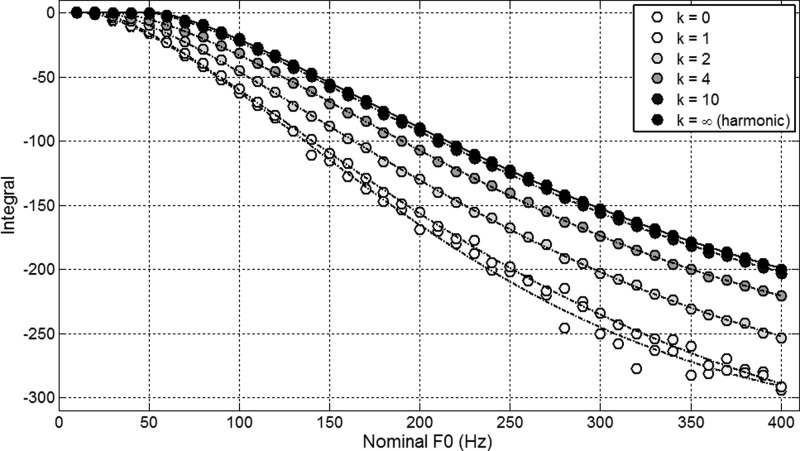
The two vertical lines in each panel of Fig. 3 represent the median integral for inharmonic complexes and the integral for harmonic complexes for comparison. These integral values are plotted in Fig. 4 for many more F0s, sampled in 10-Hz steps between 10 and 400 Hz. The median integrals for inharmonic complexes are shown in the figure where k = 0 (the other values of k represent inharmonic complexes whose first k partials were not jittered). There are several aspects to highlight from these modeling data. First, at low F0s, the integral is about 0, meaning that the size of the peaks is roughly equivalent to the size of the dips (as was observed in Fig. 1 at 50 Hz). As F0 increases, the dips grow deeper, and the peaks grow higher; but importantly, the dips deepen more than the peaks grow (as described in Sec. 2A). Therefore, the integrals are progressively more negative. Second, for harmonic complexes (k = ∞), the integral is pretty constant at around 0 for F0s up to 60–70 Hz, suggesting that glimpsing in harmonic complexes is unlikely to play much of a role until 60–70 Hz. In contrast, finding inharmonic complexes with median integrals around 0 requires F0s as low as 20–30 Hz, suggesting that glimpsing is almost always possible with inharmonic complexes. Third, median integrals are always more negative with inharmonic than with harmonic complexes, confirming that dips are more prominent in inharmonic than in harmonic complexes (as described in Sec. 2B). Fourth, the difference in the median integral between the two complexes increases with F0. In other words, the effect of F0 (described in Sec. 2A) and the difference between harmonic and inharmonic complexes (described in Sec. 2B) interact such that the size difference between peaks and dips grows more rapidly as F0 increases for inharmonic complexes than for harmonic complexes.

Figure 4.

Integrals for harmonic complexes and median integrals for inharmonic and partially inharmonic complexes as a function of nominal F0. Partially inharmonic complexes had the first k partials fixed to their harmonic positions.

Finally, note that the present modeling only used maskers with a flat spectral profile, simply because the size of peaks and dips were easily illustrated relative to a flat-spectrum baseline. A similar modeling could easily be extended to maskers with a speech-shaped spectral profile, considering a speech-shaped baseline. Modeling results may vary a little, depending on how the averaged excitation level of speech counteracts or exacerbates certain spectral peaks and dips.

Controlling spectral dips in the measure of SI-HMLD

The key message from this modeling work is that spectral glimpsing may in general be more advantageous against inharmonic maskers than against harmonic maskers, based on the same nominal F0. As a consequence, comparisons in MDT or comparisons in SRT between harmonic and inharmonic maskers may be confounded by differences in spectral glimpsing opportunity. The present modeling predicted that masking releases provided by spectral glimpsing would in general reduce the SI-HMLD and this effect would increase as F0 increases. These predictions were tested in experiment 1.

It is possible to create inharmonic complexes that offer similar opportunities for spectral glimpsing as there are in harmonic complexes, either (a) by reducing the nominal F0 at which inharmonic complexes are generated or (b) by fixing the first partials to their harmonic positions. To illustrate solution (a), Fig. 4 shows that a harmonic complex with a 400-Hz F0 has an integral of about −200, which is similar to the median integral for inharmonic complexes (k = 0) based on a nominal F0 of 237.3 Hz. To obtain comparisons that were as fine as possible, the integrals obtained in Fig. 4 were fitted with negative Weibull functions (lines in Fig. 4), which enabled a finer resolution of F0 than 10-Hz steps. From these functions, harmonic complexes with F0s at 200, 100, and 50 Hz have the same integrals as inharmonic complexes based on F0s at 126.6, 55.0, and 13.1 Hz, respectively. The alternative solution (b) is to restrict the number of partials that are jittered from their harmonic positions. Since the size of spectral dips decreases considerably as partial number increases, differences in spectral glimpsing opportunities between harmonic and inharmonic complexes could be greatly reduced by fixing low-order partials to their harmonic positions. Integrals were computed following the same procedure as described above for complexes with many values of k and shown in Fig. 4 for k = 1, 2, 4, and 10. It is well known that the limit of resolvability in harmonic complexes is around the 10th partial (Bernstein and Oxenham, 2003, 2005), so it is not surprising that by fixing the first 10 partials, integrals for these partially inharmonic complexes are almost identical to those for harmonic complexes because inharmonicity was pushed exclusively into the unresolved regions. More interestingly, by fixing the first two partials, differences in integrals between harmonic and inharmonic complexes were halved. By fixing the first four partials, differences in integrals between harmonic and inharmonic complexes were divided by about 4. In fact, it seems that these differences were roughly divided by k by fixing the first k partials, which is a useful rule of thumb when one considers the impact of low-order partials on the size of spectral dips. Thus, the alternative solution (b) enabled comparisons between harmonic and inharmonic complexes that had very different ranges of F0. By fixing the first few partials to their harmonic positions, periodicity in auditory filters centered in low spectral regions was however preserved, but it is unclear whether this would affect the HMLD. Deroche and Culling (2011b) observed that periodicity in remote channels could affect the masking release in a given auditory filter, tapping into the across-channel nature of the underlying mechanism. Depending on how periodicity is integrated across center frequencies, these partially inharmonic complexes may or may not be perceived as inharmonic as the complexes in which all partials are jittered. These issues were examined in experiment 2 and 3 by measuring SI-HMLDs between harmonic and inharmonic complexes that were supposedly equated for spectral glimpsing opportunities.

GENERAL METHODS

Listeners

Sixteen listeners took part in experiments 1 and 2, and eighteen listeners took part in experiment 3. They were between 20 and 45 yr old and were paid for their participation. All listeners had pure tone thresholds less than 15 dB hearing level (HL) at frequencies between 0.25 and 8 kHz and English was their native language. The three experiments were performed in the same order, within about 2.5 h, with breaks in between.

Stimuli

A total of 41 blocks of ten sentences were used for the target stimuli, covering 16, 16, and 9 conditions for experiment 1, 2, and 3, respectively. In addition, 20 other sentences were used for two practice blocks occurring at the beginning of the first experimental session. The same listener could thus participate in all experiments since different materials were used in each. All sentences, taken from the Harvard Sentence List (Rothauser et al., 1969), have low predictability and five keywords. All target sentences were at most 3 s long. Maskers varied in each experiment but were always stationary, broadband (with partials up to the Nyquist frequency), flat-spectrum, i.e., had all their partials in equal amplitude, and were 3 s long with 30-ms onset and offset ramps.

Procedure

The study began with explaining the tasks and obtaining informed consent for all subjects. To familiarize listeners with the speech recognition task, two practice runs presented sentences in white noise. Within each experiment, the target sentences were presented in the same order while the order of conditions was rotated for successive listeners. SRT was measured using a 1-up/1-down adaptive method (Plomp and Mimpen, 1979), in which ten target sentences are presented one after another, each one against the same masker. The TMR starts at −32 dB and increased by 4-dB steps until the listener can hear about half of the first sentence, in which case he/she attempts to type a transcript. The correct transcript is then displayed on the screen, with five keywords written in capitals, and the listener self-marks how many keywords were obtained. Subsequent target sentences are presented only once and self-marked in a similar manner; the level of the target speech is decreased by 2 dB if the listener correctly identifies three or more of the five keywords or else increased by 2 dB. Measurement of each SRT, targeting 50% intelligibility, is taken as the mean TMR at the last eight trials.

Equipment

All experiments were performed at the Music Perception Laboratory of Johns Hopkins Hospital and were approved by an Institutional Review Board. A graphical user-interface was displayed on a touch-screen monitor, inside a sound-attenuating audiometric booth. Listeners used a keyboard to type their transcript. Signals were sampled at 44.1 kHz and 16-bit resolution, digitally mixed, D/A converted by a 24-bit Edirol UA-25 sound card and presented diotically over Sennheiser HD 280 headphones.

EXPERIMENT 1: SI-HMLD CONFOUNDED BY THE SIZE OF SPECTRAL DIPS

Rationale

The theoretical analysis above indicated that (a) spectral dips in a harmonic masker are generally smaller than in an inharmonic masker based on the same nominal F0 and (b) that this difference increases as F0 increases. Experiment 1 tested whether these predictions were correct: SRT should decrease with nominal F0 for both harmonic and inharmonic maskers but should decrease more rapidly for the inharmonic maskers.

Although not related to the primary purpose of the present study, there is another recurring methodological issue regarding the measurement of HMLDs in general; they can be influenced by stimulus uncertainty (Neff and Green, 1987). Different tokens of harmonic complexes (here different sets of random phases) provide very similar pitch percepts, whereas different tokens of inharmonic complexes provide very different pitch percepts. Multiple pitch percepts may be heard because the frequencies of resolved partials are not related by simple number ratios. In detection tasks, such stimulus uncertainty may elevate thresholds in the inharmonic condition, because percepts are very variable from one trial to the next; as a result, the HMLD may be overestimated (see, e.g., experiment 1 of Deroche and Culling, 2011b). On the other hand, it is inappropriate to use a single inharmonic complex in an entire run since one would need to find a typical complex, representative of the entire population of inharmonic complexes for a given nominal F0. The present study used both fresh and frozen complexes to examine whether stimulus uncertainty could play a role in speech recognition tasks and potentially account for some of the HMLD.

Method

In experiment 1, target sentences were unprocessed (i.e., they had naturally intonated F0 patterns and their harmonic structure was not processed through Praat, Straight, or any other speech analysis and resynthesis software) and maskers were harmonic and inharmonic complexes based on nominal F0s of 50, 100, 200, and 400 Hz. Maskers were either freshly generated or frozen. For the freshly generated conditions, 160 inharmonic complexes were created with different random jitters and random phases for each partial. The excitation pattern was calculated for each one, and an integral was computed following the procedure described in the theoretical approach. If this value was below the 2.5 percentile or beyond the 97.5 percentile of the distribution of 1000 complexes at this F0 (computed in the theoretical analysis and shown in Fig. 3), this complex was rejected on the basis that it was too extreme to be representative of the population. Another potential candidate was then generated, and so on until 160 complexes were found. For the frozen conditions, the same inharmonic complex was used for each of the ten sentences of one run for a given subject. With 16 subjects, only 16 inharmonic complexes could be generated at a given nominal F0, which needed to represent the same population. To reach this goal, the distribution of integrals (Fig. 3) was divided into 16 bands, defined by 17 percentiles regularly spaced between 2.5% and 97.5%. For each of these 16 bands, an inharmonic complex was generated at random, and the integral was extracted from its excitation pattern. If this value was not within the desired band, this complex was discarded and another potential candidate was generated and so on until a complex was found whose spectral dips fit in that band; it was then chosen for the experiment. This procedure was repeated until 16 complexes were obtained, representing the diversity of spectral dips for inharmonic complexes at a given nominal F0. The 16 frozen inharmonic complexes were then assigned randomly to the 16 subjects. For harmonic complexes, stimulus uncertainty was expected to have little effect because the only difference between fresh and frozen complexes concerned the set of random phases assigned to each partial, which had very little influence on the pitch salience.

Results

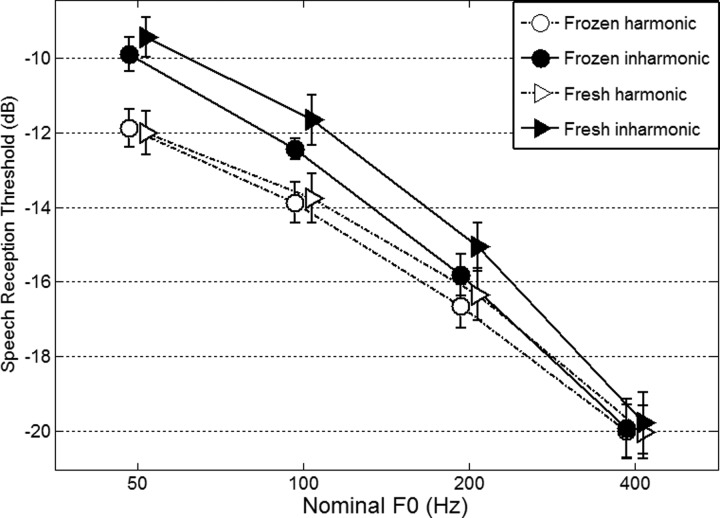
Figure 5 presents the mean SRTs over the 16 listeners. Mauchly's test of sphericity indicated that the assumption of sphericity had not been violated for any main effect or interactions [χ²(5) < 4.7, p > 0.452]. A repeated-measures analysis of variance with three within-subject factors (presentation type × F0 × harmonicity) was conducted to examine the influence of each factor on the SRT. There was a main effect of F0 [F(3,45) = 219.0, p < 0.001], a main effect of harmonicity [F(1,15) = 64.2, p < 0.001], and an interaction between them [F(3,45) = 3.6, p = 0.021]. The main effect of presentation type (fresh or frozen) was not significant [F(1,15) = 1.2, p = 0.295] and neither was its interaction with harmonicity [F(1,15) = 1.5, p = 0.236] or any other interaction [F(3,45) < 0.2, p > 0.928]. To further examine the interaction between F0 and harmonicity, post hoc pairwise comparisons were performed using Tukey's HSD test with Bonferroni corrections. The SI-HMLD was significant at 50 Hz [p < 0.001], and at 100 Hz [p = 0.002], but not at 200 Hz [p = 0.069] or at 400 Hz [p = 0.734].

Figure 5.

Speech reception thresholds measured in experiment 1 for an unprocessed, naturally intonated, voice masked by harmonic or inharmonic complexes. The same masker was used throughout one run (frozen) or changed from one sentence to the next within the ten trials in a run (fresh).

Discussion

The target voice, being naturally intonated (with a mean F0 of 104 Hz and a standard deviation of 29 Hz), produced large instantaneous ΔF0s with the complex maskers. Regardless of such ΔF0s, SRTs decreased considerably with the masker F0. This improvement in speech intelligibility presumably arose from the listeners’ ability to glimpse some useful information about the target sentences in between the resolved partials of the complex maskers. More importantly, SRTs decreased more rapidly with F0 in the inharmonic than in the harmonic conditions and as a result, the size of the SI-HMLD progressively decreased with F0, being 2.3, 1.8, 1.0, and 0.2 dB for nominal F0s at 50, 100, 200, and 400 Hz, averaged over fresh and frozen conditions. The results of this experiment therefore appear consistent with the prediction of the theoretical analysis: Inharmonic maskers allow greater glimpsing opportunities than harmonic maskers, particularly at high F0s. It may be inferred that comparisons between harmonic and inharmonic maskers based on the same nominal F0 are likely to lead to underestimations of the SI-HMLD, particularly at high F0.

The other important result of this experiment concerned the issue of stimulus uncertainty. Differences between fresh and frozen conditions were consistently less than 1 dB and neither the main effect nor any of the interactions involving the presentation type were significant. Therefore, stimulus uncertainty resulting from the variable pitch percepts from one trial to the next in inharmonic maskers plays little role in a speech recognition task. Presentation type might have more impact in a detection task because stimuli and listeners’ responses are usually short so that trials succeed each other closer in time.

EXPERIMENT 2: SI-HMLD WITHOUT CONFOUND

Rationale

Since effects genuinely related to the masker periodicity are distorted by differences in the size of spectral peaks and dips between harmonic and inharmonic complexes, the question immediately arises as to how the role of periodicity can be examined while controlling this confound. The theoretical analysis showed that it was possible to create inharmonic complexes that would offer equal opportunity for spectral glimpsing either by (a) reducing the nominal F0 from which inharmonic partials are generated or (b) fixing the first few partials to their harmonic positions since spectral dips differ less and less as center frequency increases. Experiment 2 used a combination of these two options to investigate the size of SI-HMLD for complexes that were equated for spectral glimpsing opportunities.

Method

In experiment 2, target sentences were again unprocessed and harmonic maskers had again F0s of 50, 100, 200, and 400 Hz. Inharmonic maskers were constructed using the results of the theoretical analysis to have similar spectral dips as the harmonic maskers (Fig. 4). That is, inharmonic complexes with all their partials jittered (k = 0) were based on F0s of 13.1, 55.0, 126.6, and 237.3 Hz. Inharmonic complexes with the first two partials fixed at harmonic positions (k = 2) were based on F0s of 25.3, 67.2, 151.4, and 295.1 Hz. Finally, inharmonic complexes with the first four partials fixed at harmonic positions (k = 4) were based on F0s of 29.4, 81.0, 176.7, and 348.5 Hz. All maskers were frozen, and thus generated at 16 percentiles covering the distribution of integrals following the same procedure as described in experiment 1. There were thus four groups of maskers having similar opportunities for spectral glimpsing as harmonic spectral templates at 50, 100, 200, and 400 Hz but within each group, periodicity was degraded.

Results

Figure 6 presents the mean SRTs over the 16 listeners. Mauchly's test of sphericity indicated that the assumption of sphericity had not been violated for any main effect [χ²(5) < 4.4, p > 0.493] or interaction [χ²(44) = 29.5, p = 0.965]. A repeated-measures analysis of variance with two within-subject factors (median integral × masker type) revealed a main effect of the median integral [F(3,45) = 193.1, p < 0.001] and a main effect of the masker type [F(3,45) = 41.6, p < 0.001] but revealed no interaction [F(9,135) = 0.8, p = 0.642]. To further examine the main effect of the median integral, post hoc pairwise comparisons were performed using Tukey's HSD test with Bonferroni corrections. SRT decreased by 2.0, 5.1, and 8.7 dB on average when F0 (and hence the size of spectral dips) increased [p < 0.001 in all three]. To further examine the main effect of the masker type, pairwise comparisons (again with Tukey's test and Bonferroni corrections) revealed that SRT was, on average, over the different sizes of spectral dips, 2.4 dB lower for the harmonic masker than the Inh-4 masker [p < 0.001], 2.7 dB lower for the harmonic masker than the Inh-2 masker [p < 0.001], and 3.6 dB lower for the harmonic masker than the Inh-0 masker [p < 0.001]. In other words, for maskers that displayed similar spectral dips, SRT increased incrementally as the masker periodicity was degraded. SRT was also 1.2 lower for the Inh-4 than the Inh-0 [p = 0.034] and 0.9 dB lower for the Inh-2 than the Inh-0 [p = 0.050]; but it was not different between Inh-4 and Inh-2 [p = 1.000].

Figure 6.

Speech reception thresholds measured in experiment 2 for an unprocessed, naturally intonated, voice masked by harmonic, inharmonic, and partially inharmonic complexes. Complexes had different nominal F0s such that the size of their spectral dips relative to that of their spectral peaks was similar to harmonic spectral templates at 50, 100, 200, and 400 Hz.

Discussion

The first result to consider is the large effect of the median integral (indexed by the nominal F0) which did not interact with the masker type. SRT decreased with F0 in a roughly similar way for each of the four masker types, and yet, the ranges of F0 were very different for each masker type. Thus, SRT did not decrease because of F0 itself, but rather it decreased because of the increase in spectral glimpsing opportunity it represented, which was identical for all masker types. Listeners appeared to glimpse equally well whether the spectral dips occurred in a regular or an irregular spectral template. This result is strong evidence that in the presence of harmonic maskers, SRT decreases as a function of masker F0 because spectral dips become more prominent and not because periodicity would have somehow been more effective with higher F0s.

The same result can be examined from the perspective of periodicity. Consider the difference in SRT between the harmonic and the Inh-0 masker. For F0h between 100 and 400 Hz, the SI-HMLD was constant at about 4 dB. Thus, the SI-HMLDs were not only larger than those observed in experiment 1 but also did not vary with F0 within this range. This is quite a surprising result given that the mechanisms thought to extract periodicity would in principle be F0-dependent. For example, a harmonic sieve mechanism requires more slots at low F0, and a time-domain comb-filter requires longer delays at low F0. Contrary to these dependencies, the present data suggest that periodicity provides a similar masking release for F0s between 100 and 400 Hz. In addition, this independency of the SI-HMLD on masker F0 reinforces the idea that spectral glimpsing and periodicity seem to behave as two independent mechanisms.

The partially inharmonic complexes, Inh-4 and Inh-2, resulted in higher thresholds than in the harmonic case and lower thresholds than in the completely inharmonic case (Inh-0). Therefore, low-order partials, more specifically the first two or four partials, seem to have a considerable weight in the overall periodicity of the complex. This result is consistent with the observations by Deroche and Culling (2011b) that substantial HMLDs (for MDTs) occurred in auditory filters centered as low as 500 Hz and influenced by periodicity in remote channels. The across-channel nature of this integration means that periodicity in these partially inharmonic complexes could have been integrated in low frequency regions to provide a masking release in higher frequency regions, perhaps more relevant to speech intelligibility. The weight that an individual partial carries to the overall periodicity can also be investigated by mistuning it from its harmonic position and observing an exaggerated change in its pitch. The size of this pitch shift can then be related to the strength of the harmonic frame integration. Roberts and Holmes (2006) examined how the magnitude of these pitch shifts varied as different subsets of partials were progressively jittered. They found that different parts of the harmonic frame made different contributions to the size of the pitch shift associated with mistuning the fundamental component. The second partial contributed the most, about half of the shift magnitude, while partials 6 to 12 contributed about a third. One can infer from their results that integration of periodicity is strongly dependent on the relative frequencies of adjacent partials and depends to a lesser extent on the relative frequencies of more distant partials, which is generally in line with the present results.

Finally, it is intriguing that SRT for the harmonic masker at 50 Hz was only about 2 dB lower than SRT for any of the glimpsing-equated inharmonic maskers. At such a low F0, the size of the spectral dips is very small, and the region of resolved partials is restricted to below 300 Hz; so it is presumably not very useful for speech intelligibility. Throughout the study, the use of random phase relationships between partials was intended to exclude masking release on the basis of temporal envelope modulations (the second underlying mechanism in the introduction). Yet, with F0s as low as 13 Hz, we cannot exclude the possibility that some residual modulations in these inharmonic complexes allowed listeners a better TMR over relatively long periods of time (up to 76 ms here). So, this particular experimental condition might not be adequate to evaluate the benefits attributed to masker periodicity. These phase effects were much less likely to have been involved at higher F0s (Deroche et al., 2013).

EXPERIMENT 3: SI-HMLD AS A FUNCTION OF THE SPECTRAL REGION

Rationale

Differences in spectral dips between harmonic and inharmonic complexes occur in the region of resolved partials only. One may therefore expect that SRTs against harmonic and inharmonic maskers would differ primarily in auditory filters centered at high frequencies; at low frequencies, this SI-HMLD would be reduced by the fact that inharmonic complexes facilitate a larger benefit of spectral glimpsing than harmonic complexes, reducing the advantage of harmonicity. The effect of center frequency may be different once the two maskers are equated for spectral glimpsing opportunities. Experiment 3 tested this proposition.

Method

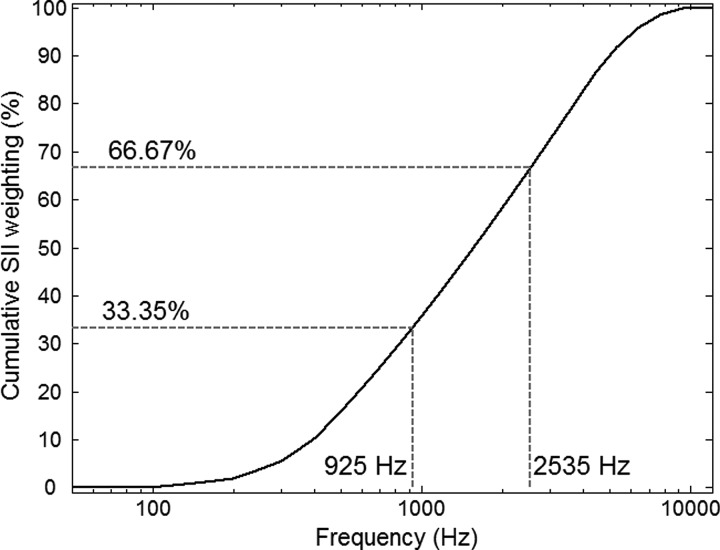
The target spectrum was divided into three spectral regions. The cut-off frequencies were chosen so as to produce three equally intelligible bands in quiet conditions. Indices such as the speech intelligibility index (SII) grant different weights to different frequency bands (ANSI, 1997). Figure 7 represents the SII-weighting plotted cumulatively as a function of frequency. Cut-offs at 925 and 2535 Hz produced three bands with equal contribution to speech intelligibility. Target sentences were consequently low-pass, band-pass, and high-pass filtered in these three spectral regions using Butterworth sixth-order filters with slopes of −30 dB per octave.

Figure 7.

Speech intelligibility index weighting plotted cumulatively as a function of frequency to delimit three spectral bands that are equally intelligible in quiet.

Three masker types were used: Harmonic complexes, glimpsing-equated inharmonic complexes, and noise. Since there were 18 subjects in this experiment, 18 frozen harmonic complexes were generated at a F0 of 200 Hz, and 18 frozen inharmonic complexes (Inh-0) were generated at a nominal F0 of 126.6 Hz, with integrals sampled at 18 percentiles covering the distribution (between 2.5% and 97.5%) calculated for 1000 different complexes. For the noise masker, 18 different broadband Gaussian white noise stimuli were created. Maskers were not filtered into different spectral regions, only the target sentences were, on the basis that periodicity in the masker might need to be integrated across the entire spectrum (Roberts and Holmes, 2006).

Results

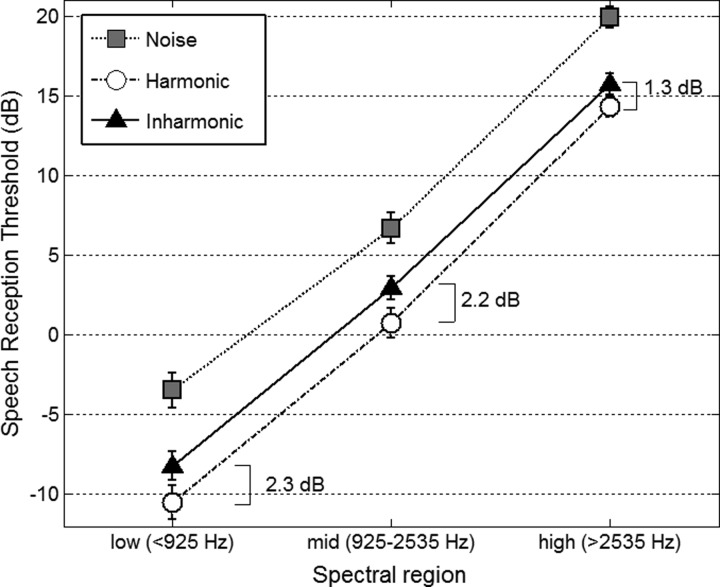
Figure 8 presents the mean SRTs over the 18 listeners. Mauchly's test of sphericity indicated that the assumption of sphericity had not been violated for any main effect [χ²(2) < 4.2, p > 0.121] or interaction [χ²(9) = 12.6, p = 0.184]. A repeated-measures analysis of variance with two within- subject factors (region × masker type) revealed a main effect of the region [F(2,34) = 819.5, p < 0.001] and a main effect of the masker type [F(2,34) = 67.0, p < 0.001], but it revealed no interaction [F(4,68) = 0.4, p = 0.783]. The main effect of the region was expected given the energy distribution of speech relative to that of a flat-spectrum masker. The main effect of the masker type reflected that SRT was lowest for the harmonic masker, increased by 1.9 dB for the inharmonic masker [p < 0.001] and increased further by 4.2 dB for the noise masker [p < 0.001]. To examine specifically how the SI-HMLD varied with the spectral region, the analysis of variance was performed again excluding the noise conditions. The main effect of harmonicity was significant [F(1,17) = 24.7, p < 0.001], but it did not interact with the spectral region [F(2,34) = 0.4, p = 0.667].

Figure 8.

Speech reception thresholds measured in experiment 3 for a voice filtered in low, mid, or high spectral region, against harmonic, inharmonic and noise maskers.

Discussion

The most obvious effect shown in Fig. 8 is that SRTs were much higher when speech was filtered in high spectral regions. This effect was simply due to a lower TMR as frequency increased. Speech has intense low frequency partials, but its excitation level decreases by 15 or 20 dB beyond 1.5 kHz. When a voice is presented against a broadband flat-spectrum masker, the TMR is much more favorable in low than in high spectral regions. Note that this main effect could largely be abolished by using speech-shaped maskers, but the modeling work had focused on flat-spectrum maskers and so did the experiments. More interestingly, the SI-HMLDs did not differ significantly across the three bandwidths, suggesting that masker periodicity can provide masking releases across a large range of center frequencies.

In addition, it is interesting to note that the SI-HMLDs in the three spectral regions added up to 5.8 dB, which is substantially larger than the 4-dB difference in SRT observed in experiment 2 for the same maskers. One possible account for this discrepancy is that there are many redundant cues in speech and the SRT only targets performance at 50% intelligibility, so listeners may not need the entire range of speech-relevant frequencies shown in Fig. 7. Low- and mid-frequency cues, being accessible at much lower TMR, are more likely to drive recognition performance for broadband speech stimuli against flat-spectrum maskers. Therefore, the masking releases provided by masker periodicity in low- and mid-frequency regions may transfer more easily to SRT for unprocessed target speech.

Finally, in noise maskers, there are no spectral dips available. Large masking releases should have occurred in inharmonic complexes on the basis of spectral glimpsing but should not have occurred for noise. Since those differences arise primarily in regions of resolved partials, one might have expected a substantial masking release between inharmonic and noise maskers, progressively disappearing in high frequency regions. This was not the case: SRT was about 4 dB lower for the inharmonic masker, irrespective of the spectral region. To understand this result, one must bear in mind the role of modulation masking (Bacon and Grantham, 1989; Dau et al., 1997a,b). A band of noise that is x-Hz wide has random envelope fluctuations with rates up to x Hz, regardless of the content of its spectral frequencies. Auditory filters with high center frequencies, being broader, might carry higher modulation rates not carried within filters with low center frequencies, but low modulation rates should be carried throughout the entire spectrum. Since the slow modulations should be mostly responsible for modulation masking with speech stimuli, one may conclude that modulation masking should have taken place in all spectral regions in the presence of the noise masker. In contrast, the extent to which modulation masking occurs for harmonic and for inharmonic complexes is less clear. It seems sensible to think that, at least in filters centered at high frequencies (passing higher rates), the fast modulation rates of the complexes would interfere little with the slow modulation rates of speech. Consequently, modulation masking might not occur to the same extent with both harmonic and inharmonic maskers, which might explain why there is a 4-dB difference in SRT between noise and inharmonic maskers above 2.5 kHz.

GENERAL DISCUSSION

Summary of the present results

A theoretical analysis was performed on the size of peaks and dips in the excitation pattern of harmonic and inharmonic complexes. It revealed that (1) spectral dips are more pronounced than spectral peaks in harmonic complexes, and this difference is amplified as F0 increases; (2) spectral dips are more pronounced in inharmonic than in harmonic complexes and this difference increases as nominal F0 increases; (3) harmonic and inharmonic complexes can present a similar ratio of peaks/dips, but they must be based on different nominal F0s; (4) fixing the first k partials of an otherwise inharmonic complex roughly reduces the differences in the size of spectral peaks/dips between harmonic and inharmonic complexes by a factor of k.

Because spectral dips are generally wider and deeper for inharmonic than for harmonic maskers, especially at high nominal F0s, there is, in principle, more opportunity for listeners to glimpse speech information against an inharmonic than a harmonic masker, especially at high nominal F0s. The width of dips may be related to how much of the target spectrum is allowed to be glimpsed, whereas the depth of dips may be related to how robust glimpsing is to adverse TMR. Experiment 1 confirmed that the SI-HMLD, measured between complexes at the same nominal F0, was relatively small (about 2 dB or less) and reduced as F0 increased from 50 to 400 Hz. By comparing harmonic to glimpsing-equated inharmonic complexes (k = 0), experiment 2 showed that the SI-HMLD was overall larger (about 4 dB) and did not vary with F0 between 100 and 400 Hz. In addition, fixing the first two or four partials to their harmonic positions in otherwise glimpsing-equated inharmonic complexes already produced some masking release. This result can be taken as evidence that low-order partials carry an important weight into the integration of periodicity of a given complex (Roberts and Holmes, 2006). Experiment 3 examined which of three speech-relevant spectral regions (low, mid, and high, contributing equally to speech intelligibility) benefitted most from the masker periodicity. The size of the SI-HMLD did not vary significantly with the spectral region, but the TMR at which these masking releases occurred increased considerably with center frequency. The benefits of periodicity at the low- and mid-frequency region might thus transfer more easily to SRT for broadband speech stimuli.

In conclusion, both spectral glimpsing and masker periodicity may offer large masking releases in a speech recognition task but behave as two independent mechanisms. Spectral glimpsing varies with masker F0, whereas the mechanism underlying the effect of masker periodicity does not, at least for F0s between 100 and 400 Hz. Spectral glimpsing offers masking release in spectral regions where partials are resolved, whereas masker periodicity offers masking release across a large range of center frequencies. The use of spectral dips in a masker is very straightforward and easily modeled. In contrast, the use of periodicity is more difficult to model. A mechanism akin to harmonic cancellation seems a valid candidate to underlie the role of masker periodicity (de Cheveigné, 1993; de Cheveigné et al., 1995, 1997a) and may therefore represent a useful starting point for a model implementation. Other mechanisms have been proposed, however, to underlie the role of masker harmonicity based upon the use of envelope modulations, and these deserve further attention as discussed below.

A different perspective on harmonicity

Treurniet and Boucher (2001) examined the detection of a 900-Hz wide band of noise against harmonic and inharmonic complexes. Inharmonic and harmonic complexes were based on the same nominal F0, 88 Hz, and inharmonic partials were jittered from their harmonic positions. Among several of their experiments, two are particularly worth contrasting with the present study. First, they measured how MDT varied as a function of center frequency for the two complexes and found that the HMLD was reduced when the masker and probe were below 1 kHz. Second, they measured MDT for complexes from which partials were omitted regularly to increase separation between partials and found that the HMLD was reduced or abolished by increasing the separation to 2 or 3 times F0. It is likely that these two results could have been influenced by spectral glimpsing. Because spectral glimpsing provides masking release only in the resolved regions of the maskers, it affects the HMLD at low center frequencies primarily. When controlling for spectral glimpsing in experiment 3, the SI-HMLD was not larger at high center frequencies (if anything, it was smaller). Second, spectral glimpsing provides more masking release as F0 increases or as partial separation increases, so it is also not surprising that the HMLD is abolished in these cases. When controlling for spectral glimpsing in experiment 2, masker periodicity provided a similar masking release for F0s between 100 and 400 Hz. Because periodicity within the first 4 partials already provided some masking release, an account based on the use of envelope modulations, as suggested by Treurniet and Boucher, seems rather unlikely. Nonetheless, the role of modulation masking in speech recognition against harmonic, inharmonic and noise maskers is not well understood. In particular, it is currently unclear (a) what spectral regions are concerned in modulation masking and (b) whether modulation masking is involved to different degrees with harmonic and inharmonic complexes, and so whether it affects the SI-HMLD at all.

Other types of inharmonicity

In the present study, inharmonicity was always generated by jittering partials from their harmonic positions with a random rove taken from a rectangular distribution between −F0/2 and F0/2. There are other types of inharmonic complexes. Two types have been examined in detail in the literature: Frequency-shifted complexes (a fixed offset is added to the frequency of each partial of a harmonic series) and spectrally stretched complexes (a cumulative increment is added to the frequency spacing of partials with increasing partial number). Although these complexes have been used primarily for studies of pitch perception and of the perceptual cohesion of complex tones (Roberts, 1998; Roberts and Brunstrom, 1998, 2001), they have been used in a few instances of studies on masking in a speech recognition task (Roberts et al., 2010) since effects of ΔF0 between competing voices may also be produced with these particular aperiodic forms of excitation. The extent to which spectral glimpsing is involved in such cases remains to be examined. The size of spectral dips should be reduced by shifting the frequency of each partial in a harmonic series upward, because the same density of partials would be shifted to a range of slightly broader filters. In contrast, the size as well as the number of spectral dips should increase in the spectrally stretched complexes because adjacent partials are more distant and less dense in any auditory filter. Because of these changes in spectral density, it is not trivial to extend the present modeling to these inharmonic complexes as resolved partials would be relatively more intense than in the harmonic case and unresolved partials would be relatively less intense than in the harmonic case. The integration between peaks and dips could not be made according to the same baseline as harmonic complexes. Evaluating the role of spectral dips in these particular types of inharmonic complexes and separating it from the role of periodicity might be a challenge.

Toward more complexity

The theoretical analysis was based on integrating peaks and dips of a given masker from a flat baseline throughout the entire spectrum. This analysis was a simplification to the problem because it completely disregarded the excitation pattern of the target voice. Speech is more intense below about 1.5 kHz than above. In addition, some frequency regions are more important to intelligibility than others, especially in masking conditions. It follows that certain spectral dips in a given masker may be more useful than others because (a) at any given TMR, speech energy is differentially available at different center frequencies; and (b) the type of speech cues being glimpsed carries different weight to intelligibility. One could imagine applying a weighting function to the integration of peaks and dips, depending on the amount of target energy relative to the amount of masker energy in any given filter, but this would itself vary somewhat with the overall TMR. At very favorable TMR, speech energy is available across a large range of center frequencies up to about 8 kHz, but as TMR progressively decreases, speech energy is eventually only available at center frequencies located at the masker spectral dips. As a consequence, the frequency region driving performance changes substantially with TMR. Such a weighting function would have to be different at each TMR and presumably would have also to be different for each token of inharmonic complexes, which would bring a much higher level of complexity to the problem. The same argument holds for experiment 3, where the target speech was band-pass filtered. It would not be sufficient to restrict the integrals to the three bandwidths because within each band the distribution of speech energy is not flat. Some spectral dips may have been more important than others, but the present study did not take such influences into account.

CONCLUSION

Among the several ways in which speech recognition can improve against a periodic as opposed to an aperiodic masker, the present study focused on the role of spectral dips and that of periodicity. When comparisons are made between harmonic and inharmonic maskers in a masked detection task or a speech recognition task, one should bear in mind that there are generally more opportunities to glimpse some energy in the target sound in between resolved partials of an inharmonic complex than in between resolved partials of a harmonic complex. This effect, occurring particularly at high F0s and in low spectral regions, can in turn counteract the masking release provided by masker periodicity and consequently reduce the observed SI-HMLD. The present study attempted to control for this confound in the measurement of SI-HMLD by designing experiments based on the predictions of a theoretical analysis that modeled the size of spectral dips relative to that of spectral peaks in the maskers’ excitation pattern. The results showed that while SRTs decreased by about 3 dB for every doubling of masker F0 due to spectral glimpsing, the size of the SI-HMLD (a) did not depend much on F0, (b) was affected by periodicity of the first four partials, and (c) occurs in low-, mid-, and high-frequency regions. Modulation masking is also important to consider when dealing with speech stimuli, but whether it is involved differentially with harmonic and inharmonic complexes remains to be investigated.