Abstract
An analysis based on the variation principle shows that in the molecules H2+, H2, B2, C2, N2, O2, F2, covalent bonding is driven by the attenuation of the kinetic energy that results from the delocalization of the electronic wave function. For molecular geometries around the equilibrium distance, two features of the wave function contribute to this delocalization: (i) Superposition of atomic orbitals extends the electronic wave function from one atom to two or more atoms; (ii) intra-atomic contraction of the atomic orbitals further increases the inter-atomic delocalization. The inter-atomic kinetic energy lowering that (perhaps counter-intuitively) is a consequence of the intra-atomic contractions drives these contractions (which per se would increase the energy). Since the contractions necessarily encompass both, the intra-atomic kinetic and potential energy changes (which add to a positive total), the fact that the intra-atomic potential energy change renders the total potential binding energy negative does not alter the fact that it is the kinetic delocalization energy that drives the bond formation.
INTRODUCTION
Covalent bond formation is a fundamental chemical reaction. Yet, its physical origin has remained obscure to most chemists.1 Most general chemistry textbooks either avoid the subject or advance incorrect explanations.
A common fundamental misconception is that chemical bonding energies are static force field energies,2 a notion that goes back three centuries.3 After the advent of quantum mechanics, this presumption was revived in the 1930s through the hypothesis that the bonding energy-lowering is due to the attractive electrostatic potential energy between the nuclei and the wave mechanically accumulated electronic charge in the bond region.4 Support for this conjecture was presumed to be seen in the virial theorem for equilibrium geometries,4 according to which the potential component of the binding energy is always negative whereas the kinetic component is always positive. Neither a formal nor a quantitative rigorous demonstration of this connection has ever been put forth, however.
By contrast, in 1933, Hellmann5 inferred from considerations based on the statistical Thomas-Fermi approximation that bond formation results from a reduction in the zero-point kinetic energy of the electronic motions due to the enlargement of the available space. Although Hellmann was aware that, at first blush, such a role of the kinetic energy seems to be at variance with the virial theorem, he did not attempt to resolve this apparent conflict by a wave mechanical analysis of the kinetic and the potential binding energy.6 His interpretation was subsequently ignored among chemists.7
The divergence of explanations showed that even the qualitative inference of physical interpretations from rigorous ab initio electronic wave functions is often not trivially self-evident. This is because the connection between conceptual physical reasoning and mathematical constructions of accurate wave functions is not as direct in quantum mechanics as in problems of classical mechanics.8
From 1962 on, Ruedenberg and coworkers9 began to develop rigorous coherent in-depth analyses aimed at discerning the physical relationships that are embedded in the rigorous framework of molecular electronic wave functions and binding energies. Examining the molecules H2 and H2+, these authors showed that, in fact, the electrostatic potential interactions of the wave mechanically accumulated charge in the bond are not bonding but actually antibonding. They moreover showed that the critical bonding contribution comes from the lowering of the kinetic energy through inter-atomic electron delocalization, a conclusion that agrees with the inference that Hellmann had drawn from different considerations.10 They furthermore demonstrated that the above mentioned signs of the total potential and kinetic energy components near equilibrium result from intra-atomic orbital contractions, which are side effects of bond formation, but do not drive it. Although this analysis was soon embraced by a number of authors,11 notably Mulliken, Fukui, Goddard, Kutzelnigg, and Schwarz, the electrostatic conjecture mentioned in the second paragraph continued to be widely taught.2 Recent high-accuracy treatments12, 13 have confirmed the kinetic explanation advanced in the papers of Ref. 9.
An important feature had, however, remained unexplained in the work of Refs. 9 and 11, 12, 13: namely, the physical reasons for the consequential intra-atomic contractions that occur on bond formation – in particular, for those internuclear distances where the virial theorem offers no rationalization (i.e., different from the equilibrium distance). This problem is solved in the present investigation. Surprisingly, and on the surface counter-intuitively (since the overlap integral decreases), these intra-atomic contractions are found to occur because they further enhance the inter-atomic delocalization and, hence, the associated inter-atomic kinetic energy lowering. This inter-atomic kinetic energy lowering through enhanced inter-atomic delocalization drives the intra-atomic contractions, which per se are antibonding, even though they generate the negative potential binding energy component at the equilibrium geometry. These conclusions are shown to be valid for the molecules H2+, H2, B2, C2, N2, O2, F2.
With this finding, the last piece for the physical understanding of the basic origin of covalent bonding has fallen in place. There remains no room for doubt that covalent bond formation is driven by the quantum mechanical attenuation of the kinetic energy due to the inter-atomic delocalization of electrons, i.e., by the quantum mechanical kinetic drive of electron waves toward expansion.
This insight places covalent bond formation into a broader perspective. According to Earnshaw's theorem,14 a collection of electrostatically interacting point charges can form a stable arrangement only if the particles are in motion. This general conclusion from classical mechanics carries over into quantum mechanics. But, it is just in the treatment of the kinetic energy and, hence, in the equation of motion, that quantum mechanics differ starkly from classical mechanics. Covalent bonding is one of the effects that are due to this difference. It is for that reason that covalent bonding and the stability of matter is inaccessible to classical mechanics.
The kinetic understanding of covalent bonding also places it in a broader chemical context. For instance, the bonding stabilization in aromatic systems is caused by delocalization, i.e., by a kinetic energy lowering, the bonding difference between atoms in the second and third period may be related to kinetic effects, and the energy differences between ground and excited states are due to orbital nodes and, hence, driven by changes in the kinetic energy.
BASIC PHYSICAL CONCEPTS FOR ENERGY ANALYSES
The ground state as optimal compromise between the kinetic drive of electron waves toward expansion and the confinement by electrostatic potentials
In order to concentrate on the fundamentals, we consider molecular ground states and assume the validity of the Born-Oppenheimer separation. The interaction between two atoms is then given by the ground state potential energy curve of this system. A stable bond results when, at some finite internuclear distance, this curve has a minimum that is lower than its value at infinity, where the atoms are separated. (For bonding in excited states, the present reasoning remains valid when the constraints of orthogonality to lower states are added.)
Since the value of the potential energy curve at any one distance is the ground state energy of the electronic Schrödinger equation at that distance, the physical understanding of the origin of the bond requires a physical understanding of the reasons for the dependence of the lowest electronic eigenvalue on the internuclear distance. The answer to this question is manifestly contingent on understanding the basic physical factors that determine the value of the lowest eigenvalue for a system of electrons in a molecule of given geometry.
Already in the 1930s, it was recognized by some15 that, in the case of bound electronic states, a solid basis for conceptual physical reasoning is provided by the framework of the variation principle. In this spirit, the present analysis takes the point of view that the “aim” to minimize the energy functional can be perceived as a “driver” that determines the characteristics of stationary wave functions for bound electrons.
According to the variation principle, the ground state is the wave function that minimizes the expectation value E of the Hamiltonian. Essential is that the existence of this minimum is a consequence of the opposing demands placed on the wave function by the kinetic energy T and the potential energy V with regard to minimizing the total energy E = T + V. While the (electrostatic) potential energy V is lowered through localizing the wave function by contracting it towards the nuclei, the kinetic energy T is lowered by a delocalizing dilution of the wave function. (That the kinetic energy is lowered by delocalization is manifest, for one electron, from the expression T = ½∫dx(∇ψ)2 in conjunction with the normalization condition ∫dx ψ2 = 1. A many-electron system has T = Σn NnTn, where the sum goes over the natural orbitals, Nn are the orbital occupations, and each Tn has the same form as in the one-electron case.) The variational energy minimum is reached by the wave function that achieves the optimal compromise in this universal variational competition between T and V.
The variational competition can be looked at in two equivalent ways. It can be said that the shape of the ground state wave function is determined by the electron wave following its innate kinetic drive towards expansion as much as it is permitted to do so by the confinement of the potential energy. Conversely, it can be said that the shape of the ground state wave function is determined by the electrostatic attractions pulling the electron cloud as close towards the nuclei as is permitted by the innate resistance of the electronic kinetic energy against such localization (and by the inter-electronic repulsions).
The drive of electron waves towards expansion embodies the fundamental difference between quantum mechanics and classical mechanics with regard to the role of the kinetic energy. It is related to the uncertainty principle.
Inferences from the basic prototype system
The prototype case, which illustrates features that are important for the subsequent bonding analysis, is the hydrogen-like system of an electron-like particle with mass m in the field of a nucleus with charge Z, which has the Hamiltonian (in atomic units)
| (1) |
Consider the normalized trial wave function
| (2) |
Since the sphere with the radius R = 2/ζ encompasses 94% of the orbital density, the parameter α = 1/ζ is a measure of the orbital size. Orbital localization increases, therefore, with increasing ζ.
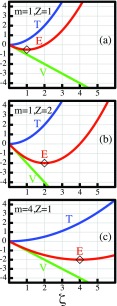
Figure 1 exhibits the variational competition between the expectation values T = ⟨ψ|T|ψ⟩ = ζ2/2m and V = ⟨ψ|V|ψ⟩ = −ζZ in lowering the expectation value E = ⟨ψ|H|ψ⟩ = T + V with respect to the variational parameter ζ, which is the abscissa. It is apparent that, in all panels, the linear decrease of V with increasing ζ describes the potential nuclear pull, while the quadratic increase of T with increasing ζ describes the kinetic resistance of the electron against localization. The energy minimum, i.e., the optimal compromise between T and V, occurs for
| (3) |
Figure 1 compares three cases. Panel (a) shows the case m = Z = 1, i.e., the hydrogen atom, where Eo = −½ h (h = hartree). Panel (b) shows the case m = 1, Z = 2, i.e., the helium +1 ion, where Eo = −2 h. Panel (c) shows the case m = 4, Z = 1, i.e., a hydrogen-like atom where the electron is replaced by a hypothetical particle with mass 4. This system has also Eo = −2 h.
Figure 1.
Variational competition between T and V determining the ground state energies (in hartree units) for three systems with the Hamiltonian of Eq. 1. The systems have different values of m and Z as indicated. Systems (b) and (c) both are 1.5 hartree lower than system (a), but for different reasons. See text.
The comparison of these plots implies the following physical interpretation of the differences in Eo. The system of case (b) has a lower Eo than the system of case (a) because the larger Z-value generates a steeper potential energy functional V = −ζZ, i.e., a stronger nuclear pull. The system of case (c) has a lower Eo than the system of case (a) because the larger value of m in the denominator of the quadratic kinetic energy functional T = ζ2/2m attenuates its rise with increasing ζ.
It is, thus, apparent that the same amount of lowering ofEo relative to system (a) can be caused either by a strengthening of the attractive potential energy functional or by a weakening of the localization-resisting kinetic energy functional. Thus, variational reasoning can elucidate the physical difference between the two situations. By contrast, the examination of the minimum valuesEo, To, Voalone manifestly cannot reveal the origin of the energy difference. This important, general insight will prove relevant in the context of the conclusions regarding the origin of covalent bonding.
Relevant for the later discussion is also the observation that small deviations from the optimal orbital size, which change E very little (quadratic in the deviation of ζ), cause very large changes in T and V (linear in the deviation of ζ).
COVALENT BONDING IN THE HYDROGEN MOLECULE ION
In order to be on firm ground, the subsequent analysis of the H2+ ion is based on a near exact wave function in terms of uncontracted (14s,6p,3d,2f,1g) basis sets of 26 σ-type spherical Gaussian atomic orbitals, with individually optimized orbital exponents, on the two atoms.12 In this basis, the hydrogen atom energy lies 0.1 μh (microhartree) above the exact value, and the molecular energy lies 0.55 μh above the exact value at the theoretical equilibrium distance of R = 1.99720 bohrs.16 All quantitative data on which the following analysis draws are documented in Ref. 12.
Wave function in terms of quasi-atomic orbitals
At all internuclear distances, the wave function can be expressed as a superposition
| (4) |
where the normalized quasi-atomic orbitals ψA and ψB each have a spherical and a polarization component:
| (5) |
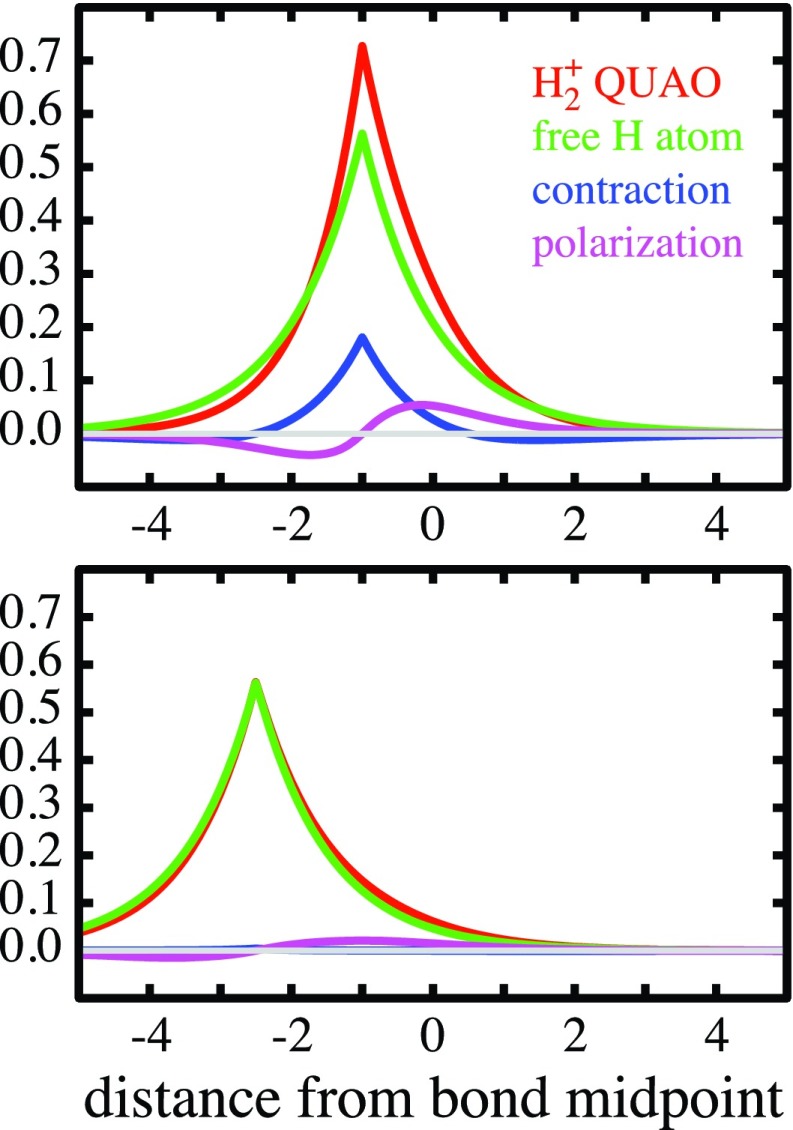
(s and p are normalized; the numbers (in brackets) indicate the number of orbitals of each type in each sum). Resolution 5 for ψA, the left atom, is exhibited along the internuclear axis in Figure 2: in the upper panel for the equilibrium geometry (2 bohrs), in the lower panel at the internuclear distance of 5 bohrs. In the figure the spherical component s has been further resolved in terms of the free-atom 1s orbital and the spherical deformation [s – (1s)]. The curves display the total respective contributions, including the coefficients in 5, so that addition of the spherical deformation (blue) and the angular polarization deformation (purple) to the free-atom 1s orbital (green) will yield the quasi-atomic orbital ψA (red).
Figure 2.
Resolution of the left quasi-atomic orbital in H2+ (red) as the sum of the free-atom orbital of H (green), the spherical contraction contribution (blue), and the polarization contribution (purple). Upper panel: For the theoretical equilibrium distance 1.9972 bohrs. Lower panel: For the intermediate distance of 5 bohrs. Abscissa in bohr, origin = bond midpoint.
At 5 bohrs, ψA and ψB differ from the 1s orbitals of the free atoms only by a polarization deformation, the spherical part remaining unchanged. At 2 bohrs, the polarization is only somewhat larger than that at 5 bohrs. But, there is now a considerable spherical deformation, namely, a contraction.
For the discussion of the contraction, it is useful to note that, at all internuclear distances, the spherical component s in Eq. 5 is, in fact, near-identical with an appropriately scaled hydrogen-like orbital 1s*, i.e., an orbital of the type formulated in Eq. 2 with an orbital exponent ζ* that is obtained by maximizing the overlap ⟨s|1s*⟩ with respect to ζ. This overlap is, in fact, always >0.99. The variation of ζ* as a function of the internuclear distance, which is displayed in Figure 3, shows that, from infinity to about 5 bohrs, ζ* remains close to unity. As the nuclei approach each other more closely, there occurs a steadily increasing contraction of both ψA and ψB. (The equilibrium geometry is indicated by the gray line parallel to the ordinate.)
Figure 3.
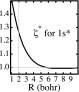
Internuclear distance dependence of the orbital exponent ζ* of the scaled 1s* orbital that has maximum overlap with the quasi-atomic orbital in H2+: Marked contraction for R < 5.5 bohrs; very slight expansion for R > 5.5. bohrs. At the theoretical equilibrium distance (1.9972 bohrs), the value of ζ* is 1.264.
The molecular orbital of H2+ differs, therefore, from the atomic orbital of a free hydrogen atom by three modifications: (i) atomic orbital superposition, (ii) atomic orbital contraction, and (iii) atomic orbital polarization. It will be seen that, of these three, the first two are most consequential.
Binding energy in terms of interactions between quasi-atomic orbitals
Resolution 4 of the molecular wave function in terms of quasi-atomic orbitals leads, by straightforward algebra, to the following decomposition of the difference between the energy expectation values of the H2+ ion and the H atom:
| (6) |
| (7) |
| (7a) |
| (8) |
| (8a) |
| (8b) |
| (8c) |
where ρI is defined by
| (8d) |
| (8e) |
| (8f) |
The formulations of these two intra-atomic contributions Tintra, Vintra and three inter-atomic components Vqc, VI, TI exhibit the following physical meanings and quantitative attributes.
The components Tintra, Vintra [Eq. 7a] represent, respectively, the intra-atomic kinetic and potential energy changes that result from the orbitals 1sA, 1sB of the free H atoms being morphed into the quasi-atomic orbitals ψA, ψB in the molecule. By virtue of the atomic variation principle, these atomic deformations necessarily raise the intra-atomic energy Eintra. Specifically, for the spherical contraction, which was observed in Figure 2 at 2 bohrs and discussed after Eq. 5, this increase of Eintra is due to an increase of Tintra prevailing over a decrease in Vintra, in accordance with the discussion in Sec. 2B and illustrated in Figure 1. As noted in the last paragraph of that section, even for small changes in Eintra, the changes in Tintra and Vintra are large.
The inter-atomic component Vqc [Eqs. 8a, 8b] represents the classical coulombic interaction between the proton B and the “deformed” hydrogen atom A, which consists of the proton A and the quasi-atomic density ψA2. It is, therefore, called the coulombic quasi-classical energy. It is positive, i.e., repulsive, when ψA is spherical. For the polarized orbital ψA in H2+, it is, however, negative, i.e., attractive, at all internuclear distances.
-
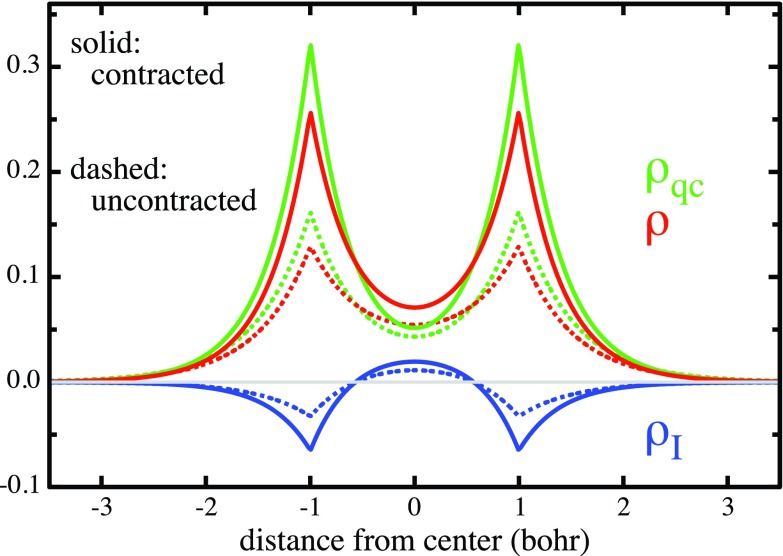
The inter-atomic component VI [Eq. 8c] is the potential energy of the density term ρI defined in Eq. 8d. According to its definition, this density ρI is the difference between the orbital density ρ = Ψ2, in which the amplitudes ψA and ψB are added before they are squared, and the “quasiclassical” density ρqc, in which these two amplitudes are squared before they are added. The term ρI represents, therefore, the interference of the superposed quasi-atomic orbital wave amplitudes when they form the molecular orbital wave Ψ. The contribution VI is, therefore, called the potential interference energy.
Since the integral over ρI manifestly vanishes, ρI describes a charge shift. As illustrated by Figure 4 for the equilibrium geometry, this charge shift is, in fact, the quantitative formulation of the frequently noted charge accumulation in the bond that results from the orbital superposition. Note that it entails the depletion of charge near both nuclei. The contribution VI that is generated by this charge shift is positive, i.e., antibonding, at all internuclear distances since the potential (–1/rA–1/rB) in the integrand of Eq. 8c is always higher in the bond region than near the nuclei. The widespread surmise that charge accumulation in the bond lowers the potential energy is quite simply wrong.
In fact, it turns out that, at all internuclear distances shown (i.e., up to 6 Å), the positive interference contribution VI is larger in absolute value than the negative quasiclassical contribution Vqc discussed under item (ii), which means that the antibonding effect of the charge accumulation in the bond prevails over the bonding effect of the quasi-classical attraction of the polarized quasi-atomic orbitals. Hence, the total inter-atomic potential interactionVinter = Vqc + VI is repulsive at all internuclear distances.
In analogy to VI the inter-atomic component TI [Eqs. 8e, 8f] is called the kinetic interference energy. From Eq. 8f, it is apparent that TI is, in fact, the difference between the kinetic energy of the molecular orbital Ψ and the kinetic energy of the quasi-atomic orbital ψA. Since Ψ is manifestly more delocalized than ψA, the kinetic energy of Ψ is lower than that of ψA, in accordance with the discussion in Sec. 2. Consequently, the kinetic interference energy TI is negative, i.e., it is bonding at all internuclear distances.
It is apparent that orbital delocalization from one to two atoms has an effect on the density of the wave function as well as on the gradient density of the wave function. The effect on the density is the charge accumulation in the bond region and yields an antibonding potential interference energy. The effect on the gradient density attenuates this quantity and yields a bonding kinetic interference energy. These two inter-atomic interference effects are coupled in as much as both are consequences of the delocalization of the electronic wave function.
Figure 4.
Resolution of the orbital density ρ (red) as a sum of the quasiclassical density ρqc (green) and the interference density ρI ≡ charge accumulation in the bond (blue), as formulated in Eq. 8d, at the equilibrium distance. Dashed curves: Using 1sH orbitals of H as quasi-atomic orbitals. Solid curves: Using the contracted 1s* orbitals (ζ* = 1.264). Note that the charge accumulation in the bond is larger for the contracted orbital than for the uncontracted orbital.
Synergism of interactions along the dissociation curve
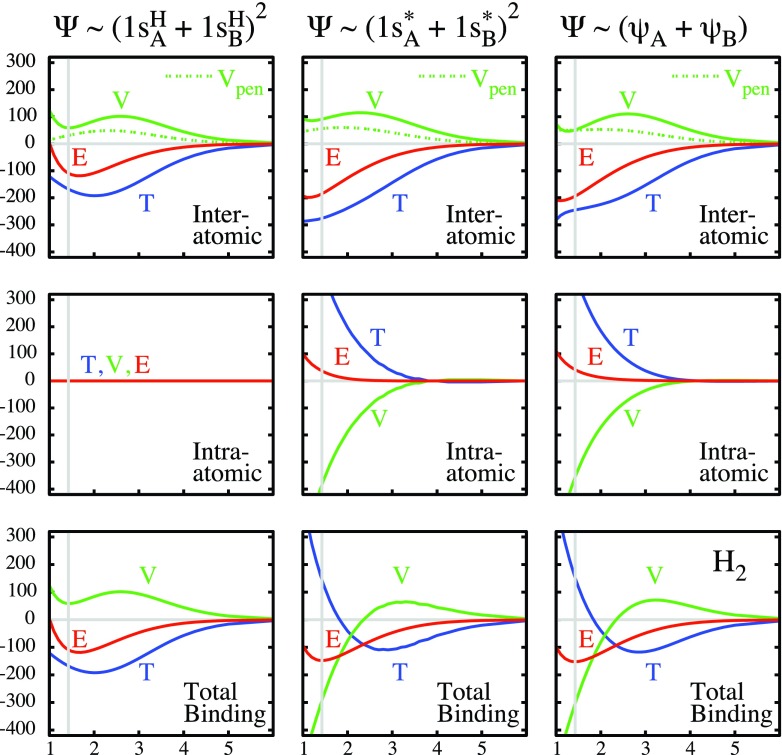
The quantitative synergism of the five contributions to the binding energy ΔE, which were identified in Sec. 3B, becomes evident by resolving each of them further into contributions corresponding to the three wave function modifications, which were identified in Sec. 3A, viz., superposition, contraction, and polarization. The synergism can be deduced from the plots of these contributions to the dissociation curve ΔE = E(Ψ) − E(H), which are displayed in Figure 5. In the interest of focusing on the essentials, only the total inter-atomic potential contribution Vinter = Vqc + VI is plotted. These graphs reveal the following.
Along the entire length of the curve in Figure 5, the total energy difference ΔE (red) is negative, i.e., bonding, because the inter-atomic interaction energy Einter is negative, i.e., bonding. Beyond about 5 bohrs, ΔE and Einter are, in fact, identical since, there, the intra-atomic contribution is negligible. As the internuclear distance decreases below 5 bohrs, there is a steady increase in the antibonding intra-atomic contribution Eintra, which is a consequence of the increasing quasi-atomic spherical contractions discussed at the end of Secs. 3A, 3B (i). Nonetheless, ΔE is becoming more and more negative because the inter-atomic energy Einter decreases more strongly than the intra-atomic energy Eintra increases. This fact implies that, in this range, the intra-atomic orbital contractions are driven by the energy lowering of the inter-atomic interaction even though the intra-atomic energies increase somewhat.
At all internuclear distances, the bonding character of the inter-atomic interaction Einter is due to the negative value of its kinetic component Tinter = TI (blue), which is a consequence of the orbital delocalization from one atom to two atoms, as discussed in Sec. 3B (iv). The potential inter-atomic energy Vinter = Vqc + VI (green) is always antibonding for the reason discussed in Sec. 3B (iii).
Since, as discussed Sec. 3C (i), the intra-atomic contributions vanish at large distances, the kinetic component ΔT = Tinter = TI of the total energy is negative and the potential component ΔV = Vinter is positive in this region. Thus, the kinetic energy is bonding and the potential energy is antibonding at large distances.
-
In the short-range region, the quasi-atomic orbitals contract, as shown by Figure 3 at the end of Sec. 3A, and discussed in Secs. 3B (i) and 3C (i). As deduced in Sec. 3C (i), the contraction is driven by Einter becoming more and more negative. It is apparent from Figure 5 that this bonding enhancement of Einter by contraction is entirely due to TI = Tinter becoming more negative. (Vinter becomes, in fact, more positive, i.e., antibonding by the contraction.)
The small total intra-atomic energy Eintra increase due to contraction, noted in Sec. 3C (i), is the result of a large increase in the positive kinetic component Tintra and a large, almost compensating lowering of the negative potential component Vintra, as mentioned in Sec. 3B (i). The origin of these large changes in Tintra and Vintra was already discussed in the last paragraph of Sec. 2B and exhibited in Figure 1.
-
Integrating these observations leads to the following conclusions. At all distances, bonding is caused by the kinetic energy lowering that is the result of the orbital delocalization from one atom to two atoms. This kinetic energy lowering is quantified by the negative kinetic interference energy TI. At large distances, TI provides directly the attractive part of the total binding energy ΔE. At shorter range, roughly less than twice the equilibrium geometry, there occurs a contraction of the quasi-atomic orbitals which further enhances orbital delocalization and renders the kinetic interference energy TI even more negative. This additional decrease in TI prevails in lowering the total energy ΔE, even though the quasi-atomic orbital contractions slightly increase the intra-atomic energies Eintra.
A side effect is that the contractive quasi-atomic deformations encompass large internally compensating changes of the intra-atomic kinetic and potential energies (in accordance with the observation made in the last sentence of Sec. 2B). As a result, the total molecular kinetic energy change ΔT is positive and the total potential energy change ΔV is negative. These signs of ΔT and ΔV, per se, have no implications regarding the cause of binding because, being coupled by the intra-atomic contractions, they yield an antibondingEintra = Tintra + Vintra. The contractions are driven by the lowering of the inter-atomic kinetic interference energy due to enhanced delocalization.
-
It should be noted that the foregoing conclusions pertain to the covalent range of R displayed in Figure 5, i.e., up to about 6 Å. Figures 23 show that, beyond 6 Å, there occurs no orbital contraction, but the orbital polarization persists into the long range region. This orbital polarization creates an induced dipole on one atom that interacts with the proton of the other atom. As shown by Coulson17 and Buckingham,18 the resulting induced dipole interaction energy decays according to (C/R4). Our high-accuracy wave function, which was formulated in the first paragraph of Sec. 3, correctly reproduces the (1/R4) decay after about 9 Å.
In as much as the induced dipole electrostatics, a potential energy effect, is causing the long range interaction, there arises the question why, according to the virial theorem, the actual potential energy goes up and the kinetic energy goes down in this region? Here, we have another example for the basic conclusion emphasized in the penultimate paragraph of Sec. 2B, namely, that the actual values of E, T, and V do not contain sufficient information to reveal the origin of energy differences between related systems. A variational analysis of the type developed in the present study, appropriately adapted to the long range regime will, no doubt, reconcile the superficial discordance also in this case.
Figure 5.
Breakdown of the binding energy curve of H2+ and its kinetic and potential components in terms of inter-atomic and intra-atomic contributions for different quasi-atomic choices: the unscaled 1sH orbitals (left), the contracted 1s* orbitals (center), and the contracted+polarized orbitals (right). Energies in milli-hartree. Abscissa = internuclear distance in bohr. The vertical gray line indicates the theoretical equilibrium distance obtained with the fully optimized quasi-atomic orbitals.
Origin of the quasi-atomic orbital contractions
The insights furnished by the analysis in Sec. 3C lead to the question: Why is the delocalization between the quasi-atomic orbitals ψA and ψB further enhanced when both contract? This effect seems to be counterintuitive in as much as the contractions decrease the overlap integral S = ⟨ψA|ψB⟩. In the preceding analysis, three quantities were found to be indicative of inter-atomic delocalization: the accumulation of charge in the bond, the negative kinetic interference energy, and the positive potential interference energy. The following direct examination of these quantities elucidates how and why they vary with the size of the quasi-atomic orbitals.
In order to focus on the essential features, consider the simple molecular wave function that is obtained by assuming the quasi-atomic orbitals ψA, ψB in Eq. 4 to be scaled 1s-type orbitals, as defined by Eq. 2, i.e., by omitting polarization.19 Thus,
| (9) |
where R = RAB.
Figure 6 exhibits contours of the interference density ρI = Ψ2 − ½(ψA2 + ψB2), which was defined in Eq. 8d. According to this plot, charge is manifestly moved from the region around the nuclei into the region between the two hyperboloid sheets ρI = 0. These sheets are given by the equation cosh[ζ(rA–rB)] = 1/S. Integration of ρI over the volume between the sheets yields the total charge Q that is accumulated into this bond region. The analytical integration yields the expression
| (10) |
where a = arcosh(1/S). The kinetic interference energy TI and the potential interference energy VI are found to be
| (11) |
| (12) |
Let us examine the variations of Q, TI, VI, with the orbital scaling parameter ζ for a fixed value of the internuclear distance R. To this end, Figure 7 displays plots of Q(σ), TI(σ) × R2, and VI(σ) × R as functions of σ. Consider, e.g., the kinetic interference energy TI. It is manifestly most bonding, i.e., negative, for σ = ζR ≈ 4.38, i.e., for ζ ≈ 4.38/R. This ζ-value is larger than 1 when the internuclear distance is less than 4.38 bohrs. For internuclear distances less than twice the equilibrium distance of H2+ (2 bohrs), the kinetic interference energy is, therefore, enhanced when the 1sA(ζ) orbitals are contracted with respect to the 1s orbitals of the free atom ground states (which have ζ = 1). Analogously, the panels for Q and VI show that contraction enhances the charge accumulation in the bond Q when R < 2.9 bohrs, and that it enhances the antibonding character of the potential interference energy VI when R < 4 bohrs.
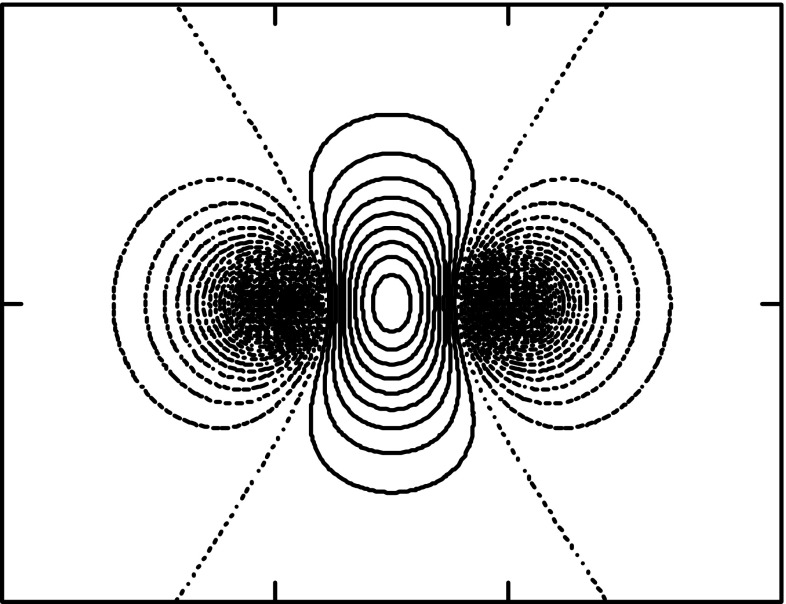
Figure 6.
Contour plots (in a plane containing the internuclear axis) of the interference density ρI ≡ charge accumulation in the bond of H2+, corresponding to the solid blue curve in Figure 4, i.e., for the contracted quasi-atomic orbitals at the equilibrium distance. Increment = 0.05 electron/bohr3/2.
Figure 7.
Variation of the charge accumulation in the bond (QI), the kinetic interference energy (TI), and the potential interference energy (VI) with the orbital size and the internuclear distance, as discussed in Sec. 3D.
These explicit properties of the quasi-atomic orbital interference with regard to orbital contraction furnish the reason for the features of the energy decomposition with regard to orbital contraction that were found in Sec. 3C. The plots of Figure 7 also imply a delocalization enhancement by orbital expansion at longer ranges. In this region the values of the interference energies are, however, too small to induce any orbital scaling changes.
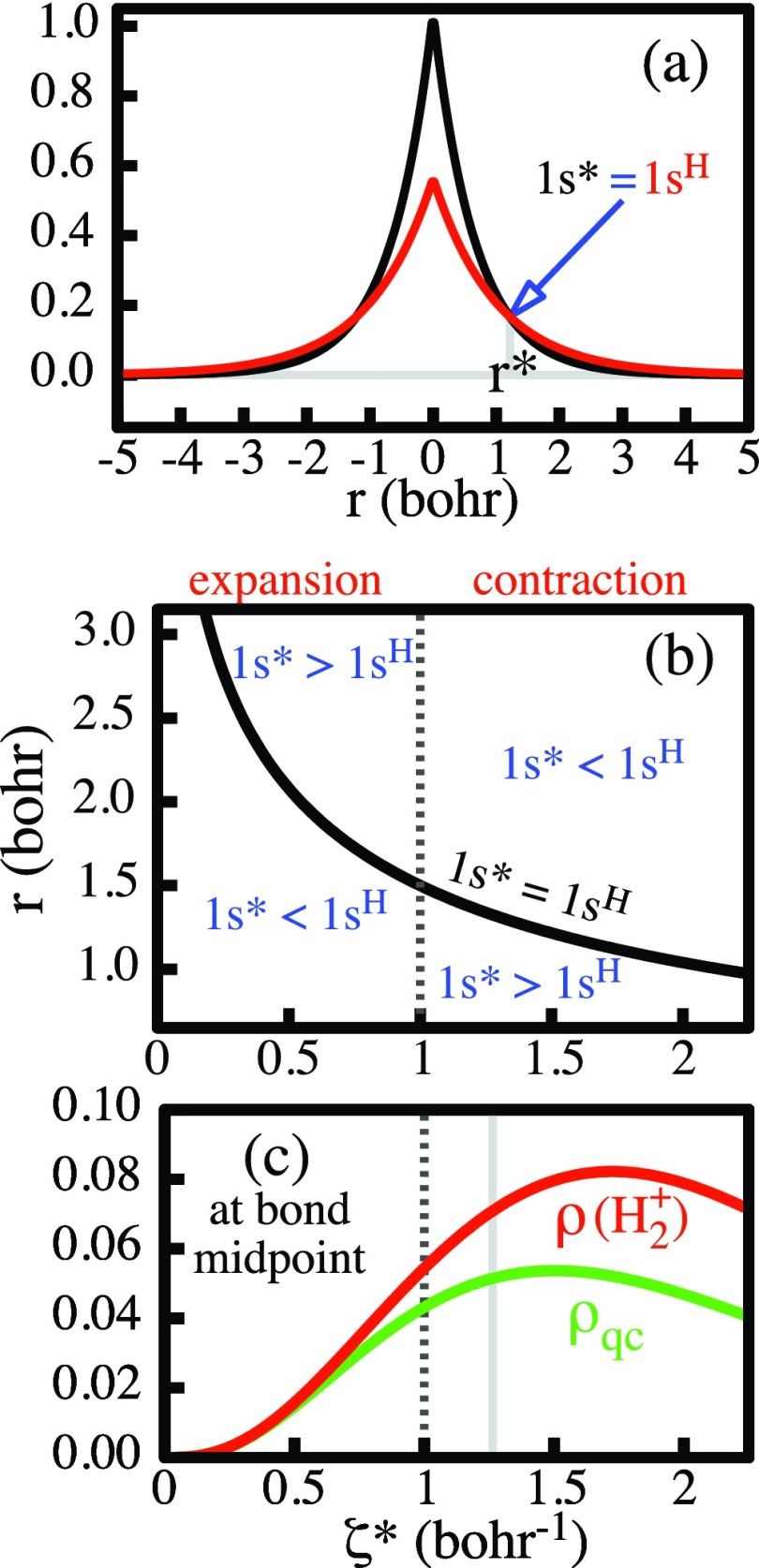
Insight into the reasons for this dependence of orbital interference on the internuclear distance can be gained by a closer examination of the superposition of the orbitals. Let 1sH(r) denote the ground state orbital of a free H atom, i.e., with ζ = 1, and let 1s*(r) denote a scaled 1s orbital with ζ*≠ 1. Since normalization is maintained, the orbitals 1sH and 1s* intersect at some radius r = r*. If 1s* is contracted with respect to 1sH, then one has ζ* > 1 and
| (13) |
as illustrated in Figure 8a. Conversely, for ζ* < 1, the orbital expands with respect to 1sH and the > signs and the < signs have to be interchanged in Eq. 13. The point of intersection manifestly depends upon the degree of scaling, i.e., it is a function r* = r*(ζ*). This function is displayed in the r-ζ* plane of Figure 8b by the curve labeled 1sH = 1s*. Critical is:
Figure 8.
Panel (a): Illustration of the relations in Eq. 13 and the intersection point r* between the unscaled 1sH orbital (ζ = 1, red) and a contracted 1s* orbital (ζ* = 1.5, black). Panel (b): Abscissa = orbital exponent ζ*of a scaled 1s* orbital. Ordinate = distance from the orbital center. The position of the unscaled 1sH orbital on the abscissa is marked by the vertical dashed line. The black curve is a plot of the intersection point r*(ζ*) between the scaled orbital and the unscaled orbital. The dashed line and the black curve create four regions, in which 1s*(r) is either larger or smaller than 1sH(r), as indicated. Panel (c): Variation of the values of ρ and ρqc (of the wave function 9 for the equilibrium distance) at the bond midpoint as a function of the orbital exponent ζ*. The vertical gray line indicates the value of ζ* for the actual wave function.
As ζ* is varied from ζ* < 1 to ζ* > 1, the function r*(ζ*) becomes = 1.5 bohrs when ζ* = 1.
In conjunction with Eq. 13, this feature implies the inequalities between 1s*(r) and 1sH(r) that are indicated in the four different regions of the r-ζ* plane in Figure 8b that are created by the black curve [1sH = 1s*] and the dashed vertical line that indicates ζ = 1, i.e., the undeformed 1sH orbital.
Consider now the molecular wave function Ψ of Eq. 9 for the equilibrium distance of 2 bohrs. Assume that ψA and ψB are initially the respective 1sH orbitals. When these orbitals are contracted, i.e., when ζ = 1 → ζ* > 1, then it is apparent from Figure 8b that the orbital ψA increases in magnitude everywhere between the nucleus A and the bond midpoint, since the latter is at a distance of 1 bohr from the nucleus, which is less than 1.5 bohrs. The analogous relation holds for the orbital ψB. Hence, the contraction raises the value of the molecular superposition Ψ of Eq. 9everywhere between the two nuclei. Additionally, the denominator in Eq. 9 gets smaller since the overlap integral decreases upon contraction, which further increases Ψ.
As an illustration, the plots in Figure 8c show, for the wave function 9 at the equilibrium geometry, how the values of ρ = Ψ2 and ρqc = {[1sA(ζ)]2 + [1sB(ζ)]2}/2 at the bond midpoint vary with the orbital exponent ζ*. The gray vertical line indicates the value of ζ* in the actual wave function. The values of ρ and ρqc are identical with the values on the corresponding solid red and green curves in Figure 4 at the bond midpoint. The values of ρ and ρqc on the dashed vertical (for ζ* = 1) are identical with the values on the corresponding dashed red and green curves in Figure 4 at the bond midpoint. While both, ρ and ρqc, increase with increasing ζ*, so does the difference between them, i.e., the interference density = the charge accumulation at the bond center, corresponding to the blue curve at the bond midpoint in Figure 4. (It is also apparent that this enhancement effect will disappear for too large a contraction.)
It manifestly follows from the foregoing analysis that, for any internuclear distance less than 3 bohrs, there are contractions of the orbitals 1sAH and 1sBH that initially increase the accumulation of charge in the bond. In fact, this also remains to be the case, when the internuclear distance is somewhat larger than 3 bohrs. But it will cease to be so for internuclear distance very much larger than 3 bohrs.
Comparison of the variational competition in H2+ with the variational competition in H
The insights gained in Secs. 3A, 3B, 3C, 3D furnish a basis for comparing the variational competition in the H2+ ion (at the equilibrium distance) with that in the H atom. The comparison implies an examination of the expectation values T = ⟨ψ|T|ψ⟩, V = ⟨ψ|V|ψ⟩, and E = ⟨ψ|H|ψ⟩ as functions of the orbital exponent ζ as variational parameter in a manner analogous to the way that was done by means of the graphs displaying variational competitions in Figure 1 of Sec. 2B.
Figure 9 exhibits plots of T, V, and E versus ζ for three systems:
Top panel: The H2+ ion using the wave function Ψ given by Eq. 9 at the equilibrium distance.
Middle panel: The free hydrogen atom, which is identical to Figure 1a in Sec. 2B.
Bottom panel: A one-electron atom, denoted as H#, using a scaled 1s# wave function, i.e., the system given by Eqs. 1, 2 of Sec. 2B, with m = 1 and Z# = 1.08273. This nuclear charge is chosen so as to yield exactly the same energy as the H2+ ion shown in the top panel.
The comparison of the H2+ plot with the H plot shows that, in H2+, the kinetic energy function increases less strongly with ζ than in H (the difference is apparent in the upper right hand corners of the panels) and that this difference in the kinetic energy is responsible for the H2+ minimum lying below the H minimum. This lowering of the minimum is very similar to the difference of the minima in the two systems discussed in Sec. 2B with reference to panels (a) and (c) of Figure 1 – except that the kinetic energy in Figure 1c was attenuated by an increase in the mass m, whereas, in H2+, the kinetic energy attenuation is caused by the wave delocalization, as discussed in Secs. 3B, 3C.
Figure 9.
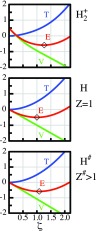
Comparison of the variational competitions in three systems. Minima marked by diamonds. Top panel: For the H2+ ion at the equilibrium distance. Middle panel: For the H atom. Bottom panel: For a hydrogen-like atom H# with a nuclear charge of Z# = 1.08273. The systems H2+ and H# have the same minimum energy value, which is 0.086152 h lower than that of the H atom. In H2+, this energy lowering is due to a lowering of the blue T curve whereas, in H#, it is due to a lowering of the green V curve. The differences between the subtle shifts of the H2+ and H# curves relative to the H curve are recognized best in the upper and lower right corners of the frames. Energies in hartree.
The plot of the hydrogen-like atom H# with ζ# = 1.08273 in the bottom panel of Figure 9 is relevant to the question whether the contraction of the atomic orbitals may simply represent an overall contraction of the molecular wave function Ψ that occurs because Ψ experiences an increased electrostatic pull due to the combined charges of both nuclei, i.e., that the contraction is simply a “united atom effect.” The plot of H# shows that it has a lower energy minimum than the H atom because the potential energy function of H# is slightly steeper, i.e., more attractive, than that of H (the difference is apparent in the lower right hand corners of the panels). By contrast, the potential energy function of H2+ (in the top panel) actually decreases slightly less steeply than that of H and, thus, opposes the energy lowering by contraction.
Thus, the lowering of the variational energy minimum of H2+ relative to the H atom is caused by the softening of the kinetic energy pressure due to delocalization whereas, in H#, the corresponding lowering of the minimum is due to the increased attractive nuclear pull of the potential energy. The orbital contraction of Ψ in H2+ can, therefore, not be considered as the result of an increase in electrostatic attraction by an effective united atom charge.
COVALENT BONDING IN OTHER MOLECULES
General considerations
The objective of the present section is to show that the factors that drive covalent bond formation in H2+ are also responsible for covalent bonding in other molecules. That this is indeed to be expected can be inferred from the following general considerations.
For all molecules, the following rigorous, general identities are valid at the equilibrium geometries: The kinetic component ΔT and the potential component ΔV of the binding energy ΔE are always related to ΔE by ΔV = 2 ΔE and ΔT = –ΔE = |ΔE|. These relations are known as the virial theorem. (An examination of the binding energy curve of H2+ in Figure 5 of Sec. 3C confirms that this is indeed so for H2+.) Furthermore, for any wave function that is expressed in terms of atomic orbitals, the virial relations are always rigorously satisfied when the variational minimization has been achieved with respect to orbital exponent scaling.20 These orbital exponent optimizations, in fact, generate the intra-atomic contractions that yield the values ΔT > 0 and ΔV < 0 that must hold at the minimum according to the virial theorem.
Within the context of the variational competition, this increase in intra-atomic localizations is, of necessity, contingent on a weakening of the kinetic resistance against localization in the molecule, and this attenuation of the kinetic energy pressure is furnished by the inter-atomic delocalization of the electron waves.
Specifically, the molecules H2, B2, C2, N2, O2, F2 are examined. The discussion of these bonding analyses in the present section is confined to a consideration of the essential aspects. In-depth analyses are worked out for these molecules in a forthcoming publication.21
Hydrogen molecule
Having opposite spins, the two electrons in the ground state of H2 can occupy the same position in space. They are, therefore, shared between the two atoms in a similar manner. Accordingly, an in-depth analysis21 shows that the electron pair bond is a result of the cumulative effect of the bonding by each electron.
The examination of the MCSCF wave function
| (14a) |
fully optimized to the same accuracy as the one achieved for H2+ (see the first paragraph of Sec. 3), leads to an overall energy analysis21 of H2 that is entirely analogous to that of H2+. The synergism of the contributions in H2 is exhibited in Figure 10. It is manifestly very similar to Figure 5 for H2+ and can be analyzed in the same manner. The analysis21 shows that, in H2 too, covalent bonding is driven by the attenuation of the kinetic energy of each of the electrons due to their delocalization from one atom to two atoms.
Figure 10.
Breakdown of the binding energy curve of H2 and its kinetic and potential components in terms of inter-atomic and intra-atomic contributions for different quasi-atomic choices: the unscaled 1sH orbitals (left), the contracted 1s* orbitals (center), and the contracted+polarized orbitals (right). The dotted green curve Vpen is the interpenetration enhancement energy of Eq. 14b. It is included in the green inter-atomic potential energy curve. Energies in milli-hartree. Abscissa = internuclear distance in bohrs.
There is, however, an additional energy contribution to the binding energy, which arises from the inter-electronic repulsion. It is a consequence of the fact that electron sharing enhances the mutual interpenetration of the electrons, each of which is originally confined to one atom. This enhanced interpenetration increases the inter-electronic repulsion and, hence, yields an anti-bonding contribution that is given by the additional potential energy term21
| (14b) |
Here, q is the probability of finding both electrons on the same atom, which has a value of about 0.14. This additional contribution is given by the curve denoted as Vpen in the top panels of Figure 10. The anti-bonding penetration effect Vpen, which is a consequence of electron sharing, is quite strong and manifestly makes the total inter-atomic potential contribution to the binding energy in H2 considerably more anti-bonding than in H2+. As a consequence, the binding energy of H2 is only 85% of twice the binding energy of H2+.
The inclusion of dynamic correlation in the analysis21 does not change these basic conclusions.
The molecules B2, C2, N2, O2, F2
The analysis21 of the molecules B2, C2, N2, O2 is based on MCSCF wave functions in the full valence space, i.e., in the full configuration space that is generated by the N valence electrons using the 8 valence orbitals in all possible ways, where N = 6, 8, 10, 12 for B2, C2, N2, O2, respectively. Calculated with Dunning's quadruple-zeta cc-pVQZ basis sets,22 these wave functions recover 91%, 99%, 93%, and 79%, respectively, of the experimental binding energies for these molecules. In F2, this approximation yields only 50% of the binding energy. For this molecule, the wave function was, therefore, chosen to be of the “14 valence electrons in 14 valence orbitals” type, by adding six correlating orbitals, two of σ-type, two of πx-type, and two of πy-type. The resulting MCSCF wave function yields 105% of the experimental binding energy.
In the MCSCF molecular orbital space of each molecule, quasi-atomic orbitals were then determined by means of the singular value decomposition, as has been described in a recent publication.23 Typical representative examples of these quasi-atomic orbitals are displayed in Figure 11. The upper set of panels in the figure display the quasi-atomic orbitals found on the left atom of the N2 molecule. They manifestly are deformed minimal basis set orbitals on that atom. The second row of panels in the figure displays the quasi-atomic orbitals found on the left atom in F2. In order to accommodate the additional orbitals in this row, the 1s-type orbital as well as the πy-type orbitals (which can be obtained from the corresponding πx type orbital by 90° rotation around the molecular axis) have been omitted. Instead, the additional correlating orbitals are shown: a 3s-type orbital and a 3px-type orbital. All of these orbitals, which are manifestly quasi-atomic, lie in the space of the optimized molecular MCSCF orbitals so that the actual molecular wave function can be expressed as a superposition of determinants formed from these quasi-atomic orbitals and the molecular energy can be resolved in terms of contributions calculated with these quasi-atomic orbitals.
Figure 11.
Quasi-atomic orbitals on the left atom from a FORS calculation of N2 and from a MCSCF calculation of F2, that includes six additional correlating orbitals, as discussed in the text. The orbitals on the same atom are mutually orthogonal. But the orbitals are not orthogonalized between atoms. Contours = 0.1 electron/bohr3/2.
In addition to the full optimal MCSCF energy, the following energies were calculated for each molecule.
Energy (i): The energies of the free atoms are calculated at the full atomic valence space MCSCF level.
Energy (ii): The energy of the molecule was calculated by a full valence space MCSCF calculation where, however, the orbitals are not optimized with respect to the quadruple-zeta AO bases, but only as linear combinations of the core and valence orbitals of the free atoms, i.e., the minimal basis set orbitals that were determined in the free-atom calculations described under (i). The resulting molecular wave function represents the analogue to the wave functions that were obtained for H2+ and H2 using the undeformed 1s ground state orbitals of the two hydrogen atoms.
Energy (iii): The energies of the quasi-atoms in the molecule were determined, which represent the analogues to the quasi-atomic energies that were obtained in H2+ and H2 by using the (contracted + polarized) quasi-atomic orbitals. For each atom, this objective was accomplished by a full atomic valence space MCSCF calculation with the same format as that used for the atomic calculation described under (i). Here, however, the atomic MCSCF orbitals were not optimized in the quadruple-zeta AO basis, but only as linear combinations of the quasi-atomic orbital orbitals obtained for that atom in the molecule as discussed above, in connection with Figure 11, in the second paragraph of this subsection. (These quasi-atomic orbitals are mutually orthogonal within each atom, but they were not orthogonalized between different atoms.)
From these energies, the following four differences were obtained:
ΔEinter(FAO): The inter-atomic energy lowering between the undeformed atoms, i.e., difference between the molecular energy calculated with the minimal basis sets of the optimal free-atom orbitals [case (ii) in the preceding paragraph] and the sum of the free-atom energies [case (i)]. This inter-atomic energy lowering is manifestly the molecular binding energy that is obtained when the free-atom orbitals are not allowed to deform.
ΔEintra = ΔEintra(FAO → QUAO): The intra-atomic energy increase due to the deformation of the minimal basis set of the free-atom orbitals that generates the minimal basis set of the quasi-atomic orbitals in the molecule, i.e., the difference between the energies of case (iii) and the energies of case (i). This represents the intra-atomic energy increase due to the formation of the quasi-atoms in the molecule.
ΔEinter(QUAO): The energy lowering of the optimized molecular energy with respect to the sum of the energies of the quasi-atoms in the molecule. This inter-atomic energy lowering is obtained by subtracting the sum of the atomic energies calculated with the deformed quasi-atomic orbitals [case (iii)] from the molecular MCSCF energy.
ΔE: The actual binding energy, i.e., the difference between the molecular MCSCF energy and the free-atom energies of case (i). This binding energy is manifestly the sum
| (15) |
The four energy differences and their kinetic and potential components are displayed in Figure 12 as functions of the internuclear distance. For comparison, the corresponding graphs of H2 and H2+ are also included in the figure. The number of calculated points from which these curves were drawn varies between 40 and 60.
Figure 12.
Resolution of the binding energy curves of the seven molecules H2+, H2, B2, C2, N2, O2, F2 in terms of intra-atomic contributions and inter-atomic contributions of the kinetic energy and the potential energy. Note that the energy unit (hartree) has different ranges and scalings on the ordinate for different molecules. Internuclear distances on the abscissa in bohr. Equilibrium distances are indicated by vertical lines. Left column: Inter-atomic interactions using unchanged free-atom-optimized minimal basis orbitals. Second column from left: Inter-atomic interactions using the molecule optimized minimal basis set atomic orbitals. Third column from left: Changes in intra-atomic energies due to deformation of atomic orbitals in the molecule (manifestly contractions). Right column: Optimized molecular binding energy curves = sum of second and third columns.
These plots show that, in all of these molecules, the factors contributing to the covalent energy lowering are very similar in as much as all plots share the following critical qualitative features of the various energy contributions.
Since ΔEintra is positive at all internuclear distances, Eq. 15 implies that it is always the inter-atomic energy decrease ΔEinter(QUAO) that is responsible for the total molecular energy decrease ΔE.
At distances larger than approximately twice the equilibrium distance, the intra-atomic energy change due to intra-atomic deformation, ΔEintra, vanishes so that ΔE = ΔEinter(QUAO) = ΔEinter(FAO).
Starting at about twice the equilibrium distance and going to shorter distances, the intra-atomic deformation energy ΔEintra increases with decreasing inter-atomic distance. But the inter-atomic interaction ΔEinter(QUAO) decreases more strongly so that the total energy decreases with decreasing distance until the equilibrium geometry is reached.
The intra-atomic energy increases always come about by large increases in the intra-atomic kinetic energy prevailing over nearly compensating decreases in the potential energy. This feature confirms that the deformations of the quasi-atomic orbitals (with respect to the free-atom orbitals) consist of overall contractions of the atoms in the molecule.
The inter-atomic energy decreases associated with these contractions always come about by decreases in the inter-atomic kinetic energy decreases prevailing over inter-atomic potential energy increases. This pattern is characteristic of an overall delocalization of the density.
At any given distance in the region where the atomic orbitals contract, the inter-atomic energy decrease ΔEinter(QUAO) is stronger than the inter-atomic energy decrease ΔEinter(FAO). Specifically, the kinetic part of ΔEinter(QUAO) is more negative than that of ΔEinter(FAO), and this change prevails over the change in the potential part of ΔEinter(QUAO), which is more positive than that of ΔEinter(FAO). These changes in the kinetic and the potential parts of the inter-atomic energy, both, reveal that an increase of the inter-atomic delocalization is generated by the intra-atomic contractions.
Remarkably, these conclusions also hold for the C2 molecule, even though a switch in configurations occurs around 3 bohrs due to an avoided crossing,24 which accounts for the jagged parts in the curves of the kinetic and potential energies.
Remarkable is that, in all cases, the inter-atomic contributions to the potential energy are anti-bonding. In light of the discussion of H2, one expects indeed that electron sharing, which drives the bonding, necessarily entails anti-bonding potential interference effects as well as increased coulombic repulsions due to enhanced penetration of the electrons from the two atoms. On the other hand, strong quasi-classical attractions are known to exist between the atoms in these molecules. One has to conclude that the quasi-classical bonding effects are weaker than the anti-bonding potential effects associated with electron delocalization.
The strikingly similar pattern exhibited by the binding energy contributions of the seven molecules in Figure 12 over the full internuclear distance range implies that the basic synergism that leads to covalent binding in H2+ and H2 is also operative in the other molecules.
CONCLUSIONS
Electron waves in bound states have an innate drive toward expansion because delocalization lowers their quantum mechanical kinetic energy. Here, the term “drive” implies the drive of the variation principle. This drive is restrained by the confinement in the nuclear potential wells. When incompletely filled atomic orbitals of comparable energies on two nuclei overlap sufficiently, then the space that becomes available to the electrons on both atoms is larger than the space on one atom. The combined space is then filled by the electron waves because of their drive toward expansion. The kinetic energy attenuation achieved by this delocalization is the physical cause of covalent bonding.
The expansion of the wave function from one atom to a wave function covering both atoms can be efficiently represented as a superposition of appropriate atomic orbitals from the bonded atoms. In this description the kinetic energy lowering appears as the result of an inter-atomic wave interference. The interference also gives rise to an accumulation of charge in the bond region, which (widespread teaching to the contrary) entails an anti-bonding increase of the potential energy, which is however less than the kinetic energy decrease.
At large internuclear distances the changes mentioned in the preceding paragraph are directly reflected in the kinetic and potential contributions to the dissociation curve.
For internuclear distances less than about twice the equilibrium distance, there occurs an additional change in the wave function, beyond that described by the superposition of the free-atom orbitals, which further enhances the delocalization of the electron wave, and correspondingly lowers the kinetic energy. This added enhancement is achieved by a contraction of the constituent atoms towards their respective nuclei. The reason is that, at these distances, the superposition of somewhat contracted atomic orbitals generates a stronger delocalization and kinetic energy lowering than the superposition of uncontracted free-atom orbitals. This enhancement of the inter-atomic kinetic energy lowering by orbital contractions prevails over the intra-atomic energy increase that is an unavoidable byproduct of orbital contractions.
The inter-atomic kinetic energy decrease through enhanced delocalization drives the contraction because the concomitant intra-atomic energy increase is small. As discussed in the penultimate paragraph of Sec. 2B, this small increase in the total intra-atomic energies is, however, the result of a large kinetic energy increase and a potential energy decrease that is only slightly smaller in magnitude. In fact, these kinetic and potential energy changes are so large that the overall molecular binding energy ends up having a negative potential and a positive kinetic contribution. Near the equilibrium distance, the signs and magnitudes of the kinetic and potential parts of the actual binding energy are, thus, determined by the anti-bonding intra-atomic contributions to the binding energy and opposite to the characteristics of the kinetic and potential parts of the inter-atomic contributions that drive the bond formation.
In the final analysis, the origin of covalent binding is no mystery: It is simply due to the drive of electron waves to lower their kinetic energy by expanding (delocalizing), which they do when partially filled atomic orbitals are available on two (or more) atoms that are sufficiently close to each other.
When a molecule is near its equilibrium geometry, matters are somewhat more complex, which is signaled by the signs of the kinetic part (>0) and the potential part (<0) of the binding energy. In order to understand these superficially confusing features, one has to recognize the following facts:
When two systems differ in their total energies, the kinetic and potential components of this energy difference per se do not, in general, reveal the physical reasons for the difference. As was shown in the second but last paragraph of Sec. 2B, this limitation is a consequence of the variational competition between the kinetic and potential energies, which is the ultimate driver.
Not only inter-atomic interactions (mainly the kinetic energy lowering) have to be taken into account but also the intra-atomic (kinetic and potential) energy changes that occur on bond formation.
In the case at hand, the inter-atomic delocalization and kinetic energy lowering is enhanced by intra-atomic contractions. This inter-atomic interaction enhancement, in fact, drives the (anti-bonding) total intra-atomic energy change. But the intra-atomic kinetic and potential contributions have their signs imprinted on the binding energy. These signs manifestly convey no information regarding the driving inter-atomic interactions and, hence, regarding the origin of covalent bond formation.
In addition to superposition and contraction there is a more subtle wave function adjustment that can be described as a polarization of the atomic orbitals. It is driven by a quasiclassical electrostatic interaction between the atoms. Since these atomic orbital deformations further increase the intra-atomic energies and, also, diminish the kinetic energy lowering due to delocalization, they yield a relatively modest overall energy lowering in the range where the covalent bonding is strong.
On the other hand, there exist non-covalent bonding patterns in which potential rather than kinetic energy changes dominate,25 viz., ionic interactions, multipolar interactions, or London dispersion forces.26, 27 In fact, these interactions determine all inter-atomic interactions at long ranges, where the covalent interactions have died out. The mix of components that contribute to these “van der Waals” interactions varies between different molecules. For instance, in H2+ the induced dipole interaction dominates, as was discussed in Sec. 3C (vi), whereas, in F2, the quadrupole repulsion and the dispersion attraction dominate.28 The transition from the covalent regime, which is the object of the present analysis, to the long range regime is often characterized by a pronounced change in the steepness of the dissociation curve, which can occur over a relatively narrow distance interval.
ACKNOWLEDGMENTS
This work was supported by the National Science Foundation (NSF) under Grant No. CHE-1147446 to Iowa State University. In part, the work was also supported (for K.R.) by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences & Biosciences through the Ames Laboratory at Iowa State University under Contract No. DE-AC02-07CH11358. The work was also supported in part with federal funds from the National Cancer Institute, National Institutes of Health, under Contract No. HHSN 261200800001E (for J.I.). The content of this publication does not necessarily reflect the views or policies of the Department of Health and Human Services.
References
- Statement by Whitesides G. M., in the Opening Plenary Lecture of the 92nd Canadian Chemistry Conference, 30 May 2009, Hamilton, Ontario, Canada (personal communication by K.R.).
- Regrettably, this misconception has been reiterated in the recent Next Generation Science Standards (NGSS) by the National Research Council, Washington, DC, 2013. (http://www.nextgenscience.org) which, according to [Google Scholar]; Cooper M. M., J. Chem. Educ. 90, 679 (2013), contains the following statements: “The first physical science core idea – PS1, Matter and its Interactions – is guided by the question: How can one explain the structure, properties, and interactions of matter?”; In high school, the “sub-atomic model and interactions between electric charges can be used to explain interactions of matter”; “The disciplinary core idea [is that] stable forms of matter are those in which the electric and magnetic field energy is minimized.” (Italics added by the present authors). 10.1021/ed400284c [DOI] [Google Scholar]
- For instance, Isaac Newton surmised that, analogous to the gravitational forces between masses, there are additional forces between atoms that are attractive at large distances and repulsive at short distances. Berzelius believed all bonds to be due to electrostatic attractions. Helmholtz conjectured the existence of short-range potentials between atoms. See, e.g., Ruedenberg K. and Schwarz W. H. E., “Three millennia of atoms and molecules,” in Pioneers of Quantum Chemistry, ACS Symposium Series Vol. 1122, edited by Strom E. T. and Wilson A. K. (ACS, Washington DC, 2013). [Google Scholar]
- This interpretation was first quoted by Slater J. C., J. Chem. Phys. 1, 687 (1933). 10.1063/1.1749227 [DOI] [Google Scholar]; A recent advocate has notably been Bader R. F. W., J. Phys. Chem. A 115, 12667 (2011). 10.1021/jp203531x [DOI] [PubMed] [Google Scholar]
- Hellmann H., Z. Phys. 85, 180 (1933); 10.1007/BF01342053 [DOI] [Google Scholar]; Hellmann H., Acta Phys. Chim. URSS 1, 333 (1934). [Google Scholar]
- Hellmann H., Quantenchemie (Deuticke, Leipzig and Wien, 1937), p. 120. [Google Scholar]
- Hellmann's interpretation was however used for solids in Sec. 5 of Peierls R. E., Quantum Theory of Solids (Clarendon Press, Oxford, 1955). [Google Scholar]
- At the Boulder Conference of 1958, Coulson C. A. famously expressed apprehension that the computer-generation of accurate, but complex wave functions might endanger conceptual interpretations, Rev. Mod. Phys. 32, 170 (1960). 10.1103/RevModPhys.32.170 [DOI] [Google Scholar]
- Ruedenberg K., Rev. Mod. Phys. 34, 326 (1962); 10.1103/RevModPhys.34.326 [DOI] [Google Scholar]; Edmiston C. and Ruedenberg K., J. Phys. Chem. 68, 1628 (1964); 10.1021/j100789a002 [DOI] [Google Scholar]; Feinberg M. J., Ruedenberg K., and Mehler E., Advances in Quantum Chemistry, edited by Löwdin P. O. (Academic Press, 1970), Vol. 5, p. 27; [Google Scholar]; Feinberg M. J. and Ruedenberg K., J. Chem. Phys. 54, 1495 (1971); 10.1063/1.1675044 [DOI] [Google Scholar]; Feinberg M. J. and Ruedenberg K., J. Chem. Phys. 55, 5804 (1971); 10.1063/1.1675751 [DOI] [Google Scholar]; Ruedenberg K., in Localization and Delocalization in Quantum Chemistry, edited by Daudel R. (Reidel, Dordrecht, Holland, 1975). Vol. 1, p. 222. [Google Scholar]
- Hellmann's work was called to Ruedenberg's attention after he first communicated his conclusions.
- Goddard W. A. and Wilson C. W., Theor. Chim. Acta 26, 195 (1972); 10.1007/BF00529306 [DOI] [Google Scholar]; Goddard W. A. and Wilson C. W., Theor. Chim. Acta 26, 211 (1972); 10.1007/BF0052930710.1007/BF00529307 [DOI] [Google Scholar]; Kutzelnigg W., Angew. Chem. 85, 551 (1973); 10.1002/ange.19730851302 [DOI] [Google Scholar]; Kutzelnigg W., Int. Edtn. 12, 46 (1973); [Google Scholar]; Bitter T. and Schwarz W. H. E., Ber. Bunsenges. Phys. Chem. 80, 1231 (1976); [Google Scholar]; Fukui K., Chemical Reactions and Electronic Orbitals (Maruzen Co, Tokyo, 1976) (Kagaku Hannoh to Denshi no Kidoh) (in Japanese); [Google Scholar]; Mulliken R. S. and Ermler W. C., Diatomic Molecules (Academic Press, New York, 1977), Sec. II.F; [Google Scholar]; Bitter T., Doctoral Thesis (University Siegen, 1982); [Google Scholar]; Rozendaal A. and Baerends E. J., Chem. Phys. 95, 57 (1985); 10.1016/0301-0104(85)80150-6 [DOI] [Google Scholar]; Baird N. C., J. Chem. Educ. 63, 660 (1986); 10.1021/ed063p660 [DOI] [Google Scholar]; Harcourt R. D., Am. J. Phys. 56, 660 (1988); 10.1119/1.15535 [DOI] [Google Scholar]; Kutzelnigg W., in The Concept of the Chemical Bond, edited by Maksic Z. B. (Springer, Berlin, 1990), Vol. 2, p. 1; [Google Scholar]; Harris F. E., in Encyclopedia of Physics, 2nd ed., edited by Lerner R. G. and Trig G. L. (VCH Publishers, Inc., New York, 1991), p. 762; [Google Scholar]; Rioux F., Chem. Educ. 2(6), 1 (1997); 10.1007/s00897-997-0007-1 [DOI] [Google Scholar]; Bacskay G. B., Reimers J. R., and Nordholm S., J. Chem. Ed. 74, 1494 (1997); 10.1021/ed074p1494 [DOI] [Google Scholar]; Gordon M. S. and Jensen J. H., Encyclopedia of Computational Chemistry, edited by Schleyer P. v. R. (John Wiley and Sons, New York, 1998), pp. 3198–3214; [Google Scholar]; Gordon M. S. and Jensen J. H., Theor. Chem. Acc. 103, 248 (2000); 10.1007/s002149900034 [DOI] [Google Scholar]; Bickelhaupt F. M. and Baerends E. J., Rev. Comput. Chem. 15, 1 (2000); 10.1002/9780470125922.ch1 [DOI] [Google Scholar]; Rioux F., Chem. Educ. 6(5), 288 (2001). 10.1007/s00897010509a [DOI] [Google Scholar]
- Ruedenberg K. and Schmidt M. W., J. Comput. Chem. 28, 391 (2007); 10.1002/jcc.20553 [DOI] [PubMed] [Google Scholar]; Ruedenberg K. and Schmidt M. W., J. Phys. Chem. A 113, 1954 (2009). 10.1021/jp807973x [DOI] [PubMed] [Google Scholar]
- Bacskay G. B. and Nordholm S., J. Phys. Chem. A 117, 7946 (2013). 10.1021/jp403284g [DOI] [PubMed] [Google Scholar]
- Earnshaw S., Trans. Camb. Philos. Soc. 7, 97 (1842); [Google Scholar]; see also Jeans J., The Mathematical Theory of Electricity and Magnetism (Cambridge University Press, 1946), pp. 167–168. [Google Scholar]
- See, for instance, Pauling L., The Nature of the Chemical Bond (Cornell University Press, 1948), Sec. 3. [Google Scholar]
- The most accurate molecular values reported so far are 1.9971933199699992 bohrs for the equilibrium distance and 0.6026346191065398 hartree for the energy. See Scott T. C., Aubert-Frecon M., and Grotendorst J., Chem. Phys. 324, 323 (2006). 10.1016/j.chemphys.2005.10.031 [DOI] [Google Scholar]
- Coulson C. A., Proc. R. Soc. Edinburgh A 61, 20 (1941). 10.1017/S0080454100006038 [DOI] [Google Scholar]
- Buckingham A. D., Q. Rev. Chem. Soc. 13, 183 (1959). 10.1039/qr9591300183 [DOI] [Google Scholar]
- This wave function was first determined by Finkelstein B. N. and Horowitz G. E., Z. Phys. 48, 118 (1928). 10.1007/BF01351582 [DOI] [Google Scholar]
- Coulson C. A. and Bell R. P., Trans. Faraday Soc. 41, 141 (1945); 10.1039/tf9454100141 [DOI] [Google Scholar]; Löwdin P. O., J. Mol. Spectrosc. 3, 46 (1959). 10.1016/0022-2852(59)90006-2 [DOI] [Google Scholar]
- Schmidt M. W., Ivanic J., and Ruedenberg K., “The physical origin of covalent bonding,” in The Chemical Bond. Fundamental Aspects of Chemical Bonding, edited by Frenking G. and Shaik S. (Wiley-VCH Verlag, 2014), Chap. 1. [Google Scholar]
- Dunning T. H., J. Chem. Phys. 90, 1007 (1989). See also the website http://tyr0.chem.wsu.edu/~kipeters/Pages/cc_append.html. 10.1063/1.456153 [DOI] [Google Scholar]
- West A. C., Schmidt M. W., Gordon M. S., and Ruedenberg K., J. Chem. Phys. 139, 234107 (2013); 10.1063/1.4840776 [DOI] [PubMed] [Google Scholar]; the quasi-atomic orbitals used in the present investigation were not orthogonalized between different atoms.
- See, e.g., Boschen J. S., Theis D., Ruedenberg K., and Windus T. L., Theor. Chem. Acc. 133, 1425 (2013). 10.1007/s00214-013-1425-x [DOI] [Google Scholar]
- Bitter T., Ruedenberg K., and Schwarz W. H. E., J. Comput. Chem. 28, 411 (2007); 10.1002/jcc.20531 [DOI] [PubMed] [Google Scholar]; Bitter T., Wang S. G., Ruedenberg K., and Schwarz W. H. E., Theor. Chem. Acc. 127, 237 (2010). 10.1007/s00214-010-0758-y [DOI] [Google Scholar]
- See, e.g., Buckingham A. D., Fowler P. W., and Hudson J. M., Chem. Rev. Washington, D.C. 88, 963 (1988); 10.1021/cr00088a008 [DOI] [Google Scholar]; Chałasiński G. and Szczęśniak M. M., Chem. Rev. Washington, D.C. 100, 4227 (2000); 10.1021/cr990048z [DOI] [PubMed] [Google Scholar]; Stone A. J., The Theory of Intermolecular Forces (Clarendon, Oxford, 1996). [Google Scholar]
- London F., Trans. Faraday Soc. 33, 8b (1937). 10.1039/tf937330008b [DOI] [Google Scholar]
- Bytautas L. and Ruedenberg K., J. Chem. Phys. 130, 204101 (2009). 10.1063/1.3139114 [DOI] [PubMed] [Google Scholar]