Tissue decomposition from dual energy CT data for MC based dose calculation in particle therapy

Abstract

Purpose: The authors describe a novel method of predicting mass density and elemental mass fractions of tissues from dual energy CT (DECT) data for Monte Carlo (MC) based dose planning.

Methods: The relative electron density ϱ_e and effective atomic number Z_eff are calculated for 71 tabulated tissue compositions. For MC simulations, the mass density is derived via one linear fit in the ϱ_e that covers the entire range of tissue compositions (except lung tissue). Elemental mass fractions are predicted from the ϱ_e and the Z_eff in combination. Since particle therapy dose planning and verification is especially sensitive to accurate material assignment, differences to the ground truth are further analyzed for mass density, I-value predictions, and stopping power ratios (SPR) for ions. Dose studies with monoenergetic proton and carbon ions in 12 tissues which showed the largest differences of single energy CT (SECT) to DECT are presented with respect to range uncertainties. The standard approach (SECT) and the new DECT approach are compared to reference Bragg peak positions.

Results: Mean deviations to ground truth in mass density predictions could be reduced for soft tissue from (0.5±0.6)% (SECT) to (0.2±0.2)% with the DECT method. Maximum SPR deviations could be reduced significantly for soft tissue from 3.1% (SECT) to 0.7% (DECT) and for bone tissue from 0.8% to 0.1%. Mean I-value deviations could be reduced for soft tissue from (1.1±1.4%, SECT) to (0.4±0.3%) with the presented method. Predictions of elemental composition were improved for every element. Mean and maximum deviations from ground truth of all elemental mass fractions could be reduced by at least a half with DECT compared to SECT (except soft tissue hydrogen and nitrogen where the reduction was slightly smaller). The carbon and oxygen mass fraction predictions profit especially from the DECT information. Dose studies showed that most of the 12 selected tissues would profit significantly (up to 2.2%) from DECT material decomposition with no noise present. The ϱ_e associated with an absolute noise of ±0.01 and Z_eff associated with an absolute noise of ±0.2 resulted in ±10% standard variation in the carbon and oxygen mass fraction prediction.

Conclusions: Accurate stopping power prediction is mainly determined by the correct mass density prediction. Theoretical improvements in range predictions with DECT data in the order of 0.1%–2.1% were observed. Further work is needed to quantify the potential improvements from DECT compared to SECT in measured image data associated with artifacts and noise.

INTRODUCTION

Monte Carlo (MC) simulation is a powerful tool for various types of verification in radiation therapy, providing the means for a deeper understanding of radiation transport within the patients’ tissue. For particle therapy, MC calculations increase the accuracy of dose calculation especially in inhomogeneous geometries. Through the advent of novel tools like TOPAS (Ref. ¹) which provide a user friendly interface, MC based dose treatment planning has become much easier to employ for proton therapy. More efficient and massively parallel based Monte Carlo codes will ultimately lead to a broad application in radiotherapy dose planning and verification.

For dose planning on patients’ computed tomography (CT) images, most MC algorithms demand mass density and elemental compositions in each CT voxel. The stoichiometric calibration presented in Refs. ² and ³ represents the state of the art approach for determining material properties on a CT voxel basis for MC simulation of external beam therapy. Here, mass density is predicted continuously by different linear fits in the CT number (“Hounsfield Unit”, HU). Elemental compositions are predicted by a table providing CT number bins of constant elemental mass fractions. Intrinsic uncertainties emerge since tissues expressing the same photon attenuation but different elemental compositions or mass densities cannot be distinguished.

Dual energy CT (DECT) may help to reduce these uncertainties by providing additional information of the scanned material. DECT comprises CT scanning with two different photon spectra.^{4, 5} Both resulting attenuation maps (CT number images) can be transformed into a second data pair of information: the relative electron density to water ϱ_e and the effective atomic number Z_eff. Different methods of calculating the ϱ_e and Z_eff from two CT numbers have been presented in the literature.^{4, 6, 7, 8, 9} A purely image based calculation of both parameters with excellent accuracy is possible [ϱ_e: ±0.4% and Z_eff: ±1.7% (Ref. ¹⁰)].

For analytical treatment planning systems, Yang et al.¹¹ presented the first DECT based approach to predict stopping power ratios (SPR) by using the Z_eff information for a mean excitation energy (I-value) estimation and allows a subsequent direct calculation of the SPR. Following the approach of Yang et al.,¹¹ Hünemohr et al.¹⁰ estimated the SPR of tissue surrogates through DECT images measured with a clinical dual source CT scanner. A mean accuracy of 0.6% (max. deviation 1.4%) for the SPR estimation was achieved. A simpler approach showed that the ϱ_e image can be sufficient to predict the SPR.¹²

For MC based dose calculation in external electron beams and brachytherapy, previous studies showed an improved determination of material composition with DECT data.^{6, 13, 14} Yang¹⁵ suggested to derive elemental mass fractions with linear fits in the Z_eff, Landry et al.¹⁶ presented an approach that calculates the minimal distance to a reference tissue composition in the ϱ_e and Z_eff space.

This paper describes a method to extract mass density and elemental compositions from the DECT ϱ_e and Z_eff information with simple linear fits in both quantities. The material decomposition is compared to the standard single energy CT (SECT) approach² and shows the theoretical potential for tissues which would benefit from DECT with respect to the predicted proton and carbon ion range. Assignment of elemental mass fractions and mass density influence not only the prediction of SPR (ϱ_e and I-value calculation) but also the subsequent assignment of nuclear cross sections.^{17, 18, 19, 20, 21, 22} More accurate material decompositions might also improve low energy photon brachytherapy,²³ PET range verification through ion beam induced tissue activation,^{16, 24} and modeling prompt gamma response in vivo.

MATERIALS AND METHODS

MC dose simulations based on CT data usually require the composition and mass density of the tissue traversed.²⁵ In this section, a novel approach for the DECT based material decomposition is presented. The DECT approach is compared to the standard SECT approach by evaluating the prediction of individual tissue properties (mass density, I-value, SPR) as well as MC range simulations with protons and carbon ions.

Extraction of elemental compositions from ϱ_e and Z_eff

For this study, the same 71 tabulated tissues as used in Ref. 2 were considered. Only the six major elements of the body were included for this work: hydrogen, carbon, nitrogen, oxygen, calcium, and phosphorus. For the sake of simplicity, trace elements were excluded from this study but can be included in the elemental mass fraction fits due to linearity in Z_eff3. Elemental mass fractions w_i were normalized to 100% by dividing single by the sum of all considered elemental mass fractions. The sum of other elemental mass fractions is smaller than 1.7%.² Readers interested in applying the method to real measured DECT data should perform fits with the full tissue composition including trace elements to calculate correct reference Z_effs. Including trace elements would cause a mean Z_eff elevation of 0.1 for the 70 tissues, excluding thyroid (maximum elevation for thyroid: 0.85 due to the high iodine content).

The relative electron density ϱ_e is defined as

$${\varrho }_{\mathrm{e}}=\frac{\varrho N_A{\sum }_i{w}_i\frac{Z_i}{A_i}}{{\varrho }_e^{H_{2}O}}$$ (1)

with the atomic number Z_i and atomic mass number A_i of each compound element. ${\varrho }_e^{{\text{H}}_2\text{O}}$ is set to 3.343 × 10²³$\frac{1}{{\text{cm}}^3}$ and N_A = 6.0221 × 10²³ denotes the Avogadro number.

The effective atomic number Z_eff is defined as

$$Z_{\text{eff}}={\left(\frac{{\sum }_i{w}_i\frac{Z_i}{A_i}{Z}_i^m}{{\sum }_i{w}_i\frac{Z_i}{A_i}}\right)}^{\frac{1}{m}}.$$ (2)

m represents the only scanner (photon spectra) specific quantity. For standard tissue compositions m ranges approximately from 2.8 to 3.8 in the diagnostic x-ray regime, dependent on the photoelectric and Compton effect portion to the overall photon attenuation.^{16, 26} For this work, m was set to 3.1 representing the scanner spectrum combination available in the second generation of dual source CT scanners (Siemens Somatom Definition Flash). The scanner provides a low energy spectrum at 80 or 100 kV tube voltage and a high energy spectrum at 140 Sn kV filtered by tin (Sn) that attenuates low energy photons to reduce the spectral overlap with the low kV spectrum.

In order to take advantage of all available information, the ϱ_e and Z_eff are used in combination for the material decomposition from DECT data in contrast to the standard SECT approach which uses CT number intervals (Fig. 1). Elemental mass fractions for each element i were derived by a linear fit of the ϱ_e, the Z_eff, and an interaction of both

$$w_{\mathrm{i}}=a_{\mathrm{i}}·{\varrho }_{\mathrm{e}}+b_{\mathrm{i}}·Z_{\mathrm{eff}}+c_{\mathrm{i}}·{\varrho }_{\mathrm{e}}{Z}_{\mathrm{eff}}+d_{\mathrm{i}}.$$ (3)

This relation shows that elemental mass fractions influence the ϱ_e and Z_eff linearly. The interaction term represents possible different linear behaviors in both quantities (i.e., the carbon and oxygen mass fractions of soft tissue behave differently dependent on the ϱ_e and Z_eff).

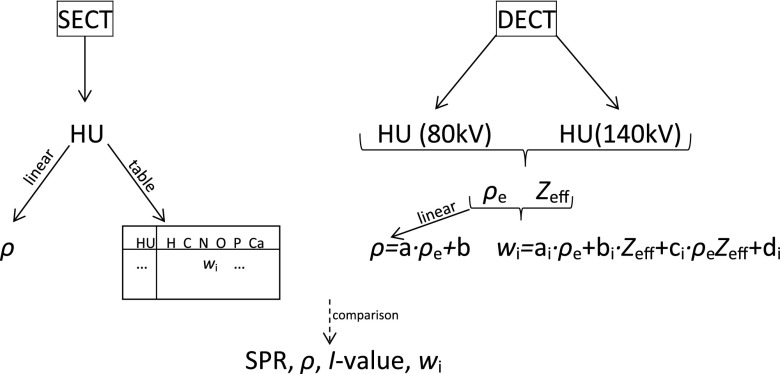
Figure 1.

Single (SECT) and dual (DECT) energy CT approach of material decomposition. MC requires mass density ϱ and elemental mass fractions w_i of every CT voxel. SECT derives mass density from different linear fits in the CT number (HU) and elemental mass fractions from a table containing CT number bins with constant elemental mass fractions. With DECT, mass density can be derived via one linear fit in the relative electron density ϱ_e. Elemental mass fractions are derived from linear fits in ϱ_e and effective atomic number Z_eff.

Elemental mass fractions dependent on Z_eff, ϱ_e, and CT number are depicted in Fig. 2. Two different regions of tissue appear: soft tissues (small Z_eff) are composed mainly of hydrogen, carbon, nitrogen, and oxygen. Since in the higher Z_eff region calcium and phosphorus gain weight, elemental fits 3 were conducted separately for soft (Z_eff < 8.2) and bone (Z_eff ⩾ 8.2) tissues. The threshold of Z_eff = 8.2 is located near thyroid when considering not only the six major elements (as done for this paper) but also the mass fractions of high Z elements. Prediction of elemental mass fractions were followed by a normalization of all predicted elemental mass fractions to the sum of 1 (100%) for every tissue.

Figure 2.

Elemental mass fractions of 70 tissues (lung tissue is not shown) dependent on CT number (HU) predicted in Ref. 2 for a 120  kV spectrum, relative electron density ϱ_e, and effective atomic number Z_eff. Ambiguous tissues in CT number can be better differentiate using the additional information of Z_eff in combination with ϱ_e.

For lung tissue (mass density ranging between air and adipose), only the ϱ_e was considered. Here, elemental mass fractions were set to the lung tissue composition and were not changed up to adipose. Lung tissue has a typical soft tissue composition with variable mass density dependent on the respiratory phase. Therefore, the ϱ_e and CT numbers are significantly lower. The presented linear elemental mass fraction fits cannot be extrapolated into the low electron density region, since the predicted lung composition would deviate significantly from the soft tissue interval.

Extraction of mass density from the relative electron density

Mass density ϱ was derived from DECT data through a linear fit in the ϱ_e from adipose tissue to cortical bone for the 70 tabulated tissues (as already showed in Ref. 23)

$$\varrho =a·{\varrho }_{\mathrm{e}}+b.$$ (4)

For lung tissue, the parameters a and b were derived by interpolating the ϱ/ϱ_e pair of air (0.00121 $\frac{\text{g}}{{\text{cm}}^3}$/0.00109) and muscle tissue (1.05 $\frac{\text{g}}{{\text{cm}}^3}$/1.041) which has a similar composition compared to lung tissue with respect to the hydrogen mass fraction. Please note the difference in the SECT approach,² where the mass density for lung tissue is derived by an interpolation of air to adipose tissue.

I-value prediction

The mean excitation energy I is one important tissue parameter (besides the ϱ_e) which influences ion ranges in tissue. Reference I-values for the 71 tissues were calculated with Bragg's additivity rule

$$\text{ln}(I/\mathrm{eV})=\frac{{\sum }_i{w}_i\frac{Z_i}{A_i}\text{ln}(I_i/\mathrm{eV})}{{\sum }_i{w}_i\frac{Z_i}{A_i}}.$$ (5)

Elemental I-values I_i were taken from Table 2.11 in Ref. 27. For the DECT prediction of the I-values, elemental mass fractions w_i were set to predicted elemental mass fractions (Sec. 2A). I-values from SECT, which are constant over each CT number bin, were calculated from the compositions in Ref. 2, normalized to the major elements.

Stopping power prediction

Reference SPR for a compound medium was approximated by the Bethe formula without any correction terms³

$$\begin{array}{ccc}\hfill \text{SPR}& =& \frac{{\varrho }_{\mathrm{e}},\mathrm{medium}}{{\varrho }_{\mathrm{e}},\mathrm{water}}·\frac{\ln \left(\frac{2m_e{c}^2{\beta }^2}{(I_{\mathrm{medium}}/\mathrm{eV})(1-{\beta }^2)}\right)-{\beta }^2}{\ln \left(\frac{2m_e{c}^2{\beta }^2}{(I_{\mathrm{water}}/\mathrm{eV})(1-{\beta }^2)}\right)-{\beta }^2}\hfill \\ & =& \frac{{\varrho }_{\mathrm{e}},\mathrm{medium}}{{\varrho }_{\mathrm{e}},\mathrm{water}}·\frac{12.77-\text{ln}(I_{\mathrm{medium}}/\mathrm{eV})}{8.45}.\hfill \end{array}$$ (6)

The particle energy was set to 200 MeV/u (assuming that the SPR is largely energy independent above energies of about 15 MeV/u); the I-value of water was set to 75 eV.²⁷

For this study with tabulated tissue compounds, the SPR prediction from DECT was calculated in two different ways. The first approach uses the ϱ_e directly for the SPR calculation (“DECT with ϱ_e”). Knowledge of elemental mass fractions is required for the calculation of the I-value 5 and the determination of the nuclear cross sections. The mass density is derived via the linear fit of the ϱ_e4 and must be assigned for MC based treatment planning on CT geometries in order to adjust continuously nuclear cross sections.²⁵ The second approach is the usual way of predicting SPR with a MC dose calculation tool. From the predicted elemental mass fractions (Sec. 2A) and mass densities (Sec. 2B) for each tissue, the ϱ_e and I-values were calculated (Sec. 2C). With both values the stopping power and nuclear cross sections for the MC simulations were accessible. The latter way was also used for the range studies with TOPAS in this paper.

All tissue reference parameters (ϱ_e, Z_eff, I-value, SPR) and compositions are listed in Table 1.

Table 1.

Reference elemental mass fractions, CT numbers (HU) at 120  kV, relative electron density ϱ_e, effective atomic number Z_eff, mean excitation energy I, and relative SPR for 71 tissues. CT numbers, compositions, densities, and CT number intervals (“HU bin”) to assign average tissue compositions according to a measured single energy CT number are taken from Ref. 2. Tissue compositions originate from Refs. ³³ and ³⁴ and were normalized to the six major elements in this work. A particle energy of 200 MeV/u was used to calculate the SPR.

			ϱ							I
Material	HU bin	HU	[g/cm3]	H	C	N	O	Ca	P	[eV]	ϱe	⟨Z/A⟩	Zeff	SPR
Lungdeflated	[−951,−120]	−741	0.26	10.4	10.6	3.1	75.7	0.0	0.2	74.54	0.258	0.5511	7.31	0.258
Adiposetissue3	[−119,−83]	−98	0.93	11.6	68.3	0.2	19.9	0.0	0.0	63.06	0.933	0.5570	6.10	0.952
Adiposetissue2	[−82,−53]	−77	0.95	11.4	60.0	0.7	27.9	0.0	0.0	64.60	0.952	0.5560	6.30	0.969
Adiposetissue1	[−82,−53]	−55	0.97	11.2	51.9	1.3	35.6	0.0	0.0	66.14	0.970	0.5551	6.48	0.985
Yellowmarrow	[−52,−23]	−49	0.98	11.5	64.6	0.7	23.2	0.0	0.0	63.72	0.982	0.5565	6.19	1.001
Mammarygland1	[−52,−23]	−37	0.99	10.9	50.8	2.3	35.9	0.0	0.1	66.73	0.987	0.5536	6.53	1.001
Yellowredmarrow	[−22,7]	−22	1.00	11.0	53.1	2.1	33.6	0.0	0.1	66.18	0.998	0.5541	6.47	1.013
Mammarygland2	[−22,7]	−1	1.02	10.6	33.3	3.0	52.9	0.0	0.1	70.05	1.015	0.5522	6.88	1.024
Redmarrow	[8,18]	11	1.03	10.6	41.7	3.4	44.2	0.0	0.1	68.70	1.024	0.5518	6.72	1.035
BrainCerebrospinalfluid	[8,18]	13	1.01	11.2	0.0	0.0	88.8	0.0	0.0	75.30	1.010	0.5551	7.45	1.010
Adrenalgland	[8,18]	14	1.03	10.7	28.5	2.6	58.1	0.0	0.1	70.92	1.025	0.5523	6.98	1.032
Smallintestinewall	[19,80]	23	1.03	10.7	11.6	2.2	75.5	0.0	0.1	73.98	1.025	0.5524	7.28	1.027
Urine	[19,80]	26	1.02	11.1	0.5	1.0	87.2	0.0	0.1	75.21	1.019	0.5548	7.45	1.019
Gallbladderbile	[19,80]	27	1.03	10.9	6.1	0.1	82.9	0.0	0.0	74.81	1.027	0.5536	7.36	1.028
Lymph	[19,80]	29	1.03	10.9	4.1	1.1	83.9	0.0	0.0	75.00	1.027	0.5536	7.38	1.027
Pancreas	[19,80]	32	1.04	10.7	17.0	2.2	69.9	0.0	0.2	73.00	1.035	0.5524	7.20	1.039
Brainwhitematter	[19,80]	34	1.04	10.7	19.6	2.5	66.8	0.0	0.4	72.50	1.035	0.5525	7.19	1.039
Prostate	[19,80]	34	1.04	10.6	9.0	2.5	77.9	0.0	0.1	74.58	1.034	0.5519	7.32	1.035
Testis	[19,80]	36	1.04	10.7	10.0	2.0	77.2	0.0	0.1	74.23	1.035	0.5525	7.31	1.037
Braingraymatter	[19,80]	40	1.04	10.8	9.6	1.8	77.5	0.0	0.3	74.17	1.036	0.5531	7.34	1.038
Muscleskeletal1	[19,80]	40	1.05	10.2	17.3	3.6	68.7	0.0	0.2	73.69	1.040	0.5501	7.21	1.042
Heart1	[19,80]	41	1.05	10.4	17.6	3.1	68.6	0.0	0.2	73.32	1.042	0.5510	7.20	1.045
Kidney1	[19,80]	41	1.05	10.3	16.1	3.4	69.9	0.1	0.2	73.79	1.041	0.5505	7.27	1.043
Stomach	[19,80]	41	1.05	10.5	14.0	2.9	72.5	0.0	0.1	73.81	1.043	0.5514	7.24	1.045
Thyroid	[19,80]	42	1.05	10.5	12.0	2.4	75.0	0.0	0.1	74.24	1.043	0.5515	7.28	1.045
Muscleskeletal2	[19,80]	43	1.05	10.3	14.4	3.4	71.6	0.0	0.2	74.03	1.041	0.5506	7.25	1.043
Liver1	[19,80]	43	1.05	10.4	15.8	2.7	70.8	0.0	0.3	73.72	1.042	0.5511	7.25	1.044
Heart2	[19,80]	43	1.05	10.5	14.0	2.9	72.4	0.0	0.2	73.80	1.043	0.5515	7.26	1.045
Aorta	[19,80]	43	1.05	10.0	14.8	4.2	70.2	0.4	0.4	74.78	1.038	0.5489	7.47	1.039
Kidney2	[19,80]	43	1.05	10.4	13.3	3.0	73.0	0.1	0.2	74.16	1.042	0.5510	7.32	1.044
Muscleskeletal3	[19,80]	44	1.05	10.3	11.3	3.0	75.2	0.0	0.2	74.66	1.041	0.5506	7.31	1.042
Heart3	[19,80]	45	1.05	10.5	10.4	2.7	76.2	0.0	0.2	74.49	1.043	0.5515	7.32	1.044
Mammarygland3	[19,80]	45	1.06	10.2	15.9	3.7	70.1	0.0	0.1	73.78	1.051	0.5503	7.21	1.053
Kidney3	[19,80]	46	1.05	10.5	10.7	2.7	75.8	0.1	0.2	74.48	1.043	0.5515	7.36	1.044
Ovary	[19,80]	46	1.05	10.6	9.4	2.4	77.4	0.0	0.2	74.52	1.044	0.5520	7.33	1.045
Eyelens	[19,80]	49	1.07	9.6	19.6	5.7	64.9	0.0	0.1	73.97	1.055	0.5474	7.16	1.057
Liver2	[19,80]	53	1.06	10.3	14.0	3.0	72.3	0.0	0.3	74.18	1.051	0.5506	7.28	1.053
Spleen	[19,80]	54	1.06	10.4	11.4	3.2	74.7	0.0	0.3	74.47	1.052	0.5510	7.32	1.053
Trachea	[19,80]	54	1.06	10.2	14.0	3.3	72.0	0.0	0.4	74.38	1.050	0.5501	7.30	1.051
Heartbloodfilled	[19,80]	56	1.06	10.4	12.2	3.2	74.1	0.0	0.1	74.22	1.052	0.5511	7.27	1.054
Bloodwhole	[19,80]	56	1.06	10.3	11.1	3.3	75.2	0.0	0.1	74.61	1.051	0.5506	7.29	1.052
Liver3	[19,80]	63	1.07	10.2	12.7	3.3	73.4	0.0	0.3	74.58	1.060	0.5501	7.30	1.061
Skin1	[19,80]	72	1.09	10.1	25.2	4.6	59.9	0.0	0.1	72.25	1.079	0.5495	7.04	1.084
Skin2	[19,80]	74	1.09	10.1	20.6	4.2	65.0	0.0	0.1	73.17	1.079	0.5495	7.13	1.082
Skin3	[19,80]	77	1.09	10.2	15.9	3.7	70.1	0.0	0.1	73.89	1.080	0.5500	7.21	1.082
Connectivetissue	[81,120]	100	1.12	9.5	21.0	6.3	63.1	0.0	0.0	73.79	1.103	0.5469	7.11	1.105
Cartilage	[81,120]	102	1.10	9.8	10.1	2.2	75.7	0.0	2.2	76.96	1.085	0.5477	7.68	1.082
Sternum	[301,400]	385	1.25	7.8	31.8	3.7	44.1	8.6	4.0	81.97	1.211	0.5378	10.27	1.199
Sacrummale	[401,500]	454	1.29	7.4	30.4	3.7	44.1	9.9	4.5	84.19	1.245	0.5357	10.63	1.228
D6L3inclcartilagem	[401,500]	466	1.30	7.4	26.7	3.6	47.6	9.9	4.8	85.38	1.253	0.5352	10.69	1.234
Vertcolwhole	[501,600]	514	1.33	7.2	26.0	3.6	47.5	10.6	5.1	86.59	1.280	0.5342	10.87	1.259
VertcolD6L3exclcartilage	[501,600]	526	1.33	7.0	28.9	3.8	44.0	11.2	5.1	86.54	1.278	0.5336	10.97	1.257
FemurHumerussphericalhead	[501,600]	538	1.33	7.1	38.1	2.6	34.3	12.2	5.6	85.43	1.279	0.5339	11.16	1.260
Femurconicaltrochanter	[501,600]	586	1.36	6.9	36.7	2.7	34.8	12.9	5.9	86.69	1.305	0.5329	11.31	1.283
C4inclcartilagemale	[501,600]	599	1.38	6.6	24.5	3.7	47.4	12.0	5.7	89.36	1.321	0.5316	11.23	1.294
Sacrumfemale	[601,700]	621	1.39	6.6	27.3	3.8	43.8	12.6	5.8	89.11	1.331	0.5315	11.33	1.304
Humeruswholespecimen	[601,700]	636	1.39	6.7	35.3	2.8	35.3	13.6	6.2	88.06	1.332	0.5318	11.48	1.307
Ribs2nd6th	[601,700]	657	1.41	6.4	26.5	3.9	43.9	13.2	6.0	90.28	1.348	0.5305	11.47	1.319
Innominatemale	[601,700]	658	1.41	6.3	26.4	3.9	43.9	13.3	6.1	90.69	1.346	0.5300	11.50	1.316
VertcolC4exclcartilage	[601,700]	672	1.42	6.3	26.3	3.9	43.9	13.4	6.1	90.78	1.356	0.5300	11.52	1.326
Femurtotalbone	[601,700]	688	1.42	6.3	33.4	2.9	36.3	14.4	6.6	90.24	1.355	0.5298	11.68	1.326
Femurwholespecism	[701,800]	702	1.43	6.3	33.2	2.9	36.4	14.5	6.6	90.34	1.365	0.5298	11.70	1.335
Innominatefemale	[701,800]	742	1.46	6.0	25.2	3.9	43.8	14.4	6.6	92.76	1.390	0.5284	11.75	1.355
Humerustotalbone	[701,800]	756	1.46	6.0	31.5	3.1	37.0	15.3	7.0	92.23	1.389	0.5283	11.89	1.355
Claviclescapula	[701,800]	756	1.46	6.0	31.4	3.1	37.1	15.3	7.0	92.26	1.389	0.5283	11.89	1.355
Humeruscylindricalshaft	[801,900]	805	1.49	5.8	30.3	3.2	37.6	15.9	7.2	93.56	1.415	0.5273	12.02	1.378
Ribs10th	[801,900]	843	1.52	5.6	23.7	4.0	43.7	15.7	7.3	95.42	1.441	0.5264	12.04	1.400
Cranium	[901,1000]	999	1.61	5.0	21.3	4.0	43.8	17.7	8.1	99.69	1.517	0.5232	12.46	1.466
Mandible	[1101,1200]	1113	1.68	4.6	20.0	4.1	43.8	18.8	8.7	102.35	1.577	0.5211	12.68	1.519
Femurcylindricalshaft	[1201,1300]	1239	1.75	4.2	20.5	3.8	41.8	20.3	9.4	105.13	1.636	0.5190	12.96	1.571
Corticalbone	[1501,1600]	1524	1.92	3.4	15.6	4.2	43.8	22.6	10.4	111.63	1.781	0.5149	13.41	1.698

Range study and comparison of dual to single energy CT material decomposition in tissues

To study the impact of the two different material decomposition approaches of SECT and DECT, a range study was done using the Geant4 based MC code system TOPAS. Monoenergetic infinitely narrow pencil beams were applied to 12 selected tabulated tissues. Three different energies were chosen for protons (117, 183, 222 MeV, 2 × 10⁶ particles) and one energy for carbon ions (350 MeV/u—equivalent to the range of the 183 MeV protons, 10⁵ particles). Default settings were applied for the proton simulations.¹ For the carbon ion simulations, the physics list in Ref. 28 was used with default hadron therapy settings from Geant4 (the g4ion-binarycascade was changed to g4ion-QMD). The dose to medium was scored along the beam axis in 0.1 mm z-steps which implies a lateral integration of absorbed dose in z-slices. Ranges were evaluated at 90% of distal falloff of the Bragg peaks.

Ion ranges in the SECT and DECT predicted material composition were compared to reference range in the ground truth composition. Therefore, three different material decompositions (elemental mass fractions, mass density, and I-value) had to be assigned for each of the 12 materials: one reference assignment with the tabulated values from Table 1, one prediction from the DECT data, and one material assignment from the standard SECT approach. DECT predictions were conducted using reference ϱ_e and Z_eff (Table 1) for the dedicated linear fits for each element [Eq. 3, Table 2] and mass density [Eq. 4, Fig. 3]. Predictions from SECT considered the published CT numbers in combination with mass density fits and a CT number bin table of tissue compositions presented in Ref. 2 (elemental mass fractions of main elements normalized to give the sum of 1).

Table 2.

Statistical properties and fit parameter results of the elemental mass fraction fits 3 for 47 soft tissues and 24 bone tissues from Schneider et al. (Ref. ²) (Table 1). Mean and maximum deviations to the ground truth are given for every element and SECT and DECT prediction separately.

		Zeff < 8.2				Zeff ⩾ 8.2
		H	C	N	O	H	C	N	O	Ca	P
DECT	ai	0.0838	−8.61591	1.38232	8.32961	−0.25201	−11.43361	1.23221	11.23761	−0.61441	−0.16981
	bi	0.0339	−1.79071	0.1104	1.81541	−0.01661	−0.42991	0.04591	0.39021	0.0049	0.00562
	ci	−0.0322	1.29691	−0.1318	−1.30481	0.01321	0.67451	−0.07341	−0.66861	0.04181	0.01251
	di	0.0153	12.30951	−1.21673	−11.26581	0.39051	10.17981	−1.01381	−8.84691	0.25771	0.0326
	R2	0.8117	0.9706	0.6933	0.9621	0.9972	0.9478	0.8510	0.9114	0.9995	0.9982
	mean diff. (pp)	0.1	2.1	0.5	2.3	0.0	1.0	0.1	1.0	0.1	0.1
	max diff. (pp)	0.6	10.2	2.1	12.1	0.2	2.6	0.4	2.5	0.2	0.1
	BIC	−435	−183	−313	−172	−277	−127	−218	−127	−263	−271
SECT	mean diff. (pp)	0.1	4.8	0.8	5.2	0.2	4.3	0.5	4.3	0.4	0.2
	max diff. (pp)	0.8	28.5	4.1	30.7	0.5	9.6	0.8	9.4	1.2	0.5

¹p < 0.01.

²p < 0.05.

³p < 0.1.

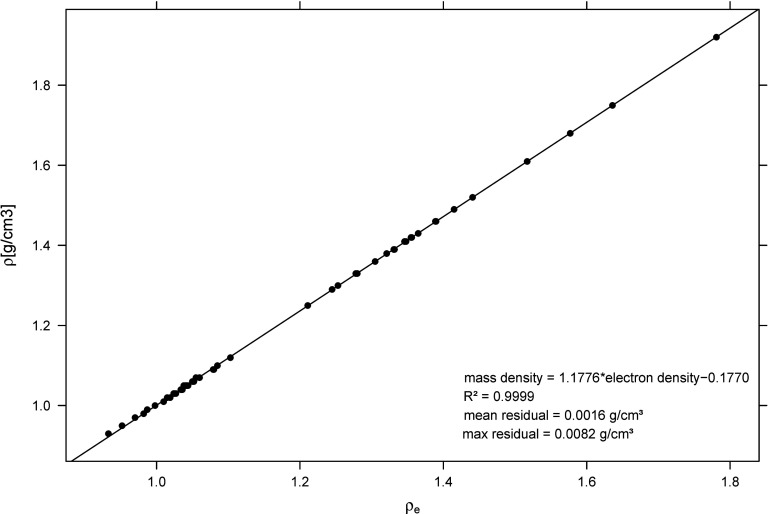
Figure 3.

Mass density ϱ to relative electron density ϱ_e fit. 70 tissues with tabulated composition (Table 1) have been considered. Mean and maximum residuals from the fit to ground truth mass densities are given.

The tissue selection covers a variety of materials in the body of different CT number bins: adipose 3, brain cerebrospinal fluid, brain gray matter, cartilage, D6 L3 cartilage male, femur total bone, humerus total bone, liver 3, muscle 3, urine, and yellow marrow. Most of these selected tissues showed the largest differences in SPR predictions from SECT compared to the ground truth (Fig. 4). One material (“HCO”) was introduced as an artificial compound representing a typical soft tissue and composed of hydrogen (10%), carbon (30%), and oxygen (60%). For “HCO,” the carbon and oxygen mass fractions were varied by ±10% since these elemental mass fractions fluctuate the most in soft tissue and cannot be predicted accurately by SECT.^{16, 20} The mass density and I-value remained constant. 10% variation in the carbon and oxygen amounts estimates the possible variation in the soft tissue region. The artificial “HCO” material enables us to study the effect of variation in these elements on ion ranges.

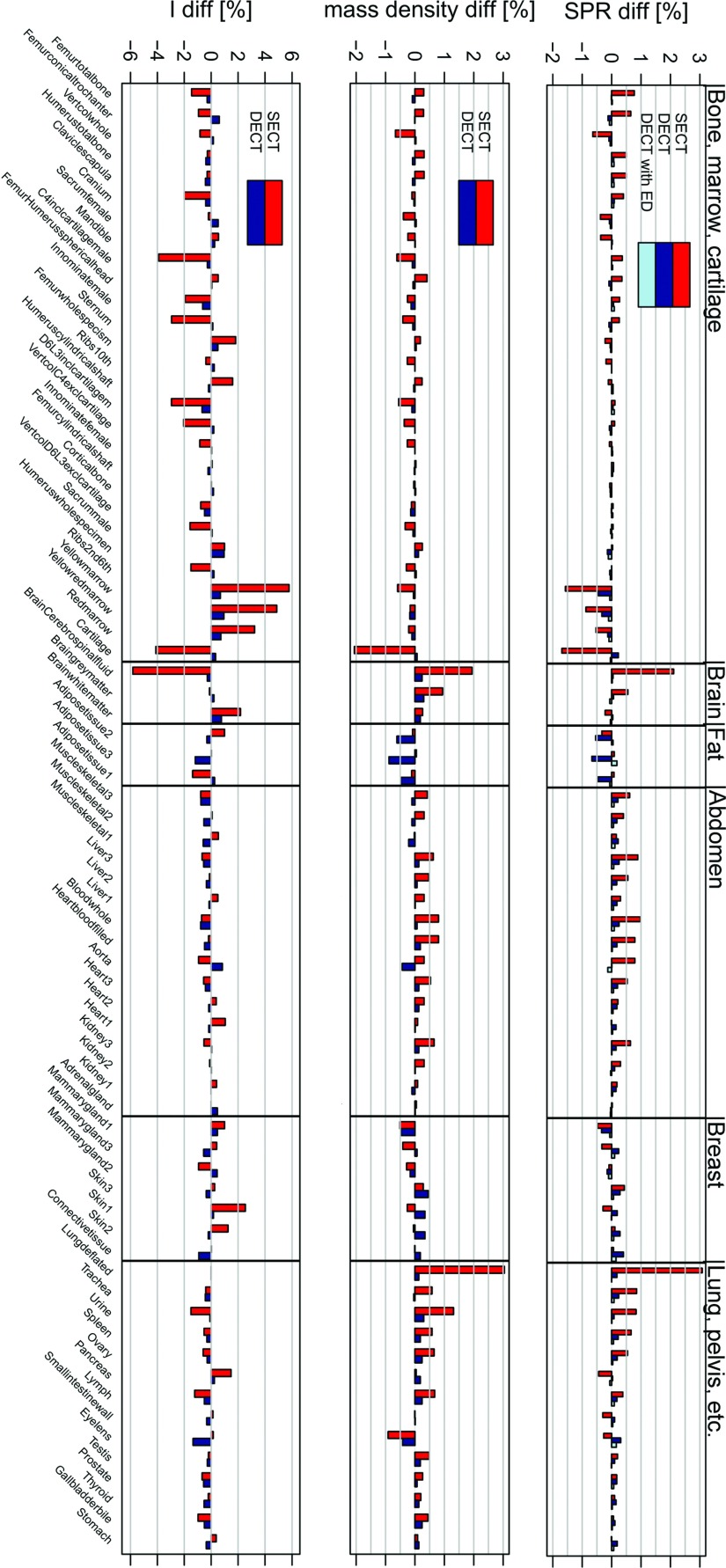
Figure 4.

Differences to ground truths for SPR, mass density, and I-value predictions from SECT and DECT for 71 tissues. With DECT the SPR can also be predicted by taking the ϱ_e directly and the elemental mass fractions for the mean Z/A and I-value prediction (“DECT with ED”).

RESULTS

Figure 4 shows the residuals of the SPR, the mass density, and the I-value predictions from SECT and DECT for the 71 tabulated tissues. Mean and maximum differences to the ground truth compositions are summarized in Table 3.

Table 3.

Mean, maximum, and standard deviations of SPR, mass density, and I-value differences to the reference values for SECT and DECT [71 Schneider et al. tissues (Ref. ²), Table 1]. DECT conversion comprehends two different ways of deriving the SPR: using the ϱ_e directly and elemental mass fractions only for the I-value (“DECT with ϱ_e”) or deriving mass density from ϱ_e and using elemental mass fractions for the I-value and mean Z/A to derive the ϱ_e for the SPR prediction 6.

(mean±sd), max differences
to ground truth [%]	CT modality	Zeff < 8.2	Zeff ⩾ 8.2
SPR	SECT	(0.53 ± 0.58), max: 3.08	(0.27 ± 0.22), max: 0.77
	DECT	(0.21 ± 0.13), max: 0.67	(0.06 ± 0.04), max: 0.14
	DECT with ϱe	(0.06 ± 0.04), max: 0.18	(0.05 ± 0.03), max: 0.11
ϱ	SECT	(0.50 ± 0.57), max: 3.04	(0.30 ± 0.15), max: 0.66
	DECT	(0.20 ± 0.17), max: 0.88	(0.05 ± 0.04), max: 0.14
I	SECT	(1.08 ± 1.42), max: 5.82	(1.26 ± 0.99), max: 3.90
	DECT	(0.44 ± 0.29), max: 1.34	(0.33 ± 0.23), max: 0.96

Extraction of elemental compositions from ϱ_e and Z_eff

Elemental mass fractions were derived by dedicated linear fits for soft and bone tissue and the corresponding statistical properties of the models are presented in Table 2.

In elemental mass fractions, the DECT was found to reduce mean deviations from the ground truth for every element by half compared to SECT (except for soft tissue hydrogen and nitrogen where the effect is slightly smaller). Predictions of the carbon and oxygen mass fractions profit especially from the access to both tissue parameters (ϱ_e, Z_eff): the maximum error in carbon mass fraction compared to the ground truth could be reduced from 29 pp (SECT) to 10 pp with DECT. Differences in the mean oxygen mass fraction compared to the ground truth could be reduced from 5 pp (SECT) to 2 pp for soft tissue. In general, bone tissue seems to profit more from the additional information than does soft tissue.

The linear elemental mass fraction fits from DECT indicate that the carbon and oxygen fluctuations compensate each other. Only one tissue (adipose 3) had a negative predicted elemental mass fraction (nitrogen, −0.4 pp) from DECT data which was set to 0 pp. The final normalization of all predicted elemental mass fractions to 100% caused only minor changes (since the maximum deviation from 100 pp was 1 pp).

Extraction of the mass density from the relative electron density

Mean deviations of mass density could be reduced for soft tissue from (0.5±0.6)% (SECT) to (0.2±0.2)% with DECT. For tabulated bone tissue mean deviations were reduced from (0.3±0.2)% (SECT) to (0.1±0.1)% (DECT).

With DECT the mass density was determined from ϱ_e via one single linear fit over the entire range of tissue from adipose up to cortical bone (due to the direct proportionality of mass to relative electron density). The decreasing $\frac{{⟨Z/A⟩}^{\text{material}}}{Z/A^{{\text{H}}_2\text{O}}}$ [Eq. 1, Table 2] toward cortical bone (due to the decreasing amount of hydrogen) is well represented by the slope greater than 1 [Eq. 4]: the linear fit parameters were a = 1.178 and b = −0.177 with R² = 0.9999. The maximum absolute difference of 0.008 g/cm³ (0.9%) appeared for adipose tissue.

The DECT lung tissue density fit resulted in a difference to the true value of 0.1% for lung in contrast to 3.1% from SECT (where the interpolation was done from air to adipose). The DECT fit interpolation from lung (instead of air) to muscle would only have a small influence on the DECT density fit parameters. The discontinuity of the two fits at the adipose tissue is smaller than 0.02 g/cm³.

I-value prediction

Using the presented DECT method, the maximum I-value difference to the ground truth could be reduced from 5.8% (SECT) to 1.3% for tabulated soft tissue and from 3.9% (SECT) to 1.0% for bone tissue. Mean I-value differences were reduced with DECT by 0.6% for soft and by 0.9% for bone tissue. The DECT approach adjusts the I-value continuously according to the elemental tissue composition derived from the ϱ_e and Z_eff information. The SECT (Ref. ²) approach provides only 24 I-values since the I-value is constant in each of the 24 CT number bins. Schneider et al.² chose the bin width according to the noise estimation in the specific CT number regions (± 50 HU in the bone region, ±15 HU in the soft tissue region).

Stopping power prediction

Stopping power prediction for MC depends on the accuracy of mass density and I-value prediction. The SPR prediction was improved by 0.3% with DECT (mean value of soft and bone tissue) compared to SECT. Maximum SPR differences were reduced with DECT from 3.1% to 0.7% for soft and from 0.8% to 0.1% for bone tissue.

Using the ϱ_e directly to derive the SPR (“DECT with ϱ_e”) is advantageous compared to deriving the mass density and I-value first and subsequently calculating SPR (upper graph in Fig. 4, Table 3).

Range study in tissues

We could not observe a significant energy dependence of absolute range differences for the different proton beams. No significant difference of protons to carbon range differences in percent to reference peak positions was observed. Therefore, this section only summarizes the range residuals for protons.

For brain gray matter and humerus bone, the DECT improved range prediction by 0.5%; in yellow marrow the DECT predicted the range 1.2% better, and in cartilage an improvement in range difference from 1.8% (SECT) to 0.2% with DECT was observed. In liver 3 range differences to reference peak positions could be improved from −0.9% (SECT) to −0.1% (DECT). The highest improvement was observed in brain cerebrospinal fluid from −2.2% (SECT) to −0.1% (DECT). These tissues have either an unusual hydrogen fraction (±0.3 pp) or an unusual carbon and oxygen fraction (±10 pp) compared to other tissues in this interval. Both effects are not well reflected by a single CT number (SECT).

The tissue selection for the MC range study included mainly materials which, according to the SPR predictions, profit the most from DECT compared to SECT (Fig. 4). In muscle and D6L3 bone (male), minor improvements of ≈0.2% were observed. In adipose 3, the DECT range prediction was 0.7% worse compared to the SECT prediction because the mass density prediction was inaccurate due to a higher hydrogen fraction (see also Fig. 5 and Sec. 4B). The HCO material with different oxygen and carbon contents showed a maximum range difference of 0.3% compared to the mean composition.

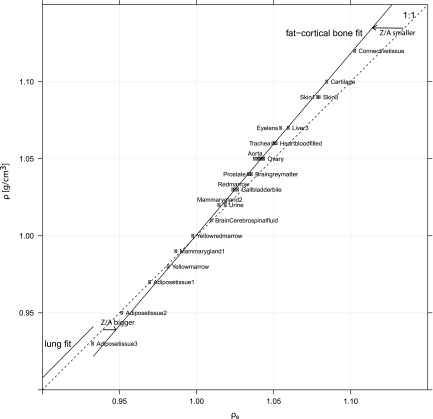
Figure 5.

Mass density to relative electron density fits in the soft tissue region. Shown are the lung and adipose-bone fits (applied in this paper in Sec. 2B), and the identity (1:1). Three different regions appear, mainly determined by different Z/A ratios: lung (Z/A similar to muscle), adipose region (Z/A bigger than water due to increased hydrogen amount), and one region with decreasing Z/A ratio toward cortical bone. An additional fit for the adipose region might improve mass density prediction for hydrogen rich tissues (Secs. 4B, 3E).

Range differences to the ground truth of the MC study with protons and carbons are summarized in Table 4. Corresponding Bragg peaks in the 12 tissues are shown in Fig. 6 for the predicted DECT and SECT tissue composition in comparison to the reference ground truth.

Table 4.

Differences in Bragg peak positions for SECT and DECT compared to reference positions in ground truth tissue decompositions. The “HCO” material denotes an artificial material with 10% different carbon and oxygen mass fractions compared to the reference composition (H = 10%, C = 20%, O = 70%).

		350 MeV/u 12C	117 MeV p	183 MeV p	222 MeV p
Material	Modality	diff [%]	diff [%]	diff [%]	diff [%]
Adiposetissue3	DECT	0.7	0.7	0.7	0.7
Adiposetissue3	SECT	0.0	0.0	0.0	0.0
BrainCerebrospinalfluid	DECT	0.0	0.0	−0.1	0.0
BrainCerebrospinalfluid	SECT	−2.1	−2.2	−2.2	−2.2
Braingraymatter	DECT	−0.1	−0.1	−0.1	0.0
Braingraymatter	SECT	−0.6	−0.6	−0.6	−0.6
Cartilage	DECT	−0.2	−0.2	−0.2	−0.2
Cartilage	SECT	1.8	1.7	1.8	1.7
D6L3inclcartilagem	DECT	0.0	0.0	−0.1	−0.1
D6L3inclcartilagem	SECT	−0.1	−0.1	−0.1	−0.1
Femurtotalbone	DECT	0.0	0.0	0.0	0.0
Femurtotalbone	SECT	−0.8	−0.8	−0.7	−0.8
HCO	C10%O80%	0.1	0.3	0.3	0.3
HCO	C30%O60%	−0.1	−0.3	−0.2	−0.2
Humerustotalbone	DECT	0.0	0.0	0.0	0.0
Humerustotalbone	SECT	−0.5	−0.5	−0.5	−0.5
Liver3	DECT	−0.2	−0.1	−0.1	−0.2
Liver3	SECT	−0.9	−0.8	−0.9	−0.9
Muscleskeletal2	DECT	−0.1	−0.2	−0.2	−0.1
Muscleskeletal2	SECT	−0.4	−0.4	−0.4	−0.3
Urine	DECT	0.0	0.0	−0.1	−0.1
Urine	SECT	−0.7	−0.8	−0.8	−0.8
Yellowmarrow	DECT	0.6	0.6	0.6	0.5
Yellowmarrow	SECT	1.7	1.8	1.7	1.7

Figure 6.

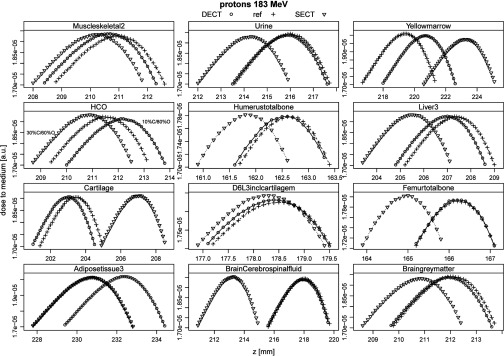
Proton Bragg peaks in 12 different tissues. Compositions were predicted by SECT and DECT. Ranges (90% distal falloff) were compared to reference ranges and are summarized in Table 4. For the HCO material, the carbon and oxygen mass fractions were varied by 10%, reference composition was H = 10%, C = 20%, O = 70%.

DISCUSSION

Extraction of elemental compositions from ϱ_e and Z_eff

p-values and Bayesian information criterion values (BIC values) in Table 2 suggest that some elements do profit more from the additional Z_eff information than others. The model parameters further show that for some elements (soft tissue hydrogen and nitrogen, bone calcium) it might not be necessary to take into account the Z_eff information or the interaction term. This fact is underscored by a low BIC value which penalizes the model complexity (hence the number of parameters). The cross correlation term (ϱ_e · Z_eff) is important for elements expressing different slopes depending on ϱ_e or Z_eff (e.g., soft tissue carbon and oxygen content in Fig. 2).

Different methods of tissue decomposition from DECT data are presented in the literature. Bazalova et al.⁶ described an elemental mass fraction assignment of tissue equivalent inserts by segmenting the ϱ_e and Z_eff space. Improvements (up to 3%–17%) of dose calculation in a phantom for low and high energy photon and electron beams with DECT data compared to the conventional SECT based approach were observed. Malusek et al.¹⁴ studied the decomposition of soft tissue to water, lipid, and protein for brachytherapy. A three-material decomposition method in the mass energy absorption and in the mass attenuation space was presented, resulting in differences smaller than 2% for both mass attenuation and energy absorption coefficients. With the three material decomposition negative elemental mass fractions were assigned for some studied soft tissues which could not be handled by MC systems. Landry et al.¹⁶ presented a method to derive carbon and oxygen mass fractions, which are crucial for PET and prompt gamma based ion treatment verification. The best results were found by assigning elemental mass fractions to a reference tissue composition which expresses the minimal Mahalanobis distance in the ϱ_e and Z_eff space. DECT based carbon and oxygen mass fractions assignments were superior to SECT based schemes also in noise associated DECT data.

In contrast, this paper presents a method that continuously assigns elemental mass fractions. As said in Ref. 11 human tissue can have significant variations dependent on health status, age, and sex. The linear fits in the ϱ_e, Z_eff, and ϱ_e · Z_eff are also able to reflect variations of compositions between reference tissues.

Influence of noise in the ϱ_e and Z_eff on elemental mass fraction predictions

Patients’ CT data are usually associated with image noise and various artifacts like partial-volume effects of different tissues on transition edges and beam hardening effects. Z_eff suffers more from noise in real DECT images than the ϱ_e (Refs. ⁶ and ⁸) and the uncertainty is higher in Z_eff. To test the presented method with realistic noise hampering, the base data (ϱ_e and Z_eff) for the elemental mass fraction fits were associated with noise. A uniform Gaussian distributed noise with one standard deviation of 0.01 units of ϱ_e and 0.2 units of Z_eff (representing two times the standard deviation measured in Ref. 10) was applied in the simulation of 1000 measurements of every material (Table 1). This noise setting represents a worst-case scenario since noise in ϱ_e and Z_eff is correlated⁸ and a covariance in both quantities would reduce the errors. Resultant mean and standard deviations of elemental mass fraction predictions from noisy ϱ_e and Z_eff pairs, in comparison to reference values, are shown in Fig. 7. Standard deviations related to noise are elevated in the main elements (carbon and oxygen) of tissues. Mean standard deviations in mass predictions of 0.1% H, 9.9% C, 0.9% N, 10.3% O, 1.1% P, and 0.2% Ca can be observed for the DECT based approach. In comparison, Landry et al.¹⁶ presented deviations in the order of 5% for the carbon and oxygen mass fraction assignments from noise associated DECT data simulated at a dose level of 40 mGy and assuming an iterative CT reconstruction algorithm which reduces noise. It was observed that DECT profits more from decreasing image noise than SECT up to a systematic shift of ±5 HU where the theoretical benefit from DECT is undermined.¹⁶

Figure 7.

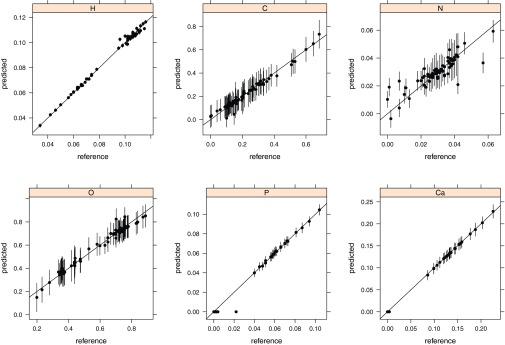
Resultant mean values and standard deviations of elemental mass fraction predictions from simulated ϱ_e and Z_eff pairs (n = 1000) associated with a Gaussian distributed noise with one standard deviation of 0.01 units of ϱ_e and 0.2 units of Z_eff (reference values in Table 1).

Extraction of the mass density from the relative electron density

The ϱ_e from DECT reflects the major influence on the stopping power for ions and is an appropriate candidate for the prediction of mass density. This result was also observed in Refs. ²⁹ and ³⁰. The key factor is mass density prediction from ϱ_e instead of using a single CT number (HU, SECT). The SECT mass density prediction suffers from the nonlinearity of the photon attenuation coefficient and the relation of HU-to-ϱ is especially nontrivial in the soft tissue region from [−200 HU, 200 HU]. Here, different elemental compositions and mass densities might express similar CT number and vice versa. This results in CT number ambiguities and five different mass density fits that cover the entire tissue spectrum with one discontinuity of 0.04 g/cm³ at the transition from soft to bone tissue. While the CT number reflects influences from the ϱ_e and the Z_eff, the ϱ_e indicates a better predictor for mass density due to the independence of the Z_eff.

The ⟨Z/A⟩ ratio is the most important influence factor for the DECT mass density fit determination from ϱ_e and depends mainly on the hydrogen mass fraction in tissues. Instead of one single fit—from adipose tissue to cortical bone—and one fit for lung tissue, three mass density fits might be a better solution for the DECT approach. In Fig. 5, three different ⟨Z/A⟩ tissue regions appear. For the lung tissue region up to adipose, the ⟨Z/A⟩ is similar to muscle. Here, an interpolation from lung to muscle instead of air to adipose is favored as mentioned before. The second region would include all hydrogen rich tissues having a higher ⟨Z/A⟩ than water (i.e., adipose, yellow marrow). This fit could reduce maximum mass density residuals for adipose tissue (Fig. 4). The last interval would begin at ϱ = 1 g/cm³ and ϱ_e = 1. From this point, the ⟨Z/A⟩ continuously decreases and one fit is sufficient. Discontinuities at transitions would be below 0.01 g/cm³.

For SECT, it would be better to interpolate the HU-to-ϱ relation from lung to muscle tissue (having the same ⟨Z/A⟩ ratio) instead of air-adipose, since the current applied fit mentioned in Ref. 2 results in a mass density residual of 3% for lung tissue.

I-value and stopping power prediction

The uncertainty in the I-value prediction can add up or compensate 6 the uncertainty in mass density which can be well observed in Fig. 4. For the SECT approach, the maximum I-value difference from the ground truth (tabulated composition) is 5.8% (DECT: 1.3 %). 10% uncertainty in the I-value translates roughly in 1% of SPR uncertainty.^{18, 31} However, Fig. 4 shows that the I-value uncertainty has only a secondary order effect on the SPR due to the logarithmic term in the Bethe formula. The assignment of the correct mass density is crucial for the calculation of the ϱ_e and therefore the accuracy of the SPR. Residual errors due to the single linear fit from ϱ_e to the mass density can be improved by 0.15% by using the ϱ_e directly for the SPR calculation. Largest residual mass errors from the ϱ_e fit appear in the soft tissue region (adipose tissue).

Range study in tissues

Range differences in tabulated tissues (Table 4) represent basically SPR differences from Fig. 4 since ion range is determined by electronic energy loss (for therapeutic ion energies) and nuclear interactions have a negligible influence on ranges. Due to this fact, analytical planning systems have one common CT number look-up table for proton and carbon ions for the translation from HU to SPR or water-equivalent path length (WEPL).

For range prediction, the correct elemental composition, as well as the correct carbon and oxygen mass fractions, are not as important as the mass density prediction and, respectively, the ϱ_e. Mass and electron density are related through the ⟨Z/A⟩ 1, which changes mainly with the hydrogen mass fraction in the compounds. As stressed before, using the ϱ_e directly to predict SPR avoids the detour through mass density. Mass density would only be needed to assign cross sections continuously according the approach presented by Schneider et al.²

Besides the accurate stopping power prediction, accurate elemental mass fraction predictions might become important for low energy brachytherapy,³² prompt gamma response, and PET range verification (especially carbon and oxygen mass fractions¹⁶) for in vivo range verification in particle therapy.

CONCLUSIONS

This paper presents a method for extracting tissue composition and mass density from DECT data for Monte Carlo dose calculation. The approach includes simple linear fits in the ϱ_e and Z_eff from tabulated tissue compositions.

The study shows that correct mass density prediction is crucial for accurate SPR prediction. Potential improvements of range predictions in the order of 0.1%–2.1% for selected tissues were observed in MC range studies with protons and carbon ions. Furthermore, the DECT is capable to predict elemental mass fractions significantly better than the SECT approach for the majority of tabulated tissues (mean and maximum differences were reduced by at least 50%) in the noiseless case. Noise associated ϱ_e and Z_eff pairs resulted in mean standard deviations of 10% in the carbon and oxygen mass fraction predictions. Further investigations are needed to quantify the potential benefit from DECT compared to SECT in measured image data associated with artifacts and noise.

Reducing uncertainties in mass density and elemental composition would lead to a reduction of range uncertainty (SPR) and target margins might ultimately be reduced. Better knowledge on tissue decomposition has a potential clinical impact on ion therapy and might also be applied in other radiotherapy disciplines which are sensitive to correct elemental tissue compositions.