Abstract
There has been consistent interest among speech signal processing researchers in the accurate estimation of the fundamental frequency () of speech signals. This study examines ten estimation algorithms (some well-established and some proposed more recently) to determine which of these algorithms is, on average, better able to estimate in the sustained vowel /a/. Moreover, a robust method for adaptively weighting the estimates of individual estimation algorithms based on quality and performance measures is proposed, using an adaptive Kalman filter (KF) framework. The accuracy of the algorithms is validated using (a) a database of 117 synthetic realistic phonations obtained using a sophisticated physiological model of speech production and (b) a database of 65 recordings of human phonations where the glottal cycles are calculated from electroglottograph signals. On average, the sawtooth waveform inspired pitch estimator and the nearly defect-free algorithms provided the best individual estimates, and the proposed KF approach resulted in a ∼16% improvement in accuracy over the best single estimation algorithm. These findings may be useful in speech signal processing applications where sustained vowels are used to assess vocal quality, when very accurate estimation is required.
INTRODUCTION
The estimation of the fundamental frequency () is a critical problem in the acoustic characterization of speech signals.1 For example, it is found in speech coding in communications, automatic speaker recognition, analysis of speech perception, and in the assessment of speech disorders.2 Typically, is evaluated over short-term time intervals and the time course of the values over the entire speech signal is known as time series (or contour). The existing difficulties in accurate estimation are well reported in the speech signal processing literature, with an excellent summary found in a study authored by Talkin.3 According to Talkin these difficulties include:3 (1) is time-varying, and may change between vocal cycles, (2) sub-harmonics (components of a waveform whose frequency is an integer fraction of the ) appear frequently, (3) may vary widely over successive vocal cycles, although often large variations are assumed to be artifacts of the estimation algorithm because such abrupt changes seem fairly rare, (4) vocal tract resonances affect the vocal folds (that is, there is feedback from the vocal tract to the vocal folds2) resulting in harmonics which are multiples of the actual , (5) it is difficult to estimate at voice onset and offset (due to transient effects), (6) there is considerable inter-observer variability on the actual values of , and (7) periodic background noise might be challenging to differentiate from breathy voiced speech (their spectra may be similar). Additional problems include differentiating between voiced and unvoiced segments of speech, and specific cases which are very hard to deal with (e.g., where the signal is of extremely short duration).3
A related task to estimation is the determination of pitch, which is the psycho-acoustic equivalent of . We emphasize that the focus of this study is estimation. Some researchers often use the terms pitch detection algorithm (PDA) and estimation algorithm interchangeably; strictly speaking, PDA is a misnomer because pitch is inherently a continuous phenomenon and estimating the fundamental frequency of a signal is not a detection problem. For this reason we will only use the expression “ estimation algorithm” to refer to the algorithms described in this study.
The assessment of vocal performance is typically achieved using either sustained vowel phonations or running speech.2 Clinical practice has shown that the use of sustained vowels, which avoids articulatory and other confounding factors in running speech, is very practical and sufficient for the assessment of general vocal performance; we refer to Titze and references therein for more details.2 In voice quality assessment sessions, subjects are often requested to produce the open back unrounded vowel /a/ at a comfortable pitch for as long and as steadily as possible.2 This vowel provides an open vocal tract configuration where the mouth is maximally open compared to other vowels, which minimizes the reflected air pulse back to the vocal folds (therefore, there is low acoustic interaction between the vocal folds and the vocal tract).2 Using the sustained vowel /a/ instead of running speech alleviates some of the difficulties highlighted previously, by avoiding (a) the need to characterize frames (segments of the original speech signal, usually pre-specified with a duration of a few milliseconds) as voiced or unvoiced, (b) reducing the range of possible values, and (c) minimizing the possible masking effects formants may have on during running speech (for example, when the formants of a word complicate the identification of because they may match its multiples—a problem often referred to as pitch halving or pitch doubling).2
Roark4 highlighted the existence of more than 70 algorithms to estimate , which reflects both the importance and difficulty of the problem. Roark emphasized that there is no simple definition of if it does not just refer to the period, and demonstrated that simple disturbances in the parameters of typical estimation algorithms may lead to divergent results. Overall, as Talkin suggests,3 it is probably impossible to find a universally optimal estimation algorithm for all applications. Some estimation algorithms may be better suited to particular applications, depending on the type of speech signals (e.g., conversational signals or singing); computational considerations may also need to be considered (for example, in speech coding applications).
Research comparing the accuracy of different estimation algorithms is not new in the speech literature.5, 6, 7, 8 However, most of these comparative studies focused on healthy, or mildly dysphonic voices. For example, Titze and Liang6 studied three estimation algorithms when perturbations in were lower than 5%. Parsa and Jamieson5 were the first to investigate the performance of various estimation algorithms in the presence of vocal disorders, a topic which has received comparatively little attention because the potentially fraught task of accurately determining is exacerbated in vocal disorders.2 Parsa and Jamieson5 ran a series of experiments to investigate the accuracy of estimation algorithms in determining the of the sustained vowel /a/. They produced synthetic signals using a stylized model which attempted to simulate the main characteristics of the vocal production mechanism generating the sustained vowel /a/. This simple model does not closely represent physiologically plausible characteristics of voice pathologies, as it is based on linear filtering of a series of impulses with added noise and perturbations. Furthermore, many more sophisticated estimation algorithms have been proposed since the publication of Parsa and Jamieson's study in 1999.5 More recently (2007), Jang et al.7 compared seven estimation algorithms in pathological voices using the sustained vowel /a/, where the ground truth time series was obtained manually. However, the estimation algorithms investigated by Jang et al.7 do not reflect contemporary advances (the two most recent estimation algorithms in that study were proposed in 1993 and 2002).
Some studies have evaluated the performance of software tools in accurately estimating the ground truth jitter ( perturbations), which can be considered a proxy for the estimation of , see, for example, Manfredi et al.8 One problem with this approach is that jitter lacks an unequivocal mathematical definition;2 another is that the time windows (reference time instances) used by each algorithm to obtain the time series may differ, which complicates the interpretation of the results. Moreover, as Parsa and Jamieson5 correctly argued, it is possible to have the same jitter values for different time series: in other words, there is no unique mapping from jitter to time series. See also the extended criticism by Ferrer et al.9 Manfredi et al.8 synthesized ten sustained vowel /a/ phonations with a physiologically plausible model and compared four estimation algorithms in their ability to detect jitter. Although this methodology can provide a general impression of the accuracy of estimation, we agree with Parsa and Jamieson5 and Ferrer et al.9 that assessing jitter does not directly quantify the accuracy of estimation, and should be avoided when comparing the performance of the estimation algorithms. Moreover, compared to the study of Manfredi et al.8 we examine a considerably larger database of speech signals, and a more comprehensive set of estimation algorithms.
The motivation for this study comes from our research on objective quantification of voice disorders using speech signal processing algorithms (dysphonia measures) to process sustained vowel /a/ phonations.10, 11, 12, 13 Since disordered voices may be highly aperiodic or even stochastic,2 the task of estimation algorithms is further complicated because some algorithms rely heavily on periodicity assumptions and their performance is known to degrade in the presence of noise.5 The dysphonia measures we typically investigate include perturbation (jitter variants),10 and some dysphonia measures which explicitly require estimates as an input;2 we refer to Tsanas et al.10 and references therein for algorithmic details. Thus, it can be inferred that those dysphonia measures which rely on estimates would benefit from accurate data.10 Moreover, researchers have attributed, at least partly, the success of some dysphonia measures to the fact that they quantify properties of the signal without requiring prior computation of estimates.10, 11, 14 We clarify that although our main research interests are in pathological voice assessment, the aim of the present study is more general: obtaining accurate estimates can be beneficial in many diverse applications which rely on speech signal processing.1, 2 Therefore, the estimates computed here are not intended to be used to compute any dysphonia measures.
Newly proposed estimation algorithms have been validated in the following scenarios: (a) values have been provided by expert speech scientists following visual inspection of the glottal cycles from plots of the signal, (b) using electroglottography (EGG) (a device placed externally to the larynx records EGG, and the glottal cycles are detected from the EGG signal), and (c) using synthetic signals where the ground truth values are known in advance. All these validation approaches have been used to assess the performance of estimation algorithms, but each approach has its limitations. First, speech experts observing a plot of a signal often do not agree on the exact length of each vocal period,3 and hence it is not clear how to define the ground truth unambiguously. Similarly, EGGs may provide faulty estimates of (particularly for pathological voices) which are often corrected manually, casting doubt on the validity of this approach.15, 16 Therefore, we argue that the third approach, using synthetic signals where the ground truth is known in advance, may be the most appropriate method for establishing the accuracy of estimation algorithms, if signals that closely resemble actual speech signals can be generated. The ability to accurately replicate disordered voice signals is related to the nature of the model used to synthesize the signals, and its capacity to mimic the origin and effects of different voice disorders. On the other hand, it could be argued that the physiological speech production model might not be able to adequately express some diverse characteristics which appear in actual speech signals, or that the error caused by the speech production model may be more severe than the errors in the EGG method. This is because, in general, physiological models attempt to develop a mathematical framework to replicate the observed data, and therefore are inherently limited both by the finiteness and measurement error of the collected data (due to sources of physiological and environmental variability that affect data recorded in real-world experiments), and also the mathematical assumptions used in the model. Hence, in practice it may be useful to also investigate a database with actual signals where simultaneous EGG recordings are available.
In this study, we use both realistic synthetic signals where the ground truth is exactly known, and also a database with actual speech signals where the ground truth is derived by simultaneous EGG measurements. The physiological model of speech production generated realistic sustained vowel /a/ signals where the values are determined from the glottal closure instants, i.e., vocal fold collision instants. If there is any type of voicing, the minimum glottal area signal (even under incomplete closure) captures all relevant physical interactions (tissue dynamics, airflow, and acoustics), and determines the periodicity of the speech signal.17 This is a more stable and reliable approach than using just the glottal airflow or radiated acoustic pressure at the lips because in those cases many additional components can impede the estimation process (e.g., added harmonic components due to acoustic coupling, noise, and other acoustic sources). Specifically, we used a numerical lumped-mass model which was described in detail by Zañartu.18 The model was capable of mimicking various normal, hyper-functional (inappropriate patterns of vocal behavior that are likely to result in organic voice disorders) and pathological voices, where the exact system fluctuations were known.
The aim of this study is twofold: (a) to explore the accuracy of ten established estimation algorithms (most of which were relatively recently proposed) in estimating in both healthy and disordered voices and (b) to investigate the potential of combining the outputs of the estimation algorithms aimed at exploiting the best qualities from each, and improve estimates. With the exception of a simple combination of three estimation algorithms,10 we are not aware of any systematic investigation into combining the outputs of estimation algorithms in the speech literature. The combination of the estimation algorithms can take place in a supervised learning setting and is known as ensemble learning in the statistical machine learning literature. Alternatively, the combination of information from various sources (here the estimation algorithms) in an unsupervised learning setting is known as information fusion (or data fusion). Ensemble learning and information fusion are particularly successful in contexts where different methods capture different characteristics of the data, and have shown great promise in diverse applications.19, 20 In this study, we extend a recently proposed information fusion framework, which relies on the adaptive Kalman filter (KF) and algorithmic robustness metrics, to weigh the estimates from each of the ten estimation algorithms. We demonstrate the adaptive KF fusion framework for estimating outperforms, on average, the single best estimation algorithm. Furthermore, we demonstrate the KF fusion approach provides robust and accurate estimates for both noisy and low sampling frequency speech signals (conditions which cause considerable performance degradation in terms of accurate estimation for most estimation algorithms).
The paper is organized as follows. In Sec. 2 we describe the data used in this study, including a brief description of the physiological model which was used to generate the simulated phonations. In Sec. 3 we review the estimation algorithms used in this study, and describe in detail the information fusion scheme that combines the individual algorithms. Section 4 compares the performance of the estimation algorithms (both individually and their combinations). Finally, Sec. 5 summarizes the main findings, outlines the limitations of the current approach, and suggests potential areas of interest for future research.
DATA
Synthetic data: Model used to generate sustained vowel /a/ signals and computation of ground truth F0 time series
The physiological model used to generate the sustained vowel /a/ signals was described in detail by Zañartu;18 here we summarize the mechanisms. This physiological model is an extended version of the original body-cover model of the vocal folds by Story and Titze,21 and allows a realistic generation of normal and pathological voices. Asymmetric vibration of the vocal folds was controlled by a single factor proposed by Steinecke and Herzel22 for modeling superior nerve paralysis. The material properties of the vocal folds and their dependence on muscle activation followed Titze and Story,23 with an extension to include neural fluctuations that affect muscle activity. These fluctuations were modeled as a zero-mean, Gaussian white noise signal. They were processed by a low-pass, finite-impulse response filter. The flow model incorporated the effects of asymmetric pressure loading.24 The airflow solver allowed for interactions with the surrounding sound pressures at the glottis and the inclusion of incomplete glottal closure from a posterior glottal opening. This model of incomplete glottal closure enhanced the ability to represent voiced speech, as it is commonly observed in both normal and pathological voices.25 The effects of organic pathologies (e.g., polyps and nodules) were modeled as described by Kuo,26 including an additional component to reduce the vocal fold contact.24 Sound propagation was simulated using waveguide models of the supraglottal and subglottal tracts, with waveguide geometries determined from previous studies.27 In addition, the wave reflection model included the mouth radiation impedance and different loss factors for the subglottal and supraglottal tracts, which allowed for nonlinear interactions between the vocal folds and the vocal tract, and also affected the vocal fold dynamics.28 A time step corresponding to a sampling frequency of 44.1 kHz was used in a fourth order Runge–Kutta ordinary differential equation solver.
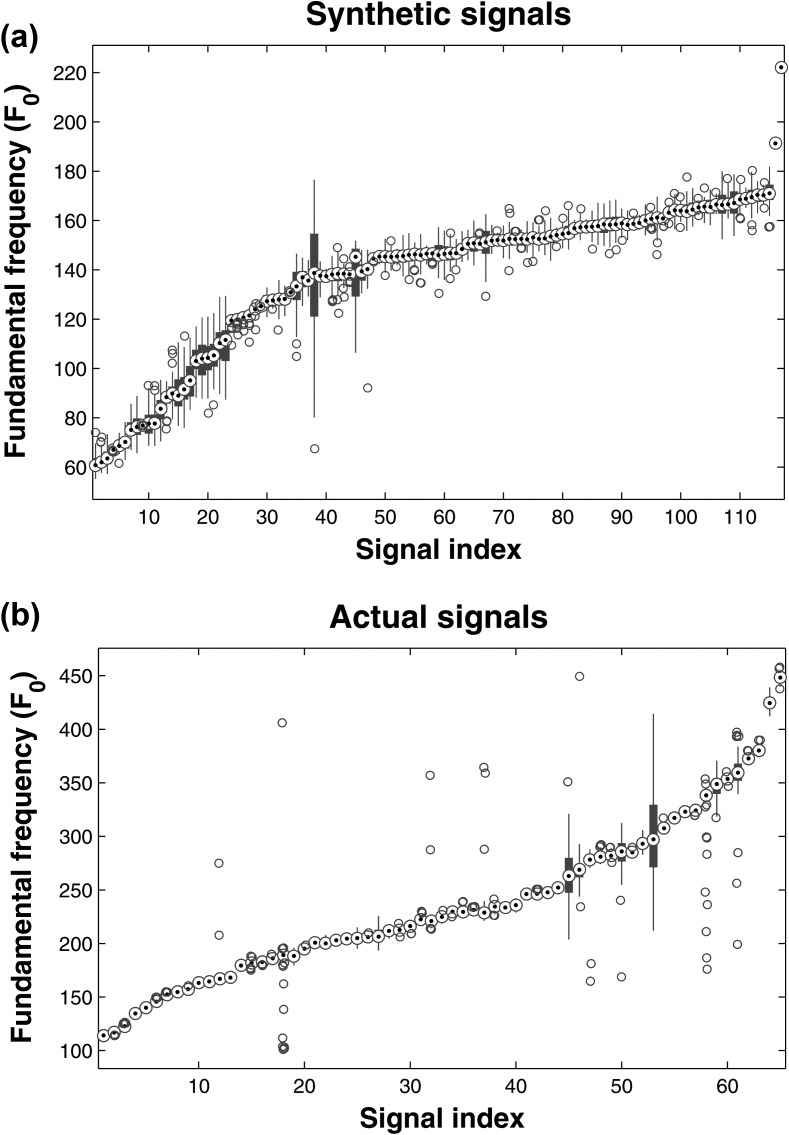
Each simulation produced 1 s of voiced speech uttering a sustained vowel /a/, where initial transients (typically about four periods) do not provide reliable information regarding the oscillating pattern of the vocal folds (until the model reaches a stable state depending on the initial conditions). To ensure that the ground truth is reliable, the initial 50 ms of each signal were discarded from further analysis. In total, 125 sustained vowel /a/ signals were generated. Cases which resulted in unnatural-sounding voices (following aural inspection by A.T.) were removed before any analysis. Thus, we processed 117 signals which were used to evaluate the performance of the estimation algorithms. The period of each cycle was computed from the instant the vocal folds begin to separate, after vocal fold collision was present (if any) or immediately after the glottal area was minimized (in cases where no vocal fold collision took place). The distributions of the ground truth values for all signals are summarized in Fig. 1, which presents the median and the interquartile range values for each speech signal. We remark that the speech signals were generated over a relatively wide range of possible values, with variable fluctuations (jitter). Care was taken to generate signals using a large range of average for each phonation (60–220 Hz), including 20 signals with low (<100 Hz), because recent research suggests such phonations are notoriously difficult for most of the commonly used estimation algorithms.29
Figure 1.
(Color online) Summary of ground truth values for (a) 117 speech signals generated using a physiological model of speech production (synthetic signals) and (b) 65 actual speech signals where simultaneous EGG recordings were available. The middle point represents the median and the bars represent the interquartile range. For convenience in presentation, the signals are sorted in ascending order of . Outliers (if any) are marked individually with circles.
The synthetic speech signals are available on request by contacting the first author.
Database with actual speech signals and computation of F0 based on EGG
We used a database consisting of 65 sustained vowel /a/ phonations from 14 subjects diagnosed with Parkinson's disease (PD). They all had typical PD voice and speech characteristics as determined by an experienced speech-language pathologist, i.e., reduced loudness, monotone, breathy, hoarse voice, or imprecise articulation. The subjects' enrolment in this study and all recruiting materials were approved by an independent institutional review board. The 14 PD subjects (8 males, 6 females), had an age range of 51 to 69 years (mean ± standard deviation: 61.9 ± 6.5 years). They were instructed to produce phonations in three tasks regarding pitch: comfortable pitch, high pitch, and low pitch, subjectively determined by each subject. The sustained vowel phonations were recorded using a head-mounted microphone (DACOMEX-059210, which is omnidirectional and has a flat frequency response with a bandwidth of 20 to 20 kHz) in a double-walled, sound-attenuated room. The voice signals were amplified using the M-Audio Mobile Pre model and sampled at 44.1 kHz with 16 bits of resolution (using the Tascam US-122mkII A/D converter). The data were recorded using a Sony Vaio computer which had an Intel display audio and Conexant 20672 SmartAudio HD device (high frequency cut-off 20 kHz). Simultaneously with the recording of the sustained vowels, EGGs were recorded using the VoceVista model. The glottal cycles were automatically determined using the EGGs with the sigma algorithm,30 which almost always correctly identifies the true vocal cycles. Visual inspection of the signals and their associated EGGs verified that the sigma algorithm was indeed very accurate at determining the vocal cycles.
METHODS
This section is comprised of (a) a review of ten widely used estimation algorithms which were tested in this study, (b) a description of a novel combination scheme using the outputs of multiple estimation algorithms, and (c) a description of the framework for validating the estimation algorithms. All the simulations and computations were performed using the matlab software package, although in some cases interfaces to other programs were used [for example, to access praat (Ref. 31) which is described in Sec. 3A2].
F0 estimation algorithms
Overall, there may be no single best estimation algorithm for all applications.3 Here, we describe some of the most established, longstanding algorithms, and some more recent, promising approaches. We tested widely used estimation algorithms for which implementations were available and hence are convenient for testing; we do not claim to have made an exhaustive comparison of the full range of estimation algorithms. There have been various approaches attempting to categorize estimation algorithms, mainly for methodological presentation purposes.3 One useful way is to cluster them as time-domain approaches (most time-domain approaches rely on autocorrelation, such as praat presented in Sec. 3A1, and some rely on cross-correlation such as rapt presented in Sec. 3A3), or frequency domain approaches (frequency spectrum and cepstral approaches). A further distinction for time-domain approaches can be made if estimation algorithms work on windows (frames), thus providing local estimates, or detect single glottal cycles, thus providing instantaneous estimates. The estimation algorithms that use short time windows are typically applied to a small, pre-specified segment of the signal (e.g., 10 ms), and the estimates are obtained by a sliding window method. A further differentiation of time-domain estimation algorithms is the method used to estimate , the most common being peak picking (for example, identifying successive negative or positive peaks) and waveform matching (matching cycle to cycle waveforms). The overall consensus is in favor of waveform matching because of its improved robustness against noise.32 We stress that the above general description is not the only practical categorization framework, and in fact some estimation algorithms can equally well be interpreted as time- or frequency-domain approaches (for example, see ndf presented in Sec. 3A8).
Many of the estimation algorithms we examine here have three main stages:3 (a) pre-processing, (b) identification of possible candidates, and (c) post-processing to decide on the final estimate. The pre-processing step depends on the actual estimation algorithm requirements. One example of pre-processing is low-pass filtering of the speech signal to remove formants. This step is useful in general, but can also introduce problematic artifacts: reducing the bandwidth increases the inter-sample correlation and could be detrimental to estimation algorithms which detect periodicity using correlations.3 Post-processing is typically used to avoid sudden jumps in successive estimates, which may not be physiologically plausible (but this is not universally true in all applications). One straightforward and simple post-processing approach is to use running median filtering (for example, see yin presented in Sec. 3A6) or dynamic programming (for example, see dypsa presented in Sec. 3A1) to refine the estimates; we will see both approaches used in the description of specific estimation algorithms.
In all cases we used the default settings for the estimation algorithms. To ensure a fair comparison, where appropriate we set the search range between 50 and 500 Hz. Although the expected physical maximum cannot, realistically, be so high in the case of comfortably produced sustained vowel /a/ signals, we wanted to test the full range of inputs to the estimation algorithms. Since this study only deals with voiced speech and there is no need to identify whether parts of the speech signal are voiced or unvoiced, that (very interesting) aspect of the estimation algorithms will not be addressed here. To avoid putting those estimation algorithms that inherently detect voiced or unvoiced frames at disadvantage, where possible this option was disabled.
dypsa
The dynamic programming projected phase-slope algorithm (dypsa) (Ref. 33) is the only estimation algorithm used in this study which aims to directly identify the glottal closure instances (i.e., works on the vocal cycles and not on time windows). It identifies candidate glottal closure events and uses dynamic programming to select the most plausible event by finding the optimum compromise for a set of criteria (such as minimizing the time difference between successive glottal cycles).
praat (two algorithms, praat1 and praat2)
The praat estimation algorithm31 was originally proposed by Boersma.34 It can be viewed as a time-domain approach which relies on autocorrelation to compute estimates. The signal is divided into frames using an appropriate window function to minimize spectral leakage, and estimates are provided for each frame. praat normalizes the autocorrelation of the signal by dividing the autocorrelation of the signal with the autocorrelation of the window function. The original algorithm34 used the Hanning window, but Boersma has later indicated that praat provides improved estimates when the Gaussian window is used. We tested both approaches: we call praat1 the estimation algorithm using the Hanning window and praat2 the algorithm using the Gaussian window. praat uses post-processing to reduce large changes in successive estimates (post-processing was used for both praat1 and praat2).
rapt
rapt is a time-domain estimation algorithm (like praat) but it uses the normalized cross-correlation instead of the autocorrelation function. It was originally proposed by Talkin.3rapt compares frames of the original speech signal with sub-sampled frames of the original signal, and attempts to identify the time delay where the maxima of the cross-correlation is closest to 1 (excepting the zero time lag which is 1 by definition). Once candidates for each frame have been chosen, rapt uses dynamic programming to determine the most likely estimate for each frame.
shrp
shrp computes estimates in the frequency domain using the sub-harmonics to harmonics ratio, and aims to estimate pitch. It was proposed by Sun35 who found in a series of experiments that pitch is perceived differently when sub-harmonics in a signal increase. Therefore, he proposed a criterion for analyzing the spectral peaks that should be used to determine pitch.
swipe
The sawtooth waveform inspired pitch estimator (swipe) algorithm was recently proposed by Camacho and Harris,36 and as with shrp, it is a frequency domain approach that estimates pitch. Instead of focusing solely on harmonic locations (peaks in the spectrum) as in shrp, swipe uses the available information on the entire spectrum using kernels. swipe identifies the harmonics in the square root of the spectrum and imposes kernels with decaying weights on the detected harmonic locations. We clarify that here we used swipe′, an extension of swipe which was also proposed in the original study,36 but we refer to it as swipe for notational simplicity.
yin
Conceptually, yin is similar to praat and relies on the autocorrelation function37 to provide estimates at pre-specified time intervals. It uses a modified version of the average squared difference function: expanding the squared expression results in the autocorrelation function and two additional corrective terms. The authors demonstrated that these two additional terms account for yin's improved performance over the naive use of autocorrelation. yin uses a final post-processing similar to median filtering to avoid spurious peaks in successive estimates.
tempo
The tempo algorithm was proposed by Kawahara et al.38 and uses the log frequency domain. A filter bank of equally spaced band-pass Gabor filters is used to map the central filter frequency to the instantaneous frequency of the filter outputs. The original proposal suggested using 24 Gabor filters in an octave, and the instantaneous angular frequency is obtained using the Hilbert transform.
ndf
The nearly defect-free (ndf) estimation algorithm was proposed by Kawahara et al.39 and relies on both time-domain and frequency-domain information to provide estimates. The algorithm combines two components to determine candidate values: (a) an instantaneous frequency based-extractor and (b) a period-based extractor. The frequency-based extractor is similar to tempo, and the period-based extractor computes sub-band autocorrelations using the fast Fourier transform, where the power spectra are initially normalized by their spectral envelope prior to the computation of the autocorrelations. Then, the candidates from the instantaneous frequency and period-based extractors are mixed using the normalized empirical distribution of side information to determine the most likely candidates.
xsx
The excitation structure extractor (xsx) was recently proposed by Kawahara et al.40 These researchers wanted to provide a fast alternative to ndf (see the preceding section), which their experiments demonstrated to be very accurate, but also computationally demanding. xsx relies on spectral division using two power spectral representations. xsx uses a set of detectors spaced equidistantly on the log-frequency axis which cover the user specified range.
Information fusion with adaptive KF
So far we have described ten popular estimation algorithms, some of which are longstanding and established, and others which were proposed more recently. Since there is no universally single best estimation algorithm3, 4 and different estimation algorithms may be in their optimal setting under different signal conditions, it is possible that combining the outputs of the estimation algorithms could lead to improved estimates. Recently, Tsanas et al.10 proposed a simple ensemble approach to obtain the time series by introducing fixed weights for three of the estimation algorithms described in the preceding sections (praat1, rapt, and shrp). In this study, we investigate more thoroughly the concept of combining an arbitrary number of estimation algorithms with adaptive weights to reflect our trust in the estimate of each estimation algorithm.
KF is a simple yet powerful technique which can be used for fusing information from different sources, and has been successfully used in many applications over the last 40 years.41 The sources (here estimation algorithms) provide information which may be potentially redundant or complementary in terms of estimating the underlying (physiological) quantity of interest, usually referred to as the state (here ). The aim is to fuse the information from the measurements (ten scalar values, one for each of the ten estimation algorithms at each step where we have estimates) recursively updating the state over time (for estimation applications, this is usually every 10 ms). Specifically, the KF in its general basic form has the following mathematical formalization:
| (1) |
| (2) |
where is the state, is the state transition model to update the previous state, is the control-input model which is applied to the control vector , is the state process noise which is assumed to be drawn from a multivariate Gaussian distribution with covariance , is the measurement of the state , is the measurement model which maps the underlying state to the observation, and is the measurement noise which is assumed to be drawn from a multivariate Gaussian distribution with covariance .
It is known from the literature that KF is the optimal state estimation method (in the least squares sense) for a stochastic signal under the following assumptions:42 (a) the underlying evolving process of successive states is linear and known, (b) the noise of the state and the noise of the measurements are Gaussian, and (c) the state noise covariance and the measurement noise covariance are known. In practice, we often assume the first two conditions are met, but the KF may not give optimal results if the estimates of the state noise covariance and the measurement noise covariance are inaccurate.41 This requirement has led many researchers to pursue intensively the notion of inferring good covariance estimates from the data.20, 42, 43 Although techniques relying solely on the data to estimate the measurement noise covariance and the state noise covariance offer a convenient automated framework,42 they fail to take into account domain knowledge which may be critical. Therefore, methods which could incorporate this potentially useful additional information have been investigated more rigorously recently. Particularly promising in this regard is the approach pioneered by Li et al.20 and more recently also applied by Nemati et al.43 with the introduction of physiologically informed signal quality indices (SQIs), which reflect the confidence in the measurements of each source. When the SQI is low, the measurement should not be trusted; this can be achieved by increasing the noise covariance. Algorithmically, the dependence of the measurement noise covariance on the SQIs is defined using the logistic function where the independent variable is the SQI.20
Both Li et al.20 and Nemati et al.43 have used SQIs to determine only the measurement noise covariance; they set the state noise covariance to a constant scalar value which was empirically optimized. Effectively, using a constant state noise covariance corresponds to assuming that the confidence in the state value does not change as a function of the a priori estimate of the state, the measurements, and their corresponding SQIs, and may well not be making full use of the potential of SQIs. In this study, both the state noise and the measurement noise covariance are adaptively determined based on the SQI (whereas in Li et al.20 and Nemati et al.43 the state noise was a priori fixed). Another difference between the current study and previous studies20, 43 is that we process a single primary signal (speech signal) from which we obtain various measurements for the quantity of interest (), whereas previously Li et al.20 and Nemati et al.43 extracted an estimate for their quantity of interest from each of the multiple primary signals they processed. Hence, the nature of the SQIs defined in those studies, which relied on the quality of each of the primary signals, will necessarily be different to the SQIs that will be defined here. Furthermore, they have used a very simplified KF setting, processing each source independently from the other sources: this facilitates the algorithmic processing since all matrices become vectors, and all vectors become scalars for a scalar state. Then, they combined the multiple KF results with an additional external function based on the KF residuals and the computed SQIs. However, we argue that the approach by Li et al.20 and Nemati et al.43 fails to capitalize on the full strength of the adaptive KF as a data fusion mechanism where measurements from all sources are combined within the KF framework. This is because in their approach each estimate from each source is only compared to the a priori state without also taking into account the estimates of the other sources. Moreover, we will demonstrate that we can advantageously exploit the fact that the information from all measurements is simultaneously processed in KF to adjust the SQIs.
Formulation of the adaptive KF setting in this study
We have so far described the general notation of the KF. Here we explicitly describe the KF setting used in this study and set values to the KF parameters. For convenience, we will now simplify notation where appropriate, e.g., to denote vectors or scalars for the current application instead of the general formulation with matrices and vectors. We start by noting that the state in this application is a single scalar . We also assume that consecutive estimates are expected to remain unchanged; that is, the a priori estimate of the current state will be the previous state: . Implicitly, we have assumed and . Similarly, we set , where the notation 1 denotes a vector with 10 elements equal to 1 (the length of the vector is equal to the number of estimation algorithms and is constant in this application). The aim of the adaptive KF then is to use the measurements (a vector with ten elements which correspond to the estimates of the ten estimation algorithms at time k) to update to the new estimated state . Next we focus on how to determine the state noise covariance (a scalar since the state is scalar) and the measurement noise covariance based on the SQIs.
SQIs
For the purposes of the current study, the SQIs can be thought of as algorithmic robustness metrics, and express our confidence in the estimate of each estimation algorithm at a particular instant. In this study, we define novel SQIs to continuously update both the measurement noise covariance and state noise covariance as functions of the SQIs using the logistic function. The final SQI, which will be used to update the noise covariances, is a combination of bonuses and penalties for each of the individual estimation algorithms at each discrete time step. The main underlying ideas for setting up the bonuses and penalties are: (a) in most cases, we expect successive estimates not to vary considerably, (b) all estimation algorithms occasionally give very bad estimates in some instances, or for entire speech signals, (c) ndf and swipe appear very robust in this application, and in most cases their estimates are trustworthy, (d) ndf is typically closest to the ground truth but sporadically gives very bad estimates, whereas swipe may be slightly less accurate but more consistent (i.e., very rarely provides poor estimates). These ideas were drawn by first investigating the behavior of the individual estimation algorithms and will become clear later when looking at Sec. 4A.
We use the standard S-shaped curved membership function (spline-based curve, very similar to the sigmoid function) to map each bonus and each penalty to a scalar in the range 0 to 1. This function relies on two independent variables and () to set thresholds, and is defined as
| (3) |
The rationale for using this function is that we want to suppress the values that are close to the thresholds and have a smooth transition in the range to . Now, we outline the layout form of the penalties which determine the SQIs, and in turn and . Overall, the confidence in the current measurement is quantified via the SQIs and is given by
| (4) |
The following paragraphs explain in detail how each of the penalties and bonuses are determined. The first penalty we introduce, , penalizes the estimation algorithms for having large absolute differences in their successive estimates: . We also penalize the estimation algorithms for exhibiting large absolute differences from their corresponding robust mean estimates (defined as the mean estimate of each of the estimation algorithms using only the corresponding estimates which fall within the 10th and 90th percentile, denoted with ): . We use the robust mean because some estimation algorithms occasionally exhibit irrational behavior (i.e., very bad estimates for some instances). Similarly, we penalize the estimation algorithms if the estimate for the current is considerably different from the a priori estimate (to be mathematically formally correct, we create a vector with 10 entries with , i.e., ): . We clarify that we penalize considerably more the algorithms which are far from the a priori estimate of with , rather than for inconsistency (penalty which penalizes large absolute successive differences focusing individually within each estimation algorithm).
Then, we determine which estimation algorithm is the “best expert at the current instant” in order to have good prior information to determine the current estimate. This essentially reflects whether to trust more ndf or swipe, and is achieved by adding up the corresponding three penalties introduced so far for ndf and swipe. Then, we apply the following logic: (a) if the estimated from ndf and swipe at the current discrete step differs by less than 50 Hz, and the sum of all penalties for both ndf and swipe is less than 0.2 (i.e., both ndf and swipe are considered trustworthy), then we trust the estimate from ndf, (b) otherwise, we trust ndf or swipe, whichever has the lowest summed penalty score. The choice of 50 Hz to quantify large deviation in the estimates of an estimation algorithm with respect to ndf or swipe was chosen empirically based on prior knowledge; we decided not to formally optimize this value to avoid overfitting the current data (also, it is possible that a relative threshold might be more appropriate).
We denote the estimate from ndf or swipe as . Next, we introduce another penalty for the estimation algorithms which at the current instant have an estimate that differs considerably from . In this case, the estimation algorithm which is believed to be “best” is not penalized. This is achieved by penalizing ndf or swipe (whichever is considered “best” at the current instance) by
It is possible that an estimation algorithm may have been substantially misguided in its previous estimate(s), but its estimate for the current is close to the “right region,” which is defined as being close to the best expert at the current instant (as described above, this is the estimate by ndf or swipe). In this case, we want to reduce the heavy penalty induced by the large successive difference in estimates. Therefore, we introduce a bonus to compensate for the penalties and , which takes into account how confident we are on the estimate of the best estimation algorithm. Specifically, we define
| (5) |
where ⊙ denotes element-wise multiplication between two vectors. We clarify that we use the multiplication dot to denote multiplication between a scalar and a vector. Moreover, if we give extra bonus to the best estimation algorithm: . This effectively means we assign greater confidence in the estimate of the estimation algorithm that we deem is most accurate if the penalties introduced so far for this algorithm sum to a value less than 0.2. As a final check, any negative is set to zero. Also, if the estimate from an estimation algorithm differs by 50 Hz or more from both the estimate of ndf and swipe, the corresponding SQI is automatically set to zero. Following Li et al.,20 we use the logistic function to estimate the measurement noise covariance . Note that Li et al.20 used a scalar for each source which was processed independently from the other sources in the KF framework, and fused information from the sources externally to KF to provide the final state estimate. Therefore, their scheme did not take advantage of the potential to fuse information internally in KF, where we determine SQIs also using information conveyed from the remaining sources. Here we retain the matrix formulation
| (6) |
where has some pre-defined constant values. We set the diagonal entries of to values that reflect our prior confidence in each estimation algorithm (higher value denotes lower confidence). Here, we set the diagonal entries in corresponding to ndf and swipe to 1, and all other entries to 3 (hence, a priori we believe more the estimates by ndf and swipe, although this prior belief is subject to be updated with the SQIs which in turn will update ). Non-diagonal entries were set to zero. It is not straightforward to optimize the appropriate non-diagonal entries so as to reflect possible interactions among the estimation algorithms (for example, a setting where an estimation algorithm provides poor estimates, whereas another estimation algorithm works particularly well).
Finally, whereas the measurement noise covariance is estimated via the logistic function and SQI, the state noise covariance is estimated as follows:
| (7) |
where L is the number of estimation algorithms with corresponding larger than 0.8. The concept behind this expression in the first clause is that the measurements of ndf and swipe cannot be trusted if both ndf and swipe have relatively low SQIs, and hence the adaptive KF will tend to trust more the a priori estimate. Conversely (in the second clause), if all estimation algorithms weighted by their respective SQI (when their SQI is larger than a threshold of 0.8) point towards a large change in successive steps in the contour, we want to increase so that KF will trust considerably more the new measurements. Note that if the estimation algorithms for which we have large respective SQIs point towards the same direction of change in (i.e., a sudden increase or decrease), then the will increase considerably and hence the KF will weight only on the current measurements and not trust the a priori estimate.
The matlab source code for the adaptive KF and the computation of the SQIs is available on request by contacting the first author.
Benchmarks: Median and ensemble learning
As standard simple benchmarks of combining information from multiple sources, we used the median from all estimation algorithms for each instant, and also two ensembles to weigh the estimates of the estimation algorithms: (a) the standard ordinary least squares (OLS) and (b) a statistically robust form of least squares, the iteratively reweighted least squares (IRLS), which is less sensitive to outliers.21 The ensembles used all but one signal for training and test on the signal left out of the training process; the procedure is repeated for all signals and the results were averaged. Because the two databases in the study have widely different ground truth distributions (see Fig. 1), the ensembles were trained separately for the two databases.
Ground truth and validation framework
Most estimation algorithms provide estimates at specific time intervals (typically at successive instances using a fixed time window of a few milliseconds). Here, wherever possible, we obtained estimates from the estimation algorithms every 10 ms, at the reference time instances [60, 70,…, 950] ms (thus, we have 90 values for each synthetic phonation signal and for each estimation algorithm or the ensemble of the estimation algorithms). Given that the synthetic speech signals exhibit inherent instabilities because the physiological model requires some 4–5 vocal cycles to settle into stable oscillation (see Sec. 2A), and that many estimation algorithms provide reliable estimates only after a few milliseconds into the speech signal, we discarded the estimates prior to 60 ms. A few estimation algorithms do not provide estimates at pre-specified time intervals, but at intervals which are identified as part of the algorithm (this is the case with rapt, for example). In those cases where the estimation algorithms do not provide estimates at the exact time instances described above, we used piecewise linear interpolation between the two closest time intervals of the estimation algorithm to obtain the estimate at the reference time instances. The time instances where was estimated in rapt did not differ considerably from the reference time instances, and thus piecewise linear interpolation should not markedly affect its performance.
The ground truth time series from the physiological model and the sigma algorithm30 is given in the form of glottal closure time instances, which are directly translated to estimates in Hz. However, we need to obtain ground truth values at the reference time instances. Hence, piecewise linear interpolation was used to obtain the ground truth at the reference instances. Similarly, we used piecewise linear interpolation to obtain estimates from dypsa at the reference time instances (dypsa is the only estimation algorithm in this study that aims to identify glottal closure instances, instead of using time windows).
Summarizing, each estimation algorithm or ensemble of estimation algorithms provides 90 estimates for every speech signal. These estimates for every speech signal are compared against the 90 ground truth scores at the reference instances. In total, we processed (a) 117 synthetic speech signals generated using the physiological model which provide values, and (b) 65 actual speech signals which provide values over which we compare the performance of the estimation algorithms and ensembles. In a few cases, the algorithms praat2 and tempo failed to provide outputs (towards the beginning or end of the signal). Those instances were substituted with the estimates from ndf for computing the praat2 and tempo overall errors (for the KF fusion we simply assumed no measurement was available by the corresponding estimation algorithm which had no estimate at those instances). Overall, the outputs from the ten estimation algorithms were concatenated into two matrices: with elements for the speech signals generated from the physiological model, and with elements for the actual speech signals. The ensembles of the estimation algorithms are directly computed using these matrices. The ground truth was stored in two vectors: which comprised elements for the generated speech signals, and which comprised elements for the actual speech signals.
The deviation from the ground truth for each signal and each estimation algorithm is computed as , where is the ith estimate (), and is the ith ground truth value. We report three performance measures: (a) mean absolute error (MAE), (b) the mean relative error (MRE), and (c) the root mean squared error (RMSE) (endorsed by Christensen and Jakobsson1 in evaluating estimation algorithms). The MRE is similar to one of the performance measures used in Parsa and Jamieson,5 but without squaring the error and the ground truth values (thus placing less emphasis on large errors). The RMSE is always equal to or greater than the MAE, and is particularly sensitive to the presence of large errors. The larger the variability of the errors, the larger the difference between MAE and RMSE. Therefore, these metrics are complementary when assessing the performance of the estimation algorithms. In this study we focus on approaches combining estimates with the aim to minimize the mean squared error (implicitly in KF). Therefore, RMSE is the primary error metric of interest to compare our findings. The metrics are defined as follows:
| (8) |
| (9) |
| (10) |
where N is the number of instances to be evaluated for each speech signal (here 90), and S contains the 90 indices of each speech signal in the estimate of each estimation algorithm and in y. Error metrics from all speech signals are averaged, and are presented in the form mean ± standard deviation.
RESULTS
This section follows the same structure as in Sec. 3: first we compare the performance of the ten individual estimation algorithms, and then we study the performance of the information fusion approach with the adaptive KF.
Performance of the ten individual F0 estimation algorithms
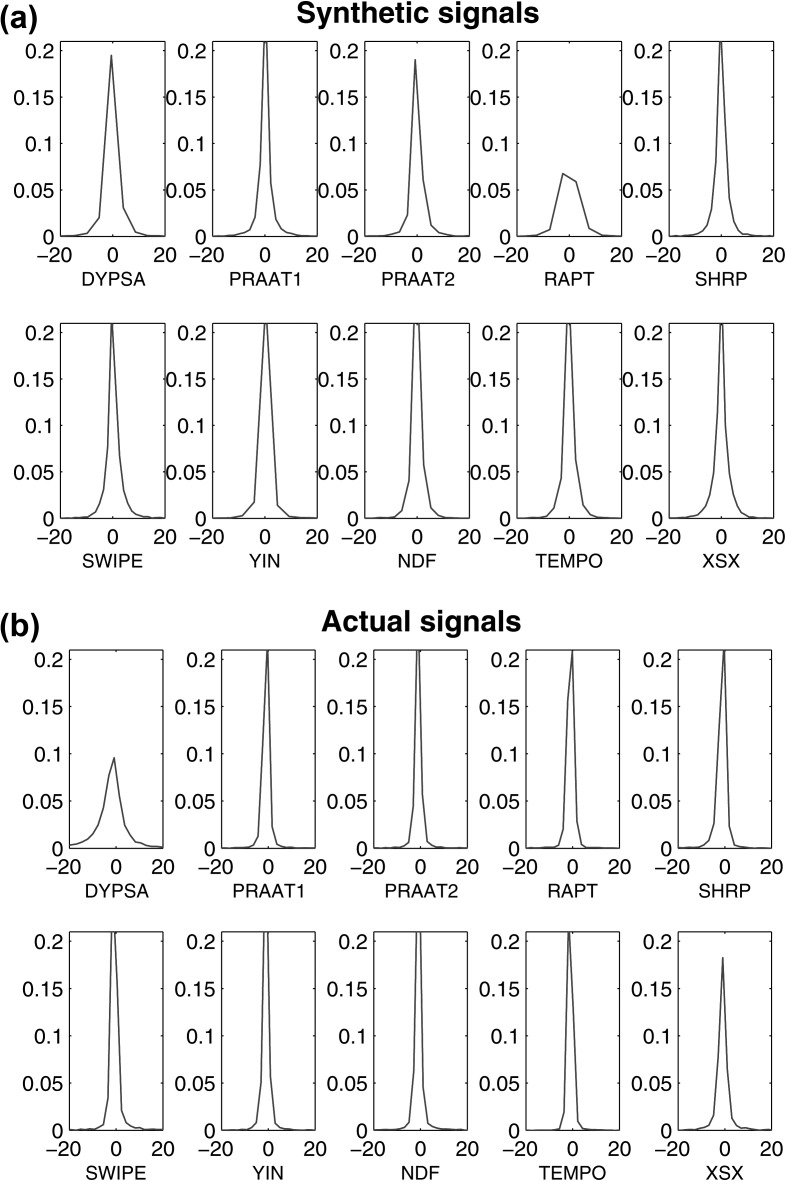
Figure 2 presents the probability density estimates of the errors for the ten estimation algorithms. The probability densities were computed using kernel density estimation with Gaussian kernels. These results provide a succinct overview of the comparative accuracy of each estimation algorithm, as well as indicating whether it is symmetric (with respect to overestimating and underestimating the true ). The error distributions of most estimation algorithms are closely symmetric, suggesting that there is no large positive or negative bias in most of the algorithms. This is also quantitatively reflected in the median errors reported in Tables 1, TABLE II., where all estimation algorithms exhibit a bias which is lower than 1 Hz. Two notable exceptions are yin and rapt which appear to underestimate considerably for the database with the synthetic signals. Figure 3 presents the number of times that each of the estimation algorithms was closer to the ground truth (reflecting the success of each of the estimation algorithms). Interestingly, there is no clear winner among the estimation algorithms in terms of accurately estimating for individual samples in the contour for the two databases [Figs. 3a, 3c]. On the other hand, ndf is clearly the most successful estimation algorithm in terms of being closer to the ground truth when studying the entire signal [Figs. 3b, 3d]. Table TABLE I. summarizes the average results in terms of estimating for the database with the generated speech signals, and Table TABLE II. summarizes the results for the database with the actual speech signals. Overall, all estimation algorithms have reasonably accurate performance.
Figure 2.
(Color online) Probability density estimates of the errors for all estimation algorithms.
TABLE I.
Performance of the estimation algorithms (synthetic speech signals). The evaluation of the estimation algorithms uses all 117 synthetic speech signals, where for each signal we use 90 estimates (thus ). The results are in the form mean ± standard deviation. The last four rows are the approaches to combine the outputs of the estimation algorithms using the median from all algorithms, OLS, IRLS, and adaptive KF. The best individual estimation algorithm and the best combination approach are highlighted in bold. The median error (ME) in the second column is used to illustrate the bias of each algorithm.
| Algorithm | ME (Hz) | MAE (Hz) | MRE (%) | RMSE (Hz) |
|---|---|---|---|---|
| dypsa | 0.02 | 3.79 ± 5.57 | 3.30 ± 5.41 | 7.20 ± 13.44 |
| praat1 | 0.00 | 10.73 ± 22.09 | 7.42 ± 14.64 | 12.46 ± 22.33 |
| praat2 | 0.02 | 6.56 ± 15.46 | 4.68 ± 10.26 | 8.81 ± 17.43 |
| rapt | −3.98 | 9.20 ± 8.91 | 6.64 ± 6.17 | 19.95 ± 14.85 |
| shrp | −0.23 | 3.67 ± 7.06 | 2.83 ± 5.08 | 7.17 ± 10.34 |
| swipe | 0.18 | 2.88 ± 7.10 | 2.37 ± 5.57 | 3.59 ± 7.59 |
| yin | −10.71 | 17.41 ± 16.87 | 11.90 ± 10.76 | 29.90 ± 22.95 |
| ndf | 0.00 | 2.38 ± 6.71 | 1.90 ± 4.92 | 3.16 ± 7.74 |
| tempo | 0.00 | 2.53 ± 6.64 | 2.01 ± 4.87 | 3.34 ± 7.53 |
| xsx | 0.01 | 3.00 ± 7.10 | 2.38 ± 5.55 | 3.73 ± 7.58 |
| Median | −0.39 | 3.00 ± 7.28 | 2.31 ± 5.23 | 4.27 ± 8.91 |
| OLS | 0.02 | 3.49 ± 5.63 | 2.72 ± 4.14 | 4.60 ± 6.49 |
| IRLS | 0.00 | 2.34 ± 7.06 | 1.89 ± 5.21 | 3.34 ± 9.43 |
| KF | 0.02 | 2.19 ± 6.54 | 1.73 ± 4.70 | 2.72 ± 6.84 |
TABLE II.
Performance of the estimation algorithms (actual speech signals). The evaluation of the estimation algorithms uses all the 65 actual speech signals, where for each signal we use 90 estimates (thus ). The results are in the form mean ± standard deviation. The last four rows are the approaches to combine the outputs of the estimation algorithms using the median from all algorithms, OLS, IRLS, and adaptive KF. The best individual estimation algorithm and the best combination approach are highlighted in bold. The ME in the second column is used to illustrate the bias of each algorithm.
| Algorithm | ME (Hz) | MAE (Hz) | MRE (%) | RMSE (Hz) |
|---|---|---|---|---|
| dypsa | −0.78 | 14.42 ± 26.32 | 5.54 ± 8.44 | 25.86 ± 32.89 |
| praat1 | −0.03 | 29.22 ± 57.23 | 13.28 ± 24.08 | 31.67 ± 57.10 |
| praat2 | −0.03 | 29.05 ± 56.86 | 13.21 ± 24.00 | 31.47 ± 56.71 |
| rapt | −0.04 | 28.30 ± 63.47 | 8.63 ± 17.98 | 34.21 ± 65.89 |
| shrp | −0.01 | 18.78 ± 47.77 | 6.85 ± 16.86 | 26.91 ± 55.21 |
| swipe | 0.10 | 3.06 ± 7.01 | 1.18 ± 2.48 | 6.22 ± 13.46 |
| yin | −0.03 | 16.36 ± 47.34 | 6.16 ± 16.32 | 23.35 ± 51.77 |
| ndf | −0.01 | 15.12 ± 60.66 | 4.16 ± 15.24 | 17.66 ± 60.87 |
| tempo | −0.03 | 50.67 ± 99.23 | 17.69 ± 31.08 | 53.21 ± 100.92 |
| xsx | −0.08 | 33.43 ± 52.11 | 16.85 ± 25.90 | 39.57 ± 56.81 |
| Median | −0.17 | 18.90 ± 46.27 | 7.71 ± 18.11 | 24.71 ± 49.15 |
| OLS | −0.78 | 4.08 ± 7.76 | 1.55 ± 2.62 | 7.58 ± 13.82 |
| IRLS | −0.03 | 3.17 ± 7.03 | 1.23 ± 2.49 | 6.53 ± 13.57 |
| KF | −0.03 | 2.49 ± 5.04 | 0.97 ± 1.82 | 4.95 ± 9.19 |
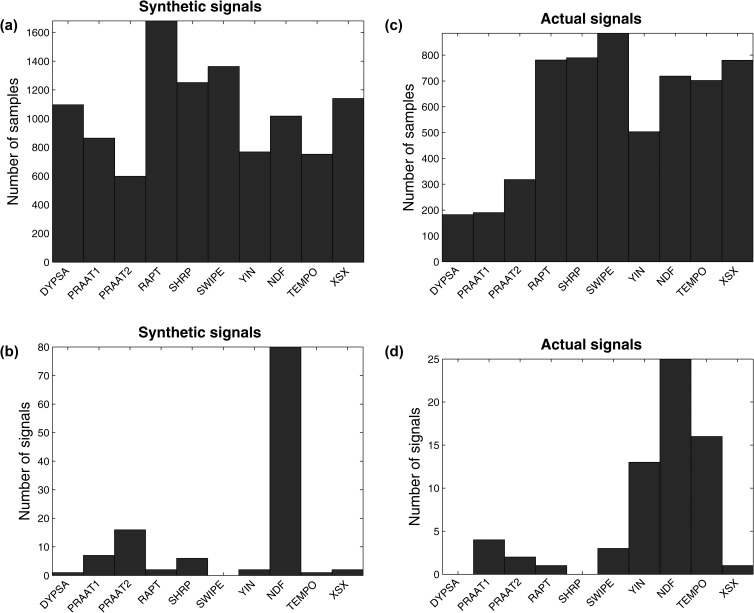
Figure 3.
(Color online) Histogram depicting the number of times each of the estimation algorithms was the most successful algorithm in estimating for each of the assessments in (a) the database with the synthetic speech signals for each of the 10 530 samples, (b) the database with the synthetic speech signals for each of the 65 signals, (c) the database with the actual speech signals for each of the 5850 samples, and (d) the database with the actual speech signals for each of the 117 signals.
The best individual estimation algorithms, on average, are ndf for the database with the synthetic signals and swipe for the database with the actual speech recordings. Some algorithms temporarily deviate considerably from the ground truth, but overall there was good agreement on the actual and estimated contour. Nevertheless, for some signals most of the estimation algorithms had consistently underestimated or overestimated for the entire duration of the signal. This was particularly evident for the database with the actual speech signals: the only estimation algorithm which did not exhibit such erratic behavior was swipe. The findings in Tables 1, TABLE II. might at first appear contradictory with the findings in Fig. 3 where we might have expected ndf and tempo to dominate. In fact, they highlight the fact that overall ndf and tempo may occasionally deviate considerably from the ground truth (this is reflected in the large standard deviation of the errors reported in Table TABLE II.).
Performance of F0 estimation combinations
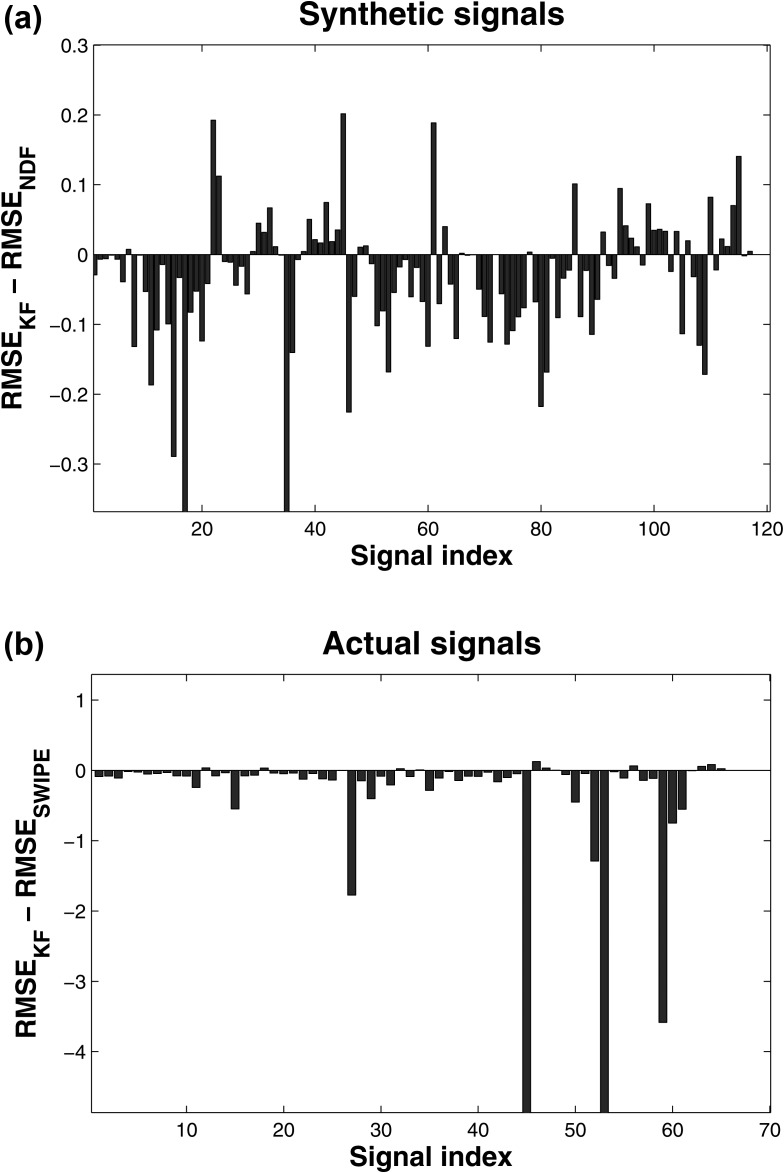
The last four rows in Tables 1, TABLE II. summarize the performance of approaches which combine the outputs of the individual estimation algorithms to obtain the final estimates. We remark that KF leads to considerable improvement for both the database with the generated speech signals (Table TABLE I.), and the database with the actual speech signals (Table TABLE II.). The relative RMSE improvement of the adaptive KF over the single best estimation algorithm is 16.2% compared to ndf for the database with the generated signals, and 25.6% compared to swipe for the database with the actual speech signals. Figure 4 presents the performance of the best individual estimation algorithm versus the best combination scheme for all signals: in the vast majority of speech signals the adaptive KF scheme is more accurate than the single best estimation algorithm, and when not, the drop in performance is negligible.
Figure 4.
(Color online) Performance comparison in terms of RMSE of the adaptive KF scheme against the best individual estimation algorithm (ndf for synthetic signals and swipe for actual signals). All error units are in Hz. For the majority of signals used in this study, the adaptive KF scheme is superior to the single best estimation algorithm, in some cases considerably so. In two cases for the synthetic signals and two cases for the actual signals the RMSE difference is larger than −15 Hz.
We can investigate the contribution of each estimation algorithm in the KF scheme by studying their corresponding SQIs, which are summarized in Table TABLE III.. In both databases, the greatest contribution comes from ndf (and to a lesser degree from swipe). The results in Table TABLE III. suggest that the KF scheme mostly considers ndf to be closest to the ground truth compared to the competing estimation algorithms (particularly for the synthetic data). The estimation algorithms were generally more accurate in predicting in the database with the synthetic signals compared to the database with the actual speech signals, which is reflected in the SQIs for the two databases. In the database with the synthetic signals, the estimation algorithms are typically not heavily penalized (the SQI values are fairly close to the default value 1); whereas in the database with the actual speech signals the SQI values for each estimation algorithm were considerably more variable.
TABLE III.
Signal quality indices in the adaptive KF. The results are in the form mean ± standard deviation. The estimation algorithm with the greatest contribution towards the adaptive KF fusion scheme is highlighted in bold.
| Algorithm | Synthetic signals | Actual signals |
|---|---|---|
| dypsa | 0.97 ± 0.11 | 0.89 ± 0.16 |
| praat1 | 0.87 ± 0.31 | 0.78 ± 0.41 |
| praat2 | 0.94 ± 0.20 | 0.78 ± 0.41 |
| rapt | 0.91 ± 0.09 | 0.85 ± 0.32 |
| shrp | 0.98 ± 0.03 | 0.92 ± 0.22 |
| swipe | 1.00 ± 0.06 | 1.12 ± 0.59 |
| yin | 0.81 ± 0.18 | 0.92 ± 0.23 |
| ndf | 3.99 ± 0.08 | 3.80 ± 0.85 |
| tempo | 1.00 ± 0.01 | 0.77 ± 0.42 |
| xsx | 0.99 ± 0.06 | 0.75 ± 0.40 |
Algorithmic robustness
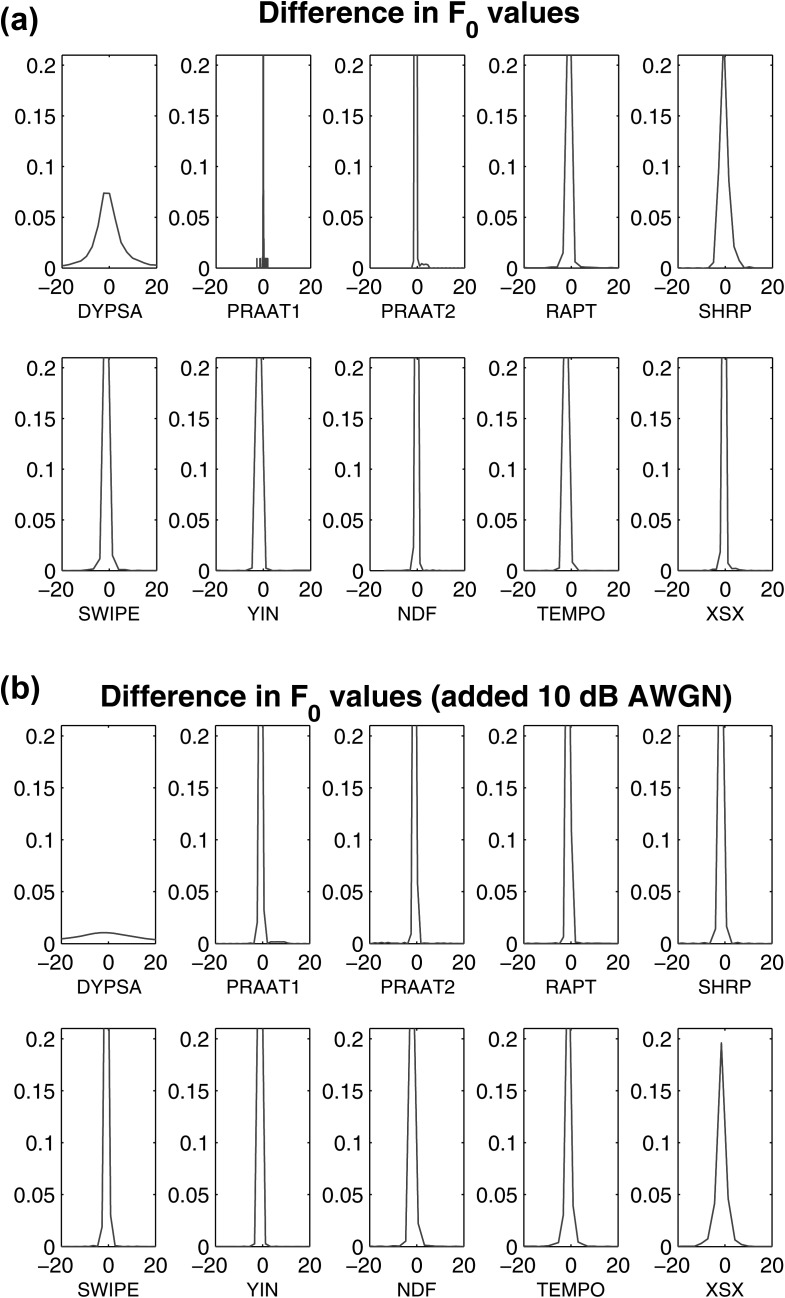
Finally, we investigated the robustness of the estimation algorithms when (a) the sampling frequency is reduced from 44.1 to 8 kHz for each of the 65 actual speech signals and (b) contaminating each actual speech signal with 10 dB additive white Gaussian noise (AWGN) prior to the computation of the . A robust algorithm should produce similar outputs in the reduced quality signals. Figure 5 illustrates the density estimates of the differences in the values computed with respect to the original actual speech signals. Down-sampling the actual speech recordings from the original sampling frequency of 44.1 to 8 kHz affects mainly dypsa, and shrp. praat1 and praat2 appear to be the least affected estimation algorithms in terms of their estimates. Interestingly, although the performance of the best individual estimation algorithm (swipe) had degraded considerably (the RMSE when using the 44.1 kHz-sampled signals was 6.22 ± 13.46 Hz and increased to 7.32 ± 15.37 Hz when using the 8 kHz-sampled signals), the RMSE in the KF approach remained virtually unchanged (originally the RMSE when using the 44.1 kHz-sampled signals was 4.95 ± 9.19 Hz and increased to 4.98 ± 9.25 when using the 8 kHz-sampled signals). That is, the KF approach is very robust in terms of accurately determining the when the sampling frequency is reduced to 8 kHz. Similar findings were observed when contaminating the actual speech signals with 10 dB AWGN: the RMSE of the best individual algorithm (swipe) increased to 6.80 ± 15.25 Hz, but the RMSE of the KF approach had only slightly changed (5.07 ± 9.30 Hz). We highlight the robustness of the KF fusion approach in both lower sampling frequency signals and in the presence of AWGN, whereas swipe and ndf both degraded considerably. Moreover, we stress that not only is the average performance of the KF better (reflected in the mean value), but it is also considerably more reliable (significantly lower standard deviation in both settings). dypsa and to a lesser degree xsx appear to be the most susceptible estimation algorithms to noise, whereas praat1, praat2, ndf, and swipe are again very robust.
Figure 5.
(Color online) Density estimates for the difference when (a) the values were estimated using a sampling frequency of 44.1 kHz versus 8 kHz and (b) the values were estimated for the actual speech signals at 44.1 kHz versus the case when 10 dB AWGN was introduced to the signals prior to computing the . In both cases we used the database with the actual speech recordings.
DISCUSSION AND SUMMARY
This study compared ten widely used estimation algorithms, and investigated the potential of combining estimation algorithms in providing estimates for the sustained vowel /a/. We focused on estimation algorithms which are widely used in clinical speech science, and some recently proposed estimation algorithms. We used two databases for our investigation: (a) a database with 117 synthetic speech signals generated with a sophisticated physiological model of speech production and (b) a database with 65 actual speech signals where simultaneous EGG recordings were available. Particular care was exercised to generate sustained vowel /a/ signals which may closely resemble pathological cases using the physiological model, and also signals with low because these signals are particularly difficult for most of the commonly used estimation algorithms.29 The ground truth in the synthetic signals was inferred from the computation of the vocal fold cycles in the model, i.e., the computation of successive instances where the glottal area was minimized. The ground truth in the actual speech signals was deduced using the sigma algorithm30 from EGG recordings, and was also verified by visual inspection of the signals and the EGG plots. Therefore, in both cases the ground truth is objective, and the aim of this study is to replicate it as accurately as possible using the speech signal alone. We remark that for the actual speech recordings the microphone and amplifier combination had a high pass cut-off frequency compared to the in sustained vowel /a/ phonations. Reducing the high pass cut-off frequency may be beneficial for some estimation algorithms but detrimental for others;33 moreover in practice it is often desirable to use the higher frequencies of the spectrum for general voice assessment analysis (in addition to determining accurately ).10 Therefore, we have not imposed a high pass cut-off frequency which would have been closer to the upper limit of the expected in the current application.
A ubiquitous problem in accurate estimation is the presence of strong sub-harmonics.2, 3 These sub-harmonics manifest as integer fractions of in the spectrum, and in practice it is often difficult to determine whether the pitch period can be considered to be, for example, doubled as a result of the amplitude of the 1/2 sub-harmonic. Some of the estimation algorithms use sophisticated methods to tackle the difficult task of overcoming sub-harmonics problems. For example, swipe imposes weight-decaying kernels on the first and prime harmonics of the signal to reduce the probability of mistakenly using the sub-harmonics as its estimates.36shrp explicitly identifies sub-harmonics and harmonics; the is then determined depending on the value of the ratio of their sums.35yin is effectively relying on the autocorrelation function with two additional corrective terms to make it more robust to amplitude perturbations.37 It uses a free parameter for thresholding a normalized version of the autocorrelation function with the two corrective terms, in order to overcome the effect of strong sub-harmonics. tempo, ndf, and xsx use parabolic time-warping using information in the harmonic structure to obtain the estimates. praat and rapt do not use any explicit mechanism for mitigating the effect of sub-harmonics.
The results reported in Table TABLE I. and Table TABLE II. strongly support the use of ndf and swipe as the most accurate individual estimation algorithms. All estimation algorithms occasionally deviated considerably from the ground truth, in particular yin and rapt. tempo was very inconsistent: overall its contour estimates may have been accurate or largely inaccurate for the entire duration of the signal. The use of Gaussian windows in praat (praat2 in this study) is beneficial compared to Hamming windows (praat1 in this study), which is in agreement with Boersma's observation. swipe was the most consistent in terms of almost never deviating considerably from the ground truth. In Table TABLE I. we have seen that, on average, can be estimated to within less than 2.4 Hz deviation from the ground truth using ndf (swipe was slightly worse). Similarly, in Table TABLE II. we reported that, on average, can be estimated to within about 3 Hz deviation from the ground truth using swipe. In most cases the standard deviations of the errors (presented as the second term in the form mean ± standard deviation) is larger than the mean error value. In general, high standard deviation indicates that the magnitude of the deviation between the estimates of an algorithm and the ground truth fluctuates substantially across samples. On the contrary, low standard deviation suggests that the deviation of the estimates of an algorithm compared to the ground truth does not fluctuate considerably around the quoted mean value (hence, we can be more confident that the mean error is a good representation of the algorithm's estimates compared to the ground truth ). Therefore, low standard deviation of an estimation algorithm suggests that the quoted mean error can be trusted more (in that sense, the algorithm can be considered more reliable). For example, swipe is not only noticeably more accurate in the database with the actual speech signals (lower mean error compared to the competing individual estimation algorithms), but also more reliable (lower standard deviation). It could be argued that the good performance of swipe might merely reflect agreement with the sigma algorithm. However, the fact that swipe demonstrated overall excellent performance in both databases (one of which used data from synthetic speech signals generated by a sophisticated model where the ground truth is known), and also that the “true” in the database with actual speech signals was visually verified, strongly suggest that swipe appears to be very successful in accurately estimating in sustained vowel /a/ phonations.
Figure 3 presents graphically the number of times each of the estimation algorithms was closest to the ground truth (for samples and also for signals in each of the two databases). However, these plots should be interpreted cautiously: first, the histograms do not quantify how much better an estimation algorithm is compared to competing approaches for a particular sample (or signal); second, in those samples (signals) that an estimation algorithm is not best, its estimates might deviate considerably from the ground truth and this is not reflected in the histogram. Therefore, although the plots in Fig. 3 illustrate nicely which estimation algorithm was better than the competing algorithms for samples (signals), for the purposes of assessing the overall performance of the estimation algorithms one should be primarily interested in the results reported in Tables 1, TABLE II..
Overall, the time-domain correlation based approaches investigated here (yin, praat, rapt) perform considerably worse than alternative estimation algorithms such as ndf and swipe. In their current implementations, yin, praat, and rapt are prone to producing large deviations from the ground truth. This finding may reflect the inherent limitations of the tools based on linear systems theory (autocorrelation and cross-correlation) used in yin, praat, and rapt. For example, autocorrelation is sensitive to amplitude changes.37 Moreover, autocorrelation and cross-correlation inherently assume that the contained information in the signal can be expressed using the first two central moments and are therefore suitable for Gaussian signals which may be embedded in noise; however, they fail to take into account nonlinear aspects of non-Gaussian signals. There is strong physiological and empirical evidence suggesting that speech signals (including research on sustained vowels) are stochastic or even chaotic, particularly for pathological cases.2, 44, 45 Therefore, nonlinear speech signal processing tools may be necessary to quantify some properties of speech signals. Interestingly, the two most successful estimation algorithms in this study, ndf and swipe, rely on nonlinear properties of the speech signals to determine the values. swipe identifies the harmonics in the square root of the spectrum and imposes kernels with harmonically decaying weights.36 Conceptually, the approach in swipe can be compared to kernel density estimation, which is widely considered one of the best non-parametric methods to estimate the unknown density of a continuous random variable, or the extension of linear concepts to nonlinear cases (for example, principal component analysis and kernel principal component analysis, or standard linear support vector machines and kernel based support vector machines).19 Therefore, introducing kernels at harmonic locations and weighting the entire harmonic spectrum to determine may explain the success of swipe over competing estimation algorithms which rely on standard harmonic analysis of the spectrum (for example, shrp). ndf is a combination of an interval based extractor (based on autocorrelations at pre-specified Gaussian filterbanks) and an instantaneous frequency based extractor, relying on a Gabor filterbank and the Hilbert transform (which promotes the local properties of the signal). The final estimate for a particular signal segment is decided following weighting of the estimates with a signal to noise ratio (SNR) estimation procedure (which is conceptually comparable to the SQIs introduced in this study). Effectively, ndf is trying to combine two different approaches in one algorithm: the standard linear autocorrelation approach with some modifications for incorporating SNR for each of the studied frequency bands, and a more complicated Hilbert-transform based weighting of Gabor filters (which is the tempo algorithm).39 The success of ndf may be attributed to incorporating information from both a modified weighted autocorrelation approach of the frequency band, and the Gabor filter Hilbert transform promoted estimates.
praat and rapt use dynamic programming, a potentially powerful optimization tool to determine the best value among a pool of candidate values for a particular signal segment (e.g., 10 ms as in this study), so one might expect these algorithms would provide accurate estimates. However, dynamic programming in the context of estimation is a post-processing technique which heavily relies on the determination of good candidate values, and requires the careful optimization of a number of free parameters. In addition to the limitations of autocorrelation (praat) and cross-correlation (rapt), a further possible reason for the relative failure of praat and rapt is that the dynamic programming parameters have probably been optimized by the developers of the estimation algorithms for running speech rather than for sustained vowels.
The results in Tables 1, TABLE II. demonstrate the adaptive KF approach consistently outperforms both the best individual estimation algorithm and the simple linear ensembles. We stress that the adaptive KF improved the accuracy in correctly determining estimates by 16% in the database with the synthetic signals, and 25.6% in the database with the actual speech signals. Notably, this improvement is not only significant, but also consistent in the vast majority of speech signals across both databases (see Fig. 4). Moreover, the adaptive KF is more reliable than the individual estimation algorithms: in addition to exhibiting lower average deviation from the ground truth (reflected in the mean value of the error), the standard deviation around the mean value of the quoted error (e.g., RMSE) was consistently lower than competing approaches in all experiments. Furthermore, the KF approach was shown to be very robust (Sec. 4C): whereas the best individual estimation algorithms (ndf and swipe) degraded considerably with increasing noise and lower sampling frequency, the KF approach was only marginally affected. Additional tests not shown in this study demonstrate that simple naive benchmarks such as the mean or median from the best subset of the estimation algorithms is also considerably worse than KF.
We have investigated the robustness of the algorithms in two settings: (a) reducing the sampling frequency of the actual speech signals from 44.1 to 8 kHz and (b) introducing AWGN to the actual speech signals. Although the speech scientists' recommendation for voice quality assessment is that the sampling frequency should be at least 20 KHz,2 in practice we might not have adequate resources to record such high-quality signals (for example, when recording signals over the telephone). Overall, in both cases we found that there is small performance degradation in terms of accurate estimation using most of the investigated estimation algorithms; moreover we verified the robustness of the proposed adaptive KF approach, where the performance degradation in terms of estimating the true values was practically negligible.
The current findings are confined to the sustained vowel /a/, and therefore cannot be generalized to all speech signals solely on the evidence presented here. It would be interesting to compare the estimation algorithms studied here, including the approaches for combining the individual estimation algorithms, for other sustained vowels (most relevant would be the other corner vowels, which are also sometimes used in voice quality assessment4). Future work could also investigate more sophisticated combinations of estimation algorithms to build on the promising results of this study.
The adaptive KF approach described in this study is an extension of the approach proposed by Li et al.20 We developed a new methodology using SQIs (which can be thought of as algorithmic robustness metrics) where the confidence in the successive estimates of the estimation algorithms is directly used to update both the measurement noise covariance and the state noise covariance. This was achieved using prior confidence in the individual estimation algorithms and taking into account their interaction in terms of difference of their estimates, and the difference with the a priori estimate which is assumed to be constant over successive time frames. We remark that our approach, where all sources are collectively used to feed the adaptive KF, is essentially different from the methodology by Li et al.20 where each source was introduced independently to the KF and the fusion of the different estimators was achieved in a subsequent step. The advantage of the new adaptive KF scheme is that we can jointly determine our confidence in the estimates of each estimation algorithm by adjusting the SQIs, seamlessly integrating the entire process within the KF framework. The proposed methodology may find use in diverse applications relying on the adaptive KF, assuming the signal quality indices are suitably defined. For example, the presented methodology could be used in the applications studied by Li et al.20 (heart rate assessment) and Nemati et al.43 (respiration rate assessment). The adaptive KF is computationally inexpensive, and hence the proposed methodology may be useful also in real-time processing applications.
ACKNOWLEDGMENTS
This study was partly supported by the Wellcome Trust through a Centre Grant No. 098461/Z/12/Z, “The University of Oxford Sleep and Circadian Neuroscience Institute (SCNi),” and partly from NIH Grant No. 1R43DC010956-01 which supported the data collection. M.Z. was supported by UTFSM and CONICYT, Grant No. FONDECYT 11110147. M.A.L. acknowledges the financial support of the Wellcome Trust, Grant No. WT090651MF.
References
- Christensen M. and Jakobsson A., Multi-pitch Estimation (Morgan and Claypool, San Rafael, CA, 2009), pp. 1–6. [Google Scholar]
- Titze I. R., Principles of Voice Production, 2nd ed. (National Center for Voice and Speech, Iowa City, 2000). [Google Scholar]
- Talkin D., “ A robust algorithm for pitch tracking,” in Speech Coding and Synthesis, edited by Kleijn W. B. and Paliwal K. K. (Elsevier Science, Philadelphia, 1995), Chap. 14, pp. 495–518. [Google Scholar]
- Roark R. M., “ Frequency and voice: Perspectives in the time domain,” J. Voice 20, 325–354 (2006). 10.1016/j.jvoice.2005.12.009 [DOI] [PubMed] [Google Scholar]
- Parsa V. and Jamieson D. G., “ A comparison of high precision F0 extraction algorithms for sustained vowels,” J. Speech Lang. Hear. Res. 42, 112–126 (1999). 10.1044/jslhr.4201.112 [DOI] [PubMed] [Google Scholar]
- Titze I. R. and Liang H., “ Comparison of F0 extraction methods for high-precision voice perturbation measurements,” J. Speech Hear. Res. 36, 1120–1133 (1993). [DOI] [PubMed] [Google Scholar]
- Jang S. -J., Choi S. -H., Kim H. -M., Choi H. -S., and Yoon Y. -R., “ Evaluation of performance of several established pitch detection algorithms in pathological voices,” Proceedings of the 29th International Conference, IEEE EMBS, Lyon, France (2007), pp. 620–623. [DOI] [PubMed]
- Manfredi C., Giordano A., Schoentgen J., Fraj S., Bocchi L., and Dejonckere P. H., “ Perturbation measurements in highly irregular voice signals: Performance/validity of analysis software tools,” Biomed. Signal Process. Control 7, 409–416 (2012). 10.1016/j.bspc.2011.06.004 [DOI] [Google Scholar]
- Ferrer C., Torres D., and Hernandez-Diaz M. E., “ Using dynamic time warping of T0 contours in the evaluation of cycle-to-cycle pitch detection algorithms,” Pattern Recogn. Lett. 31, 517–522 (2010). 10.1016/j.patrec.2009.07.021 [DOI] [Google Scholar]
- Tsanas A., Little M. A., McSharry P. E., and Ramig L. O., “ Nonlinear speech analysis algorithms mapped to a standard metric achieve clinically useful quantification of average Parkinson's disease symptom severity,” J. R. Soc. Interface 8, 842–855 (2011). 10.1098/rsif.2010.0456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsanas A., Little M. A., McSharry P. E., Spielman J., and Ramig L. O.: “ Novel speech signal processing algorithms for high-accuracy classification of Parkinson's disease,” IEEE Trans. Biomed. Eng. 59, 1264–1271 (2012). 10.1109/TBME.2012.2183367 [DOI] [PubMed] [Google Scholar]
- Tsanas A., Little M. A., Fox C., and Ramig L. O., “ Objective automatic assessment of rehabilitative speech treatment in Parkinson's disease,” IEEE Trans. Neural Syst. Rehab. Eng. 22, 181–190 (2014). 10.1109/TNSRE.2013.2293575 [DOI] [PubMed] [Google Scholar]
- Tsanas A., Little M. A., McSharry P. E., and Ramig L. O., “ New nonlinear markers and insights into speech signal degradation for effective tracking of Parkinson's disease symptom severity,” in International Symposium on Nonlinear Theory and its Applications (NOLTA), Krakow, Poland (2010), pp. 457–460.
- Godino-Llorente J. I., Gomez-Vilda P., and Blanco-Velasco M., “ Dimensionality reduction of a pathological voice quality assessment system based on Gaussian mixture models and short-term cepstral parameters,” IEEE Trans. Biomed. Eng. 53, 1943–1953 (2006). 10.1109/TBME.2006.871883 [DOI] [PubMed] [Google Scholar]
- Colton R. H. and Conture E. G., “ Problems and pitfalls of electroglottography,” J. Voice 4, 10–24 (1990). 10.1016/S0892-1997(05)80077-3 [DOI] [Google Scholar]
- Henrich N., d'Alessandro C., Doval B., and Castellengo M., “ On the use of the derivative of electroglottographic signals for characterization of nonpathological phonation,” J. Acoust. Soc. Am. 115, 1321–1332 (2004). 10.1121/1.1646401 [DOI] [PubMed] [Google Scholar]
- Mehta D. D., Zañartu M., Quatieri T. F., Deliyski D. D., and Hillman R. E., “ Investigating acoustic correlates of human vocal fold phase asymmetry through mathematical modeling and laryngeal high-speed videoendoscopy,” J. Acoust. Soc. Am. 130, 3999–4009 (2011). 10.1121/1.3658441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zañartu M., “ Acoustic coupling in phonation and its effect on inverse filtering of oral airflow and neck surface acceleration,” Ph.D. dissertation, School of Electrical and Computer Engineering, Purdue University (2010). [Google Scholar]
- Hastie T., Tibshirani R., and Friedman J., The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed. (Springer Science+Business Media, New York, 2009). [Google Scholar]
- Li Q., Mark R. G., and Clifford G. D., “ Robust heart rate estimation from multiple asynchronous noisy sources using signal quality indices and a Kalman filter,” Physiol. Meas. 29, 15–32 (2008). 10.1088/0967-3334/29/1/002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Story B. H. and Titze I. R., “ Voice simulation with a body-cover model of the vocal folds,” J. Acoust. Soc. Am. 97, 1249–1260 (1995). 10.1121/1.412234 [DOI] [PubMed] [Google Scholar]
- Steinecke I. and Herzel H., “ Bifurcations in an asymmetric vocal-fold model,” J. Acoust. Soc. Am. 97, 1874–1884 (1995). 10.1121/1.412061 [DOI] [PubMed] [Google Scholar]
- Titze I. R. and Story B. H., “ Rules for controlling low-dimensional vocal fold models with muscle activation,” J. Acoust. Soc. Am. 112, 1064–1076 (2002). 10.1121/1.1496080 [DOI] [PubMed] [Google Scholar]
- Erath B. D., Peterson S. D., Zañartu M., Wodicka G. R., and Plesniak M. W., “ A theoretical model of the pressure distributions arising from asymmetric intraglottal flows applied to a two-mass model of the vocal folds,” J. Acoust. Soc. Am. 130, 389–403 (2011). 10.1121/1.3586785 [DOI] [PubMed] [Google Scholar]
- Hillman R. E., Holmberg E. B., Perkell J. S., Walsh M., and Vaughan C., “ Objective assessment of vocal hyperfunction: An experimental framework and initial results,” J. Speech Hear. Res. 32, 373–392 (1989). [DOI] [PubMed] [Google Scholar]
- Kuo J., “ Voice source modeling and analysis of speakers with vocal-fold nodules,” Ph.D. dissertation, Harvard–MIT Division of Health Sciences and Technology (1998). [Google Scholar]
- Story B. H., “ Physiologically-based speech simulation using an enhanced wave-reflection model of the vocal tract,” Ph.D. dissertation, University of Iowa (1995). [Google Scholar]
- Titze I. R., “ Nonlinear source-filter coupling in phonation: Theory,” J. Acoust. Soc. Am. 123, 2733–2749 (2008). 10.1121/1.2832337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen M. G., “ On the estimation of low fundamental frequencies,” in Proceedings of the IEEE Workshop on Application of Signal Processes to Audio and Acoustics (2011), pp. 169–172.
- Thomas M. R. P. and Naylor P. A., “ The SIGMA algorithm: A glottal activity detector for electroglottographic signals,” IEEE Trans. Audio Speech Lang. Process. 17, 1557–1566 (2009). 10.1109/TASL.2009.2022430 [DOI] [Google Scholar]
- PRAAT: doing phonetics by computer (Version 5.1.15) [Computer program], by P. Boersma and D. Weenink. Retrieved from http://www.praat.org/ (Last viewed 3/21/2014).
- Boersma P., “ Should jitter be measured by peak picking or by waveform matching?,” Folia Phoniat. Logoped. 61, 305–308 (2009). 10.1159/000245159 [DOI] [PubMed] [Google Scholar]
- Naylor P. A., Kounoudes A., Gudnason J., and Brookes M., “ Estimation of glottal closure instants in voices speech using the DYPSA algorithm,” IEEE Trans. Audio Speech Lang. Process. 15, 34–43 (2007). 10.1109/TASL.2006.876878 [DOI] [Google Scholar]
- Boersma P., “ Accurate short-term analysis of the fundamental frequency and the harmonics-to-noise ratio of sampled signal,” IFA Proc. 17, 97–110 (1993). [Google Scholar]
- Sun X., “ Pitch determination and voice quality analysis using subharmonic-to-harmonic ratio,” ICASSP2002, Orlando, FL: (2002). [Google Scholar]
- Camacho A. and Harris J. G., “ A sawtooth waveform inspired pitch estimator for speech and music,” J. Acoust. Soc. Am. 124, 1638–1652 (2008). 10.1121/1.2951592 [DOI] [PubMed] [Google Scholar]
- de Cheveigne A. and Kawahara H., “ YIN, a fundamental frequency estimator for speech and music,” J. Acoust. Soc. Am. 111, 1917–1930 (2002). 10.1121/1.1458024 [DOI] [PubMed] [Google Scholar]
- Kawahara H., Katayose H., de Cheveigne A., and Patterson R. D., “ Fixed point analysis of frequency to instantaneous frequency mapping for accurate estimation of F0 and periodicity,” Eurospeech, Budapest, Hungary: (1999), pp. 2781–2784. [Google Scholar]
- Kawahara H., de Cheveigne A., Banno H., Takahashi T., and Irino T., “ Nearly defect-free F0 trajectory extraction for expressive speech modifications based on STRAIGHT,” Interspeech, Lisbon, Portugal: (2005), pp. 537–540. [Google Scholar]
- Kawahara H., Morise M., Takahashi T., Nisimura R., Irino T., and Banno H., “ Tandem-STRAIGHT: A temporally stable power spectral representation for periodic signals and applications to interference-free spectrum, F0, and aperiodicity estimation,” ICASSP 2008, Las Vegas; (2008), pp. 3933–3936. [Google Scholar]
- Raol J. R., Multi-sensor Data Fusion with Matlab (CRC Press, Boca Raton, FL, 2010). [Google Scholar]
- Mehra R. K., “ On the identification of variance and adaptive Kalman filtering,” IEEE Trans. Automatic Control AC-15, 175–184 (1970). 10.1109/TAC.1970.1099422 [DOI] [Google Scholar]
- Nemati S., Malhorta A., and Clifford G. D., “ Data fusion for improved respiration rate estimation,” EURASIP J. Adv. Signal Process. 2010, 926315 (2010). 10.1155/2010/926305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little M. A., McSharry P. E., Moroz I. M., and Roberts S. J., “ Testing the assumptions of linear prediction analysis in normal vowels,” J. Acoust. Soc. Am. 119, 549–558 (2007). 10.1121/1.2141266 [DOI] [PubMed] [Google Scholar]
- Tsanas A., “ Accurate telemonitoring of Parkinson's disease symptom severity using nonlinear speech signal processing and statistical machine learning,” Ph.D. thesis, University of Oxford, UK (2012). [Google Scholar]