Perturbation of nuclear spin polarizations in solid state NMR of nitroxide-doped samples by magic-angle spinning without microwaves

Abstract

We report solid state ¹³C and ¹H nuclear magnetic resonance (NMR) experiments with magic-angle spinning (MAS) on frozen solutions containing nitroxide-based paramagnetic dopants that indicate significant perturbations of nuclear spin polarizations without microwave irradiation. At temperatures near 25 K, ¹H and cross-polarized ¹³C NMR signals from ¹⁵N,¹³C-labeled L-alanine in trinitroxide-doped glycerol/water are reduced by factors as large as six compared to signals from samples without nitroxide doping. Without MAS or at temperatures near 100 K, differences between signals with and without nitroxide doping are much smaller. We attribute most of the reduction of NMR signals under MAS near 25 K to nuclear spin depolarization through the cross-effect dynamic nuclear polarization mechanism, in which three-spin flips drive nuclear polarizations toward equilibrium with spin polarization differences between electron pairs. When T_1e is sufficiently long relative to the MAS rotation period, the distribution of electron spin polarization across the nitroxide electron paramagnetic resonance lineshape can be very different from the corresponding distribution in a static sample at thermal equilibrium, leading to the observed effects. We describe three-spin and 3000-spin calculations that qualitatively reproduce the experimental observations.

INTRODUCTION

Dynamic nuclear polarization (DNP) can increase the sensitivity of nuclear magnetic resonance (NMR) measurements by transferring spin polarization from electrons to nuclei. In addition, many solid-state NMR experiments rely on magic-angle spinning (MAS) to average out anisotropic nuclear spin interactions and thereby produce sharp solid-state NMR lines. As a result, the combination of DNP with MAS has recently become prevalent in applications of solid-state NMR to a variety of chemical and biochemical systems,^{1, 2} making it important to understand how DNP mechanisms are affected by MAS.^{3, 4}

This paper reports experiments and simulations showing that MAS alone can perturb nuclear spin polarizations in frozen solutions that are paramagnetically doped with nitroxide-based compounds, even without microwave irradiation. Such samples are commonly used in solid-state NMR experiments in which DNP occurs through the cross-effect mechanism.⁵ The cross-effect mechanism involves energy-conserving three-spin transitions, in which a nuclear spin flip occurs simultaneously with the flip-flop of an electron spin pair whose electron paramagnetic resonance (EPR) frequencies differ by the NMR frequency. These three-spin transitions have the effect of equilibrating the nuclear spin polarization with the difference in spin polarization of the two electrons. In the absence of both MAS and microwave irradiation, the nuclear spin polarization is driven toward its thermal equilibrium value (since, at thermal equilibrium in the high temperature limit, the difference in spin polarizations of electrons whose EPR frequencies differ by the NMR frequency is equal to the nuclear spin polarization). However, for electron spins with large g-anisotropies as in nitroxides, MAS makes the EPR frequencies time-dependent. If the MAS rotation period is short compared with the electron spin-lattice relaxation time (T_1e), differences in spin polarization of electrons whose EPR frequencies differ by the NMR frequency can be altered by MAS, even without microwave irradiation. Three-spin transitions may then be expected to drive the nuclear spin polarization toward a steady-state value that differs from the thermal equilibrium value, provided that the cross-effect DNP mechanism is the dominant nuclear spin relaxation mechanism.

Experiments described below show that, at temperatures near 25 K and MAS frequencies near 6.7 kHz, ¹H and cross-polarized (CP) ¹³C NMR signals from uniformly ¹⁵N, ¹³C-labeled L-alanine in glycerol/water can be reduced by factors as large as six by doping with a trinitroxide compound, relative to signals from samples without nitroxide dopants. Without MAS or at temperatures near 100 K, differences between signals from samples with and without nitroxide doping are much smaller. To illustrate a likely cause of the observed effects, we present results from numerical simulations using a quantum mechanical three-spin model for cross-effect DNP, as well as a simplified 3000-spin model designed to include intermolecular electron spin diffusion. Simulations are in qualitative agreement with the experimental observations and show that intermolecular electron-electron couplings play an important role in the perturbation of spin polarizations by MAS.

In the absence of microwave irradiation, the ¹H spin polarization is reduced by MAS at low temperatures under typical experimental conditions. However, theoretically, MAS and nitroxide radical doping could produce an increase in nuclear spin polarization, especially for nuclei with low gyromagnetic ratios. Measurements comparing the ¹H, directly excited ¹³C, and CP ¹³C NMR signals in samples containing ¹³C-labeled glycerol show that the CP ¹³C and ¹H signal loss with nitroxide doping under MAS is indeed greater than the directly excited ¹³C signal loss.

EXPERIMENTAL METHODS

Experiments used the home-built ultra-low-temperature DNP-MAS NMR probe described previously² and were performed at 9.39 T (400.9 MHz and 100.8 MHz ¹H and ¹³C NMR frequencies) using a Bruker Avance III NMR spectrometer console. Sample temperatures were determined from measurements of the spin-lattice relaxation of ⁷⁹Br in KBr contained in a glass capsule placed in the MAS rotor along with the sample.⁶ All samples contained 50 mM ¹⁵N,¹³C₃-L-alanine in partially protonated glycerol/water. Nitroxide-doped samples contained 30 mM of nitroxide radicals (10 mM of the triradicals DOTOPA-4OH or DOTOPA-Ethanol^{2, 7, 8} or 15 mM of the biradical TOTAPOL⁹), while samples without nitroxides contained 0.2 mM DyEDTA to reduce the low-temperature nuclear spin-lattice relaxation times (T_1n). Sample identities and compositions are given in Table 1. Chemical structures of tri- and biradicals are shown in Fig. S1 of the supplementary material.¹⁰

Table 1.

Sample compositions for solid state NMR measurements.

			Solvent composition by volume
Sample	Dopant	13C3-L-alanine	Glycerol-d8	D2O	H2O	DMSO-d6	1,3-13C-glycerol	Buffer
1	10 mM DOTOPA-4OH	50 mM	57%	28%	10%	5%	…	25 mM phosphate, pH 7.4
2	15 mM TOTAPOL	50 mM	57%	24%	10%	9%	…	20 mM phosphate, pH 7.4
3	0.2 mM DyEDTA	50 mM	57%	33%	10%	…	…	30 mM phosphate, pH 7.4
4	10 mM DOTOPA-4OH	50 mM	6%	36%	5%	2%	51%	None
5	0.2 mM DyEDTA	50 mM	6%	38%	5%	…	51%	None
6	10 mM DOTOPA-Ethanol	50 mM	57%	28%	10%	5%	…	25 mM phosphate, pH 7.4

In ¹H and directly excited ¹³C NMR measurements, the nuclear spin polarization was first destroyed with several (3–5) 90° pulses, separated by 10 ms delays before the recycle delay (see Table 2). The NMR signal was then excited with a single pulse, either a 90° pulse for ¹³C NMR or a 20° pulse for ¹H NMR. For CP ¹³C measurements, an 800 μs CP contact time and 40 kHz ¹³C radio-frequency field strength were used, with two dummy scans to establish a steady state before NMR signal acquisition. In all ¹³C NMR experiments, 70 kHz proton decoupling fields with two-pulse phase modulation¹¹ were applied during detection of free-induction decay (FID) signals. ¹H T_1n values were measured from the dependences of ¹³C CP signals on the recycle delay between scans.

Table 2.

Summary of solid state NMR measurements.

			Signal ratio to DyEDTA-doped
	Sample	MAS	sample1			Recycle delay (s)
Sample	temperature (K)	frequency (kHz)	13C NMR	1H NMR	T1n (s)	13C NMR	1H NMR
1	24	6.7	0.14 ± 0.05 (CP)	0.15 ± 0.05	3.6 ± 0.5 (1H)	5	8
2	28	6.7	0.21 ± 0.08 (CP)	0.21 ± 0.07	5.4 ± 0.5 (1H)	6.5	8
3	23	6.8	1	1	23 ± 2 (1H)	32	128
1	19	0	0.75 ± 0.30 (CP)	0.80 ± 0.30	13.8 ± 1.5 (1H)	36	8
3	18	0	1	1	37 ± 4 (1H)	64	128
1	101	6.7	0.58 ± 0.20 (CP)	…	3.0 ± 0.2 (1H)	5	…
2	87	6.8	0.55 ± 0.20 (CP)	…	4.8 ± 0.4 (1H)	6.5	…
3	107	6.8	1	…	23 ± 5 (1H)	32	…
6	89	0	0.86 ± 0.30 (CP)	0.75 ± 0.30	7.4 ± 1.0 (1H)	9.3	128
3	81	0	1	1	20 ± 5 (1H)	32	256
4	24	6.6	0.53 ± 0.10 (DE)	0.38 ± 0.10	280 ± 50 (13C)	1600 (DE)	256
			0.35 ± 0.10 (CP)			128 (CP)
5	29	6.7	1	1	900 ± 100 (13C)	2400 (DE)	128
						128 (CP)

¹Signal ratios are corrected for differences in numbers of scans, the ratios of recycle delays to T_1n values, and temperatures. ¹³C NMR signals are either cross-polarized (CP) or directly excited (DE).

Signal ratios in Table 2 are calculated from the integrals of all ¹³C lines (including CO, Cα, and Cβ signals from ¹³C₃-L-alanine and signals from glycerol), except that broad, weak CO signals are not included in spectra of static samples, and the weak Cβ signals are not included in MAS spectra at ∼100 K. ¹H signal is measured as the peak intensity of the Fourier transform to reduce the influence of background ¹H signals. ¹³C and ¹H signal ratios are corrected for the minor differences in sample temperatures and for differences in ratios of recycle delays to ¹H T_1n values. Uncertainties in signal ratios are dominated by the signal size uncertainty, estimated at ∼25% from multiple measurements on some samples.

For experiments in which MAS was stopped during signal acquisition, the MAS drive gas pressure was shut off manually at the appropriate time point. The MAS bearing gas pressure was not changed. The MAS tachometer signal was stored on an oscilloscope and used to determine that the MAS frequency decreased approximately linearly to zero within 4 s.

For experiments in which microwave irradiation was applied, an extended interaction oscillator (EIO) from Communications & Power Industries provided 800 mW of linearly polarized microwaves at 264.0 GHz, which was transmitted through a corrugated waveguide to the quasi-optical interferometer system described previously.⁷

EXPERIMENTAL RESULTS

Effects of MAS and nitroxide doping on NMR signals

Figure 1 compares CP ¹³C NMR spectra for samples with and without nitroxide doping and also with and without MAS. Results are summarized in Table 2. Under MAS and near 24 K (Fig. 1a), there is an approximate sixfold reduction in the NMR signal amplitudes from sample 1 (DOTOPA-4OH doped) relative to sample 3 (without nitroxide), with no significant change in linewidths. The signal reduction for sample 2 (TOTAPOL doped) is approximately fivefold. CP ¹³C signal ratios and ¹H T_1n values are the same for all ¹³C lines within experimental error. In static samples near 19 K (Fig. 1c), there is a much smaller signal reduction (∼25%) from sample 1 relative to sample 3. Under MAS and near 100 K (Fig. 1b), CP ¹³C signal reductions from samples 1 and 2 relative to sample 3 are approximately 40%. Examples of ¹H NMR spectra are shown in Fig. S2 of the supplementary material.¹⁰ Nearly identical signal losses are seen for ¹H and CP ¹³C signals indicating that differences in CP efficiency are not a significant factor in the ¹³C signal losses.

Figure 1.

¹³C NMR spectra of uniformly ¹⁵N,¹³C-labeled L-alanine in partially protonated glycerol/water, containing 10 mM of the triradical dopant DOTOPA-4OH (red, a, b, c, e), 15 mM of the biradical dopant TOTAPOL (green, a, b), 10 mM of the triradical dopant DOTOPA-Ethanol (black, d), or 0.2 mM DyEDTA (blue, a–e). (a) Cross-polarized spectra of samples 1, 2, and 3 at 23–28 K with MAS at 6.7–6.8 kHz. Natural-abundance ¹³C NMR signals from glycerol are labeled “gly.” (b) Cross-polarized spectra of samples 1, 2, and 3 at 87–107 K with MAS at 6.7–6.8 kHz. (c) Cross-polarized spectra of samples 1 and 3 at 18–19 K without MAS. (d) Cross-polarized spectra of samples 3 and 6 at 81–89 K without MAS. (e) Directly excited spectra of samples 4 and 5 at 24–29 K with MAS at 6.6–6.7 kHz. Spectra in each panel are normalized by the number of scans to show signal per scan. Sample compositions, temperatures, recycle delays for each spectrum are given in Tables 1, 2.

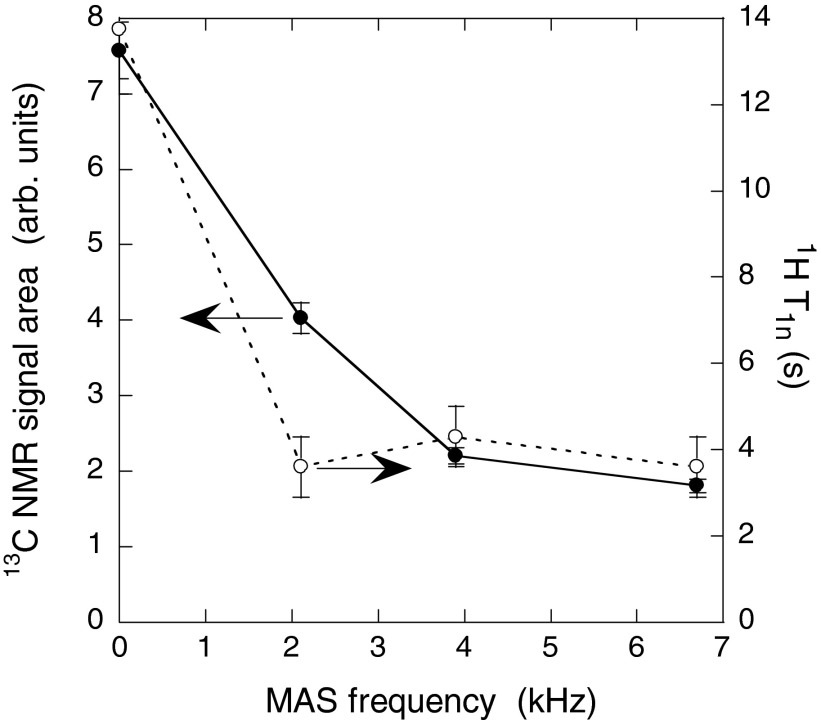
Figure 2 shows the dependences of CP ¹³C signal amplitudes and ¹H T_1n values on MAS frequency for sample 1 near 24 K. Loss of signal primarily occurs between 0 kHz and 4 kHz. ¹H T_1n values are significantly reduced by MAS at 2 kHz, but are nearly independent of MAS frequency between 2 kHz and 6.7 kHz. For sample 3 (without nitroxide), the percentage change in ¹H T_1n associated with MAS is much smaller (see Table 2).

Figure 2.

Cross-polarized ¹³C NMR signal area (●) and ¹H T_1n (○) as a function of MAS frequency for sample 1 (DOTOPA-4OH doped). Lines are drawn to guide the eye. ¹H T_1n values were measured through cross-polarized ¹³C NMR signals.

Samples 4 and 5 were used for measurements of directly excited ¹³C NMR signals. These samples contained 1,3-¹³C₂-glycerol in order to increase ¹³C signal strengths and ¹³C-¹³C spin diffusion rates, facilitating the directly excited ¹³C NMR measurements. The polarization build-up times in directly excited ¹³C NMR measurements (i.e., ¹³C T_1n values) are much longer than in CP ¹³C measurements (∼280 s and ∼900 s for samples 4 and 5, respectively, at 6.6–6.7 kHz MAS frequency and 24–29 K sample temperature). These samples also contain higher ¹H concentrations because the 1,3-¹³C₂-glycerol is not deuterated. While ¹H and CP ¹³C NMR signal amplitudes for sample 4 (DOTOPA-4OH doped) decreased by factors of approximately 2.8 relative to sample 5 (without nitroxide), the directly excited ¹³C NMR signal decreased by a factor of approximately 1.9 (see Table 2). This difference in the effect of MAS on ¹H and ¹³C spin polarizations is qualitatively consistent with the simulations discussed below, which predict a smaller reduction in spin polarization for nuclei with lower gyromagnetic ratio. The absence of quantitative agreement with simulations could result from differences in hyperfine couplings, spin diffusion, and nuclear relaxation rates between experiments and simulations. It is also worth noting that the ¹H and ¹³C CP signal losses for sample 4 are lower than for samples 1 and 2, perhaps suggesting an effect of the higher ¹H concentration in sample 4.

In DNP-enhanced solid state NMR experiments, the NMR signal enhancement factor ɛ is commonly evaluated as the ratio of the NMR signal intensity from a paramagnetically doped sample under microwave irradiation to the signal intensity from the same sample without microwave irradiation. If the “microwave off” signals are reduced relative to signals from an undoped sample (or from a sample doped with an alternative paramagnetic species that reduces T_1n but does not produce DNP, such as Dy³⁺ or Cu²⁺), then ɛ overestimates the net sensitivity gain from DNP. Nonetheless, under our experimental conditions, microwave irradiation of sample 1 (DOTOPA-4OH doped) does produce a large net sensitivity gain in CP ¹³C NMR measurements relative to sample 3 (without nitroxide). Integrated ¹³C signals from sample 1 with 800 mW microwave irradiation at 264.0 GHz are larger than signals from sample 3 by a factor of 30 with MAS at 23 K and a factor of 35 without MAS at 19 K (see Figs. S3 and S4 in the supplementary material).¹⁰ The shorter ¹H T_1n in sample 1 contributes an additional factor of 2.5 to the net sensitivity gain under MAS.

Time dependence of the effect of MAS on ¹H spin polarization

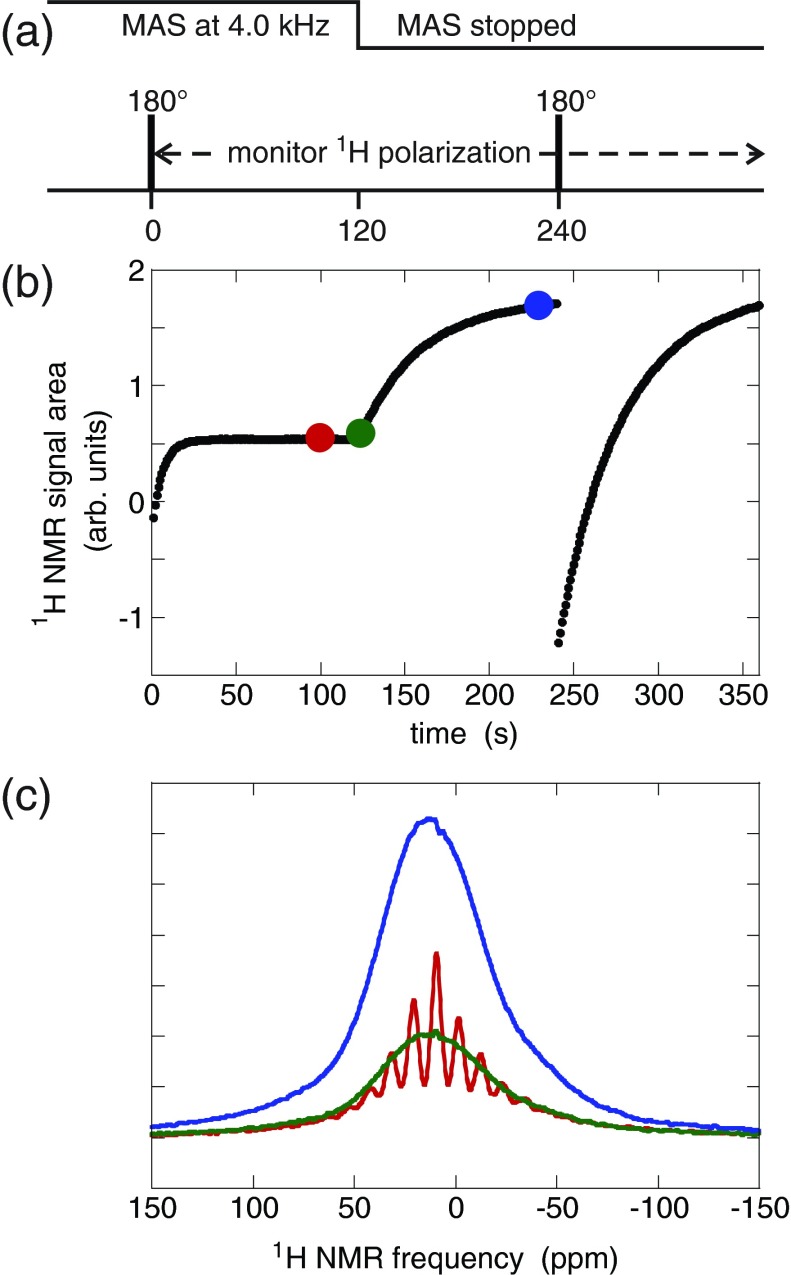
Figure 3 shows experiments to measure the time dependence of the ¹H signal when MAS is stopped. In these experiments, ¹H NMR signal intensities were monitored continuously while the MAS frequency was switched from 4.0 kHz to 0.0 kHz within several seconds, using the timing sequence in Fig. 3a. As shown in Fig. 3b, the integrated ¹H signal from sample 6 (DOTOPA-Ethanol doped) at 27 K increased slowly toward a larger steady-state value after MAS was switched off, with a time constant equal to the ¹H T_1n. As shown in Figs. 3b, 3c, integrated ¹H signals before and soon after the stoppage of MAS (red and green spectra) are nearly equal, although the ¹H NMR spectrum changes from a series of MAS sidebands to a single Gaussian-like lineshape when ¹H-¹H dipole-dipole couplings are no longer averaged out by MAS.

Figure 3.

Direct measurement of the effect of MAS on steady-state ¹H spin polarization in sample 6 (DOTOPA-Ethanol doped) at 27 K. (a) Timing sequence. After MAS at 4.0 kHz for more than 100 s, the ¹H polarization is inverted with a single 180° pulse at 0 s. The ¹H polarization is then monitored continuously by recording free-induction decay signals after 5° pulses, once per second. MAS is stopped at 120 s, changing from 4.0 kHz to 0 kHz within 4 s. A second 180° pulse is applied at 240 s. (b) Areas of ¹H spectra during the polarization monitoring period. (c) ¹H spectra at 100 s (red), 124 s (green), and 230 s (blue). The steady-state ¹H spin polarization without MAS is about four times larger than the steady-state ¹H spin polarization with MAS. The apparent ¹H T₁ value without MAS is about 6 times larger than the apparent ¹H T₁ value with MAS.

The recovery of the ¹H signal with time constant T_1n is consistent with the cross effect mechanism described in this article. Under our experimental conditions, the cross effect DNP time constant is the same as T_1n. In fact, the T_1n recovery without microwaves, and the DNP with microwaves may both result from the same underlying cross effect (three-spin flip) process. The slow recovery of the ¹H signal also excludes any mechanism with a time constant other than T_1n. Specifically, paramagnetic signal losses have generally been attributed to “bleaching” of NMR signals from molecules near the paramagnetic species, due to effects such as broadening of NMR lines, reductions in CP efficiencies, and/or interference with ¹H decoupling by strong local electron-nuclear hyperfine couplings.^{12, 13} When MAS is stopped, the modulation of the electron-nucleus hyperfine coupling stops, and in addition, the electron polarization should return to its static equilibrium with time constant T_1e (∼2 ms). Thus, we would expect MAS-dependent paramagnetic bleaching effects (if they were present) to change rapidly, contrary to our observation that the integrated ¹H NMR signal changes slowly after MAS is stopped.

The value of ¹H T_1n changes significantly when MAS is stopped, as shown by the behavior of the integrated ¹H signal after inversion of ¹H polarization by 180° pulses in Fig. 3b. The longer T_1n in the absence of MAS may be caused by two factors. First, without MAS, only a small percentage of nitroxide electron pairs are expected to have favorable orientations to create the condition for cross effect DNP, ω_e1 − ω_e2 = ω_n. In contrast, with MAS, a majority of nitroxide electron pairs should fulfill the cross effect condition, at some point in the rotor cycle.³ Second, ¹H-¹H spin diffusion from the vicinity of trinitroxide dopants to the bulk of the frozen solution, may be slower presumably due to a more pronounced spin-diffusion “barrier” in the absence of MAS.¹⁴

Similar experiments on sample 3 (without nitroxide doping) at 21 K showed a much smaller change in the integrated ¹H signal after MAS was switched off (see Fig. S5 in the supplementary material).¹⁰ The time dependence of this small signal change does not fit an exponential recovery well, and its rough time constant (∼220 s) is much longer than ¹H T_1n, which suggests that this small signal change is attributable to a gradual reduction in sample temperature. Similar experiments on sample 6 (DOTOPA-Ethanol doped) at 120 K also showed a much smaller change in the integrated ¹H signal after MAS was switched off (see Fig. S6 in the supplementary material).¹⁰ This result is consistent with the relatively small difference between signals from samples 1 and 3 with and without MAS at temperatures near 100 K.

To summarize, under our experimental conditions below 30 K, ¹H spin polarizations in nitroxide-doped frozen solutions have lower steady-state values under MAS than in the absence of MAS. When MAS is stopped within several seconds, the ¹H spin polarization increases toward the larger value on a time scale equal to the non-MAS T_1n. A sudden change in integrated ¹H signal is not observed when MAS is stopped, showing that any paramagnetic bleaching effects with a fast time constant (<1 s) do not have any dependence on MAS. Our experiments show ∼20%–25% signal loss (relative to a sample without nitroxide doping) at 19 K without MAS, which may be from conventional paramagnetic bleaching. However, the majority of the ∼6-fold signal loss with MAS recovers with time constant T_1n when MAS is stopped. Because the cross-effect DNP process can proceed even in the absence of microwaves,¹⁵ and the cross-effect buildup time is the same as T_1n, we attribute the loss of signal under MAS in nitroxide-doped samples to cross-effect DNP toward a lower nuclear polarization, as explained in detail below. At higher temperatures, the signal loss is smaller (and we do not measure any significant recovery of the signal loss on stopping MAS at 120 K under our conditions), presumably due to the shorter T_1e at higher temperatures.

NUMERICAL SIMULATIONS

General principles

The observed nuclear spin depolarization in nitroxide-doped samples under MAS can be explained by two general principles. First, the cross-effect DNP mechanism, involving transitions that flip one nuclear spin and two electron spins whose frequencies differ by the NMR frequency, does not require microwave irradiation. In the absence of microwaves, three-spin transitions still occur, and tend to equilibrate the nuclear spin polarization with the spin polarization difference between the two electrons. Second, the electron spin polarization distribution across the EPR lineshape (and thus the spin polarization difference between pairs of electrons with different EPR frequencies) can be altered by MAS. The EPR frequency of a nitroxide electron spin oscillates with time under MAS because of the large nitroxide g-anisotropy. When the EPR frequency is changing rapidly relative to 1/T_1e, the electron spin polarization is not determined simply by a Boltzmann distribution at the instantaneous EPR frequency. Instead, the spin polarization depends on the past EPR frequency history. Also important for the electron spin polarization distribution is electron spin diffusion, which can be affected by MAS. In a static sample, coupled pairs of electrons can have EPR frequency differences that are large relative to the electron-electron couplings, thus suppressing electron spin diffusion. Under MAS, however, the EPR frequencies of most electron spin pairs cross several times per sample rotation period,³ giving the electron spins a greater probability of exchanging polarization. This polarization exchange usually reduces the spin polarization differences among electrons.

The overall result of the two principles discussed above is that nuclear spin polarizations are usually reduced from their thermal equilibrium values by the cross-effect DNP mechanism and MAS, in agreement with our experiments. To examine this phenomenon in greater detail, we use two different models for simulations, namely, the three-spin model (two electrons and one nucleus within a single biradical molecule) developed in our earlier studies of cross-effect DNP under MAS³ and a new 3000-spin model (1000 three-spin groups, representing 1000 biradical molecules) that includes intermolecular electron spin diffusion.

Three-spin model

The three-spin model was described previously.³ Calculations here are similar, except that microwave irradiation is omitted. For this model of cross-effect DNP, we have the following Hamiltonian, in angular frequency units,

$$\begin{array}{ccc}\hfill H& =& {\omega }_{e1}{S}_{1z}+{\omega }_{e2}{S}_{2z}+{\omega }_n{I}_z+d(2S_{1z}{S}_{2z}-S_{1x}{S}_{2x}-S_{1y}{S}_{2y})\hfill \\ & & +h_{zz}2I_z{S}_{1z}+h_{xz}2I_x{S}_{1z}+h_{yz}2I_y{S}_{1z}.\hfill \end{array}$$ (1)

This Hamiltonian includes the interactions of the two electrons and one ¹H nucleus with the external static magnetic field in the z direction, producing EPR and NMR frequencies ω_e1, ω_e2, and ω_n, the dipole-dipole coupling between the electrons, with coupling constant d, and the hyperfine coupling between the nucleus and one of the electrons, with coupling constants h_αβ. The electron-electron coupling and hyperfine coupling are expressed in the high-field limit with respect to the EPR frequencies. However, the hyperfine coupling is not in the high field limit with respect to the NMR frequency, because the h_xz and h_yz terms (although small relative to ω_n) are not entirely negligible and are essential for DNP. Under MAS, ω_e1, ω_e2, ω_n, d, and h_αβ are time-dependent. For simplicity, we neglect the time dependence of ω_n, since the time dependence of the spin energy levels is dominated by the much larger electron g-anisotropy. Unless otherwise noted, simulations use the parameter values listed in Table 3.

Table 3.

Standard values of parameters in simulations.¹

Parameter	Standard value
Microwave frequency, ωm/2π	264.0 GHz
Microwave strength, ω1/2π	80 kHz
1H NMR frequency, ωn/2π	−400.9 MHz
Temperature, T	25 K
MAS frequency, ωr/2π	7.0 kHz
Electron-electron coupling, dmax/2π	23 MHz
Hyperfine coupling, hzz,max/2π	9 MHz
T1e	2 ms
T2e from slow fluctuations	4 μs
T2e from fast fluctuations	2 ms
T1n	1000 s
T2n	0.2 ms

¹In simulations without microwave irradiation, ω₁ = 0. T_2e, T_2n, and T_1n are not included in 3000-spin simulations. See Ref. 3 for justifications for these parameters.

The time evolution of this three-spin model is calculated numerically using the 8 × 8 density matrix description. Spin relaxation is included by periodic modification of the density matrix as previously described.³ Powder averaging is performed with 200 random biradical orientations, where each biradical orientation consists of random orientations of the electron g-tensor, electron-electron dipole-dipole coupling tensor, and electron-nucleus hyperfine coupling tensor principal axes in the MAS rotor. No correlations among the various orientation angles are used. In addition to electron-¹H hyperfine coupling, the electron-¹⁴N hyperfine coupling of each nitroxide moiety is included, with the ¹⁴N spin state randomly chosen for each nitroxide and kept fixed during the calculations. (The electron-¹⁴N hyperfine coupling effectively modifies the electron g-tensor, but has no other effect.)

For each biradical orientation, the time dependence of the density matrix is calculated starting from two different initial conditions: (i) thermal equilibrium of all spins at 25 K, based on instantaneous energy levels at the beginning of a MAS rotation period; (ii) thermal equilibrium of the electrons, and the nuclear spin polarized to 10 times its thermal equilibrium value p_n,therm. By considering two different initial conditions, we avoid the problem of distinguishing between a biradical orientation which has no net cross-effect relaxation and an orientation that happens to have a final steady-state nuclear spin polarization close to the initial nuclear spin polarization. For each of the two initial conditions, the time dependence of the density matrix is first calculated for an equilibration period of 5T_1e, without hyperfine coupling or nuclear spin relaxation. After this equilibration period, the calculation is continued with the complete Hamiltonian for 100 ms (unless otherwise noted).

We fit the time dependence of the nuclear spin polarization for the two initial conditions to exponential curves, with a common time constant (t_DNP) and steady-state nuclear spin polarization, (p_n). Orientationally averaged time constants and steady-state polarizations (t_DNP,ave and p_n,ave) are calculated according to

$$p_{n,ave}=\frac{\sum _{k=1}^N{\left(\frac{p_n}{t_{\mathrm{DNP}}}\right)}_k}{\sum _{k=1}^N{\left(\frac{1}{t_{\mathrm{DNP}}}\right)}_k},$$ (2a)

$$\frac{1}{t_{DNP,ave}}=\frac{1}{N}\sum _{k=1}^N{\left(\frac{1}{t_{DNP}}\right)}_k,$$ (2b)

where the index k represents a single biradical orientation and N is the number of orientations.

3000-spin model

The second model is designed to include electron spin diffusion by including dipole-dipole couplings among electrons in different biradicals. For this model, we use 1000 copies of the three-spin system, for a total of 2000 electron spins and 1000 nuclei spins. In order to simulate this many-spin system conveniently, we do not use a full quantum mechanical calculation. As discussed previously,³ DNP under MAS can be viewed as a series of population transfers at spin energy level crossings. The dynamics of the full quantum mechanical system can be well approximated by using the analytical Landau-Zener formula¹⁶ to calculate the probabilities of spin transitions during the level crossings. Figures S7 and S8 in the supplementary material demonstrate that level-crossing calculations using the Landau-Zener formula give results very similar to full three-spin quantum mechanical simulations.¹⁰

In total, four simplifications are made: (i) The dynamics of the many-spin system are modeled as a series of non-overlapping level crossings at which transition probabilities are evaluated with the Landau-Zener formula; (ii) Correlations between spin state populations in different three-spin systems are not preserved. This allows us to represent the state of the system by the populations of only 8000 energy levels (eight energy levels for each of 1000 three-spin systems), rather than by 2³⁰⁰⁰ states; (iii) Intermolecular electron-electron couplings are included only if the intermolecular distance is less than 45 Å and only to determine the probability that two electrons in different biradicals exchange their spin polarizations when their frequencies cross. The energy levels of one three-spin system are not perturbed by couplings to other three-spin systems; (iv) Each nucleus is coupled to only one electron.

With these simplified dynamics, the time dependences of spin polarizations for all 3000 spins are calculated as follows. First, 1000 biradical orientations are chosen randomly, and the same random orientations are used for all calculations. The positions of the biradicals are chosen randomly in a cube sized to simulate the desired biradical concentration. These positions are used to calculate intermolecular electron-electron couplings. Configurations with electron-electron distances less than 2.5 Å are rejected. (For 0 mM concentration, intermolecular couplings are not included.) Initial populations are assigned to the eight energy levels within each biradical according to Boltzmann factors. Then, the time dependences of spin energy levels within each biradical are calculated under MAS (ignoring off-diagonal terms in the electron-electron and hyperfine couplings), and the Landau-Zener formula is used to calculate probabilities of spin transitions at each energy level crossing. If a pair of levels have populations ρ₁ and ρ₂ before the crossing and if the Landau-Zener probability of a transition is p, then the populations after the crossing become ρ₁(1 − p) + ρ₂p and ρ₁p + ρ₂(1 − p).

Three types of energy level crossings are important for cross-effect DNP: (i) Electron-microwave crossings, where an EPR frequency crosses the microwave carrier frequency (ω_m), which can flip an electron spin if the microwave amplitude (ω₁) is non-zero; (ii) Three-spin crossings, where ω_e1 − ω_e2 = ω_n, which can cause a three-spin transition. Only three-spin crossings involving spins within the same biradical are included in these simulations; (iii) Electron-electron crossings, where two EPR frequencies are equal, which can produce a flip-flop transition of the two electrons. Electron-electron crossings involving electron pairs within the same biradical and electron pairs within different biradicals that are separated by less than 45 Å are included. Additionally, effects of T_1e relaxation are calculated by including partial population transfers toward a Boltzmann distribution at each time step as previously described.³T₂ relaxation is not necessary because the Landau-Zener formula does not create coherences between states.

The time dependence of the nuclear spin polarizations is calculated for two initial conditions after a 5T_1e equilibration period, as described above, resulting in two roughly exponential curves for the nuclear spin polarization in each three-spin system. These curves are then fit, and the results averaged as in Eqs. 2a, 2b.

Simulation results without microwave irradiation

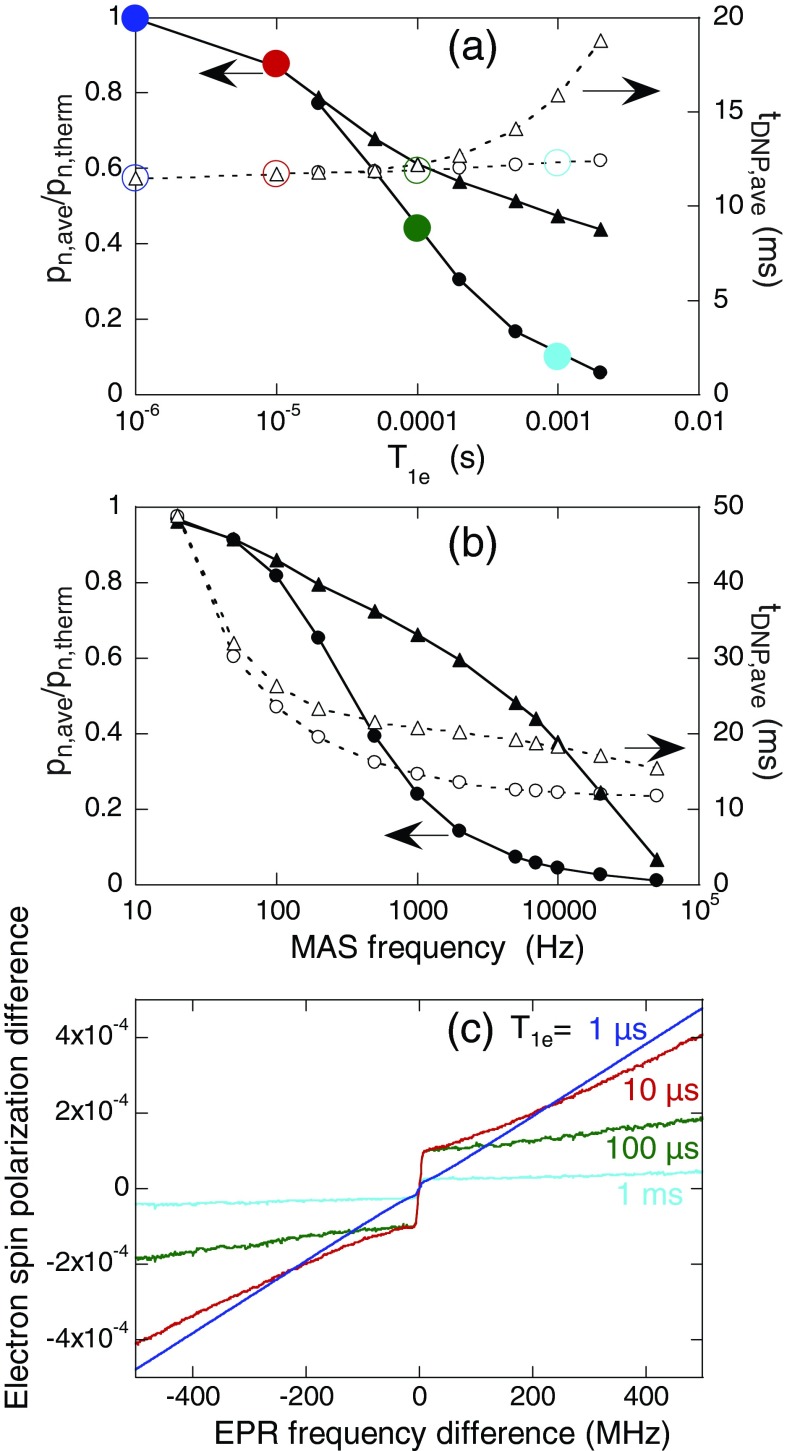
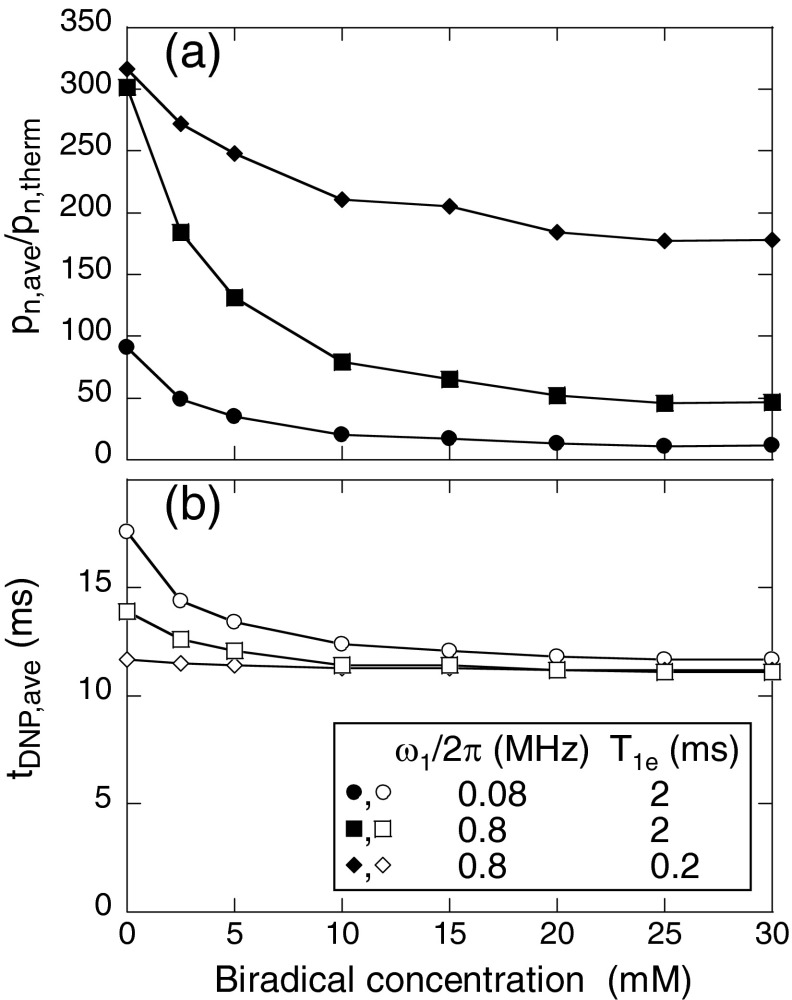
Figure 4a shows the dependences of p_n,ave and t_DNP,ave on T_1e under MAS at 7.0 kHz in the absence of microwave irradiation, calculated with the 3000-spin model. When intermolecular electron-electron couplings are not included (triangles), p_n,ave equals the thermal equilibrium nuclear spin polarization when T_1e is short compared with the MAS rotation period, but decreases as T_1e becomes longer. When intermolecular electron-electron couplings corresponding to a 15 mM biradical concentration are included, the reduction in p_n,ave is more pronounced, becoming comparable to the experimentally observed low temperature signal losses when T_1e ∼ 500 μs. The value of t_DNP,ave is nearly independent of T_1e at 15 mM biradical concentration but increases with increasing T_1e when intermolecular electron-electron couplings are not included. Figure 4b shows the dependences on MAS frequency, for T_1e = 2.0 ms. Values of p_n,ave and t_DNP,ave decrease with increasing MAS frequency, with stronger dependences on the MAS frequency at 15 mM biradical concentration, qualitatively consistent with the experimental observations.

Figure 4.

(a) and (b) Average values of steady-state nuclear spin polarizations (p_n,ave, solid symbols) and polarization time constants (t_DNP,ave, open symbols) as a function of T_1e and MAS frequency from calculations using the 3000-spin level-crossing model with biradical concentrations of 15 mM (circles) and 0 mM (i.e., without intermolecular electron-electron couplings, triangles). The nuclear spin polarization is divided by its thermal equilibrium value p_n,therm. (c) Average polarization difference between the two electrons within a biradical as a function of the frequency difference between the electrons, with 15 mM biradical concentration and with T_1e equal to 10⁻⁶ s (blue), 10⁻⁵ s (red), 10⁻⁴ s (green), and 10⁻³ s (aqua). Lines are drawn to guide the eye. Colors in panel (c) correspond to those in panel (a).

Results for p_n,ave in Figs. 4a, 4b are attributable to changes in the distribution of electron spin polarizations across the EPR lineshape under MAS, as proposed above. Figure 4c shows the simulated dependence of the spin polarization difference between the two electrons within a biradical on the instantaneous EPR frequency difference under MAS for various values of T_1e. When electron spin-lattice relaxation is very rapid, the polarization difference depends linearly on the EPR frequency difference, as expected at thermal equilibrium. As T_1e becomes longer, the polarization difference becomes less strongly dependent on EPR frequency difference, with a discontinuity at zero frequency difference. Polarization differences are generally smaller at larger T_1e. Results in Fig. 4c reflect the transport of electron spin polarizations across the EPR lineshape produced by MAS, with the discontinuity at zero frequency difference arising from the high efficiency of electron spin flip-flop transitions at the electron-electron crossings discussed above.

In the limit of rapid electron spin-lattice relaxation, biradicals in which the higher-frequency electron spin is “down” and the lower-frequency electron spin is “up” are more prevalent than biradicals with the opposite electron spin configuration. Thus, three-spin transitions at three-spin crossings flip nuclear spins (with positive gyromagnetic ratios) from “down” to “up” at a greater rate than from “up” to “down,” leading to a steady-state nuclear spin polarization equal to its thermal equilibrium value. In the limit of large T_1e, where electron spin polarization differences under MAS are reduced, the two nuclear spin-flip rates become more nearly equal, leading to a smaller steady-state nuclear spin polarization.

Dependences on biradical concentration in Figs. 4a, 4b arise from more efficient equalization of electron spin polarizations when intermolecular electron-electron couplings are included. Since intramolecular couplings are relatively strong, electron-electron level crossings involving intramolecular electron pairs are highly adiabatic, tending to preserve electron spin polarization differences within each biradical as EPR frequencies cross under MAS, as previously described.³ However, inclusion of intermolecular couplings permits electron spin diffusion by intermolecular flip-flop transitions at intermolecular electron-electron crossings. This electron spin diffusion process tends to equalize the spin polarization of the two electrons in each biradical. Then, the reduced electron spin polarization difference between the two electrons can result in reduced nuclear polarization through the cross effect DNP mechanism.

In the absence of electron-electron couplings, t_DNP,ave increases when T_1e exceeds 0.1 ms (Fig. 4a) because full equilibration of the three spin system requires relaxation of the electron spin polarizations. When electron-electron couplings are included, electron spin diffusion can cause electron spin flips in place of spin-lattice relaxation.

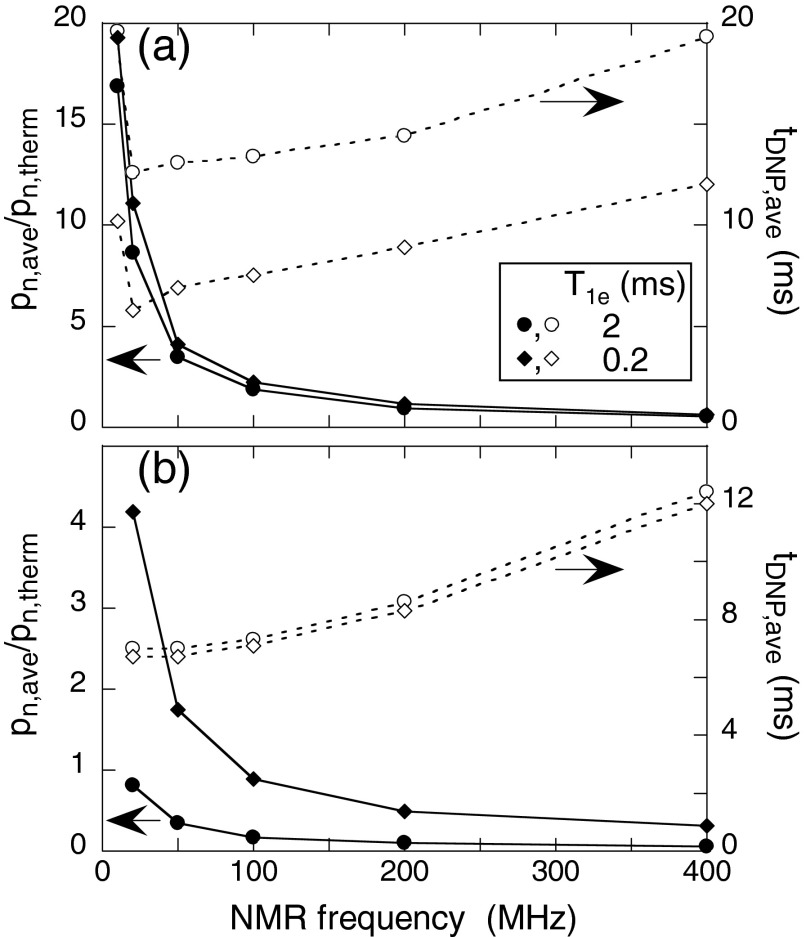
Figure 5 shows the dependences of p_n,ave and t_DNP,ave on NMR frequency, calculated with the three-spin model (Fig. 5a) and the 3000-spin model (Fig. 5b). Interestingly, both models predict that MAS can produce enhancements of nuclear spin polarization without microwave irradiation when NMR frequencies are small (relative to the EPR linewidth dictated by the nitroxide g-anisotropy). The enhancements of nuclear spin polarization arise from the increased electron spin polarization differences at small EPR frequency differences in Fig. 4c for intermediate values of T_1e. However, we should note that if ω_n is too small (ω_n < d), the cross effect mechanism described here is not effective because the electron-electron (ω_e1 − ω_e2 = 0) and three spin crossings (ω_e1 − ω_e2 = ω_n) overlap. Although enhancements of nuclear spin polarization under MAS have not yet been observed experimentally, experiments described above do show that ¹³C spin polarizations (100.8 MHz NMR frequency) can exhibit smaller reductions under MAS than ¹H spin polarizations (400.9 MHz) in the same samples, in qualitative agreement with simulations in Fig. 4c for T_1e ∼ 1 ms.

Figure 5.

Average values of steady-state nuclear spin polarization (p_n,ave, solid symbols) and polarization time constant (t_DNP,ave, open symbols) as a function of the NMR frequency from calculations with T_1e = 2 ms (circles) or T_1e = 0.2 ms (diamonds). (a) Three-spin quantum mechanical model. (b) 3000-spin level-crossing model, with biradical concentration 15 mM. In all calculations, the hyperfine coupling strength is scaled with the NMR frequency according to h_zz,max/2π = 9 MHz × (ω_n/400 MHz). Lines are drawn to guide the eye.

Simulation results with microwave irradiation

Although this paper focuses on effects that occur in the absence of microwave irradiation, it is also possible to use the 3000-spin model to simulate DNP in the presence of microwaves. Figure 6 shows results from such simulations for several combinations of microwave field amplitude ω₁ and T_1e under MAS at 7.0 kHz. Values of p_n,ave/p_n,therm (i.e., microwave-driven DNP enhancement factors) decrease with increasing biradical concentration, but remain large when ω₁ is large and T_1e is relatively short. Values of t_DNP,ave also decrease somewhat with increasing biradical concentration. (It should be noted that DNP build-up times in real samples can be limited by the time scale for nuclear spin diffusion from the vicinity of paramagnetic dopants to the bulk, a process that is not included in these simulations.)

Figure 6.

(a) and (b) Average values of steady-state nuclear spin polarization (p_n,ave) and polarization time constant (t_DNP,ave) under 7.0 kHz MAS as a function of biradical concentration from 3000-spin calculations with microwave field amplitude ω₁/2π = 0.08 MHz and T_1e = 2 ms (circles), with ω₁/2π = 0.8 MHz and T_1e = 2 ms (squares), and with ω₁/2π = 0.8 MHz and T_1e = 0.2 ms (diamonds). The microwave frequency is 264.0 GHz. Lines are drawn to guide the eye.

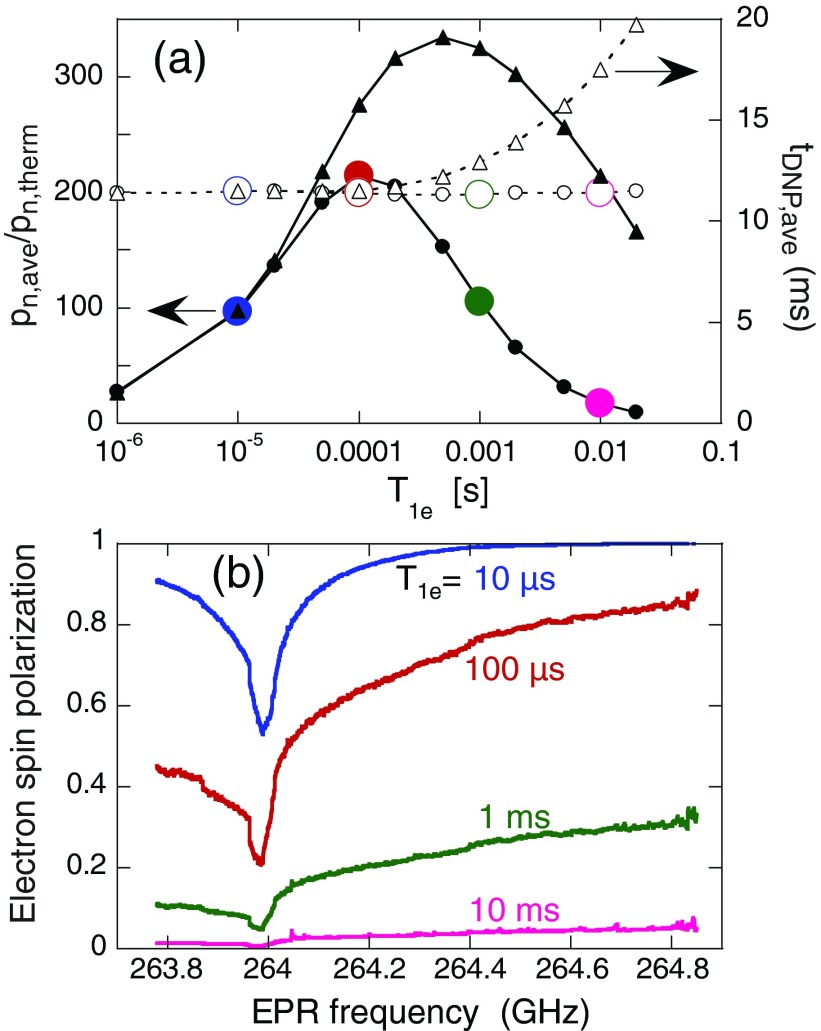
Figure 7a shows the simulated dependences of p_n,ave/p_n,therm and t_DNP,ave on T_1e under MAS with ω₁/2π = 0.8 MHz. Maximum DNP enhancement factors are observed at values of T_1e that depend on biradical concentration. When T_1e is very short, DNP enhancements are small because microwave irradiation has a relatively small effect on electron spin polarizations across the EPR lineshape. When T_1e becomes long, electron spin polarizations become small across the entire EPR lineshape, as shown in Fig. 7b. Electron spin polarization differences are then necessarily small, leading to small steady-state nuclear spin polarizations.

Figure 7.

Average values of steady-state nuclear spin polarization (p_n,ave, solid symbols) and polarization time constant (t_DNP,ave, open symbols) as a function of T_1e from 3000-spin calculations with ω₁/2π = 0.8 MHz and biradical concentrations of 15 mM (circles) and 0 mM (triangles). Lines are drawn to guide the eye. (b) Electron spin polarization across the EPR lineshape from calculations with 15 mM biradical concentration and T_1e = 10 μs (blue), 100 μs (red), 1 ms (green), and 10 ms (pink). Electron spin polarization is normalized to its thermal equilibrium value. Colors in panel (b) correspond to those in panel (a).

Additional results from 3000-spin simulations with microwave irradiation are shown in Figs. S9–S12 of the supplementary material.¹⁰

DISCUSSION

Experiments presented above show that ¹H and ¹³C NMR signal amplitudes from samples that contain nitroxide-based triradical and biradical dopants are reduced significantly under MAS at low temperatures, relative to signals from the same samples without nitroxide dopants. Data in Fig. 3 prove that the majority of the observed signal reductions below 30 K are not due to conventional paramagnetic bleaching effects or any other effects that have a time constant different from T_1n. The majority of the NMR signal loss occurs only under MAS, and has a time constant for recovery equal to ¹H T_1n. These MAS-dependent signal losses can be explained by the establishment of steady-state nuclear spin polarizations that are smaller than thermal equilibrium values, driven by the cross-effect DNP mechanism. Simulations with a 3000-spin model that includes intermolecular electron-electron couplings and thus electron spin diffusion demonstrate that the experimentally observed effects should be most significant when T_1e is larger than the MAS rotation period, which typically leads to a reduction in electron spin polarization differences within biradicals. Experimentally, we find that effects of MAS on steady-state nuclear spin polarizations become much smaller at temperatures near 100 K or higher. This temperature dependence is qualitatively consistent with the estimated temperature dependence of T_1e for nitroxide dopants. The MAS rotation period of 150 μs in most of our spinning measurements is shorter than the estimated T_1e ∼ 2 ms at 35 K and 9.4 T,⁷ but comparable to measurements of T_1e = 0.2–0.6 ms at 80 K and 5 T.¹²

Corzilius et al.¹² have recently reported measurements of doping-induced CP ¹³C NMR signal losses in frozen glycerol/water solutions at 8.9 T and 78–85 K that are relevant to our results presented above. In particular, they report signal losses (relative to an undoped sample) of 5%–10% for both TOTAPOL-doped and trityl-doped samples (20 mM electrons) without MAS and signal losses of 40%–50% under MAS at 5.0 kHz. The similarity of results for TOTAPOL and trityl-doped samples under MAS argues against a significant (i.e., >10%) contribution for nuclear depolarization via the cross effect DNP mechanism at 80 K. The results of Corzilius et al.¹² are consistent with ours, in that we also observe 40%–50% signal losses with MAS at 87–107 K for a slightly higher doping level (30 mM electrons, see Table 2). Corzilius et al. do not report results for experiments below 78 K.

We should emphasize that the observed signal reductions at low temperatures are not an inevitable feature of cross-effect DNP under MAS without microwave irradiation, but rather depend on the EPR lineshape and electron spin diffusion properties of the radicals. Simulations in Fig. 5 show that low-frequency nuclear spins could have their polarization increased if electron spin diffusion is sufficiently weak. For nitroxide biradicals, simulations suggest that the nuclear polarization could be greater than the static thermal polarization for NMR frequencies of roughly <100 MHz at 9.4 T (Fig. 5a). However, if electron spin diffusion is included for a biradical concentration of 15 mM, and T_1e = 2 ms, the simulations show reduction of the nuclear polarization even for low-frequency nuclei (Fig. 5b, circles). Additionally, perturbations of nuclear spin polarizations by MAS could be reduced or eliminated if hypothetical biradical dopants that contain two different narrow-line radicals with non-overlapping EPR lineshapes were used to satisfy the cross-effect DNP condition (ω_e1 − ω_e2 = ω_n). The lack of overlap between the EPR lineshapes of the two different radicals would suppress electron spin diffusion, and a narrow linewidth would mean that the electron spin polarizations (without microwaves) would remain close to the thermal equilibrium polarizations for the instantaneous EPR frequencies.

Qualitatively, the 3000-spin simulations fit the experimental data by predicting a larger signal loss as the temperature decreases and T_1e lengthens. Also, the simulations have a similar dependence on MAS frequency and predict a larger spin polarization reduction for ¹H nuclei than for ¹³C nuclei. Quantitatively, however, the simulations do not precisely match the experiments. In particular, the simulations predict steady-state ¹H spin polarizations under MAS that are significantly smaller than seen in experiments (see Figs. 1234). Several simplifications in the simulations could account for this discrepancy, including the neglect of correlations between electron spins in different biradicals in the 3000-spin model (which may then overestimate electron spin diffusion) and the fact that the 3000-spin simulations include only one nuclear spin per biradical.

When microwaves are applied, simulations in Fig. 7a show a maximum in nuclear polarization as a function of T_1e. T_1e must be long enough to allow saturation of one electron of a biradical, while not so long that the second electron is also saturated, by electron spin diffusion. A long T_1e could also be the limiting time constant in the entire polarization cycle, slowing the polarization of many nuclei from one biradical.¹⁷

From a practical standpoint, perturbations of nuclear spin polarizations by MAS in nitroxide-doped samples are important because NMR signal enhancement factors due to DNP are often evaluated simply by comparing signals with and without microwave irradiation. Our results show that the true DNP enhancement factor under MAS (relative to an undoped sample or relative to a sample that contains paramagnetic dopants that reduce T_1n but do not produce DNP) may differ from the ratio of signals with and without microwaves by a factor greater than five at low temperatures. Conditions that produce the largest ratio of signals with and without microwaves may not be the same as conditions that maximize NMR sensitivity. Optimizing the NMR sensitivity with DNP has been discussed in several articles,¹⁸ but in this article, we have presented an additional mechanism that affects the NMR signal not discussed previously.