An efficient algorithm for multipole energies and derivatives based on spherical harmonics and extensions to particle mesh Ewald

Abstract

Next-generation molecular force fields deliver accurate descriptions of non-covalent interactions by employing more elaborate functional forms than their predecessors. Much work has been dedicated to improving the description of the electrostatic potential (ESP) generated by these force fields. A common approach to improving the ESP is by augmenting the point charges on each center with higher-order multipole moments. The resulting anisotropy greatly improves the directionality of the non-covalent bonding, with a concomitant increase in computational cost. In this work, we develop an efficient strategy for enumerating multipole interactions, by casting an efficient spherical harmonic based approach within a particle mesh Ewald (PME) framework. Although the derivation involves lengthy algebra, the final expressions are relatively compact, yielding an approach that can efficiently handle both finite and periodic systems without imposing any approximations beyond PME. Forces and torques are readily obtained, making our method well suited to modern molecular dynamics simulations.

INTRODUCTION

Non-covalent interactions play a central role in numerous areas of chemistry and biology,^{1, 2} including protein structure,³ drug binding and molecular recognition,^{4, 5} molecular crystal structure,⁶ and nucleobase stacking.⁷ Accurate representations of these interactions, which are relatively small in magnitude, are crucial for physically realistic simulations. However, for large systems the sheer number of pairwise interactions to be considered, coupled with the need to run long simulations to sample large amounts of configurational space, necessitates a model that can be rapidly evaluated. As a compromise for these conflicting objectives, force fields can be developed by fitting classical functional forms to high-level quantum mechanical data; the choice of this functional form dictates both the accuracy and efficiency of the model.

Focusing on the classical electrostatic force field terms, the potential at a point R due to a charge distribution can be expanded⁸ in a power series about the center (r = 0) of that distribution

$$\begin{array}{ccc}\hfill V\left(\mathbf{R}\right)& =& \frac{1}{4\pi {\epsilon }_0}\int \frac{\rho \left(\mathbf{r}\right)}{|\mathbf{R}-\mathbf{r}|}\mathrm{d}\mathbf{r}\hfill \\ & =& \frac{1}{4\pi {\epsilon }_0}\int \rho \left(\mathbf{r}\right)\mathrm{d}\mathbf{r}\left(\frac{1}{R}\right)-\int r_{\alpha }\rho \left(\mathbf{r}\right)\mathrm{d}\mathbf{r}\left({\nabla }_{\alpha }\frac{1}{R}\right)\hfill \\ & & +\int \frac{1}{2!}{r}_{\alpha }{r}_{\beta }\rho \left(\mathbf{r}\right)\mathrm{d}\mathbf{r}\left({\nabla }_{\alpha }{\nabla }_{\beta }\frac{1}{R}\right)-...\hfill \\ & =& \frac{1}{4\pi {\epsilon }_0}(Q_0{T}_0-Q_{\alpha }{T}_{\alpha }+Q_{\alpha \beta }{T}_{\alpha \beta }-...),\hfill \end{array}$$ (1)

where the integrals on the second line provide a definition of Cartesian multipole moments Q, and the terms in parentheses define the interaction tensors T; the Greek subscripts represent {x, y, z} and summation over repeated indices on adjacent tensors is implied. The multipole moments may be computed ab initio, and 1 can be extended to obtain the interaction energy of two centers A and B, whose charge densities are non-overlapping:

$$\begin{array}{ccc}\hfill E_{AB}& =& \frac{1}{4\pi {\epsilon }_0}[T_0\left(Q_0^A{Q}_0^B\right)+T_{\alpha }\left(Q_0^A{Q}_{\alpha }^B-Q_{\alpha }^A{Q}_0^B\right)\hfill \\ & & +T_{\alpha \beta }\left(Q_0^A{Q}_{\alpha \beta }^B-Q_{\alpha }^A{Q}_{\beta }^B+Q_{\alpha \beta }^A{Q}_0^B\right)+...].\hfill \end{array}$$ (2)

The derivation of 2 will be discussed later. For now, we observe that two multipole moments of rank l_a and l_b are coupled via an interaction tensor of rank l = l_a + l_b, which allows us to rewrite 2 using more compact notation:

$$E_{AB}=\frac{1}{4\pi {\epsilon }_0}\sum _{l_a,l_b}^{\infty }{(-1)}^{l_a}{Q}_{l_a}^A{T}_{l_a+l_b}{Q}_{l_b}^B.$$ (3)

Using this shorthand we label the tensors only by their rank, assuming summation over all constituent components.

Most existing molecular force fields approximate electrostatic interactions by truncating 2 at the first term, thus including only isotropic point charges on the atomic centers. By extending the expansion to include the anisotropic higher-order terms, methods such as AMOEBA,^{9, 10, 11} the SSDQO water model,¹² or the effective fragment potential^{13, 14} generate more directionality in electrostatic interactions, increasing accuracy.^{15, 16, 17} Although it is well established that higher-order multipoles improve the quality of molecular force fields, they have yet to find widespread use. To remedy this, we seek the most compact representation possible, upon which an efficient algorithm can be developed.

The Cartesian quadrupole tensor has nine elements, of which only six are unique as a result of symmetry with respect to index permutations. A redundancy exists among these, which becomes evident when we consider that the Coulomb operator is harmonic, i.e., it satisfies Laplace's equation:

$${\nabla }^2\frac{1}{R}=T_{xx}+T_{yy}+T_{zz}=0(R\ne 0).$$ (4)

As a result, we can add an arbitrary constant to the diagonal elements of the quadrupole tensor without affecting its contribution to the electrostatic potential, which is generated by taking its inner product with the T tensor as in 1. A common strategy, introduced by Buckingham,¹⁸ is to redefine the Cartesian multipole moments such that they are traceless, i.e., Q_xx + Q_yy + Q_zz = 0. This constraint results in only two of the three trace elements being linearly independent. Thus, only five independent components of the quadrupole tensor are unique. More generally, the lth order Cartesian multipole moment has l(l + 1)/2 components, of which only 2l + 1 are unique. An alternative to the Buckingham Cartesian representation of multipole moments is to expand the potential in a basis of spherical harmonics, containing 2l + 1 components at each level of angular momentum l.^{19, 20, 21, 22, 23, 24, 25, 26, 27, 28} The number of components in a spherical harmonic grows linearly with angular momentum, making them a very compact, natural representation for harmonic operators when compared with the Cartesian basis, whose size increases quadratically with angular momentum. Moreover, the orthogonality properties of spherical harmonics can be exploited to achieve compact working equations (vide infra); the mathematics required to manipulate these functions is typically more involved than that required for Cartesian functions. Spherical harmonics have also been used to efficiently evaluate interactions of diffuse multipole moments.^{29, 30}

Given the relative ease of manipulating Cartesian expressions, and because trajectories are typically propagated in Cartesian space, the Buckingham representation has been widely employed in previous multipole implementations.^{9, 12, 31, 32, 33, 34, 35, 36, 37} Extensions to Cartesian multipole methods to include Ewald summation techniques have been derived.^{9, 32, 33, 34, 35, 36, 37} The Ewald summation, and its more efficient particle-mesh Ewald (PME) variant,^{38, 39, 40} involves partitioning the Coulomb operator into short- and long-ranged terms:^{41, 42, 43}

$$\frac{1}{R}\to \frac{\mathrm{erfc}\left(\beta R\right)}{R}+\frac{\mathrm{erf}\left(\beta R\right)}{R}.$$ (5)

The attenuated nature of the first term allows fewer pairwise interactions to be explicitly treated in real space, while the second term is treated in reciprocal space via a Fourier transform, allowing for an efficient treatment of periodic systems. This partitioning averts the singularity in the Coulomb operator, and replaces a single, conditionally convergent sum with two absolutely convergent sums that converge rapidly in their respective spaces. The same method may also be applied to finite systems.⁴⁴

The attenuation parameter, β, is chosen to strike a balance between longer cutoffs in direct space and larger Fourier transforms required in reciprocal space, with the optimal choice minimizing computation time for a given overall accuracy. This was powerfully demonstrated by Sagui, Pedersen, and Darden (SPD), who showed that the computational cost of treating multipoles in reciprocal space is not much greater than the equivalent point-charge only treatment. By choosing a sufficiently large β value, they were able to push most of the work into reciprocal space and evaluate systems containing multipoles up to fourth order (hexadecapoles) with a cost of only about 8.5 times the equivalent point-charge only treatment. However, even with a highly attenuated Coulomb operator, SPD's direct space computation, which was based on Challacombe's efficient McMurchie-Davidson recursive scheme,³¹ remained the computational bottleneck.

The recursive scheme implemented by SPD has a computational cost that scales with multipole order l as $\mathcal{O}\left(l^4\right)$, whereas the spherical harmonic approach developed by Hättig^{25, 27} scales as $\mathcal{O}\left(l^3\right)$. In this work, we develop a model that combines the strengths of the spherical harmonic treatment with the efficient PME treatment developed by SPD. We will demonstrate that, although spherical harmonics are not a natural fit within the PME framework, they can be manipulated into a form that results in compact expressions. Furthermore, the compactness of these equations, coupled with the orthogonality of spherical harmonics, results in a very efficient multipole implementation.

THEORY

Spherical harmonics

Following Stone,⁸ we begin by providing an alternative derivation of Hättig's method,^{25, 27} forming the basis of this work. We will use standard spherical harmonics, which are defined (using the Condon-Shortley phase) in terms of associated Legendre polynomials $P_l^m\left(\cos \theta \right)$ as⁴⁵

$$\begin{array}{cc}\hfill {\mathcal{Y}}_{lm}(\theta ,\varphi )& ={(-1)}^m\sqrt{\frac{(2l+1)(l-m)!}{4\pi (l+m)!}}{P}_l^m\left(\cos \theta \right)e^{im\varphi }\hfill \\ \hfill {\mathcal{Y}}_{lm}^{*}(\theta ,\varphi )& ={(-1)}^m{\mathcal{Y}}_{l-m}(\theta ,\varphi ).\hfill \end{array}$$ (6)

We will also encounter their Racah normalized counterparts

$${\mathcal{C}}_{lm}(\theta ,\varphi )=\sqrt{\frac{4\pi }{2l+1}}{\mathcal{Y}}_{lm}(\theta ,\varphi )$$ (7)

and the regular and irregular solid harmonics

$$\begin{array}{cc}\hfill {\mathcal{R}}_{lm}\left(\mathbf{r}\right)& =r^l{\mathcal{C}}_{lm}(\theta ,\varphi )\hfill \\ \hfill {\mathcal{I}}_{lm}\left(\mathbf{r}\right)& =r^{-l-1}{\mathcal{C}}_{lm}(\theta ,\varphi ).\hfill \end{array}$$ (8)

The multipole expansion

Our starting point is the Legendre expansion of the Coulomb operator:

$$\begin{array}{ccc}\hfill \frac{1}{|{\mathbf{r}}_{>}-{\mathbf{r}}_{<}|}& =& \sum _{l=0}^{\infty }\sum _{m=-l}^l{\mathcal{R}}_{lm}^{*}\left({\mathbf{r}}_{<}\right){\mathcal{I}}_{lm}\left({\mathbf{r}}_{>}\right)\hfill \\ & =& \sum _{l=0}^{\infty }\sum _{m=-l}^l{(-1)}^m{\mathcal{R}}_{l-m}\left({\mathbf{r}}_{<}\right){\mathcal{I}}_{lm}\left({\mathbf{r}}_{>}\right).\hfill \end{array}$$ (9)

Figure 1 depicts the quasi-internal coordinate system introduced by Hättig.^{25, 27} Invoking this coordinate system involves defining the internuclear vector, R, between centers A and B as the local z-axis, and rotating the multipole moments accordingly. Assuming non-overlapping charge distributions on centers A and B, we can write r_> = R and r_< = r_a − r_b. Because of the alignment of the coordinate system, the irregular solid harmonic in 9 becomes⁴⁵${\mathcal{I}}_{lm}\left({\mathbf{r}}_{>}\right)=R^{-l-1}{\delta }_{m0}$, simplifying the expansion to

$$\frac{1}{|\mathbf{R}-{\mathbf{r}}_a+{\mathbf{r}}_b|}=\sum _{l=0}^{\infty }\frac{{\mathcal{R}}_{l0}({\mathbf{r}}_a-{\mathbf{r}}_b)}{R^{l+1}}.$$ (10)

The addition theorem for the regular solid harmonics can be written as^{8, 45, 46, 47, 48}

$$\begin{array}{ccc}\hfill {\mathcal{R}}_{lm}({\mathbf{r}}_a-{\mathbf{r}}_b)& =& \sum _{l_a,l_b=0}^{\infty }\sum _{m_a=-l_a}^{l_a}\sum _{m_b=-l_b}^{l_b}{\delta }_{l_a+l_b,l}{\mathcal{R}}_{l_a{m}_a}\left({\mathbf{r}}_a\right){\mathcal{R}}_{l_b{m}_b}\left({\mathbf{r}}_b\right)\hfill \\ & & \times {(-1)}^{l_a+m}\sqrt{\frac{(2l+1)!}{\left(2l_a\right)!\left(2l_b\right)!}}\left(\begin{array}{ccc}\hfill l_a& \hfill l_b& \hfill l\\ \hfill m_a& \hfill m_b& \hfill -m\end{array}\right)\hfill \end{array}$$ (11)

and the Wigner 3j symbol takes the form^{8, 45}

$$\begin{array}{ccc}\hfill \left(\begin{array}{ccc}\hfill l_a& \hfill l_b& \hfill l\\ \hfill m_a& \hfill m_b& \hfill -m\end{array}\right)& =& {(-1)}^{l_a-l_b+m}\sqrt{\frac{\left(2l_a\right)!\left(2l_b\right)!(l+m)!(l-m)!}{(2l+1)!(l_a+m_a)!(l_a-m_a)!(l_b+m_b)!(l_b-m_b)!}}\hfill \\ & =& {(-1)}^{l_a-l_b+m}\sqrt{\frac{\left(2l_a\right)!\left(2l_b\right)!}{(2l+1)!}\left(\begin{array}{c}l+m\\ l_a+m_a\end{array}\right)\left(\begin{array}{c}l-m\\ l_a-m_a\end{array}\right)}.\hfill \end{array}$$ (12)

To proceed, we combine the 3j symbol selection rule m_a + m_b = −m with the δ_m0 introduced by the quasi-internal coordinate system to write m_a = −m_b = −κ. Utilizing the identity ${\mathcal{R}}_{l_a-\kappa }\left({\mathbf{r}}_a\right)={(-1)}^{\kappa }{\mathcal{R}}_{l_a\kappa }^{*}\left({\mathbf{r}}_a\right)$, we arrive at the expansion

$$\begin{array}{ccc}\hfill \frac{1}{|\mathbf{R}-{\mathbf{r}}_a+{\mathbf{r}}_b|}& =& \sum _{l_a,l_b=0}^{\infty }\sum _{\kappa =-\min (l_a,l_b)}^{\min (l_a,l_b)}\frac{{\mathcal{R}}_{l_a\kappa }^{*}\left({\mathbf{r}}_a\right){\mathcal{R}}_{l_b\kappa }\left({\mathbf{r}}_b\right)}{R^{l+1}}{(-1)}^{l_b+\kappa }\hfill \\ & & \times \sqrt{\left(\begin{array}{c}l\\ l_a+\kappa \end{array}\right)\left(\begin{array}{c}l\\ l_a-\kappa \end{array}\right)}.\hfill \end{array}$$ (13)

The interaction energy between charge densities on centers A and B, which are separated by a distance R, can now be written compactly

$$\begin{array}{ccc}\hfill E_{AB}& =& \int \int \rho \left({\mathbf{r}}_a\right)\frac{1}{4\pi {\epsilon }_0|\mathbf{R}-{\mathbf{r}}_a+{\mathbf{r}}_b|}\rho \left({\mathbf{r}}_b\right)\mathrm{d}{\mathbf{r}}_a\mathrm{d}{\mathbf{r}}_b\hfill \\ & =& \sum _{l_a,l_b=0}^{\infty }\sum _{\kappa =-\min (l_a,l_b)}^{\min (l_a,l_b)}{\tilde{Q}}_{l_a\kappa }^{A*}{t}_{\kappa }^{l_a,l_b}\left(R\right){\tilde{Q}}_{l_b\kappa }^B.\hfill \end{array}$$ (14)

This expression utilizes the regular solid harmonic definition of the multipole moments, $Q_{lm}^{*}\equiv \int {\mathcal{R}}_{lm}^{*}\left({\mathbf{r}}_{\alpha }\right)\rho \left({\mathbf{r}}_{\alpha }\right)\mathrm{d}{\mathbf{r}}_{\alpha }$, and the t tensor

$$t_{\kappa }^{l_a,l_b}\left(R\right)=\frac{{(-1)}^{l_b+\kappa }}{4\pi {\epsilon }_0{R}^{l+1}}\sqrt{\left(\begin{array}{c}l\\ l_a+\kappa \end{array}\right)\left(\begin{array}{c}l\\ l_a-\kappa \end{array}\right)}.$$ (15)

We use a tilde in 14 to denote multipoles that have been rotated into the quasi-internal frame, in which the interaction tensor elements $t_m^{l_a,l_b}\left(R\right)$ assume a very simple scalar form. The orthogonality of spherical harmonics manifests itself by allowing only those components with the same κ values to interact, greatly reducing the number of interactions that must be considered. For example, a charge on A will only interact with the ${\tilde{Q}}_{4,0}^B$ component of the hexadecapole on B, whereas 9 interactions must be considered in a general coordinate system using spherical harmonics, and 15 interactions exist when Cartesian multipoles are employed. Moreover, Hättig has demonstrated²⁷ that the quasi-internal coordinate system allows computation of the gradients using only the six translational and rotational energy derivatives, the minimal number of terms, due to a decoupling of the internal degrees of freedom. The rotation matrices that reorient the regular solid harmonic multipoles are readily formed via recursion^{25, 49, 50} and programmable equations are provided in the supplementary material.⁵¹

Figure 1.

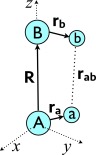
The quasi-internal coordinate system for a pair of centers A and B, whose internuclear axis, R, is coincident with the z axis. The vectors r_a and r_b represent locations within the densities associated with centers A and B, respectively.

Ewald extension

To enable treatment of periodic systems, and to utilize the reciprocal space to reduce computational expense, we now extend the method to include Ewald summation. In the Introduction, we motivated the use of spherical harmonics by noting that the Coulomb operator satisfies Laplace's equation. However, if we focus on the screened Coulomb operator which forms the short-ranged part of 5, we find that Laplace's equation is no longer satisfied

$${\nabla }^2\frac{\mathrm{erfc}\left(\beta R\right)}{R}=\frac{4{\beta }^3{e}^{-{\beta }^2{R}^2}}{\sqrt{\pi }}\ne 0.$$ (16)

An important corollary is that the screened Coulomb operator is no longer harmonic, and may not be trivially expanded in a basis of spherical harmonics. Because of this, Cartesian representations of this operator have been used in previous work.^{9, 32, 33, 34, 35, 36, 37, 52} Ángyán, Gerber, and Marsman detailed⁵³ the difficulty in formulating a spherical harmonic representation of the screened Coulomb operator. By invoking a Laplace transform and some lengthy algebra, performed with the aid of the Mathematica computer algebra system,⁵⁴ they derived the screened analog of 9,

$$\frac{\mathrm{erfc}\left(\beta r_{>}\right)}{|{\mathbf{r}}_{>}-{\mathbf{r}}_{<}|}=\sum _{l=0}^{\infty }\sum _{m=-l}^l\sum _k^{\infty }{\beta }^{2k}{D}_{l,k}\left(\beta r_{>}\right){\mathcal{I}}_{lm}^{*}\left({\mathbf{r}}_{>}\right)r_{<}^{2k}{\mathcal{R}}_{lm}\left({\mathbf{r}}_{<}\right),$$ (17)

where

$$\begin{array}{c}\hfill D_{l,k}\left(X\right)=\left\{\begin{array}{cc}\hfill \mathrm{erfc}\left(X\right)+\frac{e^{-X^2}}{\sqrt{\pi }}{2}^{l+1}{X}^{l+1}\sum _{m=1}^l\frac{2^{-m}{X}^{-2m}}{(2l-2m+1)!!}& \hfill \text{if}k=0\\ \hfill \frac{e^{-X^2}}{\sqrt{\pi }}\frac{2^{l+1}(2l+1)X^{2l+1}}{k!(2l+2k+1)}\sum _{m=1}^l\left(\genfrac{}{}{0pt}{}{m-k-1}{m-1}\right)\frac{2^{k-m}{X}^{2(k-m)}}{(2l+2k-2m+1)!}& \hfill \text{otherwise}.\end{array}\right.\end{array}$$ (18)

The k = 0 terms represent the unscreened operator, 9, while the remaining terms – hereafter referred to as “contamination” – are a result of the screened Coulomb operator not satisfying the Laplace equation, 16. To proceed in an analogous manner to Sec. 2B, we require a generalized version of the regular solid harmonic addition theorem that includes the radial prefactor, $r_{<}^{2k}$. In a series of papers, Sack outlined^{55, 56, 57, 58} the mathematics of these expansions, but showed the difficulty in formulating a symmetric generalized addition theorem.⁵⁶ Alternatively, the radial prefactor itself can be expanded⁵⁵ in a hypergeometric series involving spherical harmonics, which could then be coupled with the regular addition theorem, 11, via a Gaunt series.⁵⁹ Rather than pursue this approach, we instead derive the expansion in the more natural Cartesian basis and use Stone's Cartesian-spherical (CS) transformation^{60, 61} to obtain the desired expression. The CS transformation allows a tensor to be readily converted from Cartesian to Racah normalized spherical harmonic, cf. 7, representations

$$T_{lm}=\sum _{l_x+l_y+l_z=l}{C}_{lm,l_x{l}_y{l}_z}{T}_{l_x{l}_y{l}_z}$$ (19)

and from spherical harmonic to traceless Cartesian representations

$$T_{l_x{l}_y{l}_z}=\sum _{m=-l}^l{C}_{l_x{l}_y{l}_z,lm}{T}_{lm}.$$ (20)

This transformation is unitary, i.e.,

$$\begin{array}{cc}\hfill C_{l_x{l}_y{l}_z,lm}& =C_{lm,l_x{l}_y{l}_z}^{*}\hfill \\ \hfill \sum _{l_x+l_y+l_z=l}{C}_{lm,l_x{l}_y{l}_z,}{C}_{l^{\prime }{m}^{\prime },l_x{l}_y{l}_z}& ={\delta }_{l{l}^{\prime }}{\delta }_{m{m}^{\prime }}.\hfill \end{array}$$ (21)

To be consistent with the original Hättig approach, we seek an analogous expression involving regular solid harmonics. The CS approach is still applicable to regular solid harmonics, as long as we adjust 21 for normalization^{22, 46}

$$\begin{array}{cc}\hfill \sum _{l_x+l_y+l_z=l}{R}_{lm,l_x{l}_y{l}_z}{R}_{l^{\prime }{m}^{\prime },l_x{l}_y{l}_z}& ={\delta }_{l{l}^{\prime }}{\delta }_{m{m}^{\prime }}\frac{(2l-1)!!}{l!}.\hfill \end{array}$$ (22)

The coefficients that express a regular solid harmonic in terms of its constituent monomials can be obtained by applying the appropriate normalization to the expression derived by Schlegel and Frisch⁶²

$$\begin{array}{ccc}& & R_{lm,l_x{l}_y{l}_z}\hfill \\ & & =\frac{l_x!l_y!l_z!}{l!}\sqrt{\frac{(1-|m\left|\right)!}{(1+|m\left|\right)!}}\frac{1}{2^l}\sum _{i=0}^{\frac{1-\left|m\right|}{2}}\left(\genfrac{}{}{0pt}{}{l}{i}\right)\left(\genfrac{}{}{0pt}{}{i}{j}\right)\frac{{(-)}^i(2l-2i)!}{(1-|m|-2i)!}\hfill \\ & & \times \sum _{k=0}^j\left(\genfrac{}{}{0pt}{}{j}{k}\right)\left(\genfrac{}{}{0pt}{}{\left|m\right|}{l_x-2k}\right){(-)}^{\mathrm{sgn}\left(m\right)\left(\frac{\left|m\right|-l_x-2k}{2}\right)},\hfill \end{array}$$ (23)

where $j=\frac{l_x+l_y-\left|m\right|}{2}$ and the entire expression is nonzero only if j is an integer. By omitting the leading $\frac{l_x!l_y!l_z!}{l!}$ from 23, we can restrict the summations over Cartesian monomials in 19 to include only permutationally unique components. Finally, we can formulate the real solid harmonics by taking the following linear combinations:

$$\begin{array}{cc}\hfill {\mathcal{R}}_{l,0}\left(\mathbf{r}\right)& ={\mathcal{R}}_{l,0}\left(\mathbf{r}\right)\hfill \\ \hfill {\mathcal{R}}_{l,\left|m\right|c}\left(\mathbf{r}\right)& =\frac{{\mathcal{R}}_{l,m}\left(\mathbf{r}\right)+{\mathcal{R}}_{l,-m}\left(\mathbf{r}\right)}{\sqrt{2}}\hfill \\ \hfill {\mathcal{R}}_{l,\left|m\right|s}\left(\mathbf{r}\right)& =\frac{{\mathcal{R}}_{l,m}\left(\mathbf{r}\right)-{\mathcal{R}}_{l,-m}\left(\mathbf{r}\right)}{i\sqrt{2}}.\hfill \end{array}$$ (24)

Having set up the transformations, we now develop the Cartesian multipole expansion. This is facilitated by introducing the multipole operators

$$\begin{array}{cc}\hfill {\widehat{L}}_A& =\sum _l\sum _{l_x+l_y+l_z=l}{Q}_{l_x{l}_y{l}_z}^B\frac{{\partial }^{l_x}}{\partial x^{l_x}}\frac{{\partial }^{l_y}}{\partial y^{l_y}}\frac{{\partial }^{l_z}}{\partial z^{l_z}}\hfill \\ \hfill {\widehat{L}}_B& =\sum _l\sum _{l_x+l_y+l_z=l}{(-)}^l{Q}_{l_x{l}_y{l}_z}^A\frac{{\partial }^{l_x}}{\partial x^{l_x}}\frac{{\partial }^{l_y}}{\partial y^{l_y}}\frac{{\partial }^{l_z}}{\partial z^{l_z}},\hfill \end{array}$$ (25)

which produce the potential at center A due to the multipoles on B and the potential at B due to the multipoles of A, respectively, when applied to the Coulomb operator; the $Q_{l_x{l}_y{l}_z}$ tensors are the Cartesian multipoles introduced in 1 with a more explicit notation for the suffixes than that introduced in 3. The Cartesian expression for the electrostatic interaction energy of centers A and B is

$$E_{AB}={\widehat{L}}_B{\widehat{L}}_A\frac{1}{\sqrt{x^2+y^2+z^2}}$$ (26)

and its Ewald analog is

$$E_{AB}={\widehat{L}}_B{\widehat{L}}_A\frac{\mathrm{erfc}\left(\beta \sqrt{x^2+y^2+z^2}\right)}{\sqrt{x^2+y^2+z^2}},$$ (27)

where x, y, and z are components of the vector R. Considering 1, 21, 22, we may re-write the Cartesian multipoles in terms of their real solid harmonic analogs

$$Q_{l_x{l}_y{l}_z}=\frac{1}{(2l-1)!!}\sum _m{R}_{l_x{l}_y{l}_z,lm}{Q}_{lm}.$$ (28)

The coefficients in this expression have been adapted according to 24. Substituting 28 into 26, 27 yields expressions for the unscreened and screened interaction energies, respectively, in terms of real solid harmonic multipoles. The resulting expression can be greatly simplified by invoking the quasi-internal coordinate system, which is achieved via the substitution {x, y, z} → {0, 0, R}.

We implemented the approach outlined above, using the Mathematica 8 program.⁵⁴ To obtain compact expressions, we introduce a recursive screening function for the Coulomb operator

$$\begin{array}{cc}\hfill D_0\left(\beta R\right)& =\mathrm{erfc}\left(\beta R\right)\hfill \end{array}$$ (29a)

$$\begin{array}{cc}\hfill D_l\left(\beta R\right)& =D_{l-1}\left(\beta R\right)+\frac{2^l{\left(\beta R\right)}^{2l-1}{e}^{-{\left(\beta R\right)}^2}}{(2l-1)!!\sqrt{\pi }},\hfill \end{array}$$ (29b)

which is related to the screened Coulomb operator used in previous works,^{33, 35, 37} but has been modified to account for the R-dependence of the t tensor.

To obtain compact expressions, we define $X=-\frac{1}{\beta }\frac{\partial }{\partial R}\mathrm{erfc}\left(\beta R\right)=\frac{2e^{-{\beta }^2{R}^2}}{\sqrt{\pi }}$ and introduce contamination terms ${\chi }_{\kappa }^{l_a,l_b}$, which are listed in Table 1. We now write the Ewald analog of 15 as

$$\begin{array}{ccc}\hfill {\tau }_{\kappa }^{l_a,l_b}(\beta ,R)& =& \left[D_{\left[\frac{l_a+l_b}{2}\right]}\left(\beta R\right)+{\chi }_{\kappa }^{l_a,l_b}(\beta ,R)\right]t_{\kappa }^{l_a,l_b}\left(R\right)\hfill \\ & & -{\delta }_{l_a{l}_b}\frac{2^{l_a}{\beta }^{2l_a+1}X}{(2l_a+1)!!}.\hfill \end{array}$$ (30)

The square brackets in the term $\left[\frac{l_a+l_b}{2}\right]$ denote the integer part of the fraction. In Table 1, we have introduced the notation δ_κ⩽x, to represent terms that only contribute to multipole couplings with κ values less than or equal to x. For example, the contamination term that couples two octopoles (l_a, l_b = 3) has two contributions; the former has a factor of δ_κ⩽0 that couples only the ${\tilde{Q}}_{30}$ components, while the latter contains a δ_κ⩽1 so it couples the ${\tilde{Q}}_{30}$, ${\tilde{Q}}_{31c}$, and ${\tilde{Q}}_{31s}$ octopoles. Using this notation, it is evident that the contamination manifests itself in additional, partial contributions from the standard t tensor for the Coulomb operator. Although 30 is useful for exhibiting the nature of the contamination terms, the explicit equations for τ, provided in the supplementary material,⁵¹ are more compact. The D_x(βR), R^−x and (βR)^x intermediates can be easily formed via recursion, making the computational cost of constructing τ very low. Because τ(β, R) has a more complicated dependence on R than t(R), the expression for the derivatives are not as straightforward as those presented by Hättig. However, they are still readily obtained by applying the standard chain rule to 30, and are discussed further below. It is straightforward to show that setting β to zero yields the original t tensor.

Table 1.

The contamination contributions to the τ tensor elements.^a

la	lb	${\chi }_{l_a,l_b}(\beta ,R)$
0	0	0
0	1	0
0	2	0
0	3	$\frac{4}{15}X{\left(\beta R\right)}^5{\delta }_{\kappa \le 0}$
0	4	$\frac{8}{105}X{\left(\beta R\right)}^7{\delta }_{\kappa \le 0}$
1	1	0
1	2	$\frac{4}{9}X{\left(\beta R\right)}^5{\delta }_{\kappa \le 0}$
1	3	$\frac{2}{15}X{\left(\beta R\right)}^7{\delta }_{\kappa \le 0}$
1	4	$\frac{16}{525}X{\left(\beta R\right)}^9{\delta }_{\kappa \le 0}+\frac{8}{105}X{\left(\beta R\right)}^7{\delta }_{\kappa \le 1}$
2	2	$\frac{4}{27}X{\left(\beta R\right)}^7{\delta }_{\kappa \le 0}$
2	3	$\frac{4}{225}X{\left(\beta R\right)}^7[2{\left(\beta R\right)}^2-3]{\delta }_{\kappa \le 0}+\frac{8}{75}X{\left(\beta R\right)}^7{\delta }_{\kappa \le 1}$
2	4	$\frac{8}{4725}X{\left(\beta R\right)}^9[4{\left(\beta R\right)}^2-9]{\delta }_{\kappa \le 0}+\frac{8}{315}X{\left(\beta R\right)}^9{\delta }_{\kappa \le 1}$
3	3	$\frac{8}{1125}X{\left(\beta R\right)}^9[{\left(\beta R\right)}^2-3]{\delta }_{\kappa \le 0}+\frac{32}{1125}X{\left(\beta R\right)}^9{\delta }_{\kappa \le 1}$
3	4	$\frac{16}{55125}X{\left(\beta R\right)}^9[4{\left(\beta R\right)}^4-18{\left(\beta R\right)}^2+15]{\delta }_{\kappa \le 0}+\frac{16}{55125}X{\left(\beta R\right)}^9[20{\left(\beta R\right)}^2-25]{\delta }_{\kappa \le 1}+\frac{16}{735}X{\left(\beta R\right)}^9{\delta }_{\kappa \le 2}$
4	4	$\frac{8}{385875}X{\left(\beta R\right)}^{11}[8{\left(\beta R\right)}^4-54{\left(\beta R\right)}^2+90]{\delta }_{\kappa \le 0}+\frac{8}{385875}X{\left(\beta R\right)}^{11}[50{\left(\beta R\right)}^2-125]{\delta }_{\kappa \le 1}+\frac{8}{1715}X{\left(\beta R\right)}^{11}{\delta }_{\kappa \le 2}$

^aThe contamination terms are symmetric, i.e., ${\chi }_{l_a,l_b}={\chi }_{l_b,l_a}$. See text for the definitions of X and δ_κ⩽x.

The most demanding step in evaluating energies and gradients, using the approach outlined above, is rotation of the body-fixed multipoles Q_lm into the quasi-internal frame; explicit expressions for the rotation matrices are provided in the supplementary material.⁵¹ The rotation may be performed in two ways; either by rotating all multipoles into the lab frame in $\mathcal{O}\left(N\right)$ effort, then completing the rotation to the quasi-internal frame for each pair, or by constructing a composite rotation matrix for each atom of each pair. The former approach is more efficient in the absence of molecular symmetry, because the second half of the rotation (which is performed for each pair) requires formation of only one rotation matrix for both centers – the matrix that describes the rotation of the internuclear axis to the lab frame. The composite approach is useful when sparse multipoles, resulting from symmetry, are present, because the sparsity may be exploited to avoid computation and multiplication of certain elements of the rotation matrices. In both cases, the rotation itself is highly vectorizable, as are the ensuing dot products involving the rotated multipoles, making this approach highly amenable to efficient implementation on single instruction, multiple data hardware. In practical terms, both cases are needed; while most biologically relevant molecules lack symmetry, typical simulations are dominated by water-water, i.e., C_2v – C_2v, interactions where significant speedups are possible if symmetry is utilized.

Working equations

The decomposition of the energy, force, and torques into direct, reciprocal, self, and adjusted terms have been well described in previous developments of Ewald summation for Cartesian multipoles,^{34, 36} so we briefly outline the steps necessary to evaluate each term using spherical harmonics. The direct space energy is simply

$$E_{\text{dir}}=\frac{1}{2}\sum _{A,B}^N\sum _{l_a,l_b}\sum _{\mathbf{n}}\sum _{\kappa }{\tilde{Q}}_{l_a\kappa }^A{\tau }_{\kappa }^{l_a,l_b}(\beta ,|R+\mathbf{n}\left|\right){\tilde{Q}}_{l_b\kappa }^B.$$ (31)

The vector n represents summation over all unit cells and the term A = B is excluded for the parent cell, n = 0. We arrange the multipole and τ tensor components in the order 0, 1c, 1s, 2c, 2s … and the summation over kappa includes the first 2 min (l_a, l_b) + 1 terms. Intermediates for efficiently evaluating energies, forces, and torques have been proposed by Hättig²⁷ and are used to evaluate 31 and derivatives thereof. We have provided programmable equations for the torque intermediates in the supplementary material.⁵¹

Any pairwise interactions that are neglected in the direct summation, such as 1–2 and 1–3 interactions, must be accounted for by defining the adjusted energy. These neglected pairs are placed on a list M and we replace $\mathrm{erfc}\left(\beta R\right)$ with $-\mathrm{erf}\left(\beta R\right)$ in 29a, allowing us to define

$$E_{\text{adj}}=\frac{1}{2}\sum _{A,B\in \mathcal{M}}\sum _{l_a,l_b}\sum _{\kappa }{\tilde{Q}}_{l_a\kappa }^A{\tau }_{\kappa }^{l_a,l_b}(\beta ,R){\tilde{Q}}_{l_b\kappa }^B.$$ (32)

The self-energy may now be simply evaluated, while continuing to use $-\mathrm{erf}\left(\beta R\right)$ in 29a, as

$$\begin{array}{ccc}\hfill E_{\text{self}}& =& \underset{R\to 0}{\lim }\frac{1}{2}\sum _{A,B}\sum _{l_a,l_b}\sum _{\kappa }{\tilde{Q}}_{l_a\kappa }^A{\tau }_{\kappa }^{l_a,l_b}(\beta ,R){\tilde{Q}}_{l_b\kappa }^B\hfill \\ & =& -\frac{1}{4\pi {\epsilon }_0}\sum _A^N\sum _{l_a}\frac{2^{l_a}{\beta }^{2l_a+1}}{(2l_a+1)!!\sqrt{\pi }}{\left|{}^A\mathbf{Q}_{l_a}\right|}^2,\hfill \end{array}$$ (33)

which arises solely from the final term in 30. The reciprocal space terms can be implemented by making minor modifications to existing Cartesian PME approaches, which define the structure factor as the Fourier transform of the discretized representation of 25; the derivative operators are obtained as B-spline derivatives. Such implementations may be used, without modification, by simply back-transforming the spherical harmonic multipoles to a Cartesian representation, using 28. These elements are tabulated in the supplementary material. Alternatively, the Cartesian splines may be linearly combined using 23 to allow contraction with the real solid harmonic multipoles; this utilizes the spherical harmonic multipoles but offers no computational savings over a Cartesian formulation. As Sagui and co-workers indicated,³⁶ the addition of higher-order multipoles to the reciprocal space term does not incur much additional computational cost, with respect to a point-charge only model. This crucial result permits the use of a large attenuation parameter, β, to mitigate the high cost of evaluating 31 by reducing the number of A, B pairs that must be explicitly considered.

High order multipoles are commonly employed in concert with polarizable dipoles, which allow molecules to respond to their environment. While many implementations allow mutual polarization by iteratively allowing induced dipoles to interact with each other,^{9, 10, 13, 14} an interesting simplification to this procedure was recently proposed. In constructing the iAMOEBA force field, a robust parameterization was performed to a functional form that included polarization only as a direct response to the field generated by the permanent multiple moments, thus averting the need to self-consistently solve for the induced dipole magnitudes.¹¹ While the quasi-internal coordinate system is unlikely to be the most efficient choice for performing the iterative component of the mutual polarization scheme, it allows for extremely simple implementation of the direct contributions from permanent moments; these terms are readily obtained by scaling existing pairwise torque intermediates with the appropriate spherical harmonic Thole damping factors.⁹ Orthogonality dictates that there are at most three contributions to the field from any order of multipole in the quasi-internal frame, and the resulting field for each pairwise interaction can be simply rotated back to the lab frame.

CONCLUSIONS

By extending Hättig's spherical harmonic treatment of multipole interactions to include the Ewald summation, we have developed an efficient method for evaluating energies, torques, and forces for next-generation force fields. Although our derivation involves some lengthy algebra, the final working equations are compact and our method inherits all of the benefits of its progenitor. Specifically, the interaction tensor, τ, takes a simple form that depends only on β and R, allowing for simple evaluation of energies and derivatives. The computational cost of our method grows with angular momentum l as $\mathcal{O}\left(l^3\right)$, as opposed to the best Cartesian based approach, which scales as $\mathcal{O}\left(l^4\right)$. The incorporation of the Ewald summation allows us to aggressively shift terms into reciprocal space, where the introduction of high-order multipoles does not significantly increase the computational cost, greatly improving the efficiency of the method. Implementation details and performance benchmarks on assorted test systems will be presented in subsequent work.