Abstract
Purpose: The authors describe algorithms to control dynamic attenuators in CT and compare their performance using simulated scans. Dynamic attenuators are prepatient beam shaping filters that modulate the distribution of x-ray fluence incident on the patient on a view-by-view basis. These attenuators can reduce dose while improving key image quality metrics such as peak or mean variance. In each view, the attenuator presents several degrees of freedom which may be individually adjusted. The total number of degrees of freedom across all views is very large, making many optimization techniques impractical. The authors develop a theory for optimally controlling these attenuators. Special attention is paid to a theoretically perfect attenuator which controls the fluence for each ray individually, but the authors also investigate and compare three other, practical attenuator designs which have been previously proposed: the piecewise-linear attenuator, the translating attenuator, and the double wedge attenuator.
Methods: The authors pose and solve the optimization problems of minimizing the mean and peak variance subject to a fixed dose limit. For a perfect attenuator and mean variance minimization, this problem can be solved in simple, closed form. For other attenuator designs, the problem can be decomposed into separate problems for each view to greatly reduce the computational complexity. Peak variance minimization can be approximately solved using iterated, weighted mean variance (WMV) minimization. Also, the authors develop heuristics for the perfect and piecewise-linear attenuators which do not require a priori knowledge of the patient anatomy. The authors compare these control algorithms on different types of dynamic attenuators using simulated raw data from forward projected DICOM files of a thorax and an abdomen.
Results: The translating and double wedge attenuators reduce dose by an average of 30% relative to current techniques (bowtie filter with tube current modulation) without increasing peak variance. The 15-element piecewise-linear dynamic attenuator reduces dose by an average of 42%, and the perfect attenuator reduces dose by an average of 50%. Improvements in peak variance are several times larger than improvements in mean variance. Heuristic control eliminates the need for a prescan. For the piecewise-linear attenuator, the cost of heuristic control is an increase in dose of 9%. The proposed iterated WMV minimization produces results that are within a few percent of the true solution.
Conclusions: Dynamic attenuators show potential for significant dose reduction. A wide class of dynamic attenuators can be accurately controlled using the described methods.
Keywords: dose reduction, dynamic attenuators, dynamic bowtie, fluence field modulation
INTRODUCTION
In x-ray CT, dynamic, prepatient attenuators have been proposed as a replacement for the static prepatient attenuator (often called the “bowtie filter” because of its shape) which defines the distribution of x-rays as a function of fan angle.1 Compared to the bowtie filter, which is fixed for the entire scan, dynamic attenuators provide greater flexibility to modulate the fluence incident on the patient and can therefore reduce the dose of the scan or the variance of the reconstructed images. In systems using photon-counting x-ray detectors, a dynamic attenuator can reduce the dynamic range of flux incident on the detector, enabling photon-counting detectors with relatively modest count rates.2, 3, 4, 5 These attenuators have the potential to allow the system to more carefully control the flux distribution compared to current clinical systems, which use only the static bowtie filter and tube current modulation (TCM).6, 7, 8 Dynamic attenuators can also enable region-of-interest scanning and are more tolerant of patient miscentering.
The most important application for these dynamic attenuators may be in their use for dose reduction. Previous studies have shown that the ability to finely tune the x-ray illumination field can reduce dose by 50% in one case9 and 86% in a separate case10 without increasing the peak (or maximum) variance of the reconstruction.
Several dynamic attenuators have been proposed, some of which are described only in the patent literature. Theoretically, a dynamic attenuator that can arbitrarily adjust the number of photons incident in any ray would be ideal, and in this work we will call this the perfect attenuator. In the inverse geometry CT architecture,11, 12, 13 the “virtual bowtie” can provide very fine control of the fluence and can approximate the perfect attenuator.10 Achieving this effect in a third-generation CT scanner is more challenging.
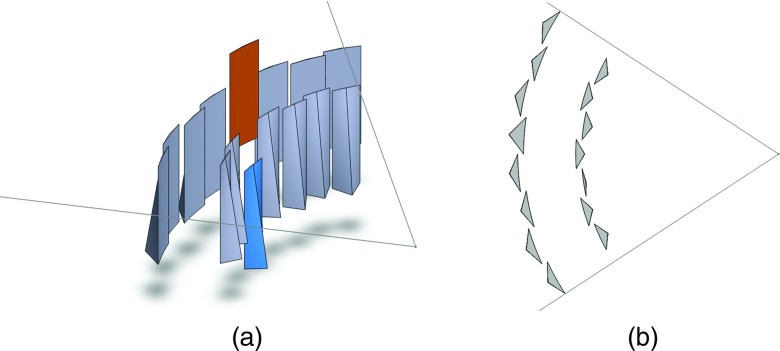
One proposed dynamic attenuator changes the attenuation profile by linear translation in the z- (or axial) direction of an appropriately shaped rigid object.14 We will call this the translating attenuator. Figure 1 shows an example of the translating attenuator. As the filter is translated, the attenuation introduced morphs into different shapes, and in general, the translating attenuator allows the system to select from a one-dimensional family of attenuator thickness functions f(γ, c), where γ is the fan angle and c is the linear translation of the attenuator. One choice of f(γ, t) is the family of attenuation functions which is optimized for circular objects of radius t5. Another is the set of parabolic attenuation functions, so that f(γ, c) = cγ2. We note that instead of translation in the z-direction, rotation about the source-detector axis using a differently shaped rigid object can also be used to achieve very similar results.
Figure 1.
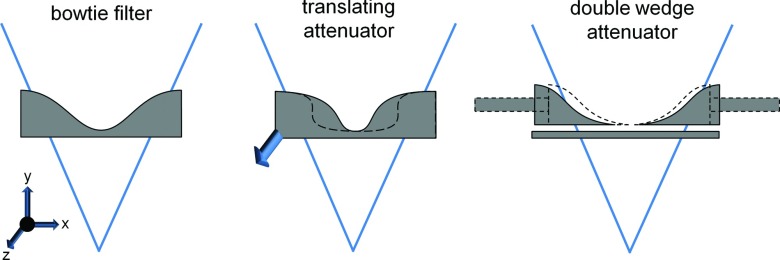
Illustrations of the (left) standard bowtie filter, (middle) translating attenuator, and (right) double wedge attenuator. The fan beam of radiation is illustrated in each figure. The bowtie filter is a static, beam-shaping filter placed several cm in front of the source. Each wedge of the double wedge attenuator can be adjusted using actuators (illustrated as long rectangles). The translating attenuator can change its shape by motion into or out of the page (the arrow is intended to convey motion in this direction). Both the dynamic wedge attenuator and the translating attenuator show examples of alternative shapes as dashed outlines.
A second dynamic attenuator configuration uses two wedges that may be translated in the fan-angle direction (Fig. 1).15 We will call this the double wedge attenuator. Let the attenuation of the two wedges be represented by fleft(γ) and fright(γ). The double wedge attenuator presents two degrees of freedom to the system, γleft and γright, so that the attenuator thickness is f(γ, γleft, γright) = fleft(γ − γleft) + fright(γ − γright). For small patients, the wedges can be pushed together and for larger patients the wedges may be moved apart. Besides this, the wedge locations could be modulated throughout the scan to better conform to the patient anatomy, and the double wedge attenuator is a natural choice for region of interest scans.
A third dynamic attenuator which we recently proposed uses a series of wedges which translate in the z-direction to produce a piecewise-linear attenuation profile. We will call this the piecewise-linear attenuator. This piecewise-linear attenuator can be viewed as an approximation of the perfect attenuator. The axial cross-sections of each wedge as a function of z translation are triangles of different heights, and by adjusting the location of each wedge, the total thickness that the beam must penetrate is piecewise-linear in fan angle. Figure 2 shows this dynamic attenuator. Two layers of triangular wedges are shown, with one layer moved by half of the triangular base so that the apex of a triangle in one layer corresponds to the meeting of corners of two triangles in the other layer. A wide range of piecewise-linear attenuation functions can be produced with this design. For details, the reader is directed toward Ref. 4. This is very similar to another dynamic attenuator which provides a piecewise-constant attenuation profile,16, 17, 18 but the use of triangular wedges may reduce imaging artifacts caused by sharp, rapid changes in attenuation as a function of fan angle. Compared to the translating and double wedge attenuators, the piecewise-linear attenuator offers greater control over the x-ray illumination field but is more complex and requires more moving parts. We note that both the translating and piecewise-linear attenuator described here accommodate miscentered patients well, which is known to be a problem for the conventional bowtie filter.19, 20
Figure 2.
The piecewise-linear dynamic attenuator, consisting of a series of wedges attached to actuators (not shown). The fan beam is also shown, and the x-ray focal spot sits at the apex of the fan. (a) The set of N wedges. Two of the wedges have been shaded and translated. (b) An axial cross-section of the wedges. The wedge which was translated introduces less attenuation, while the wedge that was translated upwards more attenuation. The path-length of attenuator as a function of fan angle is a piecewise-linear function. Within each of the two layers of wedges, adjacent wedges are displaced slightly to avoid scraping during motion. Parts of this figure are used with permission from Ref. 33.
Each of these dynamic attenuators provides one or more degrees of freedom per view, and each scan is composed of hundreds of views. In order to realize dose or image quality objectives, these attenuators should be carefully controlled. However, with hundreds of degrees of freedom per scan, these problems are intractable using techniques such as brute force search. One algorithm which has been previously used is multistage simulated annealing.9 While very general, simulated annealing does not provide guarantees on the accuracy of its solution and may converge to a local minimum. Another alternative used in previous work is convex optimization.10 Convex optimization is a very powerful tool but is only viable for convex problems, and the control of many types of dynamic attenuators, including the translating attenuator and the double wedge attenuator, appears to be nonconvex. (Control of the perfect attenuator and the piecewise-linear attenuator can be well approximated as convex.) Both simulated annealing and convex optimization require knowledge of the patient anatomy, which could be obtained by a low-dose prescan or perhaps from projection images.
The purpose of this work is to develop an optimization algorithm that is computationally tractable and that leads to provably optimal noise metrics in the reconstructed images. We will implement these algorithms with tools common to CT research such as forward- and backprojection, so that our results can be replicated by other researchers in the field, with minimal reliance on more complex numerical techniques. We use average variance and peak variance as our noise metrics. The optimization algorithm must be general enough to apply to the four dynamic attenuators described above: translating, double wedge, piecewise-linear, and perfect. For the perfect and piecewise-linear attenuators, we will additionally develop heuristic control methods which do not require a priori knowledge of the patient.
METHODS
Our goal is to find the x-ray illumination field that minimizes peak or mean variance while satisfying the constraints of a particular attenuator. We will define this problem more carefully in Sec. 2A. and we will continue by developing control algorithms for three classes of problems:
System with the perfect attenuator. This case is described in Sec. 2B. We analyze this class first because the theory developed is necessary in subsequent problems. We assume a priori knowledge about the patient's attenuation, which is used to formulate the optimization problem. This knowledge could be provided from a prior scan or from a low dose prescan. The piecewise-linear attenuator can be treated as an approximation of the perfect attenuator.
Systems with limited attenuators. This case is described in Sec. 2C. We define the limited attenuator as any attenuator that provides a small number of degrees of freedom D in each view. This includes the double wedge attenuator (D = 2) and the translating attenuator (D = 1 or D = 2 depending on the configuration). As a rule of thumb, the methods we will develop are effective for D ⩽ 3, although they could be extended to larger values of D. The piecewise-linear attenuator has too many degrees of freedom to be included as a limited attenuator.
Approximate solutions without a priori knowledge. This case is described in Sec. 2D. We will suggest control methods when a priori knowledge of the object's attenuation is not available. These will also be called heuristic control methods because they are empirically derived. We will confine ourselves to the perfect attenuator (and by extension, the piecewise-linear attenuator). We will not analyze other, limited attenuators because the control methods must be developed on an attenuator-by-attenuator basis.
The control algorithms we develop must be validated on data. Section 2E describes the simulations we conducted, the results of which are reported in Sec. 3.
Problem definition
Let the system have M detector channels and let x be a vector with xk being the incident intensity for the kth ray in the sinogram. For k = M(i − 1) + j, the kth ray xk corresponds to the jth detector channel in the ith view. xk is the x-ray illumination field, and is the key variable the dynamic attenuator controls. Our goal is to choose x to optimize the image quality under a fixed dose limit.
Let νk be the photons detected in the kth ray, and let fk be the fraction of photons transmitted through the patient for the kth ray, so that νk = fkxk. In most cases, we will use fkxk instead of vk to make the relationship to xk explicit. We assume that xk is large enough to be noiseless. Assuming Poisson statistics (no electronic noise) and neglecting polychromatic effects, νk is then a Poisson random variable with mean and variance
| (1) |
For CT reconstruction, the quantity of interest is log fk, not νk. Because fk is estimated using the basic relationship fk = νk/xk, propagation of error can be used to show that
| (2) |
In matrix form, let F be a diagonal matrix whose diagonal is f, so that Fkk = fk. The detected intensity is then a vector with average value Fx and with variance (Fx)−1, which is the componentwise reciprocal of Fx.
We will assume a linear reconstruction algorithm and we will develop our algorithm for 2D scans using either analytic parallel beam or direct fan beam reconstruction. We believe that extension to volumetric reconstruction should be straightforward. Iterative reconstruction algorithms are beyond the scope of this work, but we believe that improvements with analytic reconstruction should translate to improvements with iterative reconstruction.
In linear systems theory, filtered backprojection can be written as R = −A log F, with R being the reconstructed image in vector form and A being the mapping from the log-normalized measurements to the image via filtered back-projection (FBP). By propagation of error, the variance of the reconstructed image is
| (3) |
Here, A ○ A is the Hadamard product of A with itself and is simply the componentwise square of A. The variance in the image can be well approximated by summing the variances in the rays that pass through the pixel,21 so that we can write
| (4) |
where B corresponds to the system matrix which sums all rays which pass through a pixel, and c is a constant that we will neglect. B is therefore a sparsified approximation to A ○ A. For more details, the reader is directed to Ref. 21. B itself is a backprojection without the filtering step, or “unfiltered backprojection.” The benefit of this approximation is that the variance of the reconstruction can be produced as easily as reconstruction itself, with only two modifications: first, the ramp filter is disabled, and second, the quantity to be backprojected is (Fx)−1 rather than (filtered) log F.
Using B instead of A ○ A ignores the mixing of variance across detector channels within a view which results from the convolution and also any interpolation kernel used. In practice, the errors induced by this approximation are very minimal. The ramp kernel is very local, decreasing as the inverse of distance squared, so that the square of the kernel as in A ○ A decays as distance to the negative fourth power. Similarly, the choice of interpolation kernel can be modeled by the use of a different constant c.
In direct fan-beam reconstruction, a weighted backprojection is used, with the weight being proportional to the inverse square of the distance from the source to the voxel.22 In propagating the variance to the image, the weight must again to be squared. The nonzero elements of Bij should therefore be proportional to the inverse fourth power of the source-point distance. In this work, we will neglect the effect of the source-point distance weighting. This would be an empirically good model for a rebin-to-parallel reconstruction, used in many volumetric reconstruction algorithms.23, 24 It is known that variance alone is not sufficient to determine detectability and that the spatial correlations of the noise and object structure are important.25 For the purposes of this work, we assume that reconstructed variance is an adequate figure of merit for comparing attenuators and control algorithms.
The optimization needs a dose metric to be controlled or minimized. We use the total energy absorbed, which is simply a dot product
| (5) |
The elements of dk are proportionality constants measuring the relative energy absorbed from the average photon delivered along the kth ray. A simple choice of dk is to set dk = 1 if the ray intersects the patient, and dk = 0 otherwise. This choice of dk measures entrance energy. A better choice of dk can be derived from Monte Carlo simulations. We will impose a limit of dTx = dtot for all our optimization problems. This ensures that all systems will be compared at equal dose. Because variance and dose are inversely related (in the absence of electronic noise), any reduction seen in variance for equal dose can be equally well interpreted as a reduction in dose for equal variance.
System with the perfect attenuator
Weighted mean variance (WMV) optimization
The weighted mean variance minimization problem is posed as
| (6) |
where wT is the row vector of voxel weights. In the simple mean variance optimization, wk = 1 for all voxels k which are clinically relevant, and wk = 0 for voxels which are not relevant (for example, which may occur outside the patient). We will also consider WMV optimization, with each voxel receiving different weights. The WMV problem is relevant if the clinician is more interested in some regions of the patient than others. It will also be used later in our solution to the peak variance problem. We have dropped c and other proportionality constants which do not affect the optimization problem.
The constraint dTx = dtot enforces a dose limit on the system. An alternative constraint is dTx ⩽ dtot. In this work, these two constraints will lead to the same outcome because dose and variance are inversely related and because we do not assume a limit to the instantaneous source power. Therefore, the system will always choose to bring the dose up to the allowable limit with dTx = dtot to improve the image quality.
A similar problem has been solved in Ref. 26. We provide a modified solution here, which is necessary for Secs. 2B2, 2B3, 2C, 2C1, 2C2, 2D.
Looking more closely at Eq. 6, we note that because the objective function is scalar, it may be transposed without modification: (wTB(Fx)−1)T = (Fx)−TBTw. As B is the backprojection operator, BT is forward projection. In the unweighted case, if we assume that wk is one inside patient tissue and zero outside, BTw is the sinogram of the tissue path-lengths (the length of the intersection of the ray with the patient, not the line integral of attenuation).
Equation 6 can be solved using Lagrange multipliers. The Lagrangian and its partial derivatives are
| (7) |
| (8) |
| (9) |
Eq. 8 simply restates the dose limit. In Eq. 9, we used the fact that F is diagonal. This can be further simplified to
| (10) |
Therefore, the incident intensity for any ray, xk, is given by
| (11) |
where λ is chosen in order to meet the dose constraint. If desired, we could choose λ = 1, calculate the vector x and then scale it by a constant to meet the dose constraint.
Equation 11 solves the WMV optimization problem and can be very easily implemented. The numerator, BTw, is the forward projection of the weight map. In the unweighted case, BTw is the sinogram of tissue path-lengths. The dose costs d are assumed to be known, and Fkk is easily measured as the fraction of photons which are not attenuated by the patient.
We note that if we use the entrance energy approximation for dk and if we ignore the variation in BTw and approximate it to be uniform, Eq. 11 simplifies to
| (12) |
This is consistent with previously derived theory.26 Under the assumptions used in Ref. 7, this choice for the tube current minimizes the variance at the center pixel subject to a limit on the allowed mAs.
Peak variance optimization
Optimization of mean variance may increase the variance in one region to obtain a reduction in another. In an extreme case, this could render part of the image nondiagnostic and a repeat scan may then be required. It is therefore desirable to reduce the peak variance of the image rather than the mean variance. We define the peak variance as the maximum variance of any voxel in the reconstruction. This problem is stated as
| (13) |
This is a minimax problem and does not easily admit a closed form solution. Because all engaged functions are convex, convex optimization techniques can be used to find an accurate numerical solution, but the computational load can be significant given the number of variables involved. General-purpose convex optimization algorithms operate with computational complexity for number of variables Nvar.27 As there is one variable for each voxel in the reconstruction and measurement in the sinogram, can become prohibitively large. Special-purpose optimization algorithms could do better but are nontrivial to develop. However, it is clear that the problem is well-posed and that a solution exists. Let us call the optimized x to Eq. 13xpeak, and let xpeak achieve optimized peak variance .
We note that the piecewise-linear attenuator can be thought of as a low-resolution approximation to the perfect attenuator, and convex optimization28, 29 is effective for solving this problem. The details of this optimization have been reported in Ref. 4.
Iterated WMV to bound peak variance
Instead of solving for xpeak directly, we can relate the optimized peak variance to the solution to the WMV problem. Let us denote the choice of x which solves the WMV problem with weight wT as xWMV. Let S be the set of all voxels k with strictly positive weight, that is, wk > 0. We define two quantities
| (14) |
It can be shown that for any weight wT,
| (15) |
We prove these bounds in the Appendix.
Equations 14, 15 suggest an alternative approach to solving the peak variance problem. Rather than optimizing peak variance directly, a WMV problem could be constructed which achieves a tight bound about the minimax variance. The upper bound is the peak variance of the WMV solution. This simply states that the peak variance of the WMV solution cannot outperform the minimax variance. The lower bound is the minimum variance of the WMV solution, but only of voxels which have strictly positive weight.
If a tight bound existed, Eqs. 14, 15 predict that each voxel either attains the minimax variance with some positive weight, or outperforms the minimax variance but is assigned zero weight. While we do not prove that a tight bound exists for each dataset, we have found good results (bounds of a few percent) using this method. The challenge is only to select an appropriate weight map. We propose an iterative method here, but emphasize that a WMV solution with any weight map will produce a bound on the minimax variance.
The basic principle of the iterative technique is to increase, in each iteration, the weight for voxels with high noise and to decrease the weight for voxels with low noise. In order for the bounds in Eqs. 14, 15 to be useful, there must be a mechanism for setting the weight of a pixel to be zero, and another mechanism for increasing the weight from zero to a positive quantity if the pixel was erroneously weighted to zero in a prior step.
In our simulations, we use the following method to choose the weight map. We initialize wT = 1T, solve the unweighted mean variance optimization problem, and initialize the step size to cstep = 1. In each iteration, we perform the following steps:
Let S be the set of voxels with strictly positive weight, and sort the voxels of S in order of increasing variance. Create a function which smoothly maps the sorted variances of S uniformly to the range [−1, 1], and which uses linear interpolation or extrapolation if the variance does not match the variance of any voxel in S.
Update the weight vector for each voxel as . This increases the weight for voxels with high noise, and decreases the weight for voxels with low noise. Any other mechanism which increases the weight of voxels with high noise and decreases the weight of voxels with low noise could be substituted for steps (1) and (2).
Decrease the step size using cstep → cdecaycstep
Normalize the weight vector by dividing each element by the mean of w, setting . Scaling the weight vector uniformly does not affect optimization but is only important for selecting voxels which should be set to zero weight in the next step.
If a voxel has a small weight so that wk < ccutoff, set wk → 0. If wk = 0 and , then restore it by setting wk = crestore. The purpose of this step is only to increase the lower bound . We found that abruptly changing some wk can slow the rate of convergence for the upper bound .
Solve the WMV optimization problem using the updated weight vector.
In order to estimate BTw in the solution of the WMV optimization problem, we forward project the distribution of weights. This is the most computationally intensive step in our method. In our implementation, this is problematic for rays which are nearly tangent to the patient because our forward projector is not precisely matched with our backprojector, so that our forward projector is only an approximation to BT. We modify the WMV solution from Eq. 11 slightly
| (16) |
In the case of the perfect attenuator, we use a value of ɛ that is equivalent to 1 mm of tissue of average weight. Since most rays pass through several centimeters of tissue, we believed the error incurred in this step is minimal. For the other dynamic attenuators we studied, ε = 0 did not cause problems. This modification should not be necessary if a matched forward projector and backprojector are used.
The choice of a simple step size in the update step can lead to oscillatory behavior. We used cdecay = 0.96 and 100 iterations of weighted mean variance optimization in order to establish our bound on the minimax variance. A smaller value of cdecay leads to more rapid convergence, but we found that better bounds are obtained with a slower decay schedule. An adaptive step size could be used to reduce the number of iterations.
For the case of the perfect attenuator, a wide range of voxel weights is used and we choose ccutoff = 0.03 and crestore = 0.05. For other dynamic attenuators, we use ccutoff = 0.2 and crestore = 0.33. The reason for the difference is that the perfect attenuator has very fine detail, and some of the voxels require weights which are close to zero. The other dynamic attenuators have more sparse weight maps. This will be seen later in Figs. 710.
Figure 7.
(a) Weight map and (b) variance map for iterated WMV optimization of the thorax. These correspond to the final iteration (iteration #100). The window for the variance map is [30%, 38%] according to the units in Table 2 for the thorax. (c) Weight map and (d) variance map for the abdomen, with a window of [50%, 60%]. The weight maps are both windowed between 0 and 5, with the average weight throughout the reconstruction being one, in order to show regions of the weight map which are zero. The weight maps saturate at values over 25.
Figure 10.
Weights maps for iterated WMV show significant sparsity. This weight map is for the final iteration of the 100 iterations used. Weights are windowed from 0 to 5, with the value of the average weight being normalized to 1. The sparsity is predicted from the theory in Sec. 2B3. Top row: abdomen. Bottom row: thorax.
We emphasize that any weight map wT will produce a bound on the minimax variance, and that more elegant methods for choosing wT can be constructed. In our experiments, we found that a method which simply decreases the weight of voxels with low variance and increases the weight of voxels with high variance produces images which nearly attain the minimax variance. The discontinuous transition of some weights to zero complicates the algorithm, and is only necessary to obtain a tighter bound on the minimax variance, not to produce an image with a reduced peak variance.
One would expect this algorithm to converge to a set of weights because the step size cstep decreases exponentially with iteration number. However, convergence in weights is less important than convergence in the upper and lower bound of . Empirically, iterated WMV optimization produces bounds of several percent about the minimax variane on our test datasets, but it is beyond the scope of the paper to show that a tight bound can always be produced from this method.
Our code was written and executed in MATLAB (The Mathworks, Natick, MA) and each iteration required a few seconds of computation time.
Systems with limited attenuators
Recall that the limited attenuator is characterized by a small D, the number of degrees of freedom for each view. We assume the system is equipped with TCM (tube current modulation), so that it has a total of (D + 1) degrees of freedom for each view. Across V views, the total number of degrees of freedom is (D + 1)V. Since V is on the order of 1000, many general purpose optimization algorithms fail in finding the global minimum over (D + 1)V variables. Our strategy is to decompose the problem into V separate optimization problems over D variables, instead of a single problem over (D + 1)V variables.
Mean variance optimization
The mean variance minimization problem for this case is similar to Eq. 6 but includes an additional constraint from the limits of the attenuator
| (17) |
Recall that M is the number of rays measured in each view. The 2D sinogram has MV entries. Q is an M-dimensional space that includes all allowed x-ray illumination fields for any single view. We assume tube current modulation such that if , then for any α > 0.
We decompose the problem into views. Let Si be the set of indices for rays in the ith view, and introduce auxiliary variables such that
Let and be the dose and total variance, respectively, associated with the ith view:
Here, Δk is an auxiliary matrix that serves only to select the variance of the kth ray, and we set the variance of the remaining rays to zero. The problem in Eq. 17 can be rewritten as
| (18) |
We may now decouple the set of variables Si (the incident intensities) in each view. Note that the optimization problem for the perfect attenuator could also be decoupled into views, but this was not necessary because Lagrange multipliers could be employed directly. Suppose we are able to calculate the solution to the mean-variance problem within each view:
| (19) |
A solution to this problem with a dose limit of unity is directly proportional to the solution with any other dose limit because we can modulate the tube current. For the entire scan to be dose efficient, each view must be dose efficient.
This is a D-dimensional optimization problem, and may be solved with a number of optimization methods which are reliable with D dimensions but possibly not with (D + 1)V dimensions. For D = 1 or D = 2, exhaustive search may be acceptable. In our simulations, we used the Neadler-Mead simplex search, as implemented by the Matlab function fminsearch. Let the solution to the single-view illumination optimization problem, which consumes one unit of the allowed dose budget, be denoted as , and let the optimized using be ωi. In general, if the ith view consumes of the dose budget, then, if optimized, it will contribute to the variance.
With individually optimized views, the only question remaining is how to choose the x-ray source current for each view. This can be determined with the following problem:
| (20) |
To allocate the dose distribution between different views, we again use Lagrange multipliers and find
| (21) |
Therefore, to optimize the mean variance, the dynamic attenuator should be configured in each view to minimize the dose-variance product for that view, and the tube current should be adjusted such that the dose delivered in that view is proportional to the square root of the dose-variance product of that view.
Peak variance optimization
Peak variance optimization for the limited attenuator is a difficult problem because hundreds of degrees of freedom exist, and the problem is nonconvex. Stochastic techniques have been used in the past30 but do not provide guarantees on optimality. Fortunately, the iterated WMV developed for the perfect attenuator applies directly to the limited attenuator. The bound in Eq. 15 still holds, with any solution to the WMV minimization providing a bound on the minimax variance.
Approximate solutions without a priori knowledge
When a priori knowledge of the object transmission F is not available, heuristics must be used to approximately minimize image variance metrics. The elimination of the requirement for a priori knowledge makes these control methods more practical.
Mean variance optimization using a square-root-log function
For mean variance optimization with the perfect attenuator, our solution was Eq. 11, reproduced below for reference
For simple mean variance optimization, w, the weight map, is 1 for any voxel of clinical relevance (tissue) and 0 otherwise. With a few approximations, this solution can be used as a real time control algorithm. If the patient shape can be roughly determined prior to the scan, e.g., from scout scans, BTw can be estimated by calculating the tissue path-length from the estimated patient shape. Alternatively, the patient can be modeled as being composed of uniformly attenuating material with linear attenuation coefficient μ, choosing a value of μ representative of soft tissue. This approximation is sensible in regions of the body consisting mostly of soft tissue, but could cause problems in regions such as a thorax, with much of the lung tissue having a low μ.
With the assumption that (1TB)k is proportional the tissue path-length lk, and
| (22) |
We further assume that all rays which intersect the patient contribute equally to dose. Then Eq. 11 simplifies to
| (23) |
This expression depends only on the fraction of rays transmitted, Fkk, which can be well approximated using the previous view. If a more accurate model of dose were available, then the dependence on dk in Eq. 11 could also be included. Similarly, dose sensitive organs can be protected by increasing dk for rays which are known to intersect these organs.
The derivation of the square-root-log function used many approximations which may, in general, not be obeyed. Under very specific conditions the square-root-log function is optimal. We will study the performance of this control method under more realistic conditions in Secs. 2E, 3.
Power law control
An even simpler heuristic is to choose a power law. We have found good results with an exponent of −0.6, leading to the very simple expression
| (24) |
For values of between 10 and 100, is quite similar to , although at smaller (i.e., thin tissue path-lengths), delivers more flux. This makes the power law expression more robust than the square-root-log from Eq. 23 in the thorax where the assumption of uniform attenuation is inaccurate.
Optimized flat variance for peak variance minimization
For the task of peak variance optimization, one approach is to restrict ourselves to the minimal variance which is uniform (or flat) across the image. We will continue to assume that the dose metric is entrance energy. A similar idea has already been used in experimental studies.17
It should be noted that the flat variance assumption is not always a good one. One example is the perfect attenuator scan of an annulus of water with an air core. Because this system is radially symmetric, it is feasible to cast this as a convex optimization problem and solve for the true solution xpeak and numerically.28 This can be compared to the solution which flattens the variance. We find that xpeak does not lead to a flat variance map. For an annulus with an inner radius of 10 cm, an outer radius of 30 cm and μ = 0.2 cm−1, , where is the variance if the perfect attenuator is controlled to equalize the variance in the reconstructed image everywhere. Using xpeak results in reduced variance everywhere, both in the air core and water ring surrounding it.
However, the flat variance assumption simplifies the problem and reduces the requirements for a priori knowledge. The optimized flat variance problem is
| (25) |
We will now appeal to an argument which is strictly true only in the continuous case and not the discretized problem as written. Because the variance map is flat everywhere, its Fourier transform has power only at the origin and the central slice theorem implies that the backprojected variance should be flat on a per-view basis. This in turn means that the variance of each measurement within each view should be equalized, so that
| (26) |
In the nearest-neighbor model of B, αk is simply the variance delivered from each view. Although the variance must be flat within each view, it can vary from view to view. Choosing the optimal set of αk can again be performed using Lagrange multipliers and yields
| (27) |
Therefore, within each view the detected number of photons should be constant, and the total dose delivered in each view should be modulated with the square root of the dose-variance product of that view.
These heuristics can be applied with minor modification to the piecewise-linear attenuator. Instead of using fk for a single ray, we use a single value for a block of fk. In our simulations, we had one block per piecewise linear segment, with each block abutting its neighbors, and we used the harmonic mean of fk within the block instead of the arithmetic mean in order to increase the weight of highly attenuated rays.
Simulations
We compared five different attenuators and assumed that TCM was always available, unless noted otherwise.
Standard bowtie filter: The standard, fixed bowtie filter was modeled to be similar to a commercial body bowtie filter and is the reference system. The system has no control except for TCM in customizing the x-ray illumination field. In part because of limitations on the x-ray source, different CT scanners determine the TCM differently. For this reason, we will, in some cases, compare the other dynamic attenuators to the standard bowtie without TCM.
Double wedge attenuator: Our implementation of the double wedge attenuator assumed that each wedge was shaped like half of a head bowtie filter. The performance of the double wedge attenuator depends on the shape of the wedges used; splitting the head bowtie filter is a reasonable choice but may not be optimal. We found that splitting the head bowtie performed much better than splitting the body bowtie, which has a much shallower gradient of attenuation. The two wedges are translated independently, so our double wedge attenuator naturally accommodates off-center or asymmetric patients. To provide a sense of scale, the irradiated portion of each wedge could be about 3 cm long in the fan-angle direction if placed 5 cm in front of the source.
Translating attenuator: The translating attenuator uses translation or rotation to provide one or two degrees of freedom per view (besides TCM) in the x-ray illumination field. The performance of the translating attenuator depends on the set of shapes that the attenuator can take on. In one extreme, the attenuator is designed specifically for one patient scan and made to be exactly optimal.5 We expect most translating attenuator designs to be fairly generic, and we chose the thickness profile to be parabolic. The degree of freedom therefore allows the system to choose, for each view, a different value of c1 in the thickness function f(γ) = c1γ2, where γ is the fan angle of a ray normalized so that for the rays in the field of view, γ ∈ [−1, 1]. To increase its generality, we additionally assumed that this attenuator was mounted to an actuator which allowed the attenuator to be shifted in the lateral (or fan angle) direction throughout the scan, so that the thickness function can be modeled as f(γ) = c1(γ − c2)2. This improves performance for off-centered patient scans and for centered but asymmetric patients. As one possible geometry, the translating attenuator could be 6 cm in the fan-angle direction, 5 cm in the z-direction, and would be placed 5 cm in front of the source.
Piecewise-linear attenuator: In the limit of arbitrarily many segments, the piecewise-linear attenuator is the perfect attenuator. In practice, the resolution provided by the piecewise-linear attenuator will be limited by the number and size of the wedges as well as the maximum motor speed. We assumed that the piecewise-linear attenuator used 15 wedges uniformly spaced in fan angle. In one possible geometry, the dimension of each wedge is 11 mm wide, 40 mm long, and up to 6 mm thick.4
Perfect attenuator: We provide the results for the perfect attenuator. While probably impractical, it provides an upper bound for any other attenuator.
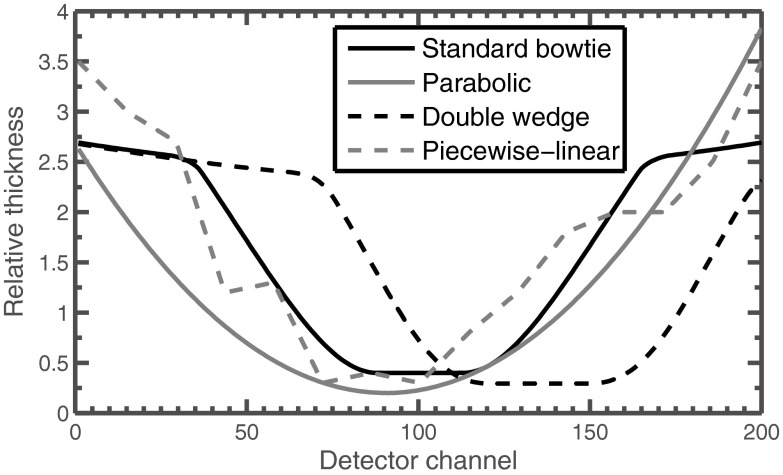
Examples of the types of thickness profiles these modulators can produce are shown in Fig. 3. The material composition of the attenuator is irrelevant for our simulations because we assumed monochromatic radiation, but we note that materials for existing bowtie filters include aluminum and carbon, which have effective atomic number similar to water but are denser. It may be necessary to use materials such as iron for the piecewise-linear attenuator.16
Figure 3.
Example thickness functions which may be provided with each dynamic attenuator concept. These thickness functions are not optimized for any shape, but are only meant to illustrate one possible attenuation choice.
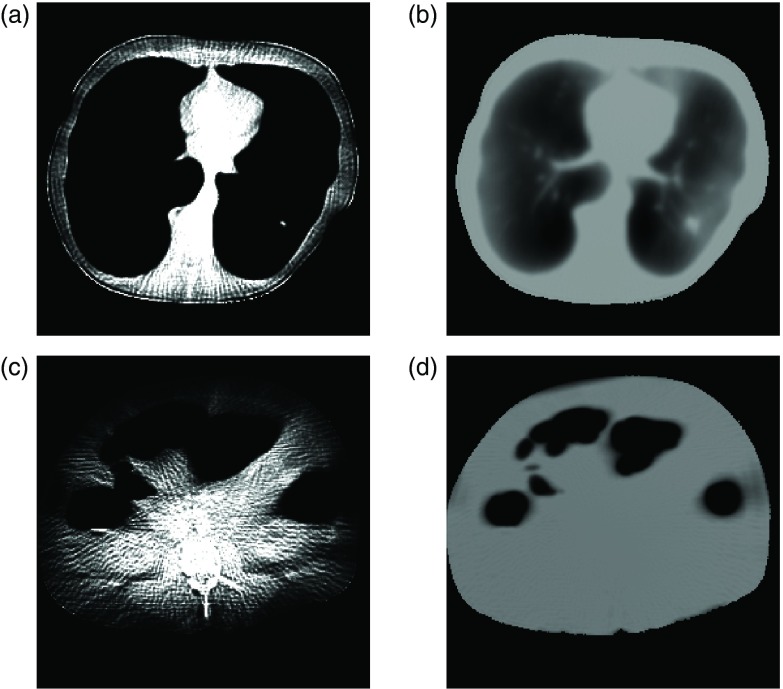
DICOM images of a thorax and an abdomen were obtained from an online source.31 Figure 4 shows our starting datasets. To simplify our calculations, we assumed a single-slice monochromatic fan-beam scan with parameters listed in Table 1. The CT number of the voxels was linearly transformed into attenuation values using a value of 0.2 cm−1 for the linear attenuation coefficient of water (∼60 keV). To reduce the computational complexity, relatively few detector channels and views were used. Raw data were estimated by forward projection, and the variance of the reconstruction was estimated by summing the variances of all rays which pass through each pixel. The effect of noise in the DICOM files was ignored, as its impact on dose and predicted variance should be small. Entrance energy was used as the dose metric.
Figure 4.
Datasets used in this study, comprising (left) an abdomen and (right) a thorax. [WL, WW] = [0, 800] HU.
Table 1.
System parameters.
| Source-isocenter distance | 50 cm |
| Detector-isocenter distance | 50 cm |
| Detector type | Equiangular |
| Energy of photons | 60 keV |
| Views used | 200 |
| Detector channels | 200 |
| Detector pixel size at isocenter | 2.5 mm |
| DICOM image dimensions | 512 × 512 |
| DICOM image voxel size | 0.78 mm |
| Reconstruction voxel size | 1.56 mm |
| Reconstructed image dimensions | 256 × 256 |
RESULTS
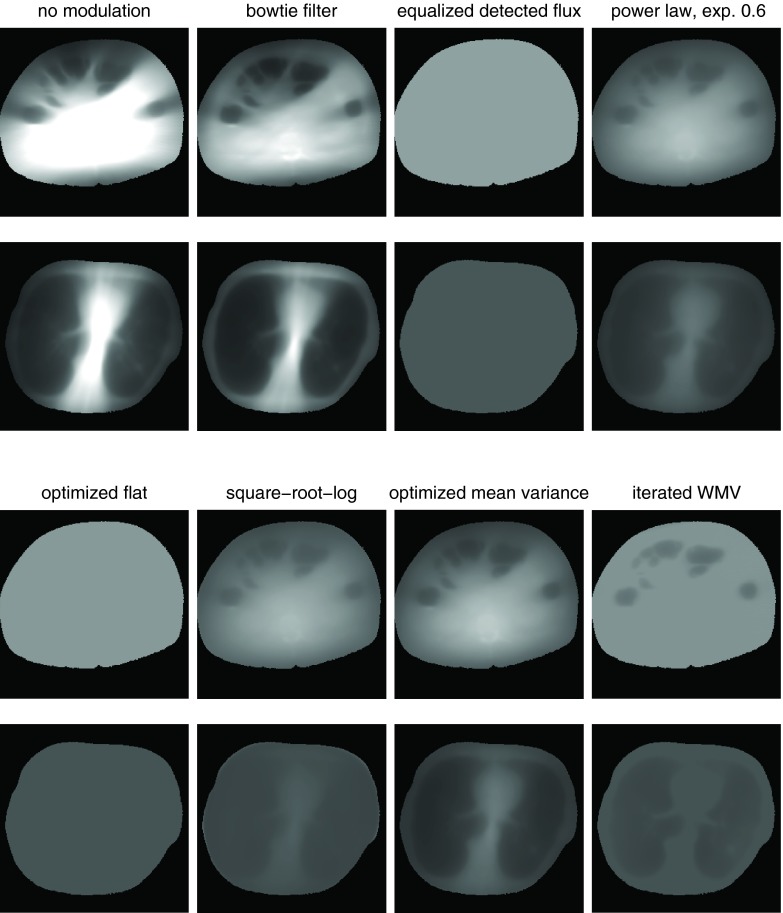
Perfect attenuator
Table 2 shows the results for different control algorithms on a system with a perfect attenuator. Figure 5 shows the variance maps for these cases. The peak and mean variances are normalized to a system that uses the body bowtie without TCM. A peak variance of 50% therefore indicates that the system is able to halve the peak variance for the same dose (or halve the dose for the same peak variance). We chose to disable TCM for the reference system for simplicity; the effects of TCM for the reference bowtie are examined in Sec. 3B.
Table 2.
Performance of different algorithms with the perfect attenuator, for both mean and peak variance in both the thorax and the abdomen. Each column is normalized to 100% for the performance of the standard bowtie filter without mA modulation. The first two control methods are reference control methods, described in Sec. 3A. All other control methods are described in the indicated sections. Numbers in parentheses for the iterated WMV solution give the bound on the minimax (or peak) variance. For example, in the thorax, the true optimized peak variance is bounded to be no less than 34.2%.
| Mean | Peak | Mean | Peak | |
|---|---|---|---|---|
| Thorax | Thorax | Abdomen | Abdomen | |
| Control method | (%) | (%) | (%) | (%) |
| No modulation | 119 | 142 | 146 | 178 |
| Bowtie filter | 100 | 100 | 100 | 100 |
| Equalized detected flux | 102 | 36.2 | 109 | 58.9 |
| (Sec. 2D2) | ||||
| Power law, | 84.8 | 45.4 | 86.1 | 71.6 |
| exponent 0.6 | ||||
| (Sec. 2D2) | ||||
| Optimized flat variance | 99.5 | 35.1 | 104 | 55.9 |
| (Sec. 2D3) | ||||
| Square-root-log | 91.1 | 42.8 | 87.1 | 67.5 |
| (Sec. 2D1) | ||||
| Optimized mean variance | 83.0 | 46.8 | 85.7 | 73.8 |
| (Sec. 2B1) | ||||
| Iterated WMV | 93.6 | 34.7 | 99.4 | 54.8 |
| (Sec. 2B3) | (34.2, 34.7) | (53.1, 54.8) | ||
| (minimax bound) |
Figure 5.
Variance distributions for the systems and control algorithms in Table 2. Both the abdomen and thorax are shown. Black is zero variance (also used for the region outside patient), and 100% for each dataset, as defined by the peak variance for a system with the standard bowtie, is set to be white. The peak variance is the largest variance within each dataset, which corresponds to the brightest pixel.
Two reference systems are provided as a comparison. A system with uniform illumination (“no modulation”), with xk constant for all rays, is provided as a comparison which achieves poor peak and mean variance on both datasets. A system with the body bowtie without TCM (“bowtie filter”) is provided as a second dataset.
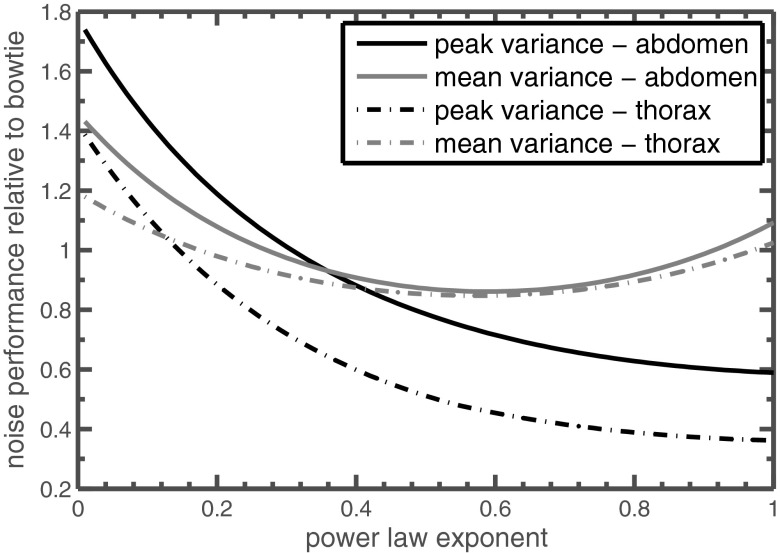
Power law control with a varying exponent, such as Eq. 24, is among the simplest control algorithms, and examples of two different exponents are included in Table 2. Figure 6 compares the mean and peak variance of power law control with different exponents. Mean variance is minimized with an exponent of about 0.6. An exponent of 1 corresponds to perfect equalization of the detected radiation (“equalized detected flux” in Table 2) and is the best simple power law control for peak variance optimization. A modest improvement on perfect equalization is optimized flat variance control [Eq. 25], which equalizes detected radiation within each view but modulates that radiation level from view to view.
Figure 6.
Performance of power law control using different exponents. Performance is relative to a standard bowtie filter without tube current modulation, so a value of 1 is equivalent to 100% in Table 2. Peak variance is minimized with an exponent of 1; larger exponent shows decreased performance.
The square-root-log control of Eq. 23 minimizes mean variance for objects composed of uniformly attenuating material and is nearly as simple as power law control. While theoretically appealing, it was outperformed on these datasets by the simpler power law control using 0.6 as the exponent. The disparity is especially large in the thorax. In the abdomen, both the power law and the square-root-log nearly reach the optimally controlled perfect attenuator in mean variance.
The proposed algorithm for minimizing peak variance, the iterated WMV method, is able to produce a fairly tight bound on the minimax variance and nearly achieves it. It outperforms the optimized flat variance by a small margin, suggesting that the flat variance assumption does not hold in these examples, possibly because of the air-filled cavities in our datasets. Figure 7 shows a rewindowed variance distribution and the weight map for iterated WMV. Areas of reduced variance are apparent. The weight maps in Fig. 7 have streaks from the repeated forward and backprojection process. These weights determine the intensity of the fluence field x. The streaks in the weights can cause minor errors in x but do not cause errors in the variance estimates of the reconstructed image, which is shown on the right side of Fig. 7.
Dynamic attenuator comparison
A comparison of the different dynamic attenuators is shown in Table 3. Each attenuator was optimized both for mean variance and peak variance using iterated WMV. A system with a standard bowtie is given as a reference, with various methods for determining the TCM. Figure 8 shows the variance distribution for these attenuators when controlled for peak variance, and Fig. 9 shows the corresponding fluence sinograms.
Table 3.
Performance of different dynamic attenuators at minimizing either peak variance or mean variance for constant entrance energy. The first two rows are reference systems, which use the standard body bowtie and the suggested tube current modulation. All percentages given relative to the standard bowtie without TCM. When iterated WMV is used to minimize peak variance, numbers in parentheses below the peak variance indicate the bound on the minimax variance. For the piecewise-linear attenuator, “peak optimized,” and “mean optimized” refer to the results from convex optimization under some approximations and are not truly optimal.
| Control | Mean variance | Peak variance | Mean variance | Peak variance | |
|---|---|---|---|---|---|
| Attenuator type | Algorithm | Thorax (%) | Thorax (%) | Abdomen (%) | Abdomen (%) |
| Standard bowtie | No TCM | 100 | 100 | 100 | 100 |
| Standard bowtie | Heuristic TCM | 123 | 76.9 | 98.4 | 96.9 |
| Standard bowtie | Mean optimized | 97.9 | 88.1 | 95.3 | 92.4 |
| Standard bowtie | Iterated WMV | 114 | 68.6 | 97.5 | 88.6 |
| (67.7, 68.6) | (85.6, 88.6) | ||||
| Translating (parabolic) | Mean optimized | 94.3 | 88.1 | 92 | 91.5 |
| Translating (parabolic) | Iterated WMV | 103.7 | 52.9 | 104 | 71.7 |
| (51.5, 52.9) | (69.4, 71.7) | ||||
| Double wedge | Mean optimized | 93.0 | 68.7 | 92.1 | 84.5 |
| Double wedge | Iterated WMV | 104 | 55.0 | 97.6 | 69.5 |
| (53.7, 55.0) | (67.5, 69.5) | ||||
| Piecewise-linear | Mean optimized | 87.2 | 59.6 | 87.7 | 80.3 |
| Piecewise-linear | Peak optimized | 92.9 | 41.8 | 96.8 | 60.1 |
| Piecewise-linear | Mean heuristic | 86.4 | 55.2 | 87.2 | 75.0 |
| Piecewise-linear | Peak heuristic | 91.8 | 46.4 | 100.4 | 63.9 |
| Perfect | Mean optimized | 83.0 | 46.8 | 85.7 | 73.8 |
| Perfect | Iterated WMV | 93.6 | 34.7 | 99.4 | 54.8 |
| (34.2, 34.7) | (53.1, 54.8) |
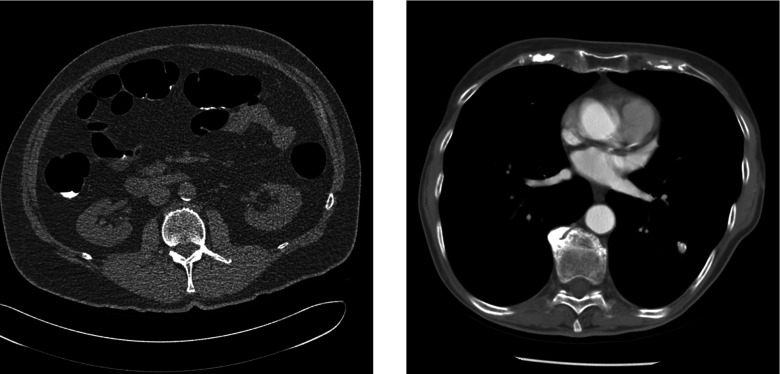
Figure 8.
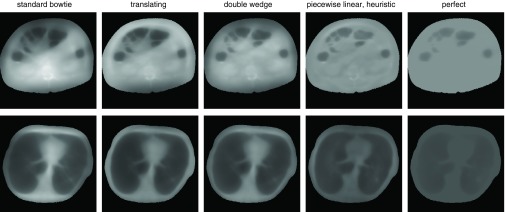
Variance distributions for the dynamic attenuators in Table 3 when controlled for minimum peak variance using iterated WMV optimization. The piecewise-linear attenuator here is not controlled using iterated WMV but using a heuristic control algorithm by approximating the solution to the optimized flat variance problem (Sec. 2D3). Black is zero variance (or the region outside patient), and 100% for each dataset, as defined by the peak variance for a system with the standard bowtie, is set to be white.
Figure 9.
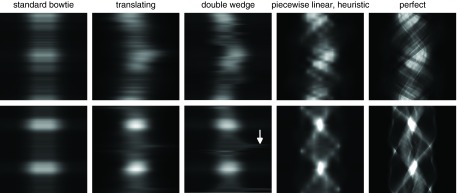
Fluence sinograms which produce the variance maps shown in Fig. 8 and are controlled for the peak variance minimization task. The top row is the abdomen dataset, and the bottom row is the thorax dataset. An arrow with the double wedge attenuator shows a discontinuous shift in the desired fluence profile on the thorax dataset. Achieving this fluence would require very rapid motion of one of the wedges, and may not be possible with actuators of limited power.
The heuristic TCM modulates flux per view with the square root of the attenuation of the central ray.7 The TCM of commercial scanners, although proprietary, can be considered only an approximation to this square-root heuristic as they are usually subject to generator limitations. Optimized TCM gives the best-case performance of a system with TCM.
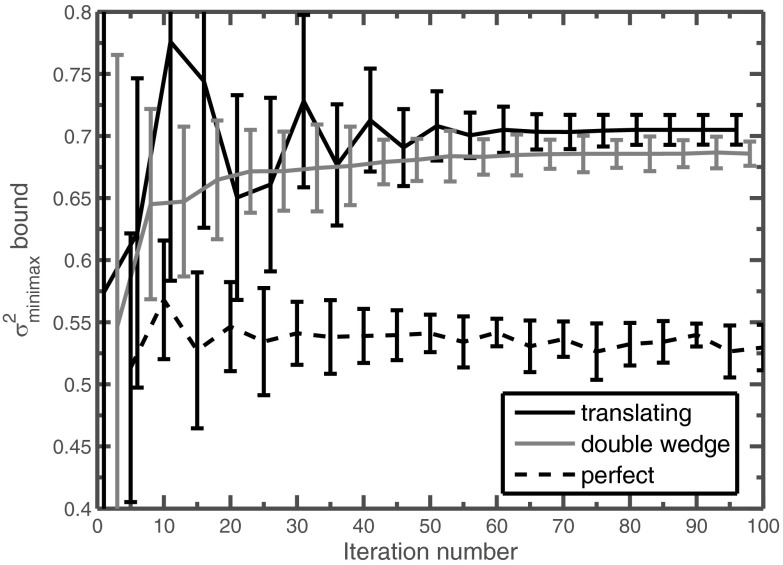
As in the perfect attenuator, we found that in most cases the iterated WMV was able to produce a bound of a few percent on the minimax variance. The final weight maps produced are quite sparse, as shown in Fig. 10. The evolution of the bound on as a function of iteration number is shown in Fig. 11. Note that the tightness of these bounds is not monotonically decreasing with iteration number but sometimes oscillates. Because all of these bounds hold, the tightest bound can be obtained by pairing the maximum lower bound with the smallest upper bound , regardless of the iteration number.
Figure 11.
Evolution of the bound on derived from iterated WMV optimization for the abdomen dataset. The error bars correspond to the lower and upper bound of , and the solid line in between simply tracks the midpoint. For readability, only every fifth bound is shown, and the bounds are reported as a percentage relative to the peak variance of the standard bowtie without TCM.
Iterated WMV could not be applied to the piecewise-linear attenuator because each view includes 15 degrees of freedom, which is too large for our general-purpose optimization methods. Instead, we used the heuristics derived in Sec. 2D, which do not require a priori knowledge and which are easy to implement. The mean variance heuristic approximates power law control (with exponent 0.6) and the peak variance heuristic approximates flat variance optimization. This is compared with the convex optimization methods described in Ref. 4. The power law control heuristic outperforms convex optimization for mean variance minimization.
Our optimization process did not include constraints related to the finite speed of actuators and motors. In Fig. 9, rapid motions can be seen in the ideal control of the double wedge attenuator (marked with an arrow) which could be impractical for actuators of limited speed. The behavior of the translating attenuator is smoother than the double wedge attenuator, and the optimized control is plotted in Fig. 12. The trajectories of the different wedges of the piecewise-linear dynamic attenuator are also shown in Fig. 12 in terms of the thickness of attenuator material (iron) per view index. For both the translating attenuator and the piecewise-linear attenuator, tradeoffs exist between the speed of the actuators, the desired fluence modulation rate and the cone angle of the system, analysis of which are beyond the scope of this work. Qualitatively, it appears that a speed of thickness modulation of about 25 mm of iron per revolution may be sufficient for the piecewise linear attenuator to approximately achieve the wedge patterns in Fig. 12. For the system parameters similar to those adopted in earlier work,4 including a 300 ms gantry rotation time, this requires actuator speed of 75 cm/s, which is nontrivial but within reach of compact motion systems.
Figure 12.
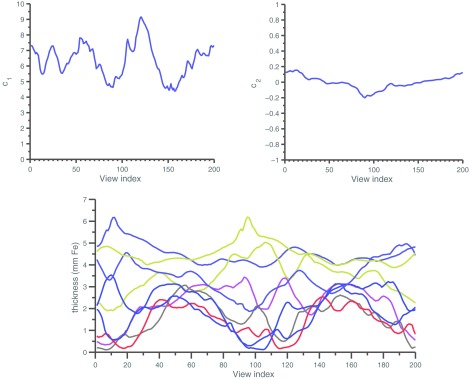
Optimized control for peak variance using different attenuators. (Top) (c1, c2) as a function of view index for the translating attenuator. As described in the text, the translating attenuator implements a parabolic thickness function of f(γ) = c1(γ − c2)2, where γ is the normalized fan angle. (Bottom) Thickness of the central nine wedges in the dynamic attenuator.
DISCUSSION
We have introduced several control algorithms for minimizing mean or peak variance using dynamic attenuators. We focused on two families of dynamic attenuators: attenuators which provide limited degrees of freedom per view (D = 1 or D = 2), and approximations to the perfect attenuator. The former includes the translating attenuator and the double wedge attenuator, but other concepts are possible. The latter includes the piecewise-linear attenuator, the related piecewise-constant attenuator,16 the virtual bowtie of inverse geometry CT,13 and the perfect attenuator itself.
For the first family of limited attenuators, we provided a method for decomposing the optimization problem into smaller problems with reduced dimensionality. In order to use these methods, a priori knowledge of the patient anatomy is needed. This is a significant assumption, and at least in some situations may not be practical and it will be necessary to develop heuristic algorithms on a case-by-case basis for each dynamic attenuator.
For the second family of attenuators, we provided methods for minimizing the mean and peak variance of the perfect attenuator. The perfect attenuator may prove very difficult to achieve, but flexible attenuator designs such as the piecewise-linear attenuator can mimic the optimal fluence field with high accuracy. For mean variance minimization and peak variance minimization, power law control and optimized flat variance, respectively, are good heuristics that eliminate the need for a priori knowledge. Optimized flat variance has similarities to power law control with an exponent of 1. A compromise between mean and peak variance can be achieved using an appropriate, intermediate exponent.
The control methods we developed can be implemented with standard CT reconstruction tools, such as forward and backprojection, and do not require detailed knowledge of numerical optimization techniques. Our proposed methods can be used on some problems (such as the double wedge or translating attenuators) which cannot be solved with convex optimization. Compared to stochastic optimization methods, our proposed methods bound the objective function and have provable accuracy. On the other hand, there are certain attenuators which are neither perfect attenuator-like nor limited attenuator-like, which cannot be analyzed by the algorithms proposed here.
For the peak variance minimization task, a tradeoff exists between attenuator complexity and dose reduction. TCM alone could be considered a degenerate dynamic attenuator and, when optimized, reduces the peak variance by 10% beyond that of the square root heuristic TCM. The translating and double wedge attenuators further reduce dose by about 20%. Although we believe we chose reasonable shapes for these attenuators, further refinement and dose reduction may be possible. The 15-wedge piecewise-linear dynamic attenuator provides an additional decrease of about 15%, and finally, the perfect attenuator provides another decrease of 15%. This tradeoff between complexity and dose reduction has also been observed in another, recent study that used multistage simulated annealing.30, 32
The dynamic attenuators were much less successful at reducing mean variance than peak variance. This is sensible because controlling the fluence field provides the system with the ability to redistribute noise. Peak variance is determined by the pixels with the highest variance, and a dynamic attenuator can redistribute fluence to reduce the variance in those pixels at the expense of increasing variance elsewhere. This is more beneficial for the peak variance metric than the mean variance metric. In any case, we suggest that in the absence of a priori information, peak variance is more appropriate than mean variance because it provides a guarantee on minimum image quality. In the clinic, it may not be acceptable to compromise diagnostic image quality in one part of the image to produce excessive image quality in another region. In the end, the variance metric that is most appropriate may depend on the clinical task. In Fig. 8, the attenuators that were most successful at reducing peak variance also increased the variance in the lung field. In many applications, this is acceptable, because contrast is much higher in the lungs than in the mediastinum. In other applications this may be disadvantageous.
If regions of interest can be delineated, further dose reduction can be achieved. These regions of interest need not be binary so that data outside the region of interest is discarded, but may instead take the form of “image quality plans” which parallel the dose plans in radiation therapy.9
The purpose of this study was to develop the theory for controlling dynamic attenuators, and we therefore invoked several simplifications. We have previously examined the effect of polychromatic spectra, Monte Carlo dose estimates, volumetric datasets, and volumetric reconstruction algorithms, and we found that the dose reductions predicted from the simple 2D studies continued to hold in the more realistic environment.33 We therefore anticipate that the dose reductions observed here would also hold in the more complex settings. However, the dose reduction may be reduced for volumetric scans with wide collimation in the z-direction. The attenuators that are described here are themselves designed for fan-beam systems. They are not intended to control modulation in the cone angle (or z) direction unless extended or combined with other concepts. For 64-slice scanners, because the field of view in the z-direction is much smaller than the field of view in the x-direction, this approximation should be acceptable. For more recent scanners with tens of centimeters of coverage in the z-direction, the dynamic attenuators will be less effective at dose reduction. Other approaches for dynamic beam shaping, such as a rotating compensator which is 3D printed for the individual,34 could be applicable. The theory developed here can still be adapted to applied to the volumetric case as it is implemented on the basis of standard forward and backprojection operators. The control of the perfect attenuator without a priori knowledge would also be similar. One difference is that if a reconstruction algorithm with data weighting is used, peak variance optimization without a priori knowledge should proceed by forcing the variance of detector channels in a view to be weighted instead of flat, similar in principle to a beam shaping filter which has already been described.35
We neglected electronic noise in the definition of our problem. A simple model of electronic noise is additive noise of fixed magnitude to each detector channel. Measurements with the fewest photons are therefore degraded the most by electronic noise. Since these measurements already dominate the noise streaks in the image, adding electronic noise would lead to even stronger noise streaks. Therefore, one of the priorities in detector design is to reduce the electronic noise as much as possible. In some cases, such as low-dose scans of very large patients, additive electronic noise cannot be neglected. Here, we expect that these control methods and dynamic attenuators could lead to greater dose reductions if they increase the flux delivered to rays with otherwise few photons.
The amount of dose reduction is expected to depend on the reconstruction algorithm used. Iterative reconstruction algorithms have recently become clinically viable, and it has been well established that simple measurements such as image variance are poor predictors for image quality with these nonlinear algorithms. One of the advantages of iterative algorithms is that they model the noise statistics and can reduce the impact of noisy measurements.36 We suggest that dynamic attenuators would still be useful with iterative reconstruction for the same reason that TCM is still useful, but that the magnitude of dose reduction may be reduced. For example, the dynamic attenuator will likely make the data statistics more uniform, reducing the impact of the iterative reconstruction algorithm.
Introducing a dynamic attenuator into a CT system is a nontrivial task. The mechanical system must be both fast and accurate, and imaging artifacts must be carefully controlled. More sophisticated beam hardening correction algorithms may also be necessary.4, 37 However, it could be argued that other routes to dose reduction, such as photon-counting detectors and iterative reconstruction, have faced similar or larger challenges and yet are being actively pursued. We believe that the dose reductions presented by dynamic attenuators are large enough to warrant further study. While the piecewise-linear dynamic attenuator showed the largest dose reduction of the practical attenuators studied, all attenuators showed potential for significant dose reductions, and some of them are relatively simple. Given the growing concern for radiation dose in CT, it seems prudent to consider adoption of these attenuators in clinical systems.
ACKNOWLEDGMENTS
This work was supported by the Lucas Foundation, the Wallace H. Coulter Foundation, the National Defense Graduate and Science Engineering Fellowship program, and the National Institutes of Health (R21 EB01557401).
APPENDIX: BOUND ON THE MINIMAX VARIANCE
The upper bound
follows from the definition of the minimax variance. The minimax variance is the smallest possible peak variance for any x, and is simply the peak variance for xWMV.
The lower bound
can be proven by contradiction. Suppose . Let us examine the objective function of the WMV problem. Because of the optimality of xWMV, we must have that
However, we may also apply an elementwise bound. Let 1 be the column vector of ones, and note that for any k, by the definition of the minimax.
If it were true that , we must have
Finally, by definition of ,
We therefore find that assuming leads us to
which contradicts the optimality of xWMV. Therefore, our supposition that must be false. The preceding arguments were independent of the particular choice of wT, so we must have that for any weight wT with elements non-negative,
References
- Hsieh J., Computed Tomography: Principles, Design, Artifacts, and Recent Advances (SPIE Press, Bellingham, WA, 2003). [Google Scholar]
- Taguchi K., Zhang M., Frey E. C., Wang X., Iwanczyk J. S., Nygard E., Hartsough N. E., Tsui B. M., and Barber W. C., “Modeling the performance of a photon counting x-ray detector for CT: Energy response and pulse pileup effects,” Med. Phys. 38, 1089–1102 (2011). 10.1118/1.3539602 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taguchi K., Frey E. C., Wang X., Iwanczyk J. S., and Barber W. C., “An analytical model of the effects of pulse pileup on the energy spectrum recorded by energy resolved photon counting x-ray detectors,” Med. Phys. 37, 3957–3969 (2010). 10.1118/1.3429056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh S. S. and Pelc N. J., “The feasibility of a piecewise-linear dynamic bowtie filter,” Med. Phys. 40, 031910 (12pp.) (2013). 10.1118/1.4789630 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu F., Wang G., Cong W., Hsieh S. S., and Pelc N. J., “Dynamic bowtie for fan-beam CT,” Journal of X-ray Science and Technology 21(4), 579–590 (2013). [DOI] [PubMed] [Google Scholar]
- Kalra M. K., Maher M. M., Toth T. L., Schmidt B., Westerman B. L., Morgan H. T., and Saini S., “Techniques and applications of automatic tube current modulation for CT,” Radiology 233, 649–657 (2004). 10.1148/radiol.2333031150 [DOI] [PubMed] [Google Scholar]
- Gies M., Kalender W. A., Wolf H., Suess C., and Madsen M. T., “Dose reduction in CT by anatomically adapted tube current modulation. I. Simulation studies,” Med. Phys. 26, 2235–2247 (1999). 10.1118/1.598779 [DOI] [PubMed] [Google Scholar]
- Kalender W. A., Wolf H., and Suess C., “Dose reduction in CT by anatomically adapted tube current modulation. II. Phantom measurements,” Med. Phys. 26, 2248–2253 (1999). 10.1118/1.598738 [DOI] [PubMed] [Google Scholar]
- Bartolac S., Graham S., Siewerdsen J., and Jaffray D., “Fluence field optimization for noise and dose objectives in CT,” Med. Phys. 38, S2–S17 (2011). 10.1118/1.3574885 [DOI] [PubMed] [Google Scholar]
- Sperl J., Beque D., Claus B., De Man B., Senzig B., and Brokate M., “Computer-assisted scan protocol and reconstruction (CASPAR)—Reduction of image noise and patient dose,” IEEE Trans. Med. Imaging 29, 724–732 (2010). 10.1109/TMI.2009.2034515 [DOI] [PubMed] [Google Scholar]
- Mazin S. R., Star-Lack J., Bennett N. R., and Pelc N. J., “Inverse-geometry volumetric CT system with multiple detector arrays for wide field-of-view imaging,” Med. Phys. 34, 2133–2142 (2007). 10.1118/1.2737168 [DOI] [PubMed] [Google Scholar]
- Schmidt T. G., Star-Lack J., Bennett N. R., Mazin S. R., Solomon E. G., Fahrig R., and Pelc N. J., “A prototype table-top inverse-geometry volumetric CT system,” Med. Phys. 33, 1867–1878 (2006). 10.1118/1.2192887 [DOI] [PubMed] [Google Scholar]
- Schmidt T. G., Fahrig R., Pelc N. J., and Solomon E. G., “An inverse-geometry volumetric CT system with a large-area scanned source: A feasibility study,” Med. Phys. 31, 2623–2627 (2004). 10.1118/1.1786171 [DOI] [PubMed] [Google Scholar]
- Arenson J. S., Ruimi D., Meirav O., and Armstrong R. H., General Electric Company, “X-ray flux management device,” U.S. patent 7,330,535 (12 Feb 2008).
- Toth T. L., Tkaczyk J. E., and Hsieh J., General Electric Company, “Method and apparatus of radiographic imaging with an energy beam tailored for a subject to be scanned,” U.S. patent 7,076,029 (11 July 2006).
- Szczykutowicz T. P. and Mistretta C. A., “Design of a digital beam attenuation system for computed tomography: Part I. System design and simulation framework,” Med. Phys. 40, 021905 (12pp.) (2013). 10.1118/1.4773879 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczykutowicz T. P. and Mistretta C. A., “Design of a digital beam attenuation system for computed tomography. Part II. Performance study and initial results,” Med. Phys. 40, 021906 (9pp.) (2013). 10.1118/1.4773880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczykutowicz T. P. and Mistretta C., “Practical considerations for intensity modulated CT,” Proc. SPIE 8313, 83134E (2012). 10.1117/12.911355 [DOI] [Google Scholar]
- Li J., Udayasankar U. K., Toth T. L., Seamans J., Small W. C., and Kalra M. K., “Automatic patient centering for MDCT: Effect on radiation dose,” Am. J. Roentgenol. 188, 547–552 (2007). 10.2214/AJR.06.0370 [DOI] [PubMed] [Google Scholar]
- Toth T., Ge Z., and Daly M. P., “The influence of patient centering on CT dose and image noise,” Med. Phys. 34, 3093–3101 (2007). 10.1118/1.2748113 [DOI] [PubMed] [Google Scholar]
- Chesler D. A., Riederer S. J., and Pelc N. J., “Noise due to photon counting statistics in computed x-ray tomography,” J. Comput. Assist. Tomogr. 1, 64–74 (1977). 10.1097/00004728-197701000-00009 [DOI] [PubMed] [Google Scholar]
- Kak A. and Slaney M., Principles of Computerized Tomographic Imaging (SIAM, Philadelphia, 1988). [Google Scholar]
- Tang X., Hsieh J., Nilsen R. A., Dutta S., Samsonov D., and Hagiwara A., “A three-dimensional-weighted cone beam filtered backprojection (CB-FBP) algorithm for image reconstruction in volumetric CT—Helical scanning,” Phys. Med. Biol. 51, 855–874 (2006). 10.1088/0031-9155/51/4/007 [DOI] [PubMed] [Google Scholar]
- Tang X., Hsieh J., Hagiwara A., Nilsen R. A., Thibault J. B., and Drapkin E., “A three-dimensional weighted cone beam filtered backprojection (CB-FBP) algorithm for image reconstruction in volumetric CT under a circular source trajectory,” Phys. Med. Biol. 50, 3889–3905 (2005). 10.1088/0031-9155/50/16/016 [DOI] [PubMed] [Google Scholar]
- Boedeker K. and McNitt-Gray M., “Application of the noise power spectrum in modern diagnostic MDCT: Part II. Noise power spectra and signal to noise,” Phys. Med. Biol. 52, 4047–4061 (2007). 10.1088/0031-9155/52/14/003 [DOI] [PubMed] [Google Scholar]
- Harpen M. D., “A simple theorem relating noise and patient dose in computed tomography,” Med. Phys. 26, 2231–2234 (1999). 10.1118/1.598778 [DOI] [PubMed] [Google Scholar]
- Boyd S. P. and Vandenberghe L., Convex Optimization (Cambridge University Press, New York, 2004). [Google Scholar]
- Grant M. and Boyd S., CVX: Matlab Software for Disciplined Convex Programming, version 1.21, 2011.
- Grant M. and Boyd S., “Graph implementations for nonsmooth convex programs,” in Recent Advances in Learning and Control, edited by Blondel V., Boyd S., and Kimura H. (Springer-Verlag Limited, London, 2008), pp. 95–110. [Google Scholar]
- Bartolac S. and Jaffray D., “Compensator models for fluence field modulated computed tomography,” Med. Phys. 40, 121909 (15pp.) (2013). 10.1118/1.4829513 [DOI] [PubMed] [Google Scholar]
- CASIMAGE Radiology Teaching Files Database (available URL: http://pubimage.hcuge.ch).
- Bartolac S. and Jaffray D., “Strategies for fluence field modulated CT,” Paper Presented at AAPM 55th Annual Meeting, Indianapolis, August 2013.
- Hsieh S. S., Fleischmann D., and Pelc N. J., “Dose reduction using a dynamic, piecewise-linear attenuator,” Med. Phys. 41, 021910 (14pp.) (2014). 10.1118/1.4862079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roessl E. and Proksa R., “Dynamic beam-shaper for high flux photon-counting computed tomography,” Paper Presented at Workshop on Medical Applications of Spectroscopic X-ray Detectors, Geneva, Switzerland, 2013.
- Köhler T., Brendel B., and Proksa R., “Beam shaper with optimized dose utility for helical cone-beam CT,” Med. Phys. 38, S76–S84 (2011). 10.1118/1.3577766 [DOI] [PubMed] [Google Scholar]
- Thibault J. B., Sauer K. D., Bouman C. A., and Hsieh J., “A three-dimensional statistical approach to improved image quality for multislice helical CT,” Med. Phys. 34, 4526–4544 (2007). 10.1118/1.2789499 [DOI] [PubMed] [Google Scholar]
- Joseph P. M. and Spital R. D., “A method for correcting bone induced artifacts in computed tomography scanners,” J. Comput. Assist. Tomogr. 2, 100–108 (1978). 10.1097/00004728-197801000-00017 [DOI] [PubMed] [Google Scholar]