Skip to main content
PMC home page
Medical Physics logoLink to Medical Physics
. 2014 May 15;41(6):062102. doi: 10.1118/1.4875704

Video-rate optical dosimetry and dynamic visualization of IMRT and VMAT treatment plans in water using Cherenkov radiation

Adam K Glaser 1,a), Jacqueline M Andreozzi 1, Scott C Davis 1, Rongxiao Zhang 2, Brian W Pogue 3,a), Colleen J Fox 4, David J Gladstone 4
PMCID: PMC4032443  PMID: 24877829

Abstract

Purpose: A novel technique for optical dosimetry of dynamic intensity-modulated radiation therapy (IMRT) and volumetric-modulated arc therapy (VMAT) plans was investigated for the first time by capturing images of the induced Cherenkov radiation in water.

Methods: A high-sensitivity, intensified CCD camera (ICCD) was configured to acquire a two-dimensional (2D) projection image of the Cherenkov radiation induced by IMRT and VMAT plans, based on the Task Group 119 (TG-119) C-Shape geometry. Plans were generated using the Varian Eclipse treatment planning system (TPS) and delivered using 6 MV x-rays from a Varian TrueBeam Linear Accelerator (Linac) incident on a water tank doped with the fluorophore quinine sulfate. The ICCD acquisition was gated to the Linac target trigger pulse to reduce background light artifacts, read out for a single radiation pulse, and binned to a resolution of 512 × 512 pixels. The resulting videos were analyzed temporally for various regions of interest (ROI) covering the planning target volume (PTV) and organ at risk (OAR), and summed to obtain an overall light intensity distribution, which was compared to the expected dose distribution from the TPS using a gamma-index analysis.

Results: The chosen camera settings resulted in 23.5 frames per second dosimetry videos. Temporal intensity plots of the PTV and OAR ROIs confirmed the preferential delivery of dose to the PTV versus the OAR, and the gamma analysis yielded 95.9% and 96.2% agreement between the experimentally captured Cherenkov light distribution and expected TPS dose distribution based upon a 3%/3 mm dose difference and distance-to-agreement criterion for the IMRT and VMAT plans, respectively.

Conclusions: The results from this initial study demonstrate the first documented use of Cherenkov radiation for video-rate optical dosimetry of dynamic IMRT and VMAT treatment plans. The proposed modality has several potential advantages over alternative methods including the real-time nature of the acquisition, and upon future refinement may prove to be a robust and novel dosimetry method with both research and clinical applications.

Keywords: Cherenkov, Cerenkov, IMRT, VMAT, dosimetry, quality assurance, optical

INTRODUCTION

Recent advances in radiation therapy have led to increasingly complex treatments. Modern techniques such as intensity-modulated radiation therapy (IMRT) and volumetric-modulated arc therapy (VMAT) have added additional degrees of freedom to treatment planning and delivery which have increased efficacy but also created a need for more robust quality assurance (QA) methods for delivery verification.

Traditionally, QA methods focused on the use of radiographic or Gafchromic® film dosimetry for obtaining planar two-dimensional (2D) dose distributions inside a dosimetry phantom.1, 2, 3 Although film dosimetry is high resolution and near water equivalent, the process is cumbersome, not real-time, and may exhibit processing-dependent variability. More recent techniques include portal imaging,4, 5, 6 ionization chamber arrays,7 and semiconductor arrays.6 A digital analogue to film dosimetry, portal imaging is easy to use, but the true experimental measurement may only be made at a single planar slice. Array-based systems inherently lack the resolution required for accurate dose verification, due to the finite spacing of the detectors. Additional methods currently under development include gel and plastic or liquid scintillation dosimetry.8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 Despite several advantages, gel dosimetry is time consuming, requires postprocessing and a readout mechanism such as optical computed tomography (CT) or magnetic resonance imaging (MRI), and scintillation methods require careful calibration and suppression of the stem effect.21, 22, 23, 24, 25 Finally, all of the current techniques are not truly water equivalent, as the active medium is not water itself. This point is of particular importance, as water is the gold standard dosimetry medium due to its equivalence to tissue, cheap abundance, high-purity, and ease of interinstitution standardization. Therefore, there is interest in a simple, accurate, quick, robust, and real-time water-based method for routine QA of patient-specific IMRT and VMAT treatments.

THEORY

A number of recent studies have proposed using light generated by the Cherenkov effect (light emission from charged particles traveling through a dielectric medium at a speed greater than that of the local speed of light) for water-based dosimetry26, 27, 28, 29, 30, 31 and other radiotherapy applications.32, 33, 34, 35, 36, 37 In an initial study, a simple theoretical interpretation to the correlation between Cherenkov light emission and dose deposition for a single monoenergetic x-ray photon beam was given.26 The formalism can be summarized by expressing the number of Cherenkov photons emitted per unit mass at any spatial location in the irradiated medium, N, as

N=∫ΦρdNdxdE, (1)

where E is the particle energy, Φ is the polyenergetic electron fluence spectrum, dNdx is given by the Frank-Tamm formula, and ρ is the density of the irradiated medium. Similarly, the dose, D, can be expressed as

D=∫Φρ−dTdxdE, (2)

where −dTdx is the electron collisional stopping power. Although in the initial study, the similarity between the two quantities was attributed to the approximate proportionality between the Frank-Tamm formula and electron collisional stopping power above the threshold energy for Cherenkov light emission (under this formalism, there exists an obvious disproportionality at lower energies where Cherenkov light emission is not possible), here we reform this notion and suggest that the correlation between the two phenomena is independent of the form of dNdx and −dTdx under the pretense that the relative electron fluence spectrum remains the same. It should be noted that this assumption is valid in the beam interior and may break down at the beam edges, leading to a disproportionality between Eqs. 1, 2.

If we assume that the relative shape of Φ remains constant in the majority of the irradiated medium, Eqs. 1, 2 can be rewritten as

N=A∫ΦrρdNdxdE, (3)
D=A∫Φrρ−dTdxdE, (4)

where A represents a scalar constant at each point in the irradiated medium, which simply scales the constant relative electron fluence spectrum Φr. In this case, the integrals in Eqs. 3, 4 can be easily calculated and represent single scalar values. N and D therefore scale in identical ways simply based upon A. Referring to the scalar values as BN and BD, respectively, the relationship between the number of emitted Cherenkov photons and deposited dose, R, in the medium can then be defined as

R=BNBD (5)

which holds true at all spatial locations in the irradiated medium. Therefore, for relative dosimetry, the correlation is independent of the two energy loss mechanisms (i.e., the Frank-Tamm formula and collisional stopping power), although changes in R would need to be considered for absolute dosimetry.

Although this notion is true for a monoenergetic x-ray photon beam, (i.e., after the buildup region, due to exponential attenuation the medium will be in transient charged particle equilibrium and the assumption of a constant relative electron fluence spectrum is valid), for any realistic polyenergetic x-ray photon beam this is not be the case. If we consider a single x-ray photon beam incident on a homogenous volume, the fluence of primary x-ray photons at a given energy, ψ, reaching a certain depth, z, will be exponentially attenuated as

ψ=ψre−μz, (6)

where ψr is the initial fluence at the volume surface and μ is the linear attenuation coefficient of the medium for the given x-ray photon energy. Due to the fact that the linear attenuation coefficient of most materials (e.g., water for the purposes of radiotherapy QA) vary in the clinical x-ray photon energy range, the x-ray photon spectrum will change as a function of depth due to the preferential attenuation of lower energy x-ray photons (i.e., beam hardening). As a result, Φr will exhibit some degree of depth dependence.

However, if we consider multiple beams (as is the case in IMRT and VMAT delivery), and simplify the scenario for two parallel-opposed beams irradiating a rectangular volume, the x-ray photon fluence at any depth can be given by the superposition of the two beams as

ψ=ψr[e−μz+e−μd−z], (7)

where it is assumed that ψr is constant for the two beams, and d is the thickness of the irradiated volume. As an approximation, this superposition of the fluence from both beams mitigates the beam hardening effect. (i.e., near either of the entrance surfaces the superposition is of a hard and soft beam, whereas in the center of the volume the superposition is of two moderate beams). Therefore, the validity of using Cherenkov light emission as a surrogate for the deposited dose may be best for dynamic treatment IMRT and VMAT treatment plans in which the plan can be approximated as the superposition of a number of parallel opposed beams.

In the present study, we investigate this topic through video-rate optical dosimetry of dynamic IMRT and VMAT plans for QA and verification for the first time.

MONTE CARLO SIMULATIONS

To investigate the correlation of Cherenkov light emission and dose deposition, as well as its validity for IMRT and VMAT treatment plans, Monte Carlo simulations were run using the GEANT4 package through the GAMOS (GEANT4 architecture for medically oriented simulations) interface.38, 39 In the simulations, a 10 × 10 cm 6 MV field was used to irradiate a 40 × 40 × 40 cm volume of water parameterized into 1 mm cubic voxels. The deposited dose and number of Cherenkov photons (between 450 and 750 nm, assuming a spectrally constant refractive index of 1.33) produced within each voxel was recorded using 108 primary particles. Although in these simulations the visible wavelengths were simulated, due to the constant spectrum of Cherenkov radiation (inversely proportional to the square of the emission wavelength), widening or narrowing the waveband would simply scale the number of recorded photons in each voxel up or down, respectively. The phase space file used for the simulation was generated for a Varian 2100C Linear Accelerator (Linac) using the BEAMnrc package and a previously validated accelerator geometry.40

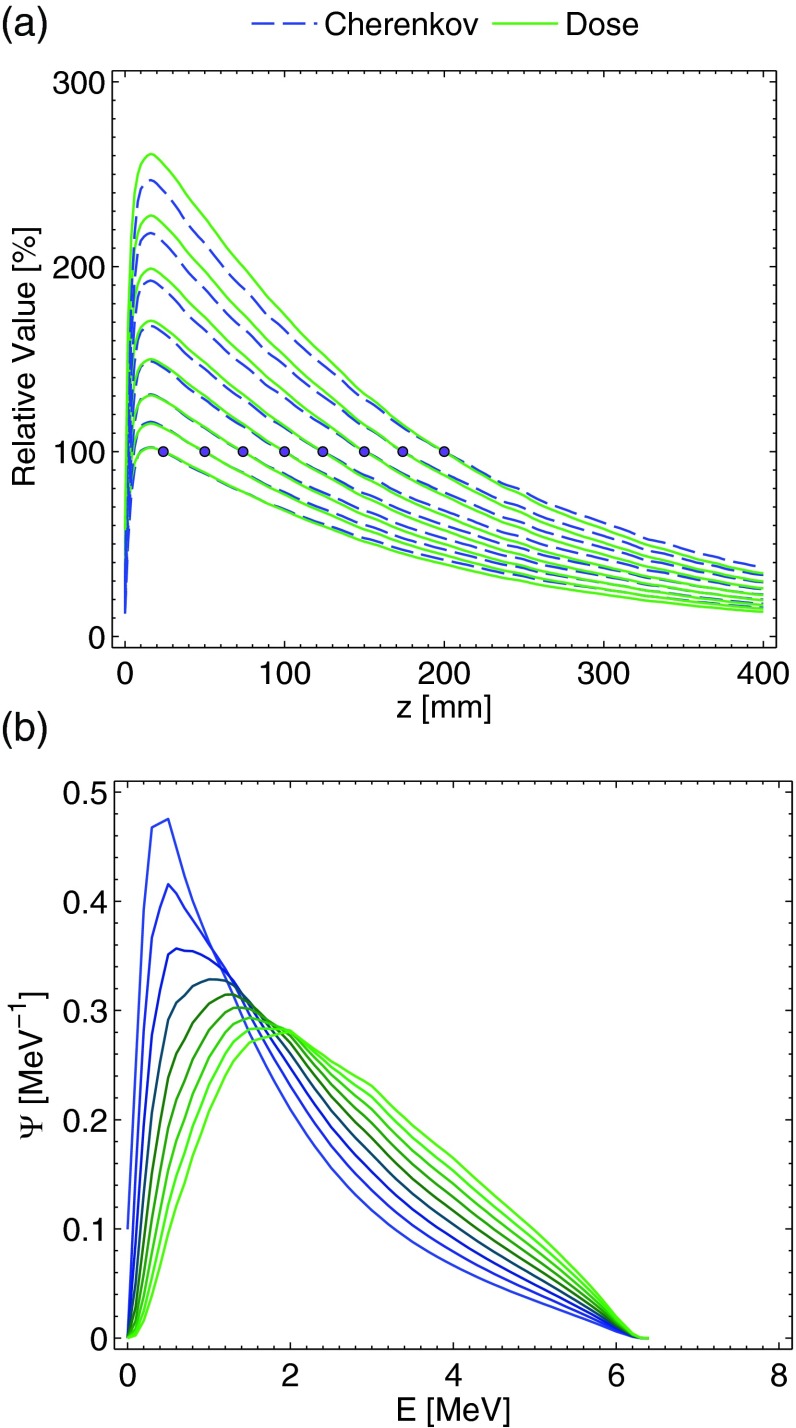
The resulting percent depth dose (PDD) and light emission curves are plotted in Fig. 1a, normalized to a value of 100% at depths of 25, 50, 75, 100, 125, 150, 175, and 200 mm, respectively. These normalization depths were chosen for the secondary simulation experiment that was performed using the superposition of the results of the single beam to mimic the anterior-posterior-posterior-anterior (AP-PA) parallel-opposed beam geometry through water volume thicknesses of 50, 100, 150, 200, 250, 300, 350, and 400 mm (i.e., the normalization depths are at the isocenter of these thickness values). As can be seen, due to the beam hardening and resulting x-ray fluence spectral differences, in general the Cherenkov light emission underpredicts the dose prior to the normalization depth, and overpredicts the dose beyond the normalization depth (i.e., relative to x-ray fluence spectrum at the normalization point, the fluence is softer prior resulting in an electron fluence spectrum weighted at lower energies with respect to Φ at the isocenter, leading to underprediction, and harder post, leading to overprediction due to an electron fluence spectrum weighted at higher energies). The error trend prior to the normalization depth also appears to increase for deeper depths of normalization, although the relative error with respect to the maximum value at the depth of maximum dose is similar. The x-ray fluence spectra from the Monte Carlo simulations at depths of 50, 100, 150, 200, 250, 300, 350, and 400 mm are plotted in Fig. 1b.

Figure 1.

Figure 1

Open in a new tab

In (a), the Monte Carlo simulation results for the normalized PDD curves of the dose and Cherenkov light emission, normalized at depths of 25, 50, 75, 100, 125, 150, 175, and 200 mm are plotted. In (b), the x-ray fluence spectra at depths of 0, 50, 100, 150, 200, 250, 300, 350, and 400 mm are plotted. Both graphs are for a 10 × 10 cm 6 MV beam.

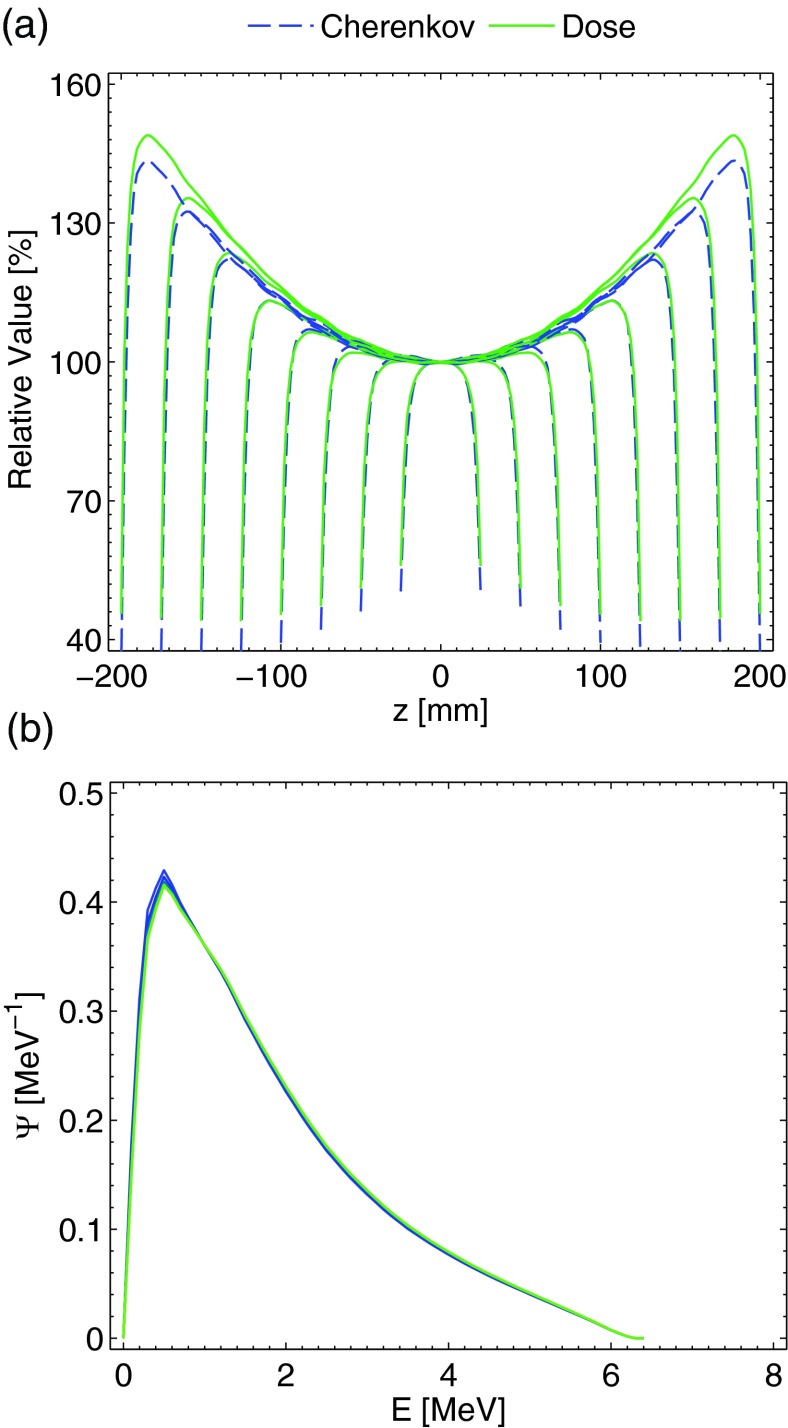
The results for the AP-PA irradiation of the thicknesses mentioned previously are plotted in Fig. 2a. For thicknesses less than roughly 300 mm, the agreement between the Cherenkov light emission and dose at all depths is within 2%–3%, and within 1% for the majority of the thinner thicknesses. The increased agreement relative to the single beam can be explained by examining the x-ray fluence spectrum. As postulated in Sec. 2, the parallel-opposed beam geometry and resulting fluence spectrum superposition effectively averages out much of the beam hardening effect. The x-ray fluence spectra at depths of 0, 10, 20, 30, 40, and 50 mm for the 100 mm thickness irradiation scenario are plotted in Fig. 2b. As can be seen, at all of the depths the relative spectrum is substantially similar, leading to a direct correlation between the Cherenkov light emission and dose deposition curves. However, for thicknesses greater than 300 mm (i.e., the 350 and 400 mm plots), the error in the hot spot regions is larger (7–8%) and the averaging out of the beam-hardening phenomenon is less applicable, although the relative error with respect to the range of dose values from zero to the hotspot remains similar.

Figure 2.

Figure 2

Open in a new tab

In (a), the Monte Carlo simulation results for the PDD curves of the dose and light emission for the AP-PA geometry, normalized at isocenter for thicknesses of 50, 100, 150, 200, 250, 300, 350, and 400 mm are plotted. In (b), the x-ray fluence spectra at depths of 0, 10, 20, 30, 40, and 50 are plotted for the 100 mm thickness phantom. Both plots are for a 10 × 10 cm 6 MV beam.

MATERIALS AND METHODS

Experimental setup

The experimental setup is shown in Fig. 3 and consists of a gated intensified-charged-coupled device (ICCD) (PIMAX3, Princeton Instruments, Acton, MA) positioned to image the induced Cherenkov light in a water-phantom during irradiation. The camera, which was equipped with a fixed focal length high aperture lens was placed 3 m from the isocenter of a Varian TrueBeam Linear Accelerator (Linac) (Varian Medical Systems, Palo Alto, CA). To increase the signal-to-background (SBR), the camera was synced with the Linac pulses by a trigger signal to acquire only when the beam was on. In this configuration, images (512 × 512 resolution) were acquired at 23.5 frames per second, and each image consisted of one accumulation (3 μs in duration), i.e., single pulse imaging. Stray radiation striking the intensifier and CCD sensor causes significant image noise; however, this was addressed by applying a moving temporal noise median filter such that each filtered image represented the pixel-by-pixel median of a stack of 23 total images (11 frames before and after the image of interest, corresponding to just under 1 s of acquisition). The filtering was also used to improve the signal-to-noise-ratio (SNR) of the captured images due the Poisson photon counting statistics associated with imaging the weak Cherenkov radiation from a single radiation pulse. The high frame rate was chosen over a lower frame rate with an increased number of pulses accumulated into an individual frame to provide the highest possible temporal data resolution, as well as the highest temporal density of frames for effective removal of the stray radiation noise.41

Figure 3.

Figure 3

Open in a new tab

The experimental setup, consisting of the linear accelerator, cubic water tank phantom, and externally placed camera system is shown. The working distance of the camera to water phantom is 3 m.

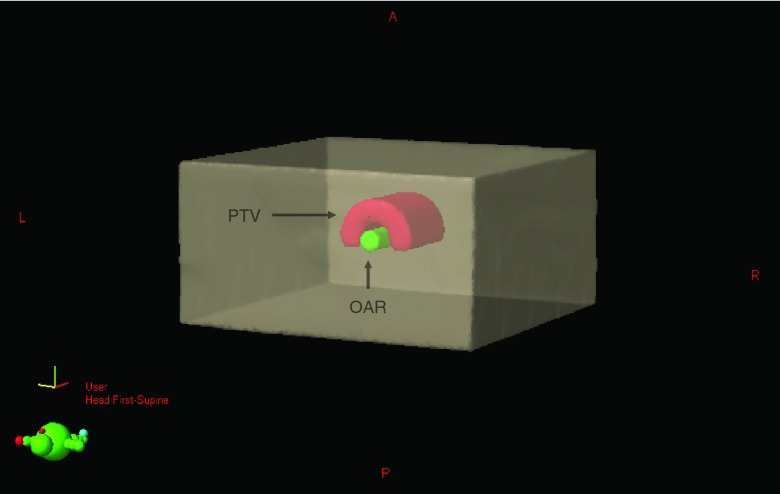
The AAPM Task Group 119 (TG-119) C-Shape plan for IMRT and VMAT were used to assess the accuracy of Cherenkov imaging dose estimates. This plan maximizes the dose in a half-ring planning target volume (PTV) about a central volume organ at risk (OAR), in which the dose is minimized. IMRT and VMAT treatment plans were designed using the Varian Eclipse TPS (Varian Medical Systems, Palo Alto, CA) on a virtual phantom. The geometry is shown in Fig. 4, where the PTV has an inner and outer radius of 1.5 and 3.7 cm, respectively, with a length of 8.0 cm and the OAR has a radius of 1.0 cm and length of 10.0 cm. More specifics on the virtual phantom geometry can be found in the report.42 The resulting optimized treatment plans were then planned on an x-ray CT scan of a 25.4 × 25.4 × 40.6 cm rectangular aquarium filled with water to a height of 34 cm doped with 1.0 g/L of quinine sulfate, which was used as the QA phantom for all experiments. The quinine sulfate serves as a means for converting the anisotropic Cherenkov radiation to isotropic fluorescence (at 400–500 nm in which the self-absorption due to water is minimal) which allows for undistorted imaging of the induced light distribution.27 The isocenter of both treatment plans was centered laterally in the tank and located 14.5 cm above the bottom surface of the tank. The specifics of each plan and the dose optimization goals are shown in Table 1.

Figure 4.

Figure 4

Open in a new tab

The geometry of the TG-119 C-Shape phantom is shown. The geometry consists of a cylindrical OAR with a radius of 1.5 cm, and an outer PTV with an inner and outer radius of 1.5 and 3.7 cm, respectively. The length of the OAR is 10.0 cm, and the length of the PTV is 8.0 cm.

Table 1.

Details of the delivered IMRT and VMAT treatment plans.

IMRT
95% of PTV to receive at least 1000 cGy, 10% of PTV to receive no more than 1100 cGy, 5% of OAR to receive no more than 200 cGy
Beam Gantry angle Collimator angle Field X Field Y SSD Dose
[#] [deg] [deg] [cm] [cm] [cm] [MU]
1 160.0 0 9.8 9.3 84.4 396
2 120.0 0 8.6 9.6 85.3 407
3 80.0 0 7.8 9.6 87.0 307
4 40.0 0 9.3 9.0 80.3 389
5 0 0 10.0 9.0 80.8 392
6 320.0 0 9.3 9.0 80.1 400
7 280.0 0 7.8 9.6 86.9 300
8 240.0 0 8.6 9.6 85.2 404
9 200.0 0 9.8 9.6 84.4 395
VMAT
95% of PTV to receive at least 400 cGy, 10% of PTV to receive no more than 440 cGy, 5% of OAR to receive no more than 1000 80 cGy
Arc Gantry rotation Collimator angle Field X Field Y SSD Dose
[#]
 [deg]
 [deg]
 [cm]
 [cm]
 [cm]
 [MU]
1 359.9 CCW 0 8.6 10.7 85.5 1087
2 359.9 CW 45.0 11.2 11.1 85.5 1082
Open in a new tab

Accuracy analysis

To quantify the accuracy of the proposed technique, the experimentally captured images of the Cherenkov light distribution were compared to the predicted dose from the TPS. To accomplish this, the resulting filtered image stack was first summed to obtain the integrated light distribution for the entire dynamic treatment plan. The resulting image represents a 2D projection of the 3D light volume induced within the water phantom and contains geometric distortion due to the parallax associated with regular imaging lenses (i.e., as opposed to telecentric lenses which provide a constant magnification with imaging distance). To account for this, the 3D dose matrix obtained from the TPS was summed in the following manner. Under the assumption that the experimentally captured images were focused at the focal plane encompassing the treatment isocenter, the 2D planes of the dose matrix closer to the camera were appropriately magnified, and the 2D planes farther from the camera appropriately demagnified based upon the known experimental setup (e.g., tank dimensions, camera working distance, and refraction at the air tank interface). The resulting experimental 2D projection of the light distribution and nonlinearly summed 2D dose projection from the TPS were normalized to 100% at their maximum values at isocenter, and compared using the gamma-index analysis feature in the 3D SlicerRT program with a 3%/3 mm dose difference and distance-to-agreement (DTA) criterion.43, 44

RESULTS AND DISCUSSION

Representative experimental images for both a single frame (i.e., single Linac pulse), the corresponding median filtered frame, and summed composite image for the VMAT treatment plan is shown in Fig. 4. In the raw image shown in Fig. 5a of a single pulse (3 μs in duration), both the stray radiation noise and Poisson photon counting statistical noise are apparent. The counts due to the induced Cherenkov radiation are sparse and appear as blooms due to single photons striking the intensifier of the ICCD. However, the temporal median filter of the stack of 23 images effectively removes the stray radiation noise and elucidates the radiation beam, as is shown in Fig. 5b. The resulting summed composite image for the VMAT treatment plan is shown in Fig. 5c.

Figure 5.

Figure 5

Open in a new tab

In (a), a representative experimental raw image for the VMAT treatment plan is shown. The resulting frame after the pixel-by-pixel temporal median filtering of 23 frames is shown in (b). In (c) the resulting summed composite image for the VMAT treatment plan is shown.

To demonstrate the temporal abilities of the method, a region of interest (ROI) was drawn about the PTV and OAR in the experimentally acquired projection images. The cumulative intensity within each ROI was then calculated as a function of time, the results of which are shown in Figs. 6a, 6b. The former plot clearly shows that as a function of time, the intensity (or dose) is preferentially deposited in the PTV rather than the OAR. It is interesting to note that directly following the conclusion of the first arc, the second arc begins with a spike in counts suggesting that at this point in the VMAT treatment a large portion of the dose is being deposited. In addition, the temporal profile of the OAR shows four distinct periodic spikes in counts, which correspond roughly to beam angles of 0°, 90°, 180°, 270°, and 360°. At these angles the OAR receives a nominal amount of dose relative to the other angles due to the inability of the beam to treat the PTV while completely sparing the OAR. Finally, despite the axial symmetry of the geometry, the profiles of the two arcs with respect to the PTV are not symmetric due to different collimator rotations.

Figure 6.

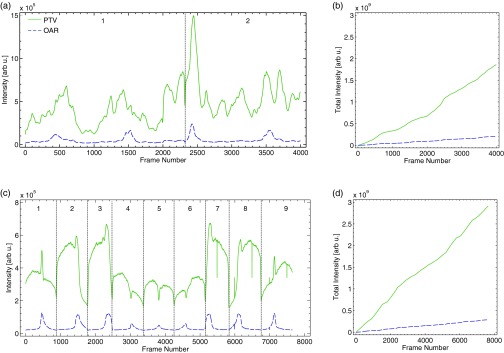
Figure 6

Open in a new tab

In (a), the temporal time profile for the PTV and OAR ROIs of the VMAT treatment plan are shown. The divider indicates the transition between arcs 1 and 2. In (b), the cumulative accumulation of intensity within both ROIs is plotted. Commensurate plots for the IMRT treatment plan are shown in (c) and (d), with the dividers indicating the transitions between fields 1 and 9.

Similar plots for the IMRT plan are shown in Figs. 6c, 6d. The dividers in the temporal plot clearly indicate the nine different fields of the plan. In the IMRT plan, for each field the MLC shapes the beam in a sliding window approach in which the beam passes over the aperture, which directly irradiates the OAR. This can be seen in the single spike in the time profile for each field of the OAR. The PTV temporal profile also reveals that the intensity or dose deposited by beams 2 and 3 (and 7 and 8 due to symmetry), is larger than that of beams 4, 5, and 6 due to the difference in attenuation through the water tank prior to reaching the isocenter. Finally, due to identical collimator settings for all nine fields, the temporal profiles of both the PTV and OAR appear symmetric.

The resulting summed dose distribution, projection image of the experimentally captured 3D Cherenkov light volume, and gamma-index map for the nine-field IMRT treatment plan are shown in Figs. 7a, 7b, 7c. The commensurate images for the VMAT treatment plan are shown in Figs. 7d, 7e, 7f. Visual inspection of the dose distributions predicted by the TPS and the experimentally captured images shows excellent agreement, which is confirmed by the quantitative gamma-index analysis. In the case of the nine-field IMRT treatment plan, 95.9% of the pixels exhibit a passing criteria, whereas for the VMAT treatment plan 96.2% of the pixels pass the 3%/3 mm dose difference and DTA criterion. This is in good agreement with the 95% pass rate typically used for clinical IMRT and VMAT treatment plans.

Figure 7.

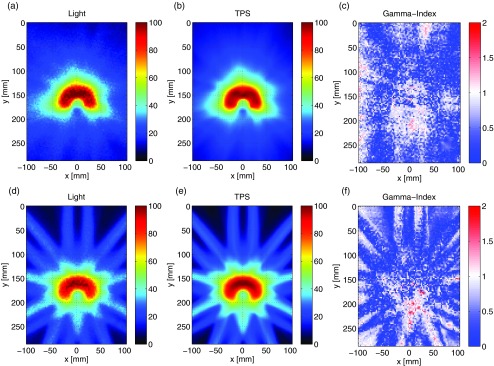
Figure 7

Open in a new tab

In (a) and (b), the 2D projections of the experimentally imaged 3D Cherenkov light volume and nonlinearly summed 3D dose matrix from the TPS are shown for the VMAT treatment plan. The resulting gamma-index map is shown in (c) for a 3% /3 mm dose difference and DTA criterion. In (d)–(f), the same images for the nine-field IMRT treatment plan are shown.

The observed discrepancies between the light distribution and TPS could be due to misalignment of the two images in the rigid transformation, as well as to the fundamental differences between the deposited dose and Cherenkov light volumes, stemming from the assumption that Φr remains constant in Eqs. 1, 2 for all regions of the water tank. This would be most apparent at the beam edges, which is confirmed by the gamma-index map for the IMRT treatment plan. In addition, Monte Carlo simulations indicate that the validity of the Cherenkov approximation for a 6 MV field breaks down at larger thicknesses (i.e., beyond 300 mm), limiting the accuracy and applicability of this technique to irradiation of larger clinical volumes. An investigation into additional beam energies, as well as the potential calibration for the sources of error enumerated above will be investigated in future studies.

CONCLUSION

We have shown for the first time that a novel optical technique can accurately estimate delivered dose of IMRT and VMAT in real time in water phantoms. This capability is enabled by imaging the induced Cherenkov radiation in a water tank using an ICCD synchronized to a Linac. This technique is simple and robust and is able to collect video-rate temporal dosimetric images at 23.5 frames per second. Comparison of the temporally summed experimental images to the predicted dose yielded results which were in good agreement with the expected 95% gamma index pass criterion of dynamic radiotherapy plans based upon a 3%/3 mm dose difference and DTA criterion. While additional studies are required for further validation, to our knowledge, this study represents the first to show real-time dosimetry of IMRT and VMAT in water phantoms. Although currently limited to indirect, time-resolved 2D projection imaging of 3D dose (similar to portal imaging), the use of multiple cameras and optical tomography, or a single plenoptic camera could yield 4D data at a higher spatial resolution with respect to current ionization chamber array techniques (e.g., 3D ArcCHECK). This capability could have a significant impact on quality assessment for the treatment modalities.

ACKNOWLEDGMENT

This work has been funded by NIH Grant Nos. RO1CA109558, R21EB017559, and P30CA23108.

References

  1. Low D. A., “Quality assurance of intensity-modulated radiotherapy,” Semin. Radiat. Oncol. 12, 219–228 (2002). 10.1053/srao.2002.33700 [DOI] [PubMed] [Google Scholar]
  2. Dempsey J. F., Low D. A., Mutic S., Markman J., Kirov A. S., Nussbaum G. H., and Williamson J. F., “Validation of a precision radiochromic film dosimetry system for quantitative two-dimensional imaging of acute exposure dose distributions,” Med. Phys. 27, 2462–2475 (2000). 10.1118/1.1290488 [DOI] [PubMed] [Google Scholar]
  3. Niroomand-Rad A., Blackwell C. R., Coursey B. M., Gall K. P., Galvin J. M., McLaughlin W. L., Meigooni A. S., Nath R., Rodgers J. E., and Soares C. G., “Radiochromic film dosimetry: Recommendations of AAPM Radiation Therapy Committee Task Group 55. American Association of Physicists in Medicine,” Med. Phys. 25, 2093–2115 (1998). 10.1118/1.598407 [DOI] [PubMed] [Google Scholar]
  4. Van Esch A., Depuydt T., and Huyskens D. P., “The use of an aSi-based EPID for routine absolute dosimetric pre-treatment verification of dynamic IMRT fields,” Radiother. Oncol. 71, 223–234 (2004). 10.1016/j.radonc.2004.02.018 [DOI] [PubMed] [Google Scholar]
  5. Mans A., Remeijer P., Olaciregui-Ruiz I., Wendling M., Sonke J. J., Mijnheer B., van Herk M., and Stroom J. C., “3D dosimetric verification of volumetric-modulated arc therapy by portal dosimetry,” Radiother. Oncol. 94, 181–187 (2010). 10.1016/j.radonc.2009.12.020 [DOI] [PubMed] [Google Scholar]
  6. Partridge M., Ebert M., and Hesse B. M., “IMRT verification by three-dimensional dose reconstruction from portal beam measurements,” Med. Phys. 29, 1847–1858 (2002). 10.1118/1.1494988 [DOI] [PubMed] [Google Scholar]
  7. Poppe B., Blechschmidt A., Djouguela A., Kollhoff R., Rubach A., Willborn K. C., and Harder D., “Two-dimensional ionization chamber arrays for IMRT plan verification,” Med. Phys. 33, 1005–1015 (2006). 10.1118/1.2179167 [DOI] [PubMed] [Google Scholar]
  8. Guillot M., Beaulieu L., Archambault L., Beddar S., and Gingras L., “A new water-equivalent 2D plastic scintillation detectors array for the dosimetry of megavoltage energy photon beams in radiation therapy,” Med. Phys. 38, 6763–6774 (2011). 10.1118/1.3664007 [DOI] [PubMed] [Google Scholar]
  9. Beddar S., Archambault L., Sahoo N., Poenisch F., Chen G. T., Gillin M. T., and Mohan R., “Exploration of the potential of liquid scintillators for real-time 3D dosimetry of intensity modulated proton beams,” Med. Phys. 36, 1736–1743 (2009). 10.1118/1.3117583 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Frelin A. M., Fontbonne J. M., Ban G., Colin J., Labalme M., Batalla A., Vela A., Boher P., Braud M., and Leroux T., “The DosiMap, a new 2D scintillating dosimeter for IMRT quality assurance: Characterization of two Cerenkov discrimination methods,” Med. Phys. 35, 1651–1662 (2008). 10.1118/1.2897966 [DOI] [PubMed] [Google Scholar]
  11. Collomb-Patton V., Boher P., Leroux T., Fontbonne J. M., Batalla A., and Vela A., “DOSIMAP: A high-resolution 2-D tissue equivalent dosemeter for linac QA and IMRT verification,” Radiat. Prot. Dosim. 131, 100–109 (2008). 10.1093/rpd/ncn228 [DOI] [PubMed] [Google Scholar]
  12. Goulet M., Archambault L., Beaulieu L., and Gingras L., “High resolution 2D dose measurement device based on a few long scintillating fibers and tomographic reconstruction,” Med. Phys. 39, 4840–4849 (2012). 10.1118/1.4736526 [DOI] [PubMed] [Google Scholar]
  13. Ponisch F., Archambault L., Briere T. M., Sahoo N., Mohan R., Beddar S., and Gillin M. T., “Liquid scintillator for 2D dosimetry for high-energy photon beams,” Med. Phys. 36, 1478–1485 (2009). 10.1118/1.3106390 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Olding T. and Schreiner L. J., “Cone-beam optical computed tomography for gel dosimetry II: Imaging protocols,” Phys. Med. Biol. 56, 1259–1279 (2011). 10.1088/0031-9155/56/5/003 [DOI] [PubMed] [Google Scholar]
  15. Olding T., Holmes O., and Schreiner L. J., “Cone beam optical computed tomography for gel dosimetry I: Scanner characterization,” Phys. Med. Biol. 55, 2819–2840 (2010). 10.1088/0031-9155/55/10/003 [DOI] [PubMed] [Google Scholar]
  16. Oldham M., Siewerdsen J. H., Shetty A., and Jaffray D. A., “High resolution gel-dosimetry by optical-CT and MR scanning,” Med. Phys. 28, 1436–1445 (2001). 10.1118/1.1380430 [DOI] [PubMed] [Google Scholar]
  17. McJury M., Oldham M., Cosgrove V. P., Murphy P. S., Doran S., Leach M. O., and Webb S., “Radiation dosimetry using polymer gels: Methods and applications,” Br. J. Radiol. 73, 919–929 (2000). 10.1259/bjr.73.873.11064643 [DOI] [PubMed] [Google Scholar]
  18. Kelly R. G., Jordan K. J., and Battista J. J., “Optical CT reconstruction of 3D dose distributions using the ferrous-benzoic-xylenol (FBX) gel dosimeter,” Med. Phys. 25, 1741–1750 (1998). 10.1118/1.598356 [DOI] [PubMed] [Google Scholar]
  19. Maryanski M. J., Ibbott G. S., Eastman P., Schulz R. J., and Gore J. C., “Radiation therapy dosimetry using magnetic resonance imaging of polymer gels,” Med. Phys. 23, 699–705 (1996). 10.1118/1.597717 [DOI] [PubMed] [Google Scholar]
  20. Gore J. C., Ranade M., Maryanski M. J., and Schulz R. J., “Radiation dose distributions in three dimensions from tomographic optical density scanning of polymer gels: I. Development of an optical scanner,” Phys. Med. Biol. 41, 2695–2704 (1996). 10.1088/0031-9155/41/12/009 [DOI] [PubMed] [Google Scholar]
  21. Liu P. Z., Suchowerska N., Lambert J., Abolfathi P., and McKenzie D. R., “Plastic scintillation dosimetry: Comparison of three solutions for the Cerenkov challenge,” Phys. Med. Biol. 56, 5805–5821 (2011). 10.1088/0031-9155/56/18/003 [DOI] [PubMed] [Google Scholar]
  22. Archambault L., Beddar A. S., Gingras L., Roy R., and Beaulieu L., “Measurement accuracy and Cerenkov removal for high performance, high spatial resolution scintillation dosimetry,” Med. Phys. 33, 128–135 (2006). 10.1118/1.2138010 [DOI] [PubMed] [Google Scholar]
  23. Beddar A. S., Suchowerska N., and Law S. H., “Plastic scintillation dosimetry for radiation therapy: Minimizing capture of Cerenkov radiation noise,” Phys. Med. Biol. 49, 783–790 (2004). 10.1088/0031-9155/49/5/009 [DOI] [PubMed] [Google Scholar]
  24. Clift M. A., Johnston P. N., and Webb D. V., “A temporal method of avoiding the Cerenkov radiation generated in organic scintillator dosimeters by pulsed mega-voltage electron and photon beams,” Phys. Med. Biol. 47, 1421–1433 (2002). 10.1088/0031-9155/47/8/313 [DOI] [PubMed] [Google Scholar]
  25. Clift M. A., Sutton R. A., and Webb D. V., “Dealing with Cerenkov radiation generated in organic scintillator dosimeters by bremsstrahlung beams,” Phys. Med. Biol. 45, 1165–1182 (2000). 10.1088/0031-9155/45/5/307 [DOI] [PubMed] [Google Scholar]
  26. Glaser A. K., Davis S. C., McClatchy D. M., Zhang R., Pogue B. W., and Gladstone D. J., “Projection imaging of photon beams by the Cerenkov effect,” Med. Phys. 40, 012101 (14pp.) (2013). 10.1118/1.4770286 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Glaser A. K., Davis S. C., Voigt W. H., Zhang R., Pogue B. W., and Gladstone D. J., “Projection imaging of photon beams using Cerenkov-excited fluorescence,” Phys. Med. Biol. 58, 601–619 (2013). 10.1088/0031-9155/58/3/601 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Glaser A. K., Voigt W. H., Davis S. C., Zhang R., Gladstone D. J., and Pogue B. W., “Three-dimensional Cerenkov tomography of energy deposition from ionizing radiation beams,” Opt. Lett. 38, 634–636 (2013). 10.1364/OL.38.000634 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Jang K. W., Yagi T., Pyeon C. H., Yoo W. J., Shin S. H., Jeong C., Min B. J., Shin D., Misawa T., and Lee B., “Application of Cerenkov radiation generated in plastic optical fibers for therapeutic photon beam dosimetry,” J. Biomed. Opt. 18, 027001 (2013). 10.1117/1.JBO.18.2.027001 [DOI] [PubMed] [Google Scholar]
  30. Jang K. W., Yoo W. J., Shin S. H., Shin D., and Lee B., “Fiber-optic Cerenkov radiation sensor for proton therapy dosimetry,” Opt. Express 20, 13907–13914 (2012). 10.1364/OE.20.013907 [DOI] [PubMed] [Google Scholar]
  31. Helo Y., Rosenberg I., D’Souza D., Macdonald L., Speller R., Royle G., and Gibson A., “Imaging Cerenkov emission as a quality assurance tool in electron radiotherapy,” Phys. Med. Biol. 59, 1963–1978 (2014). 10.1088/0031-9155/59/8/1963 [DOI] [PubMed] [Google Scholar]
  32. Zhang R., Glaser A. K., Gladstone D. J., Fox C. J., and Pogue B. W., “Superficial dosimetry imaging based on Cerenkov emission for external beam radiotherapy with megavoltage x-ray beam,” Med. Phys. 40, 101914 (12pp.) (2013). 10.1118/1.4821543 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Zhang R., Gladstone D. J., Jarvis L. A., Strawbridge R. R., Jack Hoopes P., Friedman O. D., Glaser A. K., and Pogue B. W., “Real-time in vivo Cherenkoscopy imaging during external beam radiation therapy,” J. Biomed. Opt. 18, 110504 (2013). 10.1117/1.JBO.18.11.110504 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zhang R. X., Fox C. J., Glaser A. K., Gladstone D. J., and Pogue B. W., “Superficial dosimetry imaging of Cerenkov emission in electron beam radiotherapy of phantoms,” Phys. Med. Biol. 58, 5477–5493 (2013). 10.1088/0031-9155/58/16/5477 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Teymurazyan A., Rowlands J. A., and Pang G., “Monte Carlo simulation of a quantum noise limited Cerenkov detector based on air-spaced light guiding taper for megavoltage x-ray imaging,” Med. Phys. 41, 041907 (12pp.) (2014). 10.1118/1.4867867 [DOI] [PubMed] [Google Scholar]
  36. Silva I. and Pang G., “Electronic portal imaging using Cerenkov radiation,” Radiother. Oncol. 84, S93–S103 (2007). 10.1117/12.772023 [DOI] [Google Scholar]
  37. Mei X., Rowlands J. A., and Pang G., “Electronic portal imaging based on Cerenkov radiation: A new approach and its feasibility,” Med. Phys. 33, 4258–4270 (2006). 10.1118/1.2362875 [DOI] [PubMed] [Google Scholar]
  38. Arce P., Rato P., Canadas M., and Lagares J. I., Nuclear Science Symposium Conference Record, NSS'08, 2008 (IEEE, 2008) (unpublished).
  39. Agostinelli S., Allison J., Amako K., Apostolakis J., Araujo H., Arce P., Asai M., Axen D., Banerjee S., Barrand G., Behner F., Bellagamba L., Boudreau J., Broglia L., Brunengo A., Burkhardt H., Chauvie S., Chuma J., Chytracek R., Cooperman G., Cosmo G., Degtyarenko P., Dell’Acqua A., Depaola G., Dietrich D., Enami R., Feliciello A., Ferguson C., Fesefeldt H., Folger G., Foppiano F., Forti A., Garelli S., Giani S., Giannitrapani R., Gibin D., Gómez Cadenas J. J., González I., Gracia Abril G., Greeniaus G., Greiner W., Grichine V., Grossheim A., Guatelli S., Gumplinger P., Hamatsu R., Hashimoto K., Hasui H., Heikkinen A., Howard A., Ivanchenko V., Johnson A., Jones F. W., Kallenbach J., Kanaya N., Kawabata M., Kawabata Y., Kawaguti M., Kelner S., Kent P., Kimura A., Kodama T., Kokoulin R., Kossov M., Kurashige H., Lamanna E., Lampén T., Lara V., Lefebure V., Lei F., Liendl M., Lockman W., Longo F., Magni S., Maire M., Medernach E., Minamimoto K., Mora de Freitas P., Morita Y., Murakami K., Nagamatu M., Nartallo R., Nieminen P., Nishimura T., Ohtsubo K., Okamura M., O’Neale S., Oohata Y., Paech K., Perl J., Pfeiffer A., Pia M. G., Ranjard F., Rybin A., Sadilov S., Di Salvo E., Santin G., Sasaki T., Savvas N., Sawada Y., Scherer S., Sei S., Sirotenko V., Smith D., Starkov N., Stoecker H., Sulkimo J., Takahata M., Tanaka S., Tcherniaev E., Safai Tehrani E., Tropeano M., Truscott P., Uno H., Urban L., Urban P., Verderi M., Walkden A., Wander W., Weber H., Wellisch J. P., Wenaus T., Williams D. C., Wright D., Yamada T., Yoshida H., and Zschiesche D., “Geant4—A simulation toolkit,” Nucl. Instrum. Methods Phys. Res. A 506, 250–303 (2003). 10.1016/S0168-9002(03)01368-8 [DOI] [Google Scholar]
  40. Siebers J. V., Keall P. J., Libby B., and Mohan R., “Comparison of EGS4 and MCNP4b Monte Carlo codes for generation of photon phase space distributions for a Varian 2100C,” Phys. Med. Biol. 44, 3009–3026 (1999). 10.1088/0031-9155/44/12/311 [DOI] [PubMed] [Google Scholar]
  41. Archambault L., Briere T. M., and Beddar S., “Transient noise characterization and filtration in CCD cameras exposed to stray radiation from a medical linear accelerator,” Med. Phys. 35, 4342–4351 (2008). 10.1118/1.2975147 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Ezzell G. A., Burmeister J. W., Dogan N., LoSasso T. J., Mechalakos J. G., Mihailidis D., Molineu A., Palta J. R., Ramsey C. R., Salter B. J., Shi J., Xia P., Yue N. J., and Xiao Y., “IMRT commissioning: Multiple institution planning and dosimetry comparisons, a report from AAPM Task Group 119,” Med. Phys. 36, 5359–5373 (2009). 10.1118/1.3238104 [DOI] [PubMed] [Google Scholar]
  43. Pinter C., Lasso A., Wang A., Jaffray D., and Fichtinger G., “SlicerRT: Radiation therapy research toolkit for 3D Slicer,” Med. Phys. 39, 6332–6338 (2012). 10.1118/1.4754659 [DOI] [PubMed] [Google Scholar]
  44. Fedorov A., Beichel R., Kalpathy-Cramer J., Finet J., Fillion-Robin J. C., Pujol S., Bauer C., Jennings D., Fennessy F., Sonka M., Buatti J., Aylward S., Miller J. V., Pieper S., and Kikinis R., “3D slicer as an image computing platform for the quantitative imaging network,” Magn. Reson. Imaging 30, 1323–1341 (2012). 10.1016/j.mri.2012.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Medical Physics are provided here courtesy of American Association of Physicists in Medicine

RESOURCES