Extraction of diffuse correlation spectroscopy flow index by integration of Nth-order linear model with Monte Carlo simulation

Abstract

Conventional semi-infinite solution for extracting blood flow index (BFI) from diffuse correlation spectroscopy (DCS) measurements may cause errors in estimation of BFI (αD_B) in tissues with small volume and large curvature. We proposed an algorithm integrating Nth-order linear model of autocorrelation function with the Monte Carlo simulation of photon migrations in tissue for the extraction of αD_B. The volume and geometry of the measured tissue were incorporated in the Monte Carlo simulation, which overcome the semi-infinite restrictions. The algorithm was tested using computer simulations on four tissue models with varied volumes/geometries and applied on an in vivo stroke model of mouse. Computer simulations shows that the high-order (N ≥ 5) linear algorithm was more accurate in extracting αD_B (errors < ±2%) from the noise-free DCS data than the semi-infinite solution (errors: −5.3% to −18.0%) for different tissue models. Although adding random noises to DCS data resulted in αD_B variations, the mean values of errors in extracting αD_B were similar to those reconstructed from the noise-free DCS data. In addition, the errors in extracting the relative changes of αD_B using both linear algorithm and semi-infinite solution were fairly small (errors < ±2.0%) and did not rely on the tissue volume/geometry. The experimental results from the in vivo stroke mice agreed with those in simulations, demonstrating the robustness of the linear algorithm. DCS with the high-order linear algorithm shows the potential for the inter-subject comparison and longitudinal monitoring of absolute BFI in a variety of tissues/organs with different volumes/geometries.

Near-infrared (NIR) diffuse correlation spectroscopy (DCS),^{1, 2} also called diffusing-wave spectroscopy (DWS),^{3, 4} is an emerging technology for probing microvascular blood flow in deep tissues. DCS for the measurement of blood flow variations has been broadly validated against other standards, including power spectral Doppler ultrasound, Doppler ultrasound, laser Doppler flowmetry, Xenon computed tomography, fluorescent microsphere flow measurement, and arterial-spin-labeled magnetic resonance imaging.^{2, 5} DCS has also been used for blood flow monitoring in a variety of tissues/organs including brain, tumor, and skeletal muscle.^{2, 5} Conventionally, blood flow index (BFI) was extracted by fitting the autocorrelation function measured by DCS to analytical solutions of correlation diffusion equation under regular tissue boundaries (e.g., semi-infinite homogenous media,^{6, 7, 8, 9} multi-layer slabs,^{10, 11} a sphere inside a slab¹²). Some of those analytical solutions were proposed to account for the influence of non-scattering layer tissues¹¹ or to improve the signal-to-noise ratio in deep tissues.⁹ However, the commonly used semi-infinite approximation may lead to BFI estimation errors in small volume tissues with large curvature.¹³ Seeking analytical solutions is mathematically complicated^{10, 12} and likely impossible for irregular geometries. With more and more clinical and pre-clinical applications of DCS, there is an urgent need to develop an algorithm that can accurately extract BFI without restrictions to tissue volume and geometry.

In this study, we created an algorithm to overcome these restrictions. Instead of solving the correlation diffuse equation analytically, we integrated an Nth-order linear model of light electric field temporal autocorrelation function with the Monte Carlo simulation of photon migrations in the tissue volume measured. This algorithm is thus not restricted by the tissue volume and geometry because such information has been incorporated in the Monte Carlo simulation. We validated this Nth-order linear model for the extraction of BFI using computer simulations on four tissue models with varied volumes/geometries and applied it on an in vivo stroke model of mouse.

The theory and instrumentation of DCS have been described elsewhere.¹³ Briefly, a laser launches long-coherence NIR light (650 to 900 nm) into the tissue via a source fiber placed on the tissue surface, and the light transported/scattered through the tissue is collected by a single-mode detector fiber placed millimeters to centimeters away from the source fiber. The collected light by the detector fiber is then delivered to an avalanche photodiode (APD) detector, wherein the count of photons per unit time (i.e., light intensity) is recorded. The APD output is connected to a correlator board yielding light intensity autocorrelation function which is related to the motion of moving scatterers (primarily red blood cells in microvasculature). The normalized electric field temporal autocorrelation function g₁(τ) of the detected light through highly scattering media can be determined by^{3, 4, 12, 13}

$$g_1(\tau )=\frac{⟨E(0)E^{*}(\tau )⟩}{⟨{|E(0)|}^2⟩}={\displaystyle {\int }_0^{\infty }P(s)\exp }(-\frac{1}{3}{k}_0^2⟨\Delta r^2(\tau )⟩\frac{s}{l^{*}})ds.$$ (1)

Here, P(s) is the normalized distribution of detected photon pathlength s, k₀ is the wave vector magnitude of the light in the medium, l^* is the photon random-walk step length which is equal to 1/${\mu }_s^{\prime }$ (${\mu }_s^{\prime }$ is the reduced scattering coefficient), and τ is the delay time of autocorrelation function. ⟨Δr²(τ)⟩ represents the mean-square displacement of the moving scatterers and its form depends on specific flow model adopted; diffuse model has been found to fit experimental data well over a wide range of tissues,⁶ i.e., ⟨Δr²(τ)⟩ = 6D_Bτ. Here, D_B is the effective diffusion coefficient. A factor α is added to ⟨Δr²(τ)⟩ (i.e., ⟨Δr²(τ)⟩ = 6αD_Bτ) to account for the fact that not all scatterers are “moving” in the tissue; α is the ratio of “moving” scatterers to the total number of scatterers. The combined term, αD_B, is referred to as BFI in biological tissues.¹⁴

From DCS theory, the unnormalized electric field temporal autocorrelation function G₁(τ) = ⟨E(0)E^*(τ)⟩ also satisfies the correlation diffusion equation^{6, 12}

$$\left(D{\nabla }^2-v{\mu }_a-\frac{1}{3}v{\mu }_s^{\prime }{k}_0^2⟨\Delta r^2\left(\tau \right)⟩\right)G_1\left(\overrightarrow{r},\tau \right)=-vS(\overrightarrow{r}).$$ (2)

Here, v is the light speed in the medium, μ_a is the medium absorption coefficient, D ≈ v / $3{\mu }_s^{\prime }$ is the medium photon diffusion coefficient, and $S(\overrightarrow{r})$ is continuous-wave isotropic source. Frequently, the analytical solution to Eq. 2 with semi-infinite geometry is used to extract αD_B.^{6, 7, 8} By contrast, our algorithm starts from the original definition of g₁(τ) in Eq. 1; g₁(τ) is extended to a form of Nth-order Taylor polynomial

$$g_1(\tau )=g_1(0)+g_1^{(1)}(0)\tau +{\displaystyle \sum _{i=2}^N\frac{g_1^{(i)}(0)}{i!}{\tau }^i}+\frac{g_1^{(N+1)}(\xi ){\tau }^{N+1}}{(N+1)!},\hspace{1em}(0<\xi <\tau ).$$ (3)

From Eq. 1 with the diffuse model ⟨Δr²(τ)⟩ = 6αD_Bτ, we get

$$g_1(0)={\displaystyle {\int }_0^{\infty }P(s)ds}=\hspace{0.17em}1,$$ (4)

$${g_1}^{(i)}(0)={\displaystyle {\int }_0^{\infty }P(s)s^i{(-2k_0^2{\mu }_s^{\prime }\alpha D_B)}^{i}ds}={(-Z)}^i\overline{s^i},\hspace{1em}i\ge 1,$$ (5)

$${g_1}^{(i)}(\xi )={(-Z)}^i{\displaystyle {\int }_0^{\infty }P(s)s^i\exp (-Z}s\xi )ds.$$ (6)

$$\text{Here},\hspace{0.17em}\overline{s^i}={\displaystyle {\int }_0^{\infty }P\left(s\right)s^{i}ds}\hspace{1em}\text{and}\hspace{1em}Z=2k_0^2{\mu }_s^{\prime }\alpha D_B.$$ (7)

Combining Eq. 3, 4, 5, 6, 7, we get

$$g_1(\tau )-\hspace{0.17em}1-{\displaystyle \sum _{i=2}^N\frac{{(-Z)}^i\overline{s^i}}{i!}{\tau }^i}=(-Z\overline{s})\tau +\frac{{(-Z)}^{N+1}{\displaystyle {\int }_0^{\infty }P(s)s^{N+1}\exp (-Z}s\xi )ds}{(N+1)!}{\tau }^{N+1},\hspace{1em}(0<\xi <\tau ).$$ (8)

When τ is sufficient small, the second term on the right side of Eq. 8 can be ignored (see the error estimation below). The first-order (N = 1) and Nth-order (N > 1) approximations are thus derived from Eq. 8, respectively,

$$g_1(\tau )-1=(-Z)\overline{s}\tau ,$$ (9)

$$g_1(\tau )-1-{\displaystyle \sum _{i=2}^N\frac{{(-Z)}^i\overline{s^i}}{i!}{\tau }^i}=(-Z)\overline{s}\tau .$$ (10)

Here, $\overline{s^i}={\int }_0^{\infty }P\left(s\right)s^{i}ds$ can be determined from the Monte Carlo simulation of photon migrations in the tissue measured.¹³ For the first-order approximation (N = 1) in Eq. 9, $Z_1=2k_0^2{\mu }_s^{\prime }\alpha D_B^{(1)}$ (Eq. 7) can be readily calculated from the slope of linear regression. For the Nth-order approximation (N > 1) in Eq. 10, which has unknown αD_B on both left and right sides, αD_B can be derived iteratively using following equations:

$$g_1(\tau )-\hspace{0.17em}1-{\displaystyle \sum _{i=2}^N\frac{{(-Z_{N-1})}^i\overline{s^i}}{i!}{\tau }^i}=(-Z_N\overline{s})\tau ,\hspace{1em}N\ge 2$$ (11)

$$\alpha D_B^{(N)}=Z_N/\left(2k_0^2{\mu }_s^{\prime }\right),\hspace{1em}N\ge 2.$$ (12)

Note that Eq. 11 utilizes the linear regression between the Nth-order Taylor polynomial of g₁(τ) and delay time τ to extract the BFI (αD_B). This algorithm is thus called “Nth-order linear model.” To estimate the errors of αD_B determined by Eq. 9, 10, 11, 12, we rewrite Eq. 8 as

$$g_1(\tau )-\hspace{0.17em}1-{\displaystyle \sum _{i=2}^N\frac{{(-Z_{N-1})}^i\overline{s^i}}{i!}{\tau }^i}=(-Z\overline{s})\tau +{\displaystyle \sum _{i=2}^N\frac{{(-Z)}^i-{(-Z_{N-1})}^i}{i!}\overline{s^i}{\tau }^i}+\frac{{(-Z)}^{N+1}{\displaystyle {\int }_0^{\infty }P(s)s^{N+1}\exp (-Z}s\xi )ds}{(N+1)!}{\tau }^{N+1}.$$ (13)

Comparing Eqs. 11, 13, we have

$$(-Z_N\overline{s})\tau =(-Z\overline{s})\tau +{\displaystyle \sum _{i=2}^N\frac{{(-Z)}^i-{(-Z_{N-1})}^i}{i!}\overline{s^i}{\tau }^i}+\frac{{(-Z)}^{N+1}{\displaystyle {\int }_0^{\infty }P(s)s^{N+1}\exp (-Z}s\xi )ds}{(N+1)!}{\tau }^{N+1}.$$ (14)

Note that Z (Eq. 7) and Z_N (Eq. 12) contain the true αD_B and estimated $\alpha D_B^{(N)}$, respectively. As seen from Eq. 14, the errors between the Z and Z_N (as well as the αD_B and $\alpha D_B^{(N)}$) result from Z_N−1 and N + 1 order Taylor expansion residual. These errors can be estimated as follows:

$$\begin{array}{c}err(\tau )=\left|\frac{\alpha D_B^{(N)}-\alpha D_B}{\alpha D_B}\right|=\left|\frac{Z_N-Z}{Z}\right|=\left|\frac{(-Z_N\overline{s}\tau )-(-Z\overline{s}\tau )}{(-Z\overline{s}\tau )}\right|\\ =|{\displaystyle \sum _{i=2}^N\frac{{(-Z)}^i-{(-Z_{N-1})}^i}{i!}\overline{s^i}{\tau }^i+\frac{{(-Z)}^{N+1}{\displaystyle {\int }_0^{\infty }P(s)s^{N+1}\exp (-Z}s\xi )ds}{(N+1)!}{\tau }^{N+1}}|/|(-Z)\overline{s}\tau |\\ \le |{\displaystyle \sum _{i=2}^N\frac{{(-Z)}^i-{(-Z_{N-1})}^i}{\overline{s}(-Z)i!}\overline{s^i}{\tau }^{i-1}}|+|\frac{{(-Z)}^N}{(N+1)!}\frac{{\displaystyle {\int }_0^{\infty }P(s)s^{N+1}\exp (-Z}s\xi )ds}{\overline{s}}{\tau }^N|\\ \le |{\displaystyle \sum _{i=1}^{N-1}\frac{{(-Z)}^{i+1}-{(-Z_{N-1})}^{i+1}}{\overline{s}(-Z)(i+1)!}\overline{s^{i+1}}{\tau }^i}|+|\frac{{(-Z)}^N}{(N+1)!}\frac{\overline{s^{N+1}}}{\overline{s}}{\tau }^N|.\end{array}$$ (15)

When $\Delta Z_{N-1}=Z_{N-1}-Z\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$ is sufficient small,

$${(-Z)}^{i+1}-{(-Z_{N-1})}^{i+1}\hspace{0.17em}\hspace{0.17em}\approx (i+1)\Delta Z_{N-1}{(-Z)}^i.$$ (16)

With this approximation, Eq. 15 becomes

$$err(\tau )\le \left|{\displaystyle \sum _{i=1}^{N-1}\frac{{(-Z)}^{i+1}-{(-Z_{N-1})}^{i+1}}{(-Z)(i+1)!}\frac{\overline{s^{i+1}}}{\overline{s}}{\tau }^i}\right|+\left|\frac{{(-Z)}^N}{(N+1)!}\frac{\overline{s^{N+1}}}{\overline{s}}{\tau }^N\right|\hspace{0.17em}\hspace{0.17em}\approx \left|\frac{\Delta Z_{N-1}}{Z}{\displaystyle \sum _{i=1}^{N-1}\frac{{(-Z\tau \overline{s})}^i}{i!}\frac{\overline{s^{i+1}}}{{(\overline{s})}^{i+1}}}\right|+\left|\frac{{(-Z\tau \overline{s})}^N}{(N+1)!}\frac{\overline{s^{N+1}}}{{(\overline{s})}^{N+1}}\right|.$$ (17)

When $Z\tau \overline{s}=2k_0^2\alpha D_B{\mu }_s^{\prime }\tau \overline{s}\ll 1\hspace{0.17em}$, i.e., $\tau \ll \frac{1}{2k_0^2{\mu }_s^{\prime }\alpha D_b\overline{s}}\hspace{0.17em}\hspace{0.17em}$, err(τ) is approximately equal to zero.

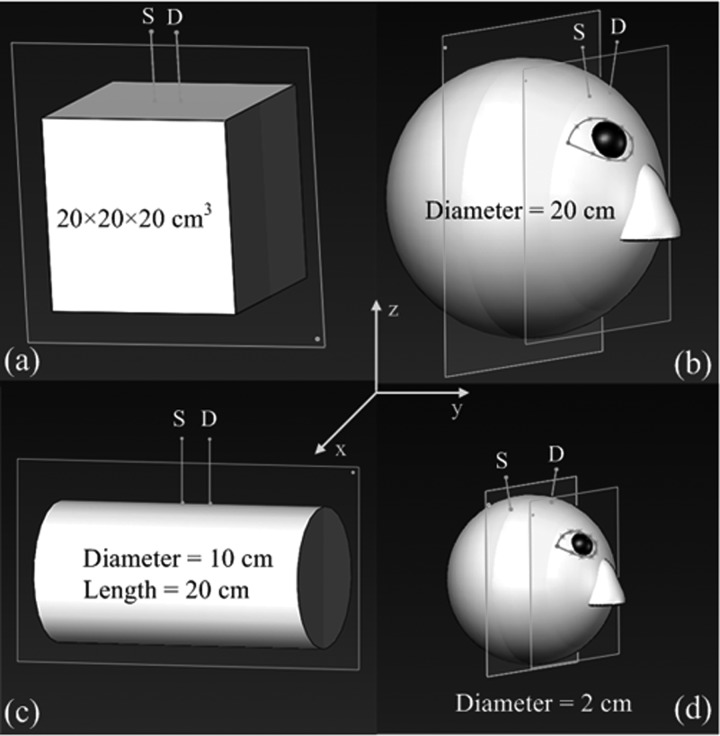
In order to evaluate the proposed Nth-order linear model (Eq. 11) and corresponding errors (Eq. 17), we created four tissue models with different volumes and geometries in computer simulations: (1) a large slab representative of an approximate semi-infinite tissue (Fig. 1a), (2) a large sphere representative of a human head (Fig. 1b), (3) a large cylinder representative of a human lower leg (Fig. 1c), and (4) a small sphere representative of a mouse head (Fig. 1d). The source-detector (S-D) separations were set as 2.5 cm for the tissues with large volumes (Figs. 1a, 1b, 1c) and 0.8 cm for the small mouse head (Fig. 1d). The dimensions and measurement setups for these tissue models matched approximately in vivo experiments.^{13, 14} The Monte Carlo simulation of 10 × 10⁶ photon migrations in the tissue was utilized to generate the normalized distribution of detected photon pathlengths P(s) in each tissue model.¹³ The calculated P(s) was then combined with the assigned BFI (αD_B) as well as optical properties (e.g., μ_a and μ_s′) reported in literature¹³ to generate an autocorrelation function g₁(τ) based on Eq. 1. Ten levels of αD_B with a step decrement of 10% was assigned (i.e., αD_B (i) = [1 − (i−1)/10] × 10⁻⁸ cm²/s, i = 1, 2,…, 10) for the evaluation of relative changes in BFI. Random noises generated by an established noise model¹⁵ were added to 1000 g₁(τ) curves in all tissue models, respectively. The levels of noise were determined by the detected light intensity which depended on tissue optical properties and S-D separation. A larger separation resulted in a lower light intensity, leading to a greater noise. As such, larger noises were added to the larger tissue models (by assigning a lower light intensity of 50 kHz based on previous in vivo human studies¹³) using the larger S-D separation of 2.5 cm (Figs. 1a, 1b, 1c) while smaller noises were added to the mouse head model (by assigning a higher light intensity of 200 kHz based on previous in vivo mouse studies¹⁴) using the shorter S-D separation of 0.8 cm (Fig. 1d). From the generated g₁(τ) curves, we extracted αD_B using the semi-infinite solution and Nth-order linear model. DCS data with the delay time 0.2 ≤ τ ≤ 30 μs (78 data points) were used in the linear model to satisfy the approximation made in Eqs. 9, 10, 11, 12, 13, 14, 15, 16, 17. The mean and standard derivation (mean ± SD over the 1000 g₁(τ) simulations) of αD_B errors between the reconstructed and assigned values are quantified for evaluations.

Figure 1.

Four tissue models with different volumes and geometries: (a) a large slab representative of large flat tissue, (b) a large sphere representative of human head, (c) a large cylinder representative of human lower leg, and (d) a small sphere representative of mouse head. The separations between the source (S) and detector (D) fibers were 2.5 cm for the models of (a), (b), and (c), and 0.8 cm for that of (d). The S-D fibers were placed in the ways to mimic in vivo experimental configurations. Note that the illustration scales may not be the same among different models.

After computer simulations, we applied our Nth-order linear model on an in vivo stroke model of mouse. The experimental protocol was approved by the University of Kentucky Institutional Animal Care and Use Committee. Ten C57BL/6 mice (male, 10–12 weeks old, Harlan Laboratories, Inc., IN, USA) were utilized. The mouse was anesthetized throughout cerebral ischemic procedure via inhalation of 1%–2% isoflurane in oxygen and a warm blanket was used to maintain the rectal temperature at 37 °C.¹⁴ For installation of optical probe on the skull, scalp was surgically removed from the mouse head.¹⁴ Left common carotid artery ligation (CCAL) was applied first, followed by a permanent left middle cerebral artery occlusion (MCAO) to induce a stroke. A foam pad (5 mm × 10 mm) containing a pair of source and detector fiber was glued on the mouse skull.¹⁴ The S-D separation was set as 0.8 cm, matching the simulation setup for mouse head (Fig. 1d). Cerebral BFI was continuously monitored by a DCS device throughout the ischemic procedure and extracted using the Nth-order linear model with small sphere tissue model, and compared with the semi-infinite solution.

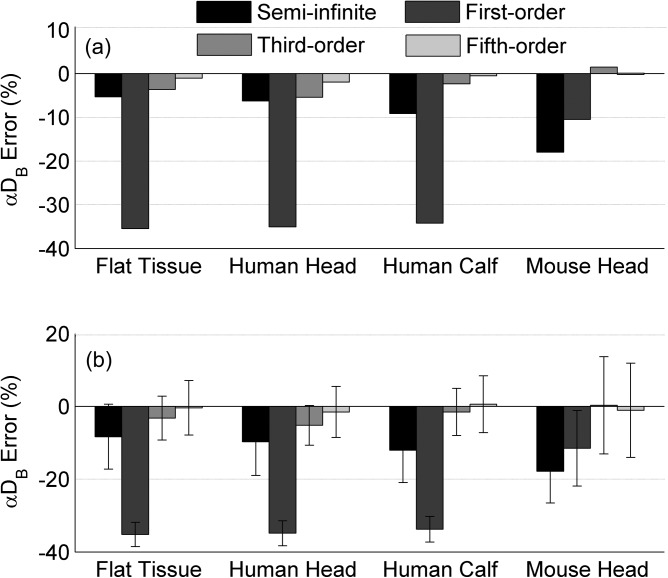
Figure 2 shows the percentage errors of αD_B at the first step of BFI variation (i.e., αD_B (1) = 1 × 10⁻⁸ cm²/s) reconstructed from the simulated DCS data without (Fig. 2a) or with noises (Fig. 2b). For comparisons, αD_B was calculated using the semi-infinite solution and the Nth-order linear model (N = 1, 3, 5,…). For all tissue models without noises (Fig. 2a), the reconstructed errors of αD_B decreased with the increase of the order number, and the solutions with higher orders (i.e., N ≥ 3) generated smaller αD_B errors than the semi-infinite solution. The accuracy of the semi-infinite solution relied on tissue geometry and volume; αD_B errors increased with the increase of tissue curvature and the decrease of tissue volume (large slab: −5.3%; human head: −6.3%; human lower leg: −9.1%; mouse head: −18.0%). By contrast, higher order solutions of the linear model retrieved more accurate αD_B values consistently regardless of the variations in tissue volumes and geometries. The reconstructed errors of αD_B using the third-order and fifth-order solutions were less than ±5.5% and ±2.0%, respectively, for all tissue models. Note that the errors using the linear model at higher orders (N > 5) were too small (< ±0.5%) to be displayed (data are not shown). Furthermore, the BFI errors generated by the high-order linear algorithm (N ≥ 5) and semi-infinite solution were not correlated (p > 0.05). All BFI errors observed in the simulations fell into the range estimated by Eq. 17. Adding random noises to DCS data resulted in variations in the errors of reconstructed αD_B (Fig. 2b). However, the mean values of these errors (Fig. 2b) were similar to those obtained from the noise-free DCS data (Fig. 2a).

Figure 2.

Percentage errors of αD_B at the first step of BFI (i.e., αD_B (1) = 1 × 10⁻⁸ cm²/s) in four tissue models reconstructed from the simulated DCS data (a) without and (b) with noises. The average errors calculated from the simulated 1000 autocorrelation curves with noises (b) are presented as means ± standard deviations (error bars).

For the αD_B values at different variation steps (i.e., from 0.1 × 10⁻⁸ to 1 × 10⁻⁸ cm²/s) with or without noises, the absolute BFI errors reconstructed by both the semi-infinite solution and Nth-order linear model were found to be proportional to the assigned absolute αD_B values. As a result, the errors in extracting the percentage changes of BFI (relative to the baseline BFI at the first step) were small (< ±2.0%) for all tissue models with and without noises, which did not rely on the tissue volume and geometry (data are not shown).

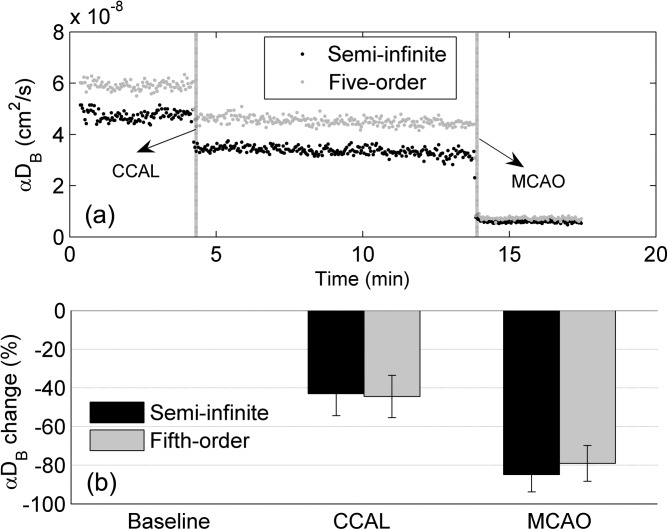
Figure 3 shows cerebral blood flow data reconstructed using the semi-infinite solution and fifth-order linear model from 10 mice with stroke. As illustrated from a representative mouse (Fig. 3a), time course changes in αD_B during ischemic procedures were continuously monitored and reconstructed by the two solutions for comparisons. An immediate large decrease in αD_B occurred at the onset of the left CCAL, followed by another deep reduction after the left MCAO. The two solutions yielded substantial difference in baseline αD_B. On average (n = 10), the significant differences in baseline αD_B (−20.7% ± 3.6%, p < 10⁻⁷, paired t-test) reconstructed by the two solutions were similar to those (−17.8% ± 8.7%, p < 10⁻¹⁰, paired t-test) observed in the simulated data with noises (Fig. 2b). However, the percentage changes in αD_B during CCAL and MCAO (Fig. 3b) were not significantly different (p = 0.47, one-way repeated measures ANOVA), which also agreed with our simulation results.

Figure 3.

Cerebral BFI (αD_B) data measured from 10 mice during the ischemic procedures to induce a stroke: (a) time course changes of αD_B extracted from a representative mouse and (b) percentage changes of αD_B during CCAL and during MCAO relative to their baselines (assigning 0), respectively. The αD_B was reconstructed using the semi-infinite solution and fifth-order linear algorithm, respectively. The percentage changes of αD_B were averaged over 10 mice and presented as means ± standard deviations (error bars).

In the simulations and in vivo tests, DCS data with delay time 0.2 ≤ τ ≤ 30 μs were selected to extract αD_B. According to Eq. 17, using DCS data with smaller τ to extract αD_B would result in smaller errors. On the other hand, the linear regression model (Eqs. 9, 11) needs more data points involved to yield a stable and accurate slope for extracting αD_B. Based on a few simulations, 78 DCS data points with 0.2 ≤ τ ≤ 30 μs were thus selected to balance the contradictory requests.

In summary, BFI is often extracted by fitting DCS data to the semi-infinite solution of correlation diffusion equation,^{6, 7, 8, 13, 14, 16} which assumes the homogeneous tissue to have a semi-infinite volume and flat surface. However, ignoring geometrical/volume influence (i.e., using semi-infinite approximation) may lead to remarkable evaluation errors in BFI (e.g., 5.3% to 18.0% observed in this study). Minimizing these errors is particularly crucial for these studies to compare the small differences in BFI at different time points or different regions of tissues (e.g., 10% to 28% differences observed in the infant's brain with a small volume and large curvature^{7, 16}). The linear algorithm created in this study overcomes the restrictions of semi-infinite solution and our results demonstrate that high-order linear solutions (N ≥ 5) can accurately extract absolute BFI values in homogenous tissue models with different geometries and volumes. Although we have tested this linear model only on several simple geometries/volumes (i.e., slab, sphere, cylinder), arbitrary geometry/volume can be obtained and tested in the future by incorporating other imaging modalities (e.g., MRI). It is also possible to extend the capability of the linear algorithm for extracting BFI values in heterogeneous tissues from DCS measurements at multiple S-D separations. Overall, our linear algorithm enables accurate quantification of absolute blood flow index, which is crucial for the inter-subject comparison and longitudinal flow monitoring in a variety of tissues/organs with different volumes and geometries.