Pathway structure determination in complex stochastic networks with non-exponential dwell times

Abstract

Analysis of complex networks has been widely used as a powerful tool for investigating various physical, chemical, and biological processes. To understand the emergent properties of these complex systems, one of the most basic issues is to determine the structure and topology of the underlying networks. Recently, a new theoretical approach based on first-passage analysis has been developed for investigating the relationship between structure and dynamic properties for network systems with exponential dwell time distributions. However, many real phenomena involve transitions with non-exponential waiting times. We extend the first-passage method to uncover the structure of distinct pathways in complex networks with non-exponential dwell time distributions. It is found that the analysis of early time dynamics provides explicit information on the length of the pathways associated to their dynamic properties. It reveals a universal relationship that we have condensed in one general equation, which relates the number of intermediate states on the shortest path to the early time behavior of the first-passage distributions. Our theoretical predictions are confirmed by extensive Monte Carlo simulations.

INTRODUCTION

Complex networks consisting of discrete states connected by dynamic transitions have been successfully applied for investigating many physical, chemical, and biological processes.^{1, 2, 3, 4, 5} Since the functioning of these complex systems is strongly influenced by their structures, the most important step in theoretical analysis is to determine the topology of underlying networks. Despite recent strong advances in understanding the dynamical and structural properties of complex chemical and biological networks,^{6, 7, 8, 9, 10, 11, 12, 13, 14} revealing the hidden structures of networks and their relations to dynamics remains a challenging task. One of the main reasons for this is a relatively small number of theoretical methods that can be employed.

Significant experimental progress in measuring dynamic properties of various chemical and biological processes has been reported. For many complex systems specific events between two arbitrary states can be measured with high temporal resolution.^{15, 16} Although the underlying structural information is contained in those experimental measurements, it is very difficult to extract it and to determine the unique mechanism of the process. It was realized that the analysis of distributions of such events is connected with a first-passage problem,^{19, 20, 21} which is a powerful method successfully applied to many stochastic chemical and biological problems.^{17, 18} Other theoretical methods for uncovering network structures, including hidden Markov models^{22, 23} and the absorbing boundary method,²⁴ have been developed recently. However, their practical application is limited to small networks and systems where one has prior knowledge of some details of the network structure.

Recently, a new theoretical approach to determine the relationship between structural and dynamic properties of complex networks has been developed based on the first-passage idea.^{25, 26} At early time, the probability density of the first-passage time between two states on a linear network has been found to follow a power law behavior.²⁵ It was proposed that similar relationships hold for general complex networks, and it was supported by Monte Carlo computer simulations. Later, the conjecture was proved to be correct for the network of any topology by deriving the Taylor series of first-passage time probability density using graph theory methods.²⁶ It was found that the smallest number of intermediate states between two arbitrary states of the network is given by the corresponding exponent of the power law function. By applying this theoretical method for several motor protein systems, it was argued that it might be especially useful for analyzing single-molecule experiments in various chemical and biological systems.²⁵ However, this approach explicitly assumed that all dynamic transitions between states are Poissonian, i.e., the corresponding dwell times on each single state are exponential. However, there is a large number of natural and industrial processes that involve non-exponential waiting times.^{27, 28, 29, 30} For example, coupling of mechanical degrees of freedom with chemical processes in motor proteins might lead to non-exponential waiting time distributions.²⁸ More generally, when a given state has an internal structure, for instance, a smaller sub-network of states, we should expect non-exponential dwell time distributions and violations of the Markov property. Since this is a more general case than systems modeled by Markov chains, it is important to extend the first-passage approach for investigating these more complex systems.

In this article, we study the coupling between structure and dynamic properties of complex networks with non-exponential dwell time distributions for each transition. We have found a universal identity that connects dynamic information, which can be obtained from experimental measurements, with the number of states along the selected path as a first step to unveil the complete structure of the complex network. It is shown that this general result reduces to previously found relations^{25, 26} for exponential dwell times. Our theoretical predictions are supported by Monte Carlo computer simulations for several networks with different topology.

RESULTS

Laplace transforms of the first-passage distribution functions

We consider a general network composed of a series of discrete states k which form the state space of the network σ. We identify the state i ∈ σ as the initial state and the state j ∈ σ as the final state for which we would like to know the distribution f_ij(t) of the first-passage times when starting from the state i. We associate to each state k ∈ σ a set of transition probabilities 0 ⩽ P_kℓ ⩽ 1 to reach any of the states ℓ ∈ σ in the state space of the network in one step. The normalization condition ∑_{ℓ ∈ σ}P_kℓ = 1 must hold for these transition probabilities and P_kk = 0. The matrix P whose elements are the P_kℓ is thus the embedded Markov chain in discrete time.

We now assign to each state k a general dwell time probability density ϕ_k(t) in the following form:

$${\varphi }_k\left(t\right)=C_k{\left(t/t_0\right)}^{\alpha }\exp \left(-a_k{(t/t_0)}^{{\gamma }_k}\right),$$ (1)

where C_k has a dimension of inverse time (s⁻¹) and is fixed by the normalization. The parameters a_k, γ_k are both larger than zero and can depend on the state k. We initially restrict our analysis to the case where the parameter α is the same for all states of the network and satisfies α > −1. In the following, we assume that t₀ = 1 s. For γ_k = 1 and α = 0 we recover the exponential waiting times from previous studies.^{25, 26} Equation 10 is, in essence, a mathematical generalization of the Gamma distribution, which can be obtained by setting γ_k = 1. We have allowed for the possibility to take γ_k ≠ 1 in order to have the most general dwell time distribution that we are able to treat mathematically with the method described in this work. Apart from the Gamma distribution, which arises naturally in many stochastic natural phenomena or as the convolution of several exponential dwell times, other choices for the value of γ_k > 0 do not have an obvious physical or chemical origin.

Now consider a first-passage time from the initial state i to the final state j for general networks as shown in Fig. 1. Since we are using the more general dwell time distributions 1, we cannot use the approach based on the chemical Master equation to derive the first passage time. Let τ_ij be the random number that gives the first-passage time from the state i to the state j, and $t_{i{k}_1}$ be the time from i to any of its nearest neighbors k₁. With the assumptions given above, the time to reach any of the neighbors is independent of the neighbor and is distributed according to 1. We will thus put $t_{i{k}_1}=t_i$. We also define ${\tau }_{k_{1}j}$ as the first-passage time from each of the neighbors of i to the final state j. These times are related by

$${\tau }_{ij}=t_i+{\tau }_{k_{1}j},$$ (2)

if k₁ is the first state visited by the process after leaving the state i. In terms of the Laplace transforms from Eq. 2 we obtain

$$F_{ij}\left(s\right)=D_i\left(s\right)F_{k_{1}j}\left(s\right),$$ (3)

under the condition that k₁ is the first visited state. Here we have defined $F_{ij}\left(s\right)={\int }_0^{\infty }{e}^{-st}{f}_{ij}\left(t\right)dt$. Each neighbor k₁ of the state i can be visited with the corresponding probability $P_{i{k}_1}$ after leaving state i. Therefore, the final Laplace transforms of the first-passage time from i to j is given by

$$F_{ij}\left(s\right)=\sum _{⟨k_{1}i⟩}{D}_i\left(s\right)P_{i{k}_1}{F}_{k_{1}j}\left(s\right),$$ (4)

where D_i(s) is the Laplace transform of the dwell time distribution density at state i defined as,

$$D_i\left(s\right)={\int }_0^{\infty }{e}^{-st}{\varphi }_i\left(t\right)dt.$$ (5)

Note that the notation ${\sum }_{⟨k_{1}i⟩}$ means a sum over all k₁ that are neighbors of the state i, i.e., they can be reached from the state i in a single transition.

Figure 1.

A schematic view of a general network. The nodes represent individual states of the system and the arrows describe reversible transitions between states. The red vertex i is the initial state and the green vertexes j_k (k = 0, 1, 2, 3) correspond to the final states investigated in this work. Other states are shown in blue. There are many different paths between the initial and any final state in this network, but the shortest path is always unique for this scheme.

In Eq. 2 we split the random time to go from the state i to the state j as the time to reach one of the first neighbors of the state i plus the first-passage time to reach the state j from this neighboring state. In terms of Laplace transforms it is expressed as the product of the respective functions as given in Eq. 3. Since the first-passage time from any k₁ to j can also be split into a dwell time to be in k₁ and the first-passage time to one of its neighbors, one can extend the expansion in Eq. 4 into sums of products,

$$\begin{array}{ccc}\hfill F_{ij}\left(s\right)& =& \sum _{⟨k_{1}i⟩}\cdots \sum _{⟨k_{\ell }{k}_{\ell -1}⟩}{D}_i\left(s\right)D_{k_1}\left(s\right)\cdots D_{k_{\ell -1}}\left(s\right)\hfill \\ & & \times P_{i{k}_1}{P}_{k_1{k}_2}\cdots P_{k_{\ell -1}{k}_{\ell }}{F}_{k_{\ell }j}\left(s\right),\hfill \end{array}$$ (6)

where ℓ can be arbitrarily large and ${\sum }_{⟨k_b{k}_a⟩}$ means a sum over all k_b that are neighbors of the state k_a.

The universal identity for the shortest path

We assume that the shortest path from the state i to the state j is unique in the network and it has exactly m intermediate states. Notice that the sums in Eq. 6 stop whenever they reach the final state j. Thus, as ℓ → ∞, Eq. 6 will be split into an infinite sum of generic terms like

$$G_n\left(s\right)=P_{i{k}_1}{P}_{k_1{k}_2}\cdots P_{k_{n}j}{D}_i\left(s\right)D_{k_1}\left(s\right)\cdots D_{k_n}\left(s\right),$$ (7)

where k₁, k₂, …, k_n are the state members of an arbitrary random walk from the state i to state j and n is the length of the walk. The dwell time distribution densities ϕ_k(t) from Eq. 1 have the following asymptotic behavior at early times t → 0:

$${\varphi }_k\left(t\right)\sim C_k{t}^{\alpha }+o\left(t^{\alpha }\right),$$ (8)

where the second term goes to zero faster than the first term. Recall that early times correspond to large Laplace variables (s → ∞). Therefore, the Laplace transforms D_k(s) of the ϕ_k(t) for all states k ∈ σ at large s can be written as

$$D_k\left(s\right)\sim B_k{s}^{-(\alpha +1)}+o\left(s^{-(\alpha +1)}\right),$$ (9)

where B_k is some constant. Then, the Laplace transform G_n(s) in Eq. 7 is simply given by

$$G_n\left(s\right)\sim {\mathcal{B}}_n{s}^{-(n+1)(\alpha +1)}+o\left(s^{-(n+1)(\alpha +1)}\right)$$ (10)

for large s with ${\mathcal{B}}_n$ being another constant. Thus, under the assumption that there exists a unique shortest path with m intermediate states between the state i and the state j, this path gives a contribution similar to Eq. 10. One can see that, apart from a multiplicative constant, the expression of 10 for n = m necessarily dominates the expansion in Eq. 4 at large s since m is the smallest possible value that n can take. It yields the asymptotic result,

$$F_{ij}\left(s\right)\sim {\mathcal{B}}_m{s}^{-(m+1)(\alpha +1)}+o\left(s^{-(m+1)(\alpha +1)}\right)$$ (11)

in the limit of s → ∞. Other paths with larger number of intermediate states have contributions of smaller order of magnitude. Then, by inverting the Laplace transform, the asymptotic behavior of the probability density f_ij(t) at early times can be obtained as

$$f_{ij}\left(t\right)\sim A_m{t}^{(m+1)(\alpha +1)-1},$$ (12)

where A_m is a constant. It suggests that the first-passage time probability function f_ij(t) at early times has a power-law dependence (∼t^β), which is similar to results derived in previous studies with exponential waiting times.^{25, 26} The corresponding exponent β satisfies the equation

$$\beta =(m+1)(\alpha +1)-1.$$ (13)

Note that this exponent does not depend on the parameter γ_k and it reproduces the known identity β = m for continuous time Markov chains, i.e., if α = 0.^{25, 26} One important consequence of Eq. 13 is that for any given β, derived for instance after fitting experimental data, the number of intermediate states m and the parameter α cannot be chosen arbitrarily and independently from each other. Therefore, Eq. 13 delivers a strong constraint that couples the structural properties along the pathway and the dynamical properties at the level of the individual dwell times. As a side remark, using the general expansion given in Eq. 6 it is easy to see how Eq. 13 can be generalized when the parameter α does depend on the state k. Using the same method that relates early times to large s we indeed obtain

$$\beta =({\alpha }_i+1)+({\alpha }_{k_1}+1)+\cdots +({\alpha }_{k_m}+1)-1,$$ (14)

where α_i is the parameter α associated to the initial state i and ${\alpha }_{k_{\ell }}$ is the parameter α associated to the state k_ℓ.

Numerical test with Monte Carlo simulations

To test our theoretical prediction, Eq. 13, we performed a series of computer simulations, analyzing complex networks presented in Fig. 1. Many distinct paths with varied numbers of intermediate states exist between the initial state and any of the final states in the system. For the four final states j_k with k = 0, 1, 2, 3 considered in the network, the numbers of intermediate states m for the shortest paths starting from the initial state i are given by 0, 1, 2, and 3, respectively. Equation 13 suggests that the relationship between α, β, and m does not depend on other parameters such as a_k, γ_k which appear in Eq. 1. Therefore, we simply set a_k = γ_k = 1. We fix, instead, the parameter α in Eq. 1 to take one of the two possible values, α = 0.5 and α = 1, as examples. Each state in the network shown in Fig. 1 is labeled by a number starting from 1 to 11.

Since we want to compare our results both in the case of exponential (Markov) and non-exponential dwell times, we first proceed by creating a continuous time Markov chain by assigning transition rates between connected states. We assume that the transition rate from the state k to the state ℓ r_kℓ = 0.5 s⁻¹ for k < ℓ and r_kℓ = 0.1 s⁻¹ if k > ℓ. The transition probabilities from the state k to one of its neighbors ℓ is given by

$$P_{k\ell }=\frac{r_{k\ell }}{{\sum }_{⟨nk⟩}{r}_{kn}},$$ (15)

where the notation ∑_⟨nk⟩ means a sum over all n that are neighbors of the state k. The probability matrix 15 defines our embedded discrete time chain introduced in Sec. 2A. Notice that the continuous time chain thus created corresponds to the case of α = 0 and γ_k = 1, but with varying parameters a_k depending on the transition rates from the state k to their neighbors.

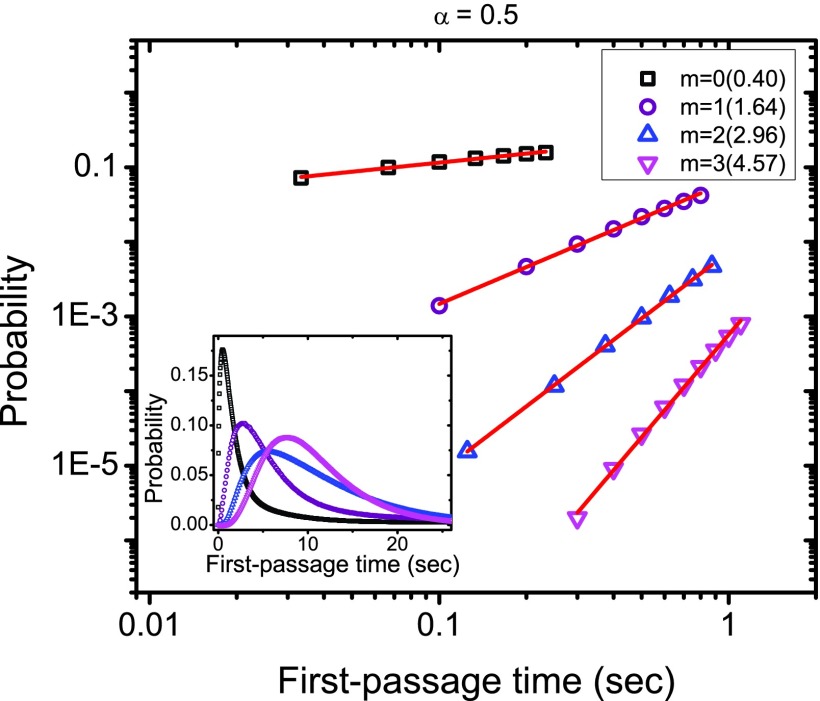
To proceed to the non-exponential dwell times, we instead consider the embedded chain 15 and define the dwell times according to the distribution 1. We first consider the case when α = 0.5 for the dwell time distribution at each state of the network. The first-passage time probability densities starting from the initial state i to the final state j_k with k = 0, 1, 2, 3 are presented in Fig. 2. The early time behavior of the probability densities is shown in the main figure on log-log scale, while the inset gives the full time picture. The solid lines in Fig. 2 correspond to linear fits of the logarithm of the simulation results at early times, i.e., before the distribution reaches its maximum value (hereafter we will refer to the linear fit of the logarithm of the distribution simply as linear fit). The slopes of these solid lines approximate the values of β as expressed in Eq. 13. The number m of the intermediate states for the shortest path between the initial state i and final state j_k with k = 0, 1, 2, 3 is also indicated in Fig. 2. From Eq. 13 with α = 0.5 we expect that the corresponding value for β is equal to 0.5, 2, 3.5, 5 with m varied from 0, 1, 2 to 3, respectively. The slopes obtained from the linear fit of the early times in Fig. 2 are close to the expected values calculated from Eq. 13. Similarly as was observed before,²⁵ the slopes are slightly smaller than the expected values of β as given by Eq. 13. However, as discussed below, we notice that the slopes approach the expected values as the time span used for fitting is reduced. One can see that the number of intermediate states for the shortest path between the initial and the final states can be derived from the slope of first-passage time densities at early times. As shown in Fig. 2, the slope increases with the number of intermediate states, in agreement with the prediction of Eq. 13.

Figure 2.

First-passage time probability densities for the network shown in Fig. 1 with the parameter α = 0.5. The initial state i is the red vertex i and the final states are green vertexes labeled from j₀ to j₃ as given in Fig. 1. The main figure shows the probability densities at early times and the inset gives the probability densities over all times. The data from computer simulations are presented by different symbols for various final states. The solid lines correspond to the linear fits of the simulation results. The number m of intermediate states for the shortest path between the initial and final states and the slope for each curve are also indicated.

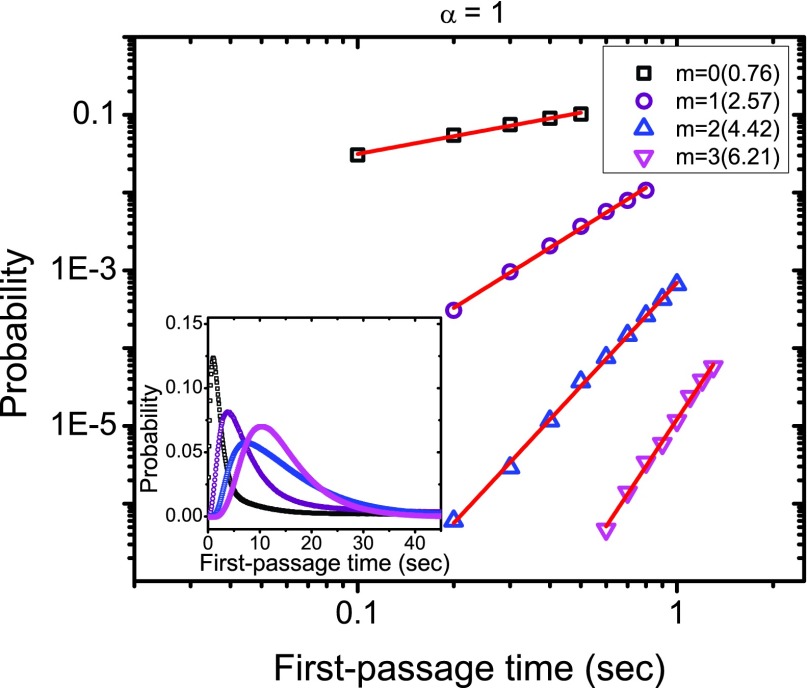
To test further predictions from Eq. 13 we calculated the first-passage probability densities using α = 1 for the networks shown in Fig. 1. As presented in Fig. 3, the slope for the solid lines from linear fit increases with the number of intermediate states for the shortest path between the initial and final states, fully supporting our theoretical predictions. Compared with Fig. 2, we can also find that the corresponding slopes with the same number m of intermediate states become larger as the value of α increased from 0.5 to 1, which is again consistent with Eq. 13. The expected values for β are equal to 1, 3, 5, and 7 for α = 1 when the number m of intermediate states on the shortest path between the initial and final states takes the values 0, 1, 2, and 3, respectively. One can see that the slopes obtained from linear fits (Fig. 3) are close to the expected values. For a fixed value of α we can also determine the number of intermediate states on the shortest path between any two states on a complex network from the early time behavior. For α = 1, a slope between 0 and 1 means m = 0, i.e., there are no intermediate states in the shortest path between the two states. A slope between 1 and 3 means there is one intermediate state, i.e., m = 1. These arguments can be extended to any number of intermediate states (see Fig. 3).

Figure 3.

First-passage time probability densities for the network shown in Fig. 1 with the parameter α = 1. The initial state and the final states are same as discussed in Fig. 2. The main figure shows the probability densities at early times and the inset gives the probability densities at all times. The data from computer simulations are presented by different symbols for various final states. The solid lines correspond to linear fittings of the simulation results. The number m of intermediate states for the shortest path between the initial and final states and also the slope for each curve are also indicated.

For the network in Fig. 1 we analyzed the case with exponential dwell time distributions, as was discussed previously,^{25, 26} and obtained the corresponding first-passage time probability densities from the initial state i to final states j_k. The results are presented in Fig. 4. In this case, where α = 0, Eq. 13 reduces into a simple form, β = m, as was found in previous studies.^{25, 26} Following the procedure described above, one can obtain the number of intermediate states for the shortest path directly from the early time behavior of the first-passage time probabilities (see Fig. 4). The probability density is an exponentially decaying function of time if the final state is one of the neighbors of the initial state, and the corresponding slope has a value close to zero (Fig. 4). As the number of the intermediate states becomes larger, a rising phase followed by a decaying phase appears in the probability density function, as demonstrated in Fig. 4. We also find that the slope of the fitting curves is very close to the expected value of β for each case as discussed above. The number m of intermediate states can even be obtained directly by rounding to the upper integer of the slope for each linear fitting curve, as indicated in Fig. 4. The same results were found previously.²⁵ However, the number m of the intermediate states between two states of a complex network with general dwell time distributions cannot be read out directly from these fittings, but one can still easily obtain them using Eq. 13 as discussed above.

Figure 4.

First-passage time probability densities for the network shown in Fig. 1 with exponential dwell time distribution at each state corresponding to the case with α = 0. The initial state and the final states are same as discussed in Fig. 2. The main figure shows the probability densities at early times and the inset gives the probability densities at all times. The data from computer simulations are presented by different symbols for various final states. The solid lines correspond to linear fittings of simulation results. The dotted line describes the slope equal to zero for m = 0. The number m of intermediate states for the shortest path between the initial and final states and also the slope for each curve are also indicated.

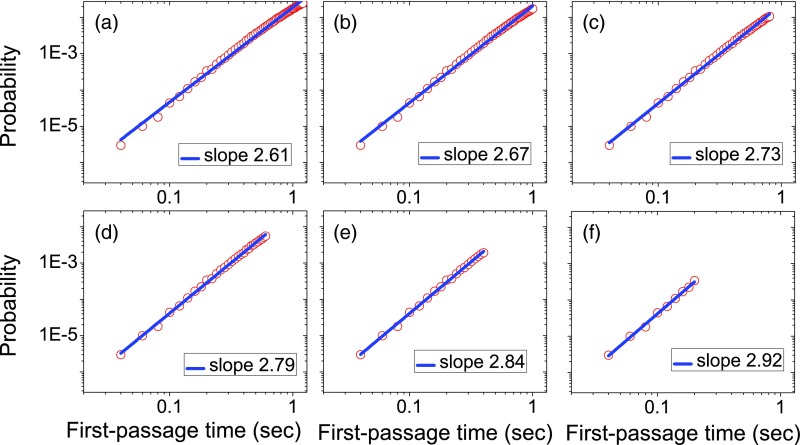
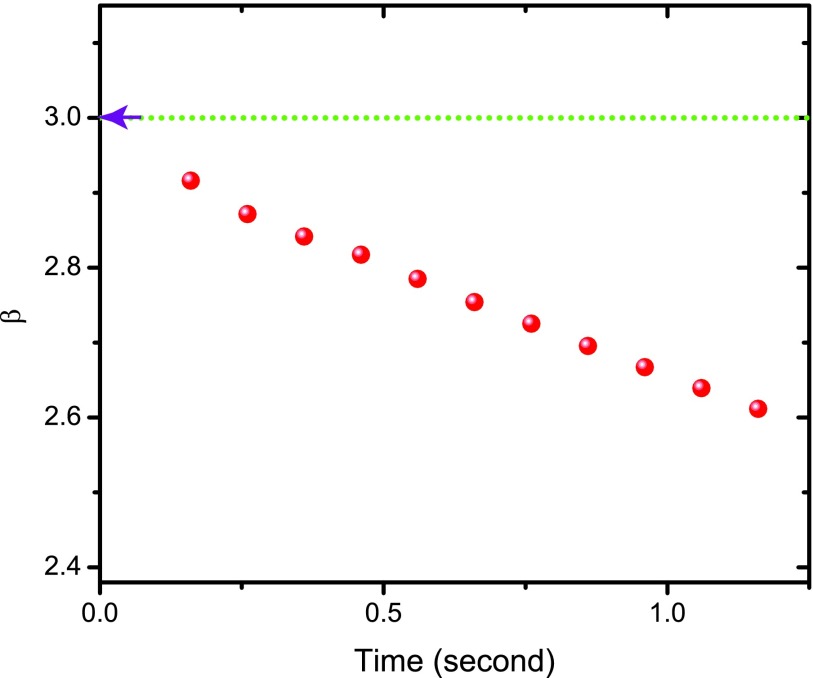
Analyzing first-passage distribution functions for various sets of parameters, one can notice that slopes obtained by linear fitting of the first-passage distributions at early times are always smaller than suggested by Eq. 13. It is found that predictions from Eq. 13 are getting more accurate with decreasing the time interval utilized for fitting. It is not surprising since our theoretical conclusions were obtained in the limit of t → 0. To illustrate this, let us consider the network shown in Fig. 1 with the initial state i, the final state j₁, and the parameter α = 1. Different slopes obtained by linear fittings of first-passage probability functions for varying time intervals are given in Fig. 5. As we reduce the time range the corresponding slope values increase monotonically. In order to see this trend clearly these slopes are also presented in Fig. 6. For this case there is 1 intermediate state (m = 1) and Eq. 13 predicts the slope should be equal to 3. The fitted slope values approach this number fast as the size of the time segment decreases, supporting our theoretical arguments.

Figure 5.

First-passage time probability densities for the network shown in Fig. 1 with the initial state i, the final state j₁, and the parameter α = 1 at early times. The data from computer simulations are presented by red open circles. The blue solid lines correspond to linear fittings of the simulation results. We considered different time ranges for linear fittings of the probability densities. The simulation data shown are same in all figures but the time range used for the linear fitting is reduced from (a) to (f), and the value of the slope from each fitting is also indicated.

Figure 6.

The slope from the linear fit of first-passage time probability densities as a function of the time range used for the fitting. The red dots are the slopes from Fig. 5. The purple arrow points to the expected value of β as calculated from Eq. 13.

DISCUSSION AND CONCLUSIONS

We investigated the relationship between topology and dynamic properties of general networks via theoretical analysis of first-passage probability distribution functions for various transition events. In contrast to previous studies^{25, 26} where simple exponential dwell time distributions were assumed, more general dwell time probabilities were used in this work. Using analytical calculations based on asymptotic analysis of Laplace transforms it is shown that there is a universal behavior of the first-passage distribution functions at early times. It is specified by a power-law temporal dependence of the probability functions for events starting and finishing at different sites of the network. We found that the exponent of the power-law is directly related to the number of intermediate states on the shortest path connecting the initial and the final states. For purely exponential waiting times this exponent simply reduces to the number of intermediate states, as was already shown before.^{25, 26} In general case, the exponent depends on details of transition dynamics at each site. Furthermore, our analysis suggests that the universal behavior of first-passage probability function is observed if the power-law component of waiting time distributions is the same for all states on the network.

The physical mechanism of this universal behavior can be easily explained using the following arguments. At early times, only trajectories that follow the shortest path between the specified start and end states can be observed since the system should pause at each intermediate state. This argument is more precise the shorter the time for observations, and the arrival dynamics should reflect the number of intermediate states. Even for very fast transitions, i.e., for very short dwell times at some sites, there is a time when this universal behavior should be observed. In other words, this dynamic picture is independent of the absolute values of the average dwell times at each state.^{25, 26} The reversibility of individual transitions and therefore the probability that one path is taken instead of another also does not play any role at this level of analysis.

Our theoretical ideas were tested in extensive Monte Carlo simulations for various networks with different parameters to describe the non-exponential waiting times. In all cases it was found that analytical predictions correctly describe first-passage arrival dynamics at early times. The analysis also shows that the agreement with theoretical calculations is asymptotic in time: decreasing the time segment for extracting the universal exponents leads to convergence to predicted values. It supports the universal nature of presented theoretical results, and it also provides a direct method for connecting structural and dynamic properties for any network. The most significant outcome of this study is the development of an explicit theoretical framework for analyzing complex physical, chemical, and biological processes in order to extract relevant microscopic information. It will be critically important to test our theoretical predictions in real experimental systems.