Through the eyes of a bird: modelling visually guided obstacle flight

Abstract

Various flight navigation strategies for birds have been identified at the large spatial scales of migratory and homing behaviours. However, relatively little is known about close-range obstacle negotiation through cluttered environments. To examine obstacle flight guidance, we tracked pigeons (Columba livia) flying through an artificial forest of vertical poles. Interestingly, pigeons adjusted their flight path only approximately 1.5 m from the forest entry, suggesting a reactive mode of path planning. Combining flight trajectories with obstacle pole positions, we reconstructed the visual experience of the pigeons throughout obstacle flights. Assuming proportional–derivative control with a constant delay, we searched the relevant parameter space of steering gains and visuomotor delays that best explained the observed steering. We found that a pigeon's steering resembles proportional control driven by the error angle between the flight direction and the desired opening, or gap, between obstacles. Using this pigeon steering controller, we simulated obstacle flights and showed that pigeons do not simply steer to the nearest opening in the direction of flight or destination. Pigeons bias their flight direction towards larger visual gaps when making fast steering decisions. The proposed behavioural modelling method converts the obstacle avoidance behaviour into a (piecewise) target-aiming behaviour, which is better defined and understood. This study demonstrates how such an approach decomposes open-loop free-flight behaviours into components that can be independently evaluated.

1. Introduction

Animals moving in the natural environment need to routinely avoid obstacles on route to a destination. This task becomes critically challenging when moving at high speeds, such as in flight. Many flying animals have evolved impressive abilities to avoid obstacle collisions [1]. For example, echolocating big brown bats (Eptesicus fuscus) forage at night, avoiding obstacles while tracking flying insects, whereas diurnal goshawks (Accipiter gentilis) chase aerial preys through dense woodlands at high speed. Apart from these specialists, other flying birds and bats must also routinely deal with obstacles. For example, sparrows and pigeons have successfully colonized cities, which are highly three-dimensional environments, similar to their natural habitats [2]. These birds manoeuvre around lampposts, buildings and vehicles with proficiency, relying on vision to navigate through their environment. Here, we examine guidance strategies that pigeons (Columba livia) use to successfully navigate cluttered environments using a combined experimental and modelling approach.

Limitations of the visual system necessarily affect any visually guided locomotion. Similar to other birds at risk of aerial predators, pigeons have a wide more than 300° panoramic field of view for predator detection. The associated retinotopic trade-off limits a pigeon's binocular field to approximately 20° [3–5]. Binocular stereoscopic depth perception has been demonstrated in falcons, owls and pigeons, but only in close-range discrimination tasks [6–8]. Hence, binocular vision is unlikely to provide depth sensing for flight. A pigeon's broad panoramic visual field also reduces the overall visual acuity: pigeons can resolve up to 12 sinusoidal cycles/degree within their lateral visual field, which declines towards their frontal view, much less than predatory eagles (approx. 140 cycles/degree) and humans (approx. 70 cycles/degree) [9]. Although high resolution is important for distant target tracking (which raptors do routinely), it is not a requirement for flight control. Most insect compound eyes have even worse visual acuity (less than 4 cycles/degree) [10], yet flying insects have quite robust flight control [11–15]. Finally, in order to perceive rapid motion in flight, birds generally possess flicker fusion frequencies above 100 Hz (pigeon: 116–146 Hz) [16]. Taken together, these properties of pigeon vision suggest a more reactive approach to obstacle negotiation. In contrast to a conventional path-planning paradigm where sensory information is used to construct an internal model of the world for evaluation [17–19], we hypothesize that pigeons may react to obstacles over short distances and time scales based on local information and simple rules.

Such a view of visual guidance is shared by others in the field. In particular, Warren and co-workers [20–23] termed this ‘information-based control’, which they used to derive various behavioural models for humans navigating in virtual reality. These models treat goals as attractors and obstacles as repellers. The superposition of attraction/repellence potential fields continuously shapes steering, causing the locomotor trajectories to ‘emerge’ [23]. This potential field method describes human goal-directed walking well [22] and also is a classic approach in reactive robotic obstacle avoidance [24–27]. However, the main limitation to this method (attractor–repeller) is the treatment of multiple goals and obstacles [28]. For instance, if there are two goals affecting the agent (robot, human or other animal), the model might predict an average path that misses both targets. Similarly, an agent approaching three obstacles might steer head-on to the middle obstacle due to the average repellence from the two side obstacles. This so-called ‘cancellation effect’, as recognized by Fajen et al. [29], can be solved by differentiating the ‘valence’ of different obstacles and goals. Indeed, it seems conceptually unlikely that a navigating agent would avoid all obstacles simultaneously or steer towards an average goal direction, in which no real goal exists. In practise, the agent only needs to guide movement through one opening (or gap) at a time. A natural alternative to the potential field method is to always aim for a gap [30]. Although all available gaps affect the gap selection process, once the choice is made the actual steering should be unaffected by the other, non-selected gaps. Here, we propose a new procedure for modelling avian obstacle flight by introducing the gap-aiming method with two underlying assumptions: (i) we treat obstacle avoidance as a series of gap-aiming behaviours and (ii) we assume that the agent steers towards one selected opening (gap) at each instance and never attempts to simultaneously aim for multiple openings. Under these assumptions, obstacle flight becomes a piecewise target-aiming behaviour, in which the selected gaps are the steering aims.

In this study, we examine short-range guidance of pigeons flying through randomized sets of vertical obstacles. Under our proposed framework, the pigeon must first identify relevant obstacles and then select a suitable gap aim. A general strategy for gap selection may be decomposed into two concurrent and possibly competing objectives [31]: maximizing clearance between obstacles and minimizing required steering (i.e. change in path trajectory). Whereas a bird should select the largest gap to maximize clearance, it should simultaneously select the gap most aligned with its flight direction in order to minimize steering. We refer to this decision process as the guidance rule. Once the desired flight direction is chosen, the bird must implement the steering that changes the flight path. A steering controller that dictates the motor behaviours and ultimately the flight dynamics is needed to accomplish the required steering. Sensory and biomechanical delays exist for any motor controller. Here, we formulate the steering controller by simply combining the delays and steering dynamics into a generic proportional–derivative (PD) controller with a constant visuomotor delay.

We strategically simplified the sensory task by presenting the pigeons with a vertical pole array of relatively short depth (figure 1), minimizing the birds' depth perception challenge and inducing steering cues only about the yaw axis. The scale of the flight corridor also minimized the global navigation challenge for the pigeon. The direction along the corridor is practically the direction of the destination (figure 1a). Using PD control theory [32], we established a steering controller assuming that the pigeon steers to one gap at a time. We subsequently reproduced pigeon flight trajectories using several different guidance rules, each based on the same, established steering controller, with varying levels of perception noise. In particular, we ask whether pigeons prioritize clearance over steering minimization during the obstacle flights.

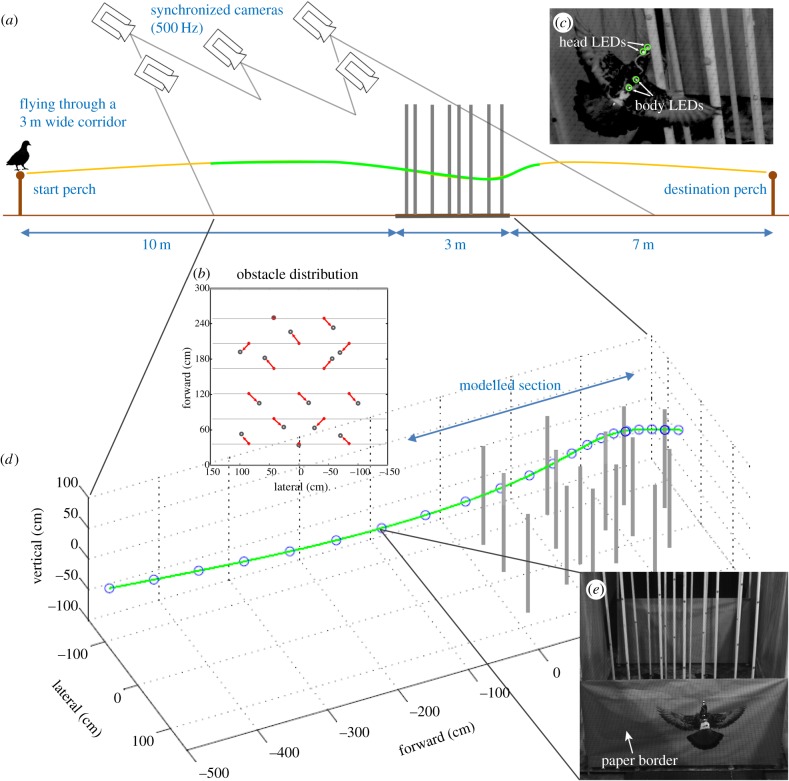
Figure 1.

Obstacle avoidance flight corridor and motion tracking. (a) Pigeons were trained to fly between two perches located at either end of a 20 m indoor flight corridor. An obstacle ‘pole forest’ was erected 10 m from the take-off perch to elicit obstacle negotiation. Five high-speed cameras captured the flight trajectories (green section) throughout the entire obstacle forest, including 5 m of the approach. (b) Starting from a standard grid (red dots), for each flight obstacles were randomly assigned one of five positions (the grid centre) or one of four orthogonal locations 25 cm from the grid centre (illustrated by red arrows). (c) Four 2.4 mm LEDs were attached to each pigeon in combination with a small battery-pack (16.5 g total) to facilitate positional tracking of the head and body. (d) Three-dimensional flight trajectories were reconstructed from the high-speed videos. An example trajectory (green trace) is marked every 200 ms (blue circles). To model steering through the obstacle field, we considered a section of the flight from 50 cm in front of the obstacle field to 20 cm before the pigeon left the obstacle field (blue arrow). (e) Three-dimensional head positions and pole distributions were used to reconstruct the in-flight visual motion of obstacles with respect to the pigeon's head (and eyes). The modelling process assumed that pigeons always aimed towards visual centres of gaps.

2. Material and methods

2.1. Animal training and the obstacle course

Seven wild-caught adult pigeons (C. livia) were trained to fly through an indoor corridor without obstacles. The four birds that flew most consistently between the perches were selected for experiments.

To study path planning and manoeuvring flight in a cluttered environment, we challenged pigeons to fly between two perches (1.2 m high) through an indoor flight corridor (20 m long, 3 m high, 3 m wide) with an obstacle field located 10 m from the take-off perch (figure 1a). The obstacle field comprised a 3 × 3 m area over which 15 poly(vinyl chloride) poles (3.81 cm outer diameter) were erected vertically in predetermined random distributions. In order to maintain the overall obstacle density while introducing random variations, random pole distributions were based on a standard grid, in which each pole had an equal probability of being placed at one of five positions: at the centre position or at one of four corner positions approximately 25 cm from the centre position (figure 1b). For every obstacle flight, the poles were repositioned according to this randomizing procedure, so that the pigeons experienced a new obstacle distribution for each flight. Each obstacle pole was digitized every flight to verify its placement. The walls of the flight corridor were lined with translucent white plastic sheeting to provide a homogeneous visual environment. The front and rear borders of the obstacle field were guarded by 0.9 m high paper to ensure the pigeon flight paths remained within a calibrated three-dimensional volume (figure 1e).

2.2. Pigeon flight tracking

Each pigeon carried two pairs of infrared, surface mount high-intensity light-emitting diode (LED) markers (Vishay Intertechnology, Inc., Malvern, PA, USA) for tracking purposes: one pair defined the head vector and one pair defined the body vector (figure 1c). These were securely strapped on the head and torso along with a battery (overall weight: 16.5 g). We limited the added components to less than 5% of the pigeon's body mass to minimize the effect on manoeuvring. Multiple views of the flight trajectories were obtained by five synchronized Photron high-speed cameras (three SA3; two PCI-1024, Photron USA, Inc., San Diego, CA, USA) mounted on the ceiling, operating at 500 Hz. This provided a calibrated volume covering the obstacle field and 5 m of the flight corridor leading up to the obstacle field (figure 1a). Three-dimensional reconstruction of the marker trajectories was achieved using DLTdv5 and EasyWand2 Matlab scripts [33].

To establish the birds’ indoor flight characteristics, eight flights per bird were recorded without obstacles (32 flights total). Following this, a total of 64 obstacle flights were recorded for novel obstacle distributions from the four birds, after training the birds with five to eight obstacle flights. The 32 initial flights without obstacles were used to establish a behavioural reference. From the 64 obstacle flights, we used eight flights per bird from the first three pigeons to tune the steering controller (24 flights). The remainder of the flights from the first three pigeons and 10 obstacle flights from the fourth pigeon were used to test the guidance strategy simulations (10 obstacle flights per bird). These data allocations allowed us to demonstrate the universality of the PD controller, as well as test for the robustness of the guidance rules simulations.

2.3. Data processing and flight path analysis

Pigeons’ body and head positions were computed from sampled 500 Hz three-dimensional marker data. Because we were only interested in the body trajectory and the visual experience determined by the body velocity vector (the flight direction), head and body orientations were not computed for this study. Specifically, we used the rear head marker to compute in-flight visual information (i.e. obstacle angular position, angular velocities and distance), and the rear body marker (close to the estimated body centre of mass) to derive the pigeon trajectory. The visual input data were down-sampled to 100 Hz (or 10 ms time-steps) to approximate a pigeon's flicker fusion frequency of 116–146 Hz [16]. t = 0 was defined when the pigeon's rear body marker crossed the entry line of the obstacle field. In order to generate continuous steering dynamics, we evaluated steering using the same 10 ms time-step for all modelling procedures.

3. Experimental results

Without obstacles, the four pigeons flew in straight lines near the central axis of the corridor (figure 2a, light grey paths). When randomly distributed obstacles were introduced, pigeons deviated from the centre straight path to avoid obstacles, by initiating manoeuvres approximately 1.5 m before the obstacle field (figure 2b, dark grey paths). Occasional head turns were observed during obstacle flights. However, previous work suggests that head turns are more relevant to visual stabilization than targeting during obstacle avoidance [34].

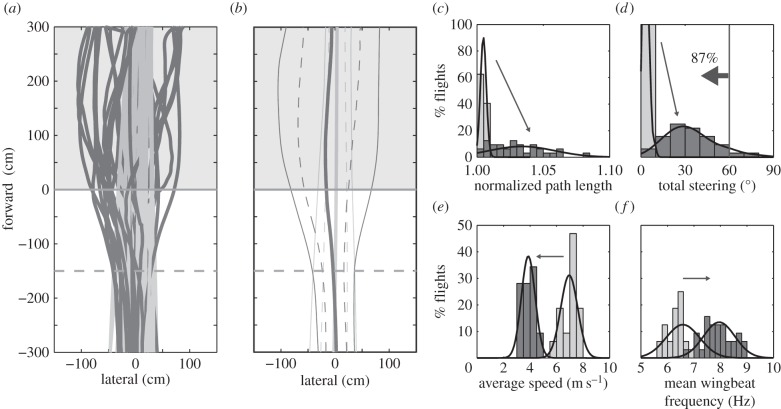
Figure 2.

Characteristics of pigeon obstacle flight. (a) The pigeons flew straight, close to the corridor midline in the absence of obstacles (light grey traces). When challenged with obstacles (dark grey traces), flight trajectories diverged within the obstacle field. (b) Steering was first observed 1.5 m in advance of obstacles, determined when the standard deviation (dark grey dash lines) and the limit (dark grey solid lines) exceeded control trajectories (light grey dash lines and solid lines). (c) Flight trajectories without obstacles were extremely straight over the 6 m calibrated section of the flight corridor, with a normalized path length of 1.00 + 0.002. Obstacle flights were slightly longer, with a normalized path length of 1.03 ± 0.025. The path length was normalized to the straight-line reference. (d) Control flights normally contained less than 5° of total steering; whereas obstacle flights involved total steering summing up to approximately 80°. However, 87% of obstacle flights contained less than 60° of total steering (thick arrow). (e) Flight speed was reduced 44.5% from 6.95 ± 0.64 m s⁻¹ to 3.86 ± 0.52 m s⁻¹, and wingbeat frequency (f) increased by approximately 21% from 6.58 ± 0.63 Hz to 7.95 ± 0.59 Hz when pigeons flew through the obstacles.

Despite pronounced manoeuvres, pigeon obstacle flight paths were only up to 8% longer than straight-line paths (figure 2c). Summed changes in flight direction over a flight, or total steering, ranged from 10° to 80° for obstacle flights (figure 2d). Eighty-seven per cent of these obstacle flights contained less than 60° of steering. Pigeons generally re-aligned their flight direction with the corridor central axis, which suggests a maximum of 30° steering to either left or right. The pigeons flew by obstacles with a clearance of 15.6 ± 5 cm (referenced to the bird's body midline), with a minimum of 9.3 cm. Given that a pigeon's torso is approximately 10 cm wide, this represents a surprisingly tight clearance for obstacle avoidance.

Cruising speeds of pigeons exceed 10 m s⁻¹ in open space [35]. In our 20 m indoor flight corridor, however, pigeons only achieved an average speed of 6.95 ± 0.64 m s⁻¹ (figure 2e). When obstacles were introduced, pigeons reduced their average flight speed to 3.86 ± 0.52 m s⁻¹ and increased their wingbeat frequency from 6.58 ± 0.63 Hz during straight corridor flights (figure 2f) to 7.95 ± 0.59 Hz when negotiating obstacles, a typical wingbeat frequency for manoeuvring flights [36]. This higher frequency likely satisfied the additional power demand of slower flight and increased manoeuvrability by providing more opportunity for changing flight direction. Without obstacles, the four pigeons maintained flight altitude at 88.1 ± 3.3 cm, 111.1 ± 4.8 cm, 63.5 ± 2.3 cm and 78.0 ± 1.9 cm, respectively. Manoeuvring through the obstacles, the four pigeons flew at similar heights but displayed more altitude fluctuation (75.8 ± 42.5 cm; 103.7 ± 41.8 cm; 106.1 ± 45.6 cm; 110.7 ± 39.4 cm). However, given that the flight negotiation task was to steer around vertical obstacles, we ignored these altitude fluctuations and analysed only the horizontal components of the flight trajectories for developing and evaluating the following guidance modelling work.

4. Pigeon obstacle flight model

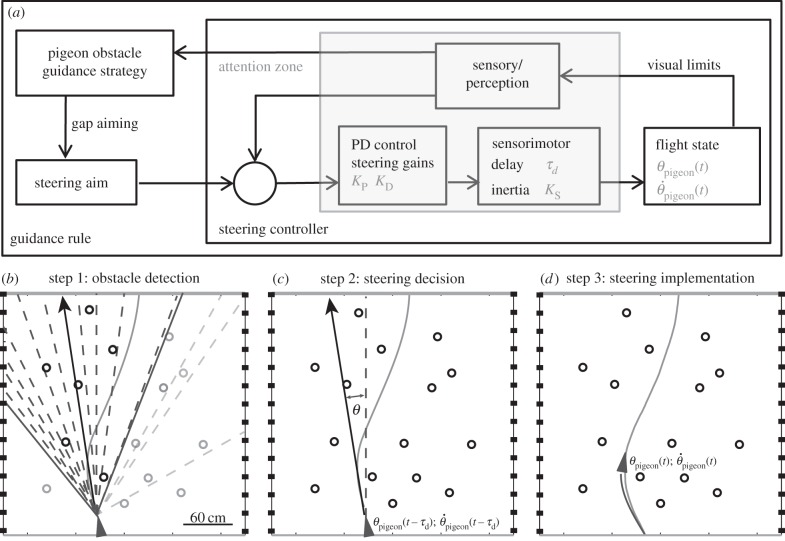
According to our framework, we consider obstacle avoidance behaviour as two levels of control: the steering controller, which directly produces the flight trajectories, is embedded within an outer guidance rule loop that determines the gap selection and thus steering direction (figure 3a). In the following sub-sections, we introduce each component and the underlying assumptions of the model.

Figure 3.

Modelling framework for pigeon obstacle negotiation. (a) The pigeon's obstacle negotiation is expressed as a feedback control system with a steering controller embedded within a guidance rule (gap selection). The model determines a steering aim at each time step based on a guidance rule. Gap-aiming behaviour suggests that this aim is represented by one of the available gaps in the obstacle field, which then becomes the reference for the steering controller. The steering controller subsequently generates a steering command based on a given set of proportional and derivative gains. After a given visuomotor delay, the steering is implemented under the influence of steering inertia. (b–d) The obstacle navigation behaviour can be broken down into three subsequent steps: obstacle detection, steering decision and steering implementation. (b) For each time step, relevant obstacles are identified within a given attention zone, establishing the available gaps (dashed lines). The model pigeon focuses on those that fall within ± 30° of the flight direction, which the model considers its ‘attention zone’ (solid lines; see text for details). The side-walls were modelled as very dense rows of obstacles (black squares). (c) Depending on the guidance rule, one of the available gaps is selected as the steering aim. The deviation angle θ and its derivative are calculated based on flight direction and the steering aim. (d) The steering controller determines the amount of steering that occurs after the visuomotor delay τ_d.

4.1. The attention zone

To limit the parameter space, we first considered only 30° on either side of the pigeon's flight direction as obstacles to which the pigeon must attend. As most flights (87%) exhibited less than 60° total turning (approx. 30° left or right) (figure 2d), we assumed that pigeons only considered steering within that 60° zone centred about their flight direction (figure 3b, solid lines). We estimated the effective range of this ‘attention zone’ by considering the typical response time of the looming-sensitive neurons of 0.48 s [37] in the pigeon's tectofugal pathway [38]. For the free-flight indoor flight speed (6.95 m s⁻¹) of the pigeons in our study, 0.48 s converts into a detection range of 3.34 m. Because the obstacle array was only 3 m in depth, we assumed that the pigeon could practically attend to all obstacles within the specified 60° attention zone, once it arrived at the obstacle forest.

4.2. Gap-aiming behaviour and side-wall avoidance

There is some established evidence regarding gap-aiming behaviours in birds, especially in the context of flying through tight spaces. Budgerigars balance contra-lateral optical flow when choosing a flight path through narrow spaces [39]. This is consistent with aiming at the angular centre between two poles when flying through a gap. Thus, we represented potential steering aims by the angular centres (and not the geometric centre) of available gaps (figure 3b, dashed lines). This assumption discretized the steering aims into a handful of gap choices. In addition, the flight corridor had side-walls with homogeneous visual texture, which the pigeon clearly could see (as observed during training). In order to impose this boundary constraint in the guidance model, we represented the side-walls as two dense arrays of vertical obstacle poles spaced 20 cm apart (figure 3b). These virtual obstacles created extremely small visual gaps that the model pigeons would never attempt to fly through.

4.3. Steering controller approximation

To test and compare gap selection strategies, we first identified a steering controller that captured the steering dynamics of the pigeons under the experimental conditions. We incorporated visuomotor delay in this phenomenological model. Even though such delay is sometimes negligible in low-speed locomotion such as human walking [23], or tracking a distant target such as prey interception by raptors [40], it is likely to be non-trivial for a pigeon in flight through a relatively densely cluttered environment. According to the convention in flight guidance [41], we identified the pigeon's flight direction angular velocity 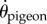as the control variable and constructed a simple PD controller with a visuomotor delay τ_d and three constant steering gains (figure 3c): the proportional gain for the steering aim K_P, the derivative gain for the steering aim K_D and the stabilizing gain for self-motion K_S. This steering controller is given by

4.1

where t is time and θ_pigeon is the flight direction. θ is the angular deviation from the steering aim θ_aim given by

4.2

Similar controllers (frequently implemented without the derivative terms) have been applied to houseflies [42], blowflies [43], bats [44] and tiger beetles [45]. However, these controllers were developed in the context of pursuit or flight stabilization, in which the animal has a clear steering aim (θ_aim). In the context of obstacle negotiation, however, both the controller parameters and steering aim need to be determined. Consequently, here we first determine the steering controller parameters with a PD controller tuning procedure and subsequently test between several potential guidance rules by means of simulations.

4.4. Proportional–derivative controller tuning

Unlike in a conventional controller tuning process, our parameters for the steering controller were determined without a priori knowledge of the steering aims. Instead, our controller tuning relied on a fitting procedure using all possible candidate gaps. In essence, we tested every possible combination of gain-delay on every possible gap steering aim. This was done by first imposing a specific set of controller parameters (three gains and one delay) for one particular flight. Gap angular centres that fell within the attention zone (±30° of current flight direction) were identified as candidate gaps. At each time step (10 ms), the angular centres of all candidate gaps were determined. The specific set of gains and delays were then applied to each candidate gap angular centre to predict the necessary steering angular velocity, which was in turn compared with the observed pigeon angular velocity. We picked the candidate gap that gave the minimum deviation for that time step and proceeded to the next time step. The average deviation over the entire trajectory became a fitting index for this set of controller parameters. We repeated this process for every possible combination of the four controller parameters within the relevant ranges (21 delays, 21 proportional gains, 21 derivative gains and 21 stabilization gain values; yielding 194 481 sets in total). To tune the controller that governs turning, time steps in which there was no appreciable steering (less than 10° s⁻¹) were excluded, covering manoeuvring sections from 0.5 m before entering the forest to 0.2 m before exiting the forest. This tuning process resulted in a four-dimensional map of the PD controller fit in the parameter space for each flight and the weighted average (weighted flights by the time steps with steering) across trails gave the animal specific map. From this map, we could extract the controller parameters that best described the pigeon's steering (see Modelling results for details).

4.5. Guidance rule simulations

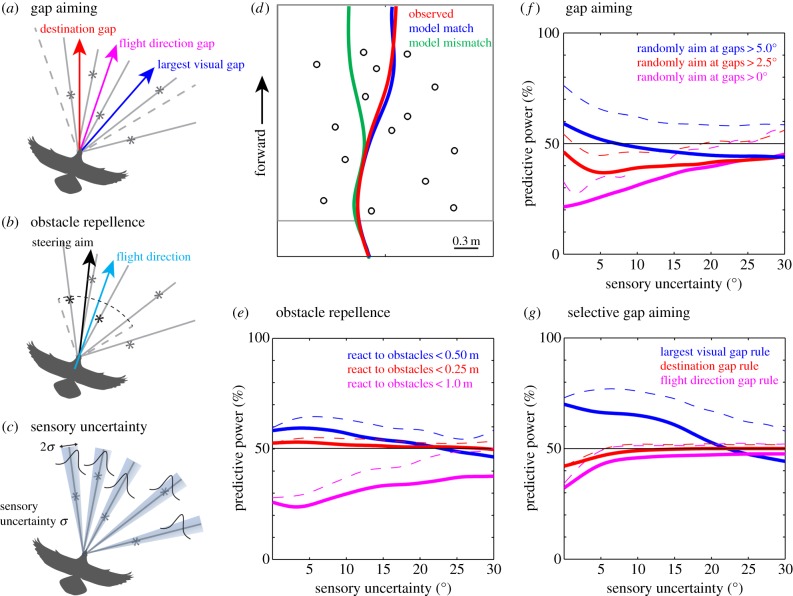
To study guidance rules, we used the determined steering controller (derived from pooled data from three pigeons) to simulate pigeon flights based on different guidance rules. The complete set of rules used by pigeons for obstacle flight guidance likely includes many behavioural variables and their interactions. Here, we merely ask which of the following two navigation objectives is more important: maximizing clearance or minimizing steering. We tested three simple rules for gap selection: (i) choosing the gap most aligned with the flight direction, (ii) choosing the gap most aligned with the destination direction or (iii) choosing the gap with the largest visual size (figure 4a).

Figure 4.

Pigeons bias their flight paths towards largest gaps. (a) Based on the gap-aiming paradigm, we proposed three potential guidance rules: (1) steer to the gap closest to the destination direction (red), (2) steer to the gap in the existing flight direction (magenta) or (3) steer to the largest visual gap (blue). (b) To establish a reference for our gap-aiming paradigm, we reconstructed a conventional obstacle repellence model with a variable range attention zone (marked by dashed lines), in which the repellent effects from all obstacles within that threshold range and angle were summed. (c) To provide the simulations with more realistic sensory information, we incorporated sensory uncertainty by assuming a Gaussian distribution centred at each obstacle position for the model to sample from. The standard deviation of this Gaussian distribution was varied to test each steering strategy across a range of noise levels. (d) We simulated 40 pigeon flights (not used for steering controller tuning) given only the initial conditions (i.e. body position, flight direction, entry speed) 0.5 m before the obstacle field. Some simulations recapitulated the observed flight trajectories (blue trace) and some did not (green trace). We quantified the percentage of flight trajectory matches for each guidance rule in each simulation set (40 flights). To examine the effect of sensory uncertainty, we ran each simulation set 100 times under each sensory uncertainty condition. (e) We varied the threshold range of the obstacle repellence model and found that a threshold of 0.5 m yielded the greatest mean predictive power of 58% with zero noise (solid blue line). The corresponding maximum predictive power (blue dashed line) reached 64% at 6° sensory uncertainty. The obstacle repellence model's predictive power was lower when reacting to the obstacles too late (less than 0.25 m) or too early (less than 1 m). (f) The gap-aiming navigational paradigm requires that pigeons always aim to a gap between two obstacles. In this set of simulations, the modelled pigeon randomly aims to a gap over a given angular size threshold. As the threshold increases, the predictive power increases for sensory uncertainty ranging from 0 to 20°, signifying the importance of gap size in the decision-making process. (g) Maintaining the gap size threshold at 5°, we ran simulations using the three basic guidance rules described in (a). The destination gap rule and flight direction gap rule both underperformed compared with random gap selection as in (f). The maximum predictive power of those simulations where the model pigeons aimed for the largest visual gap, however, approached 80% around a noise level of 6°, outperforming the alternative gap selection rules, random gap selection (f) and the obstacle repellence model (e).

A simple way to test these different guidance rules is to apply the steering controller (with the parameters from table 1) with each rule and simulate the pigeon's flight paths given only the initial conditions (position, flight direction and speed). In each time step, the guidance rule determined the steering aim, which was subsequently implemented by the steering controller that determined the steering angular velocity as described in equation (4.1). The flight speed was assumed constant at the average speed of the particular flight being simulated. The simulations produced some trajectories that closely matched the actual pigeon obstacle flights (figure 4d, blue trace). Others led to different navigation paths (figure 4d, green trace). Based on the modelled pigeon flight trajectories, we quantified the model match to observed flight paths by evaluating the poles which the model pigeon ‘correctly’ passed by on the observed side. We then quantified the percentage of flights that each guidance rule predicted (termed predictive power) from simulations of a separate set of 40 pigeon obstacle flights. For clarity, we define one simulation set as the ensemble of these 40 flights simulated under the same condition, such as a particular guidance rule. Each simulation set thus produced a predictive power value.

Table 1.

Steering controller tuning results for pigeon obstacle flights.

	visuomotor delay (ms)	proportional gain (s−1)	derivative gain	stabilizing gain	controller fit (R2)
pigeon 1	161 ± 8.8	4.31	irrelevant	<1	0.97
pigeon 2	159 ± 6.3	4.56	irrelevant	<0.5	0.97
pigeon 3	120 ± 5.7	4.95	irrelevant	<0.5	0.97
pooled	134 ± 5.0	4.74	irrelevant	<0.5	0.97

4.6. Obstacle repellence model as a reference

For comparison, we reconstructed a more conventional obstacle repellence model in relation to the gap-aiming paradigm proposed here. In order to do so, we established an obstacle repellence function similar to [23], which can fit into our PD controller (equation (4.1))

4.3

where α_i is the desired steering aim relative to the obstacle to avoid, θ_i is the angular location of a particular obstacle and R_i is the distance from this obstacle. We only considered this repellent function when the obstacle was within the avoidance attention zone thresholds (figure 4b). This avoidance attention zone had the same angular threshold (θ_th = ±30°) as the gap-aiming model. We empirically varied the range threshold R_th (from 1.5 to 0.25 m) in the guidance rule simulation and found the best range to be 0.5 m. If an obstacle was located at 30° to either side of and 0.5 m away from the model pigeon, α_i became θ_pigeon − θ_i and the steering aim became the pigeon's flight direction (no steering). As the obstacle distance and angle decreased, α_i increased rapidly and drove the steering aim away from the obstacle(s). We summed the contributions from all obstacles within the attention zone to find the steering aim

4.4

We used this model to establish a baseline comparison with respect to our gap-aiming simulations.

4.7. Sensory uncertainty

Deterministic behaviour models with exact inputs often fail to capture real-world decision processes, which involve tolerating sensory uncertainties. For instance, the pigeon might choose either of two gaps with similar qualities in real-life due to sensory uncertainty, but the model will always choose the slightly better one consistently. To address this discrepancy, we introduced random noise into the sensory information of guidance rule simulations, following the approach of Warren & Fajen [23]. For our application, we assumed a Gaussian distribution of the obstacle angular position centring at the actual angular position of each obstacle (figure 4c). At each modelling time step, we randomly sampled from this Gaussian distribution as the sensory input of each obstacle position. We varied the standard deviation of this Gaussian distribution from 0° (no sensory noise) to 30° (sufficient noise that obstacle locations are virtually unknown) at 1° increments to determine whether the introduction of noise resolved this modelling discrepancy. To obtain statistics for the effect of sensory noise, we ran each sensory noise condition 100 times for each simulation set. From these 100 simulation sets, we extracted the mean and maximum predictive power (figure 4e–g).

5. Modelling results

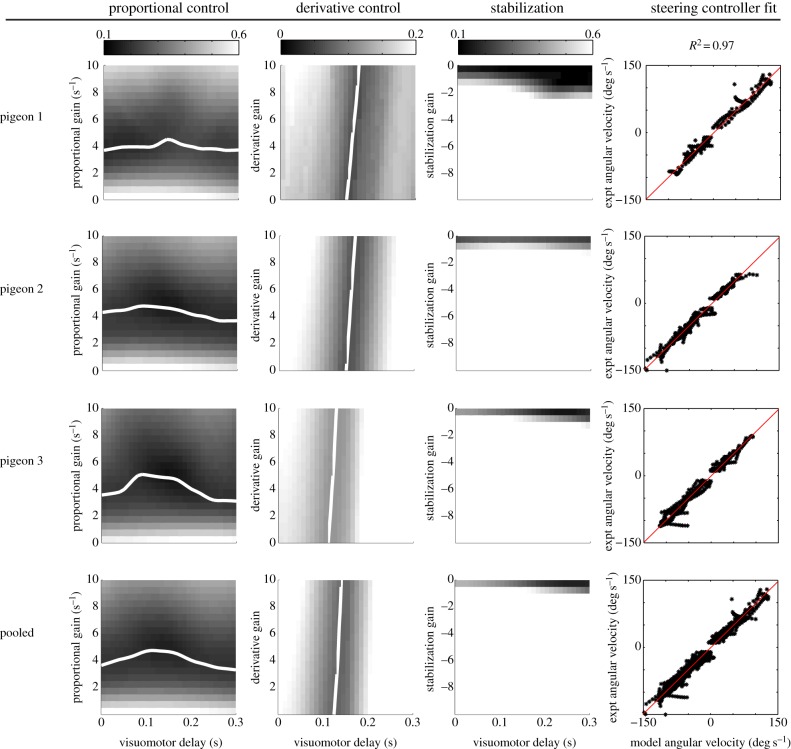
The steering controller tuning process generated a four-dimensional steering deviation map in the parameter space. We found the minimum deviation in this map and generated heat maps for two parameters at a time in order to examine the gradient around this minimum in the four-dimensional parameter space (figure 5). The proportional controller was broadly tuned with the gain centred at approximately 4 s⁻¹ that varied only slightly across different delays (figure 5, column 1). By contrast, the derivative term showed much less variation with respect to visuomotor delay, being centred at approximately 130 ms (figure 5, column 2). The stabilizing gain (negative by definition) showed a small contribution to the steering (figure 5, column 3).

Figure 5.

Steering controller tuning. Tuning was based on the average deviation between model-predicted and observed flight directions, determined every 10 ms time step for the best steering aim, for all possible combinations of gains and delay, and for all obstacle flights. To make the flight controller independent of the guidance rule, the tuning process assumed that the pigeon always aimed to one of the available gaps without imposing an a priori rule on gap selection, but instead selected the gap that resulted in the best fit with the observed flight path. The proportional controller was broadly tuned with a minimum deviation band centred about a gain of approximately 4 s⁻¹ (column 1). For the derivative control, however, a visuomotor delay of approximately 130 ms was strongly selected but with a broadly tuned derivative gain (column 2). We implemented steering inertia as a stabilizing term. The stabilization gain is, by definition, negative and is generally quite small (column 3). We extracted the controller parameters that provided the best fit to the observed data; these are presented in table 1 (see text for details). We then demonstrated that pigeon obstacle flights can be modelled as aiming to a gap by regressing the observed angular rate of change of flight direction against that predicted by the best fitting controller parameters. The steering controller predicted the observed steering extremely well (R² = 0.97 for all four cases; column 4), under the paradigm of gap aiming. (Online version in colour.)

To extract parameter values from the controller tuning maps, we first recognized the pronounced visuomotor delay selection in the derivative controller map. We averaged the delay values across the range of derivative gains reported in table 1. From this delay value, we found the corresponding proportional gain (figure 5, column 1) for each pigeon individually and for the three-pigeon-pooled dataset. This analysis showed that the controller was dominated by the proportional term, with negligible derivative gain and small stabilizing gain (table 1). These PD controller parameters were then used in the steering simulations. We could also evaluate the steering controller tuning by re-running the tuning procedure with these near-optimal controller parameters. As before, the steering aim could be any gap that gave the most consistent fit given these parameters. We plotted the observed flight angular velocity of individual pigeons against the model-predicted angular velocity derived for each pigeon. The resulting regressions showed extremely strong fits (R² = 0.97 for all cases; figure 5, column 4). The pooled data for all three pigeons showed similar fits for controller tuning and predictive performance as for the individual data (figure 5, row 4).

The guidance rule simulations produced interesting predictive power tuning curves with respect to sensory uncertainty (figure 4e–g). For clarity, we present the smoothed data for both the mean predictive power (thick solid traces) and maximum predictive power (dashed traces). The behaviour of the simulation was similar for the three pigeons on which the steering controller tuning was based, as well as for the fourth pigeon. Thus, we considered the pooled steering controller parameters generic to pigeon flight under the experimental conditions. The conventional obstacle avoidance paradigm produced a best mean predictive power of 58% at a threshold reaction range of 0.5 m (figure 4e). As the sensory uncertainty increased, the predictive power decreased steadily. The maximum predictive power never exceeded 65%. With inappropriate reaction range (e.g. 1 m), the mean predictive power started below 30% and approached 40% with increasing sensory uncertainty. A comparable set of simulations using the gap-aiming paradigm would be a random gap selection model with a minimum gap size threshold (figure 4f). The best mean predictive power for the random gap model with a 5° threshold averaged close to 60% at zero sensory uncertainty and exhibited a maximum of approximately 70%. The predictive power dropped quickly with increasing sensory uncertainty. Simulations with different gap size threshold values all converged to a predictive power of approximately 44% at maximum sensory uncertainty.

Instead of randomly selecting gaps above a certain size threshold, we individually applied the three different gap selection rules (figure 4a) as previously described. At zero sensory uncertainty, the flight direction aim strategy predicted 32.5% of the flights, whereas the destination aim strategy predicted 42.4% (figure 4g), showing that these gap selection rules perform worse than random gap selection. The maximum predictive power of these two gap selection rules approached 44%, similar to that observed for random gap selection (figure 4f). By contrast, the largest gap strategy predicted 70% of the flights accurately. With increasing sensory uncertainty, the maximum predictive power approached 80% (at approx. 6° noise). The largest gap selection strategy (figure 4g) therefore performed significantly better than any of the other strategies (including those for obstacle avoidance; figure 4e).

6. Discussion

6.1. Flight trajectory planning versus reactive navigation

We observe that pigeons can negotiate through a forest-like vertical obstacle field with less than 60 cm typical gap spacing at near 100% proficiency. Despite prior training and repeated trials recorded to negotiate the obstacle field, the pigeons showed no evidence of manoeuvring until 1.5 m before the obstacle field (figure 2a,b) and tolerated frequent wing–obstacle collisions. We did find that pigeons fly slower and use higher wingbeat frequencies during obstacle flights, compared with unobstructed flights (figure 2e). These flight changes likely reflect the demand for enhanced manoeuvrability to steer between obstacles. In general, flight paths through obstacle fields were only 8% longer than straight paths, and 87% of these flights exhibited less than 60° of total steering (figure 2d).

The lack of steering could be an energetic strategy or a consequence of the bird's relatively fast entry speed. However, once in close range of the obstacles, pigeons showed deliberate steering. Pigeons also timed their wingbeats or folded their wings to avoid contact with nearby obstacles. The closest flyby relative to the bird's midline body axis was measured at 9.3 cm (providing approx. 4.3 cm clearance from the obstacle to the side of the body). These observations suggest that, under our experimental conditions, obstacle flight is a reactive behaviour that relies on local information, rather than following a pre-planned trajectory.

6.2. Proportional versus derivative control

The steering controller tuning showed that obstacle negotiation is best described as proportional control with a constant delay. The visuomotor delay of approximately 130 ms (table 1) was comparable to, yet slightly greater than, the delay measured for the pigeon's peak flight muscle activity after the firing onset of looming-sensitive cells [38]. The visual angular velocities of obstacles did not seem to affect this control. This is an interesting and somewhat unexpected result given that most flying animals use angular velocity-based optical flow to assess their flight states, such as ground speed and drift [46–48]. However, during flights through the obstacle ‘forests’ employed in our experiments, the angular drifts of obstacles were fast and highly nonlinear. Consequently, our results suggest that pigeons focus on the angular positions of the obstacles, rather than their angular velocities induced by the bird's self-motion. This feature distinguishes obstacle flights from normal cruising flight, particularly at altitude, when most optical flow arises from distant visual features.

6.3. The effect of sensory noise

An effective obstacle negotiation strategy must tolerate some sensory noise. In principle, the increase of sensory uncertainty should reduce the mean predictive power (figure 4f, blue trace). However, in the case of a weak or poor guidance rule, increasing the sensory uncertainty allows the model to occasionally obtain correct steering aims by chance. This leads to an increase of mean predictive power with sensory uncertainty (figure 4f, magenta trace). When the sensory uncertainty increases dramatically, the model loses any knowledge of obstacle position, leading all guidance rules to converge to a baseline predictive power that represents random steering. These simulated flight trajectories are generally straight because it is equally probable to steer left or right. As a result, the baseline predictive power is slightly below 50% (almost half of the flights match the observed trajectories, which were generally fairly straight). Interestingly, in the case of the largest visual gap strategy, the maximum predictive power actually increases with a sensory uncertainty of up to 6°, after which predictive power decreases as expected. Closer inspection reveals that the increase in predictive power at low sensory uncertainty is associated with instances of choice degeneracy. Specifically, when two gaps are close in visual size, the model lacking sensory uncertainty always aims for the slightly larger gap. However, this may not be the actual choice of the pigeon due to the naturally present sensory uncertainty. These instances are captured by the maximum predictive power. Based on this, our simulations indicate that pigeon obstacle negotiation can be best described by a largest visual gap-aiming strategy (given the obstacle field is short) with a sensory uncertainty of approximately 6°.

6.4. Steering to a gap as a navigational objective for obstacle negotiation

Modelling obstacle negotiation as avoiding individual obstacles (e.g. [20–24]) has a major difficulty when more than two obstacles must be considered at the same time (high obstacle density), in which the summation of the obstacle repulsion may lead to unreasonable guidance. This problem can be avoided by limiting the avoidance attention to a small region in the flight direction, as we demonstrate here. However, in a dense obstacle field, in which multiple obstacles must often be attended to, the superposition of multiple repellent effects ultimately degrades the predictive power of an obstacle avoidance model. As described here, we instead treat obstacle negotiation as a gap-aiming behaviour. This allows us to transform the avoidance problem (which can be challenging to define) to a guidance problem. There are two major advantages to this alternative approach for phenomenological modelling of animal guidance behaviours. First, the local minima of the steering potential field due to superposition of conflicting obstacle repellence no longer exist. The agent selects an opening at any given time and, when there is no immediate need to steer, aims for the destination. Second, having one steering aim at any given time enables PD controller tuning and allows separation of the fundamentally different guidance rule and the steering controller. The guidance rule comprises decision criteria, which dictate where the agent chooses to go, whereas the steering controller represents the mechanics and skills that allow the agent to implement the steering. This separation allows for examination of different guidance rules for one individual and for comparison of the same guidance rule in different individuals. Different individuals may share the same guidance rule but may have differing steering ability.

The gap-aiming method has additional benefits in practise. For example, the attention zone can incorporate steering as well as the sensory constraints of an agent. Gap-aiming is also fundamentally safe, because the agent always heads towards a safe direction and not just turns away from potential obstacles. A very similar gap-aiming model has been implemented on a robotic vehicle with great success [30]. In essence, we methodically decompose obstacle flight into a well-defined target reference point and a controller, so that we can apply what has been learned from studies of target aiming/pursuit [21,49].

6.5. Modelling animal obstacle flights

Obstacle flight is perhaps more difficult to model than other flight behaviours, such as fixation or optomotor responses, largely because it requires the animal to make consecutive decisions. Our study shows that a simple strategy of aiming to the largest visual gap seems to capture the pigeons’ obstacle flight behaviour. However, such a simple strategy is likely only one of many decision criteria. Nevertheless, in the short obstacle field setting of our experiments, this strategy dominated the steering behaviour. Most decision processes by an animal involve the integration of multiple behavioural parameters and sensory inputs. Optimal control theories are powerful tools that can be used to interpret animal behaviour in relation to motor control and trajectory planning [50]. In general, this approach involves evaluating a cost function that contains all variables relevant to the behaviour and determining the optimal output based on some weighting of these variables. Modelling guidance, therefore, may well require construction of a decision function, in which most, if not all possible decision criteria (e.g. obstacle identification, visual gap size, destination direction, flight direction, steering bias, as well as internal states of the animal) are included (with different weights) to determine the steering decision. A good example of such an approach is the ‘open space algorithm’ previously proposed to describe the guidance strategy used by echolocating bats to fly through an obstacle field [51,52]. This algorithm divides 360° into an arbitrary number of steering directions and computes the desirability of each direction based on a target direction and all detected obstacles. Then, a so-called ‘winner-take-all’ process selects the direction with maximum evaluation. This is similar to our approach, in that the agent never steers to a summed direction of all the steering directions considered but instead only steers to a single ‘winner’ direction. Using such a framework to integrate multiple decision criteria might be something worth pursuing in the future.

Another inherent challenge in studying obstacle flight is the treatment of free-flight data. Owing to the difficulty in providing full in-flight sensory feedback, virtual reality does not always work for complex flight behaviours. Interpreting free-flight data is challenging because, although the behavioural objective of avoiding obstacles is clear, the steering aims are far less so. Additionally, under free-flight conditions, animals generate sensory input via self-motion, making it difficult to independently manipulate and evaluate the visual stimuli experienced by the flying animal. Our current study provides a new modelling procedure for describing obstacle negotiation in a flying bird. It does so by first extracting the steering controller from the observed flight behaviour and then testing different guidance rules by means of simulation–observation comparison. Such a framework was enabled by treating the obstacle negotiation as a gap-aiming behaviour instead of an obstacle avoidance behaviour. The results not only help identify the visuomotor control properties of obstacle flight in birds, but also may inspire simple ways to develop real-time controllers for guiding flying robots through cluttered environments [53].

All pigeons were housed, trained and studied at the Concord Field Station (Bedford, MA, USA) according to protocols approved by Harvard University's Institutional Animal Care and Use Committee.

Funding statement

This work was financially supported by an ONR grant (N0014-10-1-0951) to A.A.B.