On the strength of β-sheet crystallites of Bombyx mori silk fibroin

Abstract

Silk fibroin, a natural multi-domain protein, has attracted great attention due to its superior mechanical properties such as ultra-high strength and stretchability, biocompatibility, as well as its versatile biodegradability and processability. It is mainly composed of β-sheet crystallites and amorphous domains. Although its strength is well known to be controlled by the dissociation of protein chains from β-sheet crystallites, the way that water as the solvent affects its strength and the reason that its theoretically predicted strength is several times higher than experimental measurement remain unclear. We perform all-atom molecular dynamics simulations on a β-sheet crystallite of Bombyx mori silk. We find that water solvent reduces the number and strength of hydrogen bonds between β-chains, and thus greatly weakens the strength of silk fibroin. By dissociating protein chains at different locations from the crystallite, we also find that the pulling strength for the interior chains is several times higher than that for the surface/corner chains, with the former being consistent with the theoretically predicted value, while the latter on par with the experimental value. It is shown that the weakest rupture strength controls the failure strength of silk fibre. Hence, this work sheds light on the role of water in the strength of silk fibroin and also provides clues on the origin of the strength difference between theory and experiment.

1. Introduction

Being produced in silk glands under benign aqueous condition, silk fibroin exhibits impressive mechanical, chemical and biological properties, which are superior to most of synthetic and natural polymers. For example, the unique combination of high strength/ductility, biocompatibility and biodegradability enables its wide use in structural and biomedical applications [1]. Silk fibroin is composed of β-sheet crystallites (hereafter simply referred to as crystallites) and amorphous domains [2,3]. The mechanical characteristics of silk fibroin predominantly originate from the interactions between and within these building blocks. As shown in figure 1, the crystallite domains are hydrophobic and they are embedded in the amorphous regions, which are hydrophilic and hold moisture. The main structural components of the crystallite domains are the polypeptide chains mainly made of the amino acids glycine (Gly) and alanine (Ala), and adjacent chains are held together by strong hydrogen bonds in an anti-parallel arrangement to form β-sheets [4]. The strong inter-chain interactions contribute to the superior strength of the silk fibroin. The amorphous domains are largely disordered and play the role of a soft matrix in the silk fibroin [5–7]. To explore the correlation between the structure and mechanical properties of the silk fibroin, the influence of several experimental conditions has been investigated. As an example, it was shown that with increased reeling speed, there was a decrease in the size of the β-sheet crystallites in the polypeptide chain network, and as a result, the mechanical properties of silk were enhanced [8,9]. For instance, at the reeling speed of 1 mm s⁻¹, the crystallite size is 3.5 nm in width, 7.3 nm in length and 2.4 nm in thickness. At the reeling speed of 100 mm s⁻¹, the crystallite size is decreased to 2.7 nm in width, 6.4 nm in length and 2.1 nm in thickness [9], showing the influence of the reeling speed on the crystallite size. Besides the reeling speed, the mechanical properties of silk were also found to be negatively influenced by humidity [10]. These studies show that one is able to tune and improve the mechanical properties of silk by controlling the silk harvesting or processing conditions.

Figure 1.

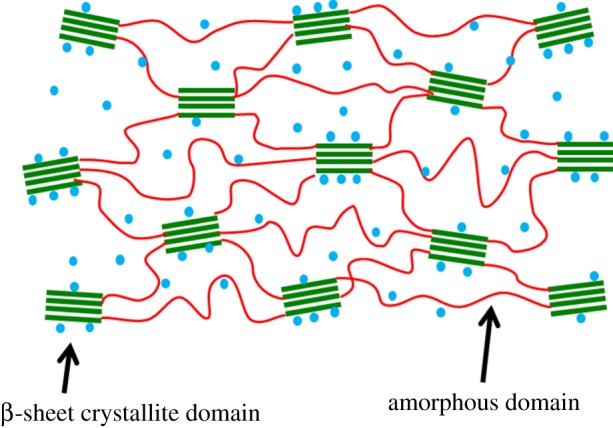
The illustration of β-sheet crystallite embedded in the amorphous matrix. Water molecules are represented by blue dots.

Given the challenges in the experimental access to the structures and mechanical properties of silk fibroin at the nanoscale [11], atomistic simulations fill in the gap in our understanding at this scale. In an earlier study, an energy minimization method was first used to evaluate the β-sheet crystallite structure [12]. All-atom molecular dynamics simulation was then performed on silk crystallite units with both parallel and anti-parallel arrangements by Xiao et al. [13]. It was found that in terms of strength, anti-parallel β-sheet crystallites outperform their parallel counterparts. Recently, with strong interest in the size effect of β-sheet crystallite on the mechanical properties of silk, all-atom molecular dynamics simulations were performed to study the stiffness, strength and toughness of silk [14]. It was found by Keten et al. that when β-sheet crystallites are confined within a few nanometres, much higher stiffness and strength can be achieved. This work presented an interesting analysis on the crystallite size effect and provided a useful guideline for the design of silk-based and other bioinspired materials with superior mechanical properties. It is also interesting to note that the predicted strength from their simulations is a few times higher than the estimated experimental value [14]. This discrepancy is compelling and certainly deserves research attention.

When silk fibre is subjected to tensile loading, the fracture should be dictated by the weakest rupture strength. An important question naturally follows: what failure process dictates the strength of silk fibre? Another important question is: how do water molecules affect the structure and failure strength of silk fibre? Despite great interest in the effect of moisture on the structure and strength of silk fibroin, previous efforts only focused on the effect of moisture on the amorphous domains or the silk fibroin as whole [10,15]. There has been no systematic experimental or modelling analysis focusing on the effect of moisture on the mechanical behaviour of the crystallite domains. In this study, we perform molecular dynamics simulations on a silk crystallite unit in environments with different degrees of hydration to investigate the effect of water molecules on its structure and strength. Pull-out tests for a β-chain within a typical crystallite unit were also carried out to investigate the chain-location-dependent strength with the aim of identifying the critical process that dictates the failure strength. We find that water molecules have the effect of hindering the formation of hydrogen bonds between β-chains in the crystallite domains. In addition, the ultimate tensile force (UTF) for pulling out a β-chain from a crystallite unit is strongly chain-location-dependent, from which we identify the weakest link that dictates the failure process.

2. Models and methods

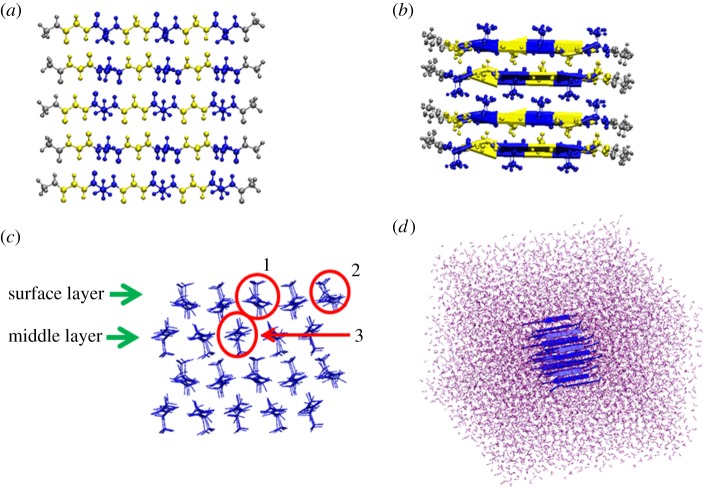
An anti-parallel β-sheet crystallite unit was selected as a model system to represent the crystallite domains of Bombyx mori silk. The initial coordinates for the atomistic model of the crystallites were obtained from Protein Data Bank with entry 2slk and the sequence of poly (Gly–Ala) [12]. Figure 2a illustrates each layer of the crystallite unit consisting of five peptide chains, where Ala residues are displayed in blue and Gly residues in yellow. Figure 2b illustrates the structure of the crystallite unit consisting of four layers of anti-parallel β-sheets. Figure 2c shows the side view of the four-layer crystallite, where the targeted β-chains to be pulled out are labelled as surface layer (SL), middle layer (ML), surface layer-middle chain (SLMC), surface layer-corner chain (SLCC) and middle layer-middle chain (MLMC). The figures were generated using the visual molecular dynamics (VMD) code [16]. Amber force field [17] was used to parametrize the protein. To simulate the mechanical response of the crystallite unit in a water environment, the system was solvated in a TIP3P water box [18] with dimensions of approximately 6.0 × 6.5 × 6.8 nm³, as shown in figure 1d. The system consisted of approximately 25 000 atoms. All simulations were carried out using the package Gromacs v. 4.5.5 [19]. Energy minimization was carried out first, followed by molecular dynamics simulation for up to 5 ns to obtain the equilibrium structure of the system. Periodic boundary conditions and a time step of 0.001 ps were adopted. Molecular dynamics simulations were performed using the NPT ensemble at the temperature of T = 300 K and a pressure of P = 1 bar. The particle mesh Ewald method was used to calculate the long-range electrostatic interactions [20].

Figure 2.

Crystallite structure and simulation set-up. (a) Structure of one layer of silk β-sheet crystallite, which consists of five single peptide chains. The residues displayed in blue represent Ala residues while those in yellow represent Gly residues. Cap residues are coloured in grey. (b) Structure of a four-layer β-sheet crystallite. (c) Side view of the β-sheet crystallite structure. SL and ML are labelled, respectively. Representative chains are highlighted in red circles: (1) SLMC, (2) SLCC and (3) MLMC. (d) β-sheet crystallite structure solvated in the water box.

The equilibrated structure was adopted as the starting configuration for mechanical tests. Pull-out tests were carried out using steered molecular dynamics (SMD) simulations [21]. For the targeted chain (or chains) to be pulled out from the unit, the terminal residues were subjected to a force along the chain direction by pulling a spring with a constant velocity. A counter force was applied to the rest of the chains. Specifically, if one layer of the β-chains is pulled away from the unit, the pulling force is applied to the end residues of all the chains on this layer, whereas a counter force is applied to all the rest chains. A pulling rate of 0.5 nm ns⁻¹ with a spring constant of 830 pN nm⁻¹ was used for SMD simulations. Note that a similar loading condition was also adopted in previous work for simulation of the mechanical response of silk crystallite domains [13].

3. Results

3.1. Water effect on strength of the crystallite

Although water environment has been known to have significant impact on the mechanical properties of the amorphous domain of silk [15], its effect on the crystallite domain remains unexplored. Equilibrium simulation was performed on the crystallite domain in both vacuum and explicit water solvent. It is found that the root-mean-square deviation (RMSD) of the β-chains is within 2 Å without unreasonable fluctuations.

3.1.1. Reduced number of hydrogen bonds

Hydrogen bond formation and strength are important in determining the stability and the failure strength of the β-sheet crystallite. Our simulations allow us to examine the different behaviour of hydrogen bonds in vacuum and in water. Figure 3a and b displays the hydrogen bond formation on the SL of the representative equilibrium structures exposed to vacuum and water, respectively. In order to analyse the hydrogen bonds, we tracked the N–O distance and set the criteria for hydrogen bond by following the VMD default definition for hydrogen bonds, i.e. the bond length cut-off of 3.5 Å and the angle cut-off of 20°. Based on these conditions, there are 22 hydrogen bonds in vacuum and eight in water in the SL. The interaction configurations of two β-chains on the SL interacting with water molecules are also shown in figure 3c.

Figure 3.

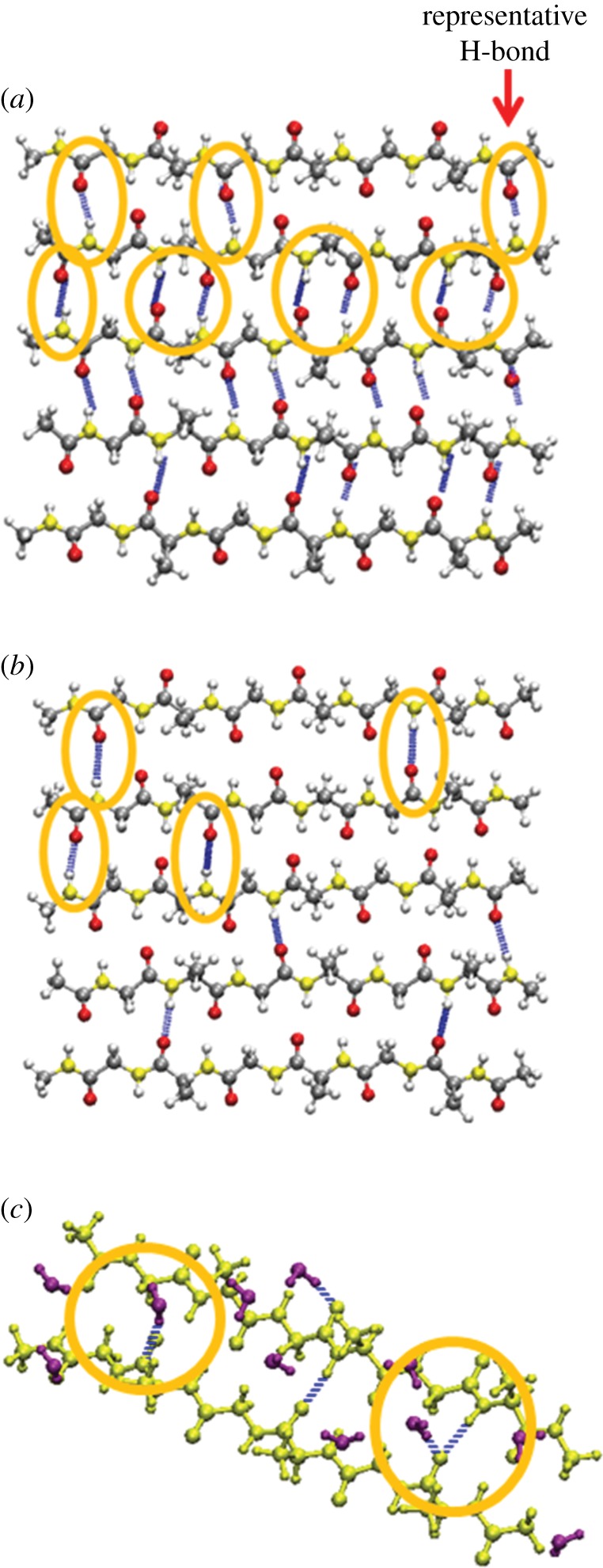
Hydrogen bond analysis on the representative β-sheet crystallite structures at equilibrium. (a) Snapshot of the β-sheet chains on the SL in vacuum. (b) Snapshot of the β-sheet chains on the SL in water. Hydrogen bonds are illustrated in blue and those located among the top three chains are highlighted. (c) Snapshot of two representative β-chains on the SL interacting with water molecules. β-chains are displayed in yellow, and water molecules are displayed in purple.

3.1.2. Reduced hydrogen bond lifetime/strength

To quantitatively investigate the stability of the β-chain structures [22,23], we calculate the lifetimes of hydrogen bonds on the SL and ML in water and in vacuum, respectively [24]. Long time molecular dynamics simulations up to 50 ns for each system were carried out in order to calculate the hydrogen bond lifetimes. As shown in table 1, the hydrogen bond lifetimes of the SL and ML in water are both lower than that in vacuum. For example, the hydrogen bond lifetime of the SL is 212.52 ps in vacuum, but decreases to 43.36 ps in water. Therefore compared to those in vacuum, both the number and strength of the hydrogen bonds between β-chains are reduced in water.

Table 1.

The hydrogen bond lifetimes of the SL and ML in vacuum and in water, respectively, calculated according to the Luzar & Chandler [24].

	hydrogen bond lifetime (ps)
targeted chains	in water	in vacuum
SL	43.36 ± 2.84	212.52 ± 13.40
ML	58.56 ± 9.37	286.16 ± 28.47

To simulate the conditions with different degrees of hydration, in addition to vacuum and the fully solvated water environment (100%), we also considered two intermediate systems with 10 and 50% of the water content used for the fully solvated water environment. The hydrogen bond activation energies of these systems were compared. Hydrogen bond activation energy is able to reflect the strength of the bond through a kinetic procedure [25]. A higher hydrogen bond activation energy corresponds to a higher bond strength. One representative hydrogen bond N–O located in the SL was selected as highlighted in figure 3a. The hydrogen bond energy was obtained by calculating the mean first passage time τ_mfp [25]. Molecular dynamics simulation was carried out for each system at 300 and 350 K for 1 ns, respectively, and the activation energy barrier is calculated via 1/τ_mfp = A exp(−(E_a/k_BT)), where A is the attempting frequency, and E_a is the activation energy. As shown in table 2, the hydrogen bond energy is 1.02 kcal mol⁻¹ in water, while the value increases to 2.86 kcal mol⁻¹ in vacuum. Hydrogen bond energies in systems with 50 and 10% of the water content take intermediate values, showing that the higher the degree of hydration, the weaker the hydrogen bond strength.

Table 2.

Hydrogen bond energy for the representative hydrogen bond on SL of the crystallite in different degrees of hydration. A is the attempting frequency, and E_a denotes the activation energy.

degree of hydration	A (ps−1)	Ea (kcal/mol)
full water	5.84	1.02
50% water	9.23	2.21
10% water	16.47	2.58
vacuum	24.34	2.86

3.1.3. Reduced peak rupture force

To prove that water molecules weaken the mechanical properties and stability of the silk β-sheet crystallites, we perform pull-out tests on the targeted peptide chains from the crystallite unit in vacuum and in water. The pull-out of the SLMC is selected as the representative case for comparison. For each system, we define the UTF as the peak rupture force when the targeted β-chain is pulled away from the crystallite unit. Figure 4 shows the force versus extension curves for the pull-out tests in the two environments. It is seen that the UTF in vacuum is much higher than that in water. A similar trend in UTF variation is also observed for chains at different locations.

Figure 4.

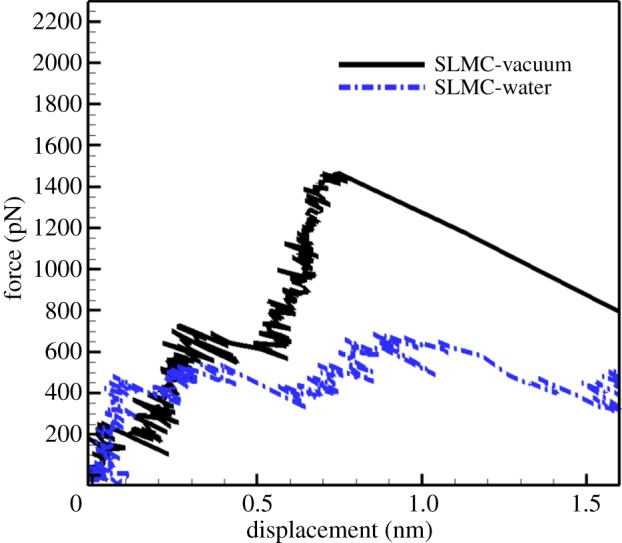
Force–displacement curves for pulling out the SLMC from the crystallite in vacuum and in explicit water solvent environment, respectively. (Online version in colour.)

3.1.4. Increased specific interaction energy

To further understand the mechanical properties and stability of the crystallite in water, we also compute the specific interaction energy, which is defined as the interaction energy between the targeted β-chain(s) and the rest of the crystallite divided by the length of the peptide. Table 3 illustrates the specific interaction energy for all the cases. It should be noted that the specific interaction energies are calculated based on the equilibrium structure of the crystallite, and consist of both electrostatic interaction energy and the van der Waals energy. From table 3, it is seen that for each representative system, the specific interaction energy in vacuum is stronger than that in water, confirming that the β-sheet structure is more stable in vacuum.

Table 3.

Specific interaction energies between selected β-chains and the rest of the chains in the crystallite unit.

	interaction energy per length (kJ/(mol nm))
targeted chain(s)	in water	in vacuum
SL	−367.55	−417.74
ML	−543.98	−582.94
SLMC	−231.56	−244.50
SLCC	−92.47	−125.32
MLMC	−275.43	−283.26

3.2. Critical process governing the tensile strength of crystallite in water solvent

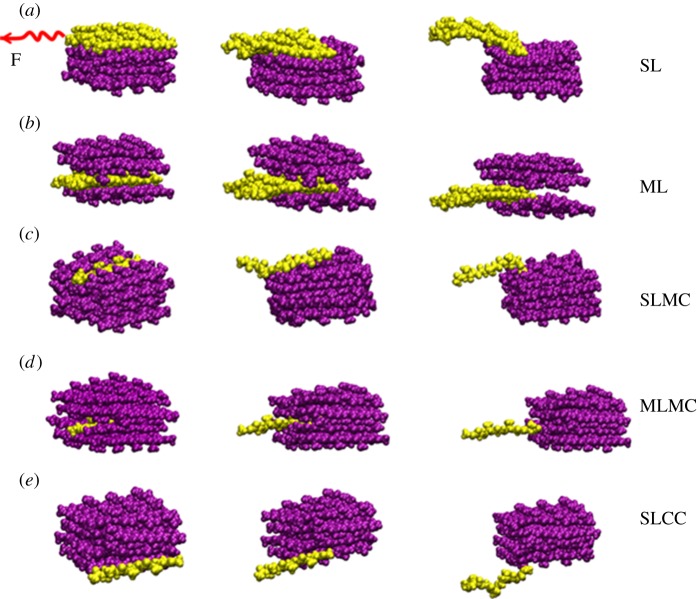
Since almost all the experimental tests on silk fibre were carried out in certain moisture environments [26], here we perform the pull-out simulations in water solvent to identify the critical process that governs the failure strength of β-sheet crystallite in silk fibre. The representative snapshots during the pull-out tests are illustrated in figure 5 for five selected locations: (a) SL, (b) ML, (c) SLMC, (d) MLMC and (e) SLCC.

Figure 5.

Representative snapshots for pulling out the β-chains from different locations of the crystallite unit. (a) SL, (b) ML, (c) SLMC, (d) MLMC and (e) SLCC. The chains being pulled out are displayed in yellow, while the rest are displayed in purple.

3.2.1. Middle layer versus surface layer pull-out

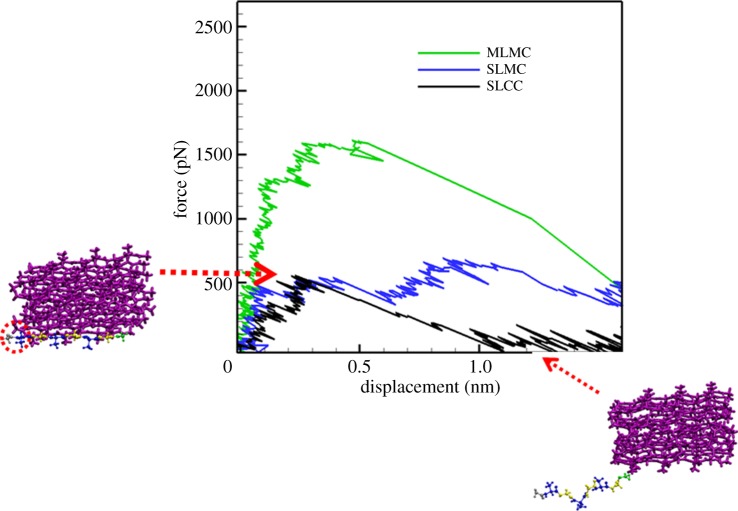
In the case of pulling out one layer of β-chains, the force–displacement curves at two different pulling locations, that is, ML and SL, are shown in figure 6. It is seen that the UTF for pulling out ML is 2550.03 pN. The configuration of the crystallite corresponding to UTF is also given in the inset of figure 6. Right after the peak force, the bonds between the pulled layer and its two adjacent layers are broken, leading to the ultimate failure of the crystallite. The abrupt decrease in the force–displacement curve indicates the brittle nature of the ML failure. In the case of the SL being pulled out, the first peak in the force–displacement curve corresponds to the initial rupture (see the inset of figure 6), subsequently during the sliding of the peptide chains, bonds are able to reform. The snapshot of the crystal configuration corresponding to the second peak is also shown in the inset of figure 6. Compared to the ML, the UTF for pulling out the SL is much lower, that is, 708.88 pN, occurring at the second peak.

Figure 6.

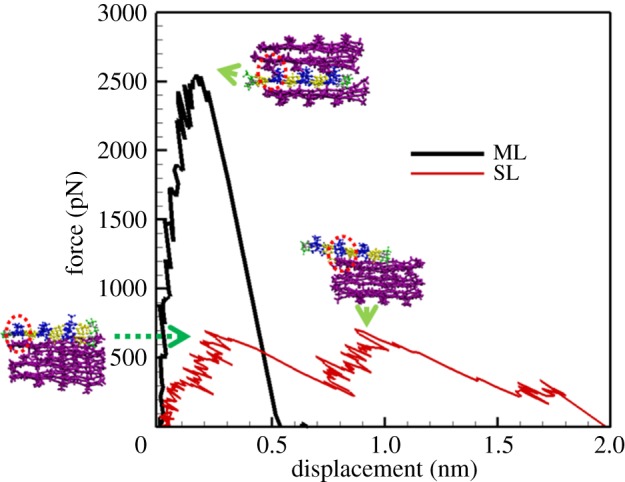
Force–displacement curves for pulling out the ML and the SL, respectively. Snapshots of the crystallite unit corresponding to the rupture force at peaks are also provided. Residues of the peptides in the targeted layer are displayed in blue and yellow, while the rest are displayed in purple.

In order to quantitatively analyse the mechanical behaviour of different layers in the crystallite unit, the resilience of the targeted layer of β-chains for the pull-out tests is also calculated. The resilience of the system is defined as the energy stored before the rupture of hydrogen bonds at UTF. Based on this definition, the resilience of the SL is 19.04 ± 1.31 kJ/(mol nm³), while that of the ML is 16.75 ± 1.36 kJ/(mol nm³). The mean value and standard deviations are calculated based on three separate simulations for each case, respectively.

3.2.2. Single chain pull-out

The force–displacement curves for pulling out a single chain from three different locations in the crystallite are shown in figure 7. The UTF for pulling out the MLMC is 1613.52 pN, which is the highest among the three cases; the UTF for SLMC is weaker, which is 691.90 pN; and that of the SLCC is the weakest, with the value of 557.11 pN. From table 3, it is also seen that the specific interaction energy between MLMC and the rest of the crystallite in the water environment is −275.43 kJ/(mol nm), which is the strongest. Representative snapshots for pulling out SLCC from the crystallite unit are also shown in figure 7.

Figure 7.

Force–displacement curves for pulling out one single chain from three different locations of the crystallite unit. Snapshots for pulling out the SLCC are also shown. The β-chain with residues displayed in blue and yellow is the targeted peptide chain, while the rest are displayed in purple.

4. Discussion

4.1. Water effects on crystallite domain

It was indicated that the hydrogen bond energy is about 4.2 kcal mol⁻¹ in vacuum, while the value dropped to 0.5 kcal mol⁻¹ in water solvent [27]. In our study, hydrogen bond lifetime is calculated as the reflection for the stability of the β-chain structures. As shown in table 1, compared to the vacuum environment, there is a 79.59% drop in hydrogen bond lifetime in the SL, and a 79.53% drop in the ML in water. In addition, the snapshot of β-chains interacting with water molecules as shown in figure 3c suggests that the interactions between β-chains and water molecules are competing with the inter-chain hydrogen bond interaction in solution. These simulation results are also consistent with previous simulations [24] carried out on short secondary structures, including α-helices and β-sheets, indicating that these structures are more stable in vacuum than in water. Our simulation results show that water molecules have a weakening effect on hydrogen bond formation and strength in the crystallite, and therefore the stability of β-sheet crystallite is reduced.

The crystallite size adopted in our simulation is 2.44 nm in width, 1.77 nm in thickness and 2.64 nm in length. The width and thickness of the crystallite in our simulation is comparable to that of the experimental reported size (3.2 nm in width, 3.82 nm in thickness) [28], while a much smaller length than that of the experimental one (10.76 nm in length) is adopted due to limitation of computational capability. Keten et al. [14] reported that beyond the length of about four amino acids (i.e. approx. 1.4 nm calculated based on peptide bond length of 3.5 Å), the length plays little effect on the mechanical property of the crystallite. Thus, our model is able to reproduce the mechanical properties of the crystallite.

4.2. Water effects on the whole silk fibroin

Water has been reported to play an important role in the mechanical properties of silk. Dehydration has been cited to be a major cause of brittleness, rigidity and decreased softness in silk (e.g. excavated silk) [29,30].

Structurally, silk fibroin is composed of β-sheet crystallite domains that are embedded in a matrix of amorphous domains (figure 1). The fibroin molecule itself is a hydrophilic–hydrophobic–hydrophilic polymer, consisting of alternate hydrophobic crystallite and hydrophilic amorphous blocks [26]. The molecule has a more extended chain structure at the initial production stage. Upon in vivo processing, the hydrophobic blocks begin to assemble and organize to form micelles, then liquid crystals. Upon spinning, they eventually form β-sheet crystallites. Meanwhile, the hydrophilic blocks promote silk solubility in water and also have the function of preventing the premature formation of β-sheets during in vivo assembly. With the presence of hydrophilic domains, silk fibroin not only retains a certain amount of water even after spinning and drying in air but also easily absorbs water from the environment [31].

Considering silk fibroin as a whole, water influences both the crystallite and amorphous domains. On the one hand, water plays the role as a plasticizer [30], which helps to enhance chain mobility in the amorphous region of silk, in this way it increases the flexibility and plasticity, and thus reduces the brittleness of the silk fibroin. Hence, dehydrated silk, which lacks water as plasticizers in the amorphous region, will be brittle, and water is thus beneficial in the amorphous region. On the other hand, concerning the β-sheet crystallite, which mainly dictates the strength of silk, in this study, we have shown via molecule dynamics simulation that water weakens the strength of the β-sheet crystallite. Previous experimental studies also showed that moisture reduces Young's modulus of silk fibroin [10,15].

In order to investigate the water effect on the mechanical properties of silk fibroin, we chose four cases for investigating the strength of hydrogen bonds between β-chains: the crystallite unit fully solvated in (i) vacuum (ii) 10% water (iii) 50% water and (iv) 100% water box, as shown in table 2. The vacuum state reflects the extreme case when the silk fibroin is fully-dehydrated (e.g. excavated silk). Comparing these different solvation states demonstrates that water has a weakening effect on the mechanical properties of silk. This finding provides useful insights to potentially tune the mechanical properties of silk, for example by controlling the humidity during silk spinning or by feeding suitable molecules to the silkworms to control the degree of hydration in the produced silk.

4.3. Middle layer versus surface layer pull-out

As listed in table 3, in water solvent, the specific interaction energy between ML and the rest of the crystallite unit is −543.98 kJ/(mol nm), while the SL has a weaker specific interaction energy of −367.55 kJ/(mol nm) with the crystallite unit. The higher energy barrier explains the larger UTF needed to pull-out the ML from the crystallite unit, when compared with SL pull-out. In addition, the difference in the specific interaction energies (ML versus SL) is greater in the water environment (176.43 kJ/(mol nm)) than in vacuum (165.2 kJ/(mol nm)). This is because from the molecular structure point of view, the ML has much less access to water molecules. As a result, the hydrogen bonds formed between the ML and neighbouring layers are less affected by the water molecules. However, owing to the re-bonding process, the resilience of the SL is comparable to that of the ML, despite its much lower UTF than the ML. Therefore within one crystallite unit, the ML shows more brittle behaviour while the SL exhibits more ductile behaviour.

4.4. Single chain pull-out

Similarly, the UTF for SLCC is only one-third of that for MLMC due to much less confinement by inter-chain hydrogen bonds, and after the initial rupture during the pull-out process, the specific interaction between this chain and the rest of the crystallite is too weak so that no obvious re-bonding process is observed.

It is noted that the UTF for MLMC obtained by previous molecular dynamics simulation [14] is about 1500–2300 pN for crystallites with sizes of approximately 6.56–1.87 nm, in good agreement with the present value of MLMC (1613.52 pN). This high UTF arises from the higher number of hydrogen bonds between MLMC and the rest of the crystallite than that of the peptide chains in the corner location.

Considering silk fibroin as a whole, the amorphous regions will unravel first during tensile loading, and the load will then be passed on to the β-sheet crystallites [32], which are linked to the amorphous regions via surface/interior β-chains. Thereafter, tensile fracture most probably happens in the surface of crystallite domains, since our findings show that rupture force of β-chains on the surface of the crystallites is much weaker than the interior ones. Based on the present structural and energetic analyses, it is concluded that when the silk fibre is subjected to tensile loading, the fracture should start from the pulling of the corner chain in the silk fibroin, which is the weakest link that dictates the failure strength.

5. Conclusion

In summary, we have investigated the mechanical response of a β-sheet crystallite unit subjected to pull-out tests via molecular dynamics simulations. It is found that water molecules play a weakening role in the formation of hydrogen bonds between β-chains, thus decreasing the stability of the β-sheet crystallite compared with that in vacuum. The rupture force for pulling out the β-chain(s) from the crystallite unit varies with the location of the chain(s) in the crystallite unit. Although the UTF for pulling out the ML is higher than the SL, the SL shows comparable resilience to the ML. The force required for pulling out the MLMC is about three times that of the SLCC. This work also shows that the pulling of the SLCC has the lowest UTF. Hence, it is the weakest link that controls the failure strength of silk fibre, clarifying the inconsistency between experimental and theoretical failure strengths of silk fibre. The understanding gained in this work regarding the moisture effect and location-dependent mechanical response of the β-sheet crystallite will be helpful in efforts to enhance the mechanical properties of silk fibroin. For example, functional moieties can be incorporated into silk to form a protective shield around the β-sheet crystallite such that the weakening effect of water is eliminated, thereby leading to stronger and tougher silk.

Funding statement

This work was supported by the A*STAR Computational Resource Centre through the use of its high-performance computing facilities. B.J. and D.L. thank the National Natural Science Foundation of China for support through grant nos. 11025208, 11221202 and 11202026.