Visualization and Dynamics of Multidimensional Health-Related Quality-of-Life-Adjusted Overall Survival: A New Analytic Approach

Abstract

VesT was a three-armed, placebo-controlled, randomized clinical trial designed to study the effects of 30mg or 60mg/day vesnarinone. Certain contradictory results involving patient health-related quality-of-life (HRQOL) and overall survival (OS) have made a definitive and unified conclusion difficult. To reconcile these findings, we have focused on the HRQOL-adjusted OS, commonly known as QALYs (quality-adjusted life years). Currently, analyses of QALYs incorporate a single HRQOL dimension or subscale. However, the VesT HRQOL instrument had two subscales, physical (PHYS) and emotional (EMOT). We sought to simultaneously analyze PHYS- and EMOT-adjusted OS in order to gain additional insight and to reach an unequivocal conclusion. Therefore, we have developed new ways to visualize and compare EMOT and PHYS-adjusted OS in the VesT by introducing a simple QALY trade-off function. In each VesT arm, there was an increased probability of superior EMOT-adjusted OS, compared to PHYS-adjusted OS. The magnitude of these findings was comparable across trial arms.

1 Introduction

Time-to-event (TTE) endpoints, such as overall survival (OS) or disease-free survival, are commonly assessed in clinical research. Often, health-related quality of life (HRQOL) is collected as a secondary endpoint of interest, as HRQOL outcomes have become more relevant in clinical trials [1]. A strong dual relationship exists between the clinical and HRQOL aspects of patient health. The TTE influences certain HRQOL dimensions, such as physical/social functioning, energy/vitality or bodily pain [2]. On the other hand, HRQOL history may be associated with extended or shortened TTE durations. Accounting for these synergistic dimensions provides additional insight into the subtle quality/quantity-of-life interplay that separate HRQOL and TTE analyses would not otherwise reveal.

Current methods for combining TTE and HRQOL often utilize overall HRQOL or a single HRQOL dimension (i.e., subscale) at a time ([3], [4]). However, patient health status is too complex to only be summarized using the overall HRQOL or a single subscale. Whenever possible, information from multiple HRQOL subscales should be incorporated into HRQOL-adjusted TTE analyses ([5], [6]). The Vesnarinone Trial (VesT) [7] was a three-arm, double-blind, placebo-controlled randomized clinical trial for patients with severe heart failure. In VesT, patients were randomized to 30mg of vesnarinone, 60mg of vesnarinone, or placebo. HRQOL data were collected at baseline, 8, 16 and 26 months thereafter, using the Minnesota Living with Heart Failure (MLHF) questionnaire [8] that has two subscales, emotional (EMOT) and physical (PHYS). Each VesT participant may value/perceive potential trial benefits differently. Some may value long-term improvements on the physical subscale, while experiencing short-time decreases on the emotional subscale. Others may prefer less emotional distress, at the expense of slight reductions in physical function.

Therefore, we sought to answer the following questions:

1. How does one visualize the interplay between EMOT-adjusted and PHYS-adjusted OS in each trial arm?

2. Within each trial arm, is there a greater benefit in the EMOT-adjusted OS than in the PHYS-adjusted OS during follow-up?

3. If so, is this benefit manifested differentially among the trial arms?

   To address these questions, we propose new visual and analytical methods to depict and quantify any trade-offs between HRQOL-adjusted OS on various subscales, such as the EMOT and PHYS subscales in the VesT example.

2 Multiply HRQOL-adjusted TTE and a trade-off measure

The HRQOL-adjusted-life-year (QALY) method is a simple and easily interpretable summarizing measure ([9]). Patient health is classified into a number of health states, each having a utility value. QALY represents the sum of the utility-weighted time periods spent in each health state. Sensitivity analyses of the utility weights in QALY have been described in the literature [10–13].

If T represents the overall survival (OS) time, define Q⁽¹⁾T and Q⁽²⁾T to be the EMOT- and PHYS-adjusted OS in the VesT, respectively. To address our first question, we propose a simple trade-off measure TOF(t) = P(Q⁽¹⁾T > t) − P(Q⁽²⁾T > t), where t ≥ 0. TOF describes how gains in HRQOL-adjusted OS on the EMOT and PHYS scales compare. Positive TOF values demonstrate that EMOT-adjusted OS is greater than PHYS-adjusted OS at time t. Confidence intervals for TOF(t) are described in the Appendix.

To address the second and third questions, we developed a method to compare TOF(t) values in two in-dependent groups. Let TOF_group1(t) and TOF_group2(t) be the TOF (t) values in groups 1 and 2, respectively. Confidence intervals for the difference TOF_group1(t) − TOF_group2(t) are derived in the Appendix. In all statistical analyses, we have used SAS v. 9.3 for and R v. 2.13.

3 The Vesnarinone TRIAL (VesT) Example

Following a 2-week stabilization period, VesT participants were randomized with equal probability. A total of 3833 patients with left ventricular ejection fraction of 30% or less were enrolled between 01/95 and 07/96. The trial was stopped on July 31, 1996, when the prespecified total number of deaths had been reached in the placebo arm. The mean follow-up time was 286 days. Patient baseline characteristics shown in Table 1 were similar across trial arms.

Table 1.

Patient Baseline Characteristics

Variable	Placebo (N=1167)	30 mg day (N=1154)	60 mg day (N=1162)	P -value
Age (years)	62.1 ± 11.9	62.1 ± 12.4	62.5 ± 12.0	0.65
Sex, No. (%)				0.09
Male	887 (76%)	867 (75%)	916 (79%)
Female	280 (24%)	287 (25%)	246 (21%)
Race, No. (%)				0.42
Caucasian	989 (85%)	989 (86%)	985 (85%)
Black	152 (13%)	137 (12%)	149 (13%)
Hispanic	18 (2%)	15 (1%)	18 (2%)
Asian	4 (0%)	3 (0%)	7 (1%)
Other	4 (0%)	10 (1%)	3 (0%)

HRQOL was assessed using the Minnesota Living with Heart Failure (MLHF) questionnaire, which has two subscales: physical (PHYS) (range from 0–40 in 5-unit increments) and emotional (EMOT) (range 0–25 in 5-unit increments). On each subscale, high values mean low HRQOL. To facilitate analysis, PHYS and EMOT have been transformed to a 0–100 scale: 2.5 × (40 – PHY S) for PHYS and 4 × (25 – EMOT) for EMOT. For the new scores, higher values mean better HRQOL. Only patients with baseline PHYS and EMOT scores were analyzed (1167 in the placebo arm, 1154 in the 30 mg/day arm and 1162 in the 60 mg/day arm).

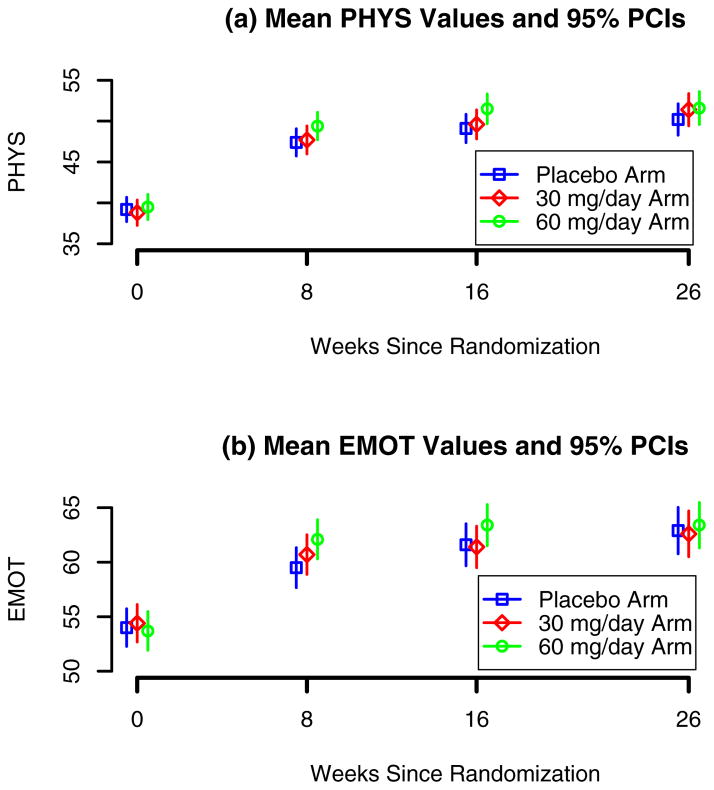
Mean PHYS and EMOT values and corresponding 95% pointwise confidence intervals at randomization, 8, 16 and 26 weeks post-baseline are shown in Figure 2. At 8 weeks post-baseline, the 60mg/day arm participants had significantly higher mean PHYS (p=0.016) and EMOT (p=0.001) scores compared to the placebo arm participants. Similar results were observed at 16 weeks (p=0.007 and 0.006, respectively). However, as revealed by the log-rank (LR) test, all-cause mortality at 8 and 16 weeks was higher in the 60mg/day arm than in the placebo arm (LR=5.80, degrees of freedom=1, p-value=0.02, Cohn et al. [7]).

Fig. 2.

Vesnarinone Trial: mean and 95% pointwise confidence intervals (PCIs) for the transformed PHYS and EMOT components the Minnesota Living with Heart Failure questionnaire at baseline, 8, 16 and 26 weeks post-randomization in the three study arms: placebo, 30mg vesnarinone/day and 60mg vesnarinone/day.

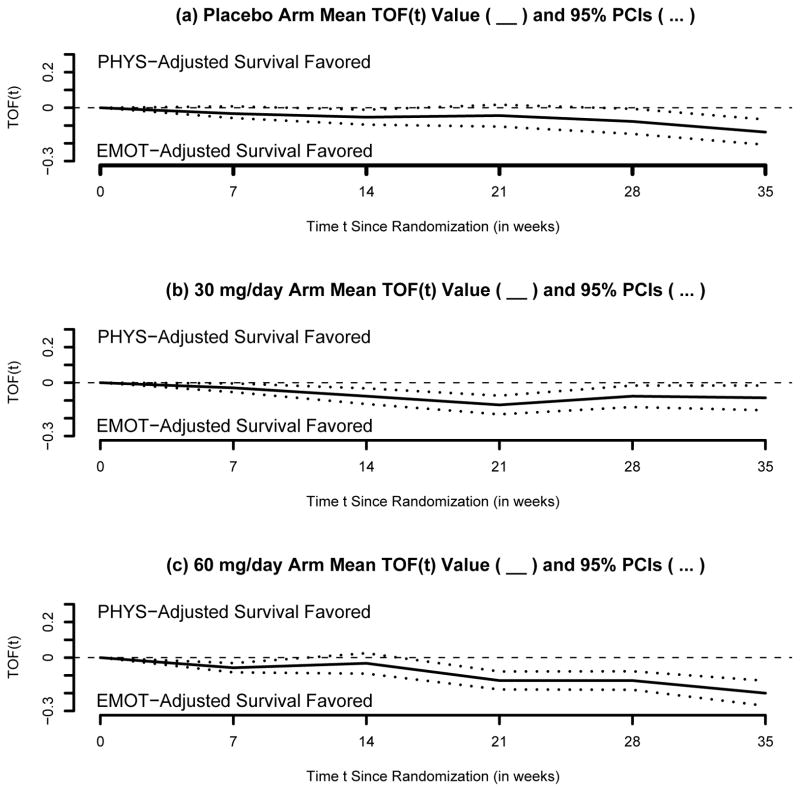
Attempting to reconcile these contradictory results, we have focused on the trade-off functions TOF instead. Let T be the OS (in weeks since randomization). Let Q⁽¹⁾T and Q⁽²⁾T be the PHYS- and the EMOT-adjusted versions of T, respectively. Let the trade-off function be TOF(t) = P(Q⁽¹⁾T > t) − P(Q⁽²⁾T > t), where Q(s) = s/100, for all s ∈ {0,···, 100}. In each VesT arm, TOF(t) was estimated t = 0, 7, 14, 21, 28 and 35 weeks post-baseline and is shown in Figure 3.

Fig. 3.

Vesnarinone Trial within-group trade-off function analyses: mean (___) and 95% pointwise confidence intervals (...) for the trade-off function TOF between PHYS-adjusted and EMOT-adjusted survival. A positive TOF(t) value indicates that PHYS-adjusted survival is favored, compared to EMOT-adjusted survival.

3.1 Within-group TOF evaluation

To address our second question, note in each arm there is a trend favoring greater EMOT-adjusted compared to PHYS-adjusted OS (Figure 3). In the placebo arm, the TOF (standard error SE) gain was 0.03 (0.02), 0.05 (0.02), 0.04 (0.03), 0.08 (0.04) and 0.14 (0.04) at weeks 7, 14, 21, 28 and 35, respectively. Statistical significance has been reached at weeks 7, 14, 21, 28 and 35, with p-values 0.049, 0.013, 0.032 and < 0.001, respectively. In the 30 mg/day arm, the TOF (SE) gains were even greater: 0.03 (0.01), 0.8 (0.02), 0.13 (0.03), 0.8 (0.03) and 0.09 (0.04) at weeks 7–35, respectively. All TOF gains were statistically significant, with p-values equal to 0.02, 0.001, < 0.001, 0.01 and 0.02, respectively. The largest TOF gains at weeks 7–35 were observed in the in the 60mg/day arm: 0.06 (0.01), 0.03 (0.03), 0.13 (0.03), 0.13 (0.03) and 0.20 (0.04), respectively. All TOF gains were statistically significant, with p-values < 0.001.

3.2 Between-groups TOF comparisons

To address the third question, the three trial arms were compared in pairwise fashion in terms of trade-off functions TOF(t) at weeks t = 0, 7, 14, 21, 28 and 35. Results are displayed in Figure 4. When comparing the placebo and the 30mg/day arms (Figure 4(a)), we found virtually no differences in TOF patterns over time, with the exception of week 21, when the TOF was borderline significantly larger in the placebo arm: TOF=0.08 (0.04), p=0.049. A similar result was seen when comparing the placebo and 60mg/day arms, with TOF reaching significance at week 21 only: TOF=0.09 (0.04), p=0.036. However, the comparison of the two active drug VesT arms (Figure 4(b)) shows that the lower dose arm is associated with a higher TOF at week 35 only: TOF=0.12 (0.05), p=0.022. This indicates that the EMOT- versus PHYS-adjusted OS tradeoff was similar in the two active drug VesT arms, with the exception of week 35 post-randomization.

Fig. 4.

Vesnarinone Trial between-groups trade-off functions comparisons: mean (___) and 95% pointwise confidence intervals (...) for difference in trade-off functions. Positive values indicate that the TOF was greater in one group than in the other.

4 Discussion

Currently, analyses of HRQOL-adjusted survival times typically involve the overall HRQOL score or a single HRQOL subscale. However, HRQOL data collection instruments such as the EQ-5D ([3], [4], [14]), the SF-12 ([15]) or the SF-36 ([16]) include multiple relevant HRQOL dimensions. They provide important information that would otherwise not be gleaned from use of overall HRQOL in the determination of QALYs. We propose new graphical methods and a trade-off function to describe the complex relationship between multiple HRQOL scales and time-to-event. This approach facilitates comparisons of trade-off functions, both within and between groups.

Robustness of conclusions in QALY studies is typically assessed using sensitivity analyses ([17], [18]). Using derivations similar to those in the Appendix, the methodology developed can be extended to study the role of the utility functions. Then, comparisons of QALY gains on the PHYS and/or EMOT dimensions can be related to the utility function specification. As a result, more robust conclusions will be obtained. This research will be disseminated in a separate report.

When more than two HRQOL dimensions are available, the trade-off function TOF is replaced by a multidimensional surface. Smoothing techniques can be used to create a more regular TOF surface and to facilitate visual assessment. The mathematical derivations necessary to extend the present results to the context of more than two HRQOL subscales are relatively straightforward.

In the VesT example, these methods indicate that the EMOT-adjusted OS tends to be favored, in comparison to PHYS-adjusted OS, in each trial arm. This demonstrates the complexity of HRQOL and the value of studying not just overall HRQOL, but also dimensions of HRQOL as they relate to survival. Furthermore, despite inferior survival and superior EMOT and PHYS scores, the 60mg/day arm presents similar EMOT- and PHYS-adjusted OS compared to the placebo arm. This finding provides important information on the relative value of treatment (i.e., 60mg of vesnarinone) versus no treatment from the perspective of HRQOL.

As HRQOL data are collected in numerous studies ([19], [20]), we anticipate that the methods developed here will help provide a fresh perspective on the complex interactions between patient health and survival. Although our example is from a heart failure trial, these methods can be applied to a wide range of disease-specific studies, including both acute and chronic diseases and the study of specific cohorts within populations of patients. Ultimately, these novel methods contribute to the burgeoning need for robust information on the interplay between survival and HRQOL from a patient, clinical care, and public policy perspective.

Fig. 1.

Vesnarinone Trial : Overall survival Kaplan-Meier estimates by group.

APPENDIX

Commonly, individual i = 1,…, n time-to-event T_i is subject to independent right-censoring by C_i, hence the follow-up time T̃_i = minimum(T_i, C_i) and the censoring indicator Δ_i = I(T_i ≤ C_i). Both T_i and C_i are assumed to be continuous. HRQOL is measured using a preference-based questionnaire with several subscales. For simplicity, assume it only has two subscales, p = 1, 2. HRQOL on the p^th scale, is quantified by a continuous-time stochastic process V^(p)(·), with state space = {0, 1,…, S_p}. Assume that the health states in are ordered increasingly, “0” being the worst and “S_p” the best state. For each individual i = 1,…, n, assume that $V_i^{(p)}(·)$ and C_i are independent and let a non-decreasing, known function Q^(p)(·) assign utilities between 0 (state “0”) and 1 (state “S_p”) to each state in .

For example, one could think of V ⁽¹⁾(·) and V ⁽²⁾(·) as being the emotional and physical health subscales in the VesT example. When using a generic pair {V (·), Q(·)}, the HRQOL-adjusted lifetime is defined as

$$QT={\int }_0^{T}Q\{V(t)\}dt$$

and its observed version is

$$\stackrel{\sim }{QT}={\int }_0^{\stackrel{\sim }{T}}Q\{V(t)\}dt.$$

Since T is adjusted on two different HRQOL scales, the resulting Q⁽¹⁾T and Q⁽²⁾T are correlated. Their joint distribution is necessary to perform testing for significance.

Assume the existence of a constant L > 0 such that P(T < L) = 1 and P(C > L) > 0. A technical assumption, First, we estimate the joint distribution of Q⁽¹⁾T and Q⁽²⁾T, namely F_1,2(q₁, q₂) = P (Q⁽¹⁾T ≤ q₁, Q⁽²⁾T ≤ q₂). Define H_1,2(q₁, q₂) as P (Q⁽¹⁾T > q₁, Q⁽²⁾T > q₂) and note that

$$F_{1,2}(q_1,q_2)=H_{1,2}(0,0)-H_{1,2}(q_1,0)-H_{1,2}(0,q_2)+H_{1,2}(q_1,q_2).$$

Thus, to estimate F_1,2(·,·) it suffices to estimate H_1,2(·,·). In the absence of censoring and based on a sample of size n, H_1,2(q₁, q₂) can be estimated by the empirical mean of the corresponding indicators of interest,

$$n^{-1}\sum _{i=1}^{n}I\{Q^{(1)}{T}_i>q_1,Q^{(2)}{T}_i>q_2\}.$$

However, when censoring is present, define $m_i^{(p)}(t)=\mathit{infimum}\left[s\ge 0;{\int }_0^s{Q}^{(p)}\{V_i^{(p)}(u)\}du\ge t\right]$ and $D_i^{(p)}(t)=m_i^{(p)}\wedge T_i$, for p = 1, 2 and i = 1,…, n. By convention, $D_i^{(p)}(0)=0$. This expression states that $D_i^{(p)}(t)$ marks the first time when the i^th individual has accumulated at least t HRQOL-adjusted lifetime on the Q^(p)(·) scale. Should this not happen until time T_i, then $D_i^{(p)}(t)$ is assigned the value T_i. The key to producing a consistent estimator for the quantity of interest is to note that if $\stackrel{\sim }{Q^{(p)}{T}_i}>q_p$, then Q^(p)T_i > q_p and censoring time C_i does not occur prior to $D_i^{(p)}(q_p)$.

Consequently, if $A_i^{(p)}(q_p)=I\{Q^{(p)}{T}_i>q_p,C_i>D_i^{(p)}(q_p)\}$ and $B_i^{(p)}(q_p)=I\{\stackrel{\sim }{Q^{(p)}{T}_i}>q_p\}$, then $A_i^{(p)}(q_p)=B_i^{(p)}(q_p)$, where p = 1, 2. Here, I{·} represents the indicator function. Define $D_i^{(1,2)}(q_1,q_2)$ to be the maximum of $D_i^{(1)}(q_1)$ and $D_i^{(2)}(q_2)$. An inverse probability-of-censoring weighted estimator becomes available after assessing when the indicator functions involved are completely observed. Further, should G(u) = P(C > u) be known

$${\stackrel{\sim }{H}}_{1,2}(q_1,q_2)=n^{-1}\sum _{i=1}^n\frac{A_i^{(1)}(q_1)A_i^{(2)}(q_2)}{G\{D_i^{(1,2)}(q_1,q_2)\}}$$

would represent an unbiased estimator for H_1,2(q₁, q₂).

This assertion is true because

$$\begin{array}{c}E\left[\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}\right]=E\left(E\left[\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}|T,V^{(1)}(·),V^{(2)}(·)\right]\right)\\ =E\left(I\{Q^{(1)}T>q_1,Q^{(2)}T>q_2\}E\left[\frac{I\{C>D^{(1,2)}(q_1,q_2)\}}{G\{D^{(1,2)}(q_1,q_2)\}}|T,V^{(1)}(·),V^{(2)}(·)\right]\right)\\ =E\{I(Q^{(1)}T>q_1,Q^{(2)}T>q_2)\}=H_{1,2}(q_1,q_2).\end{array}$$

However, G(u) being unknown, it is estimated by the Kaplan-Meier estimator Ĝ(u) of the censoring time survival function computed using {(T̃_i, 1 − Δ_i); i = 1, …, n}.

4.1 Estimator consistency

A consistent estimator for H_1,2(q₁, q₂) is

$${\widehat{H}}_{1,2}(q_1,q_2)=n^{-1}\sum _{i=1}^n\frac{B_i^{(1)}(q_1)B_i^{(2)}(q_2)}{\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}},$$

from which a consistent estimator F̂_1,2(q₁, q₂) of F_1,2(q₁, q₂) becomes immediately available. Consistency of H_1,2(q₁, q₂) is shown using arguments along the lines of [21] and [22]. Note that

$$\begin{array}{c}{\widehat{H}}_{1,2}(q_1,q_2)-H_{1,2}(q_1,q_2)={\stackrel{\sim }{H}}_{1,2}(q_1,q_2)-H_{1,2}(q_1,q_2)+{\widehat{H}}_{1,2}(q_1,q_2)-{\stackrel{\sim }{H}}_{1,2}(q_1,q_2)\\ =n^{-1}\sum _{i=1}^n\left[\frac{B_i^{(1)}(q_1)B_i^{(2)}(q_2)}{\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}}-H_{1,2}(q_1,q_2)\right]\end{array}$$ (1)

$$+n^{-1}\sum _{i=1}^n{B}_i^{(1)}(q_1)B_i^{(2)}(q_2)\frac{G\{D_i^{(1,2)}(q_1,q_2)\}-\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}}{G\{D_i^{(1,2)}(q_1,q_2)\}\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}}.$$ (2)

The expression in (1) is a sum of zero-mean i.i.d. terms, so it converges to zero in probability. In addition, $D_i^{(1,2)}(q_1,q_2)<L<{\tau }_C:=\mathit{sup}\{t;G(t)>0\}$ and Ĝ converges uniformly in probability to G on [0, τ_C). The term in (2) is bounded from above, in absolute value, by

$$\frac{\mathit{sup}\{\mid \widehat{G}(u)-G(u)\mid ;u\le {\tau }_C\}}{\widehat{G}({\tau }_C)G({\tau }_C)},$$

so it converges to zero, in probability. This shows that Ĥ_1,2(·, ·) is a consistent estimator of H_1,2(·, ·), hence an estimator for F_1,2(·, ·) can be derived easily.

Limiting Distribution Results

Let $M^c(u)=I\{C\le u,C\le T)\}-{\int }_0^{u}I(\stackrel{\sim }{T}\ge s)d{\mathit{\Lambda }}^c(s)$, where Λ^c(s) = exp{−G(s)} represents the cumulative hazard function of the censoring distribution. Using Lemma 2.4 in [23], it follows that for all t ≤ max{T̃_j; j = 1, …, n}, we have that

$$\frac{G(t)-\widehat{G}(t)}{G(t)}={\int }_0^t\frac{\widehat{G}(u-)}{G(u)}\frac{{\sum }_{j=1}^n{{dM}_j}^c(u)}{{\sum }_{j=1}^{n}I({\stackrel{\sim }{T}}_j\ge u)}.$$

When $t=D_i^{(1,2)}(q_1,q_2)$ in the previous formula, one obtains that

$$\frac{G\{D_i^{(1,2)}(q_1,q_2)\}-\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}}{G\{D_i^{(1,2)}(q_1,q_2)\}}={\int }_0^{L}I\{D_i^{(1,2)}(q_1,q_2)\ge u\}\frac{\widehat{G}(u-)}{G(u)}\frac{{\sum }_{j=1}^n{{dM}_j}^c(u)}{{\sum }_{j=1}^{n}I({\stackrel{\sim }{T}}_j\ge u)}.$$

Note that W_1,2(q₁, q₂) := n^1/2{Ĥ_1,2(q₁, q₂) − H_1,2(q₁, q₂)} = n^1/2{H̃_1,2(q₁, q₂) − H_1,2(q₁, q₂)} +n^1/2{Ĥ_1,2(q₁, q₂) − H̃_1,2(q₁, q₂)}

$$\begin{array}{c}=n^{-1/2}\sum _{i=1}^n\left[\frac{A_i^{(1)}(q_1)A_i^{(2)}(q_2)}{G\{D_i^{(1,2)}(q_1,q_2)\}}-H_{1,2}(q_1,q_2)\right]\\ +n^{-1/2}{\int }_0^L{n}^{-1}\sum _{i=1}^n\left[I\{D_i^{(1,2)}(q_1,q_2)\ge u\}\frac{A_i^{(1)}(q_1)A_i^{(2)}(q_2)}{\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}}\right]\frac{\widehat{G}(u-)}{G(u)}\frac{{\sum }_{j=1}^n{{dM}_j}^c(u)}{n^{-1}{\sum }_{j=1}^{n}I\{{\stackrel{\sim }{T}}_j\ge u\}}.\end{array}$$ (3)

Because

$$\frac{\widehat{G}(u-)}{G(u)}\frac{1}{n^{-1}{\sum }_{j=1}^{n}I({\stackrel{\sim }{T}}_j\ge u)}\stackrel{a.s.}{\to }{\left\{P(\stackrel{\sim }{T}\ge u)\right\}}^{-1},$$

it follows that the second term in (3) can be written as

$$\begin{array}{c}{n}^{-1/2}{\int }_0^L{n}^{-1}\sum _{i=1}^n\left[{\left\{P(\stackrel{\sim }{T}\ge u)\right\}}^{-1}I\{D_i^{(1,2)}(q_1,q_2)\ge u\}\frac{A_i^{(1)}(q_1)A_i^{(2)}(q_2)}{\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}}\right]\sum _{j=1}^n{{dM}_j}^c(u)+o_P(1)\\ =n^{-1/2}{\int }_0^L{[P(\stackrel{\sim }{T}\ge u)]}^{-1}E\left[I\{D^{(1,2)}(q_1,q_2)\ge u\}\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{\widehat{G}\{D^{(1,2)}(q_1,q_2)\}}\right]\sum _{j=1}^n{{dM}_j}^c(u)+o_P(1)\\ =n^{-1/2}\sum _{i=1}^n{\int }_0^L{[P(\stackrel{\sim }{T}\ge u)]}^{-1}E\left[I\{D^{(1,2)}(q_1,q_2)\ge u\}\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}\right]{{dM}_i}^c(u)+o_P(1)\\ =n^{-1/2}\sum _{i=1}^n{\int }_0^L\frac{J_{1,2}(q_1,q_2,u)}{P(\stackrel{\sim }{T}\ge u)}{{dM}_i}^c(u)+o_P(1),\end{array}$$

where

$$J_{1,2}(q_1,q_2,u):=E\left[I\{D^{(1,2)}(q_1,q_2)\ge u\}\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}\right].$$

Then, one can further write

$$\begin{array}{c}{W}_{1,2}(q_1,q_2)=n^{-1/2}\sum _{i=1}^n\left[\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}-H_{1,2}(q_1,q_2)\right]\\ +n^{-1/2}\sum _{i=1}^n{\int }_0^L\frac{J_{1,2}(q_1,q_2,u)}{P(\stackrel{\sim }{T}\ge u)}{{dM}_i}^c(u)+o_P(1).\end{array}$$

Consequently, the asymptotic covariance of W_1,2(q₁, q₂) and W_1,2(r₁, r₂) is equal to

$$\begin{array}{c}E(\left[\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}-H_{1,2}(q_1,q_2)+{\int }_0^L\frac{J_{1,2}(q_1,q_2,u)}{P(\stackrel{\sim }{T}\ge u)}{dM}^c(u)\right]\\ \times \left[\frac{A^{(1)}(r_1)A^{(2)}(r_2)}{G\{D^{(1,2)}(r_1,r_2)\}}-H_{1,2}(r_1,r_2)+{\int }_0^L\frac{J_{1,2}(r_1,r_2,u)}{P(\stackrel{\sim }{T}\ge u)}{dM}^c(u)\right])\\ =E\left(\left[\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}-H_{1,2}(q_1,q_2)\right]\left[\frac{A^{(1)}(r_1)A^{(2)}(r_2)}{G\{D^{(1,2)}(r_1,r_2)\}}-H_{1,2}(r_1,r_2)\right]\right)\\ +E\left(\left[\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}-H_{1,2}(q_1,q_2)\right]{\int }_0^L\frac{J_{1,2}(r_1,r_2,u)}{P(\stackrel{\sim }{T}\ge u)}{dM}^c(u)\right)\end{array}$$ (4)

$$+E\left(\left[\frac{A^{(1)}(r_1)A^{(2)}(r_2)}{G\{D^{(1,2)}(r_1,r_2)\}}-H_{1,2}(r_1,r_2)\right]{\int }_0^L\frac{J_{1,2}(q_1,q_2,u)}{P(\stackrel{\sim }{T}\ge u)}{dM}^c(u)\right)$$ (5)

$$+E\left\{{\int }_0^L\frac{J_{1,2}(q_1,q_2,u)}{P(\stackrel{\sim }{T}\ge u)}{dM}^c(u){\int }_0^L\frac{J_{1,2}(r_1,r_2,u)}{P(\stackrel{\sim }{T}\ge u)}{dM}^c(u)\right\}.$$ (6)

Note that the expression in (4) is equal to

$$E\left[\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}{\int }_0^L\frac{J_{1,2}(r_1,r_2,u)}{P(\stackrel{\sim }{T}\ge u)}{dM}^c(u)\right]-E\left\{{\int }_0^L{H}_{1,2}(q_1,q_2)\frac{J_{1,2}(r_1,r_2,u)}{P(\stackrel{\sim }{T}\ge u)}{dM}^c(u)\right\}$$ (7)

Terms (4) and (5) are both equal to

$$-{\int }_0^L\frac{J_{1,2}(q_1,q_2,u)J_{1,2}(r_1,r_2,u)}{P(\stackrel{\sim }{T}\ge u)}d{\mathit{\Lambda }}^c(u),$$

using arguments as in [24]. Standard results for stochastic integrals with respect to martingales, lead to the fact that the expression in (6) is equal to

$$\begin{array}{c}E\left\{{\int }_0^L\frac{J_{1,2}(q_1,q_2,u)J_{1,2}(r_1,r_2,u)}{P^2(\stackrel{\sim }{T}\ge u)}d{\mathit{\Lambda }}^c(u)d\langle M^c(u),M^c(u)\rangle \right\}\\ =E\left\{{\int }_0^L\frac{J_{1,2}(q_1,q_2,u)J_{1,2}(r_1,r_2,u)}{P^2(\stackrel{\sim }{T}\ge u)}I(\stackrel{\sim }{T}\ge u)d{\mathit{\Lambda }}^c(u)\right\}\\ ={\int }_0^L\frac{J_{1,2}(q_1,q_2,u)J_{1,2}(r_1,r_2,u)}{P(\stackrel{\sim }{T}\ge u)}d{\mathit{\Lambda }}^c(u).\end{array}$$

By applying the multivariate central limit theorem, it follows that W_1,2(·, ·) converges in finite-dimensional distribution to a 4–variate zero-mean Gaussian process whose covariance function is equal to

$$\begin{array}{c}{\sigma }_{H_{1,2}}(q_1,q_2;r_1,r_2)=E\left(\left[\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}-H_{1,2}(q_1,q_2)\right]\left[\frac{A^{(1)}(r_1)A^{(2)}(r_2)}{G\{D^{(1,2)}(r_1,r_2)\}}-H_{1,2}(r_1,r_2)\right]\right)\\ -{\int }_0^L\frac{J_{1,2}(q_1,q_2,u)J_{1,2}(r_1,r_2,u)}{P(\stackrel{\sim }{T}\ge u)}d{\mathit{\Lambda }}^c(u).\end{array}$$

Recall that F_1,2(q₁, q₂) = H_1,2(0, 0) − H_1,2(q₁, 0) − H_1,2(0, q₂)+H_1,2(q₁, q₂). Using the previous findings, it follows that $\sqrt{n}\{{\widehat{F}}_{1,2}(q_1,q_2)-F_{1,2}(q_1,q_2)\}$ converges in finite-dimensional distribution to a 4–variate zero-mean Gaussian process with covariance function

$$\begin{array}{c}{\sigma }_{F_{1,2}}(q_1,q_2;r_1,r_2)=\mathit{Cov}\{H_{1,2}(0,0)-H_{1,2}(q_1,0)-H_{1,2}(0,q_2)+H_{1,2}(q_1,q_2),\\ H_{1,2}(0,0)-H_{1,2}(r_1,0)-H_{1,2}(0,r_2)+H_{1,2}(r_1,r_2)\}\end{array}$$

Define R_1,2(q₁, q₂, u) = J_1,2(0, 0, u) − J_1,2(q₁, 0, u) − J_1,2(0, q₂, u) + J_1,2(q₁, q₂, u) and

$${\mathbf{\Gamma }}_{1,2}(q_1,q_2)=\frac{A^{(1)}(0)A^{(2)}(0)}{G\{D^{(1,2)}(0,0)\}}-\frac{A^{(1)}(q_1)A^{(2)}(0)}{G\{D^{(1,2)}(q_1,0)\}}-\frac{A^{(1)}(0)A^{(2)}(q_2)}{G\{D^{(1,2)}(0,q_2)\}}+\frac{A^{(1)}(q_1)A^{(2)}(q_2)}{G\{D^{(1,2)}(q_1,q_2)\}}-F_{1,2}(q_1,q_2).$$

After involved, but direct, computations, it follows that σ_F1,2(q₁, q₂; r₁, r₂) is equal to

$$E\left[{\mathbf{\Gamma }}_{1,2}(q_1,q_2){\mathbf{\Gamma }}_{1,2}(r_1,r_2)\right]-{\int }_0^L\frac{{\mathbf{R}}_{1,2}(q_1,q_2,u){\mathbf{R}}_{1,2}(r_1,r_2,u)}{P(\stackrel{\sim }{T}\ge u)}d{\mathit{\Lambda }}^c(u).$$

Variance Estimation

Following standard arguments, the cumulative hazard Λ^c(t) of the censoring distribution is estimated by the Nelson-Aalen estimator

$${\widehat{\mathit{\Lambda }}}^c(t)={\int }_0^t\frac{{\sum }_{i=1}^n(1-{\mathrm{\Delta }}_i)dI({\stackrel{\sim }{T}}_i\le u)}{{\sum }_{i=1}^{n}I({\stackrel{\sim }{T}}_i\ge u)}$$

The value of P(T̃ ≥ u) can be consistently estimated by $n^{-1}{\sum }_{i=1}^{n}I({\stackrel{\sim }{T}}_i\ge u)$, while an estimator for J_1,2(q₁, q₂, u) is given by

$${\widehat{J}}_{1,2}(q_1,q_2,u)=n^{-1}\sum _{i=1}^{n}I\{D_i^{(1,2)}(q_1,q_2)\ge u\}\frac{B_i^{(1)}(q_1)B_i^{(2)}(q_2)}{\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}}.$$

Furthermore, Γ_1,2(q₁, q₂) and R_1,2(q₁, q₂, u) are estimated by

$${\widehat{\mathbf{\Gamma }}}_{1,2}(q_1,q_2)=n^{-1}\sum _{i=1}^n[\frac{B_i^{(1)}(0)B_i^{(2)}(0)}{\widehat{G}\{D_i^{(1,2)}(0,0)\}}-\frac{B_i^{(1)}(q_1)B_i^{(2)}(0)}{\widehat{G}\{D_i^{(1,2)}(q_1,0)\}}-\frac{B_i^{(1)}(0)B_i^{(2)}(q_2)}{\widehat{G}\{D_i^{(1,2)}(0,q_2)\}}+\frac{B_i^{(1)}(q_1)B_i^{(2)}(q_2)}{\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}}]-{\widehat{F}}_{1,2}(q_1,q_2)$$

and R̂_1,2(q₁, q₂, u) = Ĵ_1,2(0, 0, u) − Ĵ_1,2(q₁, 0, u) − Ĵ_1,2(0, q₂, u) + Ĵ_1,2(q₁, q₂, u), respectively.

In conclusion,

$$\begin{array}{c}{\widehat{\sigma }}_{{\widehat{H}}_{1,2}}(q_1,q_2;r_1,r_2)=n^{-1}\sum _{i=1}^n(\left[\frac{B_i^{(1)}(q_1)B_i^{(2)}(q_2)}{\widehat{G}\{D_i^{(1,2)}(q_1,q_2)\}}-{\widehat{H}}_{1,2}(q_1,q_2)\right]\\ \times \left[\frac{B_i^{(1)}(r_1)B_i^{(2)}(r_2)}{\widehat{G}\{D_i^{(1,2)}(r_1,r_2)\}}-{\widehat{H}}_{1,2}(r_1,r_2)\right])-{\int }_0^L\frac{{\widehat{J}}_{1,2}(q_1,q_2,u){\widehat{J}}_{1,2}(r_1,r_2,u)}{n^{-1}{\sum }_{j=1}^{n}I({\stackrel{\sim }{T}}_j\ge u)}d{\widehat{\mathit{\Lambda }}}^c(u)\end{array}$$

and

$${\widehat{\sigma }}_{{\widehat{F}}_{1,2}}(q_1,q_2;r_1,r_2)={\widehat{\mathbf{\Gamma }}}_{1,2}(q_1,q_2){\widehat{\mathbf{\Gamma }}}_{1,2}(r_1,r_2)-{\int }_0^L\frac{{\widehat{\mathbf{R}}}_{1,2}(q_1,q_2,u){\widehat{\mathbf{R}}}_{1,2}(r_1,r_2,u)}{n^{-1}{\sum }_{j=1}^{n}I({\stackrel{\sim }{T}}_j\ge u)}d{\widehat{\mathit{\Lambda }}}^c(u)$$

are consistent estimators of σ_H1,2(q₁, q₂; r₁, r₂) and σ_F1,2 (q₁, q₂; r₁, r₂), respectively.

Confidence Intervals

Based on these derivations, a 100 × (1 − α)-level confidence interval for TOF(t) is $[\widehat{\mathit{TOF}}(t)-z_{1-\alpha }\sqrt{{\widehat{\sigma }}_{H_{1,2}}(t,0;0,t)/n},\widehat{\mathit{TOF}}(t)+z_{1-\alpha }\sqrt{{\widehat{\sigma }}_{H_{1,2}}(t,0;0,t)/n}]$, where n is the group size and z_1−α is the upper α^th quantile of the N(0, 1) distribution.

We now focus on the two-group setting. Let n₁ and n₂ be the sample sizes of the two groups, respectively. A 100 × (1 − α)-level confidence interval for TOF_group1(t) − TOF_group2(t) is

$$\begin{array}{l}[{\widehat{\mathit{TOF}}}_{\mathit{group}1}(t)-{\widehat{\mathit{TOF}}}_{\mathit{group}2}(t)-z_{1-\alpha }\sqrt{{\widehat{\sigma }}_{H_{1,2}^{\mathit{group}1}}(t,0;0,t)/n_1+{\widehat{\sigma }}_{H_{1,2}^{\mathit{group}2}}(t,0;0,t)/n_2},\\ {\widehat{\mathit{TOF}}}_{\mathit{group}1}(t)-{\widehat{\mathit{TOF}}}_{\mathit{group}2}(t)+z_{1-\alpha }\sqrt{{\widehat{\sigma }}_{H_{1,2}^{\mathit{group}1}}(t,0;0,t)/n_1+{\widehat{\sigma }}_{H_{1,2}^{\mathit{group}2}}(t,0;0,t)/n_2}].\end{array}$$