Using a Shared Parameter Mixture Model to Estimate Change during Treatment when Termination is Related to Recovery Speed

Abstract

Objective

This study demonstrates how to use a shared parameter mixture model (SPMM) in longitudinal psychotherapy studies to accommodate missing that are due to a correlation between rate of improvement and termination of therapy. Traditional growth models assume that such a relationship does not exist (i.e., assume that data are missing at random) and will produce biased results if this assumption is incorrect.

Method

We use longitudinal data from 4,676 patients enrolled in a naturalistic study of psychotherapy to compare results from a latent growth model and a shared parameter mixture model (SPMM).

Results

In this dataset, estimates of the rate of improvement during therapy differ by 6.50 – 6.66% across the two models, indicating that participants with steeper trajectories left psychotherapy earliest, thereby potentially biasing inference for the slope in the latent growth model.

Conclusion

We conclude that reported estimates of change during therapy may be underestimated in naturalistic studies of therapy in which participants and their therapists determine the end of treatment. Because non-randomly missing data can also occur in randomized controlled trials or in observational studies of development, the utility of the SPMM extends beyond naturalistic psychotherapy data.

It is important for clinicians, patients, policy-makers, and researchers to know how much time in therapy patients need in order to accrue clinically significant benefits. Such information is essential for planning and allocating resources, and it can be used as a benchmark against which an individual patient’s progress is tracked (cf. Finch, Lambert, & Schaalje, 2001). Characterizing the typical rate of improvement in response to a particular dose of therapy is complicated in naturalistic settings in which the dose of therapy is determined by the patient and therapist rather than by a researcher or other independent influence (Feaster, Newman, & Rice, 2003). In naturalistic settings, the amount of time that one spends in therapy is inversely related to speed of recovery; patients who recover most quickly leave therapy earliest (Baldwin, Berkeljon, Atkins, & Nielsen, 2009; Barkham, Connell, Stiles, Miles, Margison, Evans, et al. 2006). Moreover, data collection often only occurs when patients are in therapy. Consequently, we will have far more observations on patients who remain in therapy (i.e., those who change the slowest) than we will on patients who terminate.

This type of missing patient data can be considered non-ignorable or non-random because the longitudinal process which governs change in psychological functioning is related to the process governing termination. This is patient data from sessions following termination are considered missing in situations for which it would be desirable to know what the symptomatology of a patient would have looked like had they continued therapy. In particular, this type of non-random missingness is random coefficient-dependent because the latent trajectory underlying an individual’s rate of change is directly related to missingness.¹ In contrast, many common approaches to accommodating missing data, such as those implemented in latent growth and multilevel growth models, assume that missing data are missing at random (MAR; e.g., when maximum likelihood or multiple imputation is implemented) or missing completely at random (MCAR). MCAR is a subtype of MAR that is rarely observed in practice unless data are missing by design. Violating the assumption of random missingness can lead to biased results and inaccurate information about expected rates of change.

In this manuscript we illustrate a method for incorporating information about random coefficient-dependent missing data into a growth model in order to obtain results that are directly comparable to those obtained using a standard growth model. We apply this model, referred to as a shared parameter mixture model (SPMM), to a naturalistic dataset where dose of therapy was not controlled by the researcher. In previous work, Gottfredson et al. (in press) presented technical details on the SPMM, along with results from a Monte Carlo study of the model’s relative performance under a variety of data conditions. Here, we minimize the presentation of technical details and instead aim to provide an accessible overview of the SPMM and an illustration of how it can be applied to strengthen research in clinical psychology.

The outline of the manuscript is as follows. We begin by orienting the reader to our motivating data analysis problem – we desire to measure psychological change in a naturalistic study of psychotherapy treatment. Second, we briefly review the MAR assumption inherent in standard methods for modeling change and discuss how violations of this assumption lead to biased results in the context of a naturalistic treatment study. Third, we introduce the SPMM as a statistical method that is useful when individual differences in change (e.g., differences in rate of improvement during treatment) may be related to the presence, pattern, or amount of missing data. Fourth, we apply the SPMM to the naturalistic psychotherapy dataset and contrast the results with a traditional latent growth curve model. Finally, we discuss implications of our results for the study of naturalistic change during therapy.

Motivating Example: Naturalistic Change during Psychotherapy Treatment

We wish to obtain reliable estimates of expected change over time in psychological functioning based on repeated outcome measures collected from patients enrolled in psychotherapy. Furthermore, we are interested in how expected rates of improvement vary as a function of a patient’s diagnosis (i.e., adjustment disorder, anxiety disorder, mood disorder, or some other disorder) and demographic characteristics (i.e., age and gender). Such information is useful for establishing a benchmark against which the progress of new patients can be measured. In this study, as in most other naturalistic studies of change during treatment, assessment of psychological functioning was not attempted after the termination of therapy. Thus, one might argue that data are not literally ‘missing’ for individuals who have completed therapy because they were never intended to be collected. However, not all patients decide to leave therapy at the exactly the same level of psychological functioning and thus the process governing termination is inherently unobservable. Therefore, the absence of data past an individual’s completion of therapy are indeed ‘missing’ in the sense that an analyst wishing to make an inference about the expected trajectory of a future patient with similar characteristics will not have data with which to make an informed prediction.

Missing Data Assumptions

The MAR assumption is violated when the cause of missingness is related to the outcome of interest but this cause is not included as a measured variable in the analytic model. Given this definition, any situation in which the cause of treatment termination is related to treatment trajectories (i.e., not random), and not modeled using measured variables, is a violation of the MAR assumption. If the MAR assumption is violated, then the probability that a given repeated outcome measure (y_ti) is missing depends on the underlying value of y_ti itself, even after accounting for all measured variables in the model. This would occur, for instance, if latent (i.e., inherently unmeasured) individual differences in rates of change give rise to earlier or later termination of therapy. For example, patients who improve relatively rapidly leave treatment sooner than patients who improve relatively slowly. In this case, the missing data can be said to be missing not at random (MNAR) due to a random coefficient-dependent missingness process, where the random coefficients in this context refer to patient-specific rates of change. If a standard growth model is used to analyze data in which this type of non-random missingness is present, bias may occur in any of the parameter estimates and/or their standard errors (Gottfredson et al., in press). There is no formal test to evaluate whether missing data are MAR, parameter bias will not be detectable with fit statistics (Enders, 2011), and parameter bias will lead to incorrect inference about typical growth trajectories and about the degree of normative variation around typical growth trajectories. The degree of parameter bias that may exist within a single application may not be exceptional. Over time and across many studies, however, consistently biased results may have a serious impact on effect size estimates and practical implications drawn from such biased effect size estimates. The only way to detect whether bias due to non-random missingness might plausibly be occurring in one’s model is to employ sensitivity analyses with alternative models that do not rely on the assumption that missing data are MAR.²

Random coefficient dependent missingness is likely to occur in naturalistic treatment studies because the decision to end treatment may depend upon an individual’s latent change trajectory. But concerns about this type of MNAR missingness should not be limited to naturalistic studies. Even if the duration of treatment is specified by design, as in many randomized control trials, patients may drop out of a study at will. Even intermittent missing data may be MNAR and arise as a function of latent growth trajectories. Intermittent missingness may occur if patients are assessed on a schedule and they fail to show up at one time point, but do not fully drop out of the study. If a patient’s therapeutic trajectory is related to the probability of missing an assessment, random coefficient dependent missingness is present. Morgan-Lopez and Fals-Stewart (2007) discussed this type of missing data within the context of group-based therapy. Although our motivating example involves the termination of treatment, which can be thought of as a kind of dropout, the model described in this manuscript is also appropriate to use with intermittent random coefficient missingness.

Although we regard the SPMM as a useful supplement to the data analytic toolkit of clinical researchers, like any other tool it should be applied only when appropriate. There are three situations when the SPMM is not appropriate. The first is when missing data are MNAR, but missingness does not depend on a patient’s underlying trajectory. An example would be the occurrence of an unpredictable, catastrophic event leading to sudden worsening of a patient’s depression and need for hospitalization and discontinuation of the treatment plan. Second, the SPMM performs poorly when there are relatively few measurement occasions. Gottfredson et al. (in press) found that the model performs well with ten assessments, but not with five. For research designs with five or fewer measurement occasions, we recommend using less complex pattern mixture models (Little, 1993; Hedeker & Gibbons, 1997; described below). Finally, Gottfredson et al. (in press) found that a U-shaped missingness mechanism is difficult to approximate using a SPMM. If patients are most likely to leave therapy if they are doing exceptionally well or exceptionally poorly, then a U-shaped selection mechanism exists. If a U-shaped missingness mechanism is known to exist, then a parametric shared parameter model (Wu & Carroll, 1988; described below) may be a better choice.

Missing Data Models

Three popular models for handling non-ignorable missing data include pattern mixture models (Little, 1993; Roy, 2003), parametric shared parameter models (Albert & Follman, 2009; Wu & Carroll, 1988), and selection models (Diggle & Kenward, 1994; Heckman, 1979). Pattern mixture models are useful when only a relatively small number of repeated measures have been collected and few missing data patterns are present (Hedeker & Gibbons, 1997); parametric shared parameter models and selection models are useful when the non-ignorable missing data mechanism is well-understood and can be modeled with great accuracy (Winship & Mare, 1992). In addition, selection models are the only choice for handling a particularly difficult type of non-randomly missing data—those that are missing as a function unmeasured, time-varying variables or residual error (e.g., a catastrophic event). However, all of these methods rely on stringent implicit or explicit assumptions about the process giving rise to missing data (Kenward, 1998; Little, 1994; Tsonaka, Verbeke, & Lesaffre, 2009; Vonesh, Greene, & Schlucher, 2006; Winship & Mare, 1992).

Pattern mixture models condition growth parameters on observed patterns of missing data. In practice, this means that the pattern of missing data is included in the model (e.g., via binary coding variables) as a predictor of trajectory intercepts and slopes (Hedeker & Gibbons, 1997). When there are more than a handful of observed patterns of missing data, it is often necessary to combine some patterns together. In the case of a naturalistic study of psychotherapy, such an approach would involve an ad hoc decision by the analyst regarding which patterns of missingness are unique from one another and which may be combined. A further drawback to this approach is the pragmatic difficulty that some patterns necessarily contain much less information about the shape of growth than other patterns, leading to great uncertainty about trajectories of the patients who terminate therapy after a few sessions. A recent extension of this approach by Roy (2003) uses latent rather than observed missing data patterns to help avoid pitfalls related to sparse missingness patterns; however, the other concerns remain.

Traditional shared parameter models and selection models require the user to provide a specific model for the missing data and the parameter estimates for the trajectory model depend on this missing data model. In the case of a naturalistic psychotherapy study, these models would require the analyst to specify, using a parametric model, the underlying cause(s) of termination or intermittent missingness. The difficulty is that these causes are often not known precisely. Because the longitudinal model for change during therapy is conditioned on this model, any misspecification in the missing data model will propagate to the growth parameters. Thus, although shared parameter models and selection models have the benefit of being conceptually straightforward, they are heavily model-dependent and sensitive to misspecification of the missing data model (e.g., omitted covariates, misspecification of the form of missingness, or violations to distributional assumptions; Kenward, 1998; Tsonaka, Verbeke, & Lesaffre, 2009; Vonesh, Greene, & Schlucher, 2006; Winship & Mare, 1992).

In contrast, the shared parameter mixture model (SPMM)³ that we describe requires relatively few assumptions about the causes underlying the decision to terminate treatment or reasons for intermittently missing treatment sessions. Furthermore, results obtained using SPMM are directly comparable to those obtained using a standard growth modeling technique such as latent curve modeling or multilevel modeling. The SPMM procedure works by, first, empirically approximating the association between patterns of missing data and the growth trajectory using latent classes. This step is akin to the step of creating a missing data model in a parametric shared parameter model, but the model is determined empirically rather through an explicit, user-inputted model. More specifically, one determines the number of latent classes needed to account for the dependence between the missing data process and the latent change process. Second, the analyst averages across latent missingness classes to obtain a solution that is comparable to that which would be obtained using a standard growth model.⁴

Unlike a standard growth model, the SPMM allows for an association between repeated measures and missing data. The SPMM is a semi-parametric model (e.g., Heckman & Singer, 1984) in the sense that the analyst is not required to specify an explicit parametric association between individual growth trajectories and missing data; the association is instead approximated during estimation. This empirical approximation is achieved via a mixture of latent classes, each with its own set of growth parameter estimates and missing data patterns. Enough latent classes are estimated so that the overall association between missing data and growth trajectories can be characterized by the differences across the latent classes. The number of latent classes chosen for a specific analysis is purely data-driven and, if enough classes are estimated, will necessarily result in conditional independence between missing data indicators and growth parameters. As described more fully below, independence between missing data and latent growth parameters, conditional on latent class, is the key to reducing parameter bias due to an MNAR missing data process.

Details on Estimating a SPMM

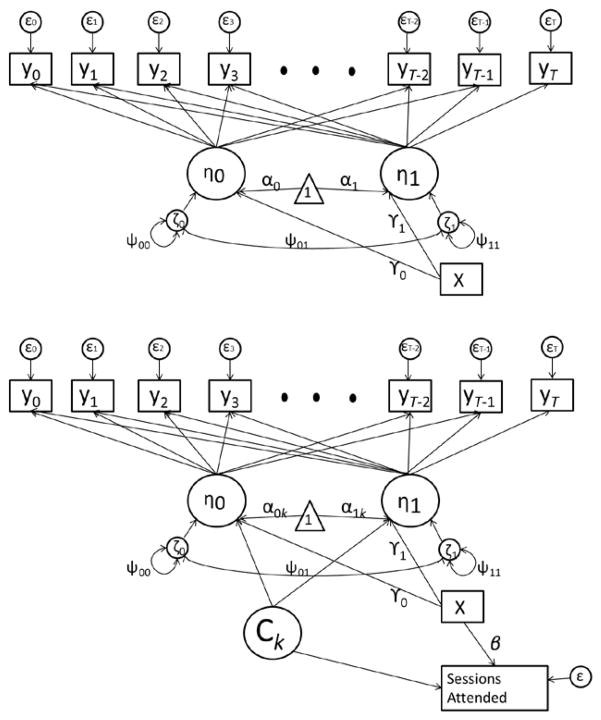
To estimate a SPMM, it is useful to first specify a latent curve model to characterize the individual trajectories, as shown in the top panel of Figure 1 (Bollen & Curran, 2006). Trajectories may take on a variety of forms (e.g., quadratic, exponential, piecewise). The linear model shown in the figure predicts T repeated measures (a T × 1 vector) for individual i as a function of two individually-varying growth factors—a latent intercept (η_0i) and a latent slope (η_1i). In our case, the repeated measures are T = 12 repeated assessments of psychological functioning. The random intercept is an individual’s baseline level of functioning, and the slope is an individual’s rate of change. Average trajectories in the sample are characterized by the mean intercept (α₀) and the mean slope (α₁). In the figure, growth factor means are informed by a time-invariant predictor, X_i. X_i may represent treatment modality, a clinical diagnosis, or gender, for instance.

Figure 1.

Contrasting path diagrams of a LCM (top) and a SPMM (bottom). McArdle and Epstein’s (1987) RAM notation is used. Circles represent unobserved/latent variables (i.e., growth factors η, latent classes C_k, disturbances ζ, and error terms ε); rectangles represent measured variables; the triangle represents the mean structure (i.e., intercepts α) for the growth factors. The SPMM semi-parametrically incorporates information about the dependence between missing data (operationalized as the number of sessions attended) and the trajectory of psychological functioning (y_t). This is done by allowing the growth factor means α₀ and α₁, as well as the mean number of sessions attended, to vary across K latent classes.

The next step in fitting an SPMM is to include one or several missing data indicators (R_i). This approach is shown at the bottom of Figure 1. Like our analysis, Figure 1 uses a single indicator—the number of sessions attended by a given individual—to summarize missingness. A variety of alternative methods for summarizing the missing data patterns are possible, and many choices are described by Roy (2007). One method is to use a dichotomous missing data indicator (i.e., missing or not missing) for every observation occasion. Alternatively, one might condense this information using meaningful summary variables. Gottfredson (2011) showed via simulation methodology that it is desirable to limit the number of missing data indicators when information about missingness can be adequately summarized with fewer indicators because doing so increases computational and statistical efficiency. In this instance, the bulk of the useful information about missingness can be condensed into a single number summary: number of sessions attended.

In lieu of an explicit, parametric model that lays out the precise causes underlying termination of treatment (i.e., a shared parameter model specifying a direct path between latent growth factors η_i and missingness indicators R_i), the association between R_i and the growth factors η_i is approximated using a mixture of latent classes, represented as C_k (k = 1, … K) in Figure 1. The termination process is assumed to be random (i.e., unrelated to the growth trajectory) within each of the K missingness classes (i.e., there is no association between growth parameters and number of sessions attended within each class). As mentioned previously, this assumption is reasonable so long as one has allowed a large enough K, as dictated by information criteria and parameter sensitivity (the process for enumerating classes is described below). Conceptually, if the individuals within a latent class are sufficiently homogeneous in their patterns of change and missing data, no residual relationship should exist between missing data and change trajectories within the class. In other words, it is assumed that the selection process that generates non-randomly missing data can be adequately approximated by splitting the population into a finite number of relatively homogeneous groups, each with their own mean growth trajectory and missing data pattern. As shown in Figure 1, each class has a different intercept and slope, and a different average number of sessions attended, with individual variability in both the trajectories and number of sessions attended within each class. Once the dependence between missing data and growth trajectories has been approximated using latent classes, trajectories within each class are weighted proportionally to the percent of the population that is estimated to ‘belong’ to each class and averaged. This averaging process is described later.

In practice, one chooses a handful of possible values for K (e.g., K = 1, 2, 3, or 4), compares the fit across these models, and evaluates the degree of parameter sensitivity as a function of the number of latent classes in the model. As a result, it is possible to empirically meet or approximate the condition of random missingness within each latent class. Each latent class k is characterized by a mixing proportion π_k that indicates the relative weight of the class in determining the overall pattern of growth. These mixing proportions are used to aggregate within-class trajectory estimates (α_k and ψ_k) in order to obtain overall growth parameters that are comparable with those produced by an LCM, but account for the possibility of random coefficient-dependent missing data. We now describe this process.

Obtaining Results that are Comparable to a Standard Growth Model

Because the classes estimated in a SPMM are not thought to be literal, distinct groups, but are used only as a statistically expedient method for approximating the association between trajectories of change and missing data, and because the goal of such an analysis is to obtain results that are directly comparable with a standard growth model, it is recommended that these class-specific parameters not be interpreted as substantively meaningful. Alternative models exist for researchers who desire to use direct applications of mixture modeling to make inferences about latent groups of people (Morgan-Lopez & Fals-Stewart, 2007; Muthén et al., 2011). However, in our view, focusing on within-class parameter estimates may lead to a mistaken reification of these parameter estimates (Bauer, 2007; Eggleston, Laub, & Sampson, 2004; Sampson & Laub, 2003).

Aggregate values for the growth parameter means or intercepts are calculated by averaging over the estimated latent-class specific growth factor means. Averages are taken by weighting each latent group’s mean using the estimated class proportion, π_k (Bauer, 2007; Vermunt & van Dijk, 2001):

$$\widehat{\mathbf{\alpha }}=\sum _{k=1}^K{\widehat{\pi }}_k{\widehat{\mathbf{\alpha }}}_k.$$

Similarly, aggregate variance and covariance estimates for the longitudinal growth factors can be calculated by combining the between-class covariance matrix (i.e., the (co)variance in the intercept and slope accounted for by between-class differences in means for these growth factors; class proportions and growth factor means from different classes are denoted using the subscripts j and k) with the estimated within-class covariance matrix for the growth factors (i.e., the degree to which individuals deviate from the average trajectory within their latent class; Φ̂), as shown below (Bauer, 2007; Vermunt & van Dijk, 2001):

$$\widehat{\mathbf{\Psi }}=\sum _{k=1}^K\sum _{j=k+1}^K{\widehat{\pi }}_k{\widehat{\pi }}_j({\widehat{\mathbf{\alpha }}}_k-{\widehat{\mathbf{\alpha }}}_j){({\widehat{\mathbf{\alpha }}}_k-{\widehat{\mathbf{\alpha }}}_j)}^{\prime }+\widehat{\mathbf{\Phi }}.$$

Standard errors for the aggregate estimates can be computed via the delta method (available in Mplus, Raykov & Marcoulides, 2004). The delta method is a technique for estimating standard errors via a linear approximation when the analytical computation of exact standard errors is not possible.

Demonstration of SPMM

In a prior analysis of this data, Baldwin et al. (2009) showed that individual trajectories of psychological functioning differ as a function of the number of psychotherapy sessions attended, that is, that the amount of change observed over sessions was related to the dose of psychotherapy received. The purpose of Baldwin et al.’s (2009) manuscript was to demonstrate that the effectiveness of therapy is dose-dependent. The lack of independence between therapy termination and rate of improvement that was demonstrated by these authors provided the motivation for this manuscript: rate of change that depends on the dose (i.e., termination date) is a clear violation of the MAR assumption, making these data ideal for illustrating the application of the SPMM.

For the purpose of this manuscript, we are interested in obtaining a description of the average response to therapy as a function of sessions attended (and variability around the average), irrespective of the dose that is ultimately received by any one patient.⁵ We are also interested in obtaining trajectory estimates conditional on psychological diagnosis, gender, and age. For this purpose, the SPMM provides an optimal modeling approach. We use the number of sessions attended as the observed missing data indicator, R_i. We first estimate change during treatment with a latent curve model (LCM). Second, we estimate a SPMM to examine the sensitivity of LCM results to the suspected non-random termination of therapy.

Method

Participants and Procedure

Participants were drawn from an archival dataset of therapy outcomes that is maintained by a large university counseling center. See Baldwin et al. (2009) for a full description of the sample, measures, and study procedures. Participants in this study were completing their first round of individual psychotherapy. Patients who attended at least three, but no more than 27 sessions were included in the sample (most clients attended fewer than 27 sessions and those attending only two sessions did not provide enough information to calculate growth trajectories). All participants completed therapy within a 40 week period (M = 6.89; SD = 7.46). Patients discontinued therapy at their (and their therapists’) discretion. Only data from the first 12 sessions are analyzed because 75% of patients had dropped out of therapy by this point; extrapolation beyond this point would be imprecise. The first session is coded as ‘0’ to represent baseline functioning and the last is coded as ‘11’.

Of the 4,676 patients analyzed in the sample, the median length in treatment was eight sessions. The majority of patients had adjustment disorders (37.96%), mood disorders (24.59%), or anxiety disorders (12.13%). Most patients were single (65.06%), White (89.07%), and female (62.32%). Ages ranged from 17–60, with a mean age of 22.28 (SD = 3.70).

Psychotherapy Outcome Measure

The Outcome Questionnaire-45 (OQ-45), a 45-item self-report sum score measure of overall psychological functioning (Lambert, Morton, Hatfield, et al., 2004), was used to assess patients’ symptom trajectories over time. The measure assesses three domains: subjective discomfort (e.g., “I feel blue”), inter-personal relationships (e.g., “I feel lonely”), and social role performance (e.g., “I have too many disagreements at work/school”). Patients indicated level of agreement on a five-point scale. Possible scores range from 0 (high functioning) to 180 (low functioning), and they ranged from 0 to 166 in this sample. The OQ-45 has been shown to have high internal consistency, test-retest reliability, and concurrent validity (Baldwin et al., 2009; Lambert et al., 2004; Snell, Mallinckrodt, Hill, & Lambert, 2001). Participants completed the OQ-45 at initial intake and prior to each therapy session.

Time Metric

Time may be coded using a variety of different metrics (e.g., weeks or days in treatment; treatment session; Biesanz, Deeb-Sossa, Papadakis, Bollen, & Curran, 2004). Sessions were the preferred unit of time for this analysis because it was the most relevant to the substantive question of interest: what is the typical rate of response to the receipt of psychotherapy, and how much individual variation exists in response to therapy.

Latent Curve Model Analysis

We assessed a variety of unconditional growth models using a latent curve model (LCM) before deciding to model change as a function of the log of time, which allowed us to capture the more rapid changes that occur early in treatment followed by more gradual changes at subsequent sessions: OQ45 _it =η_01i +η_1it ln(Session + 1) + ε_it. A visual inspection of individual trajectories, observed using OLSTraj (Carrig, Wirth, & Curran, 2004), supported this transformation. Here, OQ45_ti represents patient i’s score on the OQ-45 at session t, η_0i represents baseline psychological functioning for individual i, η_1i represents individual rate of change in psychological functioning, and ε_ti represents an individual’s time-specific deviation from their expected trajectory. η_0i and η_1i are assumed to be normally distributed in the population and they are free to covary.

After settling on an unconditional trajectory model, we added the following predictors of the latent intercept and slope: disorder status (anxiety, mood disorder, and other diagnosis were contrasted with adjustment disorder); gender (females were used as the reference group); and mean-centered age. Finally, we determined that the model fit better when the variances of the residuals ( $\mathit{VAR}({\epsilon }_{ti})={\sigma }_t^2$) were allowed to vary over time.

Shared Parameter Mixture Model Analysis

The next step of the analyses involved fitting a series of SPMMs to the data, increasing the number of latent classes as necessary. A single summary indicator was used to indicate the termination occasion—the log of the total number of sessions attended. Total number of sessions attended is used as the single summary variable with which to model the non-random missing data mechanism. We use this single indicator because we expect that all of the important information about missing data that is associated with an individual’s growth trajectory will be contained number of therapy sessions that an individual attended.⁶ Total number of sessions attended ranged from 3 – 27 for the sample and was heavily skewed right. Log number of sessions was distributed with Mean = 2.05, Median = 2.08, SD = .60, Skew = .07, and Kurtosis = −.74. Thus, by using the log-transformed summary indicator, we were able to assume conditional normality and reduce the computational burden of the model.

SPMMs were estimated with and without predictors of the OQ-45 trajectories. The former is called a ‘conditional model’ and the latter is called an ‘unconditional model’. One- through four-class SPMMs were fit to the data. A decision to stop adding classes was made after small class proportions appeared in the four class model (i.e., the estimated class proportion, π_k, was less than .05), and because aggregate parameter estimates did not change substantially as more classes were added. Classes with small values for π_k tend to be unstable, greatly increasing standard errors of the parameter estimates. Mplus version 6 was used to estimate the models, and the Model Constraints command was used to calculate the aggregated intercept, slope, and variance component parameter estimates so that standard errors (computed by the delta method) would be output by the program. Growth factor and summary indicator means/intercepts were free to vary across latent classes; growth factor variances were fixed to equality across all classes to speed convergence.⁷ Model syntax for a two-class model is included in the appendix.

Results

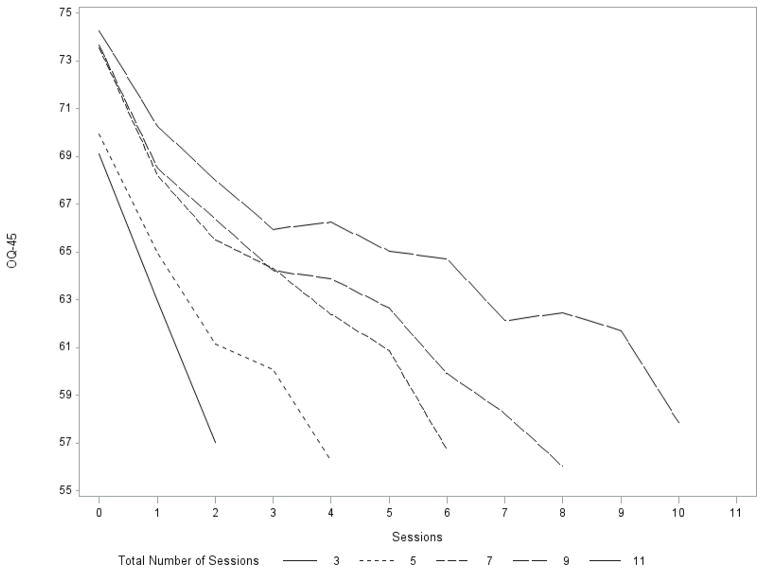
Figure 2 shows a descriptive depiction of psychological functioning over time. Average observed OQ-45 scores decrease quickly at first and then level off. The sample size at each time point is indicated by the diameter of the bubble at that point. It is important to recognize that sample-level mean change over time will only accurately convey information about individual-level rates of change if patients who leave therapy early change no more rapidly than those who do not leave early. Otherwise, the sample that remains at later points in time will differ systematically from the larger sample at earlier points in time. In contrast, Figure 3 plots average OQ-45 scores as a function of time separately for patients who attended a total of three, five, seven, nine, and eleven sessions. It is visually apparent that rate of change is strongly linked with total number of sessions attended; Figure 2 portrays a misleading characterization about the shape individual change during therapy.

Figure 2.

Psychological symptoms (OQ-45) as a function of time in psychotherapy. Bubble width and color gradient indicates sample size at each time point.

Figure 3.

Average OQ-45 scores by session as a function of total number of sessions attended.

Unconditional Models for Growth: Testing Sensitivity to the MAR Assumption

It is useful to assess model fit in a conventional growth model before moving on to a sensitivity analysis for the assumption of random missingness. However, it must be stressed that conventional model fit criteria for evaluating LCMs are insensitive to the nature of missingness (Enders, 2011). That is, a model that assumes a MAR mechanism may fit the data well even when missing data are not truly MAR. This point is supported by subsequent SPMM analyses.

The unconditional LCM has an acceptable fit (χ²(73)=1153.79; p<.001; CFI = .95; TLI = .95; RMSEA 90% confidence interval (.05,.06)). Parameter estimates from the unconditional models are shown on the left side of Table 1. This model suggests that on average, people were estimated to have an OQ-45 score of α₀ =71.37 (SE =.37) upon starting psychotherapy treatment. This is well above the 63-point threshold on the OQ-45 for clinically significant symptoms. However, there is substantial individual variability at baseline. The LCM-implied intercept variance (ψ₀₀) is estimated to be 445.05 (SE =10.40; a standard deviation of about 21 points on the OQ-45 scale). The model for change was log-linear; for the average individual, each log-session was estimated to be linked with an improvement of α₁ = −7.81 points (SE = .23) on the OQ-45 symptom severity score. There was also substantial heterogeneity in the slope (ψ₁₁ =80.13) and a significant negative covariance between the intercept and slope (ψ₀₁ = −61.33) —individuals who began psychotherapy with worse symptoms tended to improve more quickly than those with less severe symptoms.

Table 1.

Comparison of unconditional models: Assessing sensitivity to the MAR assumption

	LCM		SPMM		Parameter Sensitivity
	Estimate	SE	Estimate	SE	% Change	CSK
Fixed Effects
Intercept	71.37***	.37	71.60***	.37	.32	−62.13
Slope (Time-Logged)	−7.81***	.23	−8.33***	.24	6.66	226.09
Variance Components
Intercept Variance	445.05***	9.47	445.09***	9.45	.01	−.42
Slope Variance	80.13***	2.76	78.97***	2.70	1.45	42.03
Covariance	−61.33***	4.34	−61.10***	4.31	.38	−5.30

^***p<.001

Note. Residual variances not tabled. Values range from 74.80 at baseline to 155.66 at last time point for the LCM and from 76.27 at baseline to 155.47 at last time point for the SPMM. MAR: Missing at random; CSK: Collins-Schafer-Kam index of model sensitivity; LCM: Latent curve model; SPMM: Shared parameter mixture model.

We next estimated an unconditional SPMM. Indices used to judge fit for standard structural equation models are generally not valid for mixture models, so other metrics must be used for model comparisons (McLachlan & Peel, 2000). The Bayesian Information Criterion (BIC; Schwarz, 1978) works well in the context of indirect applications of mixture models such as the SPMM because it favors more parsimonious models than the Akaike Information Criterion (AIC; Akaike, 1977), and it is therefore statistically more efficient than the AIC. The Lo-Mendell-Rubin (Lo, Mendell, & Rubin, 2001) and the Bootstrap Likelihood Ratio Test (McLachlan, 1987) are good alternatives to the BIC; however, these approaches are more computationally intensive than the BIC. Because indirect applications of mixture modeling do not attempt to identify an objective ‘true’ number of latent classes, model parsimony is the objective and the BIC has been shown to accomplish this objective well (Gottfredson et al., in press; Morgan-Lopez & Fals-Stewart, 2008).

To test parameter sensitivity to the assumption that the number of sessions attended was independent from individual growth trajectories, a one-class SPMM was compared with a two-class SPMM. A one-class SPMM implies independence between missing data and growth parameters, and is essentially equivalent to a LCM. The BIC was lower for the two-class SPMM (236,784 for the one-class model versus 235,931 for the two-class model). Although this is not a formal statistical test, this finding is suggestive of a non-random missing data mechanism. Because the two-class SPMM fit the data better than a one-class model, a three-class SPMM was then estimated. The three-class model had a lower BIC value than the two-class model (235,633). The three-class solution was favored over the four-class solution because the four-class model contained a very small, unstable, latent class. Aggregate parameter estimates for the unconditional 3-class SPMM are shown in the center of Table 1.

Because the purpose of mixture models is to recover the empirical distribution as closely as possible, information criteria often indicate that more classes are superior to fewer classes (Bauer & Curran, 2003; Bauer, 2007). Even when the conservative BIC metric is used in model selection, there are several features of the data that might lead to the extraction of more than one latent class. Outside of non-random missingness, plausible causes for extracting extra latent classes include violation of the assumption of normality for the repeated measures or a misspecified trajectory model. Even though care was taken to model the shape of the trajectory appropriately and the repeated measures were approximately normal, Bauer and Curran (2003) have shown that very slight departures from model assumptions can lead to the extraction of additional latent classes. For this reason, it is important to inspect parameter estimates for evidence of meaningful change when missing data indicators are included as part of an SPMM, rather than relying on the number of classes (i.e., one class versus more than one class) alone as evidence for non-random missingness. Extracting unnecessary classes will not lead to parameter bias in the fixed effects but it will lead to somewhat inflated standard errors, confidence intervals that are too wide, and a concomitant reduction in power. Furthermore, Gottfredson et al. (in press) showed via simulation that variance component estimates tend to be more upwardly biased as the number of classes increases unnecessarily.

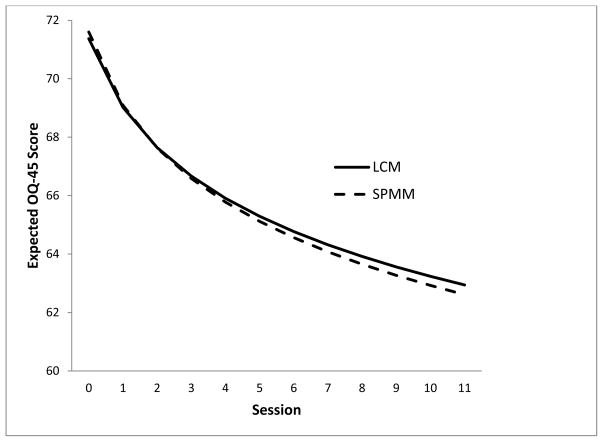
One way to quantify the degree of parameter sensitivity to the assumption of random missingness is percent change in the parameter estimates. Percent change is calculated by subtracting the SPMM-implied estimate from the LCM-implied estimate and dividing this quantity by the LCM-implied estimate. The absolute value of this result is multiplied by 100. Because percent change is highly dependent upon the magnitude of the effect, Collins, Schafer, and Kam (2001) introduced an alternative metric. Their measure, which we call the CSK index, can be computed in our study by subtracting the SPMM estimate from the LCM estimate, dividing by the standard error of the LCM estimate, and multiplying this value by 100. Collins et a. (2001) indicate that CSK value of +/− 40% is considered problematic.⁸ Both percent change and CSK are shown on the right side of Table 1. Data visualization is another method for evaluating growth parameter sensitivity to the MAR assumption. A comparison of LCM-implied average trajectories with SPMM-implied average trajectories is shown in Figure 4. Although the difference between the two implied trajectories is slight, the difference between the symptom scores at later sessions is not trivial.

Figure 4.

Comparison of average unconditional model-implied trajectories for LCM versus SPMM.

As expected, most of the parameter sensitivity occurred in the estimate of the slope (CSK = 226.09; a 6.66% change). When dropout patterns are simultaneously modeled with the growth trajectory, the average rate of change becomes larger in magnitude (the estimate of α₁ changes from −7.81 to −8.33). In other words, the assumption that therapy termination is ignorable leads to a presumed underestimate of the average rate of change. This occurs because people who leave the study earliest due to rapid improvement provide less information about the shape of change than people who continue in psychotherapy for longer.

Assessing the Impact of Covariates on Missing Data Assumptions

The MAR assumption implies that missing data are randomly missing conditional on observed data (Schafer, 1997). Thus, it follows that including more covariates into a model may help to explain missing data patterns, thereby approximating a MAR mechanism. Indeed, Collins et al. (2001) showed that it is best to use an inclusive strategy when adding covariates to a model, as this tends to decrease parameter bias. The logic behind multiple imputation is similar—even if predictors are not necessarily of interest for the research question, they may be useful for predicting missing values. We encourage the incorporation of predictors that have the potential to explain missing data patterns. Of course, researchers may not know the cause of their missing data or they may not have measured the variables that are responsible for missingness. In the case of missingness that is presumed to depend upon individual differences in growth, the cause of missingness is inherently latent and unmeasured. However, including measured covariates that explain some of the variance in growth may reduce the severity of violations to the MAR assumption.

In the next set of analyses, we added demographic predictors as well as clinical diagnosis in an effort to better explain growth trajectories, but also in an effort to make the MAR assumption more plausible by conditioning on these measured variables. Results for the conditional LCM are shown on the left side of Table 2. The conditional LCM had acceptable fit (χ²(123)=1326.96; p<.001; CFI = .95; TLI = .95; RMSEA 90% confidence interval (.04,.05)). Diagnosis was strongly linked with the baseline OQ-45 scores: individuals with mood disorders were estimated to be substantially worse at baseline than individuals with adjustment disorders (γ =18.01; SE =.96), and people with anxiety disorders were worse than people with adjustment disorders (γ =6.81; SE =1.38). Females had higher baseline symptom severity score than males (γ =4.10; SE =.63). People with mood disorders tended to have steeper trajectories of improvement (γ = −3.33; SE =.45). Older age was related to slower recovery (γ =.08; SE =.04).

Table 2.

Conditional models: Assessing sensitivity to the MAR assumption conditional on covariates

	LCM		SPMM		Parameter Sensitivity
	Estimate	SE	Estimate	SE	% Change	CSK
Fixed Effects
Intercept	63.23***	.82	63.56***	.82	.52	−40.24
Slope (Time-Logged)	−6.77***	.40	−7.21***	.39	6.50	110.00
Covariate Effects on Intercept
Anxiety	6.81***	1.38	6.76***	1.39	.73	3.62
Mood	18.01***	.96	17.84***	.97	1.44	27.08
Other Disorder	1.29	.99	1.21	1.00	6.20	8.08
Female	4.10***	.63	4.06***	.63	.98	6.35
Age (Centered)	.07	.09	.06	.09	14.29	11.11
Covariate Effects on Slope
Anxiety	−.47	.61	−.55	.58	17.02	13.11
Mood	−3.33***	.45	−3.49***	.44	4.80	35.56
Other Disorder	.82*	.39	.74	.39	9.76	20.51
Female	−.59	.37	−.62	.37	5.08	8.11
Age (Centered)	.08*	.04	.08a	.04	0	0
Variance Components
Intercept Variance	386.55***	8.75	384.01***	8.95	.66	28.38
Slope Variance	77.82***	2.78	73.32***	2.71	5.78	166.05
Covariance	−49.69***	3.88	−52.26***	3.79	5.17	67.81

^*p<.05;

^***p<.001

Note. Adjustment disorders and males are the referent groups. Residual variances are not tabled. Values range from 73.39 at baseline to 156.57 at the last time point for the LCM. Values range from 74.61 at baseline to 156.41 at the last time point for the SPMM. MAR: Missing at random; CSK: Collins-Schafer-Kam index of model sensitivity; LCM: Latent curve model; SPMM: Shared parameter mixture model.

^aThe SPMM-implied point estimate and standard error appears identical to the LCM-implied point estimate and standard error due to rounding error. The latter effect is statistically significant and the former is not.

In line with the idea that covariates reduce MNAR severity, the two-class SPMM fit better than a one-class or three-class model according to the BIC (one-class BIC = 236,282.09; two-class BIC=235,448.91; three-class BIC=235,157.74). Parameter estimates are shown in the center of Table 2 and model comparison statistics (percent change and CSK) are shown on the right side of Table 2. It is noteworthy that the degree of parameter sensitivity in the slope parameter estimate (quantified using CSK) has been greatly reduced by the inclusion of covariates. CSK for the slope has changed from 226.09 (a 6.66% change from the LCM estimate) to 110.00 (a 6.50% change from the LCM estimate). Because the covariates that were included in the model explain a portion of the variance in individual trajectories, these variables are also useful for helping to explain termination timing.

The most important point of this analysis is that a small degree of parameter sensitivity remains in the conditional LCM estimate of the slope, even after including the important covariates about diagnostic status in model. That is, even though we used an inclusive strategy with a full information maximum likelihood estimator by incorporating diagnostic information and relevant background variables into the LCM, significant unexplained dependence remains between psychological functioning and termination. Although it is not known for certain which of these models is more “correct,” we view the SPMM as being theoretically more plausible than the LCM.

Discussion

Projections about expected length and course of voluntary treatment programs are useful for practitioners for a variety of reasons. However, with voluntary treatment comes dropout or intermittent attendance. Patient adherence to treatment and timing of termination is intrinsically linked with the psychological or behavioral phenomenon that is being addressed by the treatment. Because many standard growth models rely on the assumption that the process underlying missing data is unrelated to the outcome of interest (after accounting for all relevant covariates), the estimates generated by these models are not always suitable for describing change in studies that permit dropout or intermittently missing data, including naturalistic treatment studies, randomized controlled trials, or developmental studies. Because there is no test to determine whether missing data are MAR, it is essential to conduct a sensitivity analysis whenever a non-random missingness mechanism is plausible.

In this paper, we showed how the SPMM could be used to directly assess the sensitivity of traditional growth model results to the assumption of random dropout.⁹ In our analysis, we found evidence to suggest that individual trajectories of psychological functioning over time are related to time spent in therapy. Further, we used the SPMM to obtain growth estimates that do not depend on the MAR assumption. A comparison of the LCM-implied slopes with SPMM-implied slopes showed that the growth parameters are sensitive to the assumption that the total number of sessions attended is unrelated to individual growth trajectories. Incorporating covariates into the model helped to reduce this parameter sensitivity to some degree, but differences in the parameter estimates generated by the two models were still non-trivial. Using the SPMM, we conclude that the average individual recovers from negative psychological symptoms more quickly than would be suggested by standard growth models.

In our dataset, we relied on a single indicator of missingness/dropout (i.e., number of sessions attended) to inform growth parameter estimates. In a more complicated setting, such as when patients skip appointments or re-enroll in therapy after a hiatus, it is still possible to utilize a SPMM and model these intermittent missingness patterns as well as dropout. This would involve modeling more than one indicator of missingness – for example, one might include number of sessions attended plus average time between sessions, or an indicator of re-enrollment. In other words, it is essential for the analyst to carefully consider the suspected missingness mechanism and include missingness indicators that will adequately inform growth parameters.

Limitations

Unfortunately, there is no method to determine whether missingness is truly non-ignorable. However, we did evaluate several sources of evidence that suggested the MAR assumption was unlikely: 1) the idea that therapy termination would be uncorrelated with rate of improvement in psychological functioning seemed implausible; 2) BIC values indicated that two- and three-class solutions provided a better fit to the data than a one class solution; 3) model-implied estimates for the slope differed substantially as the number of latent classes increased whereas other parameter estimates were not affected by the addition of latent classes. Each of these pieces of evidence is consistent with our expectation that the decision to leave therapy is related to rate of improvement. Simulation analyses reported in Gottfredson et al. (in press) suggest that non-random missingness is strongly associated with the tendency of the BIC to support two or more latent classes.

Whereas Gottfredson et al. (in press) found that SPMM-based fixed effect estimates were always equal or superior to LCM-based fixed effect estimates, they also found that SPMM-based variance component estimates tend to be more biased than LCM-based estimates, particularly when the MAR assumption is actually correct. Thus, we avoided interpreting the sensitivity of the variance component estimates. Variance component estimates were quite stable across the two models; however, the variance estimates for the slope were somewhat smaller in the SPMM analysis. It is difficult to know whether this discrepancy is a result of missing data assumptions in the LCM or to model approximation error in the SPMM. When the fixed effect estimates do not differ between the LCM and SPMM, we recommend interpretation of the LCM both because the variance component estimates are more likely to be trustworthy and because the LCM is a more parsimonious model.

The SPMM technique is useful for circumstances in which non-ignorable missing data arise as a function of individual trajectories (e.g., speed of improvement, baseline levels of functioning). However, other causes for non-ignorable missing data are conceivable. For instance, a sudden and unexpected worsening of symptoms might require patient hospitalization and a new treatment plan. In such a case, the SPMM will not be able to get leverage on the sudden worsening of symptoms from the patient’s prior trajectory. We advise researchers to consider whether this type of missing data might exist. If so, it will be important to follow-up with patients to identify reasons for treatment termination so that this information can be accounted for, or to use another MNAR model to conduct a sensitivity analysis. Enders (2011) describes a variety of options.

The archival data used in these analyses were drawn from a sample of volunteers seeking therapy at a university counseling center. Thus, the psychological functioning of participants may have been less impaired than that which might be observed in a community health setting. The reduced clinical severity of the average client may have limited the range of the typical length of therapy received by the participants in the sample. However, the number of sessions provided by the psychologists and psychiatrists was never limited and no cases were referred outside of the clinic. In the case that the range of psychological functioning or number of sessions attended was limited in our sample, this would reduce the degree of non-random missingness that would be observed. This is because patients with the longest treatment times and slowest rate of change would be selected out of the sample. Thus, the degree of parameter sensitivity due to potential non-random missingness that we observed in this analysis likely represents a lower bound of what might be observed in other naturalistic clinical settings.

Additional Research and Clinical Implications

Up to this point, we have detailed a number of important implications for the analysis of data involving non-ignorable missing data. In addition, non-ignorable missing data can impact choices about timing of measurement in treatment studies and can point to potentially important clinical processes in need of study. For example, an implication for naturalistic psychotherapy studies is that researchers must attend carefully to when they choose to measure outcomes. In many, if not all, naturalistic studies outcomes are measured only when a participant is in treatment. This is both practical (i.e., fairly inexpensive) and reasonable (i.e., we care about change during treatment). However, this measurement schedule also opens up the possibility of non-ignorable missing data due to the relationship between change and termination. Thus, researchers could consider obtaining measurements independent of treatment over a fixed time window (e.g., weekly for 4 months). Considering such issues is critical for patient-focused research (Lambert, 2007; Lutz, Martinovich, Howard, & Leon, 2002), which relies heavily on data collected in naturalistic treatment settings. Of course, randomized clinical trials are not immune to non-ignorable missing data due to a relationship between dropout and rate of change. Thus, researchers conducting clinical trials need to carefully consider the reasons for missing data in their trials and whether methods such as the SPMM should be implemented as a sensitivity analysis.

Non-ignorable missing data are not just a statistical nuisance but may provide important clinical information. Indeed, missing data are not ignorable, by definition, when the mechanism for the missing data is systematic rather than random. The systematic reasons for the missing data can be substantively important and understanding those mechanisms could improve theory and practice. For example, the correlation between missing data and rate of change can inform us clinically about how patients and therapist regulate the length of treatment. Barkham et al. (2006) proposed what they called the good-enough level model. The idea is that patients stay in therapy until they decide they have achieved sufficient improvement, and then terminate. This model suggests that fixed doses of treatment for all patients is not appropriate and is not a good use of resources. The good-enough level model also challenges the long-held conclusion in psychotherapy research that as the number of sessions increases, the benefits of each additional session decreases (Howard, Kopta, Krause, & Orlinsky, 1986). Furthermore, understanding the systematic decision processes patients go through when deciding whether to return to treatment is an important area for researchers to study as it could help clinicians in their treatment planning and monitoring.

Conclusion

We believe that the SPMM is a valuable tool for evaluating the sensitivity of trajectory estimates to missing data and that its application has the potential to improve clinical research on change over time. Sample Mplus syntax is provided in the appendix to facilitate the application of the SPMM.

Appendix

TITLE: Two class SPMM with covariates
DATA: file=psychotherapy.dat;
VARIABLE:
! Variable names should be 8 characters or less
names are age minor single anx mood otherdx lognumvi total0-total11;
! Estimating two latent classes here
classes=class(2);
! Missing data should be coded with ‘.’ In the dataset
missing=.;
ANALYSIS:
! Allows for missing data at later sessions
coverage=0;
! 50 random starts. Top 5 iterate to full solution.
starts=50 5;
type=mixture;
MODEL:
%OVERALL% ! True for all classes
! Factor loadings fixed for a log-linear growth model
! Using standard piping syntax for growth models in Mplus
i s  |  total0@0 total1@.6931 total2@1.0986 total3@1.3863
total4@1.6094 total5@1.7918 total6@1.9459 total7@2.0794
total8@2.1972 total9@2.3026 total10@2.3979 total11@2.4849;
! Item intercepts should be fixed to zero; latent factors imply item means
[total0-total11@0];
! Allows residual variances to be unconstrained over time
total0-total11;
! Saving covariance parameters for the model constraints command by using () notation
i (varint);
s (varslp);
i with s (cov);
! [] indicates a mean or intercept
[i s];
[lognumvi];
! Regressing latent growth factors and missing data indicator on demographic variables
i on age minor single anx mood otherdx;
s on age minor single anx mood otherdx;
lognumvi on age minor single anx mood otherdx;
!Missing data indicator lognumvi is conditionally independent from the intercept and slope
lognumvi with i@0;
lognumvi with s@0;
! Save to class proportion for Class#1. Need to do this for K-1 classes
[Class#1] (logit1);
!Growth factor means vary by class, as does missing data indicator mean
!Save the growth factor means for model constraints command
%Class#1%
[i] (ba1);
[s] (bb1);
[lognumvi];
%Class#2%
[i] (ba2);
[s] (bb2);
[lognumvi];
ODEL CONSTRAINT:
! Create new variables based on parameter estimates that were saved earlier
NEW(p1 p2 mba mbb va vb covab);
! Create estimated class proportions to weight within-class estimates
p1 = exp(logit1)/(exp(logit1)+1);
p2 = 1-p1;
! Overall intercept and slope
mba = (p1*ba1 + p2*ba2);
mbb = (p1*bb1 + p2*bb2);
! Overall growth factor variances and covariances
va=p1*p2*(ba1-ba2)**2+varint;
vb=p1*p2*(bb1-bb2)**2+varslp;
covab=p1*p2*(ba1-ba2)*(bb1-bb2)+cov;
! Results based on model constraints can be found near the end of the Mplus output