Abstract
Though sequence differences between alleles are often limited to a few polymorphisms, these differences can cause large and widespread allelic variation at the expression level. Such allele-specific expression (ASE) has been extensively explored at the level of transcription but not translation. Here we measured ASE in the diploid yeast Candida albicans at both the transcriptional and translational levels using RNA-seq and ribosome profiling, respectively. Since C. albicans is an obligate diploid, our analysis isolates ASE arising from cis elements in a natural, nonhybrid organism, where allelic effects reflect evolutionary forces. Importantly, we find that ASE arising from translation is of a similar magnitude as transcriptional ASE, both in terms of the number of genes affected and the magnitude of the bias. We further observe coordination between ASE at the levels of transcription and translation for single genes. Specifically, reinforcing relationships—where transcription and translation favor the same allele—are more frequent than expected by chance, consistent with selective pressure tuning ASE at multiple regulatory steps. Finally, we parameterize alleles based on a range of properties and find that SNP location and predicted mRNA-structure stability are associated with translational ASE in cis. Since this analysis probes more than 4000 allelic pairs spanning a broad range of variations, our data provide a genome-wide view into the relative impact of cis elements that regulate translation.
Translation plays a pivotal role in determining levels of gene expression. In prokaryotes, ribosomes alone comprise nearly 25% of cellular mass (Bremer and Dennis 1996), and in rapidly growing yeast 60% of total gene expression is devoted to the synthesis of ribosomes (Warner 1999). An intricate network of trans-acting factors and cis-regulatory elements ensures that mRNAs are translated into proteins at the appropriate rate, location, and time (Preiss and Hentze 1999; Gebauer and Hentze 2004). Improper translation is linked to a variety of pathologies; for instance, mutations in trans regulators are linked to cancer (Stumpf and Ruggero 2011), and ribosomal-subunit haploinsufficiencies cause inherited anemias or specific loss of the spleen (Bolze et al. 2013).
A variety of cis elements embedded in mRNA sequences affect translation, and mutations in these sequences can cause disease (Jacobson et al. 2005; Barbosa et al. 2013). It is known that the Kozak sequence, upstream open reading frames (uORFs) in untranslated regions (UTRs), and mRNA tertiary structure all affect translational efficiency (Preiss and Hentze 1999; Gebauer and Hentze 2004; Gingold and Pilpel 2011). As expected, point mutations disrupting these features impact gene expression and consequently can result in a pathological phenotype. For example, a SNP in the 5′ UTR of MYC perturbs the structure of an internal ribosome entry site and leads to higher translational efficiency, which is associated with an increased likelihood of developing multiple myeloma (Stumpf and Ruggero 2011; Hsieh et al. 2012; Cunningham et al. 2013).
Until very recently, there have only been a few systems-level studies that have investigated how cis elements of mRNA affect translation, but they share in common two key features: a large panel of incrementally variant mRNAs and a quantitative assay to detect translational differences. For example, Plotkin and colleagues engineered a panel of 154 synonymous mRNA variants—each encoding a single GFP polypeptide—and used quantitative fluorescence measurements to assess translation, finding that mRNAs with high folding stability near the 5′ end tend to have lower translational efficiency (Kudla et al. 2009). Pursuing a very different strategy, Kruglyak and colleagues exploited the natural variation between alleles of 643 budding-yeast genes and quantitatively measured protein abundance using large-scale liquid chromatography–mass spectrometry, enabling dissection of the relative contributions of cis elements and trans regulators to expression levels (Khan et al. 2012). Such quantitative measurements of allele-specific expression (ASE) have the ability to reveal novel and general features of translational control as shown recently (Artieri and Fraser 2014; McManus et al. 2014), but thus far they have largely been applied to transcriptional studies (Ge et al. 2009; Pastinen 2010; Pickrell et al. 2010; Montgomery et al. 2010; Lefebvre et al. 2012).
Here we advance our understanding of the cis regulation of translation: Our panel of variant mRNAs comprises the allelic pairs of the entire Candida albicans genome, and our quantitative assay for translation is ribosome profiling (Ingolia et al. 2009; Brar et al. 2011). We chose C. albicans as a model for several reasons. First, the pathogenic budding yeast exists almost exclusively in a diploid state (Hickman et al. 2013); thus, unlike hybrid organisms used in other recent translational ASE studies (Artieri and Fraser 2014; McManus et al. 2014), the alleles in C. albicans will have evolved physiologically relevant interactions at the transcriptional and translational levels. Second, we recently assembled a completely phased diploid genome for C. albicans (Muzzey et al. 2013); thus, for the 54% of genes that have multiple SNPs, we can both pool and cross-validate the sequencing data across phased SNPs. Our data not only enable us to decipher some of the cis features that influence translational efficiency, but they also reveal the respective roles and interactions that transcription and translation have in determining a gene’s expression level.
Results
Measuring ASE in transcription and translation
We used RNA-seq and ribosome profiling to probe ASE at the transcriptional and translational levels, respectively. From two independent vegetatively growing wild-type C. albicans cultures in log phase, we prepared mRNA fragments (“mRNAs”) for RNA-seq and ribosome footprints (“FPs”) for ribosome profiling (Supplemental Fig. S1,2; Methods). Any read spanning a SNP contains information about allele-specific expression (Fig. 1A). We aligned reads to our phased diploid assembly of the C. albicans genome, requiring a perfect match at SNP positions in order to identify allele-specific reads. For each allele, we summed the mRNA and FP reads from both replicates across all SNPs; the allelic ratio of mRNA reads reflects transcriptional ASE, and the allelic ratio of translational efficiency (“TE” where TE = FP/mRNA) represents translational ASE.
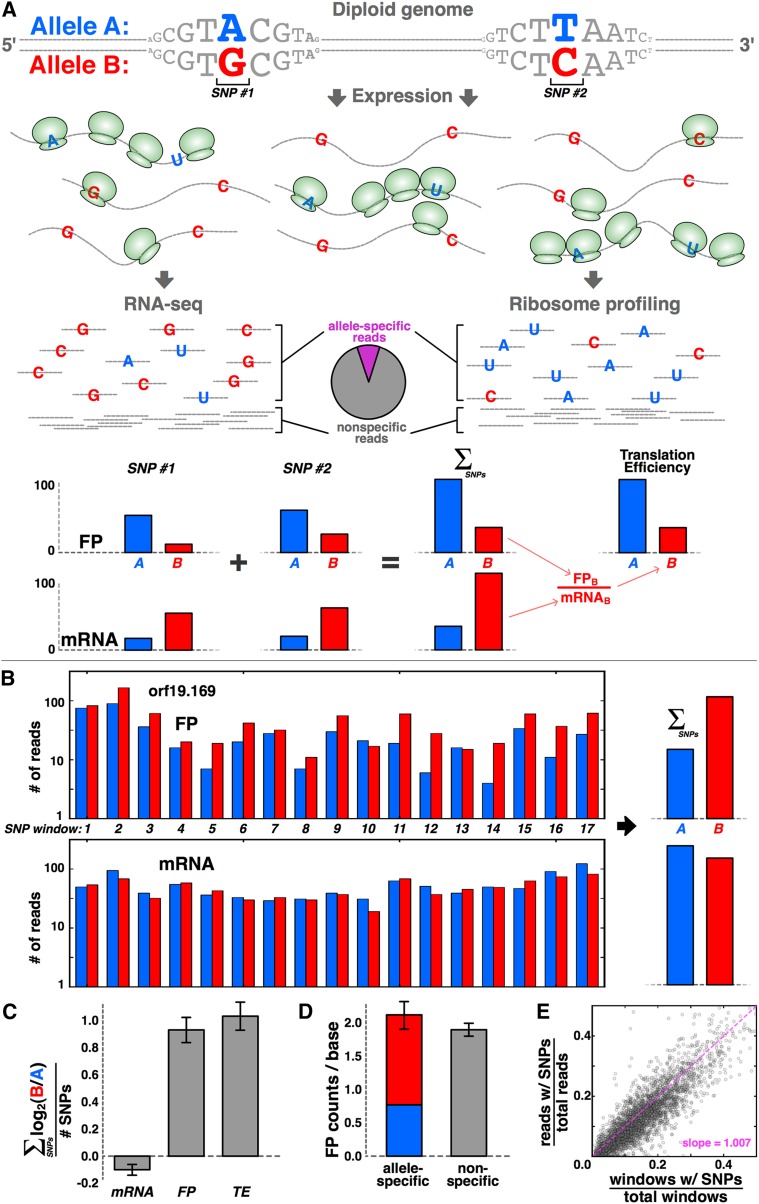
Figure 1.
Sensitively detecting ASE at translational level with ribosome profiling. (A) Schematic of the approach. For a given gene with two SNPs, transcripts from the B allele may be more abundant, whereas translation favors the A allele, as indicated by increased density of ribosomes, shown in green. These biases are revealed by RNA-seq and ribosome profiling, respectively. Allele-specific reads are summed across all SNPs in the gene, and translational efficiency (“TE”) is calculated from the mRNA and footprint (“FP”) levels. (B,C) Signal is consistent across many SNPs. There are 17 distinct SNP windows in orf19.169/CHO2, and the majority indicates a translational bias toward the B allele, but roughly equal transcript levels (B), with little error across SNPs (C); error bars, ±SEM. (D) The sum of allele-specific reads (red and blue bar) matches the level of nonspecific reads that do not include SNPs (gray bar) for orf19.169; error bars, ±SEM. (E) Across all genes, the fraction of SNP-containing reads corresponds strongly to the fraction of gene length comprised of SNP-containing windows.
We validated our data by several analyses. First, if our data were reliable, we would expect to observe a consistent ASE bias across many SNPs within the same gene. Figure 1B shows CHO2, a representative gene with 17 discrete SNP windows, where a SNP window contains all nucleotides that are 30 or fewer nucleotides upstream of a SNP, since—with our average read length of 30 nt—all such positions will contain allele-specific expression information. The sum across SNP windows indicates favored translation of the B allele and comparable transcription of both alleles. Importantly, these features are also apparent within the large majority (15 out of 17) of the 17 SNP windows (Fig. 1B,C). For CHO2, the agreement among SNP windows in terms of which allele was favored at the FP level was 88% (15/17 = 0.88); such agreement is very unlikely to occur if SNP windows randomly favored either allele (P = 0.0023, binomial test). Across all genes, we find average signal coherence across multiple SNPs of 80%–89% for mRNAs and 76%–80% for FPs (ranges depend on sequence coverage, with higher coverage giving higher coherence; see Methods). Coherence among FPs may be slightly lower than for mRNAs due to ribosome-progression effects: For instance, an allele with low overall TE relative to its homolog may nonetheless have higher FP signal in a particular SNP window if the sequence or structural features of the mRNA at that SNP window cause the ribosome to pause or slow down.
We next considered the impact of alignment error potentially arising from three sources: (1) allele-specific biases in library generation and sequencing, (2) inadequacies with the diploid genome assembly, and (3) errors in the scripts we used to process the data. We reasoned that such errors would manifest as systematic disparities between the levels of allele-specific reads and nonspecific reads. For instance, if our phased assembly only contained half of the real SNPs in the genome, then reads harboring the neglected SNPs would fail to align, leading to lower counts in our ostensibly nonspecific regions. We calculated the coverage by allele-specific reads and compared it with the level of coverage by the nonspecific reads that lack SNPs, and indeed they were closely matched for both CHO2 (Fig. 1D) (P > 0.05, KS test) and across all SNP-containing genes more generally (Fig. 1E) (regression slope = 1.007).
Assessing the significance of ASE
To determine which genes have significant translational ASE bias, we used a bootstrapping strategy. In assigning significance it is important to note that since our measurement of ASE involves a ratio of two sums, our calculations could be highly susceptible to noise. We wanted to distinguish among several scenarios, depicted schematically in Figure 2A for a mock gene with a single SNP. In particular, we aimed to differentiate those genes that have allelic bias reproducibly across allele-specific positions in the gene (scenario #1) from those whose calculation of TE is dominated by a minority of positions (scenario #2), or those that simply lack allelic bias (scenario #3).
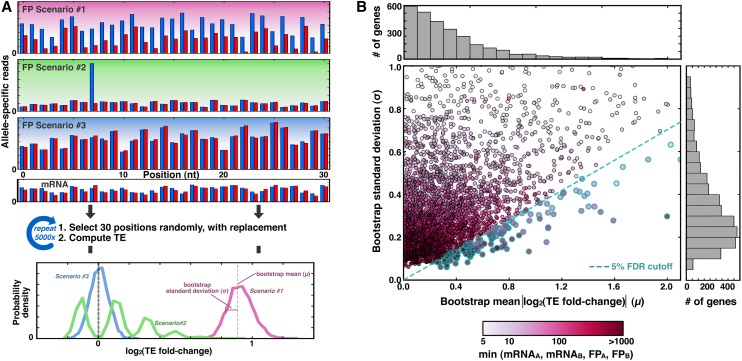
Figure 2.
A total of 4.2% of genes show translational allelic bias. (A) Schematic of the bootstrapping procedure. (Top) For a mock gene containing a single SNP, ∼30 consecutive positions contain allele-specific information, and three scenarios for read distributions are shown: (#1) shows reproducible bias toward allele A in blue; (#2) shows how a single position could suggest a bias that is not supported by other positions, and (#3) shows a consistently reported lack of bias. (Middle) For each of 5000 iterations, 30 positions are selected randomly and with replacement, and a TE value is calculated from the mRNA and FP reads from those positions. (Bottom) The results are tabulated into a histogram, where the mean and standard deviation of the bootstrap distribution reflect the magnitude and confidence, respectively, of allele-specific bias in TE. (B) Scatterplot and accompanying histograms (top and right) showing the bootstrap means and standard deviations for the 3285 genes with at least five reads for mRNAA, mRNAB, FPA, and FPB (shading indicates the metric with the fewest read counts, as shown in the legend at bottom). Blue-rimmed circles indicate genes that pass the 5% FDR threshold.
For each gene, we compiled the list of all nucleotide positions in SNP windows (i.e., all reads mapping to these positions contain allele-specific information) that span the open reading frame (see Methods). Since each SNP window is ∼30 nt in length, this list generally contained ∼30 positions per SNP window. For a list of length x, we next created 5000 new lists, each containing x positions that were chosen at random and with replacement from the original list. For each random list, the TE was calculated from the mRNA and FP reads at the randomly chosen positions and compiled into a “bootstrap distribution.” The bootstrap distribution shows the likelihood of a given ASE bias based on the empirically observed read counts. For scenarios #1 and #3, the bootstrap distributions are narrow, since nearly all positions have the same balance between FPA, FPB, mRNAA, and mRNAB. Thus, random lists comprised of these positions will tend to report similar TE values. Conversely, for scenario #2, the bootstrap distribution is wide, since the eighth position—which alone has strong allelic disparity—may be included once, many times, or not at all, in the random lists.
We used the means and standard deviations of the bootstrap distributions to classify whether or not genes have a significant translational ASE bias. The bootstrap distributions for the majority of genes in the genome have both low means and low standard deviations, consistent with a high confidence of no allelic bias (Fig. 2B, high gene density in lower left). However, a subset of genes has bootstrap distributions with means that are many standard deviations away from zero, suggestive of allelic bias. To identify such genes systematically, for each gene we calculated a P-value from a Z-score reflecting the number of standard deviations separating the bootstrap mean from zero. From the resulting distribution of P-values (Supplemental Fig. S3), we selected a cutoff such that the false-discovery rate is 5%. These analyses adjust for multiple hypothesis testing and revealed that 139 genes—4.2% of those tested—show strong and high-confidence allelic bias in TE. We used FuncAssociate (Berriz et al. 2003) and the Candida Genome Database GO Term Finder (Inglis et al. 2012) to identify significantly enriched functional categories among genes with allelic TE bias (see Methods) and found an unexpected abundance of nuclear-encoded transcripts for mitochondrially targeted proteins (FuncAssociate corrected P-value < 0.015; GO Term Finder corrected P-value < 0.007; see Discussion).
Transcription and translation have comparable effects on ASE
Since our data set measures ASE at both the transcriptional and translational levels, we sought to determine the relative ASE contributions of these two mechanisms. For genes with bootstrap standard deviations below 0.4 at the TE level (Fig. 2B), we compared the respective allelic levels of mRNA, FP, and TE (Fig. 3A–C) and further compiled these values into histograms that depict allelic log-fold-difference (“ALFD”) (Fig. 3D). The standard deviations of ASE differences between biological replicates were less than half of the respective standard deviations of the observed ALFD distributions (Fig. 3D; Supplemental Fig. S1), arguing against a common noise floor that similarly affects each distribution. Additionally, noise in ALFD from low-sequencing coverage is not a main driver of the distribution widths, since median read counts for genes at the extremities of the distributions are in excess of 50 (Supplemental Fig. S4).
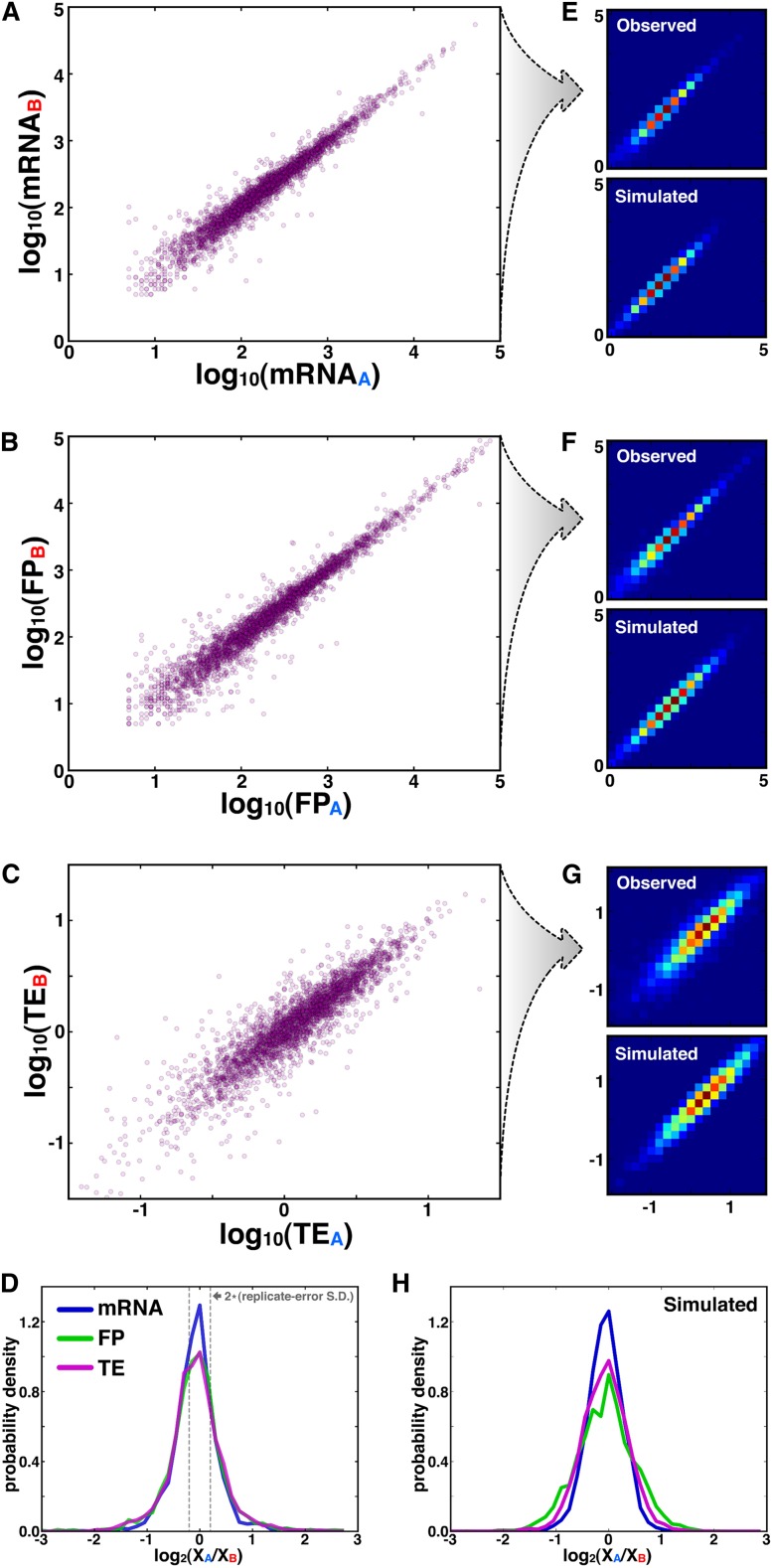
Figure 3.
ASE at translational level is as strong as at transcriptional level. (A–C) Scatterplots of the respective allelic levels of mRNA (A), FP (B), and TE (C). (D) Histograms of mRNAALFD, FPALFD, and TEALFD, where gray dotted lines indicate the two-standard-deviation boundary of error distributions from biological replicates (Supplemental Fig. S1). (E–G) Top panels show 2D heatmap PDFs of observed data from A–C, and bottom panels depict predicted data from simulation; cool and warm colors indicate lowly and highly populated bins, respectively. (H) Simulated data in E–G was used to plot histograms of mRNAALFD, FPALFD, and TEALFD.
The ALFD histograms for all three metrics were largely superimposable (P > 0.05 for all three pairwise comparisons among distributions, Mann-Whitney U-test), indicating that allelic variability at all three levels affects a comparable number of genes by a similar amount. However, interpreting the overlap in mRNAALFD, FPALFD, and TEALFD distributions is complicated by the fact that FP levels are a function of mRNA levels, and TE is a function of both FP and mRNA. Overlap between the FPALFD and mRNAALFD distributions could result trivially from a perfect correlation between mRNAALFD and FPALFD levels. However, such a perfect correlation would lead to a delta function for the TEALFD distribution, since TEALFD = FPALFD – mRNAALFD. If distributions for mRNAALFD and FPALFD overlapped but the values were uncorrelated, then the distribution width for TEALFD would be higher than the respective widths for mRNAALFD and FPALFD, since the variances for independent values would be additive. Indeed, the congruence among all three distributions reflects the positive but not perfect correlation (R = 0.50) that we observe between mRNAALFD and FPALFD levels.
To further explore our results, we implemented a simple simulation that models transcription and translation of two alleles (see Methods). In brief, for a given gene, we chose its transcriptional and translational propensities randomly from lognormal distributions. To get allelic values for mRNA and FP, we scaled the respective propensities by normally distributed noise terms to get mRNAA, mRNAB, FPA, and FPB values. The parameters for transcription were drawn directly from the empirical distribution in Figure 3A, and the mean translational propensity was derived from Figure 3B. Two fit parameters—one for the width of the lognormal translational propensity and the other for translational noise—allowed the model to match the dispersion of points in both the FP and TE 2D histograms (Fig. 3F,G). In total, the simulation corresponds well with the observed data both at the single-gene level (Fig. 3E–G) (R2 = 0.946; parameters listed in Supplemental Table S1) and in aggregate in the ALFD histograms (Fig. 3H), and we performed cross-validation to exclude the possibility of overfitting (Supplemental Fig. S5). As expected from the observed overlap in mRNAALFD and FPALFD distributions, the noise-strength parameters that drive allelic differences for transcription and translation in the model are of similar magnitude (0.16 and 0.2, respectively). Further, correlation between mRNAALFD and FPALFD is effectively built into the simulation by the fact that FPA is a function of mRNAA but not mRNAB, and vice versa. Thus, the overlap among ALFD distributions for mRNA, FP, and TE in both the observed data and the model arises from comparable levels of allelic variability in mRNA and FP, coupled with correlation between these two values.
Allelic TE bias tends to reinforce transcriptional bias more than expected by chance
Our measurements of ASE at both the transcriptional and translational levels allowed us to explore whether the two processes interact in a systematic fashion to influence allelic bias. For instance, allelic disparity at the transcriptional level that favors one allele may be offset by higher TE for the opposite allele, a compensatory interaction that stabilizes FP levels (Fig. 4A). Alternatively, if transcription and TE favor the same allele in a reinforcing manner, FP levels are highly disparate (Fig. 4B). We sought to assess the prevalence of such interactions from a scatter plot of mRNAALFD versus TEALFD (Fig. 4C), where genes with reinforcing interactions have fold changes of the same sign, and those with compensatory interactions have opposite signs. There is a negative correlation of −0.33 between the twofold changes, which would seem to suggest a prevalence of compensatory interactions, as reported recently from analysis of comparable plots (Artieri and Fraser 2014; McManus et al. 2014). However, since TEALFD is a monotonically decreasing function of mRNAALFD, this negative correlation is to be expected and must be factored into subsequent analyses of enrichment.
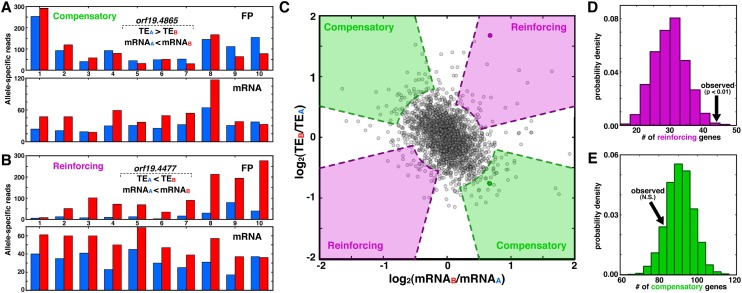
Figure 4.
Biases in transcription and translation are often coordinated, with interactions favoring compensation over reinforcing. (A,B) Specific examples of compensatory (A) and reinforcing (B) interactions between transcription and translation. Genes with compensatory interactions have higher allelic difference at the mRNA level than at the FP level, whereas those with reinforcing interactions differ more at the FP level than at the mRNA level. (C) Scatterplot of mRNAALFD and TEALFD levels, where genes from A and B are indicated as darkened circles, and shaded regions indicate compensatory and reinforcing interactions, as indicated. The purple and green regions’ curved portions reflect the two-standard-deviation spread of the data along the y = x and y = −x lines, respectively, and straight segments are based on a heuristic chosen to ensure that both the mRNAALFD and TEALFD values are nonzero (see Methods). (D,E) PDFs indicating the number of reinforcing (D) and compensatory (E) genes from permuted data; arrows indicate the number of genes from the observed data.
To determine whether compensatory or reinforcing interactions are enriched, we performed a permutation analysis. First, from the empirical plot in Figure 4C, we demarcated regions shown in purple and green that represent reinforcing and compensatory interactions, respectively. Next, we generated 1000 randomized null data sets in which the empirical mRNAALFD distribution was used to create randomized FP′ALFD and TE′ALFD distributions that match key features of the empirical data (e.g., mean, standard deviation, and correlation with mRNAALFD) but lack bias toward compensatory or reinforcing relationships (see Methods). From each randomized data set, we counted the number of genes in the compensatory and reinforcing colored regions and compiled the results into histograms (Fig. 4D,E). This analysis revealed that compensatory interactions are not more abundant than expected by chance. However, reinforcing interactions are significantly enriched (P < 0.01), suggesting that allele-specific bias can be coordinated at multiple expression levels, with a trend toward maximizing expression differences.
Identification of cis elements that affect translational efficiency
We sought to identify cis features of mRNAs that affect how well they are translated. Specifically, from our set of 2132 allelic pairs that have high-confidence measurements of allele-specific TE (i.e., all genes in Fig. 3), we wanted to determine sequence properties that distinguish genes with strong allelic bias in TE from those lacking such bias.
We first investigated how well codon bias might explain differences in allelic translational efficiency. We considered three gene sets based on their TEALFD values (Fig. 5A), calculated the codon adaptation indices (“CAI”) (Sharp and Li 1987) for alleles in each set, and found no significant disparity among the resulting distributions (Fig. 5B), consistent with codon bias playing a minor role, if any, in determining allelic TE bias in C. albicans. We similarly observed no correspondence between codon-pair bias and TEALFD (Supplemental Fig. S6).
Figure 5.
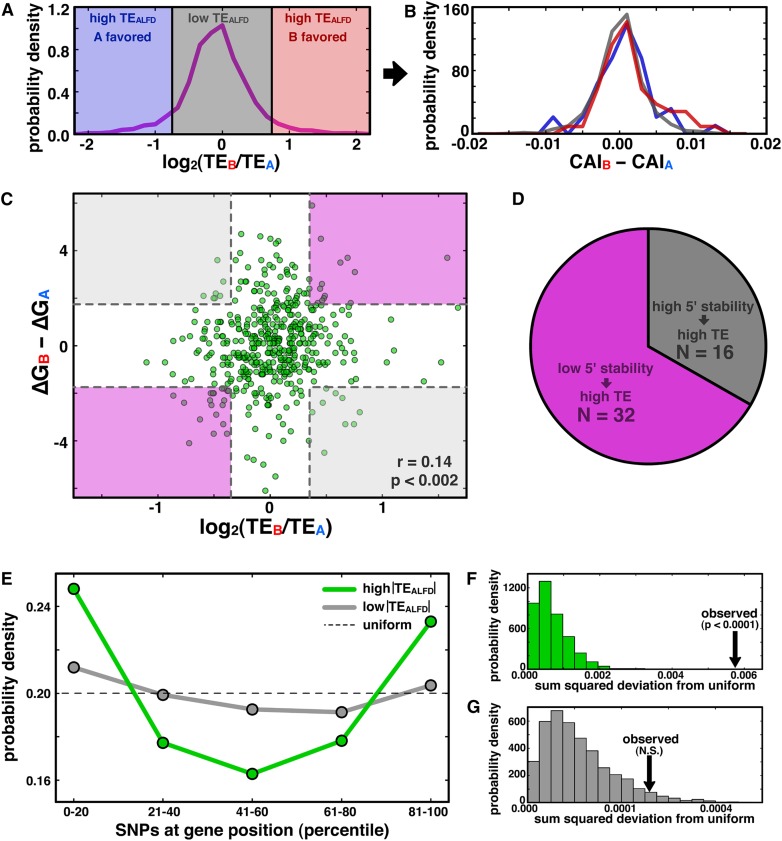
mRNA structure stability near start codon and SNP positioning near termini correlate with translational ASE bias. (A) Genes with high TEALFD are shaded in blue and red, and those with low TEALFD are shaded gray. (B) Allelic disparities in codon bias are not different among the gene sets in A. (C) Scatterplot of TEALFD versus the difference in predicted folding energy of the 60-nt window surrounding the start codon for all genes with at least one SNP in the window. Shading indicates regions that are at least one standard deviation away from zero on each axis, with purple regions representing the expected relationship between structure stability and TE, and gray indicating the unexpected relationship. (D) Pie chart quantifying the number of genes falling in each region demarcated in C. (E) PDF of SNP density as a function of position for genes with high (green) or low (gray) TEALFD (see Methods); the dashed line shows the uniform distribution. (F,G) PDFs indicating the sum-squared deviation from the uniform distribution from permutation analyses for genes with high (F) and low (G) TEALFD (see Methods); observed values indicated by black arrows.
We next considered whether the computed stability of mRNA structure near the start codon was predictive of TEALFD in C. albicans, since it has been found to play a role in bacteria (Kudla et al. 2009). We focused on the 60-nt window centered on the start codon; for each allele with at least one SNP in this window, we used Mfold (Zuker 2003) to predict the potential mRNA-folding structures. Figure 5C shows TEALFD versus the difference in folding energy for the most stable structure predicted for each allele. There is a weak but significant correlation between these quantities (Pearson correlation = 0.14, P < 0.002), and we also observe that the number of allelic pairs with the expected relationship between 5′ stability and TEALFD is twofold greater than the number with the unexpected relationship (Fig. 5D). These data are consistent with previous observations from E. coli, but they show a weaker effect and argue that stability around the start codon is not sufficient to explain the majority of translational ASE bias.
Finally, we explored how SNP position along the mRNA affects allelic TE bias. Using the gene boundaries defined from our ribosome-density data (see Methods), we divided the gene length into five equal-size bins, and compiled probability density functions (PDFs) of SNP location for each gene. These PDFs for genes with high or low |TEALFD| values were separately summed and again normalized to yield averaged PDFs (Fig. 5E; see Methods) that allow comparison of the respective groups’ SNP-location distributions in aggregate. Among genes with high |TEALFD|, we observed high SNP density in the 5′- and 3′-proximal quintiles of the averaged PDF, whereas genes with low |TEALFD| appear to have roughly uniform SNP positioning (the number of SNPs per gene was not significantly different between the high- and low-|TEALFD| sets; Supplemental Fig. S7). Using permutation tests, we first assessed whether these averaged PDFs differed from each other and next considered whether they were different from a uniform distribution. Relative to the averaged PDFs from randomly subsampled gene subsets of the low-|TEALFD| set (see Methods), we found that the high-|TEALFD| averaged PDF has a significantly elevated sum-squared deviation from the low-|TEALFD| averaged PDF (P < 0.001; Supplemental Fig. S8), arguing that the two averaged PDFs are different. Next, we examined whether these averaged PDFs differed significantly from a uniform distribution (Fig. 5E; see Methods): High |TEALFD| significantly differed from randomly permuted data (P < 0.0001) (Fig. 5F), but the distribution of SNPs within genes with low allelic TE bias did not deviate significantly from a uniform distribution (P > 0.05) (Fig. 5G). Taken together, these results are consistent with |TEALFD| arising from an enrichment of SNPs near the termini of the ribosome’s path along an mRNA.
Discussion
Expression variation among alleles in diploid organisms is important for both clinical and research applications. Studies of allele-specific expression have appreciably advanced our understanding of transcriptional control, both in cis and trans. Here we have performed the first highly sensitive, genome-wide, allele-specific assays of both transcription and translation in a natural organism. Though previous sequencing-based assays of allele-specific expression have been cast in doubt due to inconsistencies in signal across SNPs of the same gene (Gregg et al. 2010; DeVeale et al. 2012; Kelsey and Bartolomei 2012), our RNA-seq and ribosome profiling data sets have high consistency across phased SNPs within a gene. The reproducibility across biological replicates further supports the quality of our data, and we were careful to filter genes using our bootstrapping approach to ensure that our analyses focused on genes with high-confidence measures of ASE.
There is consensus between our work and two recent investigations of translational ASE (Artieri and Fraser 2014; McManus et al. 2014) that the prevalence and magnitude of ASE bias are similar for both transcription and translation. In our data, this is indicated both by the overlap among the ALFD distributions of mRNA, FP, and TE and by the allelic-bias parameters of our simulation. Among the many implications of this observation is that the steps are not optimized for specific size biases. In other words, for a gene to achieve a particular allelic expression bias, either its transcriptional or translational control can be tuned. Given their comparable magnitude, we anticipated that there would be widespread compensation between transcription and translation, such that alleles tend to be comparably expressed. However, statistical analysis using our null model indicated that compensatory interactions were no more prevalent than expected by chance, and instead it is the reinforcing interactions that were overrepresented. Though we found no functional enrichments among the reinforcing genes, it will be interesting to attribute the transcriptional and translational effects to particular SNPs, to assess their evolutionary history, and to determine whether the reinforcing interaction confers a fitness advantage to the cell.
A priori, we expected allelic bias at the translational level to be indiscriminate with respect to function, and thus we were surprised to see enrichment for allelic bias among genes with mitochondrial roles. Importantly, our analyses only considered genes encoded on the eight nuclear chromosomes, not those in the mitochondrial genome. Since mitochondrial genomes are known to be fast evolving relative to nuclear genomes (Brown et al. 1979), we speculate that mitochondrially targeted proteins encoded on the nuclear chromosomes may need to evolve at a similarly rapid rate to keep pace functionally with their counterparts encoded in the mitochondrial genome. This possible source of evolutionary pressure may manifest as the observed ASE bias, and, interestingly, this ASE bias is restricted to translational control, since mRNA allelic variability was the same for mitochondrial genes as for other genes.
Resolving all of the cis determinants of translational control is beyond the scope of a single study, but our work reveals a few important pieces of information. For instance, codon bias appears not to be a major factor in driving translational ASE in C. albicans. This finding differs from the observation in hybrids of Saccharomyces cerevisiae and Saccharomyces paradoxus (Artieri and Fraser 2014; McManus et al. 2014), where codon bias differences between alleles were reported to correlate with allelic bias in TE. We expect that the discrepancy arises from the fact that SNPs are far less common in C. albicans (one per 283 coding bases) (Muzzey et al. 2013) than in the interspecific hybrid (one per 10 coding bases) (Kellis et al. 2003); therefore, the dynamic range of codon-usage-bias differences in C. albicans is sufficiently low that any signal is obscured by noise.
Our results are consistent with recent findings (Dvir et al. 2013; Shah et al. 2013; Artieri and Fraser 2014) showing that sequence diversity near the 5′ end of a transcript—especially variations that affect the stability of mRNA structure near the start codon—affect allelic TE bias, likely by impacting initiation. However, we also observed significant enrichment of SNPs near the 3′ ends of genes that exhibit high allelic TE bias. We argue that these 3′-proximal SNPs are not exerting their effect on allelic TE bias via impaired ribosome progression, since our ASE signal was highly coherent in SNP windows across entire genes, and genes with strong bias contributions from a minority of SNP windows were filtered out by our bootstrapping analysis. Thus, we postulate that the 3′-proximal SNPs affect allelic TE bias by impacting reinitiation of translation. It is well established that poly(A)-binding proteins at the 3′ end interact with translation-initiation factors at the 5′ end to stimulate initiation (Imataka et al. 1998; Mangus et al. 2003), and recent reports find that factors binding 3′-UTRs upstream of the poly(A) tail can also enhance initiation (Bai et al. 2013; Lee et al. 2014). Thus, SNPs causing disparity between 3′-proximal sequences of alleles may affect allelic TE bias via 3′-mediated differences in initiation efficiency.
It is likely that each gene’s ASE bias is a combination of multiple determinants, many of which we may not have yet identified. Resolving the effect of mRNA secondary structure on allele-specific TE will be greatly facilitated by recent techniques that probe RNA structure genome-wide (Rouskin et al. 2014; Wan et al. 2014). However, for SNPs that do not affect mRNA structure, it is likely that the variants in cis sequences alter the interaction with trans factors in a way that influences ASE. Thus, additional work will be needed to search for disrupted RNA-binding protein motifs in alleles with high translational ASE bias and to verify a role for RNA-binding proteins via perturbation of the trans-factor composition of the cell. C. albicans is a well-suited model organism for these trans-factor perturbations because it can exist as a homozygous diploid for certain chromosomes (thereby only expressing a subset of trans-factor alleles), or as a haploid amenable to genetic manipulation (Hickman et al. 2013). Future studies of both cis- and trans-regulation of ASE also have a promising future in human cells, where the number of phased genomes is growing rapidly (Ma et al. 2010; Fan et al. 2011; Peters et al. 2012) and haploid cell lines are now available (Carette et al. 2009).
Methods
RNA-seq and ribosome profiling
Libraries for RNA-seq and ribosome profiling from the SC5314 strain of C. albicans were prepared as described in Brar et al. (2011), with a few exceptions. Cells were harvested via filtration in a 30°C room and then flash frozen in liquid nitrogen without the pretreatment of a translational inhibitor. To guard against post-lysis translation in the ribosome-profiling sample, we supplemented the lysis buffer with 50 µg/mL GMPPNP and 10 µg/mL Blasticidin S (InvivoGen), since cycloheximide does not affect the ribosomes of C. albicans (Yamaguchi and Iwata 1970). Oligos used for rRNA subtraction are listed in Supplemental Table S2. Deep sequencing was performed on the Illumina Genome Analyzer IIx and HiSeq 2000. Reads from the two biological replicates were pooled to enhance total signal.
Alignment
Reads were aligned using Bowtie v0.12.7 (Langmead et al. 2009), allowing no mismatches but up to 16 match locations per read. The Bowtie library was built from the diploid FASTA file of the C. albicans genome containing SNPs but not indels (Muzzey et al. 2013); indels are almost exclusively noncoding and were excluded to facilitate analysis. Custom programs in C and scripts in PHP were used to parse Bowtie output and assign reads to their respective alleles based on their SNP composition. To minimize cloning-bias artifacts, reads in which the SNP occurred at the first or last position were not assigned to a particular allele. A two-state, strand-specific hidden Markov model (“HMM”) was used to delineate gene boundaries based on our observed FP sequencing data. This unsupervised method of gene-boundary detection was used to enhance ASE signal measurements by maximizing the number of nucleotide positions that have FP density contiguous with a gene’s annotated coding region. Thus, the HMM performs two main functions. First, it corrects for misannotations in gene boundaries that could underestimate gene length and thereby compromise the accuracy of ASE measurements. Second, since FP reads range in length from 28 to 32 nt and were mapped to the genome based on their 5′ ends as in Ingolia et al. (2009), the HMM automatically accounts for the fact that there is a variable offset between the 5′ end of a read and the part of the read that was in the P site; rather than readjust 5′-end alignment positions by subtracting a fixed and potentially flawed offset value to approximate the P-site position, the HMM simply identifies the empirical gene boundary based on the density of the 5′ ends of reads. The HMM had two states—“Coding” and “Noncoding”—and focused only on strand-specific FP reads, since FP regions are embedded within mRNA regions by definition. For simplicity, it converted the FP signal to a binary string, where positions with zero read counts were called “0” and those with nonzero read counts were assigned “1.” Transition and emission probabilities were tuned with two considerations: (1) maximizing the number of open-reading frames spanned by a single, contiguous “Coding” region, and (2) minimizing the number of contiguous “Coding” regions that spanned multiple open-reading frames. The parameters noted in Table 1 were used in the final HMM, with performance illustrated in Supplemental Fig. S9:
Table 1.
Parameters used in the final HMM

A gene’s final boundaries were determined as follows:
5′ boundary: If the start-codon position from the Assembly 21 GFF file ([Inglis et al. 2012] and http://www.candidagenome.org/) was embedded in an HMM-identified “Coding” region, the 5′ end of the “Coding” region was used; otherwise the start-codon position was used.
3′ boundary: If the stop codon was embedded in an HMM-identified “Coding” region, the 3′ end of the “Coding” region was used; otherwise the stop-codon position was used.
In general, the HMM-demarcated boundaries differed little from the annotated gene boundaries, with a median length increase of 1.7%. Read counts per gene are included in Supplemental Table 3.
Signal coherence across SNPs
The main goal of our assessment of signal agreement across SNPs is to ensure that SNPs reporting a large mRNA or FP bias in favor of one allele do not reside in the same gene as other SNPs strongly favoring the opposite allele. To this end, we restricted our analysis to genes where at least 75% of SNPs each report an allelic difference of 25% or more, giving 185 genes at the mRNA level and 320 genes at the FP level. For such genes, we counted the number of all SNPs that favor the A allele and divided by the total number of SNPs in the gene to get the A-allele coherence. We calculated the B-allele coherence as 1-(A-allele coherence) and called the gene’s SNP coherence the maximum of the A-allele and B-allele coherence values. We evaluated signal coherence at two different coverage thresholds. The first threshold required min(mRNAA, mRNAB, FPA, FPB) > 5, giving 540 and 754 genes, respectively, for mRNA and FP coherence analysis. The other threshold required minimum coverage of at least 20 reads, giving 185 and 320 genes, respectively, for mRNA and FP analyses.
Bootstrapping
Bootstrapping was performed for all genes specified in the C. albicans Assembly 21 GFF file (http://www.candidagenome.org/) with custom PHP scripts using the algorithm described in the main text. For each gene, the results from the 5000 iterations were written to a text file and processed in batch with Python to get the mean and standard deviation of bootstrap distributions. These data were then analyzed in Excel. Bootstrapping means and standard deviations are included in Supplemental Table 3.
Functional enrichment analysis
We performed two functional-enrichment tests, one on the set of genes shown to have strong ASE bias in TE at a 5% FDR (N = 139), and a larger set in which we included the top 1000 genes based on their Z-score (i.e., how many standard deviations the bootstrap mean is from zero). The gene universe was all genes for which min(mRNAA, mRNAB, FPA, FPB) > 5 reads (N = 3285 genes). The large set—but not the small set—had significant functional enrichments after correcting for multiple hypothesis testing in FuncAssociate (Berriz et al. 2003) and on the GO Term Finder on the Candida Genome Database (Inglis et al. 2012).
Simulation and fitting
The stochastic simulation was implemented and fit using a custom Python script with the following equations:
where ntxn and ntnl are the log-normally distributed transcription and translation propensities, respectively; k1 and k2 are the mean and standard deviation of the normal distribution exponentiated to yield ntxn, and k4 and k5 are the corresponding parameters for ntnl; k3 and k6 represent the allelic noise variables for transcription and translation, respectively; finally, randn() is a normally distributed random variable with mean 0 and variance of 1. Only k5 and k6 were fit parameters; the others were calculated directly from the data as follows: k1 is the mean of the empirical ln(mRNA) data (Fig. 3A); k2 is the standard deviation of the ln(mRNA) data (Fig. 3B); k3 is the standard deviation of the distances of ln(mRNA) data from y = x (Fig. 3A), and k4 is the mean of the ln(FP) data divided by k1 (Fig. 3B). All parameter values are summarized in Supplemental Table S1. Each run of the simulation iteratively executed equations 1 through 8 3285 times, once for each gene in the observed data set. The mRNA, FP, and TE allelic log-fold differences were then plotted as a 2D PDF, shown as heatmaps in Figure 3, E–G. Error for a single run of the simulation was calculated as the sum of squared differences between the simulated and observed values for each bin in the heatmap grids shown in Figure 3, E–G. For each set of parameter values k5 and k6 (each parameter sampled over the range [0,5]), the model was run 10 times to yield an average error, and the parameters generating the smallest average error are reported in Supplemental Table S1, and correspondence between the observed and fit data is in Supplemental Figure S5.
Significance testing of compensatory and reinforcing interactions
For each gene i with observed allelic log-fold difference (“ALFD”) value of mRNAALFD[i], a random FPALFD[j] (with j ≠ i) was selected from the empirical FPALFD distribution and then scaled to yield FP′ALFD[i] such that the correlation between mRNAALFD and FP′ALFD matched the observed correlation between mRNAALFD and FPALFD (r = 0.50) using the following equation: FP′ALFD[i] = r * mRNAALFD[i] + (1 − r2) * FPALFD[j]. Importantly, after this scaling, the mean and standard deviation of FPALFD and FP′ALFD are equivalent. Finally, we calculated TE′ALFD[i] = mRNAALFD[i] – FP′ALFD[i]. The number of genes falling in shaded regions delineated in Figure 4C were counted from the scatterplot of mRNAALFD and TE′LFD. These regions were specified based on the spread of the observed data. Specifically, for compensatory shaded regions, all datapoints were projected onto the line y = −x, the standard deviation of the projected data was calculated, and the green shaded region indicates distances of at least two standard deviations from the origin. For reinforcing interactions, corresponding steps were performed after the data were projected onto the line y = x. Finally, we imposed the heuristic requirement that abs(log10(abs(mRNAALFD[i] / TEALFD[i]))) < 0.5 such that we focus specifically on genes for which both mRNAALFD and TEALFD change.
CAI and mRNA structure prediction
With a custom PHP script, CAI and codon-pair-bias scores were calculated for each gene using their frequencies in coding genes. mRNA structure predictions were generated using Quikfold (http://mfold.rna.albany.edu/?q=DINAMelt/Quickfold), with the output processed with custom scripts.
SNP positional enrichment at 5′ and 3′ ends
Two hundred genes with TEALFD > 0.58 (a 50% difference between alleles) were defined as the “high |TEALFD|” group, and the 1000 genes with lowest |TEALFD| were defined as the “low |TEALFD|” group. In each group, for each gene with at least three SNPs a five-bin PDF of SNP location was calculated, and all such PDFs were summed and normalized to yield the averaged PDFs in Figure 5E. Deviation of averaged PDFs from the uniform distribution was determined by tabulating the empirical number of genes with at least three SNPs from each group (i.e., 200 genes in the high TEALFD group and 1000 genes in the low TEALFD group) as well as their empirical number of SNPs per gene, and then generating random single-gene PDFs based on uniform distribution of SNPs among the bins. As with the empirical data, these random PDFs were summed, normalized, and then compared with a uniform distribution using the sum-squared deviation across the five bins. Ten thousand iterations of this procedure for each group yielded the distributions in Figure 5, F and G. Deviation of the two averaged PDFs from each other was determined by creating 1000 random subsampled sets from the low-|TEALFD| group (N = 1000), with each subsampled set having 200 genes such that the subsampled sets had the same number of genes as the high-|TEALFD| group (N = 200 genes). For averaged PDFs from all subsampled sets as well as the high-|TEALFD| group, the sum-squared deviation was calculated relative to the averaged PDF of the entire low-|TEALFD| group (i.e., gray trace in Fig. 5E) and shown in Supplemental Fig. S8.
Data access
All raw and processed data from this study have been submitted to the NCBI Gene Expression Omnibus (GEO; http://www.ncbi.nlm.nih.gov/geo/) under accession number GSE52236.
Acknowledgments
We thank Suzanne Komili, Frank Albert, and Leonid Kruglyak for helpful advice, and Murat Tasan and Fritz Roth for FuncAssociate support. D.M. is an HHMI Fellow of the Damon Runyon Cancer Research Foundation. This work was also supported by the Howard Hughes Medical Institute (J.S.W.) and NIH grants R01-HG003468 (G.S.) and R01-DE015873 (G.S.).
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.166322.113.
References
- Artieri CG, Fraser HB 2014. Evolution at two levels of gene expression in yeast. Genome Res 24: 411–421 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai Y, Zhou K, Doudna JA 2013. Hepatitis C virus 3′UTR regulates viral translation through direct interactions with the host translation machinery. Nucleic Acids Res 41: 7861–7874 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbosa C, Peixeiro I, Romão L 2013. Gene expression regulation by upstream open reading frames and human disease. PLoS Genet 9: e1003529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berriz GF, King OD, Bryant B, Sander C, Roth FP 2003. Characterizing gene sets with FuncAssociate. Bioinformatics 19: 2502–2504 [DOI] [PubMed] [Google Scholar]
- Bolze A, Mahlaoui N, Byun M, Turner B, Trede N, Ellis SR, Abhyankar A, Itan Y, Patin E, Brebner S, et al. 2013. Ribosomal protein SA haploinsufficiency in humans with isolated congenital asplenia. Science 340: 976–978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brar GA, Yassour M, Friedman N, Regev A, Ingolia NT, Weissman JS 2011. High-resolution view of the yeast meiotic program revealed by ribosome profiling. Science 335: 552–557 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bremer H, Dennis PP 1996. Modulation of chemical composition and other parameters of the cell by growth rate. In Escherichia coli and Salmonella typhimurium: cellular and molecular biology (ed. Neidhard FC, et al.), Vol. 2, pp. 1553–1569. ASM Press, Washington, DC [Google Scholar]
- Brown WM, George M, Wilson AC 1979. Rapid evolution of animal mitochondrial DNA. Proc Natl Acad Sci 76: 1967–1971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carette JE, Guimaraes CP, Varadarajan M, Park AS, Wuethrich I, Godarova A, Kotecki M, Cochran BH, Spooner E, Ploegh HL, et al. 2009. Haploid genetic screens in human cells identify host factors used by pathogens. Science 326: 1231–1235 [DOI] [PubMed] [Google Scholar]
- Cunningham JT, Pourdehnad M, Stumpf CR, Ruggero D 2013. Investigating myc-dependent translational regulation in normal and cancer cells. Methods Mol Biol 1012: 201–212 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeVeale B, van der Kooy D, Babak T 2012. Critical evaluation of imprinted gene expression by RNA-Seq: a new perspective. PLoS Genet 8: e1002600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dvir S, Velten L, Sharon E, Zeevi D, Carey LB, Weinberger A, Segal E 2013. Deciphering the rules by which 5′-UTR sequences affect protein expression in yeast. Proc Natl Acad Sci 110: E2792–E2801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan HC, Wang J, Potanina A, Quake SR 2011. Whole-genome molecular haplotyping of single cells. Nat Biotechnol 29: 51–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge B, Pokholok DK, Kwan T, Grundberg E, Morcos L, Verlaan DJ, Le J, Koka V, Lam KCL, Gagné V, et al. 2009. Global patterns of cis variation in human cells revealed by high-density allelic expression analysis. Nat Genet 41: 1216–1222 [DOI] [PubMed] [Google Scholar]
- Gebauer F, Hentze MW 2004. Molecular mechanisms of translational control. Nat Rev Mol Cell Biol 5: 827–835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gingold H, Pilpel Y 2011. Determinants of translation efficiency and accuracy. Mol Syst Biol 7: 481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregg C, Zhang J, Weissbourd B, Luo S, Schroth GP, Haig D, Dulac C 2010. High-resolution analysis of parent-of-origin allelic expression in the mouse brain. Science 329: 643–648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickman MA, Zeng G, Forche A, Hirakawa MP, Abbey D, Harrison BD, Wang Y-M, Su C-H, Bennett RJ, Wang Y, et al. 2013. The “obligate diploid” Candida albicans forms mating-competent haploids. Nature 494: 55–59 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh AC, Liu Y, Edlind MP, Ingolia NT, Janes MR, Sher A, Shi EY, Stumpf CR, Christensen C, Bonham MJ, et al. 2012. The translational landscape of mTOR signalling steers cancer initiation and metastasis. Nature 485: 55–61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imataka H, Gradi A, Sonenberg N 1998. A newly identified N-terminal amino acid sequence of human eIF4G binds poly(A)-binding protein and functions in poly(A)-dependent translation. EMBO J 17: 7480–7489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inglis DO, Arnaud MB, Binkley J, Shah P, Skrzypek MS, Wymore F, Binkley G, Miyasato SR, Simison M, Sherlock G 2012. The Candida genome database incorporates multiple Candida species: multispecies search and analysis tools with curated gene and protein information for Candida albicans and Candida glabrata. Nucleic Acids Res 40: D667–D674 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingolia NT, Ghaemmaghami S, Newman JRS, Weissman JS 2009. Genome-wide analysis in vivo of translation with nucleotide resolution using ribosome profiling. Science 324: 218–223 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobson EM, Concepcion E, Oashi T, Tomer Y 2005. A Graves’ disease-associated Kozak sequence single-nucleotide polymorphism enhances the efficiency of CD40 gene translation: a case for translational pathophysiology. Endocrinology 146: 2684–2691 [DOI] [PubMed] [Google Scholar]
- Kellis M, Patterson N, Endrizzi M, Birren B, Lander ES 2003. Sequencing and comparison of yeast species to identify genes and regulatory elements. Nature 423: 241–254 [DOI] [PubMed] [Google Scholar]
- Kelsey G, Bartolomei MS 2012. Imprinted genes … and the number is? PLoS Genet 8: e1002601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan Z, Bloom JS, Amini S, Singh M, Perlman DH, Caudy AA, Kruglyak L 2012. Quantitative measurement of allele-specific protein expression in a diploid yeast hybrid by LC-MS. Mol Syst Biol 8: 602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kudla G, Murray AW, Tollervey D, Plotkin JB 2009. Coding-sequence determinants of gene expression in Escherichia coli. Science 324: 255–258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B, Trapnell C, Pop M, Salzberg SL 2009. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol 10: R25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K-H, Kim S-H, Kim H-J, Kim W, Lee H-R, Jung Y, Choi J-H, Hong KY, Jang SK, Kim K-T 2014. AUF1 contributes to Cryptochrome1 mRNA degradation and rhythmic translation. Nucleic Acids Res 42: 3590–3606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefebvre JF, Vello E, Ge B, Montgomery SB, Dermitzakis ET, Pastinen T, Labuda D 2012. Genotype-based test in mapping cis-regulatory variants from allele-specific expression data. PLoS ONE 7: e38667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma L, Xiao Y, Huang H, Wang Q, Rao W, Feng Y, Zhang K, Song Q 2010. Direct determination of molecular haplotypes by chromosome microdissection. Nat Methods 7: 299–301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangus DA, Evans MC, Jacobson A 2003. Poly(A)-binding proteins: multifunctional scaffolds for the post-transcriptional control of gene expression. Genome Biol 4: 223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McManus J, May GE, Spealman P, Shteyman A 2014. Ribosome profiling reveals post-transcriptional buffering of divergent gene expression in yeast. Genome Res 24: 422–430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montgomery SB, Sammeth M, Gutierrez-Arcelus M, Lach RP, Ingle C, Nisbett J, Guigo R, Dermitzakis ET 2010. Transcriptome genetics using second generation sequencing in a Caucasian population. Nature 464: 773–777 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muzzey D, Schwartz K, Weissman JS, Sherlock G 2013. Assembly of a phased diploid Candida albicans genome facilitates allele-specific measurements and provides a simple model for repeat and indel structure. Genome Biol 14: R97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pastinen T 2010. Genome-wide allele-specific analysis: insights into regulatory variation. Nat Rev Genet 11: 533–538 [DOI] [PubMed] [Google Scholar]
- Peters BA, Kermani BG, Sparks AB, Alferov O, Hong P, Alexeev A, Jiang Y, Dahl F, Tang YT, Haas J, et al. 2012. Accurate whole-genome sequencing and haplotyping from 10 to 20 human cells. Nature 487: 190–195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell JK, Marioni JC, Pai AA, Degner JF, Engelhardt BE, Nkadori E, Veyrieras J-B, Stephens M, Gilad Y, Pritchard JK 2010. Understanding mechanisms underlying human gene expression variation with RNA sequencing. Nature 464: 768–772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preiss T, Hentze MW 1999. From factors to mechanisms: translation and translational control in eukaryotes. Curr Opin Genet Dev 9: 515–521 [DOI] [PubMed] [Google Scholar]
- Rouskin S, Zubradt M, Washietl S, Kellis M, Weissman JS 2014. Genome-wide probing of RNA structure reveals active unfolding of mRNA structures in vivo. Nature 505: 701–705 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah P, Ding Y, Niemczyk M, Kudla G, Plotkin JB 2013. Rate-limiting steps in yeast protein translation. Cell 153: 1589–1601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp PM, Li WH 1987. The codon Adaptation Index–a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res 15: 1281–1295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stumpf CR, Ruggero D 2011. The cancerous translation apparatus. Curr Opin Genet Dev 21: 474–483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan Y, Qu K, Zhang QC, Flynn RA, Manor O, Ouyang Z, Zhang J, Spitale RC, Snyder MP, Segal E, et al. 2014. Landscape and variation of RNA secondary structure across the human transcriptome. Nature 505: 706–709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warner JR 1999. The economics of ribosome biosynthesis in yeast. Trends Biochem Sci 24: 437–440 [DOI] [PubMed] [Google Scholar]
- Yamaguchi H, Iwata K 1970. In vitro and in vivo protein synthesis in Candida albicans. 3. Protein synthesis and inhibition. Sabouraudia 8: 201–211 [PubMed] [Google Scholar]
- Zuker M 2003. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res 31: 3406–3415 [DOI] [PMC free article] [PubMed] [Google Scholar]