Abstract
Introduction
The transcatheter mitral valve repair (TMVR) technique utilizes a stent to cinch a segment of the mitral annulus (MA) and reduces mitral regurgitation. The cinching mechanism results in reduction of the septal-lateral distance. However, the mechanism has not been characterized completely. In this study, a method was developed to quantify the relation between cinching tension and MA area in an ex vivo ovine model.
Method
The cinching tension was measured from a suture inserted within the coronary sinus (CS) vessel with one end tied to the distal end of the vessel and the other end exited to the CS ostium where it was attached to a force transducer on a linear stage. The cinching tension, MA area, septal-lateral (S-L) and commissure-commissure (C-C) diameters and leakage was simultaneously measured in normal and dilated condition, under a hydrostatic left ventricular pressure of 90 mmHg.
Results
The MA area was increased up to 22.8% after MA dilation. A mean tension of 2.1 ± 0.5 N reduced the MA area by 21.3 ± 5.6% and S-L diameter by 24.2 ± 5.3%. Thus, leakage was improved by 51.7 ± 16.2 % following restoration of normal MA geometry.
Conclusion
The cinching tension generated by the suture acts as a compensation force in MA reduction, implying the maximum tension needed to be generated by annuloplasty device to restore normal annular size. The relationship between cinching tension and the corresponding MA geometry will contribute to the development of future TMVR devices and understanding of myocardial contraction function.
Introduction
Functional mitral regurgitation (MR) is associated with mitral annular dilation and alternations in subvalvular apparatus such as papillary muscular displacement. Annuloplasty is the most common repair procedure to correct functional MR. Recently, the development of transcatheter mitral valve repair (TMVR) offers a great promise for patients who cannot undergo surgery due to its minimally invasive approach. One of the TMVR techniques utilizes the proximal location of the coronary sinus (CS) to the mitral annulus (MA) to deploy a TMVR device within the CS and the great cardiac vein (GCV) (Fig.1). When the device contracts, it indirectly reshapes the MA by shortening the septal-lateral direction to decrease MR (Deharrera and Sun, 2007). Several TMVR devices have been developed including Viacor (Viacor, Inc.), Carillon (Cardiac Dimensions, LLC) and Monarc System (Edwards Lifesciences, Inc.). Animal studies have demonstrated the short term effectiveness of TMVR devices to reduce MR (Condado and Velez-Gimon, 2003; Kaye et al., 2003a; Maniu et al., 2004). However, the initial outcomes from human trials were suboptimal (Duffy et al., 2006; Harnek et al., 2011; Sack et al., 2009; Siminiak et al., 2009b; Webb et al., 2006) with report of adverse events including compression of the left circumflex artery, vessel perforation, device migration and fracture (Duffy et al., 2006; Hoppe et al., 2009; Siminiak et al., 2007; Siminiak et al., 2009a; Webb et al., 2006). As a result, TMVR devices are not yet commercialized.
Figure 1.
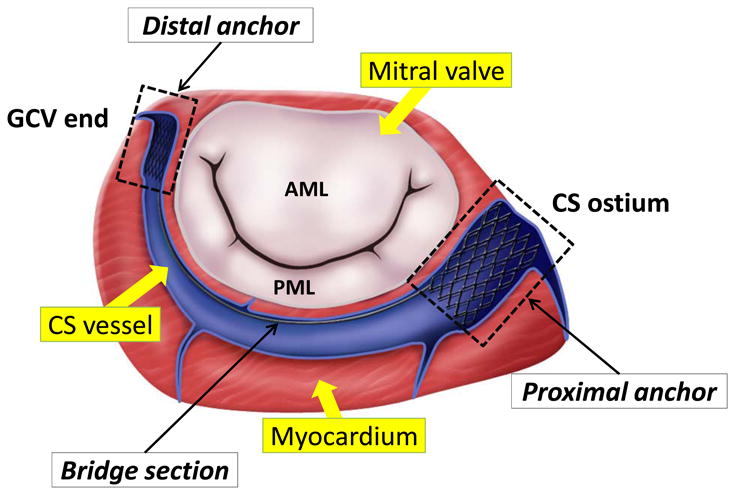
An illustration of one of the transcatheter mitral valve repair devices, the Monarc system (Edward Lifesciences, Inc.). The device consists of proximal, distal and bridge sections. The distal anchor is placed within the great cardiac vein (GCV) and the proximal anchor is deployed near the coronary sinus (CS) ostium.
Previous investigation on MA mechanics demonstrated the tension was lower in the commissural section (17.8 N/m) compared to anterior (40.0 N/m) or posterior (30.6 N/m) sections of the annulus (Bhattacharya and He, 2009, 2012; He and Bhattacharya, 2008, 2010). These studies offered insights into the underlying mechanism of annular dilatation. Annuloplasty complicates the annular mechanics by undersizing the dilated MA geometry (Rabbah et al., 2013). Some studies measured the forces generated by the myocardium on a prosthetic device and correlated them with changes in MA geometry. The maximum in-plane MA force generated by the myocardium on a rigid annulplasty ring was 6 – 8 N at mid-systole (porcine model) (Hasenkam et al., 1994). The maximum force in flexible rings was in a range of 4.4 – 13.9 N (swine models) (Shandas et al., 2001). Later, the development of saddle-shape bioprosthetic valve represented a novel advance in design to reduce the leaflet stress (Gorman et al., 2004; Jensen et al., 2011; Padala et al., 2009; Salgo et al., 2002). In a comparative study, the forces on the anterior and commissural annular segments of the flat ring were 0.72 ± 0.14 N and 1.38 ± 0.27 N, respectively, while the saddle-shaped ring exhibited nearly zero(Jensen et al., 2008).
These studies, however, only provided knowledge of cyclic forces that a device could experience during implantation, e.g. myocardial forces acting on the device, but not the force generated by devices necessary to reduce dilated MA. A fundamental question arises: what are the contributions from active and passive myocardial deformation, hydrostatic pressure and MA tension to the forces on the devices? The answer will not only facilitate the design and increase safety of annuloplasty devices but help to understand myocardial function and MA dilatation mechanism. In this study, an ex vivo technique was developed to quantify the CS cinching tension. The goal is to form a baseline value of cinching tension needed to correct dilated MA. The ovine model has been used extensively in experimental mitral valve mechanics studies (Gorman Iii et al., 1997; Randall Green et al., 1999) and pre-clinical studies of TMVR (Byrne et al., 2004; Kaye et al., 2003b; Liddicoat et al., 2003). The impact of cinching tension on the MA area, septal-lateral (S-L) and commissure-commissure (C-C) diameters and leakage in dilated valves were investigated.
Materials and Methods
Specimen preparation
Ten fresh adult ovine hearts (313.5 ± 51.9 g) were obtained from a local slaughter house. The hearts, which were not tested within 48 hours upon arrival, were cryopreserved at −80°C (Bia et al., 2006). Studies have shown that a short period of cryopreservation do not induce significant changes in passive vascular tissue mechanical properties (Bia, 2006; Delgadillo et al., 2010; Langerak et al., 2001; Stemper et al., 2007). For each heart, the left atrium was carefully removed to expose the mitral valve (MV), the MA, the CS vessel and CS ostium. Small graphite markers were affixed to the MA to demarcate the area to be measured (Fig. 2c). A suture was inserted within the CS vessel with one end tied at the GCV end and the other end exited the CS ostium. The coronary arteries and CS attributes were occluded by sutures.
Figure 2.
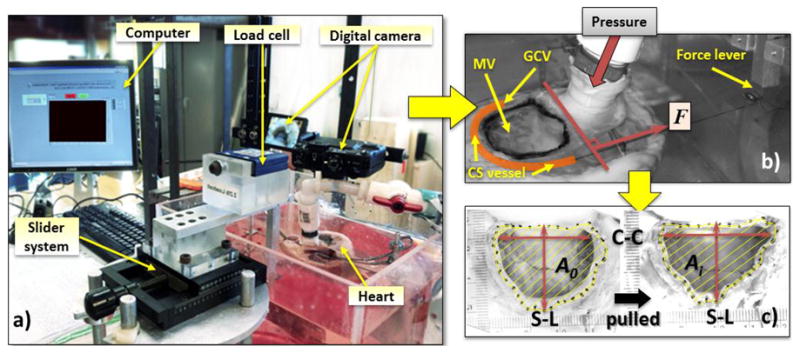
a) An image of the mitral valve (MV) cinching system consists of a computer acquisition system, a force transducer connects to a slider and a digital camera; b) a top view of a representative heart showing the location of the MV, the tissue dye highlighting the measured MV area, the coronary sinus (CS) vessel, the Great Cardiac Vein (GCV) vessel and the cinching force, F; c) the representative captured digital images of the reference area, A0 and the area after pulled at a distance, Ai.
The MV cinching system setup
The experimental system consists of a water column, a pump, a clear Plexiglas solution chamber, a custom-made rigid supporting structure, a slider system, one digital camera and a computerized data acquisition system (Fig.2a). Each heart was stabilized by fixing the right ventricle to the custom-made supporting structure placed inside the Plexiglas chamber. The left ventricle (LV) pressurization was achieved by injecting saline solution into the LV through a cannula, which was inserted into the ascending aorta vessel and passed the aortic leaflets. The water column, fabricated with a large-bore tubing attached to the aortic cannula. Ethylene-Glycol-Tetraacetic acid (EGTA, 2.0 mM) and papaverine (0.1M) were added to the saline solution (37°C) to minimize the active contraction of muscle fibers in order to obtain the passive mechanical properties of the heart (Alastrué et al., 2008; Carboni et al., 2007; Desch and Weizsäcker, 2007; García et al., 2011; Schulze-Bauer et al., 2003). The LV pressure was controlled by the height between the saline level in the water column and the mitral annular plane (Yamauchi et al., 2012). A quasi-static system was chosen as the MV experiences a highest force during peak systole or when it is fully closed. A peak hydrostatic systolic pressure of 90 mmHg is chosen for the physiological pressure of an ovine heart (Sakamoto et al., 2006; Siefert et al., 2012c). The leakage volume was measured by an amount of fluid regurgitated back into the left atrium during pressurization. The testing chamber was threaded with an outlet tube that drained the regurgitated fluid into a graduated cylinder for leakage measurements.
The slider system consists of a force lever, which was connected to a 10 N force transducer mounted on a linear stage. The handle of the linear stage can be manually rotated to linearly displace the force lever with an accuracy of ± 0.01 mm. The force transducer was connected to data acquisition device (National Instrument, NI SCC-68/SCC-SG24, NI 6351). A LabVIEW program recorded the force transducer data at each displacement. The force transducer was calibrated prior to each experiment. The MA area was obtained from a digital camera mounted perpendicular to the annular plane.
Experimental protocol
Each heart was preconditioned by applying 10 consecutive pressure loading (90 mmHg) cycles. The experimental measurements including the MV cinching tension, MV area and leakage measurements were obtained during the three phases when the mitral valve was: 1) open (no pressure, P0), 2) closed (pressurized at 90 mmHg, P90), and 3) altered or dilated at 90 mmHg pressure (P90-D). The P0 was performed to measure the cinching force generated by the suture inside the CS vessel during the passive relax state. The P90 was chosen as a baseline value for normal valve function during LV filling. For P90-D, the MV dilation was achieved by injecting phenol (95%), into the muscular MA using a needle. The toxic substance in phenol can damage the structure and function of muscles and has been utilized in an in vivo study to simulate MA dilation (Green et al., 1999). To cinch the MA, the CS ostium suture end was pulled in the direction perpendicular to the C-C direction of the MA (Fig. 2b). For each pull, a linear displacement, d, of 2 mm for a total of 9 displacements in each phase was achieved (di, i = 0, 2, 4…12, 16 and 20 mm).
Data acquisition and analysis
The cinching tension (T) and the corresponding image of MA were measured simultaneously at an instant of a displacement. All the MA dimensions were measured using ImageJ (National Institute of Health). The MA area, A, was defined as the area encompassed by the markers. The S-L diameter was calculated as the distance between the two markers placed on the mid-septal and mid-lateral MA, and the C-C diameter was measured as the distance between the two markers placed on the commissures (Fig. 2c). The leakage (L/min) was measured after visualization of full expansion of the LV and closing of the MV for 20 seconds.
Statistics
All measurements are shown as mean ± standard deviation (SD). The analysis of variance (ANOVA) test followed by the Holm-Sidak test and the Dunn's Method test were used to compare measurements between three phases. Data were tested for normality using the Shapiro-Wilk test. The Student's t-test was used to determine significant differences. The paired Student's t-test was employed to determine the significant changes within each phase. Correlations between the parameters were determined using the Pearson's (for normal) and Spearman (for non-parametric data) correlation coefficient (r). A probability value less than 0.05 was considered statistical significant, with high significance indicated by p < 0.001. All statistical analyses were performed using SigmaPlot (Systat Software Inc., San Jose, CA) and SYSTAT (Systat Software, Chicago, IL).
Results
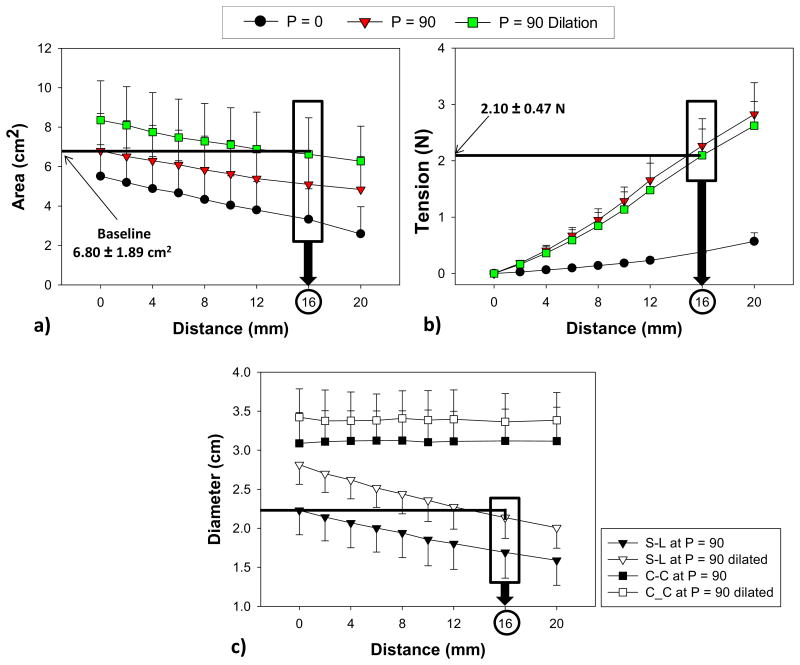
The MA deformation after each incremental load increase of a representative ovine heart during the three phases is shown in Fig. 3. The decrease in the mean MA area after each pull in each phase is shown in Fig. 4a. Prior to pulling, the MA area increased 23.3 ± 18.0% from P0 to P90 and dilated further by 22.8 ± 0.1% in P90-D. Upon pulling about 16 mm (d16), the dilated MA area was reduced by 26.2% (from 8.4 ± 2.0 cm2 to 6.6 ± 1.9 cm2) and similar to the baseline value (6.8 ± 1.9 cm2). From Fig. 4b, at d = 16 mm, T required to reduce the dilated MV area to the baseline was 2.1 ± 0.5 N. It can also be seen that T generated by the suture (P0) alone without pressurization was 0.4 ± 0.1 N.
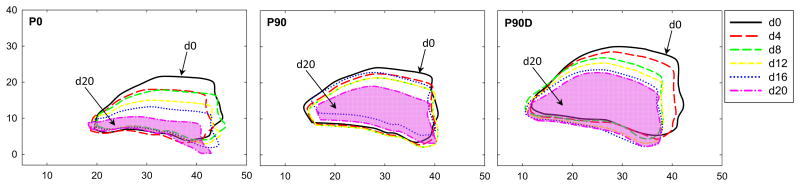
Figure 3.
Images of a representative mitral valve deformation at d = 0, 4, 8, 12, 16 and 20 mm during the three phases: (P0) when the mitral valve was open at zero pressure), (P90) close or pressurized at 90 mmHg, and (P90D) after the mitral annulus was dilated and pressurized. (Dimension is in millimeter)
Figure 4.
The relations between distance pulled and a) area (cm2), b) force (N) and c) septal-lateral (S-L) and commissure-to-commissure (C-C) diameter of the ovine hearts in three phases of valve open (P=0), valve close at 90 mmHg pressure (P=90) and valve dilation at 90 mmHg (P=90 Dilation). Data are shown as mean ± standard deviation.
The mean S-L diameter increased significantly by 26% from the baseline to dilation (from 2.2 ± 0.3 cm to 2.8 ± 0.3 cm, p < 0.001). At d16, the mean S-L diameter was significantly lower than d0 (2.1 ± 0.3 versus 2.8 ± 0.3, p < 0.001) and below the baseline value (2.1 ± 0.3 cm to 2.2 ± 0.3 cm, p = 0.485). The C-C diameter was increased by 11% after dilation. However, the C-C diameters obtained during P90-D remained unaffected throughout the experiment (Fig. 4c). The mean C-C diameter in P90 at d0 was 3.1 ± 0.4 cm and in P90-D at d16 was 3.4 ± 0.4 cm, p = 0.121. A summary of comparisons of the MV area, the S-L and C-C diameters and the leakage rate between baseline at no pull (d = 0) and dilated condition at 16 and 20 mm pulling distances (d = 16 and 20) are listed in Table 1.
Table 1. During pressurization of 90 mmHg.
| Baseline | Dilated | at d=20 | ||
|---|---|---|---|---|
| at d=0 | at d=0 | at d=16 | ||
| MV(cm2) | 6.80±1.89 | 8.35±2.00 | 6.62±1.85 | 6.27±1.77 |
| S-L dia(cm) | 2.23±0.31 | 2.81±0.25* | 2.14±0.27† | 2.01±0.26† |
| C-C dia (cm) | 3.09±0.39 | 3.42±0.36 | 3.36±0.36 | 3.38±0.35 |
| Leakage (L/min) | 0.09±0.07 | 0.18±0.09 | 0.09±0.07 | 0.08±0.05‡ |
comparedtobaselined=0,P<0.001,
comparedtodilatedd=0,P<0.001,
comparedtodilatedd=16,P<0.05
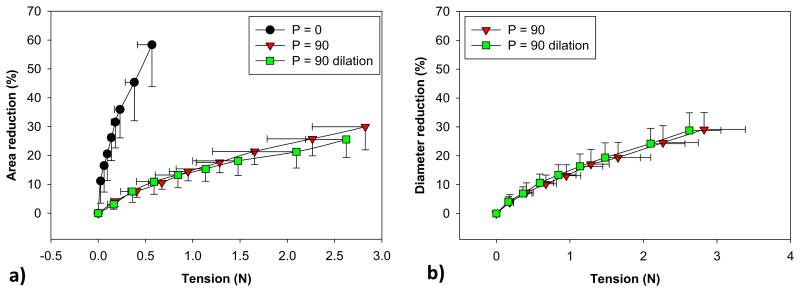
The relation between MA area and T in each phase is shown in Fig. 5a. At a maximum pulling distance (d20), a small tension of 0.6 N was required to shrink 58% of the MA area during P0. At the same tension, as expected, only 9% and 11% MA reduction were achieved for P90 and P90-D, respectively. At 15% MA area reduction, the tension of both P90 and P90-D was 1 N. After this point, the P90-D response curve shifted down slightly, indicating a larger tension would be required to shrink the MA area. The decrease in the MA area was accompanied by the reduction in the S-L and C-C diameters, and no difference was observed between P90 and P90-D, see Fig. 5b. At 2.1 ± 0.5N, when the dilated MA area returned back to the baseline value, a 21.30 ± 5.6% reduction in the MA area and a 24.18 ± 5.28% reduction in the S-L diameter were achieved.
Figure 5.
The relation between (a) mitral annulus area and cinching tension, and between (b) S-L and C-C diameters and cinching tension. Data are shown as mean ± standard deviation.
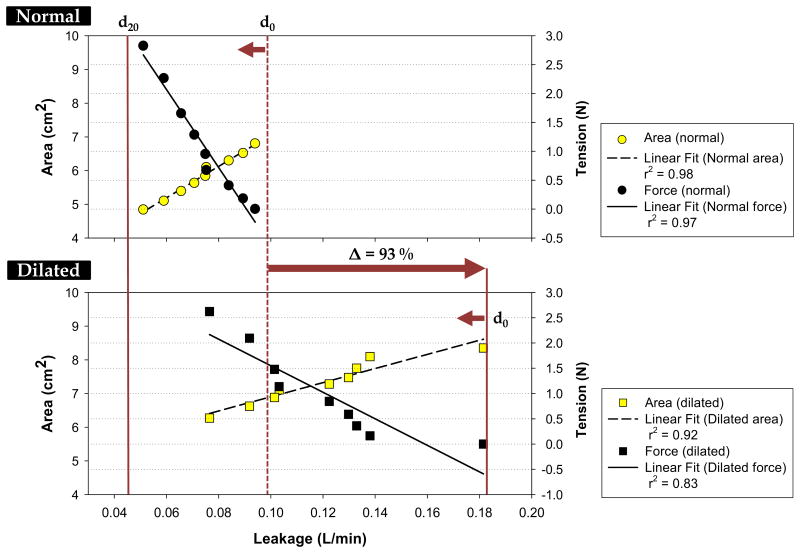
Figure 6 shows the changes in the MA area, the tensions and the leakage rates from the initial (d0) to the final (d20) pulling distances. In the normal hearts, we observed a small leakage of 0.1 ± 0.1 L/min. After phenol application, the leakage rate increased to 0.2 ± 0.0 L/min or by 93%. The progression of annular cinching caused the MA area to decrease progressively with leakage rate (r = 0.99, p < 0.001 for P90 and r = 0.96, p < 0.001 for P90-D). The T was inversely correlated with leakage rate (r = -0.98, p < 0.001 for P90 and r = -0.91, p < 0.001 for P90-D). Leakage was reduced to normal leakage rate at 1.71 N, and the MV area approached to normal at 6.8 cm2.
Figure 6.
The correlations between the mean leakage rate and mean mitral area and mean cinching tension in the a) normal and b) dilated conditions. Solid and dashed lines are the linear fits of the data. The d0 indicates no pull, and d20 is 20-mm pulling distance.
Discussion
At present, limited information is available on TMVR devices regarding device forces required to restore normal valve function. An ex vivo technique developed in this study aims to quantify the cinching tension (T) needed to restore normal MA from dilation in the passive ovine heart model. The MA dilation was achieved up to 22.8% and the S-L and C-C diameters were increased by 26% and 11% upon dilation, respectively. An in vivo animal study demonstrated that in chronic ischemic MR condition, the entire mitral annular regions dilates proportionally (Tibayan et al., 2003). Timek et al. (Timek et al., 2010) showed that the progression of acute ischemic MR in ovine models was characterized as 20% - 28% increase in MA area and 14% -19% increase in S-L diameter. For human study, significant MR caused by ischemic cardiomyopathy was characterized as 31% increase in MA area and 17% and 11% increase in S-L and C-C diameters (Kwan et al., 2003). Thus, the increase in both MA area and S-L and C-C diameters in this study showed an indication of MA dilation.
The loading condition on the MA is primarily due to the LV pressurization achieved by the hydrostatic pressure. Therefore, T is an additional force on the LV wall and leaflets connecting to the MA to balance this hydrostatic pressure force. From Fig. 4, during P0, T generated by the suture was 0.1 ± 0.0 N (P0, d = 4 mm), resulting in MA area of 4.9 ± 1.6 cm2. The T required to reduce to a similar MA area with a presence of the hydrostatic pressure was 2.8 ± 0.6 N (P90, d = 20 mm). Thus, the increase in T as the result of hydrostatic pressure can be calculated as P90 - P0, approximately 2.7 N or increased by 4557%. This drastic increase in T between P0 and P90 indicates that LV pressure is an important factor in determining the effective T of the device. To determine the change in T with the presence of MA dilation, the difference between T at P90 and P90D was obtained. At a MA area of 6.3 ± 1.8 cm2, T of P90 and P90D were 0.4 ± 0.1 N and 2.6 ± 0.4 N, respectively, resulting in 2.2 N, or increased by 539%. Since the pressure was constant for both phases, this increase in tension directly relates to the impaired muscular tissue around the MA due to phenol. Thus, we can view this suture cinching tension as a compensation force in MA reduction. In other words, T indicates the maximum force to be generated by the device necessary to restore normal MA geometry without active myocardial contraction, and usually depends on severity of annular dilatation.
The cinching tension, however, can be less in magnitude during LV contraction. In an in vivo ovine study (Siefert et al., 2012b), the MA forces were measured using a custom-made device with strain gauges placed directly on the MA in S-L and C-C directions. They reported the mean S-L and C-C forces of normal ovine group at 90 mmHg were 3.9 ± 0.8 N and 2.6 ± 0.6 N, respectively. In another study (Siefert et al., 2012a), the same group found a significant decrease in the S-L forces as the result of ischemic MR with inferior LV infarction. Their findings support the notion that the active contraction mechanism might have been impaired in ischemic MR (Daimon et al., 2010; Kaplan et al., 2000; Yiu et al., 2000). Daimon et al. (Daimon et al., 2010) found that their IMR patient group had an attenuated mitral annular motion and a reduction in MA contraction by 23.0 ± 6.5% compared to the normal group of 42.6 ± 7%. In addition, their analysis showed that MA contraction was the strongest determinant of the severity of MR among the annular measurement. The hydrostatic pressure in this study is not considering in vivo MA contraction and expansion of myocardial fibers. Thus, the active contraction properties of the MA might relieve this suture tension. However, active contraction in relation to cinching tension is remained to be determined.
The experimental technique used in this study for MA restoration only allowed a significant reduction in the S-L dimension while the C-C dimension remained unchanged (Figs. 3&4). The impact of C-C dimension in restoring MV competency, however, is still a debate. Several clinical and experimental studies have shown that S-L dimension has a prominent role in functional MR (Timek et al., 2001) and that reduction in S-L diameter alone is sufficient to restore leaflet coaptation (Glasson et al., 1998; Lai et al., 2000).
Restoration of normal MV by cinching the MA was adopted by several novel methods. A percutaneous annuloplasty device called the Cerclage was tested in 16 swine subjects to shrink both the MA and the LV outflow tract (Kim et al., 2009). The S-L diameter reduction was measured at 200g, 400g and 600g tension, and a maximum of 20% reduction at 600g was observed. This high magnitude of tension could be the result of shrinking a massive muscular structure that included both MA and aorta. Timek et al. demonstrated that S-L diameter reduction was achieved by more than one trans-annular sutures connected from locations on the anterior fibrous region to the posterior annulus (Timek et al., 2004; Timek et al., 2002) but no force was measured. Recently, Jensen et al. (Jensen et al., 2013) found that at 32% of trans- annular trigone-posterior annulus distance reduction at three different location, the peak forces were 1.2 ± 0.9 N, 1.5 ± 1.0 N, and 0.8 ± 0.2 N with no significant difference between them. Interestingly, the sum of the forces ranged from 0.12 ± 0.03 N to 3.5 ± 1.3 N, which matches our results even though force directions and suture techniques were different. Their cyclic traction suture forces increased with increasing levels of downsizing as our cinching tensions increased with increasing MA area reduction. It should be noted that the magnitude of forces measured is dependent on the type of device (Jensen et al., 2013) and how it shapes the MA. Difference in the locations of device implantation (e.g. within the CS or directly on the MA) and various hemodynamic and boundary condition could affect both MA geometry and mechanics.
In this study, tissue damage from the suture tension was not considered. It is possible that the suture might have eroded into the vessel wall during tensioning. However, it is unknown whether these damages, if any, were caused by compressive force or relative slipping motion. The Cerclage annuloplasty exerted a maximum of 600 g force without evidence of tissue erosion. Given the significant lower forces experienced in this study, we assumed minimal or negligible damage to the vessel wall.
Currently, there is a lack of understanding of biomechanics involved in the device design and optimization of TMVR devices, possibly due to the complex MV geometries. Fortunately, in the past decade, the mechanical testing techniques and constitutive modeling in cardiovascular mechanics have improved tremendously. Human tissue material properties can now be tested extensively (Pham and Sun, 2013), modeled and implemented in computational studies (Wang and Sun, 2013). Improved computational models of MV has evolved (Krishnamurthy et al., 2009; Kunzelman et al., 1993; Pouch et al., 2012; Prot et al., 2009; Stevanella et al., 2011; Weinberg and Kaazempur Mofrad, 2007) and predicted several diseased states (Kunzelman et al., 1997; Prot et al., 2010; Wenk et al., 2010; Xu et al., 2012). Thus, the data in this study can be used in validation of computational models to predict the functionality of TMVR devices.
Limitations
There are several limitations in this study. The data are valid for isolated MA dilation model which is distinctly different from ischemic MR model (Timek and Miller, 2011). The mitral valve closure due to the hydrostatic pressure could alter the native MA mechanics by the expansion of the global LV. Leaflet coaptation height, depth and tethering length were not recorded as the result of 2D imaging, thus, MR grade was not classified. Future study using 3D echocardiography will provide a new insight into the 3D dynamic behavior of the MV during cinching. This study did not account for global expansion and contraction of LV, in vivo annular contraction and expansion of myocardial fibers. Thus, the active contraction properties of the MA and LV may relieve this suture cinching tension.
Conclusion
This study investigated the cinching tension required to reduce MA dilation in passive ovine heart model. The MA was dilated up to 22.8%. A mean force of 2.1 ± 0.5 N was required for 21.3 ± 5.6% in MA area reduction, reduced leakage by 51.72 ± 16.19% and restored the normal condition with a significant reduction in the S-L dimension. The cinching tension generated by the suture acts as a compensation force in MA reduction, implying the maximum tension to be generated by annuloplasty device to restore normal MA geometry. Several approaches that utilize the CS to rectify MA dilation have been developed, but long-term durability is yet to be achieved due to current fatigue and fracture events. Therefore, knowledge of the cinching force with the corresponding MA geometry will greatly contribute to the development and design of future TMVR devices and understanding of myocardial contraction function.
Acknowledgments
The authors would like to thank the Animal Technologies (Texas) and Brothers Quality, Inc. (Stafford Springs, CT) for animal tissue supplies, Kaitlyn Clarke, Andrew Reynolds, Brittany Depoi, Adarsha Selvachandran and Kewei Li for system support, and the American Heart Association SDG grant (0930319N) and the NIH NRSA F31 Pre-doctoral Fellowship grant (HL097722) for funding resources.
Footnotes
Conflict Of Interest: The authors have no conflict of interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alastrué V, Peña E, Martínez MA, Doblaré M. Experimental study and constitutive modelling of the passive mechanical properties of the ovine infrarenal vena cava tissue. Journal of Biomechanics. 2008;41:3038–3045. doi: 10.1016/j.jbiomech.2008.07.008. [DOI] [PubMed] [Google Scholar]
- Bhattacharya S, He Z. Role of annulus tension in annular dilatation. J Heart Valve Dis. 2009;18:481–487. [PubMed] [Google Scholar]
- Bhattacharya S, He Z. Annulus tension of the prolapsed mitral valve corrected by edge-to-edge repair. J Biomech. 2012;45:562–568. doi: 10.1016/j.jbiomech.2011.11.005. [DOI] [PubMed] [Google Scholar]
- Bia D. Cryopreservation procedure does not modify human carotid homografts mechanical properties: an isobaric and dynamic analysis. Cell and Tissue Banking. 2006;7:183–194. doi: 10.1007/s10561-005-0655-0. [DOI] [PubMed] [Google Scholar]
- Bia D, Pessana F, Armentano R, Perez H, Graf S, Zocalo Y, Saldias M, Perez N, Alvarez O, Silva W, Machin D, Sueta P, Ferrin S, Acosta M, Alvarez I. Cryopreservation procedure does not modify human carotid homografts mechanical properties: an isobaric and dynamic analysis. Cell and Tissue Banking. 2006;7:183–194. doi: 10.1007/s10561-005-0655-0. [DOI] [PubMed] [Google Scholar]
- Byrne MJ, Kaye DM, Mathis M, Reuter DG, Alferness CA, Power JM. Percutaneous mitral annular reduction provides continued benefit in an ovine model of dilated cardiomyopathy. Circulation. 2004;110:3088–3092. doi: 10.1161/01.CIR.0000146904.13677.E4. [DOI] [PubMed] [Google Scholar]
- Carboni M, Desch GW, Weizsäcker HW. Passive mechanical properties of porcine left circumflex artery and its mathematical description. Medical Engineering & Physics. 2007;29:8–16. doi: 10.1016/j.medengphy.2006.01.004. [DOI] [PubMed] [Google Scholar]
- Condado JA, Velez-Gimon M. Catheter-based approach to mitral regurgitation. J Interv Cardiol. 2003;16:523–534. doi: 10.1046/j.1540-8183.2003.01052.x. [DOI] [PubMed] [Google Scholar]
- Daimon M, Saracino G, Fukuda S, Koyama Y, Kwan J, Song JM, Agler DA, Gillinov AM, Thomas JD, Shiota T. Dynamic change of mitral annular geometry and motion in ischemic mitral regurgitation assessed by a computerized 3D echo method. Echocardiography. 2010;27:1069–1077. doi: 10.1111/j.1540-8175.2010.01204.x. [DOI] [PubMed] [Google Scholar]
- Deharrera M, Sun W. Year Simulation of the Forming of a Superelastic Anchoring Stent and its Deployment in the Coronary Vein. ABAQUS annual conference; Pairs, France. [Google Scholar]
- Delgadillo JOV, Delorme S, El-Ayoubi R, Diraddo R, Hatzikiriakos SG. Effect of freezing on the passive mechanical properties of arterial samples. Journal of Biomedical Science and Engineering. 2010;3:645–652. [Google Scholar]
- Desch GW, Weizsäcker HW. A model for passive elastic properties of rat vena cava. Journal of Biomechanics. 2007;40:3130–3145. doi: 10.1016/j.jbiomech.2007.03.028. [DOI] [PubMed] [Google Scholar]
- Duffy SJ, Federman J, Farrington C, Reuter DG, Richardson M, Kaye DM. Feasibility and short-term efficacy of percutaneous mitral annular reduction for the therapy of functional mitral regurgitation in patients with heart failure. Catheter Cardiovasc Interv. 2006;68:205–210. doi: 10.1002/ccd.20810. [DOI] [PubMed] [Google Scholar]
- García A, Peña E, Laborda A, Lostalé F, De Gregorio MA, Doblaré M, Martínez MA. Experimental study and constitutive modelling of the passive mechanical properties of the porcine carotid artery and its relation to histological analysis: Implications in animal cardiovascular device trials. Medical Engineering and Physics. 2011;33:665–676. doi: 10.1016/j.medengphy.2011.01.016. [DOI] [PubMed] [Google Scholar]
- Glasson JR, Komeda M, Daughters GT, Bolger AF, Karlsson MO, Foppiano LE, Hayase M, Oesterle SN, Ingels NB, Jr, Miller DC, Bolling SF. Early systolic mitral leaflet ‘loitering’ during acute ischemic mitral regurgitation. Journal of Thoracic and Cardiovascular Surgery. 1998;116:193–205. doi: 10.1016/s0022-5223(98)70117-5. [DOI] [PubMed] [Google Scholar]
- Gorman JH, Iii MD, Gorman RC, Md, Jackson BM, Ms, Hiramatsu Y, Md, Gikakis N, Bse, Kelley ST, md, St John Sutton MG, Mbbs, Plappert T, Cvt, Edmunds LH., Jr MD Distortions of the Mitral Valve in Acute Ischemic Mitral Regurgitation. The Annals of Thoracic Surgery. 1997;64:1026–1031. doi: 10.1016/s0003-4975(97)00850-3. [DOI] [PubMed] [Google Scholar]
- Gorman JH, 3rd, Jackson BM, Enomoto Y, Gorman RC. The effect of regional ischemia on mitral valve annular saddle shape. Ann Thorac Surg. 2004;77:544–548. doi: 10.1016/S0003-4975(03)01354-7. [DOI] [PubMed] [Google Scholar]
- Green GR, Dagum P, Glasson JR, Daughters GT, Bolger AF, Foppiano LE, Berry GJ, Ingels NB, Jr, Miller DC. Mitral annular dilatation and papillary muscle dislocation without mitral regurgitation in sheep. Circulation. 1999;100:II95–II102. doi: 10.1161/01.cir.100.suppl_2.ii-95. [DOI] [PubMed] [Google Scholar]
- Harnek J, Webb JG, Kuck KH, Tschope C, Vahanian A, Buller CE, James SK, Tiefenbacher CP, Stone GW. Transcatheter implantation of the MONARC coronary sinus device for mitral regurgitation. JACC: Cardiovascular Interventions. 2011;4:115–122. doi: 10.1016/j.jcin.2010.08.027. [DOI] [PubMed] [Google Scholar]
- Hasenkam JM, Nygaard H, Paulsen PK, Kim WY, Hansen OK. What force can the myocardium generate on a prosthetic mitral valve ring? An animal experimental study. Journal of Heart Valve Disease. 1994;3:324–329. [PubMed] [Google Scholar]
- He Z, Bhattacharya S. Papillary muscle and annulus size effect on anterior and posterior annulus tension of the mitral valve: an insight into annulus dilatation. J Biomech. 2008;41:2524–2532. doi: 10.1016/j.jbiomech.2008.05.006. [DOI] [PubMed] [Google Scholar]
- He Z, Bhattacharya S. Mitral valve annulus tension and the mechanism of annular dilation: an in-vitro study. J Heart Valve Dis. 2010;19:701–707. [PubMed] [Google Scholar]
- Hoppe UC, Brandt MC, Degen H, Dodos F, Schneider T, Stoepel C, Kroener A, Haude M. Percutaneous Mitral Annuloplasty Device Leaves Free Access to Cardiac Veins for Resynchronization Therapy. Catheterization and Cardiovascular Interventions. 2009;74 doi: 10.1002/ccd.22097. [DOI] [PubMed] [Google Scholar]
- Jensen Mÿ, Jensen H, Nielsen SL, Smerup M, Johansen P, Yoganathan AP, Nygaard H, Hasenkam JM. What forces act on a flat rigid mitral annuloplasty ring? Journal of Heart Valve Disease. 2008;17:267–275. [PubMed] [Google Scholar]
- Jensen MO, Honge JL, Benediktsson JA, Siefert AW, Jensen H, Yoganathan AP, Snow TK, Hasenkam JM, Nygaard H, Nielsen SL. Mitral valve annular downsizing forces: Implications for annuloplasty device development. Journal of Thoracic and Cardiovascular Surgery. 2013 doi: 10.1016/j.jtcvs.2013.07.045. [DOI] [PubMed] [Google Scholar]
- Jensen MO, Jensen H, Levine RA, Yoganathan AP, Andersen NT, Nygaard H, Hasenkam JM, Nielsen SL. Saddle-shaped mitral valve annuloplasty rings improve leaflet coaptation geometry. Journal of Thoracic and Cardiovascular Surgery. 2011;142:697–703. doi: 10.1016/j.jtcvs.2011.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplan SR, Bashein G, Sheehan FH, Legget ME, Munt B, Li XN, Sivarajan M, Bolson EL, Zeppa M, Martin RW. Three-dimensional echocardiographic assessment of annular shape changes in the normal and regurgitant mitral valve. American Heart Journal. 2000;139:378–387. doi: 10.1016/s0002-8703(00)90077-2. [DOI] [PubMed] [Google Scholar]
- Kaye DM, Byrne M, Alferness C, Power J. Feasibility and short-term efficacy of percutaneous mitral annular reduction for the therapy of heart failure-induced mitral regurgitation. Circulation. 2003a;108:1795–1797. doi: 10.1161/01.CIR.0000096051.23734.28. Epub 2003 Oct 1796. [DOI] [PubMed] [Google Scholar]
- Kaye DM, Byrne M, Alferness C, Power J. Feasibility and Short-Term Efficacy of Percutaneous Mitral Annular Reduction for the Therapy of Heart Failure-Induced Mitral Regurgitation. Circulation. 2003b;108:1795–1797. doi: 10.1161/01.CIR.0000096051.23734.28. [DOI] [PubMed] [Google Scholar]
- Kim JH, Kocaturk O, Ozturk C, Faranesh AZ, Sonmez M, Sampath S, Saikus CE, Kim AH, Raman VK, Derbyshire JA, Schenke WH, Wright VJ, Berry C, McVeigh ER, Lederman RJ. Mitral cerclage annuloplasty, a novel transcatheter treatment for secondary mitral valve regurgitation: initial results in swine. J Am Coll Cardiol. 2009;54:638–651. doi: 10.1016/j.jacc.2009.03.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnamurthy G, Itoh A, Bothe W, Swanson JC, Kuhl E, Karlsson M, Craig Miller D, Ingels NB., Jr Stress-strain behavior of mitral valve leaflets in the beating ovine heart. J Biomech. 2009;42:1909–1916. doi: 10.1016/j.jbiomech.2009.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunzelman KS, Cochran RP, Chuong C, Ring WS, Verrier ED, Eberhart RD. Finite element analysis of the mitral valve. The Journal of heart valve disease. 1993;2:326–340. [PubMed] [Google Scholar]
- Kunzelman KS, Reimink MS, Cochran RP. Annular dilatation increases stress in the mitral valve and delays coaptation: A finite element computer model. Cardiovascular Surgery. 1997;5:427–434. doi: 10.1016/s0967-2109(97)00045-8. [DOI] [PubMed] [Google Scholar]
- Kwan J, Shiota T, Agler DA, Popovi—ç ZB, Qin JX, Gillinov MA, Stewart WJ, Cosgrove DM, McCarthy PM, Thomas JD. Geometric differences of the mitral apparatus between ischemic and dilated cardiomyopathy with significant mitral regurgitation: Real-time three-dimensional echocardiography study. Circulation. 2003;107:1135–1140. doi: 10.1161/01.cir.0000053558.55471.2d. [DOI] [PubMed] [Google Scholar]
- Lai DTM, Timek TA, Dagum P, Green GR, Glasson JR, Daughters GT, Liang D, Ingels NB, Jr, Miller DC. The effects of ring annuloplasty on mitral leaflet geometry during acute left ventricular ischemia. Journal of Thoracic and Cardiovascular Surgery. 2000;120:966–975. doi: 10.1067/mtc.2000.110186. [DOI] [PubMed] [Google Scholar]
- Langerak SE, Groenink M, Van der Wall EE, Wassenaar C, Vanbavel E, Van Baal MC, Spaan JAE. Impact of current cryopreservation procedures on mechanical and functional properties of human aortic homografts. Transplant International. 2001;14:248–255. doi: 10.1007/s001470100309. [DOI] [PubMed] [Google Scholar]
- Liddicoat JR, Mac Neill BD, Gillinov AM, Cohn WE, Chin CH, Prado AD, Pandian NG, Oesterle SN. Percutaneous Mitral Valve Repair: A Feasibility Study in an Ovine Model of Acute Ischemic Mitral Regurgitation. Catheterization and Cardiovascular Interventions. 2003;60:410–416. doi: 10.1002/ccd.10662. [DOI] [PubMed] [Google Scholar]
- Maniu CV, Patel JB, Reuter DG, Meyer DM, Edwards WD, Rihal CS, Redfield MM. Acute and chronic reduction of functional mitral regurgitation in experimental heart failure by percutaneous mitral annuloplasty. J Am Coll Cardiol. 2004;44:1652–1661. doi: 10.1016/j.jacc.2004.03.085. [DOI] [PubMed] [Google Scholar]
- Padala M, Hutchison RA, Croft LR, Jimenez JH, Gorman RC, Gorman JH, Iii, Sacks MS, Yoganathan AP. Saddle Shape of the Mitral Annulus Reduces Systolic Strains on the P2 Segment of the Posterior Mitral Leaflet. The Annals of Thoracic Surgery. 2009;88:1499–1504. doi: 10.1016/j.athoracsur.2009.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham T, Sun W. Material properties of aged human mitral valve leaflets. Journal of Biomedical Materials Research - Part A. 2013 doi: 10.1002/jbm.a.34939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouch AM, Xu C, Yushkevich PA, Jassar AS, Vergnat M, Gorman JH, Iii, Gorman RC, Sehgal CM, Jackson BM. Semi-automated mitral valve morphometry and computational stress analysis using 3D ultrasound. Journal of Biomechanics. 2012;45:903–907. doi: 10.1016/j.jbiomech.2011.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prot V, Haaverstad R, Skallerud B. Finite element analysis of the mitral apparatus: Annulus shape effect and chordal force distribution. Biomechanics and Modeling in Mechanobiology. 2009;8:43–55. doi: 10.1007/s10237-007-0116-8. [DOI] [PubMed] [Google Scholar]
- Prot V, Skallerud B, Sommer G, Holzapfel GA. On modelling and analysis of healthy and pathological human mitral valves: two case studies. Journal of the mechanical behavior of biomedical materials. 2010;3:167–177. doi: 10.1016/j.jmbbm.2009.05.004. [DOI] [PubMed] [Google Scholar]
- Rabbah JPM, Saikrishnan N, Siefert AW, Santhanakrishnan A, Yoganathan AP. Mechanics of healthy and functionally diseased mitral valves: A critical review. Journal of Biomechanical Engineering. 2013;135 doi: 10.1115/1.4023238. [DOI] [PubMed] [Google Scholar]
- Randall Green G, Dagum P, Glasson JR, Francisco Nistal J, Daughtersii GT, Ingels NB, Jr, Craig Miller D. Restricted posterior leaflet motion after mitral ring annuloplasty. Annals of Thoracic Surgery. 1999;68:2100–2106. doi: 10.1016/s0003-4975(99)01175-3. [DOI] [PubMed] [Google Scholar]
- Sack S, Kahlert P, Bilodeau L, Pierard LA, Lancellotti P, Legrand V, Bartunek J, Vanderheyden M, Hoffmann R, Schauerte P, Shiota T, Marks DS, Erbel R, Ellis SG. Percutaneous transvenous mitral annuloplasty: initial human experience with a novel coronary sinus implant device. Circ Cardiovasc Interv. 2009;2:277–284. doi: 10.1161/CIRCINTERVENTIONS.109.855205. [DOI] [PubMed] [Google Scholar]
- Sakamoto H, Parish LM, Hamamoto H, Enomoto Y, Zeeshan A, Plappert T, Jackson BM, St John-Sutton MG, Gorman RC, Gorman JH., 3rd Effects of hemodynamic alterations on anterior mitral leaflet curvature during systole. J Thorac Cardiovasc Surg. 2006;132:1414–1419. doi: 10.1016/j.jtcvs.2006.08.036. [DOI] [PubMed] [Google Scholar]
- Salgo IS, Gorman JH, 3rd, Gorman RC, Jackson BM, Bowen FW, Plappert T, St John Sutton MG, Edmunds LH., Jr Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation. 2002;106:711–717. doi: 10.1161/01.cir.0000025426.39426.83. [DOI] [PubMed] [Google Scholar]
- Schulze-Bauer CAJ, Morth C, Holzapfel GA. Passive Biaxial Mechanical Response of Aged Human Iliac Arteries. Journal of Biomechanical Engineering. 2003;125:395–406. doi: 10.1115/1.1574331. [DOI] [PubMed] [Google Scholar]
- Shandas R, Mitchell M, Conrad C, Knudson O, Sorrell J, Mahalingam S, Fragoso M, Valdes-Cruz L. A general method for estimating deformation and forces imposed in vivo on bioprosthetic heart valves with flexible annuli: In vitro and animal validation studies. Journal of Heart Valve Disease. 2001;10:495–504. [PubMed] [Google Scholar]
- Siefert AW, Jimenez JH, Koomalsingh KJ, Aguel F, West DS, Shuto T, Snow TK, Gorman RC, Gorman JH, 3rd, Yoganathan AP. Contractile mitral annular forces are reduced with ischemic mitral regurgitation. J Thorac Cardiovasc Surg. 2012a doi: 10.1016/j.jtcvs.2012.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siefert AW, Jimenez JH, Koomalsingh KJ, West DS, Aguel F, Shuto T, Gorman RC, Gorman JH, 3rd, Yoganathan AP. Dynamic assessment of mitral annular force profile in an ovine model. Ann Thorac Surg. 2012b;94:59–65. doi: 10.1016/j.athoracsur.2012.02.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siefert AW, Jimenez JH, West DS, Koomalsingh KJ, Gorman RC, Gorman JH, Iii, Yoganathan AP. In-vivo transducer to measure dynamic mitral annular forces. Journal of Biomechanics. 2012c;45:1514–1516. doi: 10.1016/j.jbiomech.2012.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siminiak T, Firek L, Jerzykowska O, Katmucki P, Wotoszyn M, Smuszkiewicz P, Link R. Percutaneous valve repair for mitral regurgitation using the Carillon(TM)-Mitral Contour System(TM). Description of the method and case report. Kardiologia Polska. 2007;65:272–278. [PubMed] [Google Scholar]
- Siminiak T, Hoppe UC, Schofer J, Haude M, Herrman JP, Vainer J, Firek L, Reuter DG, Goldberg SL, Bibber RV. Effectiveness and Safety of Percutaneous Coronary Sinus-Based Mitral Valve Repair in Patients With Dilated Cardiomyopathy (from the AMADEUS Trial) Am J Cardiology. 2009a;104:565–570. doi: 10.1016/j.amjcard.2009.04.021. [DOI] [PubMed] [Google Scholar]
- Siminiak T, Hoppe UC, Schofer J, Haude M, Herrman JP, Vainer J, Firek L, Reuter DG, Goldberg SL, Van Bibber R. Effectiveness and safety of percutaneous coronary sinus-based mitral valve repair in patients with dilated cardiomyopathy (from the AMADEUS trial) Am J Cardiol. 2009b;104:565–570. doi: 10.1016/j.amjcard.2009.04.021. [DOI] [PubMed] [Google Scholar]
- Stemper BD, Yoganandan N, Stineman MR, Gennarelli TA, Baisden JL, Pintar FA. Mechanics of Fresh, Refrigerated, and Frozen Arterial Tissue. Journal of Surgical Research. 2007:236–242. doi: 10.1016/j.jss.2006.09.001. [DOI] [PubMed] [Google Scholar]
- Stevanella M, Maffessanti F, Conti CA, Votta E, Arnoldi A, Lombardi M, Parodi O, Caiani EG, Redaelli A. Mitral Valve Patient-Specific Finite Element Modeling from Cardiac MRI: Application to an Annuloplasty Procedure. Cardiovascular Engineering and Technology. 2011;2:66–76. [Google Scholar]
- Tibayan FA, Rodriguez F, Langer F, Zasio MK, Bailey L, Liang D, Daughters GT, Ingels NB, Jr, Miller DC. Annular Remodeling in Chronic Ischemic Mitral Regurgitation: Ring Selection Implications. The Annals of Thoracic Surgery. 2003;76:1549–1555. doi: 10.1016/s0003-4975(03)00880-4. [DOI] [PubMed] [Google Scholar]
- Timek TA, Dagum P, Lai DT, Liang D, Daughters GT, Ingels NB, Jr, Miller DC. Pathogenesis of mitral regurgitation in tachycardia-induced cardiomyopathy. Circulation. 2001;104:i47–i53. doi: 10.1161/hc37t1.094913. [DOI] [PubMed] [Google Scholar]
- Timek TA, Lai DT, Liang D, Daughters GT, Ingels NB, Jr, Miller DC. Determinants of evolution and progression of acute ovine ischemic mitral regurgitation. Journal of Heart Valve Disease. 2010;19:420–425. [PubMed] [Google Scholar]
- Timek TA, Lai DT, Liang D, Tibayan F, Langer F, Rodriguez F, Daughters GT, Ingels NB, Jr, Miller DC. Effects of paracommissural septal-lateral annular cinching on acute ischemic mitral regurgitation. Circulation. 2004;110:II79–84. doi: 10.1161/01.CIR.0000138975.05902.a5. [DOI] [PubMed] [Google Scholar]
- Timek TA, Lai DT, Tibayan F, Liang D, Daughters GT, Dagum P, Ingels NB, Jr, Miller DC. Septal-lateral annular cinching abolishes acute ischemic mitral regurgitation. J Thorac Cardiovasc Surg. 2002;123:881–888. doi: 10.1067/mtc.2002.122296. [DOI] [PubMed] [Google Scholar]
- Timek TA, Miller DC. Another multidisciplinary look at ischemic mitral regurgitation. Seminars in Thoracic and Cardiovascular Surgery. 2011;23:220–231. doi: 10.1053/j.semtcvs.2011.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, Sun W. Finite element modeling of mitral valve dynamic deformation using patient-specific multi-slices computed tomography scans. Annals of Biomedical Engineering. 2013;41:142–153. doi: 10.1007/s10439-012-0620-6. [DOI] [PubMed] [Google Scholar]
- Webb JG, Harnek J, Munt BI, Kimblad PO, Chandavimol M, Thompson CR, Mayo JR, Solem JO. Percutaneous transvenous mitral annuloplasty: initial human experience with device implantation in the coronary sinus. Circulation. 2006;113:851–855. doi: 10.1161/CIRCULATIONAHA.105.591602. Epub 2006 Feb 2006. [DOI] [PubMed] [Google Scholar]
- Weinberg EJ, Kaazempur Mofrad MR. A finite shell element for heart mitral valve leaflet mechanics, with large deformations and 3D constitutive material model. Journal of Biomechanics. 2007;40:705–711. doi: 10.1016/j.jbiomech.2006.01.003. [DOI] [PubMed] [Google Scholar]
- Wenk JF, Zhang Z, Cheng G, Malhotra D, Acevedo-Bolton G, Burger M, Suzuki T, Saloner DA, Wallace AW, Guccione JM, Ratcliffe MB. First Finite Element Model of the Left Ventricle With Mitral Valve: Insights Into Ischemic Mitral Regurgitation. The Annals of Thoracic Surgery. 2010;89:1546–1553. doi: 10.1016/j.athoracsur.2010.02.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu C, Jassar AS, Nathan DP, Eperjesi TJ, Brinster CJ, Levack MM, Vergnat M, Gorman RC, Gorman JH, Iii, Jackson BM. Augmented Mitral Valve Leaflet Area Decreases Leaflet Stress: A Finite Element Simulation. The Annals of Thoracic Surgery. 2012;93:1141–1145. doi: 10.1016/j.athoracsur.2012.01.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamauchi H, Vasilyev NV, Marx GR, Loyola H, Padala M, Yoganathan AP, Del Nido PJ. Right ventricular papillary muscle approximation as a novel technique of valve repair for functional tricuspid regurgitation in an ex vivo porcine model. Journal of Thoracic and Cardiovascular Surgery. 2012;144:235–242. doi: 10.1016/j.jtcvs.2012.01.028. [DOI] [PubMed] [Google Scholar]
- Yiu SF, Enriquez-Sarano M, Tribouilloy C, Seward JB, Tajik AJ. Determinants of the degree of functional mitral regurgitation in patients with systolic left ventricular dysfunction: A quantitative clinical study. Circulation. 2000;102:1400–1406. doi: 10.1161/01.cir.102.12.1400. [DOI] [PubMed] [Google Scholar]