Noise in Biology

Abstract

Noise permeates biology on all levels, from the most basic molecular, sub-cellular processes to the dynamics of tissues, organs, organisms, and populations. The functional roles of noise in biological processes can vary greatly. Along with standard, entropy-increasing effects of producing random mutations, diversifying phenotypes in isogenic populations, limiting information capacity of signaling relays, it occasionally plays more surprising constructive roles by accelerating the pace of evolution, providing selective advantage in dynamic environments, enhancing intracellular transport of biomolecules and increasing information capacity of signaling pathways. This short review covers the recent progress in understanding mechanisms and effects of fluctuations in biological systems of different scales and the basic approaches to their mathematical modeling.

1. Introduction

Living world is shaped by the interplay of deterministic laws and randomness Monod (1971). In the past, biologists learned to deal with fluctuations and uncertainty by drawing mostly qualitative conclusions from a large number of observations. However, in the last two decades, the situation began to change with the birth of the emerging field of quantitative biology. Perhaps not coincidentally, within the same timeframe a large contingent of physicists began to look at biology as a fertile ground for new and interesting physics. The new generation of “biological physicists”, many of them trained in nonlinear dynamics and statistical physics, started to view fluctuations not as a nuisance that makes experiments difficult to interpret, but as a worthwhile subject of study by itself. Researchers are finding more and more evidence that noise is not always detrimental for a biological function: evolution can tune the systems so they can take advantage of natural stochastic fluctuations.

All processes in Nature are fundamentally stochastic, however this stochasticity is often negligible in the macroscopic world because of the law of large numbers. This is true for systems at equilibrium, where one can generally expect for a system with N degrees of freedom the relative magnitude of fluctuations to scale as $1/\sqrt{N}$. However, when the system is driven out of equilibrium, the central limit theorem does not always apply, and even macroscopic systems can exhibit anomalously large (“giant”) fluctuations Keizer (1987). There are many examples of this phenomenon in physics of glassy systems, granular packings, active colloids, etc. Biology deals with living systems that are manifestly non-equilibrium, and so it is not surprising that noise plays a pivotal role in many biological processes.

Variability in biological populations is a result of many confluent factors. The most basic one is genetic diversity among individual organisms. This genetic diversity is crucial for survival of the species in an ever-changing environment. However, even genetically identical organisms, such as monoclonal microbial colonies, cloned animals or identical human twins exhibit significant phenotypic variability. Traditionally, this variability was ascribed to environmental fluctuations affecting development of individual organisms (extrinsic noise), but in recent years it has become clear that significant variability persists even when genetically identical organisms are kept under nearly identical conditions (intrinsic noise). Biological fluctuations span multiple spatial and temporal scales from fast cellular and subcellular processes to more gradual whole-organism multi-cellular dynamics to very slow evolutionary and population-level variability. In this review we will consider properties and sources of some of these types of biological fluctuations.

During the past several years, a number of excellent reviews have been published regarding the role of noise and fluctuations in biology, however most of these reviews were written by biologists and published in biological journals Kærn et al. (2005); Fraser and Kærn (2009); Simpson et al. (2009); Wilkinson (2011); Chalancon et al. (2012). This review is written by a physicist with some experience working on biological problems, for physicists interested in exploring and perhaps joining the new and rapidly advancing field of quantitative biology. Biology is very broad, and noise affects all biological processes. This review tries to strike a reasonable compromise between encompassing the breadth of the subject and delving into the complexities of individual systems of interest. We begin with discussion of fluctuations at the cellular level, then give several characteristic examples of noise influencing development of multicellular organisms, and finally we address the effects of fluctuations on the population dynamics. Space constraints did not permit the author to give equal justice to all aspects of this vast and diverse topic. The most glaring omission is perhaps the dynamics of neurons and neural networks that is known to exhibit ample stochasticity. Fluctuations in neuroscience is such a rich subject that it certainly requires a separate review. This review also does not touch upon fluctuations affecting the properties of intracellular transport and cellular mechanics. Instead, we pay the most attention to the fundamental source of stochasticity in biology - noisy gene expression. We show how these fluctuations propagate to the higher level of biological organization and affect crucial biological functions such as decision making, development, spatiotemporal population dynamics and even evolutionary processes.

2. Stochasticity in Cell Biology

The chief source of stochastic variability on the cellular level is the intrinsic thermal fluctuations of biochemical reactions driving gene expression, signaling, cell cycle, motility, etc. These reactions occur through random collisions and transient binding of various molecular species within a single cell. In macroscopic systems randomness of inter-molecular collisions is negligible because of very large numbers of participating molecules. But most biological molecules (chromosomes, RNAs, proteins) are present inside a cell in very small numbers. According to mass spectrometry measurements Ishihama et al. (2008), the median copy number of all proteins in a single bacterium E. Coli is approximately 500, and 75% of all proteins have a copy number of less than 250. The copy numbers of RNAs often number in tens, and the chromosomes (and so the majority of the genes) are usually present in one or two copies. Therefore, the reactions among these species can be prone to significant stochasticity.

2.1. Transcription and translation

The central dogma of molecular biology stipulates that proteins that are main structural blocks of life, are produced within the cells in two steps: genes are transcribed to synthesize messenger ribonucleic acids (mRNAs) and the latter in turn are translated to make proteins. These reactions are often modeled as zeroth- and first-order Markovian “birth” reactions ∅ → m, m → p characterized by rates k_m and k_p, respectively. The accumulation of RNAs and proteins is limited by first-order “death” reactions of degradation for mRNAs and proteins, m → ∅, p → ∅ with rates γ_m and γ_p, respectively. If fluctuations were negligible, the numbers of mRNA and protein molecules would evolve according to the ordinary differential equations

$$\frac{dm}{dt}=k_m-{\gamma }_{m}m,\frac{dp}{dt}=k_{p}m-{\gamma }_{p}p$$ (1)

(deterministic mass-action approximation), and eventually reach fixed stationary levels $m_s=\lambda =k_m{\gamma }_m^{-1}$, p_s = k_mk_p(γ_mγ_p)⁻¹. To account for stochasticity due to finite numbers of participating molecules and probabilistic reaction events, one can write a chemical master equation for the two-dimensional probability distribution to have m transcripts and p proteins at time t,

$$\frac{dP(m,p,t)}{dt}=k_m[P(m-1,p,t)-P(m,p,t)]+{\gamma }_m[(m+1)P(m+1,p,t)-mP(m,p,t)]+k_{p}m[p(m,p-1,t)-P(m,p,t)]+{\gamma }_p[(p+1)P(m,p+1,t)-pP(m,p,t)]$$ (2)

In most cases chemical master equations cannot be solved analytically, and their solutions can be approximated by averaging over an ensemble of stochastic trajectories. Such trajectories can be generated using so-called Stochastic Simulation Algorithm (SSA) Gillespie (1976). In this algorithm, often referred to as direct Gillespie algorithm, time to the “next reaction” is computed based on the current state of the system under the Markovian assumption that all reactions are Markovian. For a system of N species comprising a state vector x = {x₁, …x_N} at time t and M possible reactions with propensities w_m(x), the time to the next reaction Δt is selected from an exponential distribution with the mean 1/w(x) where w(x) = ∑ w(x) is the total rate of all possible reactions. The type of the next reaction is chosen among the M possibilities with the probabilities w_m(x)/w(x). Time t is advanced to time t + Δt and the numbers of molecules in each species are updated according to the stoichiometry of the chosen reaction. Thus, the system “jumps” from one individual reaction event to the next and generates an exact stochastic trajectory. Generating enough of these trajectories allows one to compute the probability distributions of the participation species with arbitrary accuracy. This direct method was later improved and made more computationally efficient while still keeping it exact by Gillespie and others Gillespie (1977); Gibson and Bruck (2000). It was first introduced to the field of gene regulatory networks by McAdams and Arkin (1997) and has since become very popular. Still, this brute-force approach in most realistic cases is computationally prohibitive. Many approximate computational methods were proposed in recent years that take advantage of certain small or large parameters. For example, if some reactions are slow and others are fast, one can expect the fast reaction channels to equilibrate between two rare firings of slow reactions. This forms the basis of so-called tau-leap method and its modifications Gillespie (2001); Rathinam et al. (2003); Cao et al. (2005). One can also apply hybrid algorithms which treat fast reactions using Langevin equations (or even deterministic ODEs) Haseltine and Rawlings (2002) (see also Gillespie (2007) for a review of various stochastic simulation algorithms).

Eq. (2) has only zero- and first-order reactions, and therefore it is analytically solvable. For example, differential equations for moments which can be easily derived from the master equation, do not contain higher moments and can be solved sequentially Thattai and van Oudenaarden (2001). The equations for the first moments (means) of the mRNA and protein distributions coincide with the mass-action approximation (1). The stationary variance of the mRNA distribution V_m = 〈m²〉−〈m〉² is equal to the mean m_s, which can be expected since the stationary distribution of mRNA molecules is evidently Poissonian (simple birth-death process). However, the distribution of proteins is broader than Poissonian, with variance that can be much larger than the mean

$$V_p=p_s[\frac{k_p}{{\gamma }_p+{\gamma }_m}+1]$$ (3)

A similar result for the protein distribution in a growing and dividing cell population in the absence of protein degradation was obtained much earlier by Berg (1978). This protein distribution broadening is caused by the so-called “translational bursting”, since every molecule of mRNA can produce a random integer number of proteins before it is degraded. The mRNA is translated after it binds to a ribosome (the latter actually prevents it from being rapidly degraded). It is can be shown that if mRNA binding to a ribosome and degradation and are two mutually exclusive reactions with fixed rates, the distribution of the number of proteins synthesized per single mRNA is geometric McAdams and Arkin (1997),

$$\nu (p)=\frac{1}{1+b}{\left(\frac{b}{1+b}\right)}^p$$ (4)

where b = k_p/γ_m is the mean number of proteins synthesized by a single transcript (translational efficiency). In the limit of large b the distribution approaches exponential ν(p) = b⁻¹ exp(−p/b). Figure 1 shows typical time series of protein numbers obtained by the direct Gillespie method in cases of weak (small b) and strong (large b) bursting. Of course, if many mRNAs are present in the cell at the same time, there may not be actual bursts of translational activity, however the protein distribution will still be much wider than Poisson.

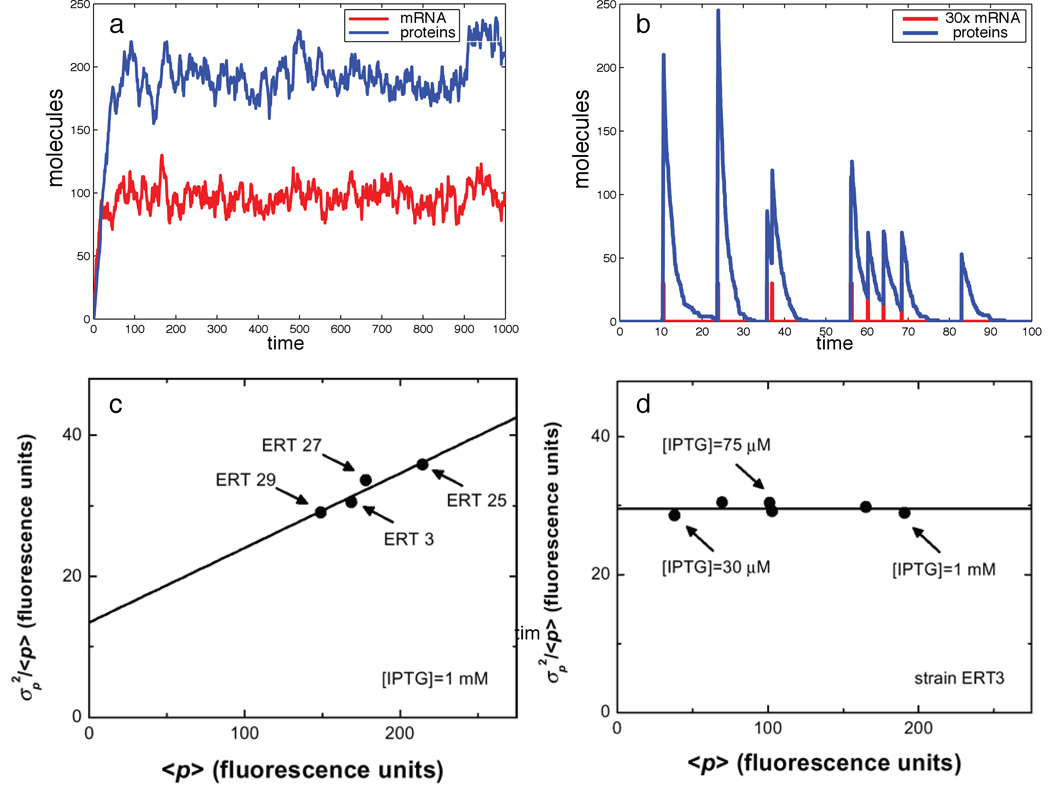
Figure 1.

Translational bursting: Time series of the protein concentration in stochastic simulations using Gillespie algorithm for (a) weak bursting, k_m = 10, k_p = 0.1, γ_m = 0.1, γ_p = 0.05, b = 1, and (b) strong bursting, k_m = 0.1, k_p = 1000, γ_m = 10, γ_p = 0.5, b = 100. (c,d) Experimentally measured Fano factor of a GFP distribution in a monoclonal bacterial population exhibits (c) strong positive correlation with the translational efficiency (ERT3, 25, 27, 29 are four mutant strains with different translation rates), but (d) shows no dependence on the transcription rate (varied by inducer concentration for a single ERT3 strain) Ozbudak et al. (2002).

Ozbudak et al. (2002) set out to test the above theoretical predictions by measuring the distribution of the green fluorescent protein in a monoclonal population of Bacillus subtilis and independently varying transcriptional and translational rates. The transcriptional rate was regulated by the concentration of IPTG (a chemical inducer), and the translation rate was modified by introducing point mutations in the ribosome binding site (RBS) and the initiation codon of the gfp gene. The strong correlation was indeed observed between the normalized width of the distribution (Fano factor, or the ratio of the variance to the mean) and the translation rate of the GFP proteins (see Fig. 1,c). In contrast, varying the transcriptional efficiency (by changing inducer concentration) did not affect the Fano factor, in agreement with the theoretical predictions (see Fig. 1,d).

Using a microfluidic-based assay in which single cells can be trapped within enclosed observation chambers, Cai et al. (2006) were able to measure the temporal fluctuations of highly fluorogenic protein β-galactosidase in E. coli cells with single molecule sensitivity in real time (see also Yu et al. (2006)). They indeed observed bursts of protein production which had exponential distribution of molecules per burst.

Friedman et al. (2006) introduced a simple model of translational bursting. This model is based on the assumption that bursting is fast compared with protein degradation, i.e. each mRNA molecules instantaneously produces random number of protein molecules. Ignoring discreteness of protein numbers, this process can be described by a continuum master equation for the protein probability distribution P(p, t),

$$\frac{dP(p,t)}{dt}=\frac{\partial }{\partial p}[\gamma pP(p,t)]+{\int }_0^{p}dp\prime w(p,p\prime )P(p\prime ,t)$$ (5)

Here the first term in the r.h.s. describes exponential degradation of the proteins with rate γ, and the second term describes discontinuous (“bursty”) synthesis of proteins. The transition probability w(p, p′) of having p proteins at time t+ and p′ proteins at time t− can be written in the form w(p, p′) = k[ν(p−p′)−δ(p−p′)] where ν(x) denotes the probability distribution of making a burst of x proteins (it is assumed stationary and independent of the current number of proteins p′). This master equation can be solved using the Laplace transform. For the exponential distribution of burst sizes, ν(x) = b⁻¹ exp(−x/b), the exact stationary solution of Eq. (5) has the form of a Gamma distribution,

$$P(p)=\frac{p^{a-1}{e}^{-p/b}}{b^a\mathrm{\Gamma }(a)}$$ (6)

The stationary protein distribution is characterized by two parameters, the mean burst frequency a = k/γ and the mean burst size b which also are equal to the ratio of variance ${\sigma }_p^2$ to the mean square of the proteins 〈p〉² (or inverse square of the coefficient of variation, CV = σ_p/〈p〉), and the Fano factor (ratio of the variance to the mean), respectively. This Gamma distribution is a continuum limit of the negative binomial distribution derived earlier by Paulsson and Ehrenberg (2000) for protein molecules produced in random geometrically-distributed bursts. It can also be obtained in the continuum limit from an explicit solution of the two-dimensional master equation for mRNA and proteins in the limit of long-lived proteins and short-lived mRNA Shahrezaei and Swain (2008). Recent high-throughput quantitative measurements of mRNA and protein expression with single-molecule sensitivity Taniguchi et al. (2010) indeed showed that almost all protein number distributions in E. coli could indeed be well-fitted by the Gamma distribution (6). However, the distribution of fitting parameter a showed a non-trivial dependence on the protein abundance 〈p〉: for low-abundance proteins, it scaled inversely with 〈p〉, as could be expected from the above model. However, high-abundance proteins (roughly 〈p〉 > 10) showed no dependence on 〈p〉, which may imply a different, most likely extrinsic source of fluctuations. If parameters a and b of the Gamma distribution (6) vary slowly, with arbitrary but peaked distributions f(a), g(b), (CV_a, CV_b < 0.3) the resulting distribution P(p̄) = ∫ ∫ P(p)f(a)g(b)dadb is still well-approximated by the Gamma distribution Taniguchi et al. (2010). However, the coefficient of variation of p in this case approaches $C{V}_a^2+C{V}_b^2+C{V}_a^{2}C{V}_b^2$ and independent on 〈p〉.

Under closer inspection, this relatively simple picture of protein synthesis begins to show strong limitations. On one hand, the transcription rate of a gene itself does not remain constant in time but is known to fluctuate, which leads to so-called transcriptional bursting. These bursts of mRNA synthesis were observed by Golding et al. (2005) in E. coli by an ingenious method of visualization of individual mRNA molecules. Similar bursts of transcription activity were also observed in other organisms Raj et al. (2006); Chubb et al. (2006). This stochastic variability of transcriptional activity can be caused by a multitude of global factors such as fluctuations of the number of RNA polymerase (RNAP) molecules and other components of transcriptional machinery (for example, σ-factors that assist RNAP binding to promoters), changes in the chromatin structure, error-correction mechanisms leading to pausing and even backtracking in the nascent RNA synthesis, etc. The transcription rate of a specific protein is also modulated by the regulatory intracellular units such as transcription factor proteins or small interfering RNAs (siRNA) whose abundance itself can fluctuate greatly. Kepler and Elston (2001) studied statistics of stochastic gene expression modeling gene activation/deactivation as a random telegraph process, see also Paulsson (2005); Sánchez and Kondev (2008) for review and generalization to arbitrarily multi-state promoter dynamics.

On the other hand, even seemingly “elementary” transcription and translation reactions are in fact very complex multi-staged biochemical reactions. For example, transcription of a single gene in a eukaryotic cell starts from initiation, or forming a so-called pre-initiation complex consisting of six sequentially recruited transcription factors that help position RNA polymerase (RNAP) over gene transcription start sites and locally unwind DNA double helix. Then a RNAP binds and begins elongation, or assembly of the nascent RNA chain which itself is a sequence of hundreds of reactions of binding of individual nucleotides. This process ends by the termination mediated by specific transcription termination factors. After that the nascent RNA chain goes through the process of splicing which is also a complex chain of biochemical reactions. Thus, even if individual steps were Markovian, the transcription taken as a whole cannot be described as a memoryless Poisson process. A somewhat more realistic approach to modeling multistep biochemical reactions such as transcription or translation consists in imposing a fixed or distributed time delay between the reaction initiation and the resulting change in the stoichiometry. Delayed reaction steps can lead to many interesting phenomena in gene expression, including oscillatory dynamics Lewis (2003); Bratsun et al. (2005); Morelli and Jülicher (2007); Mather et al. (2009). Furthermore, since many RNAP can move simultaneously on a single DNA track, they can interfere with each other’s progress Zia et al. (2011). This basic interaction can be abstracted in the form of a totally asymmetric simple exclusion process, or TASEP. It was first introduced by MacDonald et al. (1968) in the context of translation where multiple ribosomes may move along the same mRNA, and similar traffic jams may occur.

To make things even more complicated, the translocation of RNAP along the DNA chain is far from uniform, and is characterized by pausing Herbert et al. (2006) or even backtracking Nudler (2012). This leads to a broad distribution of the time intervals between successive RNAP steps Abbondanzieri et al. (2005), and consequently to heavy-tailed distribution of transcription elongation times and transcriptional bursting. A number of recent papers addressed the mechanisms of this intermittency, e.g. Voliotis et al. (2008); Ribeiro et al. (2009); Ó Maoiléidigh et al. (2011) which broadly are based on the Brownian ratchet model. Yamada and Peskin (2009) proposed an interesting “look-ahead” model of RNAP translocation which assumed that the RNA elongation happens in parallel within a certain transcription “bubble” and found that the bubble width of 4 nucleotides describe well the translocation waiting time distribution and the average speed of elongation. However, this model has yet to be tested experimentally. Voliotis et al. (2008) found that RNAP pausing Herbert et al. (2006) and possible backtracking Shaevitz et al. (2003) lead to a

2.2. Intrinsic vs. extrinsic noise

As we mentioned in the previous section, the stochastic fluctuations in the level of cellular components can be caused by the multitude of factors. They can roughly be divided into two categories: intrinsic and extrinsic. Intrinsic noise refers to the stochastic fluctuations within the system under consideration, usually caused by the inherently probabilistic nature of the underlying biochemical reactions. The stochastic processes outside the system under consideration may serve a source of extrinsic noise. Following Swain et al. (2002), we can introduce the probability distribution for the intrinsic I and extrinsic E components of noise, p(I, E), and assume that the observable x is a function of both I and E. Then the k-th moment of x can be written as

$$M_k[x]=\int d\mathbf{E}d\mathbf{I}{x}^k(\mathbf{I},\mathbf{E})p(\mathbf{I},\mathbf{E})=\int d\mathbf{E}p(\mathbf{E})\int d\mathbf{I}{x}^k(\mathbf{I},\mathbf{E})p(\mathbf{I}|\mathbf{E})=\overline{\langle x^k\rangle }$$ (7)

According to this formula, the moments can be determined by first conditional averaging over intrinsic fluctuations under fixed extrinsic noise (angular brackets) and the subsequent averaging over extrinsic variability (overbar). Using this notation, one can immediately see that the coefficient of variation of x is a linear sum of intrinsic and extrinsic components:

$$C{V}^2=\frac{\overline{\langle x^2\rangle }-{(\overline{\langle x\rangle })}^2}{{(\overline{\langle x\rangle })}^2}=\frac{\overline{\langle x^2\rangle -{\langle x\rangle }^2}}{{(\overline{\langle x\rangle })}^2}+\frac{\overline{{\langle x\rangle }^2}-{(\overline{\langle x\rangle })}^2}{{(\overline{\langle x\rangle })}^2}=C{V}_{\mathit{\text{int}}}^2+C{V}_{\mathit{\text{ext}}}^2$$ (8)

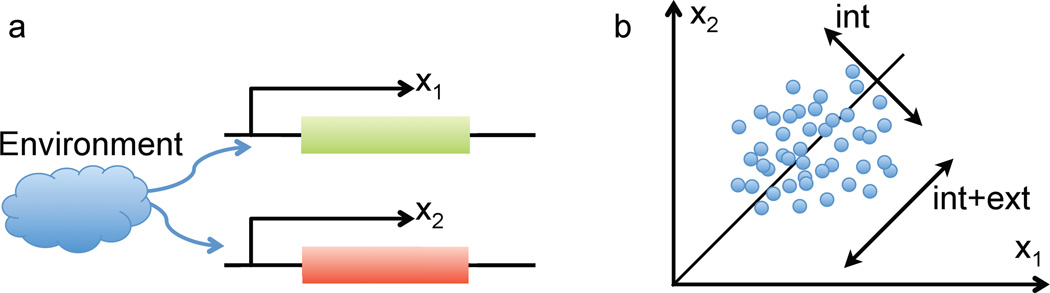
How can one experimentally measure relative contributions of intrinsic and extrinsic sources to the level of noise in a fluctuating intracellular system? An elegant way to quantify the sources of gene expression noise was proposed by Swain et al. (2002) and implemented by Elowitz et al. (2002). In this dual-reporter method, identical promoters drive transcription of two genes that produce distinguishable, but otherwise nearly identical proteins (Fig. 2A). If extrinsic sources of noise affect both promoters identically, in the absence of intrinsic noise the amount of both gene products protein in a cell would be the same at all times. This explicitly relies on the assumption that under the same extrinsic conditions both genes are transcribed and translated with the same efficiency, and both proteins degrade at the same rate. Thus, the magnitude of the difference in protein levels in different cells across a large population gives us a measure of the intrinsic noise, whereas the magnitude of the overall fluctuations characterizes the sum of intrinsic and intrinsic noise contributions. More formally, measuring x₁ and x₂ and computing $\overline{\langle x_1\rangle }=\overline{\langle x_{1,2}\rangle },\overline{\langle x_1^2\rangle }=\overline{\langle x_{1,2}^2\rangle },\text{and}\overline{\langle {(x_1-x_2)}^2\rangle }=2[\overline{\langle x^2\rangle }-\overline{{\langle x\rangle }^2}]$ allows one to find CV_int and CV_ext separately using Eq. (8). A simple graphical way to characterize the magnitudes of intrinsic vs. extrinsic noise it to create a scatter plot of (x₁, x₂) pairs for each cell in a population and estimate the widths of the resulting two-dimensional distribution along and perpendicular to the the diagonal x₁ = x₂. In the absence of intrinsic noise the points would be confined to the diagonal. In the presence of intrinsic noise but in the absence of the extrinsic noise the points will be scattered according to a wide distribution which is a direct product of two identical one-dimensional distributions for individual proteins (assuming that intrinsic noise is statistically independent for both observables). Thus, the width of the distribution perpendicular to the diagonal may serve as the measure of the intrinsic noise (see Fig. 2B).

Figure 2.

Dual-reporter method of separation of intrinsic and extrinsic noise: (a) two identical promoters driving different color fluorescent proteins; (b) scatter plot of two color fluorescence within a clonal population on a two-dimensional plane. The width of this distribution along and perpendicular to the diagonal characterizes the levels of extrinsic and intrinsic noise, respectively.

Strictly speaking, the dual-reporter method tacitly assumes that the environmental fluctuations are slow compared with the intrinsic fluctuations. As pointed out by Hilfinger and Paulsson (2011), in many biologically relevant conditions, the time scales of extrinsic and intrinsic fluctuations are comparable. Therefore the vector of extrinsic fluctuations E which was used above, has to include not just instantaneous values of extrinsic variables, but the temporal histories of the latter. This implies that in such cases a naive application of the dual-reporter method to quantification of noise sources may lead to systematic errors. Hilfinger and Paulsson (2011) proposed an alternative method of computing the extrinsic noise by time averaging the covariance between the two reporters Cov(x₁, x₂) = 〈〈x₁x₂〉〉_t − 〈〈x₁〉〉_t〈〈x₂〉〉_t. Here the inner brackets denote ensemble average, and the outer brackets denote the time average. Since presumably the two time series x₁ and x₂ share the same environmental history, this covariance should correctly characterize the variance of reporter fluctuations due to the extrinsic noise.

Elowitz et al. (2002) constructed a synthetic dual-reporter system in bacteria E.coli using yellow and cyan alleles of the green fluorescent proteins driven by the same P_lac promoter. Rather than putting them on a separate plasmid, they incorporated them into a single chromosome at equal distances from the origin of replication to ensure that the number of copies of each gene-promoter pair is exactly the same in every cell, and the rates of their transcription are as similar as possible. Since this is a fundamental assumption underlying the dual-reporter method, they checked that univariate distributions of both proteins were indeed very similar. When the P_lac promoter was fully active (in the strain that did not have lacI repressor gene), the overall noise level was rather small (CV ≈ 0.077) with similar contributions of intrinsic and extrinsic noise (CV_int ≈ 0.055, CV_ext ≈ 0.054). In a wild-type E. coli, LacI protein binds to the P_lac promoters and strongly represses transcription of both YFP and CFP. As expected, the smaller mean level of proteins contributed to the larger intrinsic noise levels (CV_int ≈ 0.19). Interestingly, the level of extrinsic noise increased even more, to CV_ext = 0.32, which presumably is explained by strong fluctuations of LacI levels across the cell population. Raser and O’Shea (2004) performed a similar experiment and analysis for eukaryotic cells by quantifying the difference in expression of two alleles in diploid budding yeast S. cerevisiae. They placed two fluorescent proteins (YFP and CFP) under control of identical promoters at exactly the same loci on two homologous chromosomes and obtained a much smaller fraction of intrinsic noise in the overall fluctuations of the fluorescence compared to bacteria (typically only 2–3%). This is to be expected because the intrinsic noise of constitutively expressed protein should scale inversely proportional to the square root of the mean number of protein molecules, and much bigger eukaryotic cells typically feature a much larger quantities of proteins expressed.

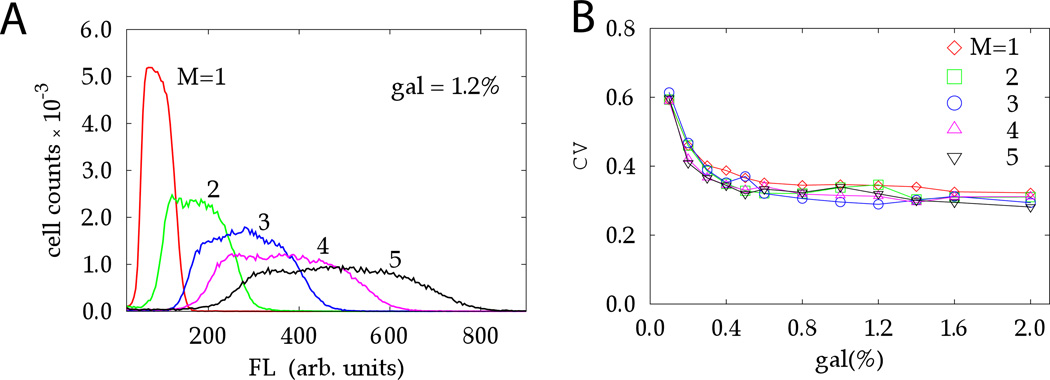
An alternative method of estimating the significance of intrinsic vs. extrinsic noise in gene expression that does not require the two-color technique was proposed by Volfson et al. (2005). This method is based on a simple observation that if multiple copies of a gene are present in the cell, and only intrinsic noise is present which is uncorrelated among the copies, the RNAs of the protein concentration will scale inversely proportional to the square root of the copy number. However, if all genes are affected by the same extrinsic noise, then the CV should be independent of the copy number. The analysis of fluctuations of fluorescence in five mono-clonal populations of S. cerevisiae with varying number M = 1, …, 5 of GFP genes embedded in the chromosome under the control of identical native GAL1 promoters showed, in agreement with the dual-reporter studies, that the gene expression in yeast is indeed dominated by the extrinsic noise (Fig. 3).

Figure 3.

Statistics of gene expression from multiple identical gene-promoter pairs in budding yeast Volfson et al. (2005): (a) Histograms of GFP measurements for copy numbers varying from M = 1 to 5; (b) Coefficient of variation for different copy number collapses on a single curve, which implies an extrinsic source of variability

What are the dominating sources of the extrinsic noise that causes fluctuations in gene expression? Volfson et al. (2005) suggested that large variability in gene expression across a cell population can be caused by the population dynamics, since even a monoclonal population consists of growing and dividing cells in different phases of their cell cycle. Using a mathematical model of population dynamics incorporating random divisions of cells, they showed that it accounts for much of the apparent extrinsic variability in monoclonal yeast populations. This mechanism should be distinguished from recently analyzed random partitioning of molecules at division Huh and Paulsson (2011) which contributes to both the extrinsic and intrinsic noise in gene expression, since it generates uncorrelated random fluctuations of copy number of participating molecules at division. Other factors, such as common upstream regulators, chromatin remodeling, and cell cycle related variability, can also contribute to the experimentally observable levels of extrinsic noise.

2.3. Gene regulatory networks

As already mentioned above, the level of expression of a particular gene (the abundance of the corresponding mRNA and protein) can be modulated by so called transcription factors (TFs). TFs themselves are proteins whose concentration can be controlled by their own transcription factors, and so on. Thus, complex gene regulatory networks are formed. A full stochastic description of such networks in principle could be based on solving the corresponding chemical master equation. However, even if one ignores the complexity of individual transcription/translation reactions discussed above, solutions of multi-dimensional master equations are rarely possible. If the system only involves zero- and first-order reactions (reaction rates are linear functions of abundances), the time-dependent moments of the corresponding distributions can still be found, for example, by using generating function approach. Thattai and van Oudenaarden (2001) obtained explicit expressions for the mean 〈p〉 and variance V_p of the protein distributions in a simple autoregulatory motif when the transcription of a single gene is linearly repressed by its own protein product (the instantaneous transcription rate is a linear function of the abundance p of the repressor protein, k_p − k₁p):

$$\langle p\rangle =\frac{1}{1+b\varphi }\frac{k_m{k}_p}{{\gamma }_m{\gamma }_p};V_p=\langle p\rangle [\frac{1-\varphi }{1+b\varphi }\frac{k_p}{{\gamma }_p+{\gamma }_m}+1]$$ (9)

where parameter ϕ = k₁/γ_p characterizes the strength of the negative feedback. These expressions show that negative autoregulation reduces the strength of stochastic fluctuations. A general scheme of solving the chemical master equation for systems containing only zero- and first-order reactions is described in Gadgil et al. (2005).

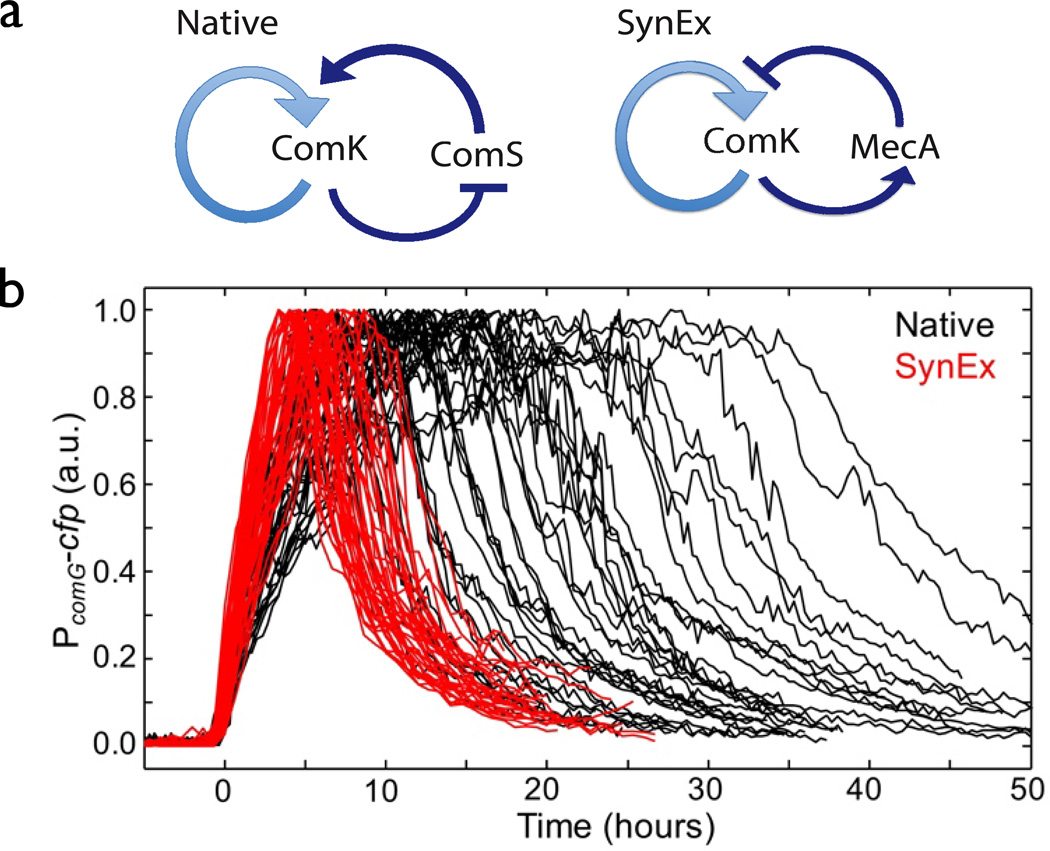
Similar functional performance can, in principle, be achieved in different network architectures. For example, a 2-stage negative feedback loop (NFL) can be based on repression of an activator or activation of a repressor. The competence system in bacterium Bacillus subtilis which will be discussed in more detail in Sec. 2.5) features the core circuit in which the master regulator ComK represses synthesis of its own activator protein ComS forming a 2-stage NFL. Çağatay et al. (2009a) compared the noise performance of this native NFL circuit with a synthetic circuit featuring an alternative architecture that employs activation by ComK of its repressor MecA (Fig. 4a). These two circuits have similar mean-field dynamics (the synthetic circuit can be tuned to produce a similar average level of competence), but they exhibit distinctly different statistics of stochastic fluctuations: the synthetic circuit exhibits a much narrower distribution of competence duration times (Fig. 4,b). Presumably, in unpredictable and fluctuating environments, significant variability of competence duration can confer a fitness advantage on the bacterial population as a whole.

Figure 4.

Comparison of two different NFL architectures Çağatay et al. (2009a): (a) Native repressed activation circuit in the competence system of B. subtilis and a synthetic activated repression circuit SynEx, (b) Single-cell time series of fluorescence that track competence in native (black) and synthetic (red) cells.

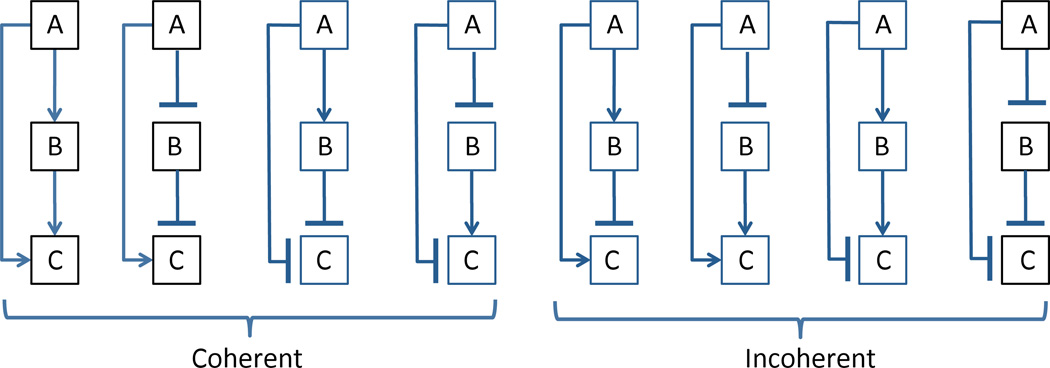
A more complex case of 3-node feed-forward loops (FFLs) have been studied by Kittisopikul and Süel (2010) There are 8 possible different types of FFLs (see Fig. 5), all of them can be found in various regulatory systems of E. coli. These architectures can be divided into two classes of coherent and non-coherent types, depending on whether the direct path from gene A to C works in accord with the indirect path or not. Coherent and non-coherent gene regulatory loops show markedly different dynamical behavior Alon (2007). But why are there multiple types of either coherent or non-coherent FFLs present within E. coli genome? One plausible explanation proposed by Kittisopikul and Süel (2010) is that these different architectures exhibit qualitatively different noise performance, and depending on the biological function, different noise properties may be beneficial. By clustering various regulatory circuits according to their functional role, they found that circuits involved in anaerobic metabolism featured FFL architectures with higher noise in their “on” states than in the “off” states, whereas stress response circuits exhibited significant enrichment of FFLs with the opposite characteristics. While many other “housekeeping” systems did not exhibit a significant preference for FFL architectures based on their noise performance (which can quite naturally be explained by the the dominant role of other factors in their selection), the observed correlation between the functional roles and the specific architectures is highly suggestive that noise performance may play a significant role in shaping the ability of biological systems to respond to distinct environmental conditions.

Figure 5.

Eight possible architectures of feed-forward loops

Unfortunately, the dynamics of gene regulatory networks are typically nonlinear (due to cooperativity, bi-molecular reactions, enzymatic processing, etc.), and therefore analytical expressions for noise performance like (9) generally cannot be found. One way to deal with such systems is to assume that the system always fluctuates very close to a deterministic (macroscopic) trajectory or a fixed point. That forms the basis of the so-called linear noise approximation (LNA) based on the Ω-expansion Van Kampen (1992). Using this approach, a full covariance matrix of molecular fluctuations can be computed from the chemical master equation Elf and Ehrenberg (2003); Paulsson (2004). If, however, the system does not remain close to a fixed point but performs a large excursions away from fixed points or deterministic trajectories, using LNA or its variants is not appropriate. In these circumstances, researchers typically resort to numerical simulations of the underlying biochemical reactions. One particularly important type of such strongly nonlinear and stochastic biological behavior is “genetic switches” that control cellular decisions in uncertain environments. This type of noisy dynamics is described later in Section 2.5.

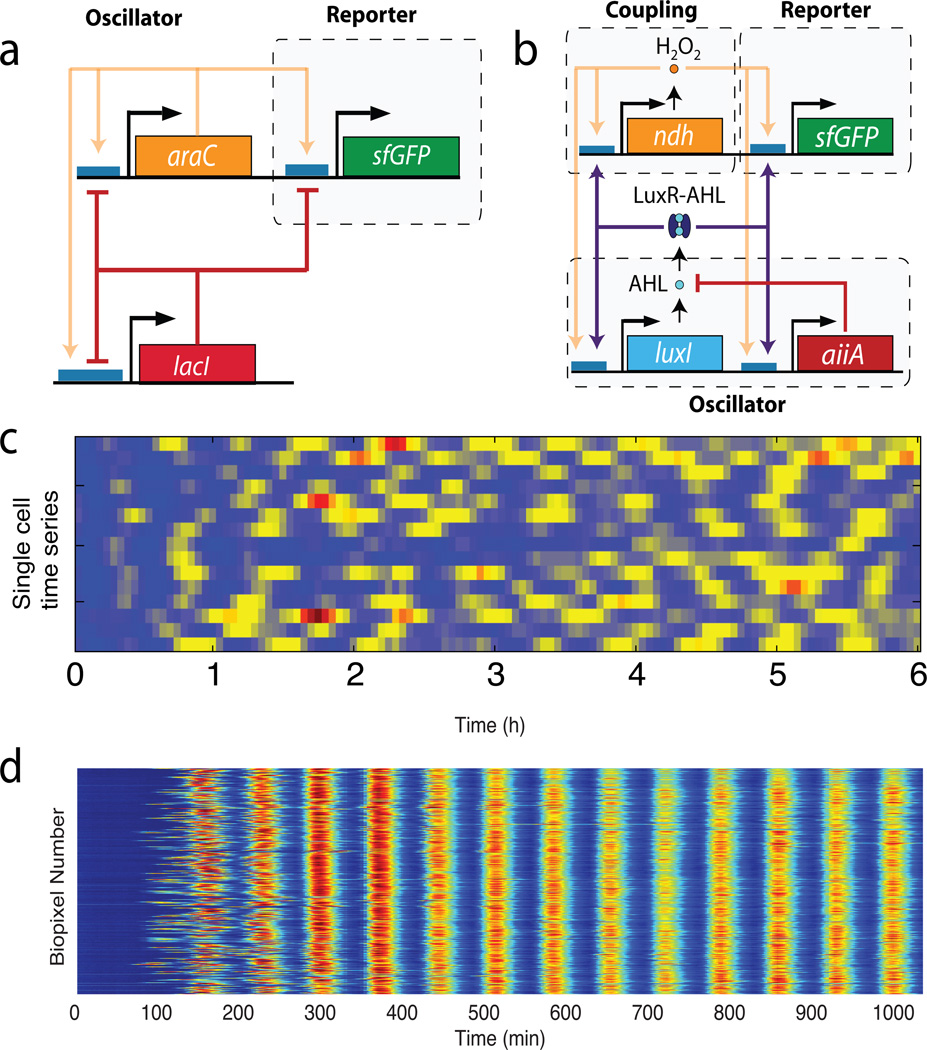
Another important class of gene circuits with non-trivial dynamical behavior are gene oscillators. Clocks play a key role in coordinating biological processes on multiple spatial and temporal scales, from individual cells to whole organisms, and from fast electrical oscillations in neurons to respiratory, glycolytic oscillations, cell division cycles to circadian rhythms. Native biological clocks are usually rather complex, with multiple layers of regulation Zhang and Kay (2010), although core gene circuits containing just a few elements have been identified in a number of cases (note however that not all native clocks are based on gene regulation, e.g. circadian clock in cyanobacteria entirely relies on phosphorylation processes Golden and Canales (2003)). In parallel to theoretical and modeling studies of native clocks, there has been a significant recent progress in forward engineering of small genetic networks generating oscillations, beginning from the seminal repressilator, in which three genes form a small loop in which one gene expressed the transcription factor that repressed expression of next one Elowitz and Leibler (2000). An even simpler 2-gene design based on a combination of one positive and one negative feedback loop was shown to exhibit robust and highly tunable oscillations Stricker et al. (2008) (see Fig. 6a). Such small circuits allow us to study the mechanisms of oscillations in greater depth and develop meaningful, yet analytically treatable models Mather et al. (2009). However, small gene oscillators they are prone to large stochastic variability of amplitudes and periods (Fig. 6c). This variability can be effectively reduced be using cell-cell coupling to coordinate the oscillatory activity of individual cells within a population. Such strategy is often used in natural settings, for example, in synchronization of oscillators driving embryo segmentation Horikawa et al. (2006). Danino et al. (2010); Prindle et al. (2011) used two modes of inter-cellular communication (quorum sensing machinery within individual micro-colony and redox signaling coupling colonies together) to achieve long-range synchronization of synthetic oscillators within a whole microfluidic device (Fig. 6b). As expected, the synchronized oscillations also have much higher temporal coherence (Fig. 6d).

Figure 6.

Synthetic gene oscillators: (a) network diagram os the single-cell gene oscillator Stricker et al. (2008): Gene araC expresses transcriptional activator AraC that activates its own transcription and that of the gene lacI and reporter sfGFP. The latter expresses transcriptional repressor LacI that represses itself, araC, and sfGFP; (b) Network diagram of the synchronized gene oscillator Prindle et al. (2011): The luxI promoter drives expression of luxI, aiiA, ndh, and sfGFP genes. The quorum-sensing genes LuxI and AiiA generate synchronized oscillations in a micro-colony within a single microfluidic chamber (“biopixel”) via quorum-sensing molecule AHL. NDH-2 protein generates H2O2 vapor, an additional activator of the LuxI promoter that migrates among colonies and synchronizes them; (c) time series of fluorescence in individual cells for the single-cell oscillator showing strong fluctuations in period and amplitude (adapted from Mondragón-Palomino et al. (2011)); (d) highly synchronized and regular oscillations in massively synchronized population of E. coli cells within a microfluidic device Prindle et al. (2011).

2.4. Information transmission in signaling cascades

Life depends on the ability of organisms to receive, process, and transmit information. Information flows occur on all scales, from population-wide social interactions and whole-organism sensory signals, all the way down to inter- and intra-cellular communication. Capacity of all these information channels is noise-limited, but cell signaling cascades provide an especially important class of biological networks constrained by intrinsic and extrinsic stochastic variability.

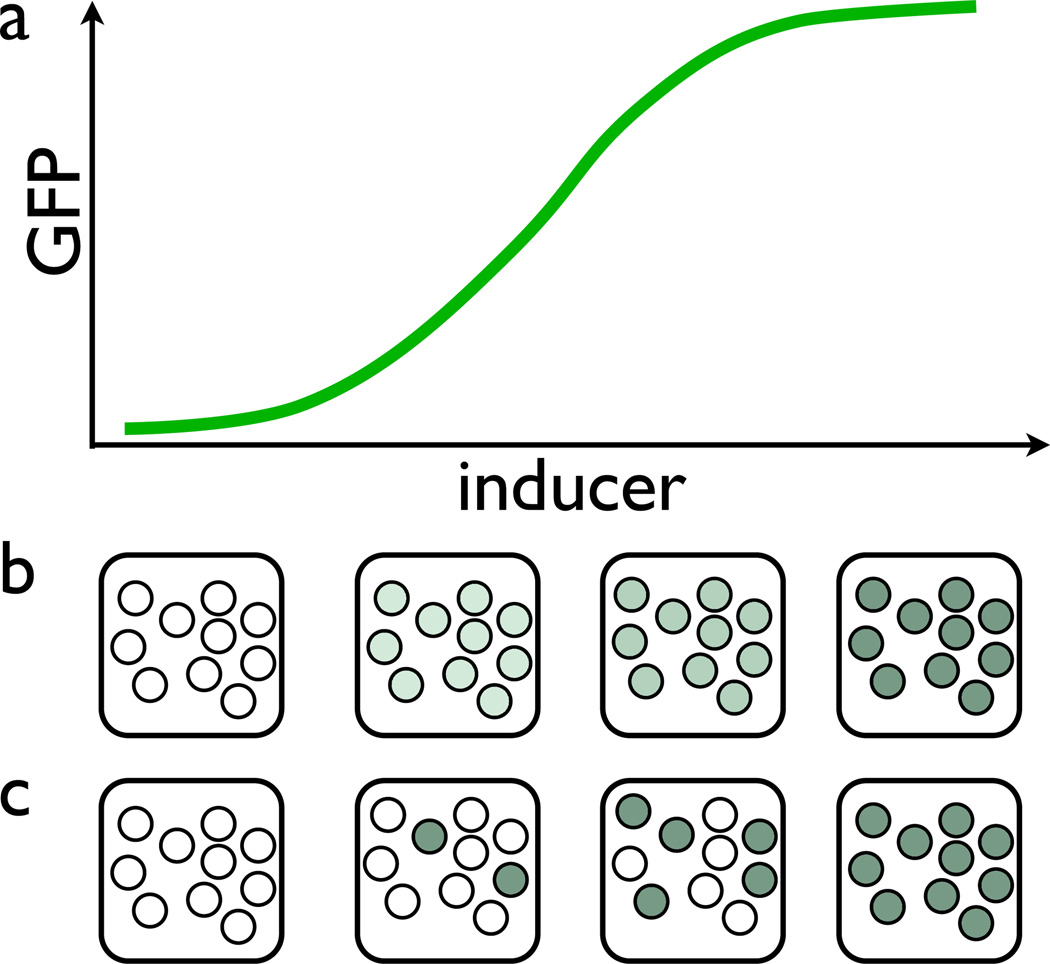
Until recently, most of the data on signaling response was collected using population-averaging methods such as Western blots or microarrays, but these approaches can often mask the important dynamical and stochastic aspects of the system response. For example, graded average response to an increased concentration of a signaling molecule may be an indication of a graded response of individual cells or a binary, but heterogeneous response with increased probability of the “on” state at higher concentration of inducer (Fig. 7). A graded chemotactic response to a transient cAMP stimulation is usually observed in a population of amoebae Dictyostelium discoideum. However, recent single-cell microfluidic experiments Wang et al. (2012) showed that the graded population-averaged response is, in fact, cased by a continuum increase of the fraction of “on” cells in an essentially bimodal population of cells. Another example of qualitatively different single-cell and population-wide signal response is presented by the NFκB immune response system: individual cells exhibit strong oscillations in nuclear localization of NFκB molecules however these oscillations are strongly dampened in the bulk because they are not phase-synchronized Paszek et al. (2010).

Figure 7.

Two alternative possibilities of producing a graded signaling response in a population: (a) a typical dose-response curve; (b) uniform graded response of individual cells; (c) binary but heterogeneous response of individual cells

Generally, one can view a signaling cascade as an input-output system with one or more inputs (signal, S) and outputs (response, R). The fidelity of signaling cascades can be characterized using information-theoretic concept of the mutual information (MI) between the signal and the response Shannon and Weaver (2002). If the joint probability distribution of signal and response is P(S, R), and P(S), P(R) are the marginal distributions of S and R, the MI is defined as

$$I={\int }_{\mathbf{S}}{\int }_{\mathbf{R}}P(\mathbf{R},\mathbf{S})\text{log}\left(\frac{P(\mathbf{R},\mathbf{S})}{P(\mathbf{R})P(\mathbf{S})}\right)d\mathbf{R}d\mathbf{S}$$ (10)

It can also be expressed as I = H(R) − H(R|S), the difference between the entropy of the output signal

$$H(\mathbf{R})=-{\int }_{\mathbf{R}}P(\mathbf{R})\log P(\mathbf{R})d\mathbf{R},$$ (11)

and the entropy of the input signal conditioned by the input signal

$$H(\mathbf{R}|\mathbf{S})=-{\int }_{\mathbf{S}}d\mathbf{S}{\int }_{\mathbf{R}}P(\mathbf{R}|\mathbf{S})\log P(\mathbf{R}|\mathbf{S})d\mathbf{R}.$$ (12)

It is easy to see from definition (10) that MI is symmetrical with respect to permutation S ↔ R and so alternatively can be defined as I = H(S) − H(S|R). MI measures (in bits when the logarithm is base 2) how much uncertainty about the input signal can be eliminated from measuring the response. The maximum possible MI is the entropy of the input signal itself,

$$H(\mathbf{S})=-{\int }_{\mathbf{S}}P(\mathbf{S})\log P(\mathbf{S})d\mathbf{S},$$ (13)

that is reached when the input completely determines output, so H(R|S) = H(S|R) = 0. Any uncertainty in the response for a given input signal due to inevitable noise in the transmission channel leads to reduction of MI below this upper bound. The maximum MI for a given channel over all possible inputs patterns constitutes the information capacity of the channel. It is tempting to think that maximizing information capacity is one of the important factors that directs the evolution of cellular signaling networks. A number of recent publications have explored this intriguing possibility by analyzing the information capacity of cellular signaling cascades.

If a signaling channel is defined by set of biochemical reactions, then evidently a simple increase of the number of signaling molecules would reduce noise and thus increase information capacity. However, such trivial “optimization” would come at a corresponding metabolic cost. Non-trivial optimization has to strike a balance between energy consumption and information flow. Tkačik et al. (2009); Walczak et al. (2010); Tkačik et al. (2012) analyzed this balance by computing optimal mutual information in several basic types of small gene networks under a constraint of a limited number of signaling molecules. They assumed that an inducible expression of a single gene activated by a “input” transcription factor c, is Gaussian, with the mean number of “output” molecules N_mg(c) characterized by the Hill function,

$$g(c)=\frac{c^n}{c^n+K^n}$$ (14)

where N_m is the maximum possible number of output molecules produced by an infinitely strong signal. There are two distinct sources of stochastic fluctuations in the output, the stochastic fluctuations of the input level amplified by the gene circuit and the intrinsic noise within the gene circuit itself due to discrete transcription, translation, and degradation processes. Assuming that both these sources of noise are Poissonian, with the variance that scales linearly with the levels of input and output molecules, the CV of the output level (the variance of the number of output molecules normalized by $N_m^2$) in the steady state can be computed in the small-noise approximation. It is given by a sum of two terms

$$CV=\frac{1}{N_m}[g(c)+c_{0}c{\left(\frac{dg(c)}{dc}\right)}^2]$$ (15)

which reflects the additive contributions of the two above-mentioned sources of noise. The relative magnitude of these contributions is determined by the input concentration scale c₀ = N_m/(Dlτ), where D is the diffusion constant for protein within the cell, l is the characteristic size of the binding site on the gene promoter, and τ is the output “measurement” time. For a variety of cells and transcription factors, this scale is ~ 15 − 150 nM. Balance of these two sources of fluctuations determines the optimal structure of the single-gene transmission circuit. Assuming that the noise is small and Gaussian, Tkačik et al. (2009) computed the MI (10) under the hard constraint of a limited maximum number of input molecules c_max

$$I=\text{log}{{\int }_0^{c_{\mathit{\text{max}}}}dc\left[\frac{N_{\mathit{\text{max}}}}{2\pi e}\frac{{(dg(c)/dc)}^2}{g(c)+c_{0}c{(dg(c)/dc)}^2}\right]}^{1/2}$$ (16)

(a similar formula can be obtained assuming a fixed mean concentration of input molecules). The analysis of this expression shows that a maximal information transmission can be achieved at particular values of dissociation constant K and Hill coefficient n if c_max ~ c₀. However, optimization is absent if c_max is much smaller or much greater than c₀. Intuitively it makes sense, because for very small input signals the circuit capacity is dominated only by the single, input source of noise, and for very large input compared to output, only the intrinsic circuit noise is the limiting factor. Obviously, the MI increases monotonously with c_max, however increasing c_max much above c₀ does yield rapidly diminishing returns since it remains limited by the intrinsic noise. Reassuringly, concentrations of most transcription factors fall within the same range ~ 15–150 nM, thus gene expression circuits indeed appear to operate effectively from the information-theoretical standpoint.

The same information-theoretical approach yields non-trivial predictions about the structure of more complex gene networks, such as multiple genes controlled by the same transcription factor Tkačik et al. (2009); Cheong et al. (2011), feed-forward circuits Walczak et al. (2010), positive and negative feedback loops Ziv et al. (2007); Tkačik et al. (2012), etc. Ziv et al. (2007) numerically compared all possible 3-gene transcriptional signaling cascades with various positive and negative feedback loops. Computing maximal achievable input-output mutual information (channel capacity) for three binary inputs (3 bits) and a single output under biologically relevant constraints on protein abundance and time scales of decision-making, they found that all circuits can be tuned to transmit more than 2 bits of information, i.e. they perform significantly better than a binary switch. Among all 24 possible circuits, the negative-feedback architectures had a slight edge that may be caused by their intrinsic noise-suppressing properties (see Sec. 2.3). In a small-noise approximation, Tkačik et al. (2012) found that feedback generally increases achievable channel capacity of single-gene input-output circuits, in that for c_max < c₀ (“genetic amplifier”) the positive-feedback circuit is optimal, and for c_max > c₀ (“genetic attenuator”) self-repression yields optimal performance.

Lestas et al. (2010) demonstrated that finite channel information capacity imposes fundamental limits on the magnitude of fluctuations in genetic regulatory systems with rather general topology. They considered a system in which a species X₁ activates synthesis of a signaling species X₂ which in turn activates an arbitrary complex “controller” that in turn determines the synthesis rate of X₁. This system can be described by three biochemical reactions

$$x_1\underrightarrow{u(x_2(-\infty ,t))}{x}_1+1x_1\underrightarrow{x_1/{\tau }_1}{x}_1-1x_2\underrightarrow{f(x_1)}{x}_2+1$$ (17)

where x_1,2 are numbers of X_1,2 molecules, τ₁ is the average lifetime of X₁ molecules, f(x₁) is the birth rate of the signaling molecules X₂, and u(x₂(−∞, t)) is the output of an arbitrary control network that may depend on the whole past history of x₂. Assuming that the dynamics of x₁ is continuous and governed by a Langevin equation, the relation between the feedback channel capacity C and the lower bound of the Fano factor of x₁ fluctuations can be deduced

$$\frac{{\sigma }_{x_1}^2}{\langle x_1\rangle }\ge \frac{1}{1+C{\tau }_1}$$ (18)

The feedback channel capacity itself depends on the magnitude of fluctuations of the synthesis function f(x₁), i.e. on fluctuations of x₁. This creates a lower bound for the magnitude of fluctuations of x₁ which for linear function f(x)αx can be expressed in the following form

$$C{V}^2={\frac{{\sigma }_{x_1}^2}{\langle x_1\rangle }}^2\ge \frac{1}{\langle x_1\rangle }\frac{2}{1+\sqrt{1+4N_2/N_1}}.$$ (19)

Here N₁ = 〈x₁〉 and N₂ = α〈x₁〉τ₁ is the number of molecules of X₁, X₂ synthesized during time τ₁. This formula shows that for a low-amplitide feedback controller, N₂ ≪ N₁, $CV\ge N_1^{-1/2}$, and for a large-amplitude feedback control N₂ ≫ N₁, CV ≥ (N₁N₂)^−1/4. Thus, feedback control of gene expression noise is fundamentally inefficient: the noise magnitude, at best, decays as a quartic root of the number of signaling molecules. For example, to reduce noise in X₁ ten times via negative feedback control, one would have to produce at least 10⁴ more signaling molecules X₂ than X₁.

Mutual information provides a useful characterization of strongly nonlinear signaling cascades when simple linear correlation analysis is not applicable. It was used for reconstructing gene regulatory networks from microarray data Basso et al. (2005); Margolin et al. (2006) However, standard MI measures fail to address certain important questions regarding the dynamics of complex biological networks. In particular, since MI between two variables x and y is symmetric with respect to permutation X ↔ Y, it cannot identify the predominant direction of the information flow between two nodes. Schreiber (2000) proposed a generalization of the MI concept called transfer entropy which quantifies how much uncertainty about the future of X is eliminated by the knowledge of the current state of Y and vice versa. It generalizes the so-called Wiener-Granger causality that characterizes how much Y improves the prediction of future X using linear regression Barnett et al. (2009). The transfer entropy has been recently used to infer the structure of the gene regulatory data from the time series microarray data for genes involved in human cell cycle Tung et al. (2007). Even more general approach Smith et al. (2002) uses dynamic Bayesian networks to inference the direction of information flows that goes beyond quantifying pair-wise interactions within a network. This method has been applied to inferring directed gene regulatory Husmeier (2003) and neural Smith et al. (2006) networks from time series data. An overview of these and many other computational methods of inferring cellular networks from experimental data can be found in Markowetz and Spang (2007).

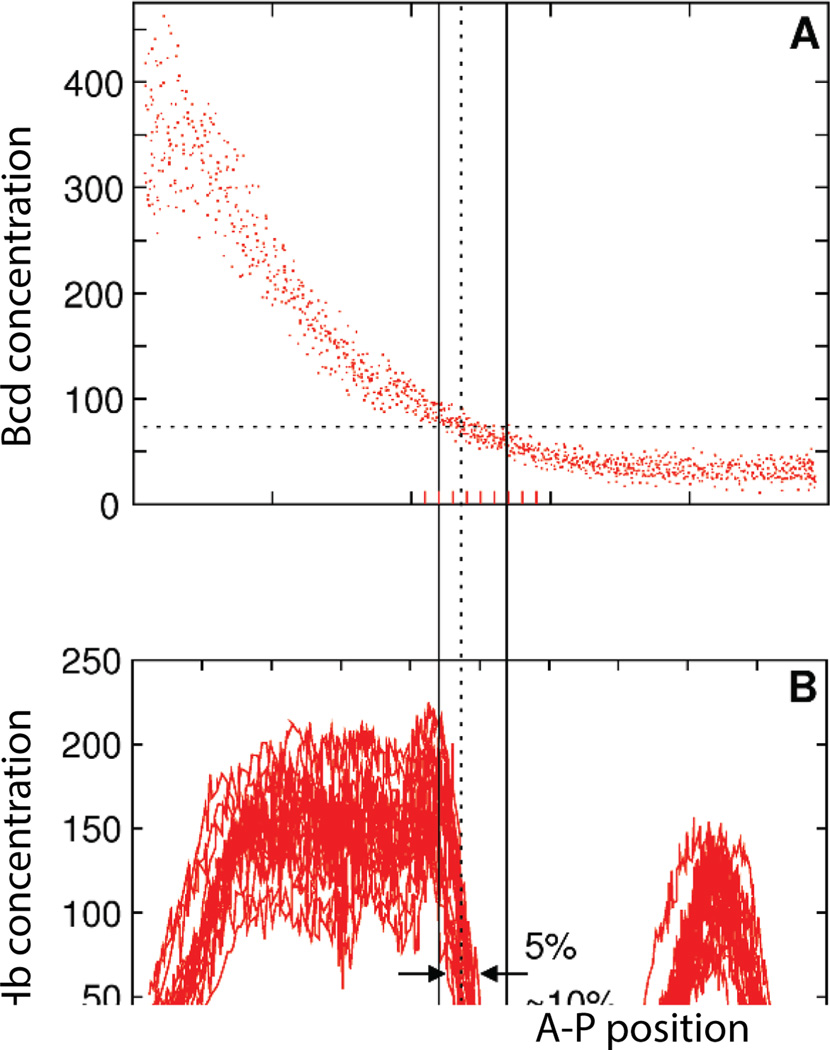
Perhaps the first experimental estimation of the channel capacity of a genetic regulatory system was done by Tkačik et al. (2008) for the gene circuit controlling morphogenesis in Drosophila melanogaster embryo using experimental measurements by Gregor et al. (2007) (this system is discussed further in Sec. 3.3). The maximal MI between the concentrations of the two main morphogens, bicoid and hunchback, was estimated to be 1.7 bits “per measurement”, which is close to the theoretical maximum information transmission rate (obtained in the small noise approximation) for a given number of signaling molecules.

Cheong et al. (2011) characterized the channel capacity of NF-κB signaling cascade in mammalian cells in response to the step-wise stimulation by tumor necrosis factor (TNF) directly from experimental data. They found that in a single cell the average MI of the NF-κB cascade is about 1 bit. Therefore, a cell appears to only be able to distinguish between two levels of input (“on” or “off”) and not the strength of the stimulation. They also found similar results for other canonical signaling cascades, such as G-protein associated receptors and epidermal growth factor pathway. However, these calculations assume that cells only measure a level of a single scalar output at a single time point. It appears likely that in order to improve information transmission capacity, biological systems employ various strategies, such as spatial or temporal averaging, using multi-branch pathways, or exploiting temporal structure of input signals. Indeed, NF-κB pathway is believed to employ sophisticated temporal coding, so different time courses of the TNF input activate different subsets of target genes and elicit distinct immune response programs Behar and Hoffmann (2010).

2.5. Noise in decision-making

Cells collect and process information to adapt to changing environmental conditions. This adaptation often takes the form of nearly-discontinuous switches in specific cell function. Abrupt phenotype changes can also be pre-programmed in the genetic blueprint of the organism development. Biology is replete with examples of drastically different phenotypes among cells with identical genomes. All cells in a human body have the same set of genes, however they code for many different cell types. The accepted view is that qualitatively different cell phenotypes are usually produced by different stable states of the underlying gene regulatory network. The developmental program forces cells to differentiate into these states. One particularly important type of strongly nonlinear gene networks is a “genetic switch” that can drastically alter the pattern of gene expression under a small change in environmental conditions. Sometimes these switches can be flipped by random intrinsic and extrinsic fluctuations, especially when the environmental conditions bring the system close to the threshold for a transition. To minimize undesirable “back-and-forth” switching and ensure phenotypic stability when the system tethers near the critical state, genetic switches usually employ positive feedback motifs that render them bistable (and hence, hysteretic) in a certain parameter range. This endows the cells with a form of memory, since the cellular state becomes history-dependent. Examples of bistable switches are abundant in cell biology at all levels from th simplest viruses and bacteria to mammalian cells. A number of such systems have been studied in great detail: lysogeny-lysis switch in λ phage Ptashne (1992), lactose utilization network in E. coli Ozbudak et al. (2004), galactose utilization network in budding yeast Acar et al. (2005), progesterone-controlled transition between two maturation stages of the Xenopus oocytes Xiong and Ferrell (2003), etc. (see Balázsi et al. (2011) for a recent review).

If the cells in a population were identical, the environmental conditions uniform, and the genetic switches deterministic, one would expect that all these cells should be in the same phenotypic state and would all switch simultaneously to another state under suitable change of environment. However there is much experimental evidence that even in isogenic populations under nearly identical environmental conditions, the cells may exhibit drastically different phenotypes. There is a certain well-defined fraction of λ-phage infected E. coli cells choosing lysogeny instead of lysis that depends on nutritional and other conditions Kourilsky (1973). Arkin et al. (1998) used Gillespie’s algorithm to simulate intrinsic stochastic fluctuations in biochemical reactions comprising the genetic switch in λ-phage and demonstrated that this probabilistic mechanism alone can satisfactorily explain the observed lysogeny/lysis fractions.

An interesting example of probabilistic decision-making involves multipotent differentiation of bacteria under unfavorable environmental conditions such as starvation, heat, toxic chemicals, etc. Bacteria deploy a number of strategies to cope with stress, including changes in motility patterns, secretion of antibiotics to compete with other microbes, etc. If all these strategies prove insufficient, as a last resort the bacteria may choose to sporulate. However, experiments in an isogenic population of Bacillus subtilis Schultz et al. (2009) showed that this transition is probabilistic in nature, and only about 50–70% of all cells make irreversible commitment to sporulation that involves lysis of cells and the release of their genetic material. The transition to sporulation is controlled by the level of phosphorylation of the master regulator Spo0A, and for a long time it was thought that heterogeneity of sporulation transition is caused by the bimodality of phosphorylated Spo0A expression due to bistability in the positive feedback loops present in the Spo0A phosphorylation pathway Dubnau and Losick (2006); Veening et al. (2008). However, more recently Chastanet et al. (2010) and de Jong et al. (2010) found that the distribution of phosphorylation activity of Spo0A was not bimodal but rather broadly heterogeneous. Similar unimodality was found in all other proteins forming the phosphorelay de Jong et al. (2010). Furthermore, Chastanet et al. (2010) showed that all positive feedback loops within the Spo0A phosphorelay were operating in a monostable regime. Presumably, the 4-component cascade that transfers phosphate groups acts as a noise generator responsible for stochastic cell-to-cell variability in timing of the sporulation entry. It can be argued that this asynchronicity is beneficial for the population as a whole in fluctuating environmental conditions.

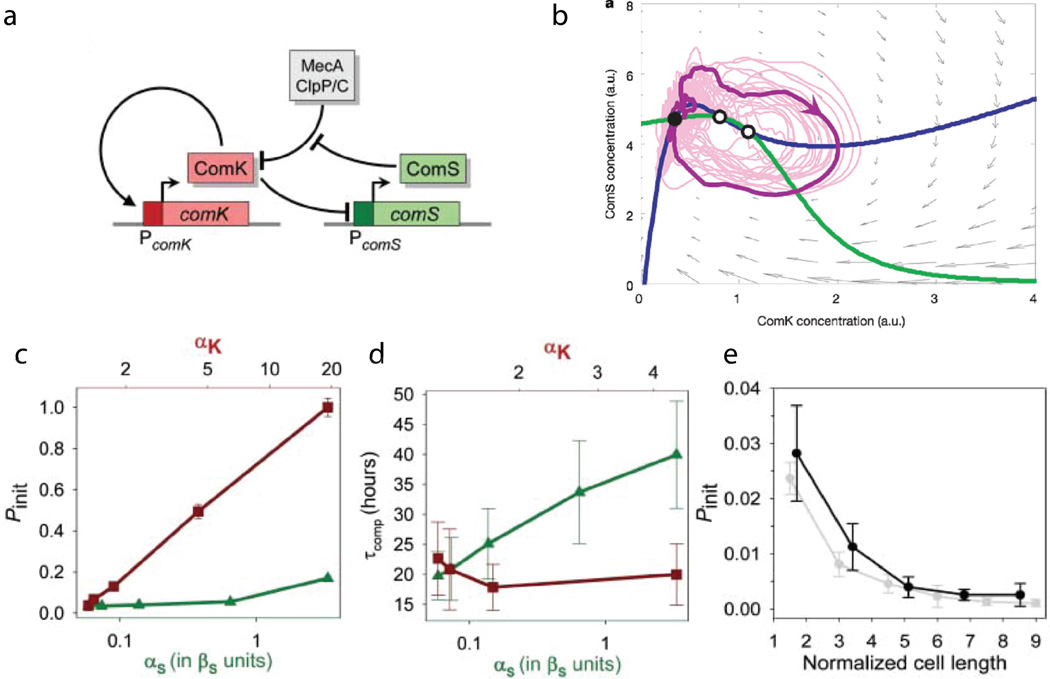
Interestingly, in the face of the same environmental stress, a small fraction of B. subtilis cells (3–15% of the colony depending on the strain) follow an alternative scenario and switch to a competent state in which a bacterium can take up exogenous DNA from already dead nearby cells. This exogenous DNA can be used for DNA repair or as mutation material to survive stressful conditions. The transition to competence is controlled by the key transcription factor protein ComK which is low in normal, non-competent cells and high in competent cells Samoilov et al. (2006); Veening et al. (2008). It was found that this transition mainly occurs within the first two hours after cells enter the stationary phase, which could be explained by the variations in basal ComK expression Leisner et al. (2007); Maamar et al. (2007). The gene circuit that controls comK gene expression contains both a positive and a negative feedback loop (see Fig. 8a). The positive feedback loop in ComK synthesis can in principle lead to bistability, and in the presence of stochastic fluctuations - to the experimentally observed bimodality in comK gene expression Maamar and Dubnau (2005). However, single-cell experiments showed that the competent state is only transient. After about 20 hours, cells spontaneously switch back to the vegetative state and continue their progress towards sporulation Süel et al. (2006); Süel et al. (2007). While this observation does not exclude a possible bistable nature of the transition, it favors an alternative model that the competence circuit operates in an excitable regime and relatively small stochastic fluctuations of comK expression can produce large “bursts” of ComK.

Figure 8.

Competence regulation in B. subtilis Süel et al. (2006); Süel et al. (2007): (a) Gene circuit controlling competence master regulator protein ComK include a positive feedback loop of autocatalytic synthesis of ComK and negative feedback loop where ComK inhibits synthesis of ComS protein that in turn inhibits degradation of ComK by the ClpP-ClpC-MecA protease complex. (b) phase plane of the model (20) with nullclines (thick solid lines), the vector field (gray arrows) and the stochastic trajectory (thin solid line) showing bursts of competence; (c)the probability of competence initiation P_int grows with the basal expression rate of comK gene (α_k, red squares), but is only weakly dependent on the comS expression rate α_s (green triangles); (d) Conversely, the duration of the competent state increases with α_s but is weakly dependent on α_k; (e) Increasing cell size (that putatively reduces intrinsic noise) reduces P_int.

The dynamics of competence can be described by two differential equations for ComK and ComS concentrations, K and S, respectively:

$$\frac{dK}{dt}={\alpha }_k+\frac{{\beta }_k{K}^n}{k_0^n+K^n}-\frac{K}{1+K+S}+{\xi }_k(t)\frac{dS}{dt}={\alpha }_s+\frac{{\beta }_s}{1+{(K/k_1)}^n}-\frac{S}{1+K+S}+{\xi }_s(t)$$ (20)

where α_k and β_k are basal and fully-activated levels of ComK synthesis, β_s is the synthesis rate of ComS in the absence of ComK, k₀ and k₁ are concentrations of ComK at which the synthesis of ComK (ComS) is increased (reduced) by 50%. Powers n and p indicate the cooperativity of ComK, ComS synthesis regulation by ComK transcription factor. Random fluctuations in ComK and ComS synthesis are modeled by Gaussian noise terms ξ_k(t) and ξ_s(t). The phase plane of Eqs.(20) with two nullclines is shown in Fig. 8b, it has a structure typical for an excitable system. Numerical simulations show that fluctuations of either ComK or ComS can lead to large excursions that correspond to the transient competent states observed experimentally.

This model is further corroborated by the measurements of the competence transitions in genetically modified cells Süel et al. (2006) which incorporated additional inducible production of ComK (in the model it can be characterized by the increased basal rate α_k) and ComS (increased α_s). The basal transcription rates of comK and comS genes could be modulated independently by chemical inducers. The measurements Süel et al. (2007) showed that the probability of switching to competence P_int (which was about 3% in their wild-type strain) was highly dependent on the basal transcription rate of comK gene but the mean duration of the competence phase was independent of it. On the other hand, P_int was independent of the basal expression level of comS but the duration of the competence markedly increased with that (see Fig. 8c,d). Furthermore, decreasing the effective transcriptional noise level by increasing the cell size also reduced P_int in agreement with the “excitable” model of competence, Fig. 8e. Still, the duration of competent state appears to be highly variable Çağatay et al. (2009b), which may still suggest a role for the stochastic switching mechanism back to the non-competent state, i.e. bistability. In fact, elevated levels of ComS, ComK expression can lead to a bifurcation towards bistability, or even oscillatory regimes Espinar et al. (2013).

Both sporulation and competence are caused by the same environmental conditions. Therefore, it is not obvious how one of these two developmental programs is ultimately selected by a particular cell. As described above, individual cells exhibit large variability in expression of master regulators ComK and Spo0A. Therefore, only single-cell measurements can unambiguously answer these questions. Until recently, it was believed that cells strongly cross-regulate these pathways, and once one pathway is selected, the other one is automatically repressed Schultz et al. (2009); Ben-Jacob and Schultz (2010). However, recent work Kuchina et al. (2011) showed that slow progression to sporulation and excursions to competence occurs independently and concurrently up to a certain irreversible decision point, and the choice of the phenotype depends on the outcome of a “molecular race” between the two independently progressing differentiation programs: whichever program reaches the decision point first, wins. On the other hand, the decision circuit itself appears to have non-trivial oscillatory that transiently open so-called “windows of opportunity” for competence Schultz et al. (2013).

In order to understand the key mechanisms of cellular memory, a number of synthetic bistable gene circuits were recently constructed that implemented positive (or double-negative) feedback motif. In fact, one of the first two papers that heralded the dawn of the new field of synthetic biology described an implementation of a synthetic toggle switch based on mutual repression of two genes borrowed from the λ-phage genome Gardner et al. (2000).

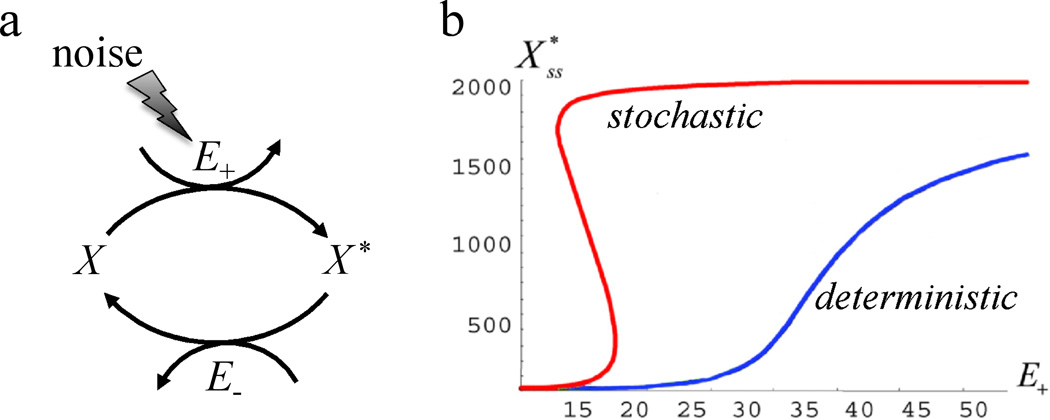
One should be very careful inferring bistability of the underlying dynamical model from the apparent bimodality of the monoclonal population-based distributions of observed quantities. It has been shown that in some biologically relevant systems, bimodality occurs just due to stochastic effects in systems which deterministically are unimodal Samoilov et al. (2005). One ubiquitous example of such systems is so-called enzymatic futile cycle, in which two enzymes counter-act to convert two substrates into each other (see Fig. 9,a). There are many examples of such cycles and their cascades in biology: phosphorylation/ dephosphorylation by kinase/phosphatase pairs, GTPase cycles, NAD+/NADH conversion in catabolism, etc. Such bidirectional enzymatic reactions are known to give rise to the zero-order ultrasensitivity Goldbeter and Koshland (1981) and are usually thought to be evolutionary selected for rapid and switch-like response to external signals. More surprising is that, when the levels of enzymes are driven by certain extrinsic noise sources, these enzymatic cycles may exhibit complex dynamical behaviors. Samoilov et al. (2005) solved the Fokker-Planck equation for the enzymatic futile cycle in which the concentration of the forward enzyme E_f is driven by a stochastic process. They showed that if the noise source is nonlinear (i.e. its strength depends on the enzyme concentration itself), the stationary distributions of substrates X,X^* can be bimodal. The mode of the distribution in a certain parameter domain becomes multi-valued (Fig. 9,b), even though for a constant level of E_f the system is always single-valued (which implies monostability). Direct numerical simulations of the underlying stochastic model reveal stochastic switches between two meta-stable states with a characteristic switching frequency that is determined by the escape rate from the corresponding basins of attractions. A similar effect of stochastic bimodality in deterministic monostable system was found by Artyomov et al. (2007) in a toy model of competing agonism/antagonism in immune response of T-cells to binding peptide-MHC complexes. This system is believed to be controlled by counteracting positive and negative feedback loops that in deterministic limit show no bistability in all parameter ranges, but intrinsic stochasticity due to small copy numbers of the molecules leads to distinct bimodality of the immune response.

Figure 9.

Enzymatic futile cycle (a) and its bifurcation diagram (b) in deterministic and stochastic regimes Samoilov et al. (2005). The red hysteretic line shows the mode of the steady-state distribution of X^* for the stochastic model of noisy enzymatic futile cycle and blue monotone line shows the steady state of the corresponding deterministic model of the noiseless system

2.6. Enzymatic queueing and inter-pathway crosstalk

Biological systems have developed robust strategies that regulate allocation of limited resources Lodish et al. (2012). On an intra-cellular level, this often leads to a significant crosstalk between pathways sharing the same limited resource. Different systems can compete for nutrient sources as well as for enzymes needed for transcription, translation, and degradation of mRNAs and proteins. This competition may lead to apparent downstream coupling Buchler and Louis (2008); Chapman and Asthagiri (2009); Genot et al. (2012) as well as retroactivity that affects upstream components Del Vecchio et al. (2008); Kim and Sauro (2010); Cookson et al. (2011); Kim and Sauro (2011); Rondelez (2012). On the other hand, cells sometimes use resource distribution itself as a global regulatory mechanism controlling cooperation among various metabolic or signaling pathways. Understanding the specific mechanisms of this regulation is far from complete Grigorova et al. (2006); Klumpp and Hwa (2008).

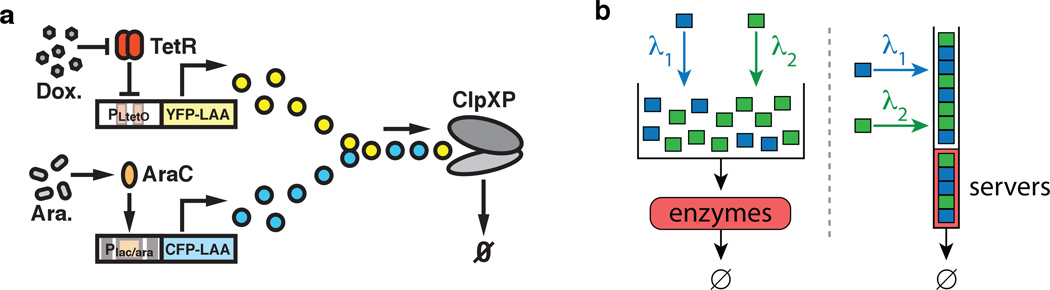
Correlated fluctuations in different intracellular components or pathways usually serve either as evidence of direct coupling among these components or as a signature of a common source of extrinsic noise. However, it is becoming increasingly clear that strong correlations within the cells can often be due to entirely different, implicit type of coupling that occurs due to limitations in common enzymatic resources shared by multiple substrates. In intracellular signaling and metabolic systems, enzymes often interact with multiple substrates, which may represent different pathways or branches of the same pathway. A ubiquitous example of this type of coupling is ribosomes that bind to and translate many different mRNA. When the number of mRNAs becomes so large that ribosomes cannot keep up with translation, a significant translational crosstalk ensues Mather et al. (2013). Downstream coupling due to common degradation machinery has recently been experimentally observed in a synthetic system where yellow and cyan fluorescent reporters were tagged for fast degradation by a common protease ClpXP Cookson et al. (2011), see Fig. 10,a. In this study, it was shown that a rate-limited interaction can lead to strong coupling between the two fluorescent reporters.

Figure 10.

a. Schematic network diagram of the synthetic circuit demonstrating coupled enzymatic degradation of yellow and cyan LAA-tagged fluorescent proteins by ClipXP machinery in E. coli Cookson et al. (2011). YFP production is controlled by the P_LtetO promoter, which is repressed by tetR in the absence of doxycycline. CFP production is under control of the P_lac/ara promoter, which is activated by araC in the presence of arabinose. Both CFP and YFP molecules are tagged with identical LAA tags and are targeted for degradation by the ClpXP complexes. b. Illustration of the prototypical model of coupled enzymatic degradation Mather et al. (2010) for m = 2 (left) and the corresponding multiclass queuing model (right). In the stochastic enzymatic degradation model proteins of both species i = 1,2 are added to a volume at different rates λ_i and are selected at random (without regard to type) for processing. In an equivalent multiclass queue jobs are analogous to molecules and servers are analogous to copies of the enzyme. Jobs of type i = 1,2 arrive at rate λ_i and are inserted randomly into a queue of jobs awaiting processing; when a server becomes free, a new job is selected for processing from the head of the queue of waiting jobs.

A theoretical description of such enzymatic correlations can be developed on the basis of the queueing theory (see for example, Bhat (2008)). Queueing theory provides a probabilistic description of waiting lines of randomly arriving and leaving customers at so-called service stations. In the biological context, molecules of different species can be thought of as “customers” that are randomly synthesized and processed or degraded via certain biochemical reactions. In recent years, queueing theory has been used to describe a cellular processes in metabolic and regulatory networks Arazi et al. (2004); Levine and Hwa (2007). However, single-class queuing models studied in Arazi et al. (2004); Levine and Hwa (2007) allow only a description of a single chemical species processed by a given enzyme, and cannot be directly applied to the analysis of inter-species correlations. Since individual enzymes can be involved in multiple biochemical reactions, enzymatic coupling can form a network of interconnected queues, an active area of research in the queueing literature known as the theory of multi-class queues Kelly (1979). Rate-limited processing can couple the numbers of different job types in a queue. If the total arrival rate exceed the processing rate, the servers become overloaded, the queue lengthens dramatically, and the numbers of jobs of different kinds competing for the attention of the servers become tightly correlated Bramson (1998); Williams (1998).

A prototypical queueing model of enzymatic correlation was considered by Mather et al. (2010). A system with m protein species X₁, …, X_m is governed by the following set of biochemical reactions. For i = 1, …, m,

$$D_i\underrightarrow{{\lambda }_i}{X}_i+D_i{X}_i+E_{{\eta }_{-}}^{{\eta }_{+}}{X}_{i}E{X}_{i}E\underrightarrow{\mu +\gamma }E{X}_i\underrightarrow{\gamma }\varnothing .$$ (21)

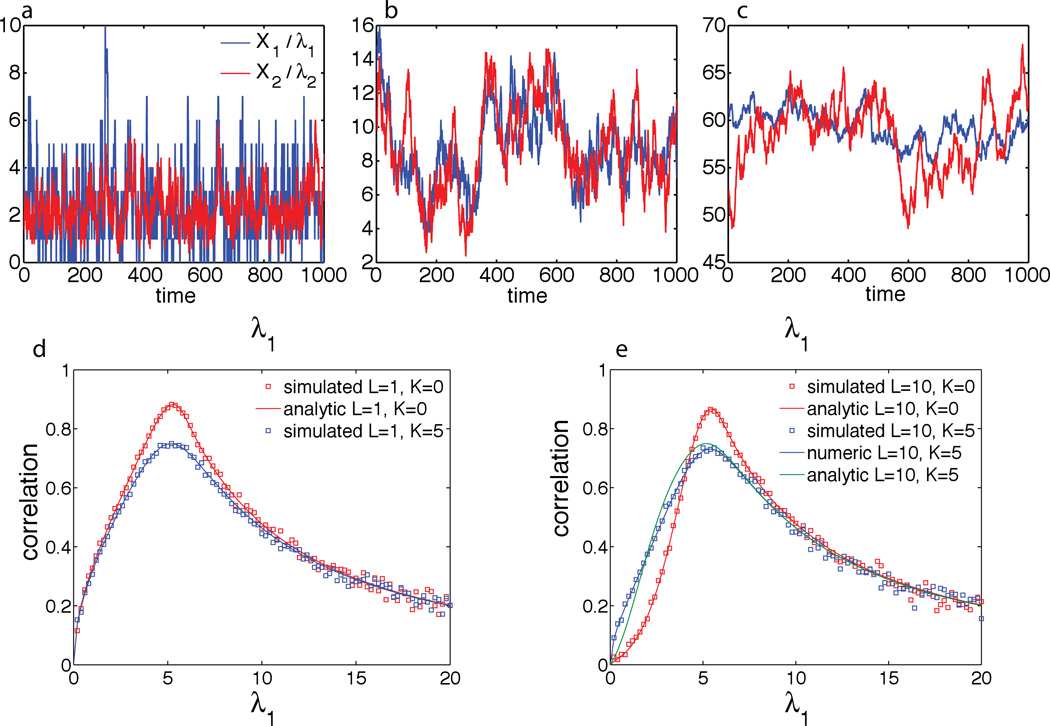
Here D_i stands for DNA producing X_i at a constant rate λ_i, X_i binds/unbinds with the enzyme E with reaction rate constants η_±, the enzyme E degrades X_i with reaction rate constant μ, and X_i is diluted in both its bound (X_iE) and unbound form with rate constant of γ. All reactions are assumed to be Poissonian (with exponentially distributed reaction times) and the reaction rate constant η is supposed to be so large that the associated reactions are effectively instantaneous. An illustration of this model for m = 2 is shown in Fig. 10,b and typical time series of the numbers of proteins X_1,2 for different production rates λ_1,2 corresponding to underloaded, balances, and overloaded conditions are shown in Fig. 11,a–c.

Figure 11.

(a–c) Time series of the two proteins in the underloaded, λ₁ + λ₂ < Lμ (a), balanced λ₁ + λ₂ = Lμ (b), and overloaded λ₁ + λ₂ > Lμ (c) regimes. (d–e) correlation resonance between the two proteins near the balance for different L and K values.

The stochastic behavior of this system may be described as follows. New molecules of species i (i = 1, …, m) are produced via an independent Poisson process with rate λ_i > 0. It is assumed there are fixed L > 0 copies of the enzyme, and when one of the L copies becomes available, it selects a protein molecule at random, binds to it instantly and begins to degrade it. The degradation time is exponentially distributed with mean 1/μ where μ > 0. In addition, the molecules can be “diluted” as follows. Each protein molecule remains in the system for at most an exponentially distributed amount of time with mean 1/γ where γ > 0. A molecule may be removed from the system by degradation before its dilution “lifetime” is up, or vice versa.

Mapping this stochastic biochemical model onto a corresponding queueing system allows one to find exact (in the limit of K ≡ η⁻/η⁺ = 0) or accurate approximate (for arbitrary non-zero K) expressions for steady-state joint probability distributions of different substrates and its moments in a closed form. In particular, the cross-correlation between the concentrations of the two protein shows a characteristic non-monotonous behavior as a function of the synthesis rate(Fig. 11,d,e). The correlation is small for very small and very large total synthesis rate (λ₁ + λ₂) and reaches maximum near the balance point, when the total synthesis rate of the proteins is equal to the the maximum processing capacity of the protease, i.e. where λ₁ + λ₂ = Lμ. In the limit of zero dilution, the correlation at the balance point becomes perfect (ρ = 1). This result is somewhat counterintuitive, because often it is tacitly assumed that correlations are a signature of direct interactions.

We already mentioned that a ubiquitous source of potential crosstalk is the competition for the resources needed for the production of proteins. For example, it is known that σ-factor competition for a finite pool of RNA polymerases leads to significant changes in RNA polymerase partitioning between transcription of housekeeping genes versus stress response genes under stress conditions Grigorova et al. (2006); Fredriksson et al. (2007). The copy number of ribosomes appears to be limiting for protein synthesis at the whole cell level Warner et al. (2001); Mauro and Edelman (2002, 2007); Shachrai et al. (2010); Scott et al. (2010); De Vos et al. (2011); Chu et al. (2011), in which case competition for a common pool of ribosomes by mRNAs can lead to crosstalk when large systematic changes in transcript abundance occur. More surprisingly, pronounced and functionally important crosstalk has been shown to arise from competition between a small number of different transcripts in the galactose utilization network of S. cerevisiae Bennett et al. (2008); Baumgartner et al. (2011), which presumably cannot overload the whole pool of ribosome in the cell. Apparently the crosstalk in this case caused by transcripts competing for a spatially-localized subset of ribosomes. Direct measurements Baumgartner et al. (2011) showed spatial co-localization of different mRNAs in the neighborhood of a nuclear pore where presumably they are being cotranslated by the same small pool of ribosomes.

The competition between mRNA molecules for translational processing resources was recently studied theoretically by Mather et al. (2013) using the methods of queueing theory. A toy stochastic model for translational crosstalk includes two different types of mRNA and a limited set of identical ribosomes. It was assumed that mRNAs instantly bind to available ribosomes, and there may be a higher probability of re-binding of a ribosome to the same mRNA than to any other after termination of translation. The analytical solution of the queueing problem for the fixed mRNA and ribosome numbers shows that again the strength of the crosstalk strongly depends on whether the ribosomes are underloaded (more ribosomes than mRNAs) or overloaded (more mRNAs than ribosomes). The model in the underloaded case recovers much of the phenomenology predicted by standard models for protein production, including a lack of crosstalk between the production rates of protein species, while the two protein species in the overloaded state exhibited substantial crosstalk. Without preferential re-binding of a ribosome to the same mRNA there is a weak positive correlation between proteins due to the finite pool or upstream mRNAs. When the number of mRNAs is allowed to fluctuate slowly or there is strong mRNA-ribosome rebinding probability, the system exhibits a negative correlation resonance (minimum) slightly above the balance point, where the number of ribosomes is equal to the total number of mRNAs. This downstream resonance is analogous, though opposite in sign, to a positive correlation resonance found upstream from a processing bottleneck as in shared degradation pathways Mather et al. (2010).

3. Noise in Developmental Biology

3.1. Developmental noise

In the previous section we touched upon the crucial role that noise plays in decision-making processes that affect the phenotypic state of unicellular organisms such as bacteria switching from normal to competent state or becoming a spore. This can be considered a part of a developmental program for these organisms, however more commonly developmental biology deals with higher multi-cellular organisms. Development of a multicellular organism from a single cell is a fascinating process during which a very complex and robust program is executed which combines growth, differentiation, and patterning Schwank and Basler (2010); Lander (2011). This program leads to sequential partitioning of an initially homogeneous cell mass into a hierarchy of smaller and smaller units which comprise the grown organism. As a result, during development of a multicellular organism, a “fossil record” of fluctuations can become “frozen” into the emerging structure of the adult organism, and therefore generate phenotypical diversity on a population level. Furthermore, during development, living organisms go through a sequence of decision-making “checkpoints” that can not only relay, but amplify microscopic stochastic fluctuations to the meso- and macroscopic levels of organization.

Most of salient characteristics of multicellular organisms are determined genetically. For example, a wild-type nematode worm C. elegans always develops into an adult organism with 959 somatic cells with precisely defined functions. The height, head shape, and eye color of humans are also genetically encoded. And yet many characteristics vary greatly even in isogenic animals. The life span of C. elegans can vary from 10 to 30 days Finch and Kirkwood (2000). While the number of neuronal cells is often conserved with a very high precision, the neuroanatomy of genetically identical species of lower animals such as locusts Steeves and Pearson (1983), fish Levinthal et al. (1976) and worms White et al. (1976) is non-identical. This combination of high precision in some aspects of developments (e.g. growth and regeneration of tissues and organs Lander et al. (2009)) with relatively lax regulation of others (e.g. life span and details of synaptic connections) poses interesting questions about the role of evolution in shaping the control of developmental variability.

Waddington (1957) defined developmental noise (DN) as a phenotypical diversity among individuals which is not caused by genetic factors. A more recent, and narrower definition of the developmental noise that excludes effect of extrinsic fluctuations is phenotypical diversity among individuals with identical genotypes under nearly identical environmental conditions Yampolsky and Scheiner (1994).

One of the often cited and studied manifestations of DN in higher organisms is a random deviation from symmetry between between bilateral organs (such as kidney size, finger length, etc.), known as fluctuating asymmetry Waddington et al. (1956); Parsons (1990). While fluctuating asymmetry can be caused by genetic, hereditary effects, there is solid evidence that most of the fluctuating asymmetry is caused by environmental or other epigenetic fluctuations during development. In normal conditions fluctuating asymmetry is rather small. For example, left and right limbs in humans on average are equal in length up to 0.2% Wolpert (2010). To explain this remarkable developmental stability Waddington (1942) introduced the idea of canalization, i.e. the insensitivity of the phenotype to changes in either genetic mutations or intrinsic stochastic fluctuations during development, and hypothesized that evolutionary pressures shaped the epigenetic landscape in a specific way to account for the canalization property. Still, given the level of stochastic fluctuations in gene expression and growth on the intra-cellular level, it is hard to imagine that such stability can be achieved without some sort of feedback control. Despite decades of intensive research, the mechanisms underlying the robustness and stability of this program are still not completely understood. One common mechanism of feedback control appears to be based on growth-dependent synthesis of specific molecules, chalones, that regulate the proliferation rate of cells in tissues and organs. Several members of the TFG-β family of proteins, in particular growth and differentiation factors (GDF) 8 and 11, as well as activin B have been implicated in control of growth and regeneration of the mammalian olfactory epithelium Wu et al. (2003); Lander et al. (2009).

3.2. Incomplete penetrance

An interesting example of large variability emerging during development is the phenomenon of incomplete penetrance that was independently discovered in Drosophila fimebris by Romaschoff (1925) and Timoféeff-Ressovsky (1925). They demonstrated that genetic mutations only result in mutant phenotype in a certain part of the population, whereas other organisms exhibit wild-type phenotype. This ambiguity persists even if the population is grown in identical conditions, which rules out the role of environmental fluctuations.

Raj et al. (2010) recently studied mechanistic origins of the incomplete penetrance of the intestinal specification in mutants of the nematode C. elegans. In a wild-type C. elegans, the intestine consists of 20 cells which proliferate from a single E cell during embryonic development. The differentiation into intestinal cells is controlled by a small gene circuit which is activated by skn-1 transcripts (see Fig. 12,a). However, in a skn-1 mutant with homozygous alleles zu67, zu129 or zu135, the number of intestinal cells in late embryos shows high variability. The accurate counting of mRNA transcripts of the genes comprising the network using fluorescent in situ hybridization (FISH) showed that this mutant contained no med-1 and med-2 transcripts, and a much smaller number of end-3 transcripts than the wild type, thereby effectively eliminating half of the regulation for the regulator end-1 (Fig. 12,b). The expression of elt-2 was strongly bimodal, whereas the expression of the upstream gene controlling it, end-1, was still unimodal as in the wild type, but much more broadly distributed (Fig.12,c). They also observed a strong positive correlation between the level of end-1 and elt-2 in individual cells. This implies that the activation of elt-2 requires end-1 to reach a certain threshold (of the order a 150–250 transcripts per cell). Wild-type E cells have a tightly controlled number of end-1 transcripts which is above this threshold and follow the prescribed developmental fate and become intestinal cells, but a large fraction of mutant E-cells fail to cross this threshold and therefore fail to differentiate into the intestinal cells.

Figure 12.

Regulation of intestinal specification in C. elegans Raj et al. (2010): (a) Gene circuit controlling intestinal differentiation in wild-type E cells: master differentiation regulator gene elt-2 is redundantly activated by both End-1 and End-3 transcription factors, which are activated by the maternal protein Skn-1 either directly (End-1) or indirectly, via Med-1, Med-2 and End-3. End-3 also co-regulates expression of end-1; (b) In a mutant skn-1 strain, med-1, med-2 are not expressed, therefore the indirect activation of elt-2 and co-regulation of end-1 by end-3 are disabled. (c) Number of transcripts of end-1 and elt-2 vs time (measured in the number of nuclei) in the wild type (left) and skn-1 mutant (right). Misregulation of the intestinal specification circuit results in a highly variable expression of end-1 and a bimodal distribution of elt-2 transcripts.

3.3. Precision of morphogenesis

The early organism development presents an interesting and still unsolved puzzle of how embryos robustly develop in a multi-cellular organisms in the face of biological noise and cell-to-cell variability. The fundamental limits of accuracy and reproducibility of development were addressed in relation to the classical problem of morphogenesis in the early stages of embryo growth of the fruit fly Drosophila melanogaster Gregor et al. (2007). The spatial pattern formation in early embryos of D. melanogaster is driven by the gradient of the morphogen proteins Bicoid. Its mRNA transcripts are maternally deposited and translated near the anterior pole, and the Bicoid protein subsequently diffuses throughout the embryo, creating a nearly exponential concentration profile with a characteristic scale λ ≈ 100µm. Bicoid activates the transcription of the hunchback (hb) and other so-called gap genes involved in the early embryo anterior segmentation. Unlike Bicoid, the profile of Hunchback concentration along the embryo is strongly nonlinear, with a sharp drop near the middle of the embryo and a smaller cap near the posterior pole (see Fig. 13). The levels of Hb in the anterior part of the embryo are quite variable, but precision with which the drop in the Hunchback concentration profile is positioned in the middle of the embryo is staggering. Expression of other gap genes (krüppel, knirps, giant, etc) is limited by similarly sharp and stable boundaries. About 3 hours after fertilization the embryo is still a single syncytial cell of about 500 µm long, and contains approximately 70 “layers” of nuclei. Nonetheless, even neighboring layers of nuclei have clearly distinguishable (and highly reproducible) levels of gap gene expression. It is easy to estimate that given the exponential profile of Bicoid, the difference between its concentration at the locations of adjacent nuclei is only about 10%. Despite this rather small difference, the adjacent nuclei reliably give rise to different cell fates, which could imply that the gene circuitry within the nuclei (in particular, hunchback genes coding for the Hb protein) can measure the absolute concentration of Bicoid with at least 10% accuracy. On the other hand, in embryos of significantly different sizes the Bicoid profiles are scaled by the length of the embryo, so the differentiation proceeds in perfect accord with the embryo size. This observation raised questions about the actual role of diffusion in forming the Bicoid gradient and the role of the absolute levels of morphogens in morphogenesis. Further experiments showed that simple linear diffusion through the cytoplasm plays a minor role in distributing Bicoid throughout the embryo, and direct exchange among nuclei is perhaps the main factor controlling the morphogen propagation and subsequent differentiation.

Figure 13.

Morphogenesis precision in D. melanogaster : (a) Exponential profiles of the morphogen Bicoid concentration (as measured by the raw fluorescent of Bcd-GFP fusion) collected from 15 different embyos Gregor et al. (2007); (b) 18 profiles of Hunchback concentration (as measured by staining) 3 min before gastrulation Manu et al. (2009a). The horizontal axis shows the position along asterior-posterior axis normalized by the embryo length

It was also confirmed by direct measurements of Hb concentration that high correlation between Bcd and Hb is maintained throughout the entire embryo. This is remarkable, since (as shown by Gregor et al. (2007)) it appears to overcome the fundamental physical limit of accuracy in estimation the transcription factor concentration This limit was originally proposed in application to the chemotaxis Berg and Purcell (1977), and is set by the random collision rates between signaling molecules and the corresponding receptors. Bialek and Setayeshgar (2005) later generalized this argument by applying the fluctuation-dissipation theorem for equilibrium chemical kinetic systems to the coupled ligand-receptor binding and ligand diffusing processes. The resulting estimate for the lower bound of the concentration measurement precision reads

$$\delta c/c>{[\pi DacT]}^{-1/2}$$ (22)

where c is the local ligand concentration, D is its diffusion constant, a is the linear receptor size, and T is the receptor occupancy integration time. Remarkably, this lower bound remains valid even for clusters of interacting receptors with arbitrary statistics of ligand-receptor kinetics Bialek and Setayeshgar (2008). Gregor et al. (2007) applied this estimate to the bicoid (b) measurement accuracy, and using biologically relevant parameters D ~ 1µm²/s, b ≈ 5 molecules/µm³, and a ≈ 3 nm, they obtained δb/b ~ (70s/T)^1/2. This formula implies that to reach 10% accuracy, the cell needs to average the receptor occupation for about 2 hours, which is much longer that the time interval between divisions (nuclear cycle) when the differentiation decision has to be made. To resolve this apparent paradox, Gregor et al. (2007) suggested that the cells use local spatial averaging over an area determined by diffusion of the morphogen during averaging time T, A ~ 4πDT. This yields a different scaling for the measurement precision as a function of time T, and for the same parameters one arrives to a much softer estimate δb/b ~ 20s/T. In this way, the observed 10% accuracy can be realistically reached within ~3 min averaging time, i.e. well within a single nuclear cycle. However, it is unclear what physical or biochemical mechanism may provide the required communication and averaging.

More recent experiments provided evidence that this high reproducibility (phenotypical canalization) could be achieved as a result of sophisticated cross-regulation among several gap genes Manu et al. (2009a); Surkova et al. (2013). Positional accuracy of Hunchback and other segmentation proteins’ distributions is significantly diminished in double mutants in which both krüppel and knirps genes are deleted, which indicates that Hunchback distribution is not controlled by the Bicoid profile alone. Furthermore, the experiments show that variability in gene expression patterns is large in early stages of embryo development, and decreases over time by the onset of gastrulation. The analysis of the mathematical model of gap genes regulatory network Manu et al. (2009b) shows that the establishment of sharp and stable boundaries among different gene expression regions can be associated with formation of domain boundaries among different attractors in the phase space of the corresponding multistable dynamical system. This dynamical model also naturally explains why the positions of gap gene bands are not accurately correlated with the local Bicoid concentrations but rather scale with the embryo size. The positions of the domain boundaries in the asymptotic regime are mostly determined by the intrinsic dynamics and the boundary conditions, and only weakly affected by the distribution of Bicoid. Further experiments and theoretical analysis will be able to clarify the relationship between the statistical and dynamical mechanisms of developmental canalization.

3.4. Morphogenesis via symmetry breaking

Another generic mechanism of pattern formation is based on an interplay between activation, inhibition, and diffusion in a spatially uniform system through a symmetry-breaking instability with respect to finite-wavenumber perturbations. The first conceptual model of this sort was proposed by Alan Turing (1952) and is considered the starting point of the field of pattern formation. Turing believed that his local self-activation/long-range inhibition model could explain stripes and spots in skin patterns of many animals, however experimental verification of this hypothesis proved difficult. Only recently, direct experimental evidence of the Turing-like mechanisms playing a role in developmental patterning started to emerge.

Nakamasu et al. (2009) studied the development of stripes on the body of zebrafish. There are three distinct types of pigment cells forming zebrafish skin patterns: melanophores (black), xanthophores (yellow), and iridophores (reflective). Using laser ablation in vivo, Nakamasu et al. (2009) showed that disrupted stripe patterns slowly regenerate themselves in a manner very reminiscent of the classical reaction-diffusion model systems. By applying controlled local perturbations, they found that xanthophores and melanophores mutually suppress each other in close proximity, however they interact cooperatively at larger distances. While the molecular basis of these interactions is still unknown, Nakamasu et al. (2009) developed a conceptual 3-field mathematical model of this system. In addition to the slowly-diffusing densities of melanophores and xanthophores, they hypothesized that the long-range coupling is provided by a fast-diffusing factor. This model exhibits a pattern-forming instability that produces stripes or round spots in certain parameter ranges. Since the characteristic width of the zebrafish stripes is only about 10 cell diameters across, the discreteness of the system and fluctuations can be expected to play a significant role in the development of stripes. Interestingly, a hybrid discrete-continuous version of the model, where discrete cells move probabilistically on a lattice in response to the diffusible signaling fields, still exhibits robust patterning despite significant noise.

A very important signaling mechanism often leading to developmental patterning in higher organisms is provided by the Delta-Notch system Bray (2006). When receptor Notch binds ligand Delta on the cell membrane, it initiates a chain of intracellular events that lead to the activation of a number of target genes. While both Delta or Notch genes are present in all cell, their expression is mutually exclusive, in a given cell only one of the two can be expressed at any given time. Direct contact-based Delta-Notch interaction can provide a mechanism for either morphogen gradient-mediated pattern formation (similar to described in Sec. 3.3), or formation of patterned state through lateral inhibition (Turing-like mechanism). Surprisingly, mutual cis-inactivation can increase the pace and precision of the developmental program. Using a discrete cell-based mathematical modeling, Sprinzak et al. (2011) compared pattern formation with and without mutual cis-inhibition. For the model of morphogen-generated wing vein formation in Drosophila, they obtained that mutual inhibition stabilizes the vein width of the interface in a broad range of morphogen gradient. Furthermore, it is also insensitive to extrinsic noise in the system (while remaining sensitive to the intrinsic noise). Another variant of the model can describe formation of checkerboard patterns in Drosophila bristles as well as vertebrate inner ear cells. In this model, Delta-Notch signaling is used to inhibit neighbors’ growth (lateral inhibition). This mechanism provides positive feedback and bistability that leads to pattern formation through symmetry breaking Plahte (2001). Sprinzak et al. (2011) showed that mutual cis-inhibition of Delta and Notch results in much faster differentiation of high-Delta and high-Notch cells. Interestingly, mutual inhibition eliminates the need for cooperativity in the lateral inhibition feedback loop that often is required for the instability.

One of the basic problems in the theory of pattern formation is, even in the presence of the instability, how do initially disordered structures emerging from small random fluctuations give rise to regular and highly precise structures in the course of development? It is well known that uncontrolled growth of patterns usually produces an array of topological defects that only slowly disappear through mutual repulsion or attraction and annihilation Cross and Hohenberg (1993). However, specific feedback control mechanisms can significantly accelerate this process. As it was demonstrated theoretically in a general reaction-diffusion context Aranson et al. (1996) and for a specific model of amoebae aggregation due to cAMP signaling Levine et al. (1996), additional slow feedback can dramatically accelerate coarsening of the overall pattern from initially disordered pattern with many small spirals to a large single spiral (see Figure 14). Similar mechanisms play a role in other pattern-forming systems, for example in chemotactic bacteria aggregation in hostile environments Budrene and Berg (1991); Ben-Jacob et al. (1995); Tsimring et al. (1995).

Figure 14.

Comparison of the pattern formation in the excitable model of cAMP signaling with (a,c) and without (b,d) genetic feedback. Top row shows early stage of pattern formation, the bottom row - late (asymptotic) regime Levine et al. (1996).

4. Fluctuations in Population Biology

4.1. Phenotypic diversity

It has long been recognized that phenotypic diversity represents an important survival strategy in fluctuating environments Philippi and Seger (1989): A phenotypically diverse population sacrifices its optimal fitness for a static environment to protect itself from possible future adverse conditions. This bet-hedging strategy would ensure that there is always a sub-group of individuals which are better prepared for a specific environmental fluctuation than the bulk of the population. Classically, the phenotypic diversity has been associated with genetic diversity, however recently it has been found in many isogenic bacterial populations. One important example of phenotypic variability is called “persistence” Balaban et al. (2004); Kussell and Leibler (2005); Gefen and Balaban (2009). Bacterial colonies often keep a small percentage of slowly growing (dormant) cells (“persisters”) that by the nature of their dormancy are strongly resistant to antibiotic drugs. This represents a major problem for antibiotic treatments of many serious infectious illnesses. Fast-growing bacteria mask the presence of slow-growing persisters under normal conditions, but in the presence of an antibiotic, persisters survive. After the antibiotic is “turned off,” most of the progeny of the persisters resume normal fast growth, and the small percentage ratio of persisters to normal cells is restored. It was shown that the probability to switch to persistence is controlled by the level of expression of toxin-antitoxin genes, which both are expressed from the same promoter that is partially repressed by the antitoxin transcription factor Gerdes and Maisonneuve (2012). Among toxin-antitoxin pairs in E. coli, the most studied is a a particular two-gene operon hipAB which represents a common toxin-antitoxin motif, in which both toxin (hipA) and antitoxin (hipB) Black et al. (1991). A particular mutation (hipA7) leading to the over-expression of hipA leads to a growth arrest and therefore a much higher percentage of persisters under normal conditions, but that growth arrest can be rescued by the over-expression of hipB. Nevertheless, themolecularmechanism of maintaining persistence in a population is still not completely clear. A recent single-cell study by Rotem et al. (2010) showed that HipA protein only affects the growth above a certain threshold of level expression (which is HipB-dependent), and the amount of HipA determines the duration of the dormant phase. Fluctuations in the levels of toxin above and below this threshold result in the coexistence of normal and dormant cells.

In stationary conditions, having a finite fraction of persistent cells reduces fitness (average growth rate) of the population as a whole, however in fluctuating environments that does not have to be the case. Thattai and Van Oudenaarden (2004); Kussell and Leibler (2005); Patra and Klumpp (2013) demonstrated theoretically that stochastic switching among different phenotypes in a monoclonal population confers fitness advantage in a fluctuating environment. Furthermore, the rate of switching can also be optimized to match the characteristic time scale of environmental fluctuations. Acar et al. (2008) tested these ideas experimentally by destabilizing a bistable galactose utilization network in Saccharomyces cerevisiae, so that it would randomly switch between two distinct phenotypes, one (“off”) with basal activity of the GAL network (measured by the amount of YFP controlled by Gal1 promoter) and another (“on”) upregulated 100-fold. The key feature of the destabilized GAL network was the possibility to control the stochastic switching rate by changing the level of regulatory protein Gal80 externally. Acar et al. (2008) engineered a synthetic gene circuit that favors growth of “on”-cells in one environment (E₁) lacking uracil, and “off”-cells in the E₂ environment where uracil was present. As expected, yeast cells in the “on” state were outcompeting “off”-cells in E₁, and “off”-cells were growing faster in E₂. Placing both fast and slow switchers in oscillating environment showed that fast switchers would out compete slow switchers in a rapidly fluctuating environment (period of switching between E₁ and E₂ was ~57h) whereas slow switchers grow faster in slow-changing environment (with period ~200h), see Fig. 15.

Figure 15.

Competitive growth of fast and slow switchers in oscillating environments Acar et al. (2008). (a) mean growth rates in a fast-changing environment (20h in E₁, 37h in E₂), (b) the same in a slowly changing environment (96h in E₁, 96h in E₂),

Many pathogenic microorganisms exhibit bet-hedging strategies which are believed to have evolved in response to the diversity and polymorphic nature of their host immune systems Moxon et al. (1994). Beaumont et al. (2009) demonstrated experimentally that bet hedging can indeed be acquired in the course of de novo evolution when the population of bacteria Pseudomonas fluorescens (that natively does not exhibit stochastically switching phenotypes) acquired this bet-hedging capability. The populations was repeatedly transferred between two contrasting environments and subjected to an exclusion rule, such the phenotype prevalent in a current environment was excluded fro the next round. This selection rule was accompanied by a bottleneck: only a single phenotype among the survivors was selected at random at the time of transfer to the new environment. The exclusion rule provided strong fitness advantage for phenotypic innovation, while the bottleneck favored diversity by alleviating the cost of bet hedging: maladapted mutants did not have to compete directly against bacteria better fit for the current environment. As a result, in two out of 12 replicate lines, the bet hedging trait evolved after just eight successive rounds of selection. Such rapid de novo evolution of bet hedging in experiment suggests that it may have emerged as a survival strategy in uncertain and fluctuating conditions at the earliest stages of natural evolution, prior to more sophisticated regulatory mechanisms.

4.2. Rare events in population dynamics

Population biology models deal with birth-death processes. These models can be very complex and include multiple sub-populations, memory effects, complex inter-species and intra-species interaction rules, spatial population variability. However, in the simplest approximation they operate on a scalar population size n and include two Markovian processes n → n+1 and n → n−1 characterized by (generally) n-dependent rates birth and death rates λ_n and γ_n, respectively. Classical population dynamics models assume deterministic continuous dynamics of the population size n, ṅ = λ_n−γ_n. The simplest of the demographic models is the Malthusian model with constant per-capita birth rate Λ = λ_n/n the per-capita death rate Γ = γ_n/n independently of the population size n. If Λ > Γ, the population size grows exponentially with the rate Λ−Γ. Obviously, the Malthusian exponential growth cannot be sustained indefinitely if resources are limited, and so the population size is saturated either due to the reduction of the birth rate, or increase of the death rate (or both). An example of the former is the logistic growth model in which λ_n = Λn(1 − n/N) and the per-capita death rate Γ is constant, whereas the classical example of the second kind is the ecological Verhulst model Nåsell (2001), in which the per-capita growth rate Λ is constant, but the per-capita death rate increases linearly with n, so γ_n = Γn(1 + nΛ/NΓ). In both models, the carrying capacity K (defined as the deterministic equilibrium population size) is K = N(1 − 1/R₀) where R₀ = Λ/Γ is called the basic reproduction ratio. For R₀ < 1 the population rapidly shrinks and goes extinct. For large N and R₀ > 1, the carrying capacity is large, K ≫ 1.

Due to intrinsic stochastic fluctuations of birth and death processes (called demographic noise) even large populations would eventually go extinct, however the extinction time can be very large. It is an important practical question to find a typical time to extinction given the population size and the environmental conditions. It can be easily shown that in a stable environment, the mean time to extinction (MTE) scales exponentially with the carrying capacity K Leigh (1981); Lande (1993). In some exceptional cases, MTE including the exponential prefactor can be obtained directly from the corresponding master equation as the mean first passage time (MFP) to the origin (n = 0). For example, the extinction time in the stochastic logistic model (λ_n = R₀n(1 − n/N), γ_n = n) at large N is given by Doering et al. (2005)

$$MTE=\frac{R_0}{{(R_0-1)}^2}\sqrt{\frac{2\pi }{N}}\exp \left(\right(\text{ln}{R}_0-1+\frac{1}{R_0}\left)N\right)$$ (23)

However, the majority of population dynamics models are not amenable to an exact analytical solution. A standard approach to finding the mean first passage time is based on the Fokker-Planck approximation to the master equation, when variable n is assumed to be continuum. However, this approximation fails to estimate MFP for large fluctuations that take the population size far away from the carrying capacity. Unfortunately, in case of large R₀ extinction belongs precisely to this class of rare events. Recently, an alternative approach to finding MTE based on the Wentzel-Kramers-Brillouin (WKB) type approximation for the master equation has been developed Dykman et al. (1994); Elgart and Kamenev (2004); Assaf and Meerson (2010). This approximation assumes that the probability distribution P(n, t) reaches a quasistationary shape that slowly decays due to the leakage to the absorbing extinction state n = 0. Finding the characteristic decay time amounts to solving an eigenvalue problem for the quasi-stationary distributions, which in the leading WKB order in small parameter 1/N is equivalent to finding a zero-energy trajectory of a classical Hamiltonian. Using this approach, an “optimal path to extinction” can be computed and the asymptotic expressions similar to (23) derived for a broad class of birth-death models. In all such cases, for large populations, the predicted mean extinction time rapidly becomes astronomical, which evidently contradicts the extinction of various species seen in reality. Note that both FP and WKB approximations treat the population size n as a continuous variable. However, close to extinction, the population size necessarily gets small, and therefore discreteness of variable n becomes important. In such cases, the WKB-approximation can be augmented by a small-n solution of the quasi-stationary master equation Assaf and Meerson (2010).

The main reason for the failure of standard demographic models to produce realistic extinction times is the neglect of environmental fluctuations. Environmental (extrinsic) fluctuations may significantly increase the probability of extinction and therefore reduce MTE. This was already understood in early work by Leigh (1981); Lande (1993) who assumed white Gaussian environmental fluctuations and used a Fokker-Planck approximation to the master equation to demonstrate that for strong environmental stochasticity the exponential scaling is replaced by the power law. In the recent literature (see Ovaskainen and Meerson (2010) for review), the effects of correlations in environmental fluctuations (colored noise) has been taken into consideration. The general result is that finite correlation time of the environmental noise greatly increases the extinction probability since the extinction risk can be strongly elevated by a prolonged period of reduced growth or increased death (i.e. small R₀). Most of this this work is numerical, however some analytical results have recently been obtained in a symmetric variant of the Verhulst model (λ_n = n(μ+r−an)/2, γ_n = n(μ−r+an)/2) with fluctuating parameter r = r₀ + ξ(t) using WKB approximation Kamenev et al. (2008). In particular, for weak environmental noise (variance v_r ≪ μa) and short correlation time of noise (t_c ≪ 1/r₀) MTE still scales exponentially with the carrying capacity K = r₀/a, MTE ~ exp(bK) for large K, however the exponential rate is reduced, b = r₀/μ − v_rt_cr₀K²/(2µ²). For strong (v_r ≫ μa) but short-correlated noise, the mean extinction time scales as the power-law (v_rt_cK/μ)^r₀/v_rt_c. Most surprisingly, for strong and long-correlated noise, the mean extinction time becomes independent of the carrying capacity and is only dependent on the difference between the growth and death rate r and the noise intensity v_e, $MTE~\text{exp}(r_0^2/2v_r)$.

As mentioned above, real population dynamics feature a number of complicating factors that make analytical estimations of the extinction probability difficult. In particular, spatial variability of growth and death parameters may produce strong qualitative effects Meerson and Sasorov (2011). Furthermore, different species usually do not live in isolation but are a part of a complex multi-species eco-system. The corresponding master equations for such multi-specie systems are high-dimensional and are notoriously difficult to analyze except for some very special cases. An example of a tractable problem is the dynamics of an outbreak of an infectious disease within the susceptible-infectious-susceptible (SIS) model close to the extinction threshold R₀ ≈ 1 Dykman et al. (2008); Meerson and Sasorov (2009).

4.3. Spatiotemporal population dynamics

Stochasticity can play an essential role in the spatiotemporal dynamics of populations. Population expansions can occur on many different scales, from microscopic (microbial biofilms) to global (viral epidemics, human mobility). The expansion speed is determined by the structure of the leading edge of the population ”wave”, where the density is low and therefore the discreteness of the populations and the inherent fluctuations are especially important. This is a particular example of a general problem of the noisy traveling wave propagation into a linearly unstable domain which is encountered in a variety of contexts, e.g. spread of advantageous mutations Kolmogorov et al. (1937); Fisher (1937), population invasion Snyder (2003), chemical kinetics Brunet and Derrida (2001), diffusion-limited aggregation Brener et al. (1991), etc.

In the continuum deterministic limit, traveling population waves can be described by the Fisher-Kolmogorov-Petrovsky-Piskunov (FKPP) equation

$${\partial }_{t}h=\gamma h(1-h)+D{\partial }_x^{2}h$$ (24)

where the first two “reaction” terms in the r.h.s. describe the usual logistic growth, and the last, diffusive term models population spreading due to random motility. It is well known that FKPP equation admits a continuous family of one-dimensional traveling wave solutions h(x − V t) with arbitrary wave speeds limited only from below by the minimum value $V_{\mathit{\text{min}}}=2\sqrt{\gamma D}$. According to the marginal stability principle Van Saarloos (1988), sufficiently steep initial profiles connecting the stable fixed point h = 1 at x → −∞ with the unstable fixed point h = 0 at x → ∞, approach the asymptotic traveling wave solution propagating with the minimal wave speed V_min. However, fluctuations can significantly alter this picture. The effect of fluctuations can be modeled by adding to the r.h.s. of the FKPP equation (24) a multiplicative noise term $\epsilon \sqrt{\gamma h(1-h)}\eta (x,t)$, where η(x, t) is δ-correlated in space and time Gaussian noise, and ε is a small parameter. This equation approximates population dynamics models with finite carrying capacity per unit area K, when the underlying kinetics of growth, death, and diffusion are discrete, in these cases ε = O(K⁻¹). It has been shown by Brunet and Derrida (1997) that due to fluctuations the asymptotic front speed becomes unique, lower than V_min, and weakly dependent on K. Intuitively, it can be expected since the fluctuations become important near the leading edge of the population where the local density of species goes to zero. For discrete birth-death kinetics, the zero state in front of the wave becomes linearly stable, since there exists a minimal density for local population growth (at least one individual needed for the birth reaction). This small O(ε) but essential “cutoff” transforms the problem of a traveling wave between a stable and unstable state into a problem of a traveling wave connecting two metastable states for which a unique asymptotic solution with well-defined propagation speed exists. Numerical simulations, as well as various asymptotic methods yield the following scaling for the front speed: V = V_min − C/ log² K. Similar logarithmic corrections to the wave speed have been obtained in a number of evolutionary models of fitness growth Tsimring et al. (1996); Desai et al. (2007); Rouzine et al. (2008); Hallatschek (2011b).

Many interesting spatiotemporal phenomena occur when the motion of individual organisms is no longer purely diffusive. We already mentioned in Sec. 3.4 highly regular patterns that are formed by populations of microorganisms in hostile environments due to attractive chemotaxis Budrene and Berg (1991); Ben-Jacob et al. (2000). These patterns can be described by deterministic reaction-diffusion systems with nonlinear diffusion and drift terms Tsimring et al. (1995); Brenner et al. (1998). However, a more realistic description can be achieved by hybrid models that combine discrete agent-based models for individual microorganisms and continuum fields for the chemoattractant, nutrients, etc. Ben-Jacob et al. (1995, 2000).

Recently, a lot of attention has been focused on swarming phenomena in groups of self-propelled particles that locally exchange directional information. Biology presents a wealth of examples of such systems on vastly different scales: herds of animals, schools of fish, flocks of birds, aggregating amoebae, clusters and rippling waves of myxobacteria, intracellular transport of biomolecules, etc. From the physics point of view, groups of motile organisms represent a nontrivial example of large out-of-equilibrium systems for which classical statistical mechanics results are inapplicable. Notably, the Mermin-Wagner theorem Mermin and Wagner (1966) which states that long-range order cannot be established at finite temperature in systems with short-range interactions in dimensions less than three, does not apply. Indeed, a finite-temperature phase transition to a long-range nematic state has been found in the paradigmatic Vicsek model Vicsek et al. (1995) in which each particle moves with a constant velocity in a direction that tries to align with the average direction of motion of neighboring particles within a certain finite range, but also is perturbed by random fluctuations. Another consequence of the non-equilibrium character of active spatiotemporal population dynamics is the presence of anomalously large (“giant”) density fluctuations when the variance σ_N of the number of objects per unit volume N grows faster than mean 〈N〉 Ramaswamy (2010). In particular, for nematically interacting driven particles, the theory Ramaswamy et al. (2003) predicts for a d-dimensional system that σ_N ~ N^1+d, so in two dimensions the standard deviation scales linearly with N and hence the fluctuations do not become negligible even in the thermodynamic limit. Examples of giant density fluctuations in biological and numerical experiments are shown in Fig. 16.

Figure 16.

a. Myxobacteria form dense clusters on an agar plate due to alignment in the course of inelastic collisions (image courtesy of M. Alber); b. A snapshot from a simulation of the Vicsek model Chaté et al. (2008) (image courtesy of H. Chate)

4.4. Stochasticity in evolutionary dynamics of finite populations

Biological evolution is driven by noise. Indeed, fitness gains are achieved by selecting beneficial mutations and purging the deleterious ones, but, as Salvador Luria and Max Delbrück showed in their famous experiment on bacteria populations attacked by virus Luria and Delbrück (1943), mutations themselves are random. Comparing their experimental data to a simple theoretical model, they were able to rule out the hypothesis of acquired hereditary resistance that every bacterium has the same chance of survival that would’ve produced a Poisson distribution of mutants. Instead they found a much broader non-Poissonian distribution of mutants that proved that bacteria has a constant mutation rate that mutations are not induced by selective pressure. Furthermore, from the distribution of mutant virus-resistant bacteria Luria and Delbrück were able to compute the mutation rate. It is worth mentioning that the giant number fluctuations in Luria-Delbrück distribution (in which variance scales as the square of the mean) and other ecological models Das et al. (2012) are reminiscent of the giant density fluctuations found in active matter (previous section). On the other hand, beneficial mutations can also be lost due to genetic drift (random fluctuations in the number of offsprings per individual with a given fitness) and have to occur repeatedly until they reach fixation Hartl et al. (1997). Generally, random sampling reduces diversity by eliminating rare variants from the gene pool in finite populations.

Stochasticity strongly affects the spread and fixation of mutations in spatially distributed populations since the number of individuals at the edge of the mutant sub-population is always small. Usually, fluctuations tend to slow down the mutation invasion in the similar way as fluctuations slow down the spread of a growing population (see Sec. 4.2). However, Hallatschek (2011a) has shown that in some cases genetic drift (random neutral mutations) can have an opposite effect: it can help the beneficial mutations to invade and fixate. Such behavior can be observed for example if the mutation changes the growth yield (the biomass produced per unit of resource), and mutants compete against the wild type for a limited spatially-distributed resource. The discrete-space discrete-time computational model of Hallatschek (2011a) assumed that both wild type and the mutant grow with the same per-capita rate Λ[1 − (n₀ + n₁)/K], but the carrying capacity of a mixed population of wild-type and mutants is linearly proportional to the fraction of mutant in a local population (deme): K = K₀[1 + εn₁/(n₀ +n₁)]. In this formula n₀ and n₁ indicate the numbers of wild-type and mutant species in the deme. Additionally, a linear diffusion between demes was assumed with the diffusion constant D.

In the deterministic limit (large carrying capacity), the interface between the wild type and mutant populations does not move (as expected since the deterministic FKPP theory predicts the traveling wave speed to be proportional to the square root of the growth advantage and the diffusion constant), and only widens diffusively. However, in a finite population where genetic drift is non-vanishing, the more economical mutants outcompete the wild type and form a traveling wave (see Fig. 17). The mechanism of this noise-driven invasion is that mutant species are more likely to be surrounded by other mutants (ancestors or descendants) and vice versa, so their more effective resource utilization confers preferential advantage on the mutant subpopulation. In the continuum (well-mixed) limit, this effect is absent.

Figure 17.

Stochastic (left) and deterministic (right) simulations of the the model of competition between two species (wild type and mutant for common resource Hallatschek (2011a). Despite the higher growth yield, mutants are only able to invade the wild-type population in the stochastic simulations. Interestingly, the width of the transition region between mutants and wild type remains constant in stochastic simulations but grows in the deterministic case. The parameters of the model are K₀ = 30, D = 0.05, ε = 0.01.

5. Outlook: pinning down the noise

As we have attempted to demonstrate in this review, noise permeates biology on all levels, from the most basic molecular, sub-cellular processes to the tissue, organismal, and population dynamics. The functional roles of noise in biological processes are also very diverse. Along with standard, entropy-increasing effects of limiting robustness, fidelity, and channel capacity of signaling relays and eliciting sub-optimal performance, it occasionally plays more surprising constructive roles, accelerating the pace of evolution, increasing the fitness of populations in dynamic environments (bet-hedging), enhancing intracellular transport of biomolecules and increasing information capacity of signaling pathways, etc. Still, it appears that randomness more often presents a hinderance for the proper biological function and reaching optimal fitness Wang and Zhang (2011), and therefore biology has evolved a number of strategies to cope with randomness. An obvious strategy to reduce the intrinsic intracellular fluctuations is to increase the copy numbers of the molecules. However, this strategy carries a metabolic cost, so a balance between the cost and the noise has to be achieved. This balance is different depending on the functional role of a particular gene product, and so it can be one reason why the abundances of different proteins vary greatly. Newman et al. (2006) and Bar-Even et al. (2006) performed systematic measurements of noise in gene expression across a large cross-section of genes and environmental conditions in yeast and found that noise levels vary along with copy numbers depending on the function of the corresponding proteins: structural genes are usually less noisy, whereas stress-response genes that are not required at all times and only have to be synthesized as necessary, usually exhibit greater amount of noise.

An alternative, less trivial way of confronting noise is to use regulatory systems that can suppress the noise or at least shape its spectral properties in order to enhance the performance of downstream cascades without the metabolic cost of overproducing the intermediate components. We have discussed in this review (Sec. 2.3) that negative auto-regulatory loops can suppress fluctuations caused by transcriptional translational bursting. Nested positive feedback loops effectively suppress fluctuations and enhance memory in decision-making circuits Acar et al. (2005). Non-negligible transcriptional delays can further reduce the probability of switches in multi-stable gene regulatory networks Gupta et al. (2013). The new frontier in studies of biological fluctuations is to figure out how the noise that originates at the gene expression level propagates up the developmental ladder to the levels of tissues, whole organisms, and populations. Along this ladder there are multiple layers of regulation, both intra-cellular (transcriptional, post-transcriptional and epigenetic) and extra-cellular that can shape the characteristics of noise. Analyzing such complex nonlinear, non-equilibrium, multi-scale systems not only poses serious technical challenges but calls for new conceptual paradigms. One intriguing possibility that is being currently explored is that the structure of complex inter- and intracellular networks may have evolved towards a self-organized critical state in which the networks exhibit high susceptibility to external perturbations and large degree of correlation among different components Mora and Bialek (2011). If the cellular networks are indeed poised near criticality, understanding the properties and effects of noise in these networks will require development of new theoretical tools since standard approximations such as moment closure, Poisson, or small-noise may no longer be valid.

The past two decades brought about a wealth of new quantitative information about the properties of noise in biological systems. These rapid advances were enabled by the explosive progress in developing single-cell and single-molecule tools and techniques, including novel fluorescent markers and multi-channel, high- spatial and temporal resolution fluorescence microscopy Fernández-Suárez and Ting (2008), microfluidic technology Bennett and Hasty (2009) and optogenetics Fenno et al. (2011). On the other hand, now standard high-throughput microarray-based genome-wide expression data Schulze and Downward (2001) and recent Next Generation sequencing methods Wang et al. (2009) provide quantitative multi-channel information about the structure and dynamics of cellular networks. These developments allow researchers not only characterize the levels of noise but measure spatial and temporal correlations between fluctuations in different gene products and pathways in dynamic but well-controlled environmental conditions Selimkhanov et al. (2012). The multi-channel correlation analysis of gene expression noise can reveal much about the structure of genetic regulatory networks themselves Dunlop et al. (2008); Munsky et al. (2012). However, many of these new techniques still suffer from limited temporal resolution that may filter out important high-frequency components of stochastic fluctuations and their possible dynamical correlations. To achieve further progress in understanding stochastic intracellular processes it will be necessary to address these experimental limitations.

Synthetic biology has recently emerged as a new and powerful tool for tackling fundamental biological questions Mukherji and van Oudenaarden (2009). The difficulty in analyzing native gene networks lies in their ultimate complexity, “everything is connected to everything.” Since synthetic circuits can be engineered to operate in relative isolation from the rest of intracellular network (they still share transcription, translation, and degradation machinery with the rest of the cell), they provide an alternative, bottom-up approach to elucidating the role of circuit architecture on its performance in noisy environments Murphy et al. (2010). On the other hand, synthetic circuits can be used as well-characterized and controllable testing elements to perturb cellular networks in prescribed ways and thereby probe the system response to non-trivial perturbations.

Finally, the future progress in understanding the origins and consequences of biological noise hinges on the tight integration between quantitative experiments and computational modeling. The development of reliably predictive computational models of biological processes that account for their stochasticity is still in infancy. In vast majority of cases, multiple simplifying assumptions about the biological noise properties are made, such as Poissonian nature of underlying biochemical reactions, statistical independence among different reactions and pathways, neglect of epigenetic effects and retroactivity, lack of multi-scale integration, etc. All these challenges will definitely be in the center of attention of computational biologists in the coming years.