The Movement of a Nerve in a Magnetic Field: Application to MRI Lorentz Effect Imaging

Abstract

Direct detection of neural activity with MRI would be a breakthrough innovation in brain imaging. A Lorentz force method has been proposed to image nerve activity using MRI; a force between the action currents and the static MRI magnetic field causes the nerve to move. In the presence of a magnetic field gradient, this will cause the spins to precess at a different frequency, affecting the MRI signal. Previous mathematical modeling suggests that this effect is too small to explain the experimental data, but that model was limited because the action currents were assumed to be independent of position along the nerve, and because the magnetic field was assumed to be perpendicular to the nerve. In this paper, we calculate the nerve displacement analytically without these two assumptions. Using realistic parameter values, the nerve motion is less than 5 nm, which induced a phase shift in the MRI signal of less than 0.02°. Therefore, our results suggest that Lorentz force imaging is beyond the capabilities of current technology.

1. INTRODUCTION

There has been much interest recently in the detection of neural currents using magnetic resonance imaging [1, 9, 10, 13-18]. This new method of functional MRI would not be based on measuring changes in perfusion--Blood Oxygen Level Dependent (BOLD) MRI--but rather on the detection of neural activity directly. If successful, this development would have enormous potential for imaging electrical activity in the brain as well as in peripheral nerves. Indeed, Koretsky [6] calls direct MRI recording of nerve activity the “holy grail” of brain imaging. Such a technique could provide information about current sources similar to that obtained from electroencephalography or magnetoencephalograpy, but without requiring the solution of an ill-posed inverse problem. However, this method faces great technical challenges because of the small size of the signal, and the possibility of developing this technique is still being debated [1]. Two mechanisms could provide the contrast necessary for MRI detection: 1) the influence of the neural biomagnetic field on the magnetic resonance signal [1, 9, 10, 15, 17, 18], and 2) movement of a nerve caused by the Lorentz force [13, 14, 16]. In this paper, we consider the second of these mechanisms.

“Lorentz Effect Imaging” has been proposed as a method for MRI detection and imaging of biocurrents [13, 14, 16]. When exposed to a magnetic field, nerve action currents are subjected to the Lorentz force that causes the current-carrying nerve fibers to move. If a magnetic field gradient is also present, this displacement causes the spins to move into a region of different Larmor frequency, resulting in an artifact in the MR signal. Truong and Song measured a frequency change in the MR signal associated with electrical activity in the median nerve of the arm, and concluded that “neural activation can be imaged noninvasively by MRI” using Lorentz force imaging [16].

In a previous paper, we calculated the displacement of a nerve carrying an action current in the presence of a static magnetic field [12]. We solved the elasticity problem including the Lorentz force, and found that the resulting displacement (13 nm) was too small to be observed using MRI. The results of our previous study [12] were not consistent with the original interpretation of the measured data [16]. When experimental observations and the theoretical calculations disagree, the assumptions behind the calculation need to be analyzed carefully.

One limitation of our previous calculation [12] is that we assumed the axial current density along the axon did not vary along the axon length, thereby treating the axon as a long wire. In this paper, we develop a more accurate model that accounts for the variation of the current along the axon. Another limitation of our previous calculation was that we only considered the case when the magnetic field was perpendicular to the nerve. In this paper, we consider both cases of the magnetic field parallel to and perpendicular to the nerve. Our goal is to calculate the nerve displacement, and to estimate its resulting affect on a magnetic resonance image.

Our mathematical model has potential applications beyond functional MRI. For instance, nerve motion could impact the study of health hazards caused by strong DC magnetic fields [3]. Moreover, imaging techniques have been proposed to measure electrical conductivity by detecting ultrasonic waves produced by oscillating Lorentz forces on currents in tissue [11].

2. METHODS

Consider a long, cylindrically symmetric, straight axon of radius a and intracellular conductivity σ_i lying in an unbounded volume conductor of conductivity σ_e. We treat the case of a single axon, and then generalize this result to a nerve consisting of many, simultaneously active axons by taking a to be the radius of the entire nerve.

Potential and Current Density Along an Axon

The calculation of potential and current density is identical to that presented by Clark and Plonsey [2] (see Appendix). The transmembrane potential, current density, and displacement are expressed in terms of Fourier transforms in z (the direction along the axon) and modified Bessel functions in r (the radial direction). All these quantities depend on time, because the action potential is propagating along the axon. In our results, we show the behavior at one instant of time; other times would correspond to a shift of the results along the z axis.

Magnetic Field Perpendicular to the Axon

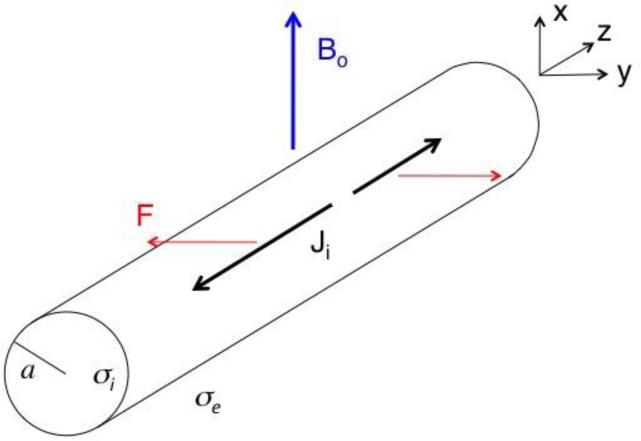
Assume that a magnetic field of strength B₀ points in the x direction, perpendicular to the axon (Fig. 1). In our mechanical model, the tissue experiences pressure and undergoes displacements. We assume that the tissue is incompressible, implying that the displacement u has zero divergence. Our model for the stress contains three terms: one containing the hydrostatic pressure p, another depending on the displacement and shear modulus μ, and a third containing the Lorentz force, F = J × B. From the stress we obtain an equation that describes the elastic state of the medium in static equilibrium, which says that the sum of the forces (elastic plus magnetic) is zero. Expressions for the displacement of the nerve are given in the Appendix.

Figure 1.

A schematic diagram of a nerve of radius a carrying action current J_i (black, thick arrows) along the z axis in a static magnetic field (blue, thick arrow) of strength B_o oriented perpendicular to the axon (the x direction). The Lorentz force F (red, thin arrows) causes the nerve to move in the y direction. The intracellular conductivity is σ_i, and the extracellular conductivity is σ_e.

In general, the spatial extent of the action potential (or more specifically, the length along the axon of the rising phase of the action potential) is much greater than the nerve radius. For instance, if the rise time of the action potential is 0.5 ms and the conduction velocity is 100 m/s, then the depolarization phase of the action potential will extend over a distance of 50 mm, which is much greater than the 2 mm radius of the median nerve in the arm. In the limit when the axial extent of the action potential is much greater than the radius, the displacement in the y-direction (perpendicular to both the nerve and the magnetic field directions) is $u_y=-\frac{B_o{J}_{iz}}{4\mu }{a}^2\ln \left(\frac{\mid k\mid a}{2}\right)$, where k is the spatial frequency and J_iz is the distribution of axial current density (see Appendix for details). This expression is nearly equivalent to the result we derived previously [12], $u_y=\frac{BJ}{4\mu }{a}^2\ln \left(\frac{b}{a}\right)$, which was found assuming that the action current is independent of z. The only difference is that the ln(b/a) factor derived previously, where b was the radius of the volume conductor surrounding the nerve (the radius of the arm, for the case of the median nerve), is replaced by $-\ln \left(\frac{\mid k\mid a}{2}\right)$. Thus, |2/k| takes the place of b. Both factors appear only as the argument of a logarithm, so the solution depends weakly on them.

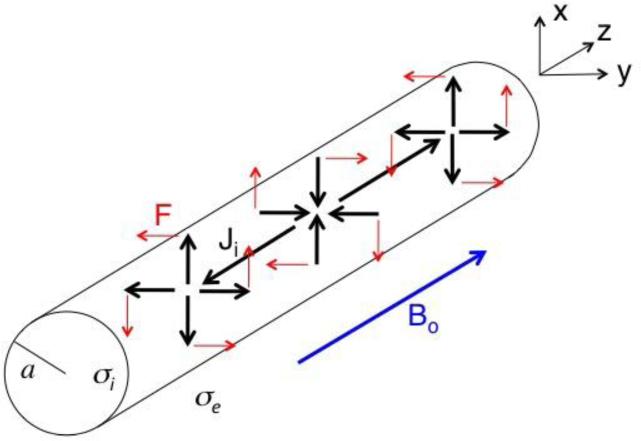
Magnetic Field Parallel to Axon

Now assume that the magnetic field points in the z direction, parallel to the axon (Fig. 2). In this case, the force is entirely in the θ direction, is independent of θ, and causes a twisting motion about the axis of the axon. Using the same mechanical model as described earlier, the pressure is zero and displacement is given in the Appendix.

Figure 2.

A schematic diagram of a nerve of radius a carrying action current J_i (black, thick arrows) along both the z axis and in the radial direction, in a static magnetic field (blue, thick arrow) of strength B_o oriented parallel to the axon (the z direction). The Lorentz force F (red, thin arrows) causes the nerve to rotate about the z axis. The intracellular conductivity is σ_i, and the extracellular conductivity is σ_e.

In our numerical calculations, we use the following parameters: σ_i = 1 S/m [12], σ_e = 1 S/m [12], a = 2 mm (approximately the radius of the median nerve in the arm [4]), B = 4 T (the magnetic field used by Truong and Song [16]), and μ = 10⁴ Pa (typical of soft tissue [8]). The transmembrane potential is represented using a three-Gaussian approximation [2].

3. RESULTS

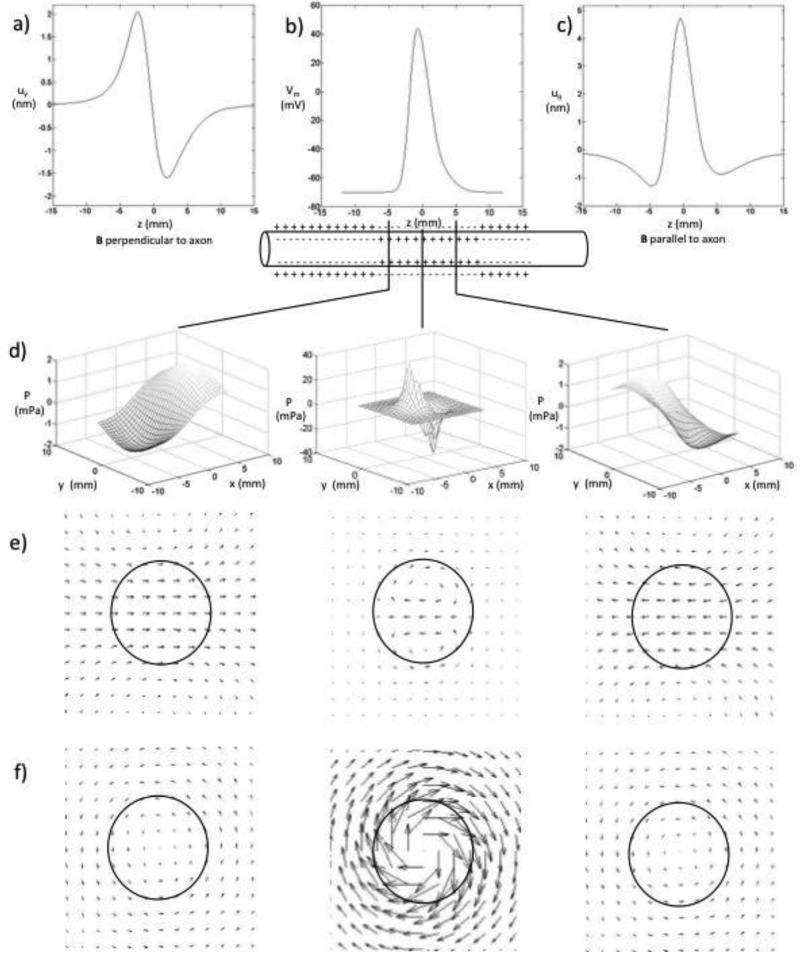
Figure 3 shows the calculated displacement distributions. The peak displacement is about 2 nm when B is perpendicular to the axon, and about 5 nm when B is parallel to the axon. This is the same order of magnitude as, but somewhat smaller than, the displacement (13 nm) calculated with our previous model [12]. When the magnetic field is perpendicular to the axon, the displacement is to the right at z = -5 mm and to the left at z = 5 mm. When the magnetic field is parallel to the axon, the displacement is largest near z = 0, where the nerve rotates clockwise. At z = ± 5 mm, the nerve rotates counterclockwise with smaller amplitude.

Figure 3.

a) The displacement in the y direction, calculated at r=0, for the magnetic field perpendicular to the nerve. b) The transmembrane potential as a function of z. c) The displacement in the direction, calculated at r=a, for the magnetic field parallel to the nerve. d) The pressure as a function of x and y for three axial locations: z = -5, 0, and 5 mm, for the magnetic field perpendicular to the nerve. When the magnetic field is parallel to the nerve, the pressure vanishes. e) The displacement for the magnetic field perpendicular to the nerve (x is vertical, y is horizontal) ), at z = -5, 0, and 5 mm. f) The displacement for the magnetic field parallel to the nerve), at z = -5, 0, and 5 mm.

We can estimate the effect of nerve displacement by calculating the phase shift it induces. Spins in a magnetic field precess at the Larmor frequency. If the displacement of the nerve causes the spins to move to a location with a different Larmor frequency they will precess faster or slower, thereby changing their phase, providing a source of contrast in the image. In their MRI experiment, Truong and Song [16] use a magnetic field gradient of 36 mT/m. If the nerve moved only 5 nm in this gradient, and if the action potential lasted 5 ms, the calculated phase shift caused by the nerve motion is 0.00024 radians, or 0.014°. This phase shift would be very difficult to detect with current technology. Poplawsky et al. [9] claim to have detected phase shifts on the order of 10⁻⁵ radians using magnetic resonance spectroscopy, but these experiments did not perform imaging and required 7-10 hours to obtain the signal. Bandettini et al. [1] estimate that the smallest measureable phase shift during imaging is on the order of 10⁻³ radians under ideal circumstances. Therefore, our results suggest that the Lorentz force mechanism is not responsible for the signal detected by Truong and Song [16].

4. DISCUSSION

A nerve in a magnetic field, such as occurs during magnetic resonance imaging, experiences a Lorentz force that causes the nerve to move. The goal of this paper was to calculate this motion, and to determine its effect on an MRI signal.

Our analysis leads to two main conclusions. First, for the case when the magnetic field is perpendicular to the axon and the axial extent of the action potential is much greater that the radius of the nerve, our previous result [12] and our current result are the same if we replace the arm radius b by |2/k|, where k is the spatial frequency. Since b and |2/k| both appear as the argument of a logarithm, the impact of this difference will be small.

Second, in our previous study we examined only a magnetic field perpendicular to the fiber, but in this paper we consider both the cases of the magnetic field parallel or perpendicular to the fiber. When the magnetic field is along the axis of the axon, it creates a force by interacting with the radial current, producing a twisting motion, like the wringing of a wet towel. This result was not examined in our previous study, because a magnetic field along the axon will only exert a force on the radial component of the current density, not the axial component, and in our previous calculation there was no radial component of the current density. Interestingly, the twisting motion caused in this case is larger than the lateral displacement when the magnetic field is perpendicular to the axon. The general case of a magnetic field in any direction is just the linear superposition of these two cases.

Our results predict that the displacements caused by the Lorentz force are too small to be responsible for the signal Truong and Song observed experimentally [16]. Our previous paper [12] speculated about several alternative explanations for their observations. One possibility is that a few skeletal muscle fibers may have been excited, resulting in small contractions. Truong and Song stimulated the median nerve below the motor threshold to avoid skeletal muscle activity. Although their electromyography recordings did not indicate any muscle signal, if only a few fibers were excited their presence may not be obvious but could cause tiny (say, 1 micron) displacements that might explain the data. Such an alternative explanation is speculative, but we present it to suggest that other interpretations of the data are possible without invoking Lorentz forces.

Our previous article [12] analyzed many of the assumptions of our model. In this study, we relax several of these assumptions. In particular, the transmembrane potential (and therefore the axial current) is distributed along the length of the nerve, the intracellular current density is not uniform across the cross section, a radial component of the intracellular current density exists, and the extracellular current density is not uniform but is large near the axon and falls off with radial distance. However, many of the assumptions are common in both models. 1. We assume a steady-state elastic model, ignoring effects associated with acoustical wave propagation. 2. We assume the nerve and surrounding tissue are homogeneous and isotropic. Anisotropy may be important in peripheral nerves or white matter in the brain. 3. We ignore viscoelastic and poroelastic behavior. Generally these dissipative effects will reduce tissue displacement, so we expect that including these effects will make the disagreement between theory and experiment worse. 4. We use a linear approximation to the strain tensor. Given the small strains predicted by the model, this assumption appears safe. 5. We assume the surrounding volume conductor is unbounded. Adding a bounded volume conductor is possible, but will make the calculation even more complicated. 6. We use a value of 10,000 Pa for the tissue shear modulus [8], and we use the same value both inside and outside the axon. The displacement is inversely proportional to the shear modulus, so if the shear modulus were smaller than the value used, the displacements would be larger. 7. The nerve is elastically coupled to the surrounding tissue. This is particularly important when the magnetic field is along the axon, so the axon merely rotates around its axis. Analysis of this assumption may be the most important issue that remains unresolved. 8. The effect of myelination is ignored. If the distance between nodes of Ranvier is small compared to the extent of the action potential, this assumption should be valid. 9. Song and Takahashi [13] have suggested that “intravoxel incoherent phase shifts” may arise if microscopic incoherent displacements are large but our macroscopic model only predicts the smaller average displacement. We see no mechanism to produce such large microscopic displacements.

The clinical impact of being able to use MRI to detect action currents would be huge. The method could provide information similar to that now obtained from fMRI, except the signal would arise directly from neural activity rather than indirectly from changes in blood flow. Unfortunately, our results indicate that Lorentz force imaging is beyond the capabilities of current technology. On the other hand, our analysis suggests what might be needed to make this a viable imaging technique. First, because the nerve motion is detected by sensing a change in Larmor frequency caused by a magnetic field gradient, the signal will increase with gradient strength. Second, the Lorentz force is proportional to the dc magnetic field strength, so a stronger main field would increase the signal. Unfortunately, strong and rapidly changing gradients can induce neural stimulation, and there are technical limitations to how strong the main magnetic field can be, so the obstacles preventing Lorentz force imaging will be a challenge to overcome. The direct measurement of the biomagnetic field using MRI [1] may be a more promising (but still challenging) path to obtaining this “holy grail” of brain imaging.

APPENDIX

Potential and Current Density Along an Axon

The calculation of potential and current density is identical to that presented previously [2, 19]. The transmembrane potential V_m(z) varies along the axon, and can be expressed in terms of its Fourier transform V_m(k)

$$V_m\left(z\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{V}_m\left(k\right)e^{-ikz}dk,$$ (1)

where

$$V_m\left(k\right)={\int }_{-\infty }^{\infty }{V}_m\left(z\right)e^{ikz}dz,$$ (2)

and k is the spatial frequency. The intracellular potential, V_i(r,z), and extracellular potential, V_e(r,z), obey Laplace's equation. At the membrane, the difference between V_i(a,z) and V_e(a,z) is equal to the transmembrane potential, and the membrane current is continuous. Clark and Plonsey [2] showed that the Fourier transforms of the potentials are therefore

$$V_i(r,k)=\frac{I_0\left(\mid k\mid r\right)}{\beta \left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}{V}_m\left(k\right)$$ (3)

and

$$V_e(r,k)=\frac{K_0\left(\mid k\mid r\right)}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (4)

where

$$\alpha \left(\mid k\mid a\right)=-(1+\gamma \left(\mid k\mid a\right)),$$ (5)

$$\beta \left(\mid k\mid a\right)=1+\frac{1}{\gamma \left(\mid k\mid a\right)},$$ (6)

$$\gamma \left(\mid k\mid a\right)=\frac{{\sigma }_e{K}_1\left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}{{\sigma }_i{K}_0\left(\mid k\mid a\right)I_1\left(\mid k\mid a\right)},$$ (7)

and I₀, I₁, K₀, and K₁ are modified Bessel functions [5]. The intracellular (r < a) and extracellular (r > a) current densities in the r and z directions are

$$J_{iz}(r,k)-ik{\sigma }_i=\frac{I_0\left(\mid k\mid r\right)}{\beta \left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (8)

$$J_{iz}(r,k)=-\mid k\mid {\sigma }_i\frac{I_1\left(\mid k\mid r\right)}{\beta \left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (9)

$$J_{ez}(r,k)=ik{\sigma }_e\frac{K_0\left(\mid k\mid r\right)}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (10)

$$J_{er}(r,k)=\mid k\mid {\sigma }_e\frac{K_1\left(\mid k\mid r\right)}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}{V}_m\left(k\right).$$ (11)

Magnetic Field Perpendicular to the Axon

Assume that a magnetic field of strength B₀ points in the x direction, perpendicular to the axon (Fig. 1)

$${\mathbf{B}}_0={\mathit{B}}_0\widehat{\mathbf{x}}={\mathit{B}}_0(\widehat{\mathbf{r}}\cos \theta -\widehat{\theta }\sin \theta ).$$ (12)

The Fourier transform of the Lorentz force per unit volume, F = J × B, is

$$F_{ir}(r,k)=ik{\sigma }_i{B}_0\sin \theta \frac{I_0\left(\mid k\mid r\right)}{\beta \left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (13)

$$F_{i\theta }(r,k)=ik{\sigma }_i{B}_0\cos \theta \frac{I_0\left(\mid k\mid r\right)}{\beta \left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (14)

$$F_{iz}(r,k)=\mid k\mid {\sigma }_i{\beta }_0\sin \theta \frac{I_1\left(\mid k\mid r\right)}{\beta \left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (15)

$$F_{er}(r,k)=ik{\sigma }_e{\beta }_0\sin \theta \frac{K_0\left(\mid k\mid r\right)}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (16)

$$F_{e\theta }(r,k)=ik{\sigma }_e{B}_0\cos \theta \frac{K_0\left(\mid k\mid r\right)}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (17)

$$F_{ez}(r,k)=-\mid k\mid {\sigma }_e{B}_0\sin \theta \frac{K_1\left(\mid k\mid r\right)}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}{V}_m\left(k\right).$$ (18)

In our mechanical model, the tissue experiences pressure and undergoes displacements. The stress tensor, τ_ij, is [8]

$${\tau }_{ij}=-p{\delta }_{ij}+2\mu {\epsilon }_{ij}+T_{ij},$$ (19)

where p is the hydrostatic fluid pressure, ε_ij is the strain tensor, μ is the tissue shear modulus, and T_ij is the Maxwell stress tensor [5] that results in the Lorentz force. We assume that the shear modulus is the same within the nerve and in the surrounding tissue.

The stress tensor specifies the stress in the tissue, but to determine the net force on an element of tissue we must examine how the stress changes with position. For instance, if the stress is larger on the left side of an element of tissue than on the right, that tissue element will experience a net force. Mathematically, the divergence of the stress tensor gives Navier's equation that describes the elastic state of the medium in static equilibrium, and says that the sum of the forces (elastic plus magnetic) is zero. Navier's equation in polar coordinates is [7]

$$-\frac{\partial p}{\partial r}+2\mu \left(\frac{\partial {\epsilon }_{rr}}{\partial r}+\frac{1}{r}\frac{\partial {\epsilon }_{r\theta }}{\partial \theta }+\frac{\partial {\epsilon }_{rz}}{\partial z}+\frac{{\epsilon }_{rr}-{\epsilon }_{\theta \theta }}{r}\right)+F_r=0,$$ (20)

$$-\frac{1}{r}\frac{\partial p}{\partial \theta }+2\mu \left(\frac{\partial {\epsilon }_{r\theta }}{\partial r}+\frac{1}{r}\frac{\partial {\epsilon }_{\theta \theta }}{\partial \theta }+\frac{\partial {\epsilon }_{\theta z}}{\partial z}+\frac{2{\epsilon }_{r\theta }}{r}\right)+F_{\theta }=0$$ (21)

$$-\frac{\partial p}{\partial z}+2\mu \left(\frac{\partial {\epsilon }_{rz}}{\partial r}+\frac{1}{r}\frac{\partial {\epsilon }_{\theta z}}{\partial \theta }+\frac{\partial {\epsilon }_{zz}}{\partial z}+\frac{{\epsilon }_{rz}}{r}\right)+F_z=0.$$ (22)

In the linear approximation, the displacement of the tissue, u = (u_r, u_θ , u_z), is related to the strain tensor by [7]

$$\begin{array}{cc}\hfill {\epsilon }_{rr}=& \frac{\partial u_r}{\partial r},{\epsilon }_{\theta \theta }=\frac{1}{r}\frac{\partial u_{\theta }}{\partial \theta }+\frac{u_r}{r},{\epsilon }_{zz}=\frac{\partial u_z}{\partial z},{\epsilon }_{\theta z}=\frac{1}{2}\left(\frac{1}{r}\frac{\partial u_z}{\partial \theta }+\frac{\partial u_{\theta }}{\partial z}\right),\hfill \\ \hfill {\epsilon }_{zr}=& \frac{1}{2}\left(\frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right),{\epsilon }_{r\theta }=\frac{1}{2}\left(\frac{\partial u_{\theta }}{\partial r}-\frac{u_{\theta }}{r}+\frac{1}{r}\frac{\partial u_r}{\partial \theta }\right).\hfill \end{array}$$ (23)

We assume that the tissue is incompressible ( ▽ · u = 0), which implies that the displacement can be specified by a stream function ψ, a scalar function whose spatial derivatives give the components of the displacement vector [7]

$$u_r=-\frac{1}{r}\frac{\partial \psi }{\partial \theta },u_{\theta }=\frac{\partial \psi }{\partial r},u_z=0.$$ (24)

These relationships allow the solution of Navier's equation to be stated in terms of two scalar functions: the pressure and the stream function. At the boundary of the nerve (r = a), the displacement and radial components of the stress tensor are continuous.

We have found an analytical solution to Navier's equation subject to these boundary conditions. Inside (i) and outside (e) of the nerve, the Fourier transform of the stream function and pressure are given by

$${\psi }_i(r,k)=-\frac{i}{2\mu k\mid k\mid }\frac{{\sigma }_i{B}_o}{\beta \left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}\cos \theta V_m\left(k\right)\left[r\mid k\mid I_0\left(\mid k\mid r\right)-\left(2+a\mid k\mid \frac{K_0\left(\mid k\mid a\right)}{K_1\left(\mid k\mid a\right)}\right)I_1\left(\mid k\mid r\right)\right],$$ (25)

$$p_i(r,k)=\frac{ik}{\mid k\mid }\frac{{\sigma }_i{B}_o}{\beta \left(\mid k\mid a\right)I_o\left(\mid k\mid a\right)}{I}_1\left(\mid k\mid r\right)\sin \theta V_m\left(k\right),$$ (26)

$${\psi }_e(r,k)=-\frac{i}{2\mu k\mid k\mid }\frac{{\sigma }_e{B}_o}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}\cos \theta V_m\left(k\right)\left[r\mid k\mid K_0\left(\mid k\mid r\right)+\left(2-a\mid k\mid \frac{I_0\left(\mid k\mid a\right)}{I_1\left(\mid k\mid a\right)}\right)K_1\left(\mid k\mid r\right)\right],$$ (27)

$$p_e(r,k)=-\frac{ik}{\mid k\mid }\frac{{\sigma }_e{B}_o}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}{K}_1\left(\mid k\mid r\right)\sin \theta V_m\left(k\right).$$ (28)

These expressions are complicated, but become simpler if |k|a >>1, which means that the spatial extent of the action potential (and more specifically, of the rising phase of the action potential) is much greater than the radius. The intracellular stream function then becomes

$${\psi }_i(r,k)=-\frac{i}{\mu k}{\sigma }_i{B}_{o}r\cos \theta V_m\left(k\right){\left(\frac{ka}{2}\right)}^2\ln \left(\frac{\mid k\mid a}{2}\right).$$ (29)

This stream function is consistent with a displacement in the y direction of

$$u_{iy}=-\frac{i}{\mu k}{\sigma }_i{B}_o{V}_m\left(k\right){\left(\frac{ka}{2}\right)}^2\ln \left(\frac{\mid k\mid a}{2}\right).$$ (30)

In the limit of |k|a >> 1 the current density in Eq. (8) becomes J_iz = ikσ_iV_m, so the displacement is

$$u_{iy}=-\frac{B_o{J}_{iz}}{4\mu }{a}^2\ln \left(\frac{\mid k\mid a}{2}\right).$$ (31)

Magnetic Field Parallel to the Axon

Now assume that the magnetic field points in the z direction, parallel to the axon (Fig. 2)

$${\mathbf{B}}_0={\mathit{B}}_0\widehat{z}.$$ (32)

In this case, the Fourier transform of the Lorentz force is

$$F_{i\theta }(r,k)=\mid k\mid {\sigma }_i{B}_0\frac{I_1\left(\mid k\mid r\right)}{\beta \left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}{V}_m\left(k\right),$$ (33)

$$F_{e\theta }(r,k)=-\mid k\mid {\sigma }_e{B}_0\frac{K_1\left(\mid k\mid r\right)}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}{V}_m\left(k\right).$$ (34)

The force is entirely in the θ direction, is independent of θ, and causes a twisting motion about the axis of the axon.

Using the same mechanical model as described earlier, the pressure is zero and the Fourier transform of the stream function is given by

$${\psi }_i(r,k)=\frac{1}{2\mu k^2}\frac{{\sigma }_i{B}_o}{\beta \left(\mid k\mid a\right)I_0\left(\mid k\mid a\right)}{V}_m\left(k\right)\left[\left(a\mid k\mid \frac{K_0\left(\mid k\mid a\right)}{K_1\left(\mid k\mid a\right)}+2\right)I_0\left(\mid k\mid r\right)-r\mid k\mid I_1\left(\mid k\mid r\right)\right],$$ (35)

$${\psi }_e(r,k)=\frac{2}{2\mu k^2}\chi \frac{{\sigma }_e{B}_o}{\alpha \left(\mid k\mid a\right)K_0\left(\mid k\mid a\right)}{V}_m\left(k\right)\left[\left(-q\mid k\mid \frac{I_0\left(\mid k\mid a\right)}{I_1\left(\mid k\mid a\right)}+2\right)K_0\left(\mid k\mid r\right)+r\mid k\mid K_1\left(\mid k\mid r\right)\right].$$ (36)

Numerical Methods

To perform the numerical calculations, we performed the Fourier transforms and Bessel function calculations in MATLAB. We approximated the z axis with a grid of 121 points, using a distance between points of 0.2 mm. For the transmembrane potential, we used the three-Gaussian approximation to the action potential used by Clark and Plonsey [2].