Development of Wishnofsky’s Rule
Max Wishnofsky asked in a 1958 report "What is the caloric equivalent of one pound of body weight gained or lost?"1 After a thoughtful analysis of the existing literature, Wishnofsky concluded that "the caloric equivalent of one pound of body weight lost" or "gained will be 3500". Fifty years later and with thousands of citations in the scientific literature and the lay press, Hill and his colleagues repeated the oft-used statement "an energy deficit of approximately 3500 kcal is needed to lose 1 lb of body weight" in the authoritative textbook Modern Nutrition in Health and Disease.2 Hill is not alone, with the same rule of thumb posted more recently on the Mayo Clinic3, Livestrong4, and countless other web sites. But Wishnofsky's Rule as applied is inaccurate, leaving many counseled patients wondering why their prescribed weight loss is far less than expected even when they rigorously adhere to their dietitian's recommendations.
Only rarely is the actual report by Wishnofsky1 appropriately referenced and the original concept is frequently mutated (e.g., "weight" replaced with "fat" gain or loss) as it spreads virally across the internet. What exactly is inaccurate and even scientifically incorrect with this half-century old dictum?
The decade following World War II saw profound growth in knowledge about how humans gain and lose weight with changes in energy balance. Disturbances in energy balance that occur with famines, chronic wasting illnesses, and obesity were just coming into focus and subjected to experimental study. A small but scientifically rigorous experimental and analytical literature was available to Wishnofsky as he began his quest to find a simple rule governing weight loss or gain. He first drew upon the 1911 chemical analysis of Bozenrad5 showing that 87% of human adipose tissue is "fat", the remainder water and non-fat solids. We now recognize that most of adipose tissue fat is triglyceride and Wishnofsky correctly assigned this lipid fraction a bomb-calorimetry energy density of 9.5 kcal/g. Wishnofsky then reasoned one pound (454 g) of adipose tissue has an energy content of 3750 kcal. He then turned to published experimental human weight loss studies and carefully distinguished between protocols that prescribed fasting versus those providing a low calorie and/or high protein diet. Wishnofsky understood the critical importance of this distinction as with fasting there are disproportionally large losses of body carbohydrate (glycogen) and protein with associated bound water. Turning to the 1930 classic 59-day very low calorie diet studies of Strang and colleagues6, Wishnofsky used the estimated daily energy and weight balance (−2100 kcal/d and −0.6 lb/d) to derive the energy content of weight change as 3500 kcal/lb. This result was "in striking agreement with the value of 3700 kcal obtained" from computations based on Bozenrad's adipose tissue samples5.
Applying Wishnofsky's Rule to predict the amount of weight loss in pounds resulting from reducing energy intake (EI, kcal/d) or increasing exercise generated energy output (EO, kcal/d) is simple: multiply the imposed deficit in energy stores (ES, kcal/d) by duration of diet (in days) and divide by 3500 kcal/lb. Several fundamental assumptions form the basis of Wishnofsky's Rule: that the subject maintains a constant prescribed EI; that weight loss is not influenced by changes in EO; that on a low calorie balanced diet the main loss of body mass is derived from adipose tissue fat; and the energy content of weight loss is constant at 3500 kcal/lb or 7700 kcal/kg. Under what conditions do these assumptions hold? We now critically examine this question on the path to discovering why modern applications of Wishnofsky’s Rule provide an incomplete description of weight loss kinetics.
Why Wishnofsky’s Rule is Inaccurate
To understand why Wishnofsky's Rule as applied (3500 kcal deficit→1 lb weight loss or 7700 kcal→1 kg weight loss) is outdated and inaccurate, we need to first consider what we know about energy balance and weight loss with low calorie dieting today. When a subject in weight equilibrium reduces energy intake without changing voluntary energy expenditure (e.g., by increasing or decreasing physical activity), a period of negative energy balance follows that draws upon energy stores. Assuming the subject is ingesting a low calorie macronutrient-balanced diet, weight loss will proceed in two distinct phases; a rapid weight loss phase during the first few days or weeks followed by a slower weight loss phase lasting up to two years7,8.
Lost Weight ≠ 3500 kcal/lb and Energy Output is Not Constant
The early weight reduction phase lasting several days or weeks7,8 is characterized by relatively rapid loss in body mass consisting of a small carbohydrate (glycogen) pool, protein, and to a less extent fat as sources of energy. Water balance is also negative during this period as carbohydrate and protein coupled with associated water are released with their oxidation and fluid balance readjusts with changes in dietary sodium intake. Water is also a byproduct of carbohydrate and protein oxidation. The high fluid content and low proportion of weight loss as fat during the evolving early weight loss phase is accompanied by an energy content of weight change that is thus not constant and substantially less than 3500 kcal/lb7,8. As a contemporary example, men and women participants in the Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy (CALERIE I) Study at Pennington Biomedical Research Center prescribed low (25% below baseline energy requirements) and very-low (890 kcal/d for three months followed by weight maintenance) calorie diets had intensive monitoring of actual energy intake with doubly-labeled water and dual energy X-ray absorptiometry body composition measurements over the 24-week weight loss phase8,9. At week 4 the measured energy content of weight change was (X±SEM) 4858±388 kcal/kg (2208 kcal/lb), far lower than Wishnofsky’s value of 7700 kcal/kg (3500 kcal/lb).
Although the timing of metabolic adaptations with low calorie dieting is not exactly clear with respect to the early phase of weight loss, there develops over time hormonal and neural regulatory mechanisms that trigger reductions in resting energy expenditure, protein turnover, and other metabolic processes10, 11. A reduced energy intake also leads to a lowering of the thermic effects of feeding and perhaps to levels of non-exercise activity thermogenesis10. Taken collectively, exhaustion of the available glycogen pool and metabolic adaptations reduce the rates of protein catabolism and energy expenditure with a shift to increasing levels of fat oxidation7. The combined effects of these processes slows the rate of weight loss and leads into the second slower weight loss phase.
The second weight loss phase extends for months or years, although very few supervised studies go beyond six months to one year that can be used to critically evaluate theoretically derived energy balance relations7. Since glycogen is largely depleted, oxidized carbohydrate comes mainly from the diet and glucogenic amino acids in protein. Nitrogen (i.e., protein) balance approaches zero, the steady-state level depending on energy and protein intake12. Adipose tissue triglycerides constitute the main energy source during this period with the rate of weight loss substantially reduced from the early diet period. By 24 weeks the measured energy content of weight change observed in CALERIE I Study participants had increased from the mean 4-week value (4858±388 kcal/kg) to 6569±272 kcal/kg (2986 kcal/lb)8,9.
As with the early phase of dieting, the composition (and energy content) of weight change during the later phase of weight loss evolves as defined by subject baseline characteristics, degree of prescribed energy deficit, and duration of dieting12,13. An important feature of this phase of weight loss is the slowing of energy output10. As noted earlier, resting energy expenditure, the thermic effect of feeding, non-exercise activity thermogenesis, and even activity thermogenesis are or may be reduced compared to baseline. Additionally, decreasing body mass is accompanied by a reduced amount of metabolically active tissue and a lower energy cost of activity. The subject now notices a gradual slowing of weight loss, at some point almost imperceptible, and eventually cessation of weight loss occurs when energy equilibrium is restored at a new lower level.
Modern Approaches to Weight Loss Prediction
Wishnofsky’s views of weight change dynamics were based on the limited understanding of fundamental metabolic processes at the time and his simple formulation was framed with impressions gained from short term dieting studies completed in small samples of obese women6.
Today we view the kinetics of weight change with low calorie diets or overeating in the larger context of energy metabolism and thermodynamics. The three main components of simple thermodynamic models are EI, EO, and ES. Wishnofsky’s focus was on the relationship between ES (i.e., EI − EO) and changes in body weight, with ES /ΔWeight = 3500 kcal/lb based on Bozenrad’s chemical analysis of adipose tissue5. Let’s take an example from the web to see how Wishnofsky’s Rule is commonly applied and why it is inaccurate:
“To get an idea of how much weight you could lose, remember that to lose one pound you need to reduce your caloric intake by 3500 calories. So, if you replace your soda with water, and don’t replace those calories elsewhere in your diet, your potential weight loss could be substantial”. “Replace your 12 ounce can of Coke with water every day and save 51,100 calories per year or about 15 pounds per year14.”
A 12 ounce can of Coke is 140 kcal, so after 365 days (1-yr) without that can of soda ES is −51,100 kcal (−140 kcal/d × 365 d) and this value divided by 3500 kcal/lb is equal to ~15 pounds rounded to the nearest integer. Let’s begin our critical analysis by assuming that the subject’s EI decreases by 140 kcal/d by reducing intake by one can of sugar-sweetened soda each day. Under these conditions EI is constant (i.e., baseline EI minus 140 kcal/d), but rather than EO and ES/ΔWeight being constant as implied by Wishnofsky, both change over time. First, EO decreases during negative energy balance for the reasons mentioned earlier: the presence of metabolic adaptations, reduced thermic effect of food and non-exercise activity thermogenesis, possible reductions in physical activity; and a loss of body heat producing lean tissues. When the reduction in EO from baseline reaches exactly 140 kcal/d, the subject’s weight loss will plateau at a new reduced weight. To reach a stable weight plateau often takes months or even years10.
Likewise, the energy content of weight change (ES/ΔW) is not constant at 3500 kcal/lb but is changing over time. Values are substantially less than 3500 kcal/lb during the early rapid weight loss phase and approach 3500 kcal/lb or 7700 kcal/g during the second slower weight loss phase8. Both fat and lean tissues are lost and do so in a predictable way as the body remodels to a new weight loss plateau13,15.
Given these complex thermodynamic and metabolic effects from simply reducing one's energy intake by 140 kcal/d explains the half-century appeal of Wishnofsky's Rule that can be easily calculated or turned into a simple recommendation. But in the dawn of the computer age in 1973 an International Business Machine scientist Vincent Antonetti had another vision16. Antonetti recognized weight loss as part of the larger topic of human energy exchange and thermodynamics. He compared examples with his newly derived model referenced against the already “classical” Wishnofsky model. In one example, Wishnofsky's model predicted the time needed for a 30 year old man weighing 180 lbs who reduces his intake by 580 kcal/d to lose 50 lbs was 302 days as compared to 545 days for the Antonetti Model. After accurately describing the errors inherent in Wishnofsky's model, Antonetti prophetically claimed “whereas the numerical calculation technique proposed is time-consuming when performed by hand, the procedure, however, is easily programmed for a digital computer.” There lies the roadblock: in 1973 you could gain ready access to a programmable computer at International Business Machines but virtually at no other clinical health care facility in the United States. The first personal computer appeared in 1977 and the internet for public use was launched in the nineteen eighties17.
Since Antonetti’s pioneering work, others have followed with more advanced dynamic weight loss prediction models. Two widely applied models founded on thermodynamic principles are easily accessible to the dietetics community. Both models are developed around the first law of thermodynamics stating in practical terms that the rate of change in body energy stores is equal to the difference between the rates of energy intake and output (i.e., ES = EI − EO). Energy equilibrium, stable energy stores, and constant body weight are achieved over time when energy ingested as food balances energy losses through heat, skin, urine, and stool.
The available dynamic weight loss prediction models are formulated around these thermodynamic concepts and are developed using classical mathematical tools that include calculus. To understand the basis of these models we can return to our earlier web example and examine the physiological events that follow when a person lowers their daily fluid intake by switching one can of soda with an equivalent amount of water. Reducing energy intake by 140 kcal/d will place the person into immediate negative energy balance. Weight will hypothetically decrease over the first day and that weight change will have a low energy density as proportionally large amounts of glycogen, protein, and water are catabolized to make up the calorie deficit. The energy density of weight change will gradually increase over time with exhaustion of available glycogen stores and as adaptations in protein and energy metabolism are activated moving towards the later phase of weight loss. Modelers build their dynamic equations with an understanding of these processes along with the influence of individual baseline body composition, gender, age, and height, and do not rely on the assumed stable energy density value of 3500 kcal/lb (7700 kcal/kg).
Obviously, the available models are far more complex than the simple formulation conceived by Wishnofsky1. The Thomas10,18 and Hall models19,20 both assume body weight is compartmentalized into fat and fat-free mass and they link changes in the mass of these two compartments to corresponding changes in energy stores. Model energy expenditure terms are developed with some differences across the two models by considering changes in resting energy expenditure, voluntary physical activity, spontaneous physical activity, the thermic effect of feeding, and the biochemical efficiencies associated with fat and protein synthesis. Derivation of the Thomas and Hall model terms appear in more recent publications20,21. Both models have been validated by reference against experimental data18–21 and users can simulate the model estimates of weight change through freely available and downloable web-based applications22,23.
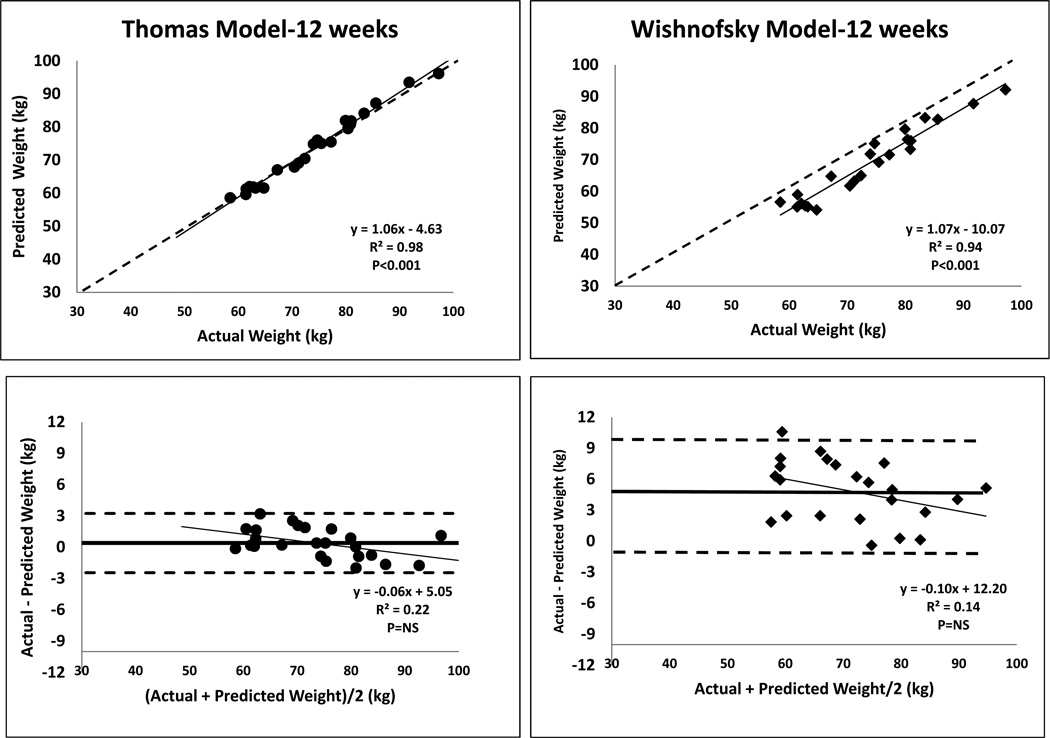
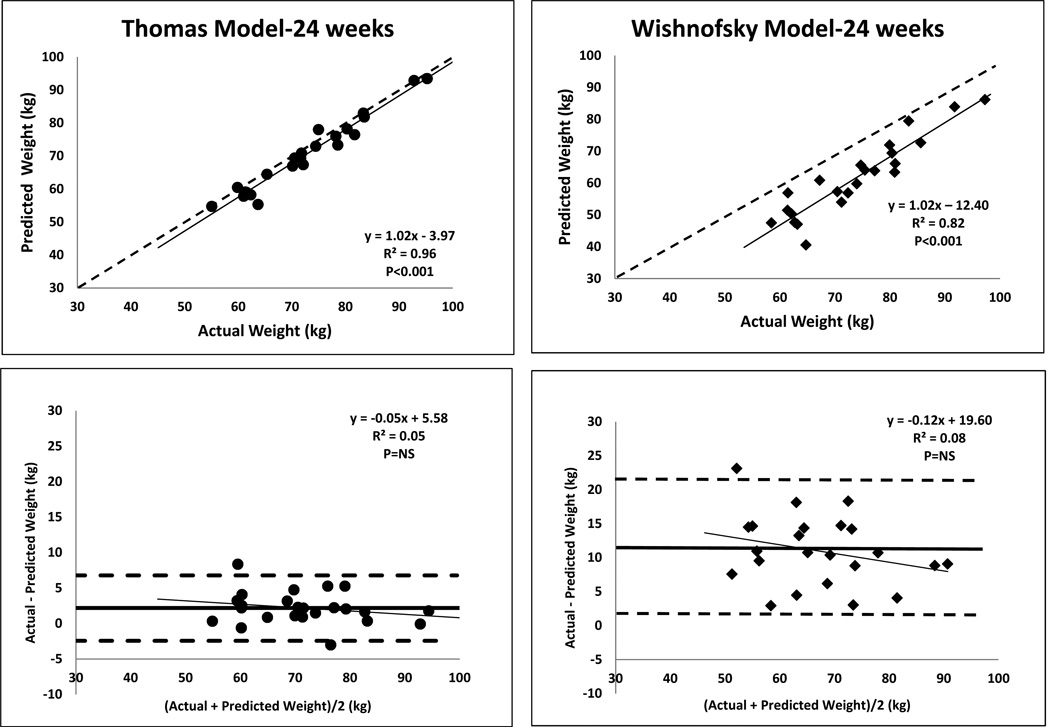
To gain perspective on the differences between the thermodynamically-based models and Wishnofsky’s model in predicted versus actual weight achieved over time with dieting we take as an example CALERIE I Study observations8,9. The results for the dynamic Thomas model and Wishnofsky model at the key protocol 12 and 24 week time points are presented in Figures 1 and 2, respectively. Even though the predicted and actual weights at 12 weeks correlate well for both models (upper panels), there is clear deviation (lower panels, Bland-Altman plots) from the line of identity for Wishnofsky’s model reflected in the bias or average error (bias = 4.8 kg) compared to the Thomas model (bias = 0.4 kg). The 95% confidence intervals, which reflect the variance in model predictions (dashed horizontal lines in lower panel of Figure 1), indicate substantially larger variance from the Wishnofsky model predictions (−1.0 kg, 10.7 kg) in comparison to the Thomas model (−2.4 kg, 3.4 kg). Similarly, at three months of dieting the mean error (95% CI) for the Hall and Antonetti models [2.5 kg (−2.2, 7.1); 2.5 kg (−2.5, 7.8)] were much smaller than those of the Wishnofsky model24. At 24 weeks the weight over-prediction by Wishnofsky’s model was even larger with a bias of 11 kg while the corresponding results for the Thomas model (bias = 2.2 kg) were more in line with that actually observed. The 95% confidence intervals for the Wishnofsky model predictions increased to over double the range from the 3-month predictions (0.9 kg, 21.1 kg) while the variance in the Thomas model remained considerably smaller (−2.4 kg, 6.8 kg).
Figure 1.
Predicted versus actual weight at 12 weeks for Thomas and Wishnofsky’s models (upper panels) among CALERIE I Study participants8,9. Simple linear regression results (solid line and equation) are included in each upper panel; the dashed line represents the line of identify. Bland-Altman plots are presented in the lower figure panels with the solid horizontal line representing the bias (mean deviation of predicted weight from actual weight). The dashed horizontal lines represent the 95% confidence intervals.
Figure 2.
Predicted versus actual weight at 24 weeks for Thomas and Wishnofsky’s models (upper panels) among CALERIE I Study participants8,9. Simple linear regression results (solid line and equation) are included in each upper panel; the dashed line represents the line of identify. Bland-Altman plots are presented in the lower figure panels with the solid horizontal line representing the mean deviation of predicted weight from actual weight. The dashed horizontal lines represent the 95% confidence intervals.
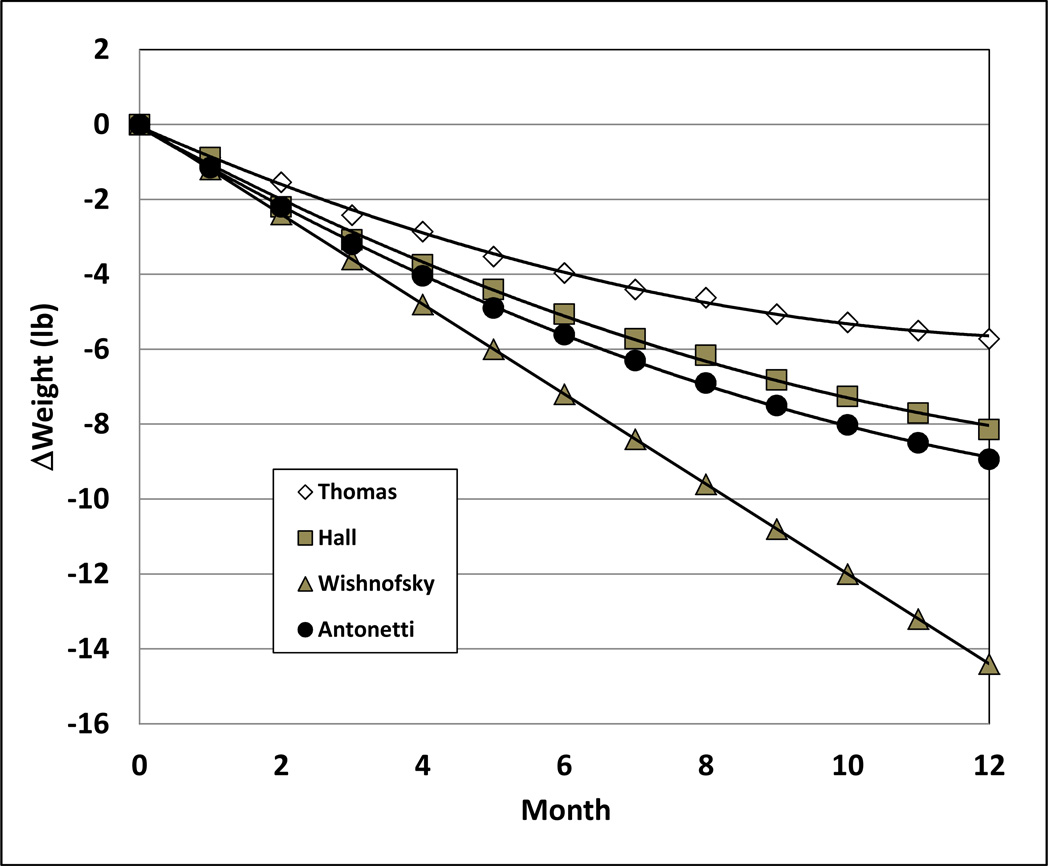
Wishnofsky’s model predicted a 15 lb weight loss over one year for our earlier web example of water replacement for calorie-containing soda (Figure 3). By contrast, the dynamic equations in this example predict a weight loss of 5.7 lbs by the Thomas model10,24, 8.2 lbs by the Hall model19,20, and 8.4 lbs for the Antonetti model16 for a representative overweight woman (age 30 yrs, height 1.68 m [5'6"], weight 76 kg [167.2 lb], and BMI 27 kg/m2).
Figure 3.
Change in body weight (expressed in lbs) predicted by Thomas10, Hall19,20, Antonetti16, and Wishnofsky1 models when an overweight woman (age 30 yrs, height 168 cm, weight 76 kg, BMI 27 kg/m2) reduces her intake by one-soda (140 kcal) per day. Variance during intake reduction for the Thomas model is expressed by the Bland Altman confidence intervals calculated for the CALERIE study as presented in Figures 1 and 29,24.
As shown by the CALERIE and soda examples, the conceptual and mathematical flaws in Wishnofsky’s model become more pronounced with greater extrapolations of weight change over time.
Conclusions
Can the laws of thermodynamics with mathematics applied in physics and chemistry be taken to a patient counseling session that includes providing weight loss expectations with dieting? On the one hand, we have Wishnofsky's Rule that is simple to apply but that lacks a contemporary scientific foundation and leads to a large error in weight loss prediction, even over the short term. On the other hand, we have complex validated dynamic weight loss equations that have strong scientific foundations and that have more accurate and realistic weight loss predictive value. The intuitive path forward is to apply these dynamic prediction models across the myriad of nutrition web sites, cellular phone applications, and in portable computer devices that are now becoming universally available.
Rather than promoting these newer dynamic weight loss prediction models as definitive, we have only started the complex construction and validation process. The thermodynamically based models rely on energy and metabolism data which contain measurement error and this error propagates into model terms. Moreover, there is always a degree of individual biological variation which cannot be captured by a model constructed in part from population averages. Far more research is needed on improving model terms, supplying more accurate empirically derived coefficients, including the dose-dependent influence of exercise or the impact of weight changes in the presence of disease, and effective delivery through software designed for clinical applications. Moving this approach forward will strengthen the links between modern dietetics and basic nutritional and physical sciences.
Acknowledgments
FUNDING/SUPPORT:
One author is supported by a Herman and Margret Sokol Institute for Pharmaceutical Life Sciences Fellowship, and NIH grant R15 DK090739 and another by NIH grants R00HD060762 and U01 DK094418.
Abbreviations
- EI, EO, and ES
energy intake, output, and storage
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
STATEMENT OF POTENTIAL CONFLICT OF INTEREST: One author is a consultant for Jenny Craig. None of the investigators report conflicts of interest for this study.
Contributor Information
Diana M. Thomas, Professor of Mathematics and Director, Center for Quantitative Obesity Research, at Montclair State University, Montclair, NJ..
M. Cristina Gonzalez, Adjunct Professor at the Post Graduate Program in Health and Behavior, Catholic University of Pelotas, Pelotas, RS, Brazil..
Andrea Z. Pereira, coordinator of the Nutrition, Obesity, and Bariatric Surgery area in the Division of Endocrinology, UNIFESP and is nutritional support physician in the Division of Oncology, HIAE, São Paulo, Brazil..
Leanne M. Redman, member of the Reproductive Endocrinology and Women' Health Laboratory, Pennington Biomedical Research Center, Baton Rouge, LA..
Steven B. Heymsfield, Professor and George A. Bray Jr. Chair in Nutrition at Pennington Biomedical Research Center, Baton Rouge, LA. He is also an Honorary Member of the American Dietetic Association..
References
- 1.Wishnofsky M. Caloric equivalents of gained or lost weight. Am J Clin Nutr. 1958;6(5):542–546. doi: 10.1093/ajcn/6.5.542. [DOI] [PubMed] [Google Scholar]
- 2.Hill JO, Catenacci VA, Wyatt HR. Obesity: Etiology. In: Shils ME, editor. Modern Nutrition in Health & Disease. 10th ed. Lippincott Williams & Wilkins; 2006. pp. 1013–1028. [Google Scholar]
- 3.Mayo Clinic staff. Exercise for weight loss: Calories burned in 1 hour. [Accessed March 1, 2013];Mayo Clinic Web site. 2011 Dec 1; http://www.mayoclinic.com/health/exercise/SM00109.
- 4.Martin M. How to burn 3,500 calories a week. [Accessed March 1, 2013];Livestrong.com Web site. 2011 Apr 17; http://www.livestrong.com/article/422797-how-to-burn-3-500-calories-a-week.
- 5.Bozenrad O. Ueber den Wassergehalt des menschlichen Fettgewebes unter verschiedenen Bedingungen. Deutsch. Arch. f. kiln. Med. 1911;103:120–123. [Google Scholar]
- 6.Strang JM, McCluggage HB, Evans FA. Further studies in the dietary correction of obesity. Am. J. M. Sc. 1930;179(5):687–693. [Google Scholar]
- 7.Heymsfield SB, Thomas D, Nguyen AM, et al. Voluntary weight loss: systematic review of early phase body composition changes. Obes Rev. 2011;12(5):e348–e361. doi: 10.1111/j.1467-789X.2010.00767.x. [DOI] [PubMed] [Google Scholar]
- 8.Heymsfield SB, Thomas D, Martin CK, et al. Energy content of weight loss: kinetic features during voluntary caloric restriction. Metabolism. 2012;61(7):937–943. doi: 10.1016/j.metabol.2011.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Redman LM, Heilbronn LK, Martin CK, et al. for the Pennington CALERIE team. Metabolic and Behavioral Compensations in Response to Caloric Restriction: Implications for the Maintenance of Weight Loss. PLoS One. 2009;4(2):e4377. doi: 10.1371/journal.pone.0004377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thomas DM, Ciesla A, Levine JA, Stevens JG, Martin CK. A mathematical model of weight change with adaptation. Math Biosci Eng. 2009;6(4):873–887. doi: 10.3934/mbe.2009.6.873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cahill GF., Jr Starvation in man. N Engl J Med. 1970;282(12):688–675. doi: 10.1056/NEJM197003192821209. [DOI] [PubMed] [Google Scholar]
- 12.Chaston TB, Dixon JB, O'Brien PE. Changes in fat-free mass during significant weight loss: a systematic review. Int J Obes. 2007;31:743–750. doi: 10.1038/sj.ijo.0803483. [DOI] [PubMed] [Google Scholar]
- 13.Thomas D, Das SK, Levine JA, et al. New fat free mass - fat mass model for use in physiological energy balance equations. Nutr Metab. 2010;7:39. doi: 10.1186/1743-7075-7-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Frey M. How much weight you can lose if you stop drinking soda. [Accessed March 1, 2013];About.com Weight Loss Web site. 2013 Jan 4; http://weightloss.about.com/od/eatsmart/a/The-Daily-Cost-Of-Your-Soda-Habit_2.htm.
- 15.Forbes GB. Body fat content influences the body composition response to nutrition and exercise. Ann N Y Acad Sci. 2000 May;904:359–365. doi: 10.1111/j.1749-6632.2000.tb06482.x. [DOI] [PubMed] [Google Scholar]
- 16.Antonetti VW. The equations governing weight change in human beings. Am J Clin Nutr. 1973;26(1):64–71. doi: 10.1093/ajcn/26.1.64. [DOI] [PubMed] [Google Scholar]
- 17.History of Personal Computers. [Accessed March 1, 2013];Wikipedia Web site. http://en.wikipedia.org/wiki/History_of_personal_computers.
- 18.Thomas DM, Martin CK, Heymsfield SB, Redman LM, Schoeller DA, Levine JA. A simple model predicting individual weight change in humans. J Biol Dyn. 2011;5(6):579–599. doi: 10.1080/17513758.2010.508541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hall KD, Jordan PN. Modeling weight-loss maintenance to help prevent body weight regain. Am J Clin Nutr. 2008;88(6):1495–1503. doi: 10.3945/ajcn.2008.26333. [DOI] [PubMed] [Google Scholar]
- 20.Hall KD, Sacks G, Chandramohan D, et al. Quantification of the effect of energy imbalance on bodyweight. Lancet. 2011;378(9793):826–837. doi: 10.1016/S0140-6736(11)60812-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Thomas DM, Martin CK, Lettieri S, et al. Can a weight loss of one pound a week be achieved with a 3500-kcal deficit? Commentary on a commonly accepted rule. Int J Obes. 2013 Apr 8; doi: 10.1038/ijo.2013.51. [Epub ahead of print]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Single subject weight change predictor. [Accessed March 1, 2013];Pennington Biomedical Research Center Web site. http://www.pbrc.edu/research-and-faculty/calculators/sswcp/.
- 23.Body Weight Simulator. [Accessed March 1, 2013];National Institute of Diabetes and Digestive and Kidney Diseases Web site. http://bwsimulator.niddk.nih.gov/.
- 24.Thomas DM, Martin CK, Redman LA, Bray G, Bouchard C, Heymsfield SB. Human Energy Balance: From Model to Clinical Application (Submitted, American Mathematical Society Notices) [Google Scholar]