Is the Gene-Environment Interaction Paradigm Relevant to Genome-Wide Studies? The Case of Education and Body Mass Index

Abstract

This study uses data from the Framingham Heart Study to examine the relevance of the gene-environment interaction paradigm for genome-wide association studies (GWAS). We use completed college education as our environmental measure and estimate the interactive effect of genotype and education on body mass index (BMI) using 260,402 single-nucleotide polymorphisms (SNPs). Our results highlight the sensitivity of parameter estimates obtained from GWAS models and the difficulty of framing genome-wide results using the existing gene-environment interaction typology. We argue that SNP-environment interactions across the human genome are not likely to provide consistent evidence regarding genetic influences on health that differ by environment. Nevertheless, genome-wide data contain rich information about individual respondents, and we demonstrate the utility of this type of data. We highlight the fact that GWAS is just one use of genome-wide data, and we encourage demographers to develop methods that incorporate this vast amount of information from respondents into their analyses.

Introduction

Many health behaviors of interest to demographers—including smoking, alcohol consumption, and obesity—are strongly affected by both environmental and genetic factors (Nelson et al. 2006). Emerging evidence from the gene-environment (GxE) interaction literature has made it clear that a full understanding of these complex phenomena requires some information about genetic risks but also a clear accounting of the social context in which individuals work, play, and eat (Boardman et al. 2008, 2012). This work has led to calls for a cogent and testable framework for GxE research (Bookman et al. 2011) from interdisciplinary teams (Mabry et al. 2008), which have been echoed by the National Academy of Sciences (Hernandez and Blazer 2006) and the National Science Foundation (e.g., IGERT).

Most examples of GxE research in the social sciences have been candidate gene or twin/sibling studies (Boardman et al. 2011; Guo and Tong 2006; Miller et al. 2010; Rodgers et al. 2001; van den Oord and Rowe 2000). Recent declines in the costs of genome-wide genotyping in conjunction with an increasing number of population-based studies with genome-wide data make a genome-wide gene-by-environment interaction (GWGEI) approach possible (Cornelis et al. 2012; Mukherjee et al. 2012; Thomas et al. 2012). For example, the Health and Retirement Study (HRS), the National Longitudinal Study of Adolescent Health (Add Health), the Framingham Heart Study (FHS), and the Wisconsin Longitudinal Study (WLS) either have collected or are collecting genetic information from their respondents. Demographers will soon be “drinking from the firehose” (Hunter and Kraft 2007). This article aims to provide a roadmap for the integration of genome-wide data into social science research through the application of GWAS and GWGEI methods to a phenotype with both genetic and environmental influences. One of the primary goals of this article is to evaluate the relevance of the current GxE models for a GWGEI study using a highly heritable phenotype (namely, body mass index (BMI)) and an established environmental determinant of BMI (education) with a well-characterized and reasonably sized (n = 1,877) sample of adults (the third generation of the FHS). We use college education as our measure of the environment because it is a valid and reliable indicator of socioeconomic position owing to its association with job status, residential quality, health, and health-related behaviors (Pampel et al. 2010). Using current genome-wide methods (Moreno-Macias et al. 2010), we examine the association between 260,402 single nucleotide polymorphisms (SNPs) and BMI, the interaction between each SNP and education, and separate GWAS models for college graduates and non–college graduates. We provide an overview of the statistical and substantive problems with these analyses, including population stratification and gene-environment correlation.

We do not find a single SNP with a p value that exceeds traditionally defined levels of genome-wide significance (p < 5 10⁻⁸; see Storey and Tibshirani 2003). Our findings point to the limitations inherent in the SNP-based GWAS and GWGEI approaches, and we suggest that demographers utilize genomic information as an indicator of relationship status or a summary indicator of risk rather than searching for associations SNP by SNP. We also highlight the difficulty of evaluating the existing GxE conceptual models using genome-wide data. Overall, we suggest some caution for the enthusiasm related to SNP based GWGEI research in general and point to clear limitations of this type of approach for population research specifically. We conclude by offering suggestions about potential uses of genome-wide data other than GWAS and GWGEI that may provide more utility for demographers.

Gene-Environment Interaction Typology

More than one-third of adults in the United States are obese (Flegal et al. 2012). Given the health consequences of obesity (Mokdad et al. 2003), understanding the causes of weight differences in the population is a critical public health issue. Social and genetic epidemiologists have a great deal of interest in using interactions between environmental and genetic factors to characterize the health of populations. This research has the potential to identify specific environments in which genetic influences on obesity-related phenotypes are enhanced or dampened. Similarly, it can highlight genetic factors that make certain individuals particularly sensitive to their environments (Caspi et al. 2003; Ellis et al. 2011). Integrating social and genetic perspectives holds the potential to enhance findings for both biologically and socially focused research.

There is strong evidence that genes determine individual differences in physical weight and weight gain (Fox et al. 2007; Haberstick et al. 2010; Yang et al. 2007). There is also a great deal of variability in the estimated influence of genotype on BMI; with an average of roughly 60 %, heritability estimates for BMI range from as little as 5 % to as high as 90 % (Loos and Bouchard 2003). This variation is in line with the GxE perspective, which anticipates differential associations between genotype and phenotype across different environments (Shanahan and Hofer 2005), and some work has demonstrated that genetic factors linked to obesity-related phenotypes are socially moderated (Boardman et al. 2012; Lee et al. 2011b). Additional evidence for the importance of the social environment with respect to the genetic influences on obesity-related phenotypes comes from a recent report by Rokholm and colleagues (2011). These researchers used measured height and weight from nearly 4,000 twin pairs from the Swedish Twin Register born between 1951 and 1985. They showed a steady increase in the contribution of genetic factors to variation in BMI for each successive birth cohort; the additive genetic variance for BMI was 4.3 (4.1, 4.5) for the earliest cohort, and 7.9 (7.3, 8.5) for the most recent cohort. They concluded that “the obesogenic environment has enhanced the influence of adiposity related genes” (p. 1).

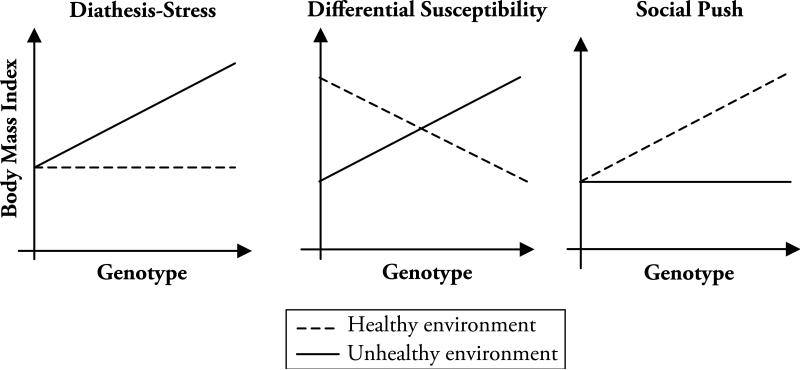
The existing GxE typology emphasizes two main interactive models: diathesis-stress and differential susceptibility (Ellis et al. 2011). These models are described graphically in Fig. 1. First, latent genetic risks for obesity may not manifest for individuals within relatively healthy social environments; risky social environments may be required to observe otherwise small genetic associations. Loos and Bouchard (2003) described environments with limited access to healthy food outlets or spaces in which to exercise regularly as “obesogenic,” and these environments “trigger” (Shanahan and Hofer 2005) otherwise latent genetic risks. In this manner, the environment is characterized as a fundamental cause (Link and Phelan 1995) of obesity although the genetic factors remain central to the etiology of physical weight gain. This social triggering mechanism in the diathesis-stress (or dual risk) model is the dominant GxE paradigm in biological, behavioral, and social science research and is supported by recent work of Rokholm et al. (2011).

Fig. 1.

Conceptual gene-environment interaction models

Second, Belsky and Pluess (2009) made a strong case that the emphasis on risky environments overlooks the possibility that environmental sensitivity is evidenced at both ends of the spectrum. According to their differential susceptibility model, some individuals may be highly sensitive to their immediate social environments and not only will experience very poor outcomes in unhealthy environments but also will have exceptionally positive outcomes in healthy environments. Given this expected crossover association, a risky allele may be common because, on average, it does not confer a risk for the population; the allele may be risky in risky environments but protective in enriching environments. Recent work has shown that alleles within the dopaminergic (DRD4) and serotonergic (5HTTLPR) system confer genetic risks for externalizing behaviors on those in the most-risky environments but protective factors on those in the least-risky environments (Simons et al. 2011).

A third model has not received the same attention as the diathesis-stress or differential susceptibility models. The social push model (Raine 2002) highlights the difference between typical and atypical social environments rather than emphasizing stressful or disorganized environments. This model hypothesizes that genetic factors will emerge as relatively more influential within stable social environments where “social noise” is minimized and the environment allows “biology to shine through” (Raine 2002:314). In other words, genetic factors become more salient when variability in the social environment is minimized.

Education as Environment

In this study, we use attainment of a college degree as our environmental indicator because educational status is regularly linked to physical size and obesity-related phenotypes (Lamerz et al. 2005). Nutrition and exercise are the more proximate determinants of weight gain, but these behaviors are distally linked to socioeconomic position (Faith and Kral 2006). Because fast-food consumption, skipping breakfast, and physical inactivity are all strongly associated with lower socioeconomic status as well as higher BMI, we characterize educational attainment as a fundamental cause of health and health behaviors (Link and Phelan 1995). Educational status is also linked to the quality of the social and built environments of people's neighborhoods (Popkin et al. 2005). In one study (Estabrooks et al. 2003), the researchers demonstrated that public exercise outlets are significantly less likely to be located in poor communities, and these same communities are perceived by the residents as less safe, making parents more likely to reduce the physical activities of their children (Lumeng et al. 2006). Relatively poor neighborhoods are also significantly closer to fast-food restaurants (Reidpath et al. 2002) and farther away from health-food outlets (Ball et al. 2009), and their residents are more likely to rely on convenience stores as opposed to supermarkets for their produce (Bovell-Benjamin et al. 2009). In sum, an exhaustive accounting of the determinants of obesity requires detailed and longitudinal information about the built and social environment, including access to healthy food, physical space to exercise, social limits to outdoor activity (including neighborhood crime), local norms about exercise and body size, and local weather patterns (Faith and Kral 2006). However, educational attainment serves as a useful proxy for many of these more complex relationships.

Extending GxE Research to the Genome-Wide Level

Earlier GxE research focused on candidate gene or twin and sibling studies, but recent statistical advances have extended GxE studies to the genome-wide level. Specifically, the GWGEI models described by Mukherjee et al. (2012), Cornelis et al. (2012), and Thomas et al. (2012) pave the way for social demographers to ask whether specific genetic polymorphisms (across the entire human genome) moderate environmental influences on health outcomes. Despite the publicized need for social science research in this area of gene-environment interplay (Bookman et al. 2011), few efforts have been made to clarify the theoretical contours of the GxE framework and the statistical methods necessary to examine these associations on a genome-wide scale. All GWAS work is plagued by multiple testing problems (e.g., hundreds of thousands or millions of regressions). This is compounded in GWGEI analyses because one will inevitably find some evidence for each of the three GxE conceptual models in Fig. 1. As we show, differentiating this evidence from chance is challenging.

Returning to Fig. 1 helps to illustrate the difficulty. Differentiating between the models requires information on the magnitude and sign of the following three components: (1) the main effect of the SNP (G); (2) the main effect of education (E); and (3) the interaction term (GxE). Although some researchers have made the case that “regions of significance” tests, such as the Johnson-Neyman approach (Preacher et al. 2007), can help us evaluate the diathesis-stress model versus the differential susceptibility model (Simons et al. 2011), this test is more relevant when one measured genotype is interacted with one measured environment. When hundreds of thousands of interactions are performed, the most significant p values for the interaction parameter estimates will be for those SNPs that have different signs for the two groups. These results conform to the differential susceptibility model but will not tell us anything meaningful about the way in which environments systematically moderate genetic factors related to BMI because they will likely be a statistical artifact.

Given the difficulties of SNP-by-SNP approaches, it is important to consider other potential uses of genome-wide data that could include efforts to characterize genetic similarity between each unique pair of unrelated observations in a study. Like quantitative genetic models that rely on assumed genetic relationships among related individuals, new methods rely on measured genetic similarity among unrelated individuals to decompose phenotypic variance into genetic and environmental components. Yang and colleagues (2011a) developed a set of statistical tools in the GCTA package (described in detail later in the article) that implements the aforementioned methods in a very simple and intuitive set of models. This method has produced heritability estimates for height and other phenotypes that are comparable to values obtained from pair-based models of twins and siblings (Yang et al. 2010). Importantly, their statistical approach also highlights the centrality of genetic similarity as a critical source of information for scientific inquiry rather than emphasizing the discovery of specific genetic loci, per se.

Research Questions

1. In the traditional GWAS approach, SNP associations and their corresponding p values are determined one at a time in an attempt to identify genetic loci that are associated with a phenotype. Given that the GxE framework is more complex, is this SNP-by-SNP approach still useful for GxE research among demographic researchers interested in health and health behaviors?

2. Given the sheer volume of information that results from GxE analyses with genome-wide data, how can researchers evaluate the evidence in support of the diathesis-stress, differential susceptibility, and social push models?

3. Given the difficulties we demonstrate in reconciling GxE results with the relationships postulated by the typology of GxE models, how can genome-wide data be used to inform future demographic research?

Methods

Data and Measures

The study sample for this project was derived from the Framingham SNP (Single Nucleotide Polymorphism) Health Association Resource (SHARe, version 6) as available through the NCBI Database of Phenotypes and Genotypes (dbGaP). The analysis for this study focused on the third generation of the Framingham Heart Study (FHS) (Splansky et al. 2007). The original cohort of the FHS was first assessed in 1948; nearly 25 years later, the respondents’ children (the G2 sample, n = 3,548) and many of their spouses participated in the offspring cohort study. Then, in 2002, roughly 4,000 adults who had at least one parent in the offspring cohort took part in the third generation (G3) cohort study. This cohort was examined for a variety of different morbidities using clinical and laboratory assessments. Crucially, study participants were measured for height and weight. Table 1 presents descriptive statistics for the FHS G3 sample that we use in our analysis by educational status. Those without a college degree have an average BMI that is 1.44 units higher than those with a college degree (p < .001). This is a moderate effect size (Cohen's D ~ .3) and translates to roughly 10 additional pounds for a 140-pound adult who is 5′8″. There are no gender differences by educational attainment, but we do see that our college-educated sample is slightly younger. We include these controls in the genome-wide association models described later.

Table 1.

Means (and standard deviations) for all variables used in the analysis

	College Degree
	No	Yes	Prob.
Body Mass Index	27.40 (5.58)	25.96 (5.20)	<.001
Sex (Female = 1)	0.50	0.54	<.103
Age (years)	40.20 (7.74)	38.79 (7.48)	<.001
Sample Size	816	1061

These samples were made available by the Framingham SHARe resource, which contains genotypes for all respondents using the Affymetrix 5.0 genotyping platform. After we reduced the Framingham SHARe data set to trios with complete (nonmissing) genetic information (i.e., genotypes for biological mother, biological father, and focal subject), our analytic sample included 1,877 trios. Because we are interested in interaction terms, we eliminated SNPs that have fairly low minor allele frequencies (those with MAF <5 %). If the minor allele frequency is .05, we would expect roughly one-quarter of 1 % (.05²) of people in the sample to be homozygous for the minor allele; in a study of our size, that translates to roughly five people. We also dropped SNPs that did not meet the Hardy Weinberg equilibrium (HWE) criterion. If the minor allele frequency is p and the alternate allele frequency is q, then the HWE is a simple one-degree-of-freedom chi-square test of independence in which the observed genotype frequencies are compared with the expected frequencies given the frequencies for each allele, where the expected frequencies are given as p², 2pq, and q². Deviations from the expected frequencies provide some evidence of deviation from the assumption of random mating and also indicate SNPs that may have genotyping errors. This initial pruning was done in PLINK (Purcell et al. 2007), and 260,402 SNPs met these criteria (the full set of SNPs is available upon request).

Statistical Analysis: Genome-Wide Gene-Environment Interaction

We used a GWGEI model that (1) protects against population stratification; (2) reduces gene-environment correlation; and (3) provides environmental, genetic, and gene-by-environment parameter estimates (Moreno-Macias et al. 2010). Consider Eq. (1), which describes the association between a SNP (X) and BMI (Y) for the ith person:

$$E(Y_i\mid X)=b_{0m}+b_1{X}_i.$$ (1)

The key aspect of this simple model is that for each SNP in the genome-wide array, it conditions the estimate of this association on the mating type (m) of the parents (where m = 1, 2, . . . 6). Mating type measures the similarity between the parents for the given SNP. Parents may both have two copies of the minor allele (AA, AA), one may have two copies of the minor allele and the other two copies of its alternate form (AA, BB), they may each have one copy of each form (AB, AB), and so on. In total, there are six potential mating types: AA-AA, AA-AB, AA-BB, AB-AB, AB-BB, and BB-BB. Controlling for mating type conditions the estimate for b₁ (the effect of a particular SNP on BMI) on the likelihood of an individual inheriting a particular allele from either or both parents. The most important aspect of this model is that the use of trios enables researchers to look at distributions of alleles within the family, nearly eliminating the risk of population stratification. This model is comparable to the FBAT approach (Laird et al. 2000; Laird and Lange 2006), which has been successfully used to identify SNPs linked to obesity (Herbert et al. 2006).

$$E(Y_i\mid X,Z)=b_{0m}+b_1{X}_i+b_{2m}{Z}_i+b_3{Z}_i{X}_i.$$ (2)

Equation (2) extends Eq. (1) to the GxE approach by including the b_2m and b₃ estimates. The b₃ estimate is the GWGEI estimate, and it describes the extent to which the effect of a SNP is moderated by the environment (Z). The effect of Z is conditioned on parental mating type (as described by b_2mZ_i), which reduces potential confounding due to gene-environment correlation. That is, if the likelihood of college graduation (E) is higher for those whose parents have a particular genetic makeup (G), then G and E are not independent and GxE parameter estimate may be biased (Jaffee and Price 2007). The use of generalized liner modeling strategies, as opposed to specific software packages such as FBAT, is attractive in that it allows for complex sampling designs, sampling weights, multilevel extensions (possibly including longitudinal mixed extensions), and virtually any way of measuring the phenotype (e.g., binary, count, time to onset, multinomial). This modeling flexibility makes genome-wide analyses more approachable for demographic researchers. This flexibility increases computational demands compared with using specialized software, but advances in the speed of modern computing technology makes this type of work a more viable option for many researchers.

Statistical Analysis: Genome-Wide Variance Decomposition

The preceding models emphasize allelic associations and corresponding interactions one SNP at a time. Researchers have recently adapted existing quantitative genetic modeling techniques to include genetic similarity among unrelated individuals (Lee et al. 2011a; Yang et al. 2010, 2011b). These methods have been organized into the GCTA suite of genome-wide association tools and are available to researchers online (http://www.complextraitgenomics.com/). Rather than estimating the cumulative influence of all known causal loci (which are, in principle, unknown), these models estimate a relationship matrix for all unrelated persons. They characterize the genetic relationships between the jth and kth individual across all genetic markers i = 1 to i = n, with minor allele frequency p as

$$A_{jk}=\frac{1}{n}\sum _{i=1}^n\frac{(x_{ij}-2p_i)(x_{ik}-2p_i)}{2p_i(1-p_i)}.$$ (3)

Related pairs will have values that, on average, correspond to the fixed values in traditional behavioral genetic models (e.g., siblings will have an average of .5), but including family members can artificially inflate heritability estimates because the shared environment is subsumed in the family coefficient. Therefore, eliminating pairs with A_jk estimates greater than .025 is recommended. Total phenotypic variance can then be decomposed into genetic and environmental components; because this method relies on unrelated individuals, there is no shared environmental variance component. Importantly, this same equation can be extended to include an additional variance estimate (A_ge) that indicates the extent to which the genetic variance is consistent across measured environments. Departure from this assumption provides evidence of gene-environment interaction without focusing on individual SNPs.

Results

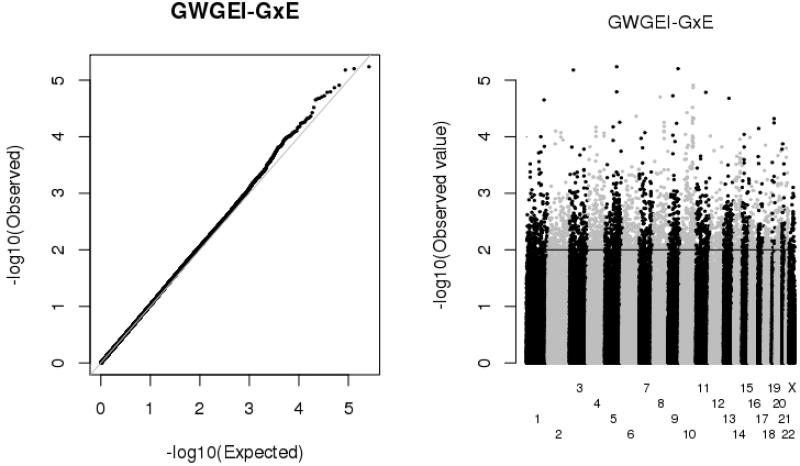
Figure 2 presents the Manhattan and QQ plots of p values for the GxE parameter estimate from the GWGEI models (b₃ in Eq. (2)). Manhattan plots efficiently summarize the vast amount of information from GWAS results because they indicate the chromosomal location (the x-axis) and the magnitude of the p value (the y-axis). Together with a QQ plot, the Manhattan plot enables an assessment of the significance and meaning of results from hundreds of thousands of regression models. For a trait like human height (see, e.g., Weedon et al. 2008), with sufficient sample size the Manhattan plot contains many loci with p values that exceed genome-wide significance, and the SNPs will tend to cluster together in similar regions across the genome. Similarly, the QQ plot will conform to the uniform distribution until the right tail, in which there is typically a notable upward departure. Neither association is evident in the plots in Fig. 2. No SNP approaches genome-wide significance; our smallest observed p value is only 5.8E–06. This is also shown in the QQ plot, in which deviation from uniform is extremely slight. This is particularly important because some researchers have argued that the threshold for significance in interaction models should be even higher (Thomas et al. 2012).

Fig. 2.

Manhattan and QQ plots for GWGEI-GxE estimates for body mass index

The next question is whether the top SNPs from the GxE associations from this GWGEI model correspond to any of the models described in Fig. 1. The estimates from the main and interactive effects for the top six SNPs identified in this model are plotted in Fig. 3. As the differential susceptibility model anticipates, the bulk of these top associations are all instances in which the allele that confers a risk of increased BMI for one group is related to decreased BMI for the other. For example, the first SNP in Fig. 3 (rs12518350) produced a main genetic effect of –1.77 (p < 8.6E-05) and a GxE effect of 2.72 (p < 5.8E-06). This translates to a 1.77 unit decrease in BMI for each additional allele for those without a college degree and a .95 unit increase for those with a college degree.

Fig. 3.

Top GWGEI results for the GxE parameter estimate

This same crossover association is also evident in nearly all the top GxE estimates. For example, when the product of the two slopes is calculated for the top 1,000 SNPs sorted in this manner, only six positive values are seen. That is, in 994 of the top 1,000 GWGEI SNPs, we observe opposite associations for the two groups, which is in line with the differential susceptibility model. However, this may simply be an artifact of the number of statistical models that are estimated. To gauge the extent to which this distribution indeed provides evidence for the differential susceptibility model, we randomly assigned each individual to an “environmental status” (with a prevalence equal to the proportion of college graduates in our study) and then estimated a similar GWGEI model. As with the GWGEI-GxE estimates, 987 of the top 1,000 SNPs (sorted by the GxE parameter estimate) evidenced crossovers in which the product of the two slopes was negative. This suggests that these top associations may not necessarily reflect real differential susceptibility in which individuals are responding differently to the environment. Equally important, six SNPs in the pseudo-GWGEI model evidenced lower p values than the top association in the “real” GWGEI model. For instance, rs17005475 and rs7609257 both had pseudo-GWGEI p values of less than 10^–6.

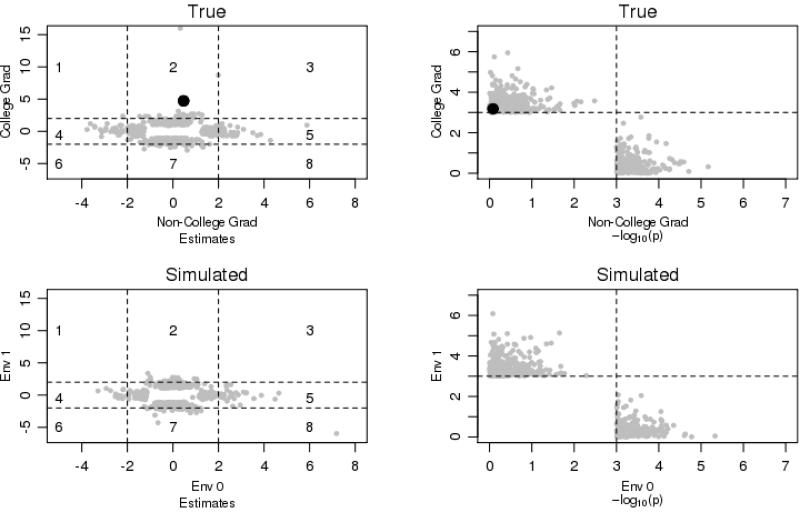
To further examine the different effects for each SNP among college graduates and for those without a college degree, we estimated comparable GWAS models separately for the two groups. Given the reduced sample size, we do not expect p values to exceed the genome-wide significance criteria. The parameter estimates and p values for college graduates and non–college graduates are plotted against one another in Fig. 4. The figure includes any SNP that had a p value of 10^–3 (p < .001) or lower for either group. This value is much weaker than the traditional level of genome-wide significance, but it provides a reasonable threshold for us to examine the distribution of these parameter estimates and corresponding p values for the two groups. The vertical and horizontal lines in the panels on the left denote estimates with a magnitude of 2. As an example, consider the SNP in zone 2 of the upper-left panel that is indicated by the dark circle. This is an example of a SNP that is associated with BMI for those with a college degree but not for those without a college degree.

Fig. 4.

Distribution of genome-wide association parameter estimates among college graduates and noncollege graduates

SNPs that fall within zones 3 and 6 are those with associations that are comparable (in size and direction) regardless of educational status and can be thought of as those providing evidence for main genetic associations. The most important observation from this figure is that there are no SNPs in zones 3 and 6; we were not able to replicate the top SNPs across the two groups. To support the main genetic association, we would expect to see SNPs aligned with a 45-degree line (a slope of 1) across this figure, but this is clearly not the case. The same conclusion is reached when referencing the comparable panel on the right, which summarizes the same models but plots the distribution of p values rather than regression coefficients. There are no SNPs in the upper-right quadrant (evidence that the SNP was even moderately significant for both groups) and only a limited number of SNPs that come close to replicating across the two groups. To further contextualize these distributions, we repeated these figures using the simulated environment described earlier; these are plotted in the bottom half of Fig. 4. As with the true environmental model, the simulated environmental model yields p values whose logarithms are negatively correlated with one another and, again, no consistent evidence for the reliability of genetic signals amid a sea of noise.

Zones 1 and 8 are those in which the association is large and positive for one group and large and negative for the other—in other words, cases that support the differential susceptibility model. As with our conclusion from the GWGEI models with the simulated environmental moderator, we find only one SNP in zone 1 and none in zone 8, which provides very little support for the differential susceptibility model when the full distribution of the SNPs is considered. In other words, although rs4358837 demonstrated a slope of –2.2 (p < .01) for non–college graduates and 2.4 (p < .0003) for college graduates (GWGEI p value 1.98E-05), it is clear from the figure that these crossovers are not the norm across the genome (the same conclusion that was drawn from the GWGEI estimates shown in Fig. 2). This SNP is in an intronic region of CYP7B1, which has been linked to cholesterol and drug metabolism (Tsaousidou et al. 2008); again, though, except for this one SNP, the overwhelming bulk of the interesting statistical associations for each group do not demonstrate any evidence of crossover effects that would support the differential susceptibility model.

The highlighted SNP in zone 2 is consistent with the social push perspective in which genetic effects emerge as more salient in the healthier environments; this SNP has an effect of roughly 4 (e.g., BMI increases by four units for each risk allele) for college graduates, but it is virtually zero for those without a college degree. A similar conclusion could be reached for SNPs in zone 7 of this panel in which the SNP would have an effect (albeit negative) for those with a college degree but not for those without a degree. Zones 4 and 5 are those in which the effect of the SNP is very large for non–college graduates but much smaller for college graduates. In this case, the distribution of effects is in line with the diathesis-stress model. For example, there is one observed SNP that increases BMI by roughly six units for each risk allele among those without a college degree but is unrelated to BMI for those with a college degree. Figure 4 illustrates the difficulty in testing the diathesis-stress (zones 4 and 5) vis-à-vis the social push (zones 2 and 7) model. There is evidence for both of the models, they seem to be equally likely, and the distribution of the effects does not appear to be different from a random environment. Consider the 349 interesting SNPs (those with p values less than 10⁻³) for the college graduates (the upper-left quadrant of the figures on the right). Among these SNPs, 316 did not reach p < .10 for the non–college group, suggesting that roughly 90 % of the SNPs that predict BMI for college graduates are not associated with BMI among non–college graduates. This might seem to provide strong support for the social push perspective. However, 87 % of the SNPs that predict BMI for non–college graduates (n = 258) are roughly equal to zero for college graduates, and very similar results are shown for the simulated environment (90 % and 94 %, respectively). Again, the difference is very slight, with no clear evidence that these are different from a random environment. In other words, although some SNPs fall within zones 2, 4, 5, and 7, their presence does not necessarily provide support for the diathesis-stress or the social push perspectives. It is possible that the environment is systematically causing SNPs to operate differently across the environments, but differentiating real GxE signals from those due to chance is difficult to achieve using traditional methods and existing data sources.

Finally, it is quite clear that the effect sizes required for deeming SNPs statistically significant are somewhat unrealistic. For example, in Fig. 4, many SNPs have slopes that exceed 2, and an increase from zero to two risk alleles would involve a four-unit increase in BMI. For a 140-pound adult who is 5′8″, this increase translates to an increase in of more than 26 pounds. This assumes an additive model and doesn't take into account the minor allele frequency, but it illustrates the rather extreme substantive implications if our understanding of genetic influences on BMI is based on SNPs that are deemed to be statistically significant from GWAS models. The same (albeit more extreme) understanding can be seen for the SNPs in the upper-left corner of Fig. 4 that have slopes that are near or exceed 10; a 20-BMI increase comparing the two homozygous groups at one loci is simply not possible.

Rather than trying to identify specific causal loci, the heritability-by-environment approach attempts to identify systematic differences in the genetic contribution to overall variance. As noted earlier, these models traditionally relied on twins and siblings to estimate the contribution of assumed genetic similarity to their observed phenotypic similarities. However, genome-wide data can also provide comparable estimates by comparing observed genetic similarity with observed phenotypic similarity of unrelated persons. The first column of Table 2 presents the genetic (Vg), environmental (Ve), and total phenotypic variance (Vp) for BMI among the third-generation participants of the FHS. The ratio of genetic variance to total variance provides an estimate of heritability. Estimated heritability of BMI is .52 and .60 for those without and with a college degree, respectively. This model is in line with the social push GxE model because the genetic factors are relatively more important for those in a relatively healthy environment. That is, the difference in heritability across the groups is due to differences in environmental variation rather than differences in the genetic effects. This can be seen in the components of the model where the genetic variance is virtually identical for the two groups (16.32 vs. 16.24), but there is more environmental variation among those with less than a college education than among college graduates (14.84 vs. 10.86). Comparable results are shown in the work of Johnson and colleagues (2011), who used a large study of twins from the Danish Twin Registry (~20,000 twin pairs) to calculate genetic and environmental contributions to BMI; increasing levels of education are associated with increasing heritability of BMI, but this is because there is less overall phenotypic variance among the most-educated. The genetic contribution to the overall variance remains virtually identical.

Table 2.

Heritability estimates for BMI using genome-wide data among unrelated persons

	<College	College +	GxE Model
Genetic Variance (Vg)	16.32 (3.21)	16.24 (2.45)	11.69 (2.44)
Environmental Variance (Ve)	14.84 (2.754)	10.86 (1.98)	12.73 (1.61)
Gene-environment Variance (Vgxe)			4.50 (2.64)
Total Phenotype Variance (Vp)	31.16 (1.61)	27.10 (1.25)	28.83 (1.00)
Heritability (Vg/Vp)	0.52 (0.09)	0.60 (0.08)	0.40 (0.08)
GxE Contribution (Vgxe/Vp)			0.16 (0.09)
N	816	1,061	1,877

Note: Cell entries are variance estimates, with standard errors in parentheses.

To examine the statistical significance of this difference, we also estimated a GxE GCTA model, which is shown in the final column of Table 2. The GxE parameter estimate (4.50) is marginally significant (t = 1.70, one-tailed p value = .047) and provides some further support for the social push GxE perspective. The heritability estimate for the full sample is the sum of the genetic and GxE components, and it allows one to consider the contribution of GxE to overall heritability. In this case, 28 % of the additive genetic influences (.28 = 4.50 / (4.50 + 11.69)) on BMI are due to GxE processes. Finally, as with the GWGEI models, we also estimated a comparable GCTA GxE model in which we randomly assigned environmental status, and the model produced a heritability of .52 and a GxE estimate of 0 (SE = 2.22). These results do not necessarily imply that the environment causes genes to operate differently; rather, it simply changes the relative importance of genes vis-à-vis the environment. However, the lack of significance of the GxE component with the simulated environment compared with the value from the empirical environment provides some tentative evidence for the social push GxE perspective and highlights the importance of considering environmental context when examining genetic contributions to complex phenotypes like BMI.

Discussion

Gene-environment interactions for obesity-related phenotypes have been shown in candidate gene (Guo et al. 2007) and twin and sibling studies (Boardman et al. 2012). To date, though, no existing study has considered GxE associations for BMI using the GWGEI approach. Several recent studies have highlighted the usefulness of GWGEI methods (Cornelis et al. 2012; Mukherjee et al. 2012; Murcray et al. 2009; Thomas et al. 2012), but none of these approaches used trios to detect main and interactive genetic effects and to reduce the risk of gene-environment correlation. Our primary goal was to situate the GWGEI findings within the existing GxE theoretical framework to provide some structure as we sifted through hundreds of thousands of main environmental, main genetic, and GxE terms. Our results suggest that the search for specific alleles that are related to health outcomes of interest to demographers, such as physical weight, may not provide useful information, and the results from GWGEI analyses are also not likely to shed any light on the existing GxE typology, especially given sample sizes in the thousands. Even with a well-established environmental factor and a highly heritable phenotype, we cannot detect overall patterns that consistently support one of the existing models vis-à-vis the others. We were able to find some evidence for each GxE model but no consistent story with biologically plausible mechanisms linking environmental sensitivity to BMI and differentiating the pattern of results from noise. This point is important because it is likely that many of the GxE associations are real, but we simply could not differentiate between real and false interactions with our current methods and data. A SNP-based approach is unlikely to provide empirical results that can be used to support the existing GxE models. We suggest that this typology be reserved for studies focusing on interactions between a candidate gene and the environment (Simons et al. 2011) or those examining heritability by environment interactions (Boardman et al. 2011).

The second important observation from our study was the genome-wide evidence for the heritability of BMI even though no single SNP emerged as a clear determinant of individual differences in BMI. Although finding the “missing heritability” has been a central issue for genetic epidemiologists (Manolio et al. 2009), it has not entered into recent demographic studies. As our methods section explains, genome-wide data provide exceptional detail on the genetic similarity of unrelated persons in our studies. These data are already available from a number of population data sources that also contain indicators of mobility, migration, mortality, marriage, birth outcomes, health, and health behaviors. If genes are associated with environmental exposure and the health outcome of interest (e.g., genes linked to novelty-seeking behaviors may predict selection into a social group of smokers and may also predict smoking behavior), then researchers may reach erroneous conclusions about the role of environmental factors. By creatively using these data to account for genetic factors that predict the independent and dependent variables, demographers can rule out alternative explanations. Lee and colleagues (2012) extended the GCTA model to include an estimate of genetic correlation using a bivariate approach. At a minimum, if genome-wide data are available, researchers can easily demonstrate absence of genetic correlation, which in turn reduces the likelihood of genetic confounding resulting from gene-environment correlation.

This point is important because it reminds us that genome-wide data continue to hold a great deal of information for the respondents of our studies. Genome-wide analysis (in the SNP-by-SNP approach) is simply one use of these data; candidate SNPs with clearly hypothesized links to environmental sensitivity via biologically plausible networks (Duncan et al. 2010) can be used in a comparable manner to construct a priori genetic profiles. We are skeptical that any one SNP will hold sufficient information to shed light on individual differences in environmental sensitivity, but summary information across a number of different loci may prove to be useful. For example, Belsky and colleagues (2012) examined 29 SNPs that have been linked to body mass phenotypes from published GWAS studies. They summed the number of risk alleles for these 29 SNPs from an independent sample to form a genetic risk score (GRS). BMI was then regressed on the GRS, and they were able to explain roughly 2 % of the variance of BMI in their study. This is a very useful approach that uses existing genome-wide data sources without performing a GWAS, per se. These genetic risk factors can be included as covariates in traditional regression based models, and they can be included as interaction terms with hypothesized environmental moderators. Such information could also be used with propensity score matching models to compare individuals with comparable propensities to engage in a particular behavior.

Future Considerations and Limitations

Several limitations in our study should be considered. First, without any information about energy intake or expenditures, it is difficult to identify the behavioral mechanisms that may undergird the link among education, genetic risk, and body mass. The FHS contains information about caloric intake, daily activities (including exercise), and sleep patterns, and additional adjustments for these behaviors may provide a cleaner signal allowing small genetic associations to manifest. However, given the limited support for any consistent genetic associations, it remains unclear whether additional controls would significantly increase the likelihood of finding SNPs that reach genome-wide significance in a sample of this size.

Second, we examined men and women together, but the work of Jackson and colleagues (2010) and others have suggested that the diathesis-stress model for obesity may be more relevant among women (who may internalize stress) than among men (who may cope with relatively stressful events through externalizing behaviors). If lack of a college degree is deemed relatively stressful, we might test this hypothesis by identifying diathesis-stress loci linked to BMI among women with and without degrees, and then look for links between these same loci and substance use or delinquent behavior among men with and without degrees (Simons et al. 2011). This would help to characterize individual differences that are linked to the likelihood that an individual may respond to their environment. More importantly, though, it structures social environment and social identities as precursors to genetic associations rather than simply byproducts of genetic makeup.

Third, our binary indicator of educational attainment (college degree) misses the wide range of educational credentials and years of completed schooling. This is particularly important because the social push model, for which we did not find clear evidence in the GWGEI models, typically focuses on the “average environment” (Shanahan and Boardman 2009) and hypothesizes that genetic factors are least important at the highest and lowest levels (for education, people with postdoctoral work and high school dropouts) but increase in salience at the average level (high school education and some college).

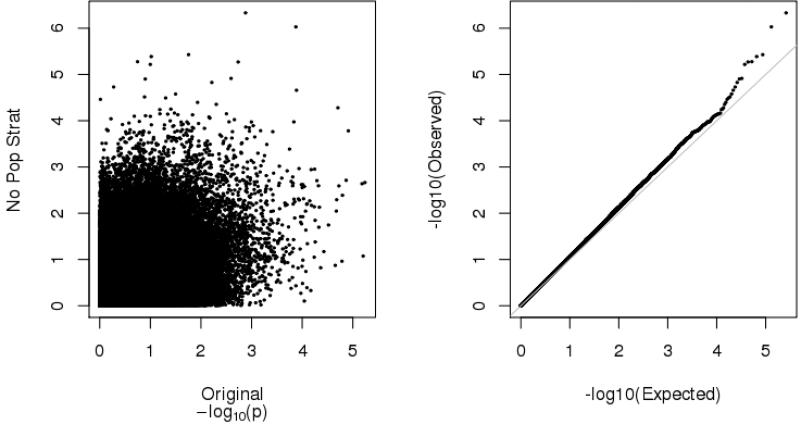
Fourth, our models are quite conservative in that they adjust for any possibility of population stratification and gene-environment correlation. It is possible that one or both of these factors account for our inability to detect associations at genome-wide significance levels. To examine this possibility, we reestimated the same GWGEI models presented in Fig. 2 without the adjustment for parental mating type (population stratification) or the interaction between parental mating type and college degree status (gene-environment correlation). These results are summarized in two diagrams in Fig. 5. The left panel plots the bivariate association between the p value (–log10) from the fully adjusted GWGEI model (those from Fig. 2) and the p values from the GWGEI models without controls for population stratification or gene-environment correlation. If these controls did not affect the p values for the two models, we would expect to see a clear linear association between the values: this is clearly not the case. In fact, the bivariate correlation between the two logged p values is only .30. The right panel is the QQ plot for the unadjusted GWGEI model. There is a notable improvement in the departure of the values from the uniform line when compared with the comparable estimates in Fig. 2, but we still do not have any SNPs that cross the genome-wide significance level, so our failure to detect true GxE SNPs in our GWGEI model is not due to overadjustment of our models. Similarly, even when the analyses are conducted with the same individuals in the full sample, the parameter estimates show tremendous variation between the two models. We do find some associations that approach genome-wide significance, but these drop precipitously with important adjustments for stratification and rGE, and some show suppressor effects so that the unadjusted estimates have p values of less than .001 but the adjusted estimates are less than .00001. In other words, the effects of each SNP are very small and are quite sensitive to the inclusion or exclusion of control variables, which may have to do with our fairly small sample size. For instance, Vrieze and colleagues (2012) stated that studies expecting to achieve genome-wide significance levels of p < 5 10^–8 need to exceed 50,000 individuals. Many health surveys used by demographers, especially those with genome-wide data, are significantly smaller than the 50,000 observations. This limitation should be considered by future researchers who are interested in genome-wide studies.

Fig. 5.

Distribution of p values from GWGEI models with and without controls for population stratification and gene-environment correlation

Conclusion

What specific genetic loci in combination with specific environmental contexts provide the most information about an individual's likelihood of exhibiting a particular behavior at a particular time in his or her life? This question is critical to both social and genetic epidemiologists because it suggests that environmental influences depend on an individual's genetic composition and that genetic influences are contingent on the social environment in which one resides, works, and plays. Little debate exists about the relevance of this question, but finding an answer has thus far proven to be quite difficult. There is little consensus on what constitutes the environment, little agreement regarding statistical versus substantive significance of interactions, little consensus about social and genetic theories explaining the mechanisms of gene-environment interplay, and a replication record that is only marginally better than chance (Risch et al. 2009). Our results suggest that these concerns may be more important when extended to the genome-wide scale. Our results do not challenge the relevance of GWAS studies, nor do they challenge GxE studies in general. Rather, we believe that the SNP-by-SNP GxE approach (GWGEI) is not likely to provide results that can be used to test existing GxE theory. In sum, we believe that SNPs indicate something important about an individual's risk of an unhealthy BMI, but taken individually, they do not hold much information. This is somewhat obvious: people do not inherit a single SNP. Rather, they inherit their entire genome from two sources—hence the importance of genome-wide data as a cumulative indicator of biological proximity among related and unrelated persons. Disentangling the genomic component of family risk from the social and behavioral component has been the work of behavior geneticists for decades, but new evidence for genetic influences on most health behaviors, new statistical methods, and new genetic data sources make this type of approach important and timely for demographic researchers.