Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 May 28;4:5090. doi: 10.1038/srep05090

Angle-resolved light scattering of individual rod-shaped bacteria based on Fourier transform light scattering

YoungJu Jo 1, JaeHwang Jung 1, Jee Woong Lee 2, Della Shin 3, HyunJoo Park 1, Ki Tae Nam 3, Ji-Ho Park 2, YongKeun Park 1,a
PMCID: PMC4035574  PMID: 24867385

Abstract

Two-dimensional angle-resolved light scattering maps of individual rod-shaped bacteria are measured at the single-cell level. Using quantitative phase imaging and Fourier transform light scattering techniques, the light scattering patterns of individual bacteria in four rod-shaped species (Bacillus subtilis, Lactobacillus casei, Synechococcus elongatus, and Escherichia coli) are measured with unprecedented sensitivity in a broad angular range from −70° to 70°. The measured light scattering patterns are analyzed along the two principal axes of rod-shaped bacteria in order to systematically investigate the species-specific characteristics of anisotropic light scattering. In addition, the cellular dry mass of individual bacteria is calculated and used to demonstrate that the cell-to-cell variations in light scattering within bacterial species is related to the cellular dry mass and growth.

Identifying and characterizing bacterial species have central functions in various fields of research in contexts of food pathogen detection, biomedical studies, diagnoses, and treatments. Among the available optical techniques for the characterization of microorganisms in rapid, non-invasive, and label-free manners1,2,3, angle-resolved light scattering (ALS) measurement techniques provide abundant information about both cellular structures and biochemical compositions of bacteria; furthermore, the implementation of ALS measurement techniques is conceptually simple and straightforward4,5,6. However, despite the increasing importance of single-cell assays7, measuring the ALS signals from individual bacteria remains challenging2,6,8,9,10,11,12, whereas the ALS of bacterial suspensions and colonies has been extensively investigated both theoretically5,6,8,9,10,11 and experimentally13,14,15,16,17.

The difficulties of measuring the ALS of individual bacteria primarily result from the technical requirements, e.g. the light scattering from a single bacterium should be isolated and collected, the scattering cross section of a single bacterium is extremely small, and the scattering signal from a single bacterium has a wide scattering angle (covering an angle range of 2π) with a significantly high dynamic range (typically six orders of magnitude in intensity). Furthermore, in order to investigate non-spherical rod-shape bacteria, information regarding the alignment of the rod-shape bacterium and the corresponding two-dimensional (2D) ALS maps should be obtained simultaneously, otherwise the characteristic light scattering patterns associated with the orientation of the rod-shaped bacterium cannot be accessed. Unfortunately, the conventional light scattering measurement techniques based on goniometers or ellipsoidal mirror have several drawbacks, including slow signal acquisition speed or limited dynamic range, that prevent them from obtaining the light scattering from individual bacteria. Thus, the measurements of 2D ALS patterns from individual rod-shaped microscopic objects have been rarely investigated.

Here, we present a novel approach for rapid measurement of the 2D ALS maps from individual bacteria. We employed the Fourier transform light scattering (FTLS) method18 based on quantitative phase imaging (QPI)19,20, which generates 2D ALS maps of individual microscopic objects by numerically propagating measured optical field image, to solve the aforementioned difficulties. The ALS patterns of four representative rod-shaped bacterial species (Bacillus subtilis, Lactobacillus casei, Synechococcus elongatus, and Escherichia coli) were measured at the single-cell level. Angular anisotropy spectroscopy (AAS) is introduced in order to systematically analyze the different characteristics in the ALS maps from each species. In addition, the cellular dry mass, which is inherently and simultaneously measured using QPI21,22, is used to demonstrate that the cell-to-cell variations in the 2D ALS patterns are related to the cellular dry mass and growth.

Results

Anisotropic Fourier transform light scattering of individual rod-shaped bacteria

In order to measure the 2D ALS patterns from individual bacteria, the QPI and anisotropic FTLS (aFTLS) techniques were employed. Using the QPI, the quantitative optical field images of individual bacteria containing both amplitude and phase information were measured first. Diffraction phase microscopy (DPM)23,24 was used for the QPI imaging in order to utilize the capability of single-shot full-field imaging with extremely high phase stability. Then, the aFTLS analyses35,36 were performed in order to retrieve the 2D ALS patterns from the measured optical field images and to address the anisotropic characteristics in the 2D ALS patterns of the rod-shaped bacterial species (see Methods).

In order to retrieve the 2D ALS patterns from the measured optical field images, the ALS patterns corresponding to the principal axes of a rod-shaped sample were selectively analyzed. The procedure for retrieving the ALS patterns of individual rod-shaped bacteria is presented in Figure 1. First, the orientation of the optical field image of a single bacterium was numerically aligned such that the principal axes of the rod-shaped bacterium, i.e. the long (major) and short (minor) axes, become parallel to the horizontal and vertical axes, respectively (Figure 1(a)). Next, using the FTLS technique, the 2D far-field ALS map was retrieved from the measured optical field image using the 2D Fourier transform (Figure 1(b)). The symmetry conservation of the Fourier transform enabled the systematic analysis of the light scattering signals along the principal axes. The light scattering intensities along the principal axes with a polar angle width of 30° were selected and then azimuthally averaged to become representative as functions of the scattering angles for both the long and short axes (Figures 1(b) and 1(c)). The maximal scattering angle that could be detected was determined through the numerical aperture (NA) of the objective lens used in the DPM setup; the current system can measure scattering signals up to a scattering angle of ~70°. The angular resolution is less than 10 mrad, which is determined by the field-of-view size.

Figure 1. aFTLS procedure.

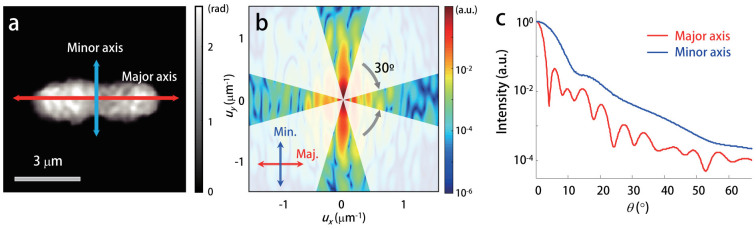
Figure 1

Open in a new tab

(a) Quantitative phase image of a S. elongatus bacterial cell after numerical alignment of the principal axes. (b) Corresponding FTLS map normalized in order that the maximum scattering intensity becomes unity. The polar angle width for the azimuthal averaging is denoted. (c) The corresponding aFTLS spectra with respect to the major and minor axes of the bacterium as a function of the scattering angle.

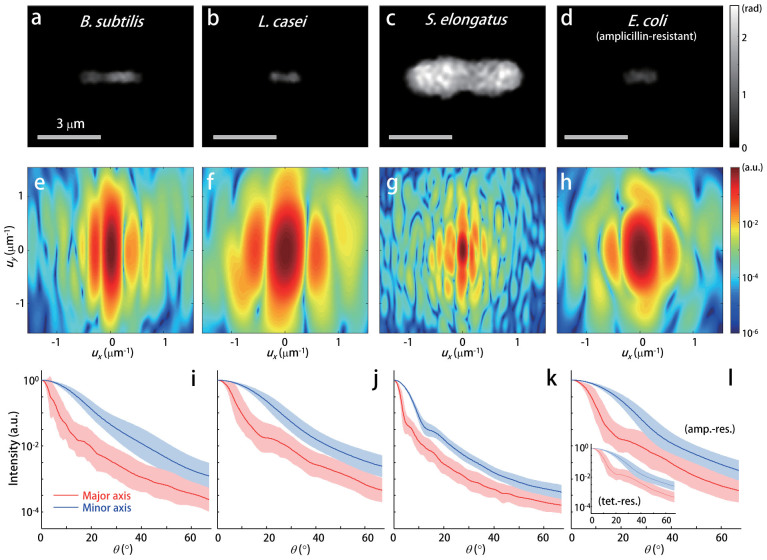
Four representative species of rod-shaped bacteria (B. subtilis, L. casei, S. elongatus, and E. coli) prepared using the standard protocols (see Methods) were analyzed using the aFTLS procedure described above and depicted in Figure 2. The representative quantitative phase images of the species are presented in Figures 2(a) to 2(d). S. elongatus, which is a species of cyanobacteria, has a relatively large cell size compared with the other species, while the phase images of all bacterial species were rod-like shapes with slightly different aspect ratios. The corresponding 2D ALS maps were obtained and are presented in Figures 2(e) to 2(h). The strong oscillatory patterns in the scattering intensity along the principal axes are clearly visible, while the periods for the oscillatory patterns are inversely proportional to the corresponding sizes of bacteria as expected from the linearity and scaling theorems of the Fourier transform. In addition, because the light scattering maps are determined using the optical properties of the cellular structures and sub-cellular biochemical compositions, the relatively complicated ALS patterns in the S. elongatus species may reflect its complex intracellular structures that possess a photosynthesizing functionality.

Figure 2. aFTLS of rod-shaped bacterial species.

Figure 2

Open in a new tab

Representative quantitative phase images of the bacterial species (a) B. subtilis, (b) L. casei, (c) S. elongatus, and (d) ampicillin-resistant E. coli. (e–h) The corresponding FTLS intensity patterns. The aFTLS spectra as function of the scattering angle, obtained from individual bacteria in the species (i) B. subtilis, (j) L. casei, (k) S. elongatus, and (l) ampicillin-resistant E. coli. The inset of (l) presents the results from the E. coli with tetracycline-resistance. The thick lines denote the average value and the areas represent standard deviation from 64, 93, 162, 143, and 129 cells of the species B. subtilis, L. casei, S. elongatus, ampicillin-resistant E. coli, and tetracycline-resistant E. coli, respectively.

The light scattering spectra along the principal axes of the four bacterial species were extracted from the 2D ALS patterns. Figures 2(i) to 2(l) present the aFTLS signals along the principal axes averaged for 64, 93, 162, 143, and 129 cells of species B. subtilis, L. casei, S. elongatus, ampicillin-resistant E. coli, and tetracycline-resistant E. coli, respectively. All the species are clinically important rod-shaped bacteria. Among them, ampicillin-resistant E. coli, and tetracycline-resistant E. coli are genetically similar to each other. The distinctive anisotropic characteristics can be seen from the measured aFTLS signals for all rod-shaped bacteria; however, the light scattering signals along the major and minor axes differ significantly to each other. This anisotropy can be understood through the asymmetry in the cellular shapes and the distributions of their intercellular organelles along the axes in the rod-shaped bacteria. The aFTLS spectra from the different species are qualitatively distinguishable, while the signals from the ampicillin-resistant E. coli and tetracycline-resistant E. coli cells were very similar, which is expected due to their genetic similarity.

Angular anisotropy spectrum

In order to quantify the anisotropic light scattering from the individual rod-shaped bacteria, the angular anisotropy spectrum (AAS) is introduced. The AAS is defined as the relative difference in scattering intensities between the minor and major axes at each scattering angle, which can be expressed as follows:

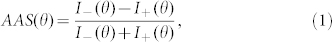graphic file with name srep05090-m1.jpg

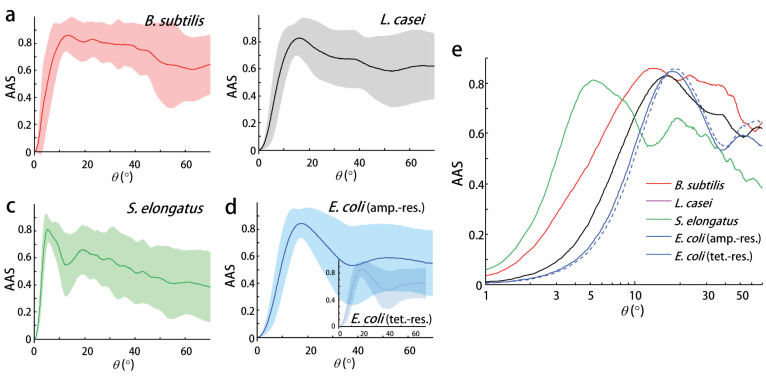
where I−(θ) and I+(θ) are the FTLS spectra along the minor and major axes, respectively. By its definition, the AAS directly and effectively quantifies the anisotropy in the 2D ALS spectra. The averaged AAS of each bacterial species are presented in Figures 3(a) to 3(d). In all species, a high AAS can be observed for large scattering angles (>10°). Importantly, the measured AAS of each species exhibited distinct AAS results with characteristic oscillatory patterns despite the large cell-to-cell deviations.

Figure 3. AAS spectra reflecting the species-specific characteristics.

Figure 3

Open in a new tab

AAS spectra as a function of the scattering angle associated with the individual bacteria in the species (a) B. subtilis, (b) L. casei, (c) S. elongatus, and (d) ampicillin-resistant E. coli. The inset of (d) presents the results of the E. coli with tetracycline-resistance. The thick lines denote the average value and the areas represent the standard deviation for 64, 93, 162, 143, and 129 cells of B. subtilis, L. casei, S. elongatus, ampicillin-resistant E. coli, and tetracycline-resistant E. coli species, respectively. (e) The averaged AAS spectra from the four species are plotted together for comparison (scattering angles are denoted in log-scale).

The averaged AAS for each species reveals the species-specific characteristics as shown in Figure 3(e). The overall AAS characteristics as a function of the scattering angles revealed species-dependent anisotropic light scattering. The scattering signal at specific angles reflects the information of the cellular components with the corresponding spatial scale; thus, these observed species-specific characteristics in the AAS indicate the species-dependency in the optical properties of the overall cellular shapes and subcellular structures. However, the AAS in low angle regimes (<10°) that represent large structures or cellular shapes were similar between the species, while only S. elongatus with its large cell sizes exhibited relatively different AAS compared with the other species. In contrast, the AAS in high angle regimes (>10°) that represents small subcellular structures significantly differed from each other. Moreover, the high AAS values at larger scattering angles (>10°) indicated significant anisotropic distribution of the local refractive index of small subcellular structures whose diameter was less than 3 μm, because the scattering angle (θ) and corresponding characteristic spatial period (Λ) are related: sin(θ)/λ = 1/Λ, where λ is the light wavelength. In addition, very similar AAS values for the ampicillin-resistant E. coli and tetracycline-resistant E. coli strains also supported that the AAS extracted species-specific characteristics.

Cell-to-cell variations in species: correlational analysis between AAS and cellular dry mass

In order to understand the cell-to-cell variations in the measured AAS, the correlation between the AAS signals and cellular dry mass were investigated. Because the cellular dry mass could be directly retrieved from the measured QPI measurement22, the QPI measurements also simultaneously provided information about the cellular dry mass of the corresponding individual bacterium25 (see Methods).

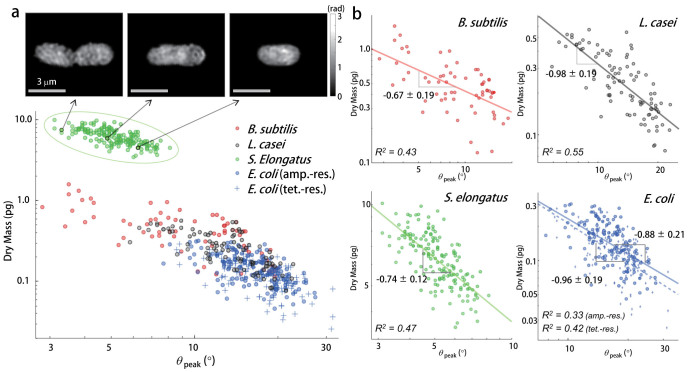
In order to examine the effects of the cellular dry mass in the AAS signals, a correlation analysis was performed between the cellar dry mass (m) and scattering angle corresponding to the first local maximum in AAS (θpeak) at the cellular level. For the individual bacteria in the four species, θpeak and m were calculated. As shown in Figure 4(a), θpeak and m exhibit a strong negative correlation for all species: θpeak shifts toward a lower scattering angle as the bacterial dry mass increases. As clearly seen in the insets of Figure 4(a), the bacterium with a larger dry mass exhibited a decrease in θpeak. The decrease in θpeak could be explained by the increased aspect ratio of the cellular shape during the cell growth and division, which is genetically controlled and affected by the cellular metabolism and morphology26.

Figure 4. Correlation between AAS peak angle and cellular dry mass.

Figure 4

Open in a new tab

(a) Scatter plots of the scattering angle for the first maximum AAS (θpeak) and the cellular dry mass of B. subtilis, L. casei, S. elongatus, ampicillin-resistant E. coli, and tetracycline-resistant E. coli species. Quantitative images for the three S. elongatus cells in various stages of cell growth are presented and the corresponding data are marked in the scatter plot. (b) The bacterial cells of each species are plotted separately in log-log scale. The fitted curves are also presented with the values for slopes and R2 obtained using least squares fitting.

The correlation between θpeak and m could be fitted with the power law with species-dependent exponents (Figure 4(b)). The exponents were −0.67 ± 0.19, −0.98 ± 0.19, −0.74 ± 0.12, and −0.88 ± 0.21 for B. subtilis, L. casei, S. elongatus, and E. coli, respectively. This result indicates the subtle differences in the growth dynamics of the bacterial species. In addition, each species occupies a different region when m is plotted as a function of θpeak (Figure 4(a)). Notably, the values of θpeak and m for S. elongatus differed significantly from the other species, and the two E. coli strains (ampicillin-resistant and tetracycline-resistant) exhibited the most similar values of θpeak and m. Thus, this result demonstrates the high sensitivity of the present method.

Discussion

The measurements of the 2D ALS patterns of individual rod-shaped bacteria are reported. The measured patterns cover a wide scattering angle range from −70° to 70° along the principal axes and are measured with unprecedented sensitivity. Using the QPI and aFTLS techniques, the holographic images of individual bacteria are obtained in a single-shot measurement that generates high quality 2D ALS patterns of individual bacteria. The anisotropy in the 2D light scattering patterns from four rod-shaped bacterial species was quantitatively analyzed at the single-cell level using the proposed AAS parameter. The AAS of the measured 2D ALS patterns systematically addressed the species-specific characteristics and cell-to-cell variations within species that originate from the cell growth and division through analysis combined with the simultaneously measured cellular dry mass.

The most attractive and direct application of the proposed approach is the implementation into microfluidics-based single-cell assays. The single-shot measurement and numerical focusing capability27 of QPI are appropriate for ultrafast high-throughput single-cell assay platforms. As a result of the recent advances in high-speed microfluidics, single-cell approaches avoid the averaging of signals from heterogeneous sub-populations in bacterial suspensions and colonies that occurs in conventional light scattering measurements. Detailed analyses of extremely small numbers of cells are also available due to the exceptionally high sensitivity of the proposed measurement technique. Furthermore, contrary to destructive biochemical characterizations, the non-invasiveness of the current approach could be combined with other modalities such as spectral28,29,30,31,32, polarimetric33,34, and tomographic35,36 imaging of the same single cell for further optical characterizations of microorganisms at the single cell level. In addition, the proposed method can also be integrated in a portable platform for field measurements when it combines with in-line holography37. Both biological studies and biomedical applications, such as label-free species identification17,38 of food pathogens, are expected to be further facilitated by the proposed aFTLS approach for measuring the 2D ALS patterns of individual bacteria.

In this study, the rod-shaped bacterial species are investigated because they are significant in numerous biomedical applications: the majority of pathologically and hygienically crucial bacterial species are rod shaped, e.g. the causes of tuberculosis (Mycobacterium tuberculosis), diphtheriae (Corynebacterium diphtheriae), listeriosis (Listeria monocytogenes), and various food poisonings (Salmonella Typhimurium, Vibrio parahaemolyticus, etc.) are rod-shaped. However, the light scattering of individual bacteria in spherical or spiral shapes can also be measured using the present approach.

For further development and enhancement of the proposed approach, several aspects could also be considered in both measurement and analysis. The detection range of the scattering angles or spatial frequencies could be extended through exploiting synthetic FTLS39 or back-scattered optical fields40. The FTLS measurements of more species and time-lapse studies would contribute to the precise characterization and sensitivity of this method, while providing unique opportunities to investigate the pathophysiology of bacteria.

Methods

Bacteria preparation

Four bacterial species, B. subtilis, L. casei, S. elongatus, and E. coli, were prepared according to the following standard protocols.

  1. B. subtilis strain (KCTC 1023, Korean Collection for Type Culture, Republic of Korea) was grown on a nutrient agar plate in a 37°C incubator.

  2. L. casei strain (KCTC 2180, Korean Collection for Type Culture, Republic of Korea) was grown on a MRS Agar plate in a 37°C incubator.

  3. S. elongatus strain (KMMCC 1063, Korea Marine Microalgae Culture Center, Republic of Korea) was propagated in a BG-11 medium photo-synthetically in a 25°C shaking incubator under a continuous white illumination of 2,000–3,000 lux. When an OD730 value of the sample reaches 0.7, the sample was moved to be cultured in a 31°C incubator under the same illumination.

  4. Ampicillin-resistant E. coli strain (DH5alpha strain with ampicillin-resistance cloning) and tetracycline-resistant E. coli strain (ER 2738, Lucigen, WI, USA) were separately grown on Luria-Bertani agar plates with either ampicillin or tetracycline (50 μg/mL), respectively. The bacterial strains were cultured in a 37°C incubator.

After culturing for 2–4 days, few tips of solid-cultured bacterial colonies (B. subtilis, L. casei, and E. coli) or drops of a weakly-centrifuged sediment solution (S. elongatus) were taken to be put into the respective epi-tubes. Within each tube, a Dulbecco's Phosphate Buffered Saline solution (LB 001-12, Welgene, Republic of Korea) was added to prepare a bacterial solution. A small volume (~10 μL) of the solution with bacteria was sandwiched between standard microscopic cover glasses (C024501, Matsunami Glass Ind., Japan) with a spacer, made of a double-sided tapes with a thickness of 20–30 μm. Aforementioned dilution step was performed until the bacterial cells were spread into a single layer when being imaged.

Diffraction phase microscopy

To quantitatively measure the optical field images of individual bacteria, DPM was employed herein. DPM employs the principle of common-path interferometry with off-axis spatial modulation23. DPM provides the single-shot full-field imaging capability and the high sensitivity for phase measurement. A diode-pumped solid state laser (λ = 532.1 nm, Cobolt Samba, Cobolt, Sweden) was used as an illumination source. An inverted microscope (IX71, Olympus American Inc., Center Valley, PA, USA), equipped with an 60× objective lens (UPLFLN 60×, 1.42 NA, oil-immersion, Olympus American Inc., Center Valley, PA, USA), was modified with additional optics to be used for a DPM setup. With the additional relay optics, the overall magnification of the system was ×199. A CMOS camera (Neo sCMOS, Andor, UK) was used to record the holograms of a sample. The optical field images were obtained from the measured holograms via a phase retrieval algorithm based on Hilbert transformation41,42. Here, other forms of QPI or digital holographic microscopy43 setups can also be employed instead of DPM. The details on the experimental setup of DPM can be found elsewhere23,24.

Fourier transform light scattering

FTLS is a numerical method to calculate the far-field scattering pattern from an optical field image18. A 2D ALS map of a microscopic sample can be directly obtained with extremely high sensitivity from a single optical field map by numerical propagation, which can be performed using the 2D Fourier transform. 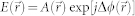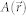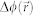QPI or digital holographic microscopy techniques can be used to measure the optical field image of a sample, Inline graphic where Inline graphic and Inline graphic are the amplitude and phase delay maps at a position 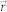Inline graphic, respectively. The optical field image is then numerically propagated to far-field using the 2D Fourier transform as,

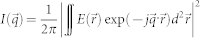graphic file with name srep05090-m6.jpg

where 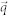Inline graphic is the lateral spatial frequency vector. Compared to traditional light scattering measurement techniques, FTLS has several advantages: simultaneous measurement of both imaging and scattering, high signal-to-noise ratio, and high angular resolution in a broad angular range. The effectiveness of the FTLS technique has been demonstrated in recent several studies in the field biophysics and cell biology44,45,46,47.

Cellular dry mass

The cellular dry mass, the mass of non-aqueous cellular contents, can be obtained from the QPI measurements of a biological cell. Because the optical phase delay is proportional to the cellular dry mass21, the total dry mass of a cell can be calculated as,

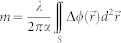graphic file with name srep05090-m8.jpg

where λ is the wavelength of an illumination source, S is the projection area for cell surface, and α is a refractive index increment for non-aqueous molecules. The refractive index increment is determined by the intracellular contents, which can be approximated as 0.18–0.21 mL/g for typical biological cells48. Here, we used α = 0.2 mL/g and the resultant cellular dry mass of bacterial cells was consistent with the previous results based on various techniques49,50.

Author Contributions

Y.-J.J. and Y.-K.P. designed the experiments, analyzed the data and wrote the paper; Y.-J.J. and J.-H.J. performed the experiments. J.W.L., D.S. prepared the bacterial samples for the experiments. H.P., K.T.N., J.-H.P. and Y.-K.P. provided advice. All authors reviewed the manuscript.

Acknowledgments

This work was supported by KAIST, KAIST Undergraduate Research Participation (URP) program, the Korean Ministry of Education, Science and Technology (MEST), and the National Research Foundation (2012R1A1A1009082, 2013K1A3A1A09076135, 2013M3C1A3063046, 2009-0087691, 2012-M3C1A1-048860, 2013R1A1A3011886). Y.-K.P. acknowledges support from TJ ChungAm Foundation. Y.-J.J. acknowledges support from KAIST Presidential Fellowship (KPF).

References

  1. Harding S. E. Applications of light scattering in microbiology. Biotechnology and applied biochemistry 8, 489–509 (1986). [PubMed] [Google Scholar]
  2. Peng L., Chen D., Setlow P. & Li Y.-q. Elastic and Inelastic Light Scattering from Single Bacterial Spores in an Optical Trap Allows the Monitoring of Spore Germination Dynamics. Anal. Chem 81, 4035–4042, 10.1021/ac900250x (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Rösch P. et al. Chemotaxonomic Identification of Single Bacteria by Micro-Raman Spectroscopy: Application to Clean-Room-Relevant Biological Contaminations. Appl. Environ. Microbiol. 71, 1626–1637, 10.1128/aem.71.3.1626-1637.2005 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Hart R. W. & Gray E. P. Determination of Particle Structure from Light Scattering. J. Appl. Phys. 35, 1408–1415 (1964). [Google Scholar]
  5. Koch A. L. Theory of the angular dependence of light scattered by bacteria and similar-sized biological objects. J. Theor. Biol. 18, 133–156 (1968). [DOI] [PubMed] [Google Scholar]
  6. Wyatt P. J. Differential Light Scattering: a Physical Method for Identifying Living Bacterial Cells. Appl. Opt. 7, 1879–1896, 10.1364/AO.7.001879 (1968). [DOI] [PubMed] [Google Scholar]
  7. Ryan D., Ren K. & Wu H. Single-cell assays. Biomicrofluidics 5, - (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Auger J. C., Aptowicz K. B., Pinnick R. G., Pan Y. L. & Chang R. K. Angularly resolved light scattering from aerosolized spores: observations and calculations. Opt Lett 32, 3358–3360 (2007). [DOI] [PubMed] [Google Scholar]
  9. Wyatt P. J. & Phillips D. T. Structure of single bacteria from light scattering. J. Theor. Biol. 37, 493–501 (1972). [DOI] [PubMed] [Google Scholar]
  10. Pan Y.-L. et al. Measurement and autocorrelation analysis of two-dimensional light-scattering patterns from living cells for label-free classification. Cytometry. Part A: the journal of the International Society for Analytical Cytology 79A, 284–292, 10.1002/cyto.a.21036 (2011). [DOI] [PubMed] [Google Scholar]
  11. Aptowicz K. B. et al. Decomposition of atmospheric aerosol phase function by particle size and asphericity from measurements of single particle optical scattering patterns. J. Quant. Spectrosc. Radiat. Transfer 131, 13–23 (2013). [Google Scholar]
  12. Crosta G. F. et al. Automated classification of single airborne particles from two-dimensional angle-resolved optical scattering (TAOS) patterns by non-linear filtering. J. Quant. Spectrosc. Radiat. Transfer 131, 215–233 (2013). [Google Scholar]
  13. Koch A. L. & Ehrenfeld E. The size and shape of bacteria by light scattering measurements. Biochim. Biophys. Acta 165, 262–273 (1968). [DOI] [PubMed] [Google Scholar]
  14. Wyatt P. J. Identification of bacteria by differential light scattering. Nature 221, 1257–1258 (1969). [DOI] [PubMed] [Google Scholar]
  15. Van De Merwe W. P., Czege J., Milham M. E. & Bronk B. V. Rapid optically based measurements of diameter and length for spherical or rod-shaped bacteria in vivo. Appl. Opt. 43, 5295–5302 (2004). [DOI] [PubMed] [Google Scholar]
  16. Bae E. et al. Analysis of time-resolved scattering from macroscale bacterial colonies. J Biomed Opt 13, 014010, 10.1117/1.2830655 (2008). [DOI] [PubMed] [Google Scholar]
  17. Banada P. P. et al. Label-free detection of multiple bacterial pathogens using light-scattering sensor. Biosensors & bioelectronics 24, 1685–1692, 10.1016/j.bios.2008.08.053 (2009). [DOI] [PubMed] [Google Scholar]
  18. Ding H., Wang Z., Nguyen F., Boppart S. A. & Popescu G. Fourier transform light scattering of inhomogeneous and dynamic structures. Phys. Rev. Lett. 101, 238102 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Popescu G. Quantitative Phase Imaging of Cells and Tissues. (McGraw-Hill Professional, 2011). [Google Scholar]
  20. Lee K. et al. Quantitative phase imaging techniques for the study of cell pathophysiology: from principles to applications. Sensors (Basel) 13, 4170–4191, 10.3390/s130404170 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Barer R. Determination of dry mass, thickness, solid and water concentration in living cells. Nature 172, 1097–1098 (1953). [DOI] [PubMed] [Google Scholar]
  22. Popescu G. et al. Optical imaging of cell mass and growth dynamics. American journal of physiology. Cell physiology 295, C538–544, 10.1152/ajpcell.00121.2008 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Popescu G., Ikeda T., Dasari R. R. & Feld M. S. Diffraction phase microscopy for quantifying cell structure and dynamics. Opt. Lett. 31, 775–777 (2006). [DOI] [PubMed] [Google Scholar]
  24. Park Y., Popescu G., Badizadegan K., Dasari R. R. & Feld M. S. Diffraction phase and fluorescence microscopy. Opt Express 14, 8263–8268 (2006). [DOI] [PubMed] [Google Scholar]
  25. Mir M. et al. Optical measurement of cycle-dependent cell growth. Proceedings of the National Academy of Sciences of the United States of America 108, 13124–13129 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Mir M. et al. Optical measurement of cycle-dependent cell growth. Proceedings of the National Academy of Sciences 108, 13124–13129 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Langehanenberg P., Kemper B., Dirksen D. & von Bally G. Autofocusing in digital holographic phase contrast microscopy on pure phase objects for live cell imaging. Appl. Opt. 47, D176–D182, 10.1364/AO.47.00D176 (2008). [DOI] [PubMed] [Google Scholar]
  28. Jung J.-H., Jang J. & Park Y. Spectro-refractometry of Individual Microscopic Objects Using Swept-Source Quantitative Phase Imaging. Anal. Chem 85, 10519–10525, 10.1021/ac402521u (2013). [DOI] [PubMed] [Google Scholar]
  29. Jung J. & Park Y. Spectro-angular light scattering measurements of individual microscopic objects. Opt Express. 22, 4108–4114 (2014). [DOI] [PubMed] [Google Scholar]
  30. Park Y., Yamauchi T., Choi W., Dasari R. & Feld M. S. Spectroscopic phase microscopy for quantifying hemoglobin concentrations in intact red blood cells. Opt. Lett. 34, 3668–3670, 10.1364/OL.34.003668 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Jang Y., Jang J. & Park Y. Dynamic spectroscopic phase microscopy for quantifying hemoglobin concentration and dynamic membrane fluctuation in red blood cells. Opt Express. 20 (2012). [DOI] [PubMed] [Google Scholar]
  32. Pham H., Bhaduri B., Ding H. F. & Popescu G. Spectroscopic diffraction phase microscopy. Opt. Lett. 37, 3438–3440 (2012). [DOI] [PubMed] [Google Scholar]
  33. Wang Z., Millet L. J., Gillette M. U. & Popescu G. Jones phase microscopy of transparent and anisotropic samples. Opt. Lett. 33, 1270–1272 (2008). [DOI] [PubMed] [Google Scholar]
  34. Kim Y., Jeong J., Jang J., Kim M. W. & Park Y. Polarization holographic microscopy for extracting spatio-temporally resolved Jones matrix. Opt Express. 20 (2012). [DOI] [PubMed] [Google Scholar]
  35. Kim K., Kim K. S., Park H., Ye J. C. & Park Y. Real-time visualization of 3-D dynamic microscopic objects using optical diffraction tomography. Opt Express. 21, 32269–32278 (2013). [DOI] [PubMed] [Google Scholar]
  36. Kim T. et al. White-light diffraction tomography of unlabelled live cells. Nat. Photonics (2014). [Google Scholar]
  37. Kim K. & Park Y. Fourier transform light scattering angular spectroscopy using digital inline holography. Opt. Lett. 37, 4161–4163 (2012). [DOI] [PubMed] [Google Scholar]
  38. Suchwalko A., Buzalewicz I., Wieliczko A. & Podbielska H. Bacteria species identification by the statistical analysis of bacterial colonies Fresnel patterns. Opt Express 21, 11322–11337, 10.1364/OE.21.011322 (2013). [DOI] [PubMed] [Google Scholar]
  39. Lee K. et al. Synthetic Fourier transform light scattering. Opt Express. 21, 22453–22463 (2013). [DOI] [PubMed] [Google Scholar]
  40. Alexandrov S. A., Hillman T. R. & Sampson D. D. Spatially resolved Fourier holographic light scattering angular spectroscopy. Opt. Lett. 30, 3305–3307 (2005). [DOI] [PubMed] [Google Scholar]
  41. Takeda M., Ina H. & Kobayashi S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 72, 156–160 (1982). [Google Scholar]
  42. Debnath S. K. & Park Y. Real-time quantitative phase imaging with a spatial phase-shifting algorithm. Opt Lett 36, 4677–4679 (2011). [DOI] [PubMed] [Google Scholar]
  43. Marquet P. et al. Digital holographic microscopy: a noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy. Opt. Lett. 30, 468–470 (2005). [DOI] [PubMed] [Google Scholar]
  44. Ding H. et al. Fourier Transform Light Scattering of Biological Structure and Dynamics. IEEE J. Sel. Top. Quant. Electron. 16, 909–918 (2010). [Google Scholar]
  45. Park Y. K., Best-Popescu C. A., Dasari R. R. & Popescu G. Light scattering of human red blood cells during metabolic remodeling of the membrane. J Biomed Opt 16, 011013 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Park Y. K. et al. Static and dynamic light scattering of healthy and malaria-parasite invaded red blood cells. J Biomed Opt 15, 020506 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yu H., Park H., Kim Y., Kim M. W. & Park Y. Fourier-transform light scattering of individual colloidal clusters. Opt. Lett. 37, 2577–2579 (2012). [DOI] [PubMed] [Google Scholar]
  48. Barer R. Interference microscopy and mass determination. Nature 169, 366-367 (1952). [DOI] [PubMed] [Google Scholar]
  49. Godin M. et al. Using buoyant mass to measure the growth of single cells. Nat Methods 7, 387–390, 10.1038/nmeth.1452 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Loferer-Krößbacher M., Klima J. & Psenner R. Determination of Bacterial Cell Dry Mass by Transmission Electron Microscopy and Densitometric Image Analysis. Appl. Environ. Microbiol. 64, 688–694 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES