Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 May 28;4:5085. doi: 10.1038/srep05085

A Bond-order Theory on the Phonon Scattering by Vacancies in Two-dimensional Materials

Guofeng Xie 1,a, Yulu Shen 1, Xiaolin Wei 1, Liwen Yang 1, Huaping Xiao 1, Jianxin Zhong 1, Gang Zhang 2,b
PMCID: PMC4035577  PMID: 24866858

Abstract

We theoretically investigate the phonon scattering by vacancies, including the impacts of missing mass and linkages (Inline graphic) and the variation of the force constant of bonds associated with vacancies (Inline graphic) by the bond-order-length-strength correlation mechanism. We find that in bulk crystals, the phonon scattering rate due to change of force constant Inline graphic is about three orders of magnitude lower than that due to missing mass and linkages 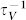Inline graphic. In contrast to the negligible 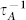Inline graphic in bulk materials, 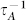Inline graphic in two-dimensional materials can be 3–10 folds larger than 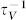Inline graphic. Incorporating this phonon scattering mechanism to the Boltzmann transport equation derives that the thermal conductivity of vacancy defective graphene is severely reduced even for very low vacancy density. High-frequency phonon contribution to thermal conductivity reduces substantially. Our findings are helpful not only to understand the severe suppression of thermal conductivity by vacancies, but also to manipulate thermal conductivity in two-dimensional materials by phononic engineering.

Thermal property of two-dimensional materials has attracted considerable attention due to the unique physical attributes1,2,3,4 and the potential applications5,6,7,8 in many areas. On the one side, because of its superior high thermal conductivity, graphene-based devices can be applied in nanoscale phononics and for thermal management9,10,11,12,13,14,15,16. On the other side, the ultra low thermal conductivity of monolayer molybdenum disulfide (MoS2) sheet and nanoribbon17,18,19 opens up the possibility to realize two-dimensional thermoelectric devices based on Transition metal dichalcogenides (TMD) materials for heat energy harvesting and refrigeration. Most materials have natural point defects, such as atomic vacancies introduced in the process of fabrication. Since the phonon frequency depends on length and energy of the local bonds20, these vacancy defects offer a possibility for tailoring the thermal conductivity of materials21,22,23,24,25.

Phonon scattering by vacancies in crystals was originally treated from perturbation theory by Ratsifaritana and Klemens. Although the role of the strain field in scattering of phonons is important since strain would change the local value of phonon frequency for a fixed wave vector, thus contributing to the perturbation, Ratsifaritana and Klemens demonstrated that the distortion effects could be neglected for vacancies, and the perturbation of vacancy defect was one that corresponds to the removal of the mass of one atom and the force constants of two atoms26. In addition to the missing mass and missing linkages (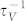Inline graphic), the change of force constant of bonds between the under-coordinated atoms near the vacancies also results in phonon scattering (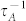Inline graphic), but it is neglected in the theoretical model of vacancy. Usually, the interatomic force constants can be obtained by the quantum chemistry calculations. However, it is not reliable to investigate the vacancy effect on phonon scattering in sizeable materials due to computational limitation.

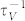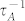In this communication, we report our findings on the phonons scattering (both Inline graphic and Inline graphic) by vacancies, including the impacts of missing mass, missing linkages, and change of force constant of the under-coordinated atoms near the vacancies based on the frame work of bond-order-length-strength (BOLS) notation27,28. We find that the phonon scattering rate due to change of force constant 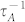Inline graphic is about three orders of magnitude less than that due to missing mass and linkages 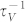Inline graphic in bulk crystals. In contrast to the negligible 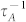Inline graphic in the bulk, 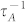Inline graphic in two-dimensional materials can be 3–10 folds larger than 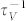Inline graphic. The critically different phonon scattering rate determines that in two-dimensional materials with vacancies, the contribution to thermal conductivity from high frequency phonons is greatly suppressed. Consistency in the present and molecular dynamics simulations29 on the thermal conductivity of defected single-layer graphene confirmed our expectations.

Results

Bond-order theory for phonon-vacancy scattering

Perturbation theory in terms of the missing mass and the missing linkages deals with the scattering of phonons by vacancy defects in crystals26,30,

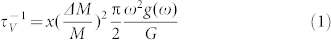graphic file with name srep05085-m1.jpg

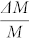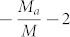where x is the density of vacancies, G is the number of atoms in the crystal, g(ω) is the phonon density of states (DOS). For vacancy defect, the effective value of Inline graphic is Inline graphic, where M is the average mass per atom, Ma is the mass of the missing atom, and the term −2 accounts for the potential energy of the missing linkages, or twice the potential energy per atom26,31.

One important fact that has been overlooked in previous modeling is that bond between under-coordinated atoms becomes shorter and stronger28. Bond shortening and strengthening not only raises the local density of charge, mass and energy but also deepens the local potential, providing perturbation to the local potential. This undercoordination effect raises the local energy density, or the elastic modulus, and subsequently the trap for phonon and electron transportation32,33. The coordination number (CN) dependence of bond-contraction coefficient (Cz) and bond energy (Ez) follow the relation28,

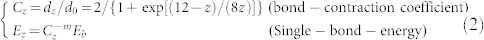graphic file with name srep05085-m2.jpg

where z is the effective coordination number, dz is the bond length. In BOLS theory, the effective CN for bulk materials is always 12, regardless of the nature of the bond or the crystal configuration34, Eb and d0 are the corresponding bulk values of single bond energy and bond length, respectively. m is an indicator for bond nature of a specific material, which is not freely adjustable. For alloys and compounds (such as MoS2 and BN) m is around 4, for C and Si the value of m has been optimized to be 2.56 and 4.88, respectively35.

Eq. (2) yields the change of force constant of bonds between under-coordinated atoms, from the perspective of dimensionality analysis28,

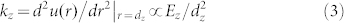graphic file with name srep05085-m3.jpg

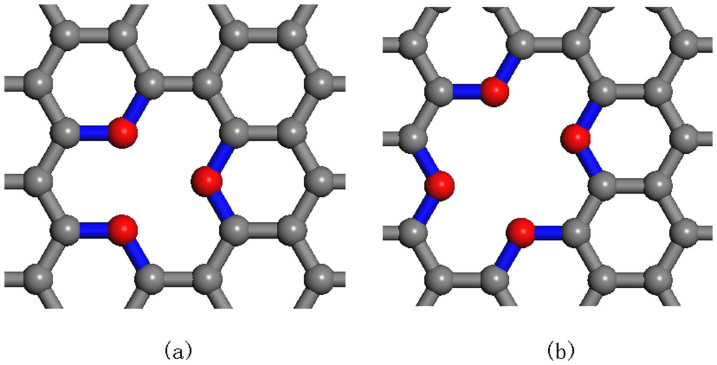
Accordingly, the bond force constant nearby the vacancies increases compared with that far away from vacancies. As shown in Fig. 1 (the schematic description of graphene flakes with single and double vacancy), the bonds displayed as blue colour between the under-coordinated atoms near the vacancy become stronger. According to the perturbation theory of Klemens, the rate of phonon scattering by atoms of different force constant is given as36,37,

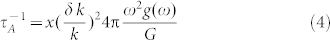graphic file with name srep05085-m4.jpg

where x is the density of imperfections, k is the force constant, and δk is the change of force constant.

Figure 1.

Figure 1

Open in a new tab

Schematic description of graphene flakes with (a) single vacancy. The CN of carbon atoms in graphene is 3. There are 3 under-coordinated atoms displayed as red colour whose CN is 2 near the single vacancy, and bonds displayed as blue colour between the under-coordinated atoms near the vacancy become stronger. (b) double vacancy.

According to Eq. (2) and Eq. (3), we can get

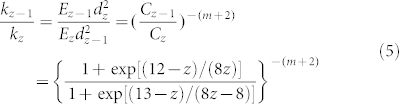graphic file with name srep05085-m5.jpg

where kz−1 is the force constant of under-coordinated atoms near the vacancies whose CN is z-1, and kz is the force constant of atom whose CN is z. Therefore, according to Eq. (4) and Eq. (5), the scattering rate of phonons by the under-coordinated atoms near the vacancies is derived as,

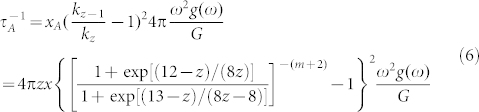graphic file with name srep05085-m6.jpg

where xA = zx is the density of the under-coordinated atoms, and x is the density of single vacancy. m is a key parameter that represents the nature of the bond.

The unusual vacancy effects on phonon scattering in 2D materials

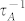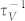The ratio of Inline graphic to Inline graphic in the case of different m and different coordination number is shown in Fig. 2. For bulk materials whose effective atomic CN is always 12 in the BOLS correlation mechanism, 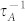Inline graphic is three orders of magnitude less than 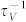Inline graphic, so the scattering of phonons by the under-coordinated atoms near the vacancies is negligible in bulk materials. The ratio 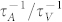Inline graphic increases quickly with decreasing the coordination number. 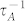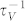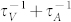For two-dimensional materials with z = 3, such as silicene, hexagonal Boron Nitride, graphene and MoS2, Inline graphic is 3- to 10-fold larger than Inline graphic, therefore the scattering of phonons by the under-coordinated atoms near the vacancies must be taken into account, and the total scattering rate of phonons by the imperfections should be Inline graphic.

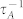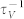Figure 2. The ratio of Inline graphic to Inline graphic in the case of different m and different CN.

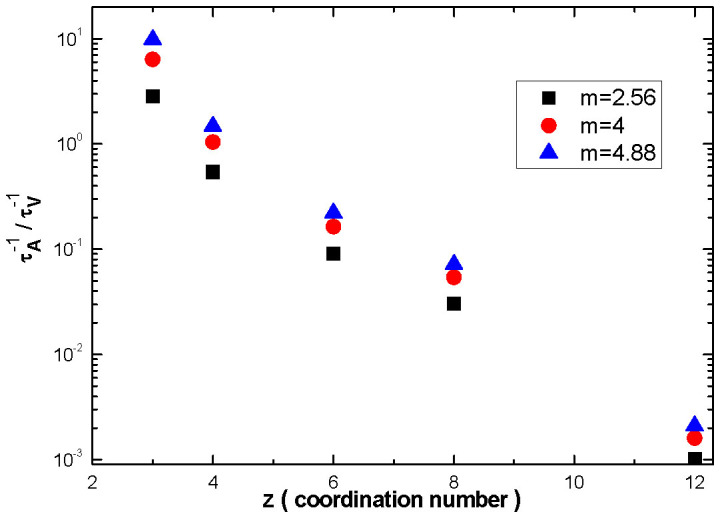
Figure 2

Open in a new tab

Coordination number z = 12 represents the phonon scattering in bulk materials.

Moreover, the ratio 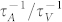Inline graphic increases with the parameter m increases. For carbon-based 2D materials, that is, graphene, m is found to be 2.56. From Fig. 2, the ratio 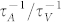Inline graphic is 2.8. For 2D alloys and compounds, such as BN and transition metal dichalcogenides (TMDs) materials, m is around 4, results to a high 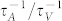Inline graphic ratio of 6.4. Very recently, monolayer MoS2, a member of TMD family, have gained considerable interest. Thus for 2D TMDs materials, the phonon scattering by under-coordinated atoms is dominated over that by vacancy itself.

Vacancy effects on phonon scattering in graphene flakes

It is an important phononic engineering technique to modulate the thermal transport by phonons with different range of frequency38. Next using graphene flake as an example, we discuss the impacts of vacancies on phonon scattering rate and thermal conductivity contributed from phonons with different frequency. The Matthiessen's rule which assumes that different scattering mechanisms are independent is adopted, so the total phonon scattering rate 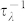Inline graphic in branch λ is given as:

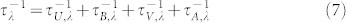graphic file with name srep05085-m7.jpg

The Umklapp phonon-phonon scattering rate (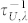Inline graphic) and the phonon-boundary scattering rate (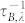Inline graphic) are given as39,

graphic file with name srep05085-m8.jpg
graphic file with name srep05085-m9.jpg

where M is the mass of a graphene unit cell, γλ is the Grüneissen parameter, W is the width of graphene ribbon, vλ,x is the component of the phonon velocity in branch λ perpendicular to the longitudinal direction of graphene ribbon, and P is the specularity parameter, which is defined as the probability of phonon's specular reflection at the lateral boundaries. In order to fit the experimental thermal conductivity value of pristine graphene, we set the specular parameter as 0.8, and the width of graphene flake as 5 μm, which are consistent with Ref. 40 and Ref. 41. As the major concern of the present work are the mechanism of phonon scattering by vacancies and the reduction of thermal conductivity by vacancies, the values of specular parameter and flake width are fixed. The Grüneissen parameters for acoustic branches originate from the results of first-principles calculations in Ref. 42. Based on the linear dispersion for in-plane branches and quadratic dispersion for out-of-plane branch (see Eq. 16 in the section of Methods), the function for phonon DOS of graphene is,

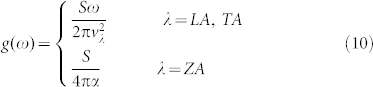graphic file with name srep05085-m10.jpg

Therefore according to Eq. (1), the rate of phonon scattering by single vacancies is given as,

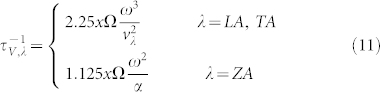graphic file with name srep05085-m11.jpg

where x is the density of vacancies, and Ω is the primitive cell area of graphene.

As shown in Fig. 1(a), the CN of carbon atoms in graphene is 3. There are 3 under-coordinated atoms whose CN is 2 near the single vacancy. Based on BOLS theory, the bond between the under-coordinated atoms becomes shorter and stronger. Girit et al.43 discovered that breaking a C–C bond of the 2-coordinated carbon atoms near the monolayer-GNR vacancy required 7.50 eV per bond, that was 32% higher than the energy (5.67 eV/bond) required for breaking one bond between 3-coordinated carbon atoms in the interior of a suspended graphene sheet. The mechanical strength of graphene increases with the density of defects44 (the reconstructed 5- and 7-atom rings forming the grain boundaries), because of the particular strength of the ring bonds and their elongation dynamics. These findings provide evidence for the BOLS prediction of the shorter and stronger bonds at vacancies. According to Eq. (5), the ratio of force constant of the 2-coordinated carbon atoms near the vacancy to that of the 3-coordinated carbon atoms is 2.03, and according to Eq. (6), the rate of phonon scattering by the 2-coordinated carbon atoms near the single vacancies is given as,

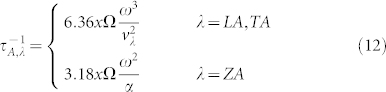graphic file with name srep05085-m12.jpg

From Eq. (12) and Eq. (11), we know that the phonon scattering by the under-coordinated atoms near the vacancy dominates over that by the vacancy in graphene.

In the pristine graphene sheet, the Umklapp phonon-phonon scattering is dominant at room temperature, but in the defective graphene, the situation is quite different. Fig. 3 presents the frequency-dependent scattering rate of LA phonons for all kinds of mechanisms in the single vacancy defective graphene. The vacancy density is 1%. For the ultra-low frequency phonons, the boundary scattering is dominant. However, for ω > 2.5 Trad/s, the scattering by the under-coordinated carbon atoms dominates over other mechanisms. The situation is similar for other branches. However, this most important scattering mechanism is neglected in previous theoretical model on phonon scattering by vacancies.

Figure 3. The phonon scattering rate as a function of phonon angular frequency.

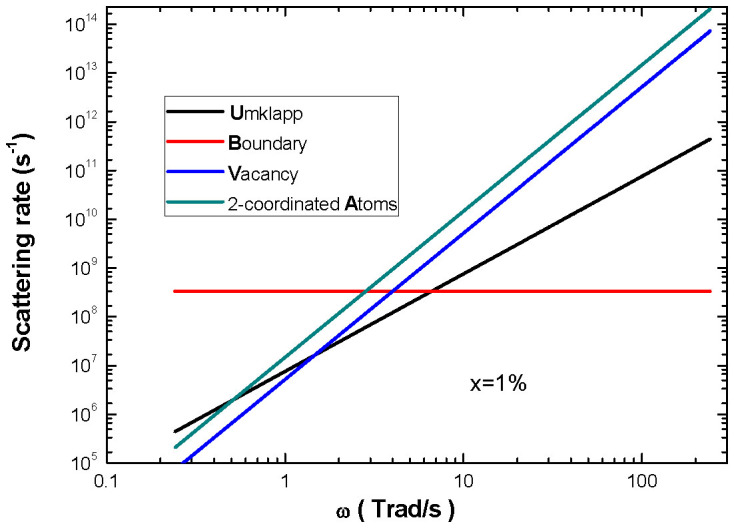
Figure 3

Open in a new tab

The phonon scattering mechanisms including Umklapp, boundary, vacancy and under-coordinated atoms scattering are considered.

Vacancy effects on thermal conductivity in graphene flakes

Many researches presented that the thermal conductivity of graphene could be remarkably reduced by point defects22,29,45, such as isotope and vacancy. The vacancy effect on the thermal conductivity is more remarkable than that of isotope. By molecular dynamics simulation, Haskins et al. found that even for a very low vacancy concentration 0.1%, a 81% reduction of thermal conductivity of graphene was achieved29. Although Klemens's model agrees well with thermal conductivity reductions by vacancies in bulk materials31,46, the severe suppression of thermal conductivity of graphene by vacancies is much over the prediction of Klemens's theory22. Incorporating phonon scattering by the under-coordinated atoms near the vacancies to the linearized phonon Boltzmann transport equation within relaxation time approximation (see in the section of Methods), we calculate the relative thermal conductivity (κ/κ0) of defective graphene (single vacancies and double vacancies) as a function of defect density at room temperature, which is shown in Fig. 4. κ0 (the thermal conductivity of pristine graphene) calculated by this work, 3750 W/mK, is coherent with various experimental measurements47,48 and theoretical calculations49,50. The dash line is the calculation results by Klemens's model from Ref. 26, in which the phonon scattering by the under-coordinated carbon atoms near the vacancies is not considered. The solid lines are the results of the present model. The squares are the molecular dynamics simulation results of single vacancies in graphene from Ref. 29. It is obvious that the results predicted by the present model agrees better with molecular dynamics simulations than the results of Klemens's theory, and the phonon scatterings by the 2-coordinated carbon atoms near the vacancies further suppress the thermal conductivity of graphene.

Figure 4. The ratio of the thermal conductivity of defective graphene to the pristine one at room temperature as a function of defect density.

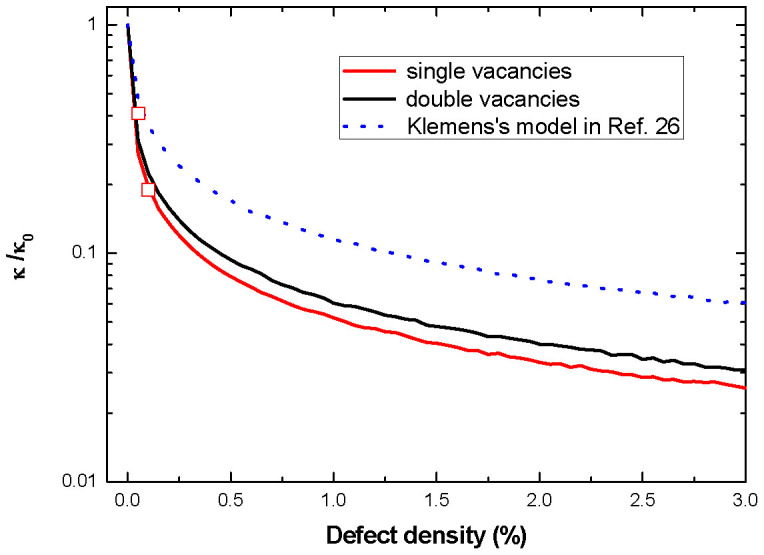
Figure 4

Open in a new tab

The squares are the molecular dynamics simulation results of single vacancy defective graphene from Ref. 29.

Fig. 5 demonstrates the normalized accumulative distribution of thermal conductivity defined as Eq. (19) (see in the section of Methods) for different single vacancy density. The curves move towards the upper-left corner as the vacancy density increases. The ultra-low thermal conductivity of vacancy defective graphene stems from the significant suppression of high-frequency phonons. With the increasing of vacancy density, the contribution of more and more high-frequency phonons to heat conductance is severely suppressed by the scattering of the vacancies and the under-coordinated atoms near the vacancies, as shown in Fig. 5. From Fig. 3, we know that the scattering by these imperfections is dominant, except for the ultra-low frequency phonons. Therefore, the thermal conductivity of vacancy defective graphene is absolutely dominated by low-frequency acoustic phonons. For example, in the case of 1% concentration of single vacancy, the phonons of ω < 3 Trad/s have about 50% contribution to the thermal conductivity, which is shown in Fig. 5. However, in the Klemens's model (the dotted line), the same phonons only have about 30% contribution which is lower than our model, because it neglects additional scattering by the under-coordinated atoms near the vacancies.

Figure 5. The normalized accumulative distribution of thermal conductivity of graphene flakes as a function of phonon angular frequency.

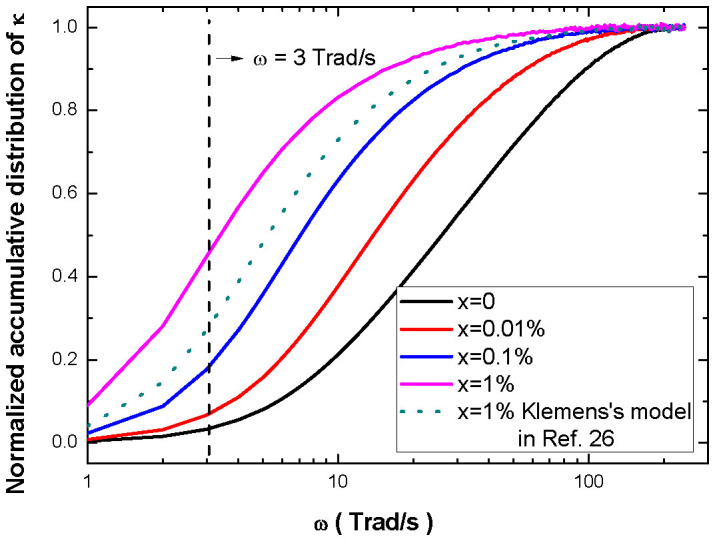
Figure 5

Open in a new tab

Here the width of graphene flake is 5 μm, concentrations of single-vacancy defect are 0%, 0.01%, 0.1%, and 1%, respectively. The solid lines are results from the present model. The dotted line is thermal conductivity of graphene flake with 1% vacancy calculated without considering the phonon scattering by under-coordinated atoms.

Discussion

The theoretical model in present work can be used to explain the different content dependence in thermal conductivity of graphene flakes with single- and double-vacancy defects. For a single vacancy, there are 3 under-coordinated atoms around each defective atom, while there are only 2 under-coordinated atoms around each defective atom for a double vacancy, as shown in Fig. 1(b). According to Eq. (6), the rate of phonon scattering by the 2-coordinated carbon atoms near the double vacancies at the same defect density x is given as,

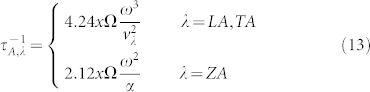graphic file with name srep05085-m13.jpg

where the defect density x is defined as the number of defected atoms divided by the total atom number in pristine graphene. The rate of phonon scattering by the 2-coordinated carbon atoms near the single vacancies is as 1.5 times as that near the double vacancies at the same defect density. Therefore, the single vacancy defective graphene possesses the lower thermal conductivity than the double vacancy defective one. For example, for graphene flakes with 0.1% defected atoms, for single vacancy defective graphene, κ/κ0 is 0.19, while for double vacancy defective graphene, κ/κ0 is 0.23. Thus under the same defected atom density, single-vacancy can result in larger reduction in thermal conductivity with respect to double-vacancy defects. This explains the phenomenon observed by molecular dynamics simulations29,51.

In summary, we find a new phonon scattering mechanism which is the scattering by the under-coordinated atoms near the vacancies. This mechanism origins from the increase of force constant of bonds associated with vacancies. The scattering of phonons by the under-coordinated atoms near the vacancies is negligible in bulk materials. However, because of the low coordination number, this mechanism has dominant effect on the phonon transport in two-dimensional vacancy defective materials. This finding is helpful not only to understand the severe suppression of thermal conductivity by vacancies, but also to apply phononic engineering to manipulate thermal conductivity in two-dimensional materials.

Methods

According to the linearized phonon Boltzmann transport equation within relaxation time approximation, the thermal conductivity in branch λ of single layer graphene (SLG) in the y direction (the longitudinal direction of graphene ribbon) is derived as:

graphic file with name srep05085-m14.jpg

where S is the area of the sample, vλ,y is the y component of the group-velocity vector in branch λ (λ = LA, TA and ZA, only acoustic branches are considered49,52), τλ is the averaged phonon relaxation time between successive scattering events, 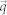Inline graphic is the wave vector, and cph is the volumetric specific heat of each mode, which is given as:

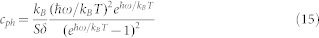graphic file with name srep05085-m15.jpg

where kB is the Boltzmann constant, δ = 0.335 nm is the thickness of graphene, 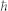Inline graphic is the reduced Planck constant, and T is the absolute temperature.

In SLG, the LA and TA acoustic branches are linear, whereas the ZA branch shows a quadratic dependence of the frequency on the wave vector49,53, so

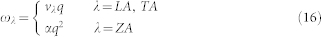graphic file with name srep05085-m16.jpg

Using this dispersion and the relationship 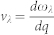Inline graphic, and transforming the integral of wave vector (q) to frequency (ω), we can get

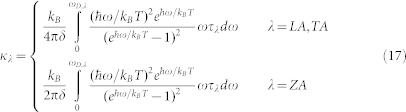graphic file with name srep05085-m17.jpg

where ωD,λ is the Debye frequency, which is given as

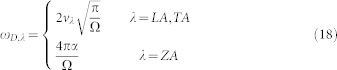graphic file with name srep05085-m18.jpg

where Ω is the primitive cell area.

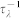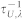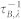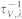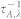The total phonon scattering rate Inline graphic is the sum of Inline graphic, Inline graphic, Inline graphic and Inline graphic, which are given as Eq. (8–12) respectively. For a flat graphene sheet lying in the x-y plane, the reflection symmetry requires that the Hamiltonian be invariant under z → −z54. Seol et al. obtained a selection rule for three-phonon scattering, which requires that an even number of ZA phonons is involved in each process. This selection rule is adopted in our calculation.

The normalized accumulative distribution of thermal conductivity is defined as,

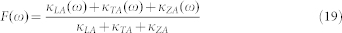graphic file with name srep05085-m19.jpg

where κλ(ω) is given as,

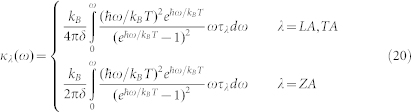graphic file with name srep05085-m20.jpg

Author Contributions

G.F.X. and G.Z. established the theoretical models and supervised the project, G.F.X. and Y.L.S. performed the calculations and data analysis, G.F.X. wrote the paper, G.Z. revised the paper. X.L.W., L.W.Y., H.P.X. and J.X.Z. discussed the results.

Acknowledgments

This work was financially supported by National Natural Science Foundation of China (NSFC) (Grant Nos. 11275163, 11274011, 11304264), and the Ministry of Education of China (Grant No. 20110001120133).

References

  1. Dubi Y. & Ventra M. D. Heat flow and thermoelectricity in atomic and molecular junctions. Rev. Mod. Phys. 83, 131–155 (2011). [Google Scholar]
  2. Yang N., Xu X. F., Zhang G. & Li B. W. Thermal transport in nanostructures. AIP Advances. 2, 041410 (2012). [Google Scholar]
  3. Liu S., Xu X. F., Xie R. G., Zhang G. & Li B. W. Anomalous heat conduction and anomalous diffusion in low dimensional nanoscale systems. Eur. Phys. J. B 85, 337 (2012). [Google Scholar]
  4. Freedman J. P., Leach J. H., Preble E. A., Sitar Z., Davis R. F. & Malen J. A. Universal phonon mean free path spectra in crystalline semiconductors at high temperature. Sci. Rep. 3, 2963 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Balandin A. A. Thermal properties of graphene and nanostructured carbon materials. Nature. Mater. 10, 569–581 (2011). [DOI] [PubMed] [Google Scholar]
  6. Sadeghi M. M., Pettes M. T. & Shi L. Thermal transport in graphene. Solid State Commun. 152, 1321–1330 (2012). [Google Scholar]
  7. Pop E., Varshney V. & Roy A. K. Thermal properties of graphene: Fundamentals and applications. MRS Bull. 37, 1273–1281 (2012). [Google Scholar]
  8. Shahil K. M. F. & Balandin A. A. Thermal properties of graphene and multilayer graphene: Applications in thermal interface materials. Solid State Commun. 152, 1331–1340 (2012). [Google Scholar]
  9. Li N. et al. Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 84, 1045–1066 (2012). [Google Scholar]
  10. Yang N., Zhang G. & Li B. Thermal rectification in asymmetric graphene ribbons. Appl. Phys. Lett. 95, 033107 (2009). [Google Scholar]
  11. Hu J., Ruan X. & Chen Y. P. Thermal Conductivity and Thermal Rectification in Graphene Nanoribbons: A Molecular Dynamics Study. Nano Lett. 9, 2730–2735 (2009). [DOI] [PubMed] [Google Scholar]
  12. Zhang G. & Zhang H. Thermal conduction and rectification in few-layer graphene Y Junctions. Nanoscale. 3, 4604–4607 (2011). [DOI] [PubMed] [Google Scholar]
  13. Sevincli H., Sevik C., Cagin T. & Cuniberti G. A bottom-up route to enhance thermoelectric figures of merit in graphene nanoribbons. Sci. Rep. 3, 1228 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Chen X. B., Tian F. Y., Persson C., Duan W. H. & Chen N.-X. Interlayer interactions in graphites. Sci. Rep. 3, 3046 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Mu X., Wu X. F., Zhang T., Go D. B. & Luo T. F. Thermal Transport in Graphene Oxide – From Ballistic Extreme to Amorphous Limit. Sci. Rep. 4, 3909 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Tian H. et al. A novel solid-state thermal rectifier based on reduced graphene oxide. Sci. Rep. 2, 523 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Liu X. J., Zhang G., Pei Q. X. & Zhang Y. W. Phonon thermal conductivity of monolayer MoS2 sheet and nanoribbons. Appl. Phys. Lett. 103, 133113 (2013). [Google Scholar]
  18. Li W., Carrete J. & Mingo N. Thermal conductivity and phonon linewidths of monolayer MoS2 from first principles. Appl. Phys. Lett. 103, 253103 (2013). [Google Scholar]
  19. Cai Y. Q., Lan J. H., Zhang G. & Zhang Y. W. Lattice vibrational modes and phonon thermal conductivity of monolayer MoS2. Physical Review B 89, 035438 (2014). [Google Scholar]
  20. Sun C. Q. Relaxation of the Chemical Bond. Vol. 108 Springer Series in Chemical Physics 795. (Berlin: Springer press, 2014). [Google Scholar]
  21. Zhang G. & Li B. W. Impacts of doping on thermal and thermoelectric properties of nanomaterials. NanoScale. 2, 1058–1068 (2010). [DOI] [PubMed] [Google Scholar]
  22. Zhang H., Lee G. & Cho K. Thermal transport in graphene and effects of vacancy defects. Phys. Rev. B 84, 115460 (2011). [Google Scholar]
  23. Yamamoto T. & Watanabe K. Nonequilibrium Green's Function Approach to Phonon Transport in Defective Carbon Nanotubes. Phys. Rev. Lett. 96, 255503 (2006). [DOI] [PubMed] [Google Scholar]
  24. Che J., Cagin T., Deng W. Q. & Goddard III W. A. Thermal conductivity of diamond and related materials from molecular dynamics simulations. J. Chem. Phys. 13, 6888–6900 (2000). [Google Scholar]
  25. Chen K. Q. et al. Effect of defects on the thermal conductivity in a nanowire. Phys. Rev. B 72, 045422 (2005). [Google Scholar]
  26. Ratsifaritana C. A. & Klemens P. G. Scattering of phonons by vacancies. Int. J. Thermophys. 8, 737–750 (1987). [Google Scholar]
  27. Sun C. Q. et al. Bond-order–bond-length–bond-strength (bond-OLS) correlation mechanism for the shape-and-size dependence of a nanosolid. J. Phys.: Condens. Matter 14, 7781–7795 (2002). [Google Scholar]
  28. Sun C. Q. Size dependence of nanostructures: Impact of bond order deficiency. Prog. Solid State Chem. 35, 1–159 (2007). [Google Scholar]
  29. Haskins J. et al. Control of Thermal and Electronic Transport in Defect-Engineered Graphene Nanoribbons. ACS Nano 5, 3779–3787 (2011). [DOI] [PubMed] [Google Scholar]
  30. Klemens P. G. & Pedraza D. F. Thermal conductivity of graphite in the basal plane. Carbon 32, 735–741(1994). [Google Scholar]
  31. Klemens P. G. Phonon scattering by oxygen vacancies in ceramics. Physica B 263–264, 102–104 (1999). [Google Scholar]
  32. Yeung T. C. A. et al. Impact of surface bond-order loss on phonon dispersion relations and thermal conductivity of cylindrical Si nanowires. Phys. Rev. B 74, 155317 (2006). [Google Scholar]
  33. Yeung T. C. A. et al. Effect of surface bond-order loss on electrical resistivity of metallic polycrystalline thin films. Phys. Rev. B 72, 155417 (2005). [Google Scholar]
  34. Sun C. Q. et al. Dimension, Strength, and Chemical and Thermal Stability of a Single C-C Bond in Carbon Nanotubes. J. Phys. Chem. B 107, 7544–7546 (2003). [Google Scholar]
  35. Sun C. Q., Li C. M., Bai H. L. & Jiang E. Y. Melting point oscillation of a solid over the whole range of sizes. Nanotechnology 16, 1290–1293 (2005). [Google Scholar]
  36. Klemens P. G. The scattering of low-frequency lattice waves by static imperfections. Proc. Phys. Soc. A 68, 1113–1128 (1955). [Google Scholar]
  37. Klemens P. G. Thermal conductivity and lattice vibrational modes. Solid State Phys. 7, 1–98 (1958). [Google Scholar]
  38. Zhang G. & Zhang Y. W. Thermal conductivity of silicon nanowires: From fundamentals to phononic engineering. Phys. Status Solidi RRL 7, 754–766 (2013). [Google Scholar]
  39. Nika D. L. & Balandin A. A. Two-dimensional phonon transport in graphene. J. Phys.: Condens. Matter. 24, 233203 (2012). [DOI] [PubMed] [Google Scholar]
  40. Nika D. L., Askerov A. S. & Balandin A. A. Anomalous Size Dependence of the Thermal Conductivity of Graphene Ribbons. Nano Lett. 12, 3238–3244 (2012). [DOI] [PubMed] [Google Scholar]
  41. Shen Y. L. et al. Size and boundary scattering controlled contribution of spectral phonons to the thermal conductivity in graphene ribbons. J. Appl. Phys. 115, 063507 (2014). [Google Scholar]
  42. Kong B. D., Paul S., Nardelli M. B. & Kim K. W. First-principles analysis of lattice thermal conductivity in monolayer and bilayer graphene. Phys. Rev. B 80, 033406 (2009). [Google Scholar]
  43. Girit C. O. et al. Graphene at the Edge: Stability and Dynamics. Science 323, 1705–1708 (2009). [DOI] [PubMed] [Google Scholar]
  44. Grantab R., Shenoy V. B. & Ruoff R. S. Anomalous strength characteristics of tilt grain boundaries in graphene. Science 330, 946–8 (2010). [DOI] [PubMed] [Google Scholar]
  45. Chen S. et al. Thermal conductivity of isotopically modified graphene. Nat. Mater. 11, 203–207 (2012). [DOI] [PubMed] [Google Scholar]
  46. Wang Y. et al. Large Thermal Conductivity Reduction Induced by La/O Vacancies in the Thermoelectric LaCoO3 System. Inorg. Chem. 50, 4412–4416 (2011). [DOI] [PubMed] [Google Scholar]
  47. Balandin A. A. et al. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 8, 902–907 (2008). [DOI] [PubMed] [Google Scholar]
  48. Ghosh S. et al. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 92, 151911 (2008). [Google Scholar]
  49. Nika D. L., Pokatilov E. P., Askerov A. S. & Balandin A. A. Phonon thermal conduction in graphene: Role of Umklapp and edge roughness scattering. Phys. Rev. B 79, 155413 (2009). [Google Scholar]
  50. Lindsay L., Broido D. A. & Mingo N. Flexural phonons and thermal transport in graphene. Phys. Rev. B 82, 115427 (2010). [Google Scholar]
  51. Zhang Y. Y. et al. Thermal conductivity of defective graphene. Phys. Lett. A 376, 3668–3672 (2012). [Google Scholar]
  52. Munoz E., Lu J. & Yakobson B. I. Ballistic Thermal Conductance of Graphene Ribbons. Nano Lett. 10, 1652–1656 (2010). [DOI] [PubMed] [Google Scholar]
  53. Kong B. D., Paul S., Nardelli M. B. & Kim K. W. First-principles analysis of lattice thermal conductivity in monolayer and bilayer graphene. Phys. Rev. B 80, 033406 (2009). [Google Scholar]
  54. Seol J. H. et al. Two-Dimensional Phonon Transport in Supported Graphene. Science 328, 213–216 (2010). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES