Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 May 28;4:5093. doi: 10.1038/srep05093

Surface Chest Motion Decomposition for Cardiovascular Monitoring

Ghufran Shafiq 1, Kalyana C Veluvolu 1,a
PMCID: PMC4035586  PMID: 24865183

Abstract

Surface chest motion can be easily monitored with a wide variety of sensors such as pressure belts, fiber Bragg gratings and inertial sensors, etc. The current applications of these sensors are mainly restricted to respiratory motion monitoring/analysis due to the technical challenges involved in separation of the cardiac motion from the dominant respiratory motion. The contribution of heart to the surface chest motion is relatively very small as compared to the respiratory motion. Further, the heart motion spectrally overlaps with the respiratory harmonics and their separation becomes even more challenging. In this paper, we approach this source separation problem with independent component analysis (ICA) framework. ICA with reference (ICA-R) yields only desired component with improved separation, but the method is highly sensitive to the reference generation. Several reference generation approaches are developed to solve the problem. Experimental validation of these proposed approaches is performed with chest displacement data and ECG obtained from healthy subjects under normal breathing and post-exercise conditions. The extracted component morphologically matches well with the collected ECG. Results show that the proposed methods perform better than conventional band pass filtering.

Advancements in health care have increased the average human life expectancy. However, individuals with complex health conditions are also becoming common1. Consequently, a significant rise in the number of patients with chronic age-related diseases (such as congestive heart failure, sleep apnoea and obstructive pulmonary disease) is observed in recent times2,3,4,5. In the United States alone, at least 180,000 deaths per year are associated with Sudden Cardiac Death and other cardiovascular diseases14,15. Limited medical resources and increasing health care costs are the major concerns4,6 that can be alleviated by continually monitoring the patient's health outside the hospital settings7,8. In this regard, efforts are being made in developing un-obtrusive personalized health care systems for long-term health monitoring. One approach for achieving this goal is to develop wearable sensors (accelerometers, electrodes or microphones, etc.) that can be placed directly or indirectly on the body9. These wearable sensors can be coupled with smart phones for self-awareness of user and automated generation of distress call in case of emergency. Accelerometers or inertial measurement units (IMUs) based wearable sensors have gained high popularity due to their small size, cost-effectiveness, little power consumption and versatility in terms of applications such as activity monitoring9, fall detection13 and physiological monitoring12,38. With the improved sensitivity, IMUs are capable of acquiring respiratory signals from the chest surface42,43. The chest surface moves predominantly due to inflation and deflation of the lungs during the breathing cycle. This movement ranges from 4–12 mm17 with a frequency range of 0.2–0.34 Hz (12–20 breaths per minute)18. In addition to respiratory motion, the chest surface motion also includes comparatively faster but weaker vibrations (precordial motion41) due to the beating of the heart. The chest surface motion due to the beating of the heart has an amplitude range of 0.2–0.5 mm19 and frequency range of 1–1.34 Hz (60–80 beats per minute)18. Applications of surface chest motion include, but are not limited to apnoea screening42, acquisition of clinically valuable parameters such as hemodynamic parameters44 and detection of early stage hemorrhage45 etc. However, it is essential to separate the precordial motion and respiratory motion from composite chest surface motion for further analysis in these applications. The purpose of this research is to employ motion sensors (IMUs) to acquire the composite surface chest motion and decompose that motion into its constituent sources (i.e. respiration and heart) for long-term monitoring of respiration and cardiovascular activity.

Several works have tried to separate the precordial motion from the surface chest motion. One of the earliest works used microwave doppler radar to detect the chest surface motion in the absence of respiration20. When respiration is suppressed, the surface chest motion is essentially the precordial motion (assuming that there is no body motion). Since then, significant efforts are put to improve the microwave doppler radar technology which can be employed for remote surveillance/detection of heart beats at a distance from subject21,35. However, this approach constraints the subject to remain within line-of-sight (LoS) of the antenna. This limitation is addressed by augmenting a visual camera system to track the subject and move antenna accordingly36. Apart from doppler radar, contraction and expansion of fiber Bragg gratings are employed under the bed or chair to obtain the surface chest wall motion16,22,23. For ubiquitous and unobtrusive monitoring of the patients without interrupting their daily life activities, the recent focus has been on wearable sensors that can be placed directly or indirectly on the body6,9,10,11,12. Recently, a wearable system equipped with accelerometer is introduced which can provide the precordial vibrations39. Nevertheless, the prototype requires the subject to remain still in order to record these vibrations. This is done in order to avoid body motions which can corrupt the desired signal. Various signal processing techniques have been employed for the separation of precordial motion from the surface chest motion. Wavelet decomposition is used to filter the respiration from the surface chest motion21. To improve the accuracy of heart beat detection with this method, a statistical method is employed to eliminate the false heartbeats and add the correct beats37. In16, a simple approach based on two band-pass filters is employed for separating respiratory motion and precordial motion. However, with the band pass filter approach, the higher harmonics of the respiratory signal often overlap with the dominant frequency band of the precordial motion24 which results in inaccurate separation. Moreover, the methods based on band-pass filters require subject-specific tuning and cannot be generalized for all the subjects and conditions.

In this paper, we approach the separation problem of respiratory and precordial motion with Independent Component Analysis (ICA) framework25. ICA can separate the constituent sources by utilizing their statistical independence rather than the spectral distinction31. One of the most successful applications of ICA is artifact removal from (multi-channel) EEG signals, where artifacts can spectrally overlap the EEG signals26. However, the application of conventional ICA yields multiple components, which require interpretation and component selection. To solve this problem and further improve the separation quality, we employ constrained ICA (cICA) or ICA with reference (ICA-R)27. ICA-R requires a reference signal that should roughly match the desired source. However, the reference generation becomes critical due to varying periodicity and morphological characteristics of the precordial motion. To address this issue, we form an idealistic reference generation technique that incorporates the periodic information from ECG and subject-specific morphological characteristics of precordial motion from the chest surface motion in the absence of respiration. Our final goal is to develop a method that is independent of ECG, and can be employed for separating the precordial motion from wearable sensors to aid the enhancement of personalized health care in various daily life scenarios. For this purpose, we employ a delayed correlation based reference generation method28 that is based on maximizing the autocorrelation of the desired source (precordial motion). The separation methods are tested under normal breathing conditions (80 trials from 9 subjects) and post exercise conditions (10 trials from 5 subjects). Results show that the performance of delayed correlation based reference generation28 is comparable to the ECG based reference generation and marks a significant improvement over conventional ICA and band-pass filtering methods.

Results

In this section, we first describe the experimental setup and protocol employed for data collection. Then the measures employed for performance analysis are discussed. Based on these measures, the results are analyzed for free breathing and post exercise trials.

Experimental Setup and Protocol

Experimental verification of the proposed approach was performed on the data acquired from 9 healthy male subjects. The ages of these subjects were in the range of 22–32 (25.6 ± 3.3) years, while their BMIs ranged from 18.3–27.2 (21.86 ± 2.56) kg/m2. The study was approved by the institutional review board of Kyungpook National University and was conducted according to the principles expressed in the declaration of Helsinki. Written consent of all the subjects was taken prior to the experiment.

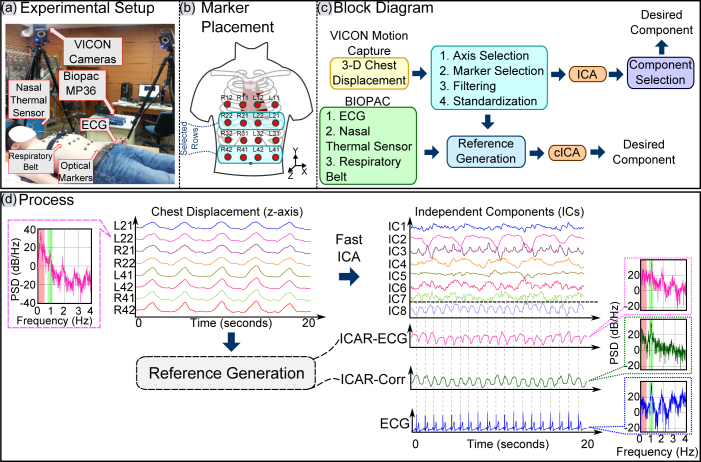
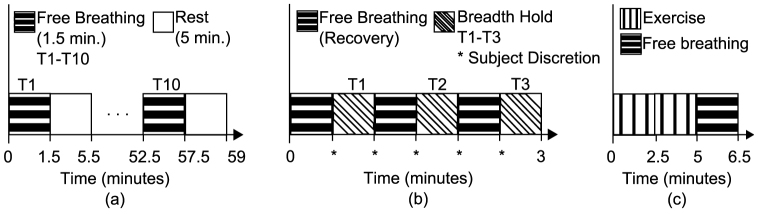
The data acquisition for the experiment consisted of two parts: i) recording the surface chest motion with multiple infrared (IR) cameras and ii) simultaneous recording of established referential signals i.e. ECG, Nasal thermal sensor signals and respiratory belt signals. The experimental setup is shown in Fig. 1(a).

Figure 1. (a) Experimental Setup, (b) Placement of markers and Labeling scheme, (c) Block diagram, (d) Process. Author G. S created the drawing.

Figure 1

Open in a new tab

A complete block diagram of data acquisition and the approach is shown in Fig. 1(c). The surface chest wall motion is acquired by the VICON IR camera system (VICON Motion Systems Ltd., UK). Six of these cameras tracked the three dimensional motion of the retro-reflective optical markers. 16 such markers were placed on the anterior upper body in a 4 × 4 grid as shown in Fig. 1(a) and Fig. 1(b). The placement of markers was done to capture the motion of full trunk. Efforts were made to adjust the markers to cover the point of maximal impulse (PMI) and the lower sternum for getting maximal and cleaner movement due to the heart. However, only 8 markers were used for the analysis (as shown in Fig. 1(b)) and the complete 16-marker configuration was used to optimize the location and number of sensors to be placed. The cameras were placed in an approximately circular pattern around the subject to ensure that each optical marker placed on the chest was visible to at least three cameras for reliable 3-D reconstruction of motion. The sampling rate for the VICON camera system was set to 100 frames per second. The ECG and the reference respiratory signals (respiration belt and thermal nasal sensor) were recorded by BIOPAC biological data acquisition system (BIOPAC Systems Inc., USA). The sampling frequency for the BIOPAC recorder was set to 500 Hz. To demonstrate the validity of approach in various daily life scenarios, we recorded the trials under: i) normal (free) breathing, ii) post-exercise and iii) breath-hold conditions. The timing diagram for experimental setup is illustrated in Fig. 2. Under normal breathing, 6–10 trials of 90 seconds each were recorded. Two trials of 90 seconds duration were recorded from 5 subjects each under post-exercise condition to simulate elevated heart rates. In this scenario, the subject was asked to perform exercise (for instance, jumping jacks) for approximately 3–5 minutes. As soon as subject completed the exercise, his heart rate was checked and recording of the trial began immediately. Three trials from 9 subjects were recorded in breath hold conditions, in which the subjects were asked to halt breathing. The duration for this maneuver was also left on subject's discretion to ensure the comfort and safety of the subject. All the trials for each scenario were recorded with the subjects in the supine position.

Figure 2. Timing diagram: (a) Free breathing, (b) Breath-hold, (c) Post-Exercise.

Figure 2

Open in a new tab

Performance Measures

This subsection discusses the performance measures employed for analyzing the performance of ICA methods for the separation of cardiac source. Further, the methods are compared with a zero-phase 4th order Butterworth bandpass filter with pass band 0.7 Hz to 2.17 Hz.

Improvement in Normalized Power Spectrum Ratio

One instance of power spectral density (PSD) comparison before and after ICA source separation is shown in Fig. 1(d). The PSD of signal before separation (chest displacement signal) shows very high power in the respiratory band (highlighted as light red). However, after the source separation, the power in respiratory band is minimized while maximizing the power in the cardiac band (highlighted as green in Fig. 1(d)). One measure to quantify the quality of separation (suppression of undesired component) is the improvement in the normalized power spectrum (INPS)29. A similar approach is used here that combines the suppression of respiratory component and boosting of cardiac component. Let α1 be the measure of respiratory component suppression which is defined as:

graphic file with name srep05093-m1.jpg

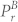where Inline graphic represents the power in the respiratory band before separation, while 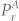Inline graphic represents the power in the respiratory band after separation. Higher value of α1 suggests more reduction in 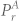Inline graphic i.e. higher attenuation of respiratory component.

Similarly, let α2 be the measure of amplification of cardiac component, which is defined as:

graphic file with name srep05093-m2.jpg

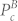where Inline graphic represents the power in the cardiac band before separation, while 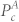Inline graphic represents the power in the cardiac band after separation. Higher value of α2 suggests an increase in 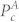Inline graphic i.e. higher amplification of the cardiac component. The overall improvement in the power spectrum α is then defined as:

graphic file with name srep05093-m3.jpg

where higher value of α indicates better separation quality.

The bounds for respiratory band were determined from the valley points (minima) around the dominant peak in the average PSD of the chest displacement signals where respiration is the major contributor of the motion. Similarly, the bounds for cardiac band were determined from the valley points (minima) around the fundamental peak in the PSD of ECG; where fundamental peak corresponds to the periodicity of heart beats.

Peak-R Offset

Since ECG is considered as the gold standard in literature for recording heart activity, the proposed approach requires comparison against ECG. However, ECG is an electrical signal and the motion of the chest due to the beating heart is a mechanical displacement. Moreover, the morphology of ECG signal and the chest displacement due to heart are entirely different. Owing to these reasons, some offset is expected between the peaks of ECG (R peaks) and the peaks of the separated signal. This offset is termed here as Peak-R offset. Since the mechanical motion of the heart is related to the electrical signal, therefore Peak-R offset should remain constant for a given trial. In other words, smaller standard deviation of this offset will imply better source separation. Peak-R offset was tested on breath-hold chest displacement signals from 9 subjects which showed an average standard deviation of less than 1 sample. Negative peaks (valleys) of the separated signals (precordial motion) are detected using auto-threshold peak detection algorithm30. Since diastole is slower than systole, valleys are sharper than peaks and provides less error in calculating the intervals. A comparison is made between FastICA, ICAR-ECG, ICAR-Correlation and zero-phase bandpass filter to analyze the performance for this measure.

Free Breathing Trials

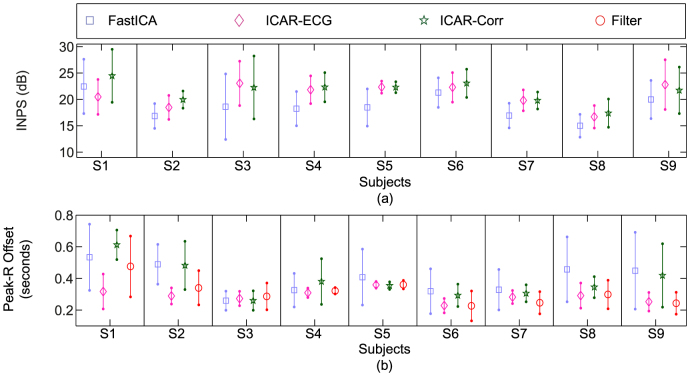
Subject-wise INPS is shown in Fig. 3(a) where the statistics (mean and standard deviation) are calculated over all the trials for the given subject. The mean INPS of ICAR-ECG and ICAR-Correlation appears to be similar; whereas the mean INPS of FastICA is better in the subject (S1). In terms of standard deviation, ICAR-ECG has the lowest standard deviation in subjects S1 to S6; whereas ICAR-Correlation shows slightly lower standard deviation than ICAR-ECG in the rest of the subjects. FastICA shows significantly higher standard deviation in subjects S3 (as compared to ICAR-ECG) and S5 (as compared to ICAR-ECG and ICAR-Correlation). In subjects S8 and S9, lower INPS deviation is observed in FastICA; however, the mean INPS of FastICA is also lower in these subjects.

Figure 3. Free breathing results: (a) Subject-wise INPS, (b) Subject-wise peak offset.

Figure 3

Open in a new tab

Subject-wise Peak-R offset is shown in Fig. 3(b) where the statistics (mean and standard deviation) are calculated over all the trials for the given subject. ICAR-ECG shows lowest deviations in subjects S2, S3, S5, S6, S7 and S9 as compared to the other methods. ICAR-Correlation shows lowest deviations in subjects S1 and S8; while similar deviations are seen for ICAR-Correlation and ICAR-ECG in subjects S3, S5, S7 and S8. Bandpass filter shows lowest deviations in subjects S4 and S9 (similar deviation values are observed in ICAR-ECG for these subjects). FastICA shows similar deviations in subject S2 in comparison with ICAR-Correlation, and S3 in comparison with other methods.

Post-Exercise Trials

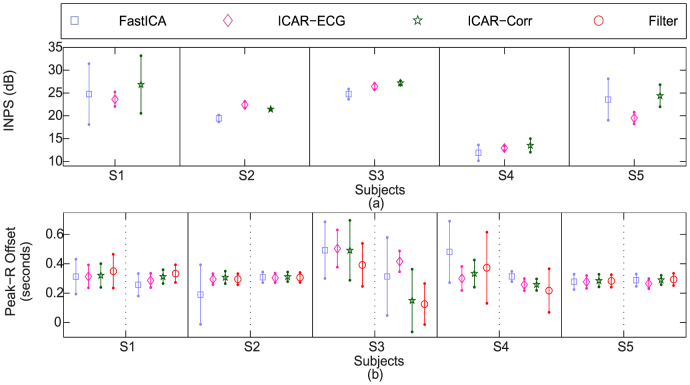
10 trials of 90 seconds each were recorded from 5 subjects after exercise to simulate tensed or anxious conditions as faster and stronger heart beats are expected in such conditions. Subject-wise INPS (statistics of INPS in all trials for a given subject) is shown in Fig. 4(a). The performance of ICAR-ECG and ICAR-Correlation is comparable in subjects S2, S3 and S4. In subject S1 and S5, ICAR-Correlation shows highest mean INPS but with higher standard deviation as compared to ICAR-ECG. FastICA performs comparable to other methods in subjects S2, S3 and S4 with slightly lower mean values. In subjects S1 and S5, mean INPS of FastICA is higher than ICAR-ECG, but with significantly higher standard deviations.

Figure 4. Post-exercise results: (a) Subject-wise INPS, (b) Subject-wise peak offset.

Figure 4

Open in a new tab

Statistics of Peak-R offset (mean and standard deviation) for each trial are shown in Fig. 4(b). Dashed line separates two trials (per subject), whereas solid lines separate the subjects. FastICA performs comparable to the other methods in S2(T2), S4(T2) and S5(T1 and T2). Bandpass filter performs comparable to ICAR-ECG and ICAR-Correlation in S2 and S5 and better than ICAR-Correlation in S3. ICAR-Correlation performs comparable to ICAR-ECG in all the subjects except S3, whereas ICAR-ECG performs best in all the subjects.

Dynamic Peak-Peak Interval Variability

This measure compares the peak-peak intervals obtained from the separated precordial motion, and the R-R intervals obtained from ECG. The higher similarity of these intervals between ECG and separated signal calculated over time suggests better separation and reliable usability of the separated signal for further Heart Rate Variability (HRV) analysis.

In order to plot peak-peak interval variability, the intervals between each peak are then averaged over a 2 second window that moves every 1 second. The resulting dynamic P-P intervals are plotted against time. A comparison is performed for Fast ICA, ICAR, ICAR-Correlation and bandpass filtering against standard ECG.

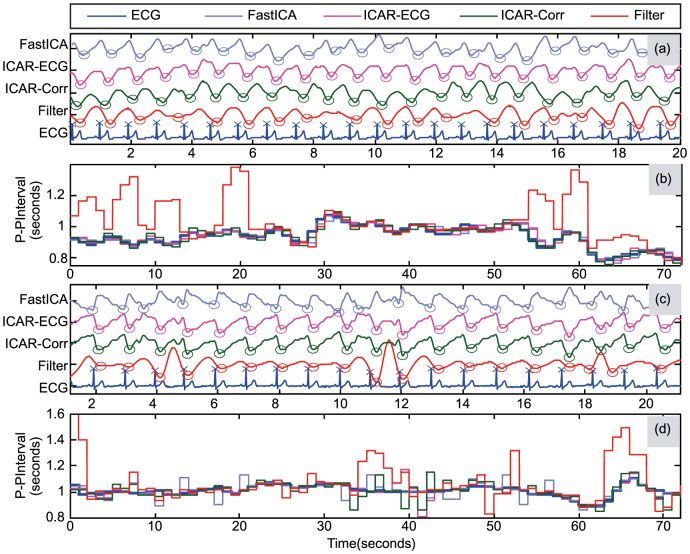
Peak detection for the separated components from two trials are shown in Fig. 5(a) and Fig. 5(c) for free breathing and post-exercise respectively (20 second segment out of full length trial is shown for better visibility). The corresponding HRV plots are shown in Fig. 5(b) and Fig. 5(d). It can be observed that the component obtained from band pass filtering shows deviated peak-peak intervals when compared against ECG. In comparison, ICA methods show similar peak-peak intervals. Moreover, peak-peak intervals calculated from ICAR-ECG shows least deviation from the peak-peak intervals calculated from ECG as compared to other methods.

Figure 5. Peak detection and P-P intervals for separated components: (a) Subject #2 Free breathing: Detection of Peaks (b) Subject #2 Free breathing: Peak-Peak intervals, (c) Subject #4 Post-Exercise: Detection of Peaks (d) Subject #4 Post-Exercise: Peak-Peak intervals.

Figure 5

Open in a new tab

Peak-Peak Interval Analysis

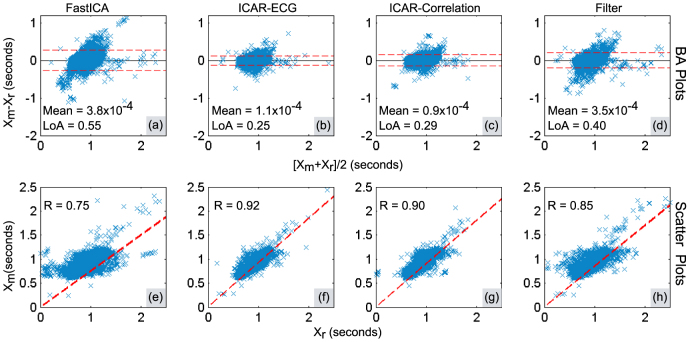
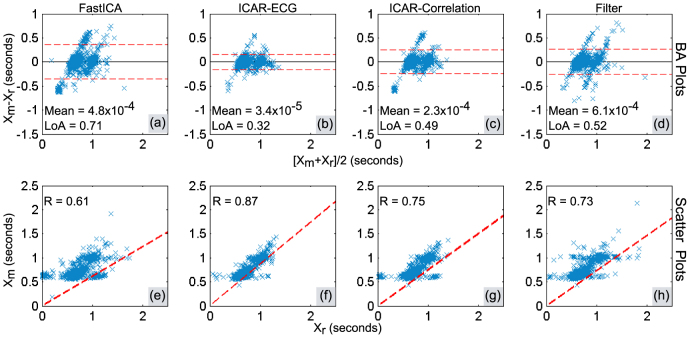
In order to evaluate the similarities between peak-peak intervals obtained from ECG (reference measurement) and separated precordial motion (test measurements), we employed Bland-Altman (BA) analysis40 and scatter plots. BA analysis identifies the presence of fixed and proportional errors. Further, it determines the reliability of the method under test by providing limits of agreement between reference method and the method under test. The scatter plots provide a visual reference for the relationship between reference measurements and test measurements precordial motion. Pearson's correlation coefficient is also found to quantify the similarity between reference measurements and test measurements.

BA plots for free breathing and post-exercise are shown in Fig. 6(a) – Fig. 6(d) and Fig. 7(a) – Fig. 7(d) respectively. The peak-peak intervals calculated from the separated heart motion are denoted by Xm; whereas the peak-peak intervals calculated from ECG are denoted by Xr. The Limits of Agreement containing nearly 95% of the errors are indicated by red dashed lines and calculated as mean(Xm − Xr) ± 1.96 × SD(Xm − Xr)40, where SD() represents the standard deviation and mean() represents the average error. The range (width) of these limits (LoA) given in BA plots is calculated as LoA = 2 × 1.96 × SD(Xm − Xr). The mean error is indicated by the black solid line. The scatter plot for showing the similarity between peak-peak intervals obtained from ECG and the separated motion is shown in Fig. 6(e) – Fig. 6(h) and Fig. 7(e) – Fig. 7(h) for free-breathing and post-exercise respectively. The similarity is quantified as correlation coefficient and the resulting linear regression line is plotted.

Figure 6. Peak-Peak interval validation analysis in free breathing trials: (a) – (d) Bland-Altman plots, (e) – (h) Scatter plots.

Figure 6

Open in a new tab

Figure 7. Peak-Peak interval validation analysis in post-exercise breathing trials: (a) – (d) Bland-Altman plots, (e) – (h) Scatter plots.

Figure 7

Open in a new tab

In the BA plots shown for free breathing in Fig. 6(a) – Fig. 6(d), it can be observed that difference intervals are least scattered for ICAR-ECG with smallest LoA. The scattering and hence LoA increases subsequently for ICAR-Correlation, bandpass filter and FastICA. The scatter plots in Fig. 6(e) – Fig. 6(h) show highest Pearson's correlation coefficient (R) for ICAR-ECG, which subsequently decreases in ICAR-Correlation, bandpass filter and FastICA. Similar conclusions can be drawn for post-exercise trials.

BA plots for post exercise trials are shown in Fig. 7(a) – Fig. 7(d). It can be observed that difference intervals are least scattered for ICAR-ECG with smallest LoA. The scattering and hence LoA increases subsequently for ICAR-Correlation, bandpass filter and FastICA. The same conclusion was drawn from the BA analysis of free breathing trials.

Discussion

The fundamental frequencies of respiratory signal and heart signal are apart in frequency domain and therefore it is intuitive to use bandpass filter to separate the two signals. However, this approach may not perform better in scenarios such as: i) presence of body movement in the subject which may spectrally overlap the desired band of frequencies and ii) presence of higher respiratory harmonic (such as 3rd or 4th harmonics) close to the beating frequency of heart. ICA methods can deal with the body motion by utilizing multiple sensors and cancelling the body motion, provided that each sensor records the same (or linearly scaled) body motion such that the ICA model can hold. The harmonics problem can be well addressed by ICA methods, as the signals are separated based on the statistical independence rather than the spectral distinction.

Experimental results demonstrate that ICAR-ECG performs best, and is subsequently followed by ICAR-Correlation, bandpass filter and FastICA. The failure of FastICA can be explained by the local minima and sign indeterminacy problems (the desired signal may come out as inverted)34. In ICAR-ECG, the reference generation process combines ECG timing as well as the breath-hold signal morphology and provides best performance compared to the rest. ICAR-Correlation marks a significant improvement over bandpass filter without ECG and makes it more attractive for practical applications.

The post-exercise trials start with higher breathing amplitude and frequency as well as stronger and faster heartbeats. However, with the passage of time, these characteristics of heart motion and the respiratory motion changes. The breathing cycle and heart beats slow down and the respiratory and cardiac motion becomes weaker. If the respiratory and cardiac motion amplitude decays at the same rate (for some time), then the two sources may become partially dependent which can affect the separation performance in the ICA methods. On the other hand, bandpass filters can have an aggravated problem with respiratory harmonics and body motion artifacts. For these reasons, all the methods show decreased performance in post-exercise trials as compared to free breathing trials. However, the performance order for post-exercise trials is same as the free breathing trials, i.e. ICAR-ECG performs best and subsequently followed by ICAR-Correlation, bandpass filter and FastICA.

The template generation for ICAR-ECG requires the subject to hold breath once for adequate time (10–15 seconds). This is possible for healthy subjects but can be inconvenient for patients with respiratory conditions. Shorter duration for breath hold segments may not be able to generate a generalized pulse template and therefore can deteriorate the separation performance of ICAR-ECG. The separation performance of ICAR-Correlation depends on the proper selection of time delay for which the autocorrelation for the desired source (precordial motion) is maximized. Estimation of the time delay requires the precordial motion to be temporally correlated, which is true in most of the cases. Band-pass filter approach relies on subject specific tuning to yield optimum results and is limited when respiratory harmonic overlaps with the fundamental heart beat frequency.

This work is a part of our continuing research in the development of wearable sensors based on inertial sensors for ubiquitous and non-obtrusive cardiopulmonary monitoring. Although the present work relies on the optical sensors, in future inertial sensors will be employed for the measurement of chest displacement. Light weight and cost effective accelerometer based smart garments will provide an affordable, personalized and long-term health monitoring. Moreover, the separation schemes with the experimental setup will be tested in more challenging real life scenarios including different postures (such as sitting and standing) and in-exercise scenarios (such as walking and running). However, employing accelerometers to obtain displacement is a major challenge. This issue will be addressed elsewhere.

Methods

Pre-processing

Chest surface motion is recorded as a 3-Dimensional signal. However, the pulsations on the chest surface due to the heart is prevalent in perpendicular direction to the frontal plane of the chest (other than ballistic force of blood flow in the head/toe direction). Therefore, we retain only z-axis motion signal for further processing (refer to Fig. 1(a)). For input selection, 2nd row and 4th row are considered. 2nd row provides the strongest contribution of heart to the chest motion as compared to the other rows. On the other hand, 4th row provides minimal heart motion contribution as compared to other rows (see Fig. 1(b)). Further preprocessing steps include bandpass filtering of the displacement signals from 0.1–4 Hz (to improve SNR) and standardizing the signals (making the signals zero-mean and unit-variance to fulfill conditions for ICA). The selected preprocessed displacement signals are then fed as input to ICA/ICA-R algorithm. As a result, precordial motion is obtained as one of the independent components.

Independent Component Analysis (ICA)

Multiple instances of surface chest motion obtained simultaneously from different markers contain different contributions from respiration and heart. It is assumed that these contributions are linearly mixed to form overall surface chest motion. It is also understood that none of these sources are Gaussian in nature. Furthermore, these contributions can be assumed to be independent in the temporal aspect (however, strict independence in not necessary31). These are the necessary conditions for ICA model25 to hold.

Let the motion from 8 markers be represented as x = {x1, x2, …, x8}T and the underlying sources (one of them corresponds to the chest motion component due to heart) be s = {s1, s2, …, s8}T, then these signals can be expressed in terms of ICA model as x = As, where A is the mixing matrix of order 8 × 8 that corresponds to the weights of the underlying source signals in the observed chest surface signals. It is assumed that the input vector x is pre-whitened (or uncorrelated) such that E{xxT = I}, where E{.} is the expectation operator. Pre-whitening is possible by a linear transformation 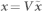Inline graphic33, where 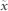Inline graphic is the raw (un-whitened) input vector and V = CD−1/2CT is the whitening matrix. C is the matrix of eigenvectors and D is the diagonal matrix consisting of eigenvalues of the raw input correlation matrix 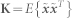Inline graphic. Whitening process significantly reduces the computational complexity by orthogonally transforming the mixing matrix34. One of the approaches to maximize the independence between estimated sources is to minimize the gaussianity for all the estimated sources. This approach is based on the central-limit theorem which states that the mixture of non-Gaussian sources tends to Gaussian. In FastICA, approximation of negentropy (differential entropy of estimated source and Gaussian random variable of same variance) is employed as a measure of gaussinaity32. The one-unit update equation ((where components or sources are found one by one) is given as33):

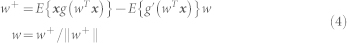graphic file with name srep05093-m4.jpg

where w is the weight vector corresponding to one of the sources y = wT x. g(u) and g′(u) are the first and second derivatives of the non-linear contrast function 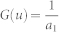Inline graphic log cosh a1u with a1 = 1 (for optimal parameter selection, see33).

Fast convergence speed, ability to separate sub-Gaussian sources (with negative kurtosis and flatter distribution than Gaussian31) and less sensitivity to parameters33 makes it a good choice for the source separation problem. After applying ICA, one of the 8 independent components (ICs) is obtained as the desired precordial motion. The precordial motion is identified (from other ICs) based on maximum relative power within the spectral range of heart beat. Further, Visual inspection is also performed to validate the selection.

ICA with reference

Conventional ICA algorithms (such as FastICA32) yield multiple independent components. Therefore, it becomes necessary to properly identify the desired source (precordial motion). If the number of undesired sources is more, the search for the desired source becomes computationally expensive27. Application of ICA with reference (ICA-R) is aimed towards automated extraction of desired source only. To achieve this goal the weight vector for the desired output component is optimized under one additional inequality constraint termed as closeness measure. The constrained contrast function is defined as27:

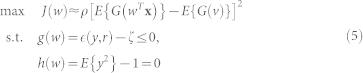graphic file with name srep05093-m5.jpg

where w is the weight vector of one component and J(w) is the objective function (approximation of negentropy) to be maximized with respect to w. x is the vector of pre-whitened observed signals and y = wT x is one source corresponding to w weight vector. ρ is a positive scaling constant for the objective function chosen as 1, whereas G() and a1 are defined above in section ICA. The equality constraint h(w) limits the variance of estimated source y equal to unity. The inequality constraint g(w) limits the closeness measure 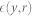Inline graphic (between the estimated source y and the reference signal r) to be less than the threshold ζ such that it follows the relationship:

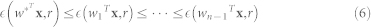graphic file with name srep05093-m6.jpg

for optimum vector w* for the desired output.

The closeness measures employed commonly are: i) Mean Square Error (MSE) and ii) Correlation between the reference signal and the estimated output at the current iteration27. However, these measures are very sensitive to the choice of the reference signal and the threshold selected. Therefore, appropriate selection of the reference signal is necessary to ensure the convergence for the desired signal.

The conventional way of generating reference signals includes determining the periodicity of the desired waveform and generating a simple pulse train having same period. However, the heart beat interval changes with time. Moreover, the correct phase offset for the reference signal has to be known in order to maximize the closeness between the reference signal and the cardiac component. Therefore, special measures are required for the reference generation.

ICA-R using Delayed Autocorrelation28

This method employs the second order statistics (correlation) to generate a reference signal for weak temporally correlated source signal. Several time-delays are identified which maximize the autocorrelation of the desired source. Based on these time delays, the desired source is roughly extracted, which is then employed as the reference signal for ICA-R.

The weight vector 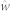Inline graphic for generating the reference signal 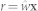Inline graphic is given as28

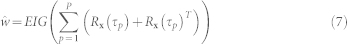graphic file with name srep05093-m7.jpg

The EIG() operator identifies the eigenvector corresponding to the maximum eigenvalue. The autocorrelation matrix of the pre-whitened input signals is given as Rx(τp) = E{xx(t − τP)T}. P is the number of time delays {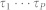Inline graphic} that maximize the autocorrelation of the desired source. In case of precordial motion, the average time period is considered as τ1 and P is set to unity. The average period is determined from the autocorrelation function of one of the whitened signals (identified by maximum relative power within the spectral range of heartbeat). The first peak of the autocorrelation at non-zero lag is set as τ1.

ICA-R using ECG

Synchronization observed between the cardiac source pattern and the QRS complex of corresponding ECG can be used to mitigate the phase effects and varying periodicity on the closeness measure. However, the QRS complex lacks the morphological similarity with the desired output component. To overcome this aspect, a new reference generation method is developed such that it incorporates the timing information of QRS complex together with the morphological characteristics of the desired output.

Chest displacement in the absence of respiration (breath hold maneuver) corresponds to the beating of the heart. Since our goal is to separate the precordial motion from respiratory dominant chest motion, the desired signal should have the same morphology as obtained from the breath hold maneuver. Moreover, each subject can have a different morphology of heart beat. Therefore, the subject-specific reference generation is required in this case. Hence, the incorporation of this breath-hold signal in reference generation can be an effective way for achieving morphological similarity.

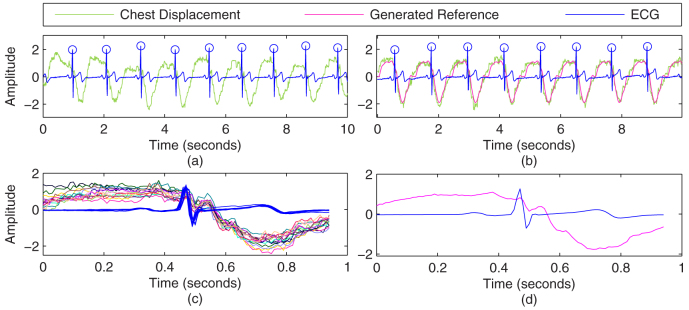
For this purpose, multiple attempts of breath hold maneuver were recorded from each subject. One such instance is shown in Fig. 8(a). All the pulses are averaged over a window length that is selected based on the average repetition of the heart beat pulses. For each heartbeat, a window is placed that is centered at each R-peak of ECG to segment the breath-hold chest displacement signal into single pulses. The resulting pulses and ECG waveform segments are overlaid and displayed in Fig. 8(c). The segmented pulses are then averaged to form a general template as shown in Fig. 8(d). To generate the reference signal, the general template is placed and repeated for each R-peak of the ECG signal. One instance of generating reference is shown in Fig. 8(b). For verification, original breath-hold chest displacement signal (for same subject but different trial that was not employed in formulating the general template) is shown as green trace in 8(b). It can be seen that the generated reference is fairly identical to the (test) breath hold signal and can yield best possible results with ICA-R.

Figure 8. Reference generation with ECG: (a) One instance of Breath hold segment, (c) Pulses of fixed length superimposed with R-peak of ECG in center, (d) Average of chest displacement pulses and ECG pulses shown in (c), (b) Reference generation for some other breath hold segment and comparison.

Figure 8

Open in a new tab

Author Contributions

K.C.V. devised the experimental protocol and experimental setup. G.S. performed all the experiments, wrote the manuscript and prepared all the figures. K.C.V. did proof reading and corrections for this manuscript.

Acknowledgments

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (Grant No. 2011-0023999).

References

  1. Gulley S., Rasch E. & Chan L. If we build it, who will come? working-age adults with chronic health care needs and the medical home. Med. Care 49, 149–155 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Pantelopoulos A. & Bourbakis N. G. Prognosis–A Wearable Health-Monitoring System for People at Risk: Methodology and Modeling. IEEE Trans. Inf. Technol. Biomed. 14, 613–621 (2010). [DOI] [PubMed] [Google Scholar]
  3. Tay F. E. H., Guo D. G., Xu L., Nyan M. N. & Yap K. L. MEMSWear-biomonitoring system for remote vital signs monitoring. J. Franklin Inst. 346, 531–542 (2009). [Google Scholar]
  4. Hao Y. & Foster R. Wireless body sensor networks for health monitoring applications. Physiol. Meas. 29, R27 (2008). [DOI] [PubMed] [Google Scholar]
  5. Abdelhafiz A. H. Heart failure in older people: Causes, diagnosis and treatment. Age Ageing 31, 29–36 (2002). [DOI] [PubMed] [Google Scholar]
  6. Patel S., Park H., Bonato P., Chan L. & Rodgers M. A review of wearable sensors and systems with application in rehabilitation. J. Neuroeng. Rehabil. 9, 1–17 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Pantelopoulos A. & Bourbakis N. G. A Survey on wearable sensor-based systems for health monitoring and prognosis. IEEE Trans. Syst. Man Cybern. Part C-Appl. Rev. 40, 1–12 (2010). [Google Scholar]
  8. Gonzalez-Valenzuela S., Chen M. & Leung V. C. M. Mobility support for health monitoring at home using wearable sensors. IEEE Trans. Inf. Technol. Biomed. 15, 539–549 (2011). [DOI] [PubMed] [Google Scholar]
  9. Chen L., Hoey J., Nugent C., Cook D. & Yu Z. Sensor-based activity recognition. IEEE Trans. Syst. Man Cybern. Part C-Appl. Rev. 42, 790–808 (2012). [Google Scholar]
  10. Paradiso R., Loriga G. & Taccini N. A wearable health care system based on knitted integrated sensors. IEEE Trans. Inf. Technol. Biomed. 9, 337–344 (2005). [DOI] [PubMed] [Google Scholar]
  11. Lee Y. & Chung W. Wireless sensor network based wearable smart shirt for ubiquitous health and activity monitoring. Sens. Actuator B-Chem. 140, 390–395 (2009). [Google Scholar]
  12. Pandian P. S. et al. Smart vest: Wearable multi-parameter remote physiological monitoring system. Med. Eng. Phys. 30, 466–477 (2008). [DOI] [PubMed] [Google Scholar]
  13. Bourke A. K., O'Brien J. V. & Lynos G. M. Evaluation of a threshold-based tri-axial accelerometer fall detection algorithm. Gait Posture 26, 194–199 (2007). [DOI] [PubMed] [Google Scholar]
  14. Coronato A. Uranus: A middleware architecture for dependable AAL and vital signs monitoring applications. Sensors 12, 3145–3161 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Andreev V. P. et al. Discrete event simulation model of sudden cardiac death predicts high impact of preventive interventions. Sci. Rep. 3, 1771 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Silva A. F., Carmo J. P., Mendes P. M. & Correia J. H. Simultaneous cardiac and respiratory frequency measurement based on a single fiber bragg grating sensor. Meas. Sci. Technol. 22, 075801 (2011). [Google Scholar]
  17. Groote A. D. E., Wantier M., Cheron G., Estenne M. & Paiva M. Chest wall motion during tidal breathing. J. Appl. Physiol. Respir. Environ. Exerc. Physiol. 83, 1531–1537 (1997). [DOI] [PubMed] [Google Scholar]
  18. Lindh W. Q., Pooler M., Tamparo C. D., Dahl B. M. & Morris J. Delmar's Comprehensive Medical Assisting: Administrative and Clinical Competencies [5th Edition] (Delmar Cengage Learning, Stamford, 2013). [Google Scholar]
  19. Ramachandran G. & Singh M. Three-dimensional reconstruction of cardiac displacement patterns on the chest wall during the P, QRS and T-segments of the ECG by laser speckle inteferometry. Med. Biol. Eng. Comput. 27, 525–530 (1989). [DOI] [PubMed] [Google Scholar]
  20. Lin J. C., Kiernicki J., Kiernicki M. & Wollschlaeger P. Microwave apexcardiography. IEEE Trans. Microw. Theory Tech. 27, 618–620 (1979). [Google Scholar]
  21. Mikhelson I., Bakhtiari S., Elmer T. & Sahakian A. V. Remote sensing of heart rate and patterns of respiration on a stationary subject using 94-GHz millimeter-wave interferometry. IEEE Trans. Biomed. Eng. 58, 1671–1677 (2011). [DOI] [PubMed] [Google Scholar]
  22. Dziuda L., Skibniewski F. W., Krej M. & Baran P. M. Fiber bragg grating-based sensor for monitoring respiration and heart activity during magnetic resonance imaging examinations. J. Biomed. Opt. 18, 057006 (2013). [DOI] [PubMed] [Google Scholar]
  23. Obeid D., Zaharia G., Sadek S. & Zein G. Microwave doppler radar for heartbeat detection vs electrocardiogram. Microw. Opt. Technol. Lett. 54, 2610–2617 (2012). [Google Scholar]
  24. Morgan D. R. & Zierdt M. G. Novel signal processing techniques for Doppler radar cardiopulmonary sensing. Signal Process. 89, 45–66 (2009). [Google Scholar]
  25. Comon P. Independent component analysis, a new concept? Signal Process. 36, 287–314 (1994). [Google Scholar]
  26. Jung T. P. et al. Removing electroencephalographic artifacts by blind source separation. Psychophysiology 37, 163–178 (2000). [PubMed] [Google Scholar]
  27. Lu W. & Rajapakse J. C. ICA with reference. Neurocomputing 69, 2244–2257 (2006). [Google Scholar]
  28. Zhang Z. L. Morphologically constrained ICA for extracting weak temporally correlated signals. Neurocomputing 71, 1669–1679 (2008). [Google Scholar]
  29. Srivastava G., Crottaz-Herbette S., Lau K. M., Glover G. H. & Menon V. ICA-based procedures for removing ballistocardiogram artifacts from EEG data acquired in the MRI scanner. Neuroimage 24, 50–60 (2005). [DOI] [PubMed] [Google Scholar]
  30. Jacobson M. Auto-threshold peak detection in physiological signals. In Proc. of the 23rd Ann. Int. Conf. of the IEEE EMBC, Istanbul. 10.1109/IEMBS.2001.1017206 (2001, OCT 25–28). [Google Scholar]
  31. Hyvarinen A., Karhunen J. & Oja E. Independent Component Analysis [Haykin, S. (ed.)] (Wiley, Hoboken, 2004). [Google Scholar]
  32. Hyvarinen A. & Oja E. A fast fixed-point algorithm for independent component analysis. Neural Comput. 9, 1483–1492 (1997). [Google Scholar]
  33. Hyvarinen A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural. Netw. 10, 626–634 (1999). [DOI] [PubMed] [Google Scholar]
  34. Hyvarinen A. & Oja E. Independent component analysis: algorithms and applications. Neural Netw. 13, 411–430 (2000). [DOI] [PubMed] [Google Scholar]
  35. Bakhtiari S., Sahakian A. V. et al. Compact Millimeter-Wave Sensor for Remote Monitoring of Vital Signs. IEEE Trans. Instrum. Meas. 61, 830–841 (2012). [Google Scholar]
  36. Mikhelson I. V. et al. Noncontact Millimeter-Wave Real-Time Detection and Tracking of Heart Rate on an Ambulatory Subject. IEEE T. Inf. Technol. Biomed. 16, 927–934 (2012). [DOI] [PubMed] [Google Scholar]
  37. Mikhelson I. V., Bakhtiari S., Elmer T. W. & Sahakian A. V. Remote sensing of patterns of cardiac activity on an ambulatory subject using millimeter-wave interferometry and statistical methods. Med. Biol. Eng. Comput. 51, 135–142 (2013). [DOI] [PubMed] [Google Scholar]
  38. Inan O. T., Etemadi M., Wiard R. M., Giovangrandi L. & Kovacs G. T. A. Robust ballistocardiogram acquisition for home monitoring. Physiol. Meas. 30, 169–185 (2009). [DOI] [PubMed] [Google Scholar]
  39. Di Rienzo M. et al. Wearable seismocardiography: Towards a beat-by-beat assessment of cardiac mechanics in ambulant subjects. Auton. Neurosci-Basic Clin. 178, 50–59 (2013). [DOI] [PubMed] [Google Scholar]
  40. Martin B. J. & Altman D. G. Statistical methods for assessing agreement between two methods of clinical measurement. Int. J. Nurs. Stud., 47, 931–936 (2010). [Google Scholar]
  41. Abrams J. Precordial motion in health and disease. Mod. Concepts. Cardiovasc. Dis., 49, 55–60 (1980). [PubMed] [Google Scholar]
  42. Morillo D. S., Ojeda J. L. R., Foix L. F. C. & Jimenez A. L. An Accelerometer-Based Device for Sleep Apnea Screening. IEEE T. Inf. Technol. Biomed., 14, 491–499 (2010). [DOI] [PubMed] [Google Scholar]
  43. Yoon J. W., Noh Y. S., Kwon Y. S., Kim W. K. & Yoon H. R. Improvement of Dynamic Respiration Monitoring Through Sensor Fusion of Accelerometer and Gyro-sensor. J. Electr. Eng. Technol., 8, 742–751 (2013). [Google Scholar]
  44. Tavakolian K., Blaber A. P., Ngai B. & Kaminska B. Estimation of hemodynamic parameters from seismocardiogram. Paper presented at Computing in Cardiology, Belfast. Missouri, USA: Computing in Cardiology [1055–1058] (2010, SEPT 26–29). [Google Scholar]
  45. Tavakolian K., Dumont G. A., Houlton G. & Blaber A. P. Precordial Vibrations Provide Noninvasive Detection of Early-stage Hemorrhage. Shock, 41, 91–96 (2014). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES