Thin-beam ultrasound overestimation of blood flow: how wide is your beam?

Abstract

It has been predicted that the development of thin-beam ultrasound could lead to an overestimation of mean blood velocity by up to 33% as beam width approaches 0% of vessel diameter. If both beam and vessel widths are known, in theory, this overestimation may be correctable. Therefore, we updated a method for determining the beam width of a Doppler ultrasound system, tested the utility of this technique and the information it provides to reliably correct for the error in velocity measurements, and explored how error-corrected velocity estimates impact the interpretation of in vivo data. Using a string phantom, we found the average beam width of four different probes varied across probes from 2.93 ± 0.05 to 4.41 ± 0.06 mm (mean ± SD) and with depth of insonation. Using this information, we tested the validity of a calculated correction factor to minimize the thin-beam error in mean velocity observed in a flow phantom with known diameter. Use of a correction factor reduced the overestimation from 39 ± 11 to 7 ± 9% (P < 0.05). Lastly, in vivo we explored how knowledge of beam width improves understanding of physiological flow conditions. In vivo, use of a correction factor reduced the overestimation of mean velocity from 23 ± 11 to −4 ± 9% (P < 0.05). Thus this large source of error is real, has been largely ignored by the early adaptors of Doppler ultrasound for vascular physiology studies in humans, and is correctable by the described techniques.

since the 1960s, it has been possible to measure the velocity of blood moving in an artery using a simple ultrasound transducer or probe embedded with both transmitter and receiver, based on the Doppler frequency shift that is induced when sound waves bounce off moving red blood cells (“Doppler” ultrasonography) (9). By the 1970s, ultrasound probes were developed that could perform Doppler ultrasound measurements of velocity and also generate images of blood vessels by analyzing the sound waves that echo back from the walls of the blood vessels (B-mode, or “echo” ultrasonography) (14). This combination of capabilities, known as “duplex” ultrasonography, provides the information needed to calculate blood flow through an artery, as blood flow is the product of mean velocity and cross-sectional area of the artery. This is sometimes referred to as volumetric blood flow, or arterial blood flow, and is most often expressed as milliliters of blood per minute. Modern clinical duplex ultrasound systems are widely used in medicine today to diagnose peripheral artery disease, among other pathologies of the peripheral vasculature. Due to its noninvasive nature, duplex ultrasound has tremendous potential to advance many areas of study in human physiology and biomedical research and has transitioned from only sparse utilization two decades ago, to being on the verge of mainstream research use, analogous to the widespread availability and use of metabolic carts. Likewise, recent research suggests that one ultrasound-based measure (known as “flow-mediated dilation”) may be a critical and modifiable cardiovascular risk factor (10). If so, we are likely to see a need for simple ultrasound-based clinical screening in the near future that quantify blood flow and shear stress. These growing markets dictate a closer evaluation of the quality of data derived from Doppler ultrasound as we shift paradigms from binary clinical decision making to quantitative assessment of more subtle physiology.

In clinical practice, it is more important to acquire high-resolution images in B-mode than to acquire accurate velocity measurements; thus most commercial ultrasound systems are designed to accommodate this prioritization. High image resolution has been achieved by designing ultrasound probes that emit a beam with a thin, finite width. These thin-width beams do not uniformly insonate the entire cross-sectional area of a large vessel, such as the femoral and brachial arteries, as illustrated in Fig. 1. When ultrasound probes emit a beam that is not wide enough to insonate the entire cross section of a vessel, the ultrasound system will not be able to measure some of the velocities at the slowest boundary layers approaching the vessel lamina. When the ultrasound system calculates an average velocity from the insonated portion, the slower velocities will not be included in the calculation, and the machine will render an overestimation of mean blood velocity. Thus, while thin-width beams provide crisp images, they may have a deleterious effect on the accuracy of blood flow estimates. Along these lines, most of the “classic” validation studies comparing Doppler ultrasound to blood flow determined by thermodilution in humans relied on earlier generation ultrasound systems (e.g., Vingmed model CFM 800) that likely did not have thin-beam technology (19). These early validation efforts cannot be generalized to later ultrasound systems.

Fig. 1.

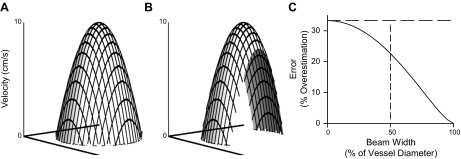
Model of parabolic flow as assessed by a finite-width ultrasound beam. A: predicted parabolic velocity profile during steady-state laminar flow across a vessel with a 4-mm diameter, a mean velocity of 5 cm/s, and a peak velocity of 10 cm/s [velocity at position r = peak velocity (1 − r²/radius²)]. B: velocity profile observed by an ultrasound beam with a beam width of 2 mm. While peak velocity remains 10 cm/s, the observed mean velocity would be 6.36 cm/s, representing a 22.6% overestimation of the true mean velocity. C: error in measuring mean velocity that is predicted by the equation of Evans (5) as a function of beam width. The horizontal dashed line highlights that the overestimation approaches an asymptote at 33% overestimation as the beam width becomes infinitely narrow relative to the vessel diameter. The vertical dashed line indicates the overestimation for the example in B, where the beam width is one-half the vessel diameter.

In the early 1980s, mathematical modeling by Evans predicted that the development of thin-beam ultrasound would lead to an overestimation of mean blood velocity of up to 33% as beam width approaches 0% of vessel diameter (5, 7, 8), as shown in Fig. 1C. This potentially large source of error has been largely ignored by the early adaptors of Doppler ultrasound for vascular physiology studies in humans, to the extent that beam width goes unreported and is neither acknowledged nor discussed in the overwhelming majority of such investigations. If both beam and vessel widths are known, in theory, this overestimation may be correctable using the equation first described by Evans (5) to estimate this error:

$$\text{Observed mean velocity}=\left[\frac{\overline{v}}{b{\left(1-b^2\right)}^{0.5}+{\sin }^{-1}\left(b\right)}\right]\left(\left[2\pi {\displaystyle {\int }_0^b}\left(y-y^3\right)dy\right]+\left\{4{\displaystyle {\int }_b^1}\left[\left(y-y^3\right){\sin }^{-1}\left(\frac{b}{y}\right)\right]dy\right\}\right)$$ (1)

where

$$b=\frac{\text{beam width}}{\text{vessel diameter}}$$

$$\overline{v}=\text{true mean velocity}$$

$$y=\frac{\text{distance r from the center of the vessel}}{\text{Radius of the vessel}}$$

Therefore, we undertook the current investigation to 1) update an older method for determining the beam width of a Doppler ultrasound system; 2) demonstrate the utility of this technique and the information it provides to reliably correct for the error in velocity measurements using the beam width to vessel diameter ratio; and 3) demonstrate how error-corrected velocity estimates impact the interpretation of in vivo data. In brief, we measured the beam width of four different probes using a novel application of a custom-built micro-positioner and a string phantom. Armed with these measurements of beam width, we tested the validity of a calculated correction factor to minimize the thin-beam error in mean velocity observed in a flow phantom with known diameter. Lastly, in vivo we explored how knowledge of beam width improves understanding of physiological flow conditions.

METHODS

Our present investigation took place in three stages. In phase 1, we updated older methodology and used it to determine the beam width of a Doppler ultrasound system (18, 22). In phase 2, we assessed the utility of this technique and the information it provides to reliably correct for the error in velocity measurements using the beam width-to-vessel-diameter ratio. Finally, in phase 3, we explored the use of these methods to correct in vivo data.

The Ultrasound Systems

We used four ultrasound systems for this study, representing a range of commercial units from different manufacturers and a range of technologies. For phase 1, we determined the beam width for the following probes/systems: 1) 10-MHz linear-array vascular probe model FLA-1A, GE Vingmed System 5 (Horton, Norway); 2) 7.0/5.0-MHz linear-array vascular probe model L7, Acuson 128XP/10-ART (Mountain View, CA); 3) 12-MHz linear-array vascular probe model 12L5, Terason t3000 (Burlington, MA); 4) a flat 4-MHz pulsed Doppler probe, Multigon 500M (Yonkers, NY). Due to logistical constraints, phase 2 used only the Vingmed and Acuson systems, and phase 3 used only the Vingmed system.

Phase 1: Determination of Beam Width

Rationale for determining beam width.

In order for the ultrasound probe to provide information regarding the velocity of blood at a given location, the probe must emit a beam that insonates the location at an angle such that the reflected sound returns to the receiver. Thus, while width of the transmitted field refers to the characteristic width of the outgoing emitted signal, “beam width” is the width of the region of interest that is insonated and returns a signal that is detected by the receiver and is a combination of the both the transmitted field width and the received field width.

Physical configuration of the technique.

We measured each probe's beam width using a computer-controlled micro-positioner stepping unit and a custom string phantom, which consisted of a silicon O-ring filament moving at a constant linear velocity. Room temperature (20°C) water was the medium for ultrasound propagation. The stepping unit was equipped with a clamp that securely held the ultrasound probe above the string phantom such that the long axis of the ultrasound probe was parallel to the string phantom, and the insonation angle was 60°. The ultrasound gate width was set to measure at the depth of the string phantom, and the power settings were adjusted to avoid saturation of the Doppler signal when the probe was directly over the string phantom. The stepping unit moved the probe horizontally (perpendicular to the string phantom) in 0.068-mm increments, pausing between steps to allow for stable measurements of the Doppler-shifted return signal. Using custom software (built in LabView version 10.0f2, 2010, National Instruments, Austin, TX), we simultaneously controlled the stepping unit and measured the sound pressure level (i.e., the volume) of the Doppler-shifted signal by calculating the root mean square of the audio signals available on the various ultrasound systems, such that we generated a plot of probe position vs. the magnitude of the returned signal, as shown in Fig. 2A. This is an adoption of older methods that are established in the ultrasound literature (18, 22). We completed five to seven trials with each ultrasound probe at each of four depths: 1, 2, 3, and 4 cm, varying the vertical distance between the probe and the string phantom.

Fig. 2.

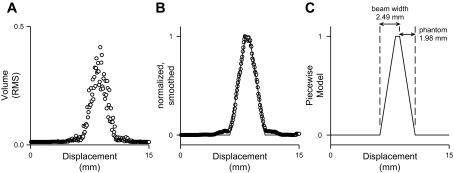
Representative data for determination of beam width. A: raw data [the root mean square (RMS) volume of the returned signal] from one trial obtained during phase 1. B: the same data after normalization and smoothing, with the piecewise model solution superimposed. C: the piecewise model solution with the beam width and phantom width indicated.

Mathematical model.

Raw values from each trial were graphed as a function of probe position (Fig. 2A), smoothed (moving average of 7 steps) and normalized (Fig. 2B), and fit to a piecewise linear model (modeled in Mathematica 8.0, Wolfram Research, Champaign, IL) that consisted of five zones (Fig. 2C) as follows:

$$y=\left\{\begin{array}{c}0,\text{if}\hspace{0.17em}x<\text{edge}\\ \frac{x-\text{edge}}{\text{phantom}},\text{if}\hspace{0.17em}x\ge \text{edge and}\hspace{0.17em}x<\text{edge}+\text{phantom}\\ \text{1, if}\hspace{0.17em}x\ge \text{edge}+\text{phantom and}\hspace{0.17em}x<\text{edge}+\text{beam}\\ \text{1}-\frac{x-\left(\text{edge}+\text{beam}\right)}{\text{phantom}},\text{if}\hspace{0.17em}x\ge \text{edge}+\text{beam and}\hspace{0.17em}x<\text{edge}+\text{beam}+\text{phantom}\\ \text{0, if}\hspace{0.17em}x\ge \text{edge}+\text{beam}+\text{phantom}\end{array}\right\}$$ (2)

where x is the horizontal displacement of the probe, edge is the location of the leading edge of the string phantom, beam is the beam width, and phantom is the phantom width, all in mm.

The model assumed that beam width was larger than the phantom width, the distance from the initial point of rise to the end of the plateau was equivalent to beam width, and the distance of either rising or falling phase was equivalent to phantom width. Thus the model parameters when solved provide estimates of both beam width and phantom width, as shown in Fig. 2C. Analysis was repeated at each depth for each probe. In turn, this value for beam width was used to determine vessel diameter-specific correction factors used in phase 2.

Phase 2: Application of Correction Factor In Vitro

Rationale for using a flow phantom.

After measuring the beam width of each of the ultrasound probes in phase 1, we compared Doppler mean velocities to simultaneously acquired half-peak velocities acquired from a flow phantom. The rationale for this in vitro comparison is that half-peak and mean velocities should have a 1-to-1 ratio if a parabolic flow profile is maintained during steady-state flow conditions, and this provides a straightforward means to assess the utility of correction factors derived from phase 1.

Physical configuration.

The flow phantom consisted of a section of taigon tubing (inner diameter 7.6 mm), supplied by a high-pressure reservoir via a flow-regulating valve. In turn, the flow phantom fed into a collecting reservoir hung from a force transducer to measure the instantaneous weight (and hence, volumetric flow) through the taigon tubing in the phantom. The system was perfused with a cornstarch suspension (10 g/l in water) as an echogenic surrogate for blood (12), and room temperature (20°C) water was the medium for ultrasound propagation outside of the tubing. A clamp securely held the ultrasound probe above the flow phantom such that the long axis of the ultrasound probe was parallel to the tubing, depth was 2 cm, and insonation angle was 60°. This angle of insonation is commonly used in human studies for linear-array vascular probes (e.g., Refs. 2, 17, 20). The ultrasound gate-width was set to measure the full width of the flow phantom, and the power settings were adjusted to avoid saturation of the Doppler signal.

Doppler signal acquisition.

Using custom software (built in LabView version 11.0.1f1, 2011, National Instruments, Austin, TX), we simultaneously measured the mean and peak frequency of the Doppler-shifted signal, by first calculating the power spectrum of the audio signals available on the various ultrasound systems. For each flow level, we measured the time-averaged mean and peak frequency during stable steady-state flow, which was repeated six times at each of five ranges of flow. We converted mean and peak frequencies into mean and peak velocities, respectively. Lastly, we calculated corrected mean velocities using a finite-beam correction factor expressed in the following equation, which we derived from the work of Evans (5). It is worth noting that Evans derived the original equation shown above by analysis of the fraction of each laminar, which is intersected by the beam. We were able to arrive at the same mathematical solution by integration across the section of the velocity profile that would be observed by the narrow-beam ultrasound, as illustrated in Fig. 1B.

$$\mathrm{Finite}\hspace{0.17em}\mathrm{Beam}\hspace{0.17em}\mathrm{Correction}\hspace{0.17em}\mathrm{Factor}\hspace{0.17em}\begin{array}{c}=100/\left\{\left[\frac{100}{b{\left(1-b^2\right)}^{0.5}+\text{ArcSin}\left(b\right)}\right]\left(\left[2\pi {\displaystyle {\int }_0^{\text{b}}}\left(y-y^3\right)dy\right]+\left\{4{\displaystyle {\int }_b^1}\left\{\left(y-y^3\right)\left[\text{ArcSin}\left(\frac{b}{y}\right)\right]\right\}dy\right\}\right)\right\}\end{array}$$ (3)

where

$$b=\frac{\text{beam width}}{\text{vessel diameter}}$$

$$y=\frac{\text{a distance r from the center of the vessel}}{\text{Radius of the vessel}}$$

Note that this equation provides a correction factor of 1.000 when beam width is equal to the diameter of the vessel (b ≥ 1), and 0.750 when beam width is infinitely narrow (b = 0). We have provided as Supplemental Material a lookup table with solutions for Eq. 3 across the full range of values for b in Microsoft Excel format.¹

Phase 3: Application of Correction Factor In Vivo

Rationale for in vivo test.

We wanted to explore the functionality of using a finite beam correction factor on data obtained in vivo, to demonstrate how error-corrected velocity estimates impacted the interpretation of in vivo data and whether they improved estimates of limb blood flow. We also wanted to explore how knowledge of beam width improved understanding of physiological flow conditions. In particular, would this approach provide insight into the generalizability of the Poiseuille equations to oscillatory flow of non-Newtonian blood, and could it differentiate between parabolic and nonparabolic flow states? Along these lines, if the blood velocity profile is parabolic in vivo, then it would be acceptable to use the half-peak velocity to calculate blood flow (which has become a common practice).

In vivo studies.

We analyzed existing data from an ongoing study on femoral and brachial artery blood flow in which we had simultaneously measured the time-averaged mean and peak frequency of the Doppler-shifted signal, as described above (insonation angle 60°), along with femoral/brachial artery diameter and depth using the Vingmed system. Vessel diameter was measured during diastole, the mean and peak velocities were averaged across time, including both retrograde and anterograde velocities. The ongoing study is approved by the University of Oregon Institutional Review Board and conforms to the Declaration of Helsinki. All subjects gave written, informed consent before participation in the study. We analyzed 51 records obtained in eight individuals under resting conditions or with limb heating to provide a wider range of blood velocities.

Statistical Analysis

We used SPSS version 21.0 (IBM, Armonk, NY) to compare “corrected” and “uncorrected” variables via paired t-test as appropriate. Differences were considered significant when P < 0.05. Values are means ± SD, unless otherwise noted.

RESULTS

Phase 1: Determination of Beam Width

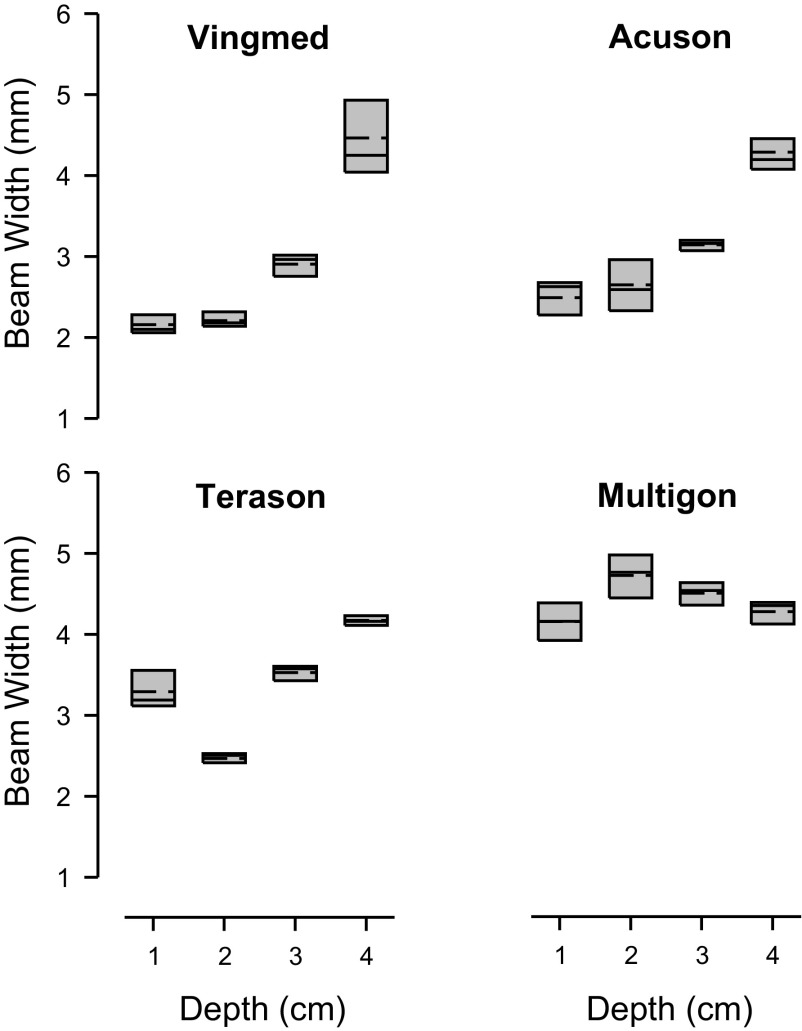
The beam width for the four ultrasound systems that were investigated in phase 1 are presented in Fig. 3. Beam width varied across ultrasound system as well as depth on insonation (both P < 0.05). Multigon had the widest beam width, which averaged 4.41 ± 0.06 mm (mean ± SD) across all depths (P > 0.05 vs. others). Vingmed had the narrowest beam width, which averaged 2.93 ± 0.05 mm, but doubled from its lowest value at 1-cm depth to its widest value at 4-cm depth. Each system was affected by depth, but the pattern varied as illustrated in Fig. 3. To put the beam widths into perspective, Table 1 shows the estimated error (based on Eq. 1) and the finite beam correction factor (based on Eq. 3) that would result in measuring from two representative sized arteries at a depth of 2 cm for each ultrasound probe.

Fig. 3.

Box plots of the beam width for four ultrasound systems. Bam width was determined at each of four depths as indicated. Boundary of the box closest to zero denotes 25th percentile, solid line within the box denotes median, dashed line denotes mean, and the boundary of the box farthest from zero denotes 75th percentile. Median beam width at each depth was used for subsequent correction of mean velocities.

Table 1.

Estimated error for representative sized arteries

		Predicted Overestimation of Mean Velocity, %		Correction Factor
	Beam width, mm	4-mm vessel diameter	8-mm vessel diameter	4-mm vessel diameter	8-mm vessel diameter
Infinitely narrow beam	0	33	33	0.750	0.750
Vingmed	2.21	20	30	0.831	0.769
Terason	2.47	17	29	0.851	0.774
Accuson	2.64	15	29	0.867	0.778
Multigon	4.72	0	19	1.000	0.842
Infinitely wide beam	∞	0	0	1.000	1.000

Phase 2: Application of Correction Factor In Vitro

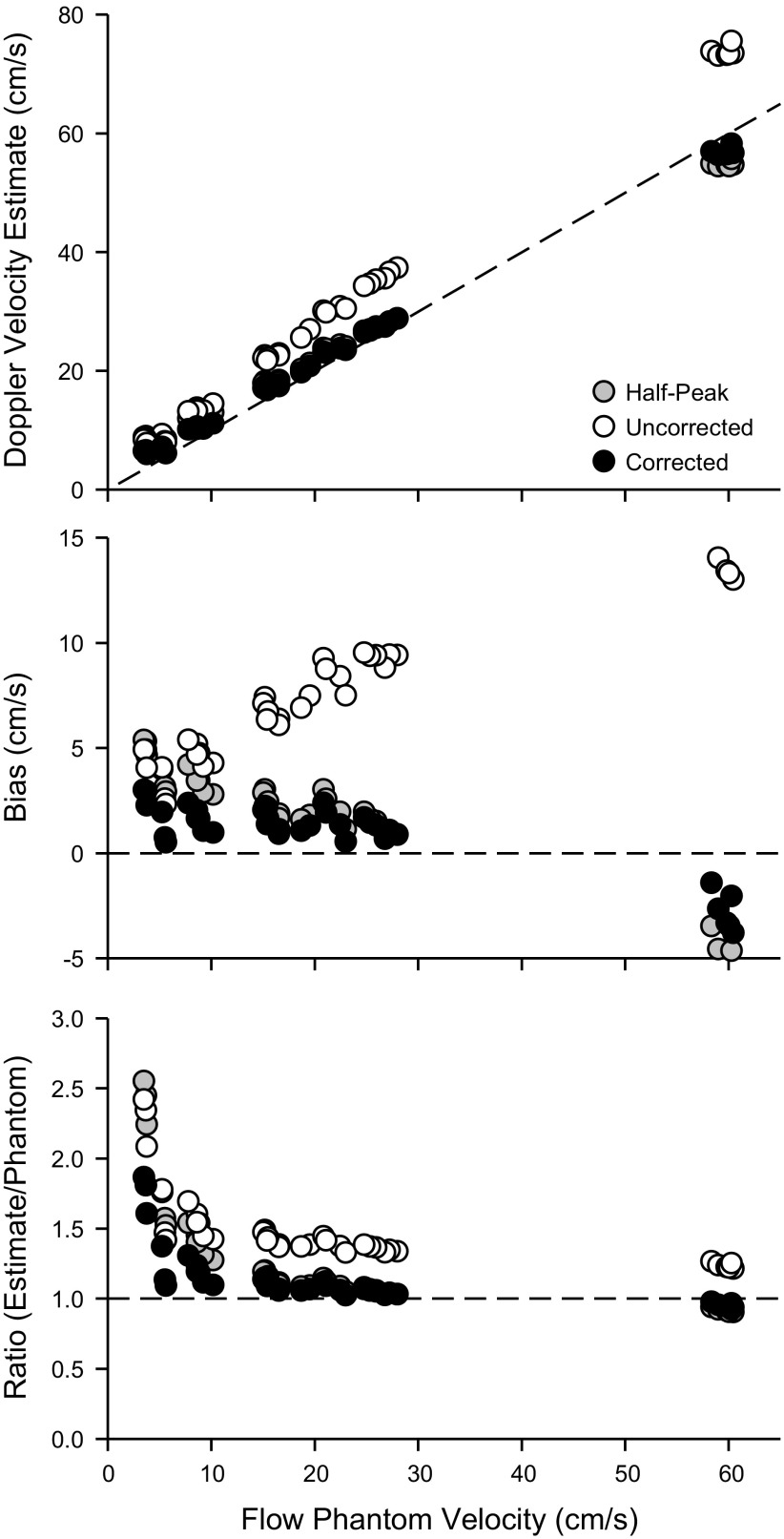
After measuring the beam width of each of the ultrasound probes in phase 1, we compared Doppler mean velocities to simultaneously acquired half-peak velocities acquired from a flow phantom. As noted above, due to logistical constraints, phase 2 used only the Vingmed and Acuson systems. Due to the similarity of outcomes for phase 2 with these two systems, we only present results for the Vingmed. The rationale for this in vitro comparison is that half-peak and mean velocities should have a 1-to-1 ratio if a parabolic flow profile is maintained during steady-state flow conditions, and this provides a straightforward means to assess the utility of correction factors derived from phase 1. Figure 4 (top) compares uncorrected mean velocity, corrected mean velocity, and half-peak velocity (all derived from Doppler velocity estimates) vs. flow phantom mean velocity, which was derived from the volumetric flow and internal diameter of the flow phantom. It is clear that uncorrected Doppler velocity estimates diverge from the line of identity (dashed line). In contrast, there is a high level of similarity between the half-peak and the corrected Doppler velocity estimates, both of which fall close to the line of identity. Likewise, the bias of the Doppler velocity estimates relative to the flow phantom velocity (Fig. 4, middle) show an increasing bias for the uncorrected Doppler velocity estimate vs. a small and largely consistent bias for the half-peak and the corrected Doppler velocity estimates. We do note some discrepancies in these trends, which appear at the lower flow phantom velocities, which we believe are representative of limitations in the ability of our particular flow phantom system to produce reliable flows at these lower rates. Above 10 cm/s, the ratio of Doppler velocity estimates to flow phantom velocity (Fig. 4, bottom) averaged 1.39 ± 0.11 to 1 for the uncorrected Doppler velocity estimate, vs. 1.12 ± 0.17 to 1 for the half-peak and 1.07 ± 0.09 to 1 for the corrected velocity estimates. Thus the overall pattern provided by Fig. 4 supports the notion that, during moderate to higher flows in the flow phantom system, 1) laminar parabolic flow velocities are likely to be present such that the mean velocity is equal to the half-peak velocity; 2) uncorrected Doppler mean velocity markedly overestimates both the true mean (by 39 ± 11%) and the half-peak velocity (by 25 ± 8%); 3) corrected Doppler mean velocity estimates the true mean (within 7 ± 9%) and the half-peak velocity (within 4 ± 6%) under these conditions (both P < 0.05 vs uncorrected); and 4) the uncorrected Doppler mean velocity is ∼1.4 times the half-peak velocity in the presence of laminar parabolic flow velocities, and this is attributable to the narrow beam width effect.

Fig. 4.

In vitro Doppler mean velocity estimates. Top: uncorrected mean velocity (open circles), corrected mean velocity (solid circles), and half-peak velocity (shaded circles) vs. flow phantom mean velocity. Dashed line represents the line of identity. Middle: bias between uncorrected mean velocity, corrected mean velocity, and half-peak velocity relative to flow phantom mean velocity (calculated as Doppler estimate minus flow phantom mean velocity). Dashed line represents bias of 0. Bottom: ratio of the Doppler estimate to the flow phantom mean velocity. Dashed line represents a ratio of 1 to 1.

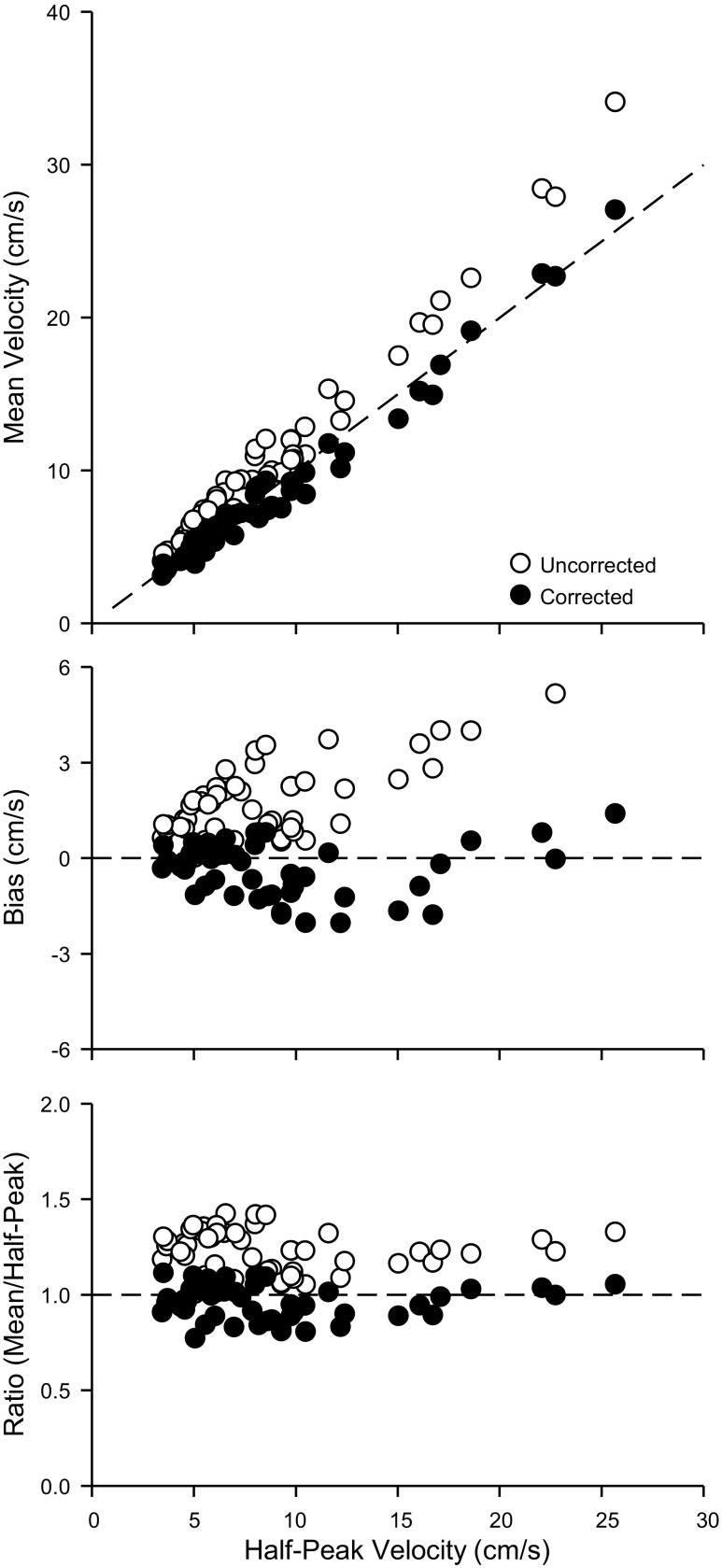
Phase 3: Application of Correction Factor In Vivo

We analyzed 51 records obtained in eight individuals to explore the functionality of using a finite beam correction factor on data obtained in vivo. The mean vessel depth was 1.43 ± 0.21 cm, the mean vessel diameter was 7.59 ± 1.81 mm, and the mean correction factor was 0.779 ± 0.024. Compared with the line of identity (Fig. 5, top), uncorrected mean values were higher than half-peak velocities, and corrected mean velocities were somewhat lower than half-peak velocities. This observation is also apparent when graphed as bias (Fig. 5, middle). Finally, the ratio of mean to half-peak velocities (Fig. 5, bottom) was higher (P < 0.05) for uncorrected velocities (1.23 ± 0.11 to 1) vs. corrected velocities (0.96 ± 0.09 to 1), with the ratio of corrected velocities being what one would predict for laminar parabolic flow (1 to 1). We do note some divergence from these ratios at the lowest velocities, which may represent velocity profiles that are more pluglike, and less parabolic, than what is observed at higher velocities. If one presumes there are uniform parabolic velocities throughout these data, then the uncorrected mean velocities overestimate by 23 ± 11% compared with −4 ± 9% for the corrected mean velocities (P < 0.05, corrected vs uncorrected). The value of 23% is similar to what would be predicted by Eq. 1 for the mean vessel diameter and beam width under these conditions (28%). For sake of comparison to the literature, the ratios of peak to mean velocities were 1.64 ± 0.15 to 1 for uncorrected velocities and 2.11 ± 0.20 to 1 for the corrected velocities, with the ratio of corrected velocities being what one would predict for laminar parabolic flow (2 to 1).

Fig. 5.

In vivo Doppler mean velocity estimates. Top: uncorrected mean velocity (open circles) and corrected mean velocity (solid circles) vs. half-peak velocity. Dashed line represents the line of identity. Middle: bias between uncorrected mean velocity and corrected mean velocity relative to half-peak velocity (calculated as corrected or uncorrected mean minus half-peak). Dashed line represents bias of 0. Bottom: ratio of the uncorrected or corrected mean velocity to the half-peak velocity. Dashed line represents a ratio of 1 to 1.

DISCUSSION

Thin-beam error is a practical concern that can be minimized by multiplying overestimated mean velocity by a correction factor. The current problem is that investigators fail to know of this issue, or do not have access to beam width specifications of their ultrasound systems. We undertook the current investigation to 1) update an older method for determining the beam width of Doppler ultrasound systems; 2) demonstrate the utility of this technique and the information it provides to reliably correct for the error in velocity measurements using the beam width to vessel-diameter ratio; and 3) demonstrate how error-corrected velocity estimates impact the interpretation of in vivo data. These three goals have generated three sets of primary observations. First, we found that beam width varies across ultrasound probes, but in general it is far from the theoretical extremes of behaving like an infinitely narrow or an infinitely wide beam. Most (but not all) of the probes we studied are narrower than a typical brachial artery, and all were narrower than a typical femoral artery. We also noted that beam width is affected by depth of insonation in measureable, but unpredictable patterns. Second, we demonstrated that knowledge of beam width provides the means to calculate a correction factor that minimizes the thin-beam error in mean velocity observed in a flow phantom with known diameter. Use of a correction factor reduces the overestimation by ∼30 percentage points. Third, in vivo use of the correction factor reduced the overestimation of mean velocity by ∼30 percentage points. It also corrects the peak-to-mean velocity ratio from one consistent with pluglike flow (1.6 to 1) to one consistent with laminar parabolic flow (2 to 1). Thus the thin-beam effect is a legitimate source of error, has been largely ignored by the early adaptors of Doppler ultrasound for vascular physiology studies in humans, and is correctable by the described techniques. Lastly, correction of this effect leads to an improved understanding of physiological flow conditions.

Hasn't Doppler Ultrasound Been Validated Against Thermodilution Blood Flow?

There are several well-respected studies comparing Doppler ultrasound to blood flow determined by thermodilution in humans. Rådegran (19) used an early-generation ultrasound systems (e.g., Vingmed model CFM 800) that likely did not have thin-beam technology. According to Rådegran, this system used a 7.5-MHz annular-array probe with a diameter of 11.5 mm (although it is possible that 11.5 mm refers to the external dimensions of the probe, the maximal gate width for pulsed Doppler measures, or the width of the beam). It appears that this same ultrasound machine was subsequently used by Wray et al. (25) and by Brothers et al. (3). All three studies reported a high degree of similarity of blood flow estimates for thermodilution and Doppler ultrasound in the femoral artery during single-leg knee extension exercise. These classic validation studies have been used to support the broader use of Doppler ultrasound for regional blood flow in humans by many investigators. However, these validation efforts, conducting on a single ultrasound machine with older probe technology, cannot be generalized to later ultrasound systems using thin-beam linear-array vascular probes. We have been unable to find evidence that modern thin-beam linear-array probes have undergone any direct validation against thermodilution.

Determining Beam Width

Transmitted field width of the outgoing ultrasound wave from a probe has traditionally been determined by use of a hydrophone target immersed in water or the “schlieren” method, which depends on light refraction in water (4). Neither of these methods is readily available to the typical vascular researcher due to their cost and complexity, nor do they determine the Doppler beam width, as they are designed to measure the transmission field. In contrast, we were able to construct constant-velocity string-phantom and computer-controlled micro-positioner on a minimal budget that is capable of determining the beam width for Doppler ultrasonography in a way that could be replicated by most laboratories, by updating methods first used several decades ago (22). Our estimates for beam width are in agreement with the few reports we have identified in which investigators have used a hydrophone to explore the transmission field of commercial Doppler ultrasounds (13, 21) and those who have used string phantoms (22). In light of the differences observed across the four ultrasound probes in the present study, it would be prudent for investigators to directly determine the beam width characteristics of the system they use, and to do so at a variety of depths that covers the in vivo insonation depths that they commonly encounter in their research.

Correcting the Thin-Beam Problem

There have been two prior attempts to create a mathematical fix to the thin-beam problem. First, Willink and Evans (23, 24) proposed an alternative calculation of mean blood velocity from the Doppler frequency spectrum that was based on the assumption of an infinitely narrow beam. This alternative calculation may be beneficial when using a “relatively thin” beam with a “relatively wide” vessel, but underestimates mean velocity by 25% as the beam width approaches the width of the vessel. It is worth noting that one must have access to the frequency spectrum data to use this approach, as it calls for an a priori modification of the calculation for mean frequency, whereas our correction method can be applied post hoc either to the mean frequency or mean velocity measurement. It does not appear that the Willink and Evans method of dealing with the thin-beam problem has seen much implementation. Second, Fei and coworkers (7, 8) proposed a correction for thin-beam ultrasound based on comparison of velocity estimates derived by two divergent methods: uniform insonation (analogous to the standard pulsed Doppler methodology) vs. the velocity profile method (the basis for color Doppler methodology). It does not appear that this method has been translated from theory to application. In contrast to these prior attempts to fix the thin-beam problem, what we propose is perhaps more “brute force” in math, less elegant in theory, but high in utility. Both in vivo and in vitro, we found that the thin-beam error estimated by the equation first described by Evans (5) was evident. Furthermore, in both settings we were able to correct the thin-beam error by applying a simple linear correction factor based on knowing the vessel diameter and the depth-specific beam width.

Possible Limitations to the Proposed Approach

Our model for calculating beam width, as illustrated in Fig. 2, treats the transmission and receiving fields of the ultrasound beam as finite and rectangular. This is likely a simplification of the real characteristics of the transmitted beam and the reflected Doppler-shifted beam. More sophisticated approaches, such as use of a hydrophone, can elude great detail regarding the shape of the transmission profile, but not the combined shape of the transmission and receiving fields. Despite this simplification, our resulting estimates of beam width appear valid for the purpose of generating a correction factor.

Our calculation of a correction factor for thin-beam is based on several assumptions that underlie the model illustrated in Fig. 3. First, we assume that velocities are axisymmetric around the center of the vessel. This is inherent in most fluid models for blood flow and Doppler ultrasound. Second, we assume that the velocity profile is parabolic. When this assumption holds true, the corrected mean velocity will be one-half the peak velocity, as we found in vitro. When the velocity profile diverges from parabolic, the corrected mean velocity will no longer be one-half the peak velocity, which we have observed under low-flow states in vivo. This is a concern, as under these conditions, neither the peak nor the corrected mean will be valid estimates of the true mean velocity across the vessel. Under such conditions, a more sophisticated approach, such as a velocity profile method or speckle tracking, may prove necessary. It is worth noting that use of the correction factor and comparison of the corrected mean vs. half-peak velocities provides for an innate test of the assumption. Such an innate test of the parabolic assumption is not readily available by other means.

Other sources of error associated with Doppler ultrasound that are well-documented include spectral broadening, insonation angle misalignment, misalignment of the ultrasound beam with the center of the vessel, and high-pass filtering that may filter out slower blood velocities. The impact of spectral broadening on peak velocity measurements becomes augmented at insonation angles >60° (11). The collective impact of these sources of error would appear minimal in our in vitro studies in which Doppler estimates of blood flow are similar to those derived from a flow phantom. It is more challenging to rule out misalignment during in vivo studies.

Finally, the in vivo velocity measurements from phase 3 of the present study were not validated using thermodilution techniques. While the results suggest that thin-beam error creates artificially inflated velocity values in vivo, this is clearly the case for measures of mean velocity relative to peak velocity.

Implications for Flow Measures and Shear Stress Estimates

The results of the present study, in support of extensive theoretical work on thin-beam ultrasonography, suggest that many of the estimates of arterial blood flow in the literature (based on uncorrected mean velocity estimates) are high by 15–30%. The degree to which these published values overestimate true flow values are affected by vessel depth, vessel diameter, and the ultrasound probe characteristics. It is intriguing to think that many of the conditions in which blood flow is believed to be reduced (e.g., aging) are conditions in which conduit arteries are also of smaller diameter and thus would exhibit lesser overestimation than the corresponding “control” group. One would likewise predict similar overestimation of reported shear rates in the literature when they have been determined from Doppler estimates of mean blood velocity.

Whether or not physiological blood velocity profiles are parabolic across all conditions in vivo remains unclear. This is an important consideration for the following reason. If velocity profiles are consistently parabolic across physiological conditions, then it is appropriate to use half-peak velocity to estimate the true mean velocity and to calculate flow and shear rates. It is worth noting that the consistency of parabolic profiles within the pulsatile cardiac cycle is not the concern, as, irrespective of how complex the instantaneous velocity profiles may be, as long as the time-averaged velocity profile is parabolic, the theory remains the same, as noted by Evans (6). The present study suggests that time-averaged in vivo flow is parabolic much of the time, but, even in this data set, representative of resting and postexercise recovery in a large conduit vessel, there appear to be divergences from parabolic flow, toward more pluglike flow, at the lower end of the blood flow spectrum.

Previously, several groups have measured mean and peak blood velocity with Doppler ultrasound with the goal of assessing the presence or absence of parabolic velocity profiles in human conduit vessels. Ade et al. (1) measured mean and peak blood velocity in both the brachial and femoral arteries across a variety of physiological stressors and concluded that both antegrade and retrograde profiles deviate from the parabolic form. However, their reports of peak-to-mean velocity ratios of ∼1.6 (brachial) and 1.7 (femoral) to 1 would “correct” to 2 to 1 ratios (i.e., parabolic), if mean velocity were overestimated by ∼20%, consistent with the present study. Likewise, in two analyses, Osada and Rådegran (15, 16) reported pluglike velocities in the femoral artery, based on peak-to-mean velocity ratios that were less than 2 to 1. However, it is unclear how wide a beam was used in these investigations, which appear to have used the same older system as discussed above. It is worth noting that these prior studies (1, 15, 16) each found changes in the peak-to-mean ratio across conditions that may suggest that blood flow is not consistently parabolic. Alternatively, changes in vessel diameter (relative to probe beam width) could contribute to this variation in the peak-to-mean ratio. Until such time as more extensive data has been analyzed, specifically data that has been beam width corrected, the question of whether or not conduit vessel velocity profiles are consistently parabolic is an unanswered concern.

Practical Suggestions

At present, we would suggest the following guidelines and recommendations that we believe are the logical extension of this work.

First, when using Doppler ultrasound to determine blood flow or shear rate in conduit vessels, such as the brachial or femoral artery in humans, investigators should document (and report) the depth and diameter of the blood vessel. This information, along with the specifications of the ultrasound probe, would allow for postpublication exploration by others to assess the potential impact of thin-beam ultrasound on the results. If relative changes in flow or shear are the primary outcome variable, it may be acceptable to merely document these variables without correcting for the beam width effect (but please note the limitation when describing methods; do not continue to ignore this effect).

Second, when absolute rates of flow or shear are the outcome variable of interest (rather than relative changes in flow or shear), investigators should determine the beam width of their ultrasound system and use a beam width correction factor, as described in the present investigation. This is also a critical recommendation for any investigation of velocity profiles. We believe that we have described an approach to determining the beam width correction factor that is inexpensive and simple to execute. However, we also suggest that an alternative approach to correcting for the thin-beam effect may be possible, based on calibration of the Doppler ultrasound against flow phantoms over a range of diameters and depths. If one presumes that corrected mean velocity is equal to half-peak velocity, one could back-calculate the appropriate correction factor for representative depths and vessel diameters. As an example, the back-calculated correction factor for the data in Fig. 4 is 0.804 ± 0.056, which is close to the correction factor of 0.771 we derived from beam width via Eq. 3. A limitation of this approach is that not many laboratories are instrumented for simultaneous peak and mean velocity measurements.

In An Ideal World

As indicated in the Introduction, most commercial ultrasound systems are designed to accommodate the priority of high image resolution via use of narrow-width beams that do not uniformly insonate the entire cross-sectional area of a large vessel, such as the femoral and brachial arteries. In the ideal world, novel ultrasound probes could be designed that are sufficiently narrow, relative to conduit vessel diameter, that one can presume them to be infinitely narrow and use a standard correction factor of 0.750 (e.g., Table 1). Alternatively, a novel ultrasound probe could use thin-beam technology for imaging, and wide beam for Doppler velocity estimates. The trade-off would be the challenges inherent in targeting a conduit artery for measurement of blood velocity with a large beam probe, and not inadvertently sampling from adjacent veins with opposing blood flow. However, we routinely use gating of pulsed ultrasound to target the correct depth and width of conduit vessels in a single plane. This approach might be replicated in a second plane or cross-sectional view of the vessel to allow matching of the sampling region to the cross section of the vessel.

In a simpler world, we may find that blood flow in conduit vessels, such as the brachial or femoral artery, is sufficiently close to the parabolic ideal, and that peak velocity can become a gold standard for estimating mean velocity. We believe that our present investigation lays the groundwork for making that determination, and that too many investigators have prematurely adapted this method with insufficient testing of its assumptions. Similarly, further validation of thin-beam flow measurement with thermodilution or other gold standard measures appears warranted.

Conclusions

It has long been suggested that Doppler ultrasound systems with modern thin-beam probes are biased toward overestimation of blood flow rates. Similarly, fluid dynamic models suggest that adequate knowledge of ultrasound probe characteristics, such as beam width, would allow correction for this overestimation. We have demonstrated the utility of using a beam width correction factor to adjust for thin-beam overestimation of blood flow. These methods are likely to be of interest to anyone engaged in the use of Doppler ultrasound to address physiological questions regarding blood flow and shear rate in the conduit vessels of humans.

GRANTS

This research was supported in part by a Summer Research Award (University of Oregon) and grants from the American Heart Association, Grant-in-Aid 11GRNT5490000, and National Heart, Lung, and Blood Institute Grant HL-115027.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: T.M.B. and J.R.H. conception and design of research; T.M.B., D.C.S., and J.R.H. performed experiments; T.M.B., D.C.S., and J.R.H. analyzed data; T.M.B. and J.R.H. interpreted results of experiments; T.M.B. and J.R.H. prepared figures; T.M.B. and J.R.H. drafted manuscript; T.M.B., D.C.S., and J.R.H. edited and revised manuscript; T.M.B., D.C.S., and J.R.H. approved final version of manuscript.