Homeostasis of functional maps in active dendrites emerges in the absence of individual channelostasis

Significance

Voltage-gated ion channels and their subcellular localization profiles mediate several continuous maps of neuronal physiological properties and confer astounding computational capabilities on single neurons. How do neurons with complex morphologies maintain these functional maps despite constant turnover of and plasticity in the ion channels that mediate them? We addressed this question through a computational framework spanning channels and measurements from the cell body and dendrites of hippocampal neurons. Our results demonstrate that individual channel properties or their densities need not be maintained at constant levels in achieving overall homeostasis of several coexistent functional maps. We suggest collective channelostasis, where several channels regulate their properties and expression profiles in an uncorrelated manner, as an alternative for accomplishing homeostasis of functional maps.

Abstract

The maintenance of ion channel homeostasis, or channelostasis, is a complex puzzle in neurons with extensive dendritic arborization, encompassing a combinatorial diversity of proteins that encode these channels and their auxiliary subunits, their localization profiles, and associated signaling machinery. Despite this, neurons exhibit amazingly stereotypic, topographically continuous maps of several functional properties along their active dendritic arbor. Here, we asked whether the membrane composition of neurons, at the level of individual ion channels, is constrained by this structural requirement of sustaining several functional maps along the same topograph. We performed global sensitivity analysis on morphologically realistic conductance-based models of hippocampal pyramidal neurons that coexpressed six well-characterized functional maps along their trunk. We generated randomized models by varying 32 underlying parameters and constrained these models with quantitative experimental measurements from the soma and dendrites of hippocampal pyramidal neurons. Analyzing valid models that satisfied experimental constraints on all six functional maps, we found topographically analogous functional maps to emerge from disparate model parameters with weak pairwise correlations between parameters. Finally, we derived a methodology to assess the contribution of individual channel conductances to the various functional measurements, using virtual knockout simulations on the valid model population. We found that the virtual knockout of individual channels resulted in variable, measurement- and location-specific impacts across the population. Our results suggest collective channelostasis as a mechanism behind the robust emergence of analogous functional maps and have significant ramifications for the localization and targeting of ion channels and enzymes that regulate neural coding and homeostasis.

Channel homeostasis, or channelostasis, refers to the regulation of the density, kinetics, voltage dependence, binding interactions, and the subcellular localization of individual ion channel types within a given cell [compared to proteostasis (1)]. Hippocampal CA1 pyramidal neurons are endowed with complex dendritic morphology and express numerous voltage-gated ion channels (VGICs), which govern critical neuronal functions across their somatodendritic arbor (2–6). Channelostasis in such neurons is an exceptionally complex puzzle, given the enormous morphological and molecular complexities accompanied by a myriad of subcellular channel localization profiles, resulting in an immense combinatorial diversity in channel expression profiles (4, 7–11). A further conundrum that compounds this complex puzzle is that neurons, despite these underlying complexities, exhibit amazingly regular gradients in several functional properties that manifest as maps along a continuous neuronal topograph (3). The coexistence of all these topographically continuous maps along the same neuronal topograph is mediated by intricately regulated subcellular localization of various VGICs.

In this study, we asked whether the topographically connected structure of a complex dendritic arbor, constrained to sustain these continuous functional maps, imposes rules on the individual and collective channelostasis of underlying ion channels. Specifically, the sustenance of the coexistent functional maps has to account for observations that several VGICs govern and modulate any given functional property within a single neuron (12–15) and that there are spatially widespread, distance-dependent influences of ionic conductances across the dendritic arbor (16, 17). Do these requirements impose constraints on the expression profiles and properties of somatodendritic ion channels, if several functional maps were to be coexistent and continuous on the same neuronal topograph? Do spatial and kinetic interactions among channel gradients across the neuronal topograph facilitate or hamper robustness of the several functional maps? Does the connected dendritic structure impose strong pairwise correlations on the expression profiles of different channels that mediate the coexistence of these functional maps? What are the location-dependent contributions of different channels to the several functional maps expressed by hippocampal neurons?

We addressed these questions by using the powerful global sensitivity analysis methodology on morphologically realistic neuronal models and dissected six functional maps with reference to 32 passive and active parameters that governed the neuron’s somatodendritic properties. We used detailed quantitative experimental measurements of channel distributions and of physiological properties from the soma and dendrites of CA1 pyramidal neurons to resolve the validity of 20,420 models generated by randomly assigning values for these 32 parameters. We found that disparate model parameters resulted in topographically analogous populations of these valid neuronal models with weak pairwise correlations between parameters, implying collective, and not individual/pairwise channelostasis as a mechanism behind homeostasis in functional maps. Finally, we derived a methodology, within the global sensitivity analysis framework, to assess the relative contribution of the different channel conductances to the various functional measurements, using virtual knockout simulations on the valid model population. Results from our study suggest that neural mechanisms involved in regulating functional homeostasis of topographically continuous maps need not maintain the density and properties of individual channels at fixed values at specific locations.

Results

We performed global sensitivity analysis on morphologically realistic (Fig. 1A), conductance-based models of hippocampal pyramidal neurons that expressed six experimentally characterized functional maps along the somatoapical trunk. The six maps were topographically continuous on the following experimentally constrained physiological measurements (Fig. 1 B–E): back-propagating action potential (bAP) amplitude, input resistance (R_in), resonance frequency (f_R), resonance strength (Q), total inductive phase (Φ_L), and maximum impedance amplitude (|Z|_max). Our sensitivity analyses spanned a total of 32 model parameters, comprising passive variables and density gradients, voltage-dependence profiles, and kinetics of five somatodendritic VGICs. We used Hodgkin–Huxley-type models for the five VGICs: Na⁺, A-type K⁺ (KA), delayed rectifier K⁺ (KDR), T-type Ca²⁺ (CaT), and hyperpolarization activated (h), and inserted them into our models with experimentally constrained somatodendritic properties (Fig. S1). The rationale behind the choice of these VGICs was their somatodendritic expression profiles and their critical roles in mediating or modulating the six chosen functional maps (3, 14, 18–24).

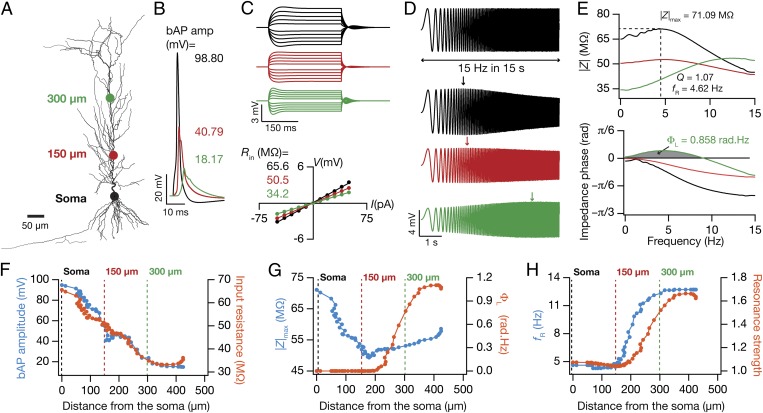
Fig. 1.

Six experimentally constrained functional maps in the base model neuron. (A) A projection of a reconstructed CA1 pyramidal neuron, depicting the locations where example measurements of electrophysiological properties are provided. The color codes of the dots represent locations in B–H. (B) Back-propagating action potential (bAP) traces in response to 1-nA somatic current injection for 2 ms. (C) Upper, voltage traces in response to a local 300-ms current injection from –50 pA to 50 pA in steps of 10 pA for different locations. Lower, steady-state voltage response, obtained from traces above, plotted against the corresponding current amplitude. Slope of the best linear fit to this V–I plot defined input resistance (R_in). (D) A chirp current stimulus, 100 pA in peak-to-peak amplitude and frequency linearly increasing from 0.1 Hz to 15 Hz in 15 s (Upper) was injected at different locations to record local voltage responses (Lower). (E) Impedance amplitude profiles [|Z(f)|, Upper] and impedance phase profiles [ϕ(f), Lower] obtained from corresponding voltage responses to the chirp stimulus (D). The frequency at which the |Z(f)| assumed its maximum value (|Z|_max) was taken as resonance frequency, f_R. Resonance strength, Q, was defined as the ratio of |Z(f_R)| to |Z(0.5)|. Gray shaded area in ϕ(f) measures the total inductive phase, Φ_L. (F–H) Functional maps corresponding to bAP and R_in (F), |Z|_max and Φ_L (G), and f_R and Q (H) along the somatoapical trunk of the baseline model. See Fig. S1 for the experimental counterparts of measurements shown in F–H.

Generation and Validation of a Randomized Model Population.

As a first step toward performing global sensitivity analysis, we hand tuned a base model that accounted for experimental constraints on all six functional maps and the underlying passive and active properties (Fig. 1, Fig. S1, and Methods). Specifically, bAP amplitude (Fig. 1 B and F), R_in (Fig. 1 C and F), and |Z|_max (Fig. 1 E and G) decreased with increase in distance of the trunk location from the soma, whereas Φ_L (Fig. 1 E and G), f_R (Fig. 1 E and H), and Q (Fig. 1 E and H) increased with increasing distance along the trunk. We matched each of these measurements with corresponding experimental values (Fig. S1), as functions of dendritic location (18–20, 24–27). We further tested the validity of our base model by assessing intrinsic measurements that we did not constrain during the tuning process. We found the firing rate profile (f–I curve) and transfer impedance characteristics to match with corresponding experimental measurements (18, 27, 28), without any requirement for additional tuning (Fig. S2).

Next, we generated a population of 20,420 models, with each model built by assigning independently random values for each of the 32 parameters in the base model. The randomization of each parameter was within a large neighborhood of its default value in the base model and followed an independent uniform distribution within that range (Table S1). Given the randomization spanning a large neighborhood, it was expected that all these models would not exhibit experimentally constrained functional maps along the somatoapical trunk. To assess this, we sampled all of the six functional maps at three locations each (Fig. 1A) and asked whether these 18 measurements (6 measurements at three defined locations) from each of the randomized models matched with experimental counterparts at the corresponding somatic or dendritic locations (Table S2) (18–20, 24–27). We fixed upper and lower bounds on each measurement such that they cover ∼80% of the corresponding experimental variability (Fig. S1) (14, 15) and declared a given model to be experimentally valid if all 18 measurements from that model fell within these bounds (Table S3). We performed this validation procedure on each of the 20,420 models and found 228 models (∼1% of the total population) to match the criteria for validity. To reconfirm the validity of these 228 models, we generated histograms of all 6 measurements corresponding to all three locations where they were measured (Fig. S3) and found them to fall within appropriate experimental constraints (Table S3).

Disparate Model Parameters Resulted in Topographically Analogous Functional Maps in the Population of Valid Neuronal Models.

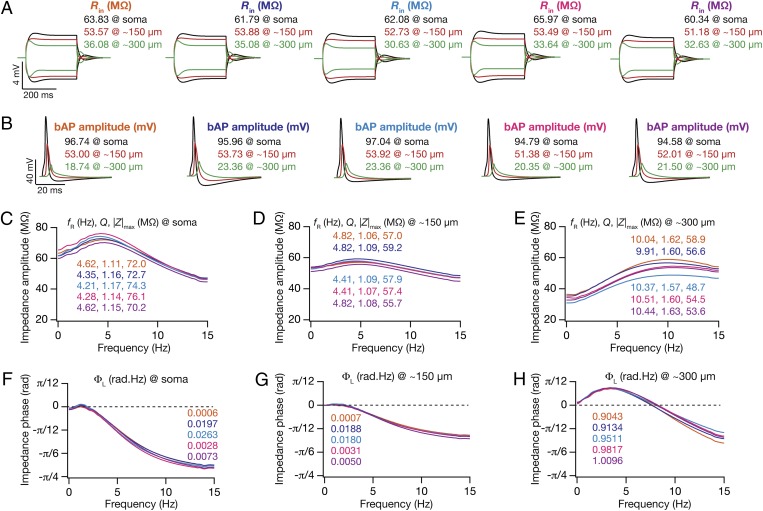
In these 228 valid models, we had constrained the six functional maps only at three specific locations. Was this procedure effective in generating experimentally constrained, topographically continuous functional maps in the entire 0- to 350-µm range, where experimental data are abundant? To test this, we randomly picked five model neurons from the valid model population, such that the 18 measurements were very similar (Fig. 2). Strikingly, when we compared the six functional maps along the trunks of these 5 models, we found that this similarity extended to locations beyond the three where they were constrained (Fig. 3 A–F). Specifically, the six coexistent functional maps inherent to these five models were topographically continuous and analogous within the 0- to 350-µm range of the apical trunk, implying that constraints laid by measurements at three locations from each of the six experimental functional maps were sufficient to confer such coexistence on model neurons.

Fig. 2.

Five randomly chosen valid models were analogous across all 18 somatodendritic measurements. All traces and measurements depicted correspond to the same set of five valid models, at the same somatodendritic locations shown in Fig. 1A. (A) Voltage traces in response to –50-pA and 50-pA current injection at three locations and corresponding input resistance (R_in) values. (B) Back-propagating action potential (bAP) traces at three locations and their corresponding amplitudes. (C–E) Impedance amplitude profile [|Z(f)|] plotted for three locations, soma (C), ∼150 µm (D), and ∼300 µm (E), with corresponding values of resonance frequency (f_R), resonance strength (Q), and maximal impedance amplitude (|Z|_max) values. (F–H) Impedance phase profile [ϕ(f)] plotted for three locations indicating corresponding values of total inductive phase (Φ_L).

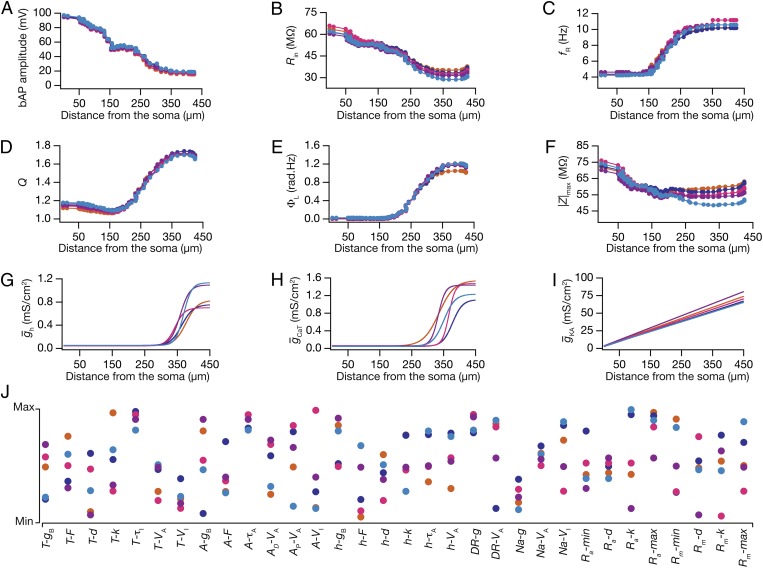
Fig. 3.

In five randomly chosen valid models, analogous functional maps of all six measurements emerged in the absence of individual channelostasis in the underlying channel population. All functional maps and underlying parametric combinations depicted here correspond to the same set of five valid models in Fig. 2. The color codes for different models in Fig. 2 are followed here as well. (A–F) Functional maps of back-propagating action potential (bAP) amplitude (A), input resistance (R_in) (B), resonance frequency (f_R) (C), resonance strength (Q) (D), total inductive phase (Φ_L) (E), and maximum impedance amplitude (|Z|_max) (F) represented along the somato-apical topograph of five valid models. (G–I) Distribution of h (G), CaT (H), and KA (I) conductances along the somato-apical trunk of the five valid models. (J) Distribution of all underlying model parameters in the five valid model neurons depicted along with their respective minimum–maximum range. Each colored circle represents parameters of the color-matched model depicted in A–I and in Fig. 2.

Neuronal properties along the somatodendritic axes are determined by nonlinear spatio-kinetic interactions among different types of VGICs that coexist across the dendritic arbor (3, 14, 16, 17). Furthermore, the spatially widespread influence of localized VGICs in an inherently continuous dendritic arbor imposes spatial relationships between physiological measurements and the channel densities that underlie these measurements (17). Given the topographically analogous nature of functional maps in these 5 models (Fig. 3 A–F), we asked whether the channel properties that underlie these maps were also constrained to express with similar somatodendritic distributions. Surprisingly, despite the severe morphologically driven constraints on the coexistence of the six functional maps, we found large variability in the somatodendritic channel densities and other parametric values (Fig. 3 G–J) that defined these models. Specifically, each of the 32 parameters from these 5 models was not clustered in its respective parametric space and exhibited large variability, almost spanning their entire assigned range (Fig. 3J and Table S1). To confirm this spread in the entire population of valid models, we constructed histograms of each of the 32 underlying parameters in all 228 valid models (Fig. 4A, bottommost row). We found the span of each of these histograms (except for that relating to the activation V_1/2 of sodium channels) to nearly cover the entire assigned range (Fig. 4A and Table S1), thus corroborating our conclusions with 5 models (Fig. 3). These results demonstrate that large variabilities in underlying channel composition (Fig. 3 G–J and Fig. 4A) could still yield robust functional homeostasis (Fig. 3 A–F and Fig. S3) despite the presence of constraints imposed by dendritic morphology and by spatio-kinetic channel interactions.

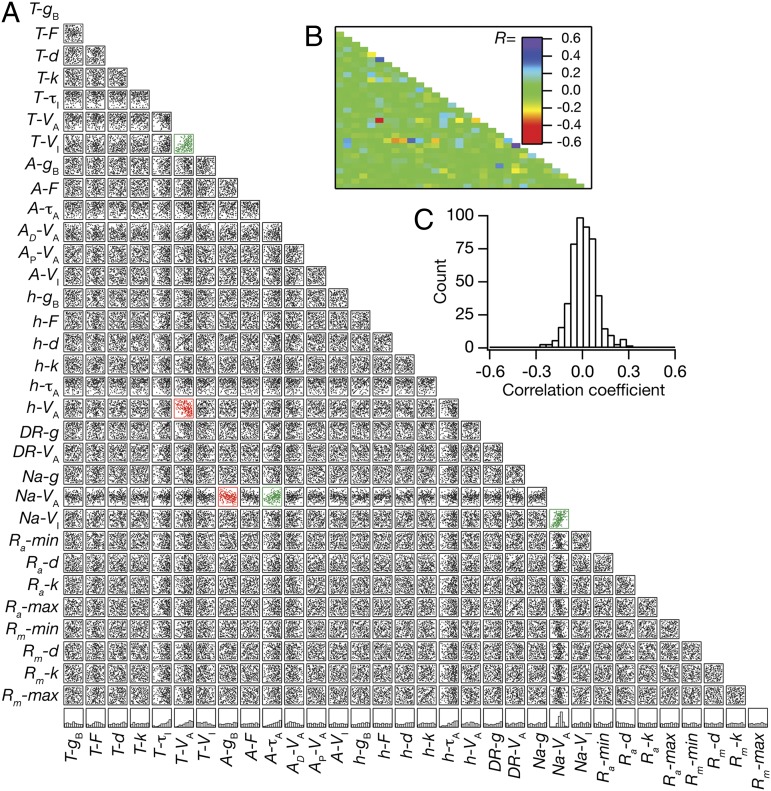
Fig. 4.

Weak pairwise correlations between parameters underlying the valid model population. (A) Lower diagonal of a matrix depicting interactions among the 32 parameters derived from all valid models (n = 228). Each subpanel depicts a scatter plot of the values of 2 parameters (labeled at bottom and at left) derived from all valid models. Correlation coefficients were computed for each of the scatter plots, and red scatter plots indicate that the value of the correlation coefficient was less than −0.3, whereas the green scatter plots indicate that the value of the correlation coefficient was greater than 0.3. The bottommost row denotes normalized histograms of individual parameters in the valid model population. (B) Lower diagonal of a color-coded matrix of correlation coefficients corresponding to the scatter plots in A. (C) Distribution of correlation coefficients for the 496 pairs corresponding to the scatter plots in A.

Weak Pairwise Correlations Between Parameters in the Valid Model Population Imply Collective Channelostasis as a Mechanism Behind Homeostasis in Functional Maps.

Our results suggested that maintaining homeostasis of coexistent functional maps (Fig. 3 A–F) did not require individual channelostasis, implying that individual channels expressed with variable densities (Fig. 3 G–I) and with disparate properties (Fig. 3J) across the dendritic arbor. However, we did not know whether such nonunique mechanisms recruited toward maintaining functional map homeostasis implied correlated expression profiles of several specific pairs of VGICs or whether a change in one parameter was compensated by changes in many other parameters (14, 15). To distinguish between these two possibilities, we analyzed pairwise correlations spanning all 32 parameters that underlie the entire population of valid models (Fig. 4). As multiple parameters could modulate any of the six analyzed measurements, maintenance of functional map homeostasis by pairwise compensation would imply a large set of high-value correlation coefficients. On the other hand, if robust functional maps were maintained by altering several parameters in response to changes in one of them, then these pairwise correlations would be weak. When we analyzed the 496 unique pairs of correlations across all 32 parameters (Fig. 4A), we found the pairwise correlation coefficients to be generally weak (Fig. 4 B and C). Specifically, 491 of the 496 pairs exhibited weak correlation coefficient values between −0.3 and +0.3, with the maximum correlation coefficient value across pairs fixed at a weak +0.508 (R² = 0.258; Pearson’s correlation), between activation V_1/2 and inactivation V_1/2 of the Na⁺ conductance (Fig. 4 A and B). These weak correlations suggest that various nonunique channel combinations could establish robust coexistence of several functional maps, where the impact of changes in one parameter was effectively compensated by changes in several other parameters. Our analyses also clearly demonstrate that the existence of topographical constraints on the maps, imposed by neuronal arborization and by nonlinear spatio-kinetic interactions among VGICs, was insufficient in enforcing strong correlations among any of the parametric combinations. Finally, to test whether these conclusions were dependent on the specific choice of parametric gradients in the base model (Fig. S1 and Table S1), we repeated our analyses on a new base model (Fig. S4) created with changes in several parametric gradients (Table S4) to match experimental map measurements (Fig. S4 and Table S3). We found that our conclusions on the absence of individual channelostasis in valid model parameters (compare Fig. 3 with Fig. S5) and on the absence of pairwise correlations among these parameters (compare Fig. 4 with Fig. S6) were consistent with results obtained from valid models generated with this new base model as the substrate.

Simulations Involving Virtual Knockouts of Specific Channels Resulted in Variable Impacts on Measurements from Neurons Within the Valid Model Population.

From our analyses so far, it was evident that channelostasis involving only individual VGICs or their pairs was expendable in the maintenance of overall homeostasis of several coexistent functional maps. A collective channelostasis, whereby several channels regulate their properties and expression profiles in an uncorrelated (but not necessarily independent) manner, appeared as a distinct alternative to such individual or paired channelostasis toward accomplishing the overall goal of functional homeostasis (Figs. 2–4). How did individual channels contribute to different measurements in the execution of such collective channelostasis? Were specific functional maps heavily reliant on distinct channel types or were such dependencies widespread without ascribing dominance to any given channel type? If the dependencies were widespread, what was the relative contribution of each channel to the different measurements at distinct dendritic locations?

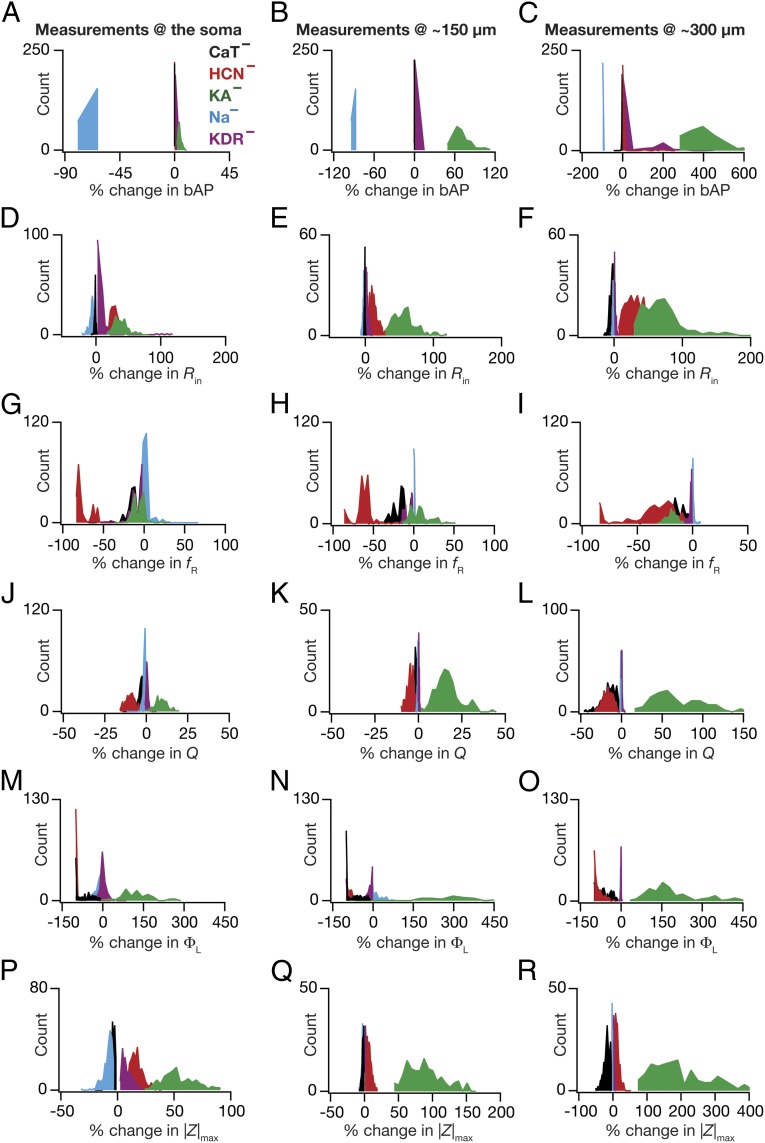
To address these questions quantitatively, we developed a virtual knockout methodology where we analyzed the impact of different VGICs on each measurement by removing the conductance mediated by that channel from each valid model. We removed a specific conductance from each of the 228 valid models and performed simulations to obtain all 18 measurements (Fig. 1) from each virtual knockout model (VKM) lacking this conductance. We repeated this entire procedure for each of the five different VGICs (Na, KDR, KA, CaT and h), obtaining 18 measurements from five classes of VKMs (one class per VGIC) in all 228 valid models (yielding a total of 5 × 228 = 1,140 VKMs, with 18 measurements each). Analyzing measurements from these models, we first found that the impact of knocking out any of the five VGICs was variable within the 228 VKMs that were specific to each VGIC. Specifically, for any given VGIC, we measured the percentage difference in each of the 18 measurements from the 228 VKMs with reference to the corresponding base model measurements. As certain VKMs sustained intrinsic oscillations, leaving them unsuitable for obtaining all measurements, and certain others elicited very high (close to infinity) percentage changes in Φ_L at the somatic and 150-µm locations (owing to low base values of Φ_L), these VKMs were eliminated from further analyses (Table S5). When we plotted histograms of these percentage differences for each measurement and each VGIC, we found the spread to encompass a wide span (Fig. 5), implying a variable impact of each channel on different valid models. As the impact of knocking out a given VGIC is directly related to the actual expression levels of that VGIC, we noted this variable impact to be a direct reflection of the large variability in VGIC conductance densities within the valid model population (Figs. 4 and 5). We also noted this to be consistent with observations from experiments, using either genetic or pharmacological elimination of channels, that blocking specific conductances results in variable effects on physiological measurements used in this study (18–20, 29–35).

Fig. 5.

Virtual knockout of specific conductances from the population of valid models had diverse impacts on physiological measurements. (A–R) Distributions of percentage changes in back-propagating action potential (bAP) amplitude (A–C), input resistance (R_in) (D–F), resonance frequency (f_R) (G–I), resonance strength (Q) (J–L), total inductive phase (Φ_L) (M–O), and maximum impedance amplitude (|Z|_max) (P–R) after removing a specific conductance from the population of valid models at three different locations (soma, 150 µm, and 300 µm; Fig. 1A). For all panels, the histograms for specific conductances are color coded as in the labels in A.

Simulations Involving Virtual Knockouts of Specific Channels from the Valid Model Population Revealed Differential Channel Contributions to Different Measurements.

Whereas these results have significant ramifications for the interpretation of experiments involving either genetic deletion or pharmacological blockade of specific channels (14, 15), we explored avenues to exploit the statistics of this variable impact of channel deletion toward understanding specific relationships between VGICs and measurements. Specifically, closer analyses of the variable impact of different VGICs on specific measurements revealed clear demarcations in the spread of variability across channels, measurements, and locations (Fig. 5). Consider the example of bAP changes at the 300-µm location in the five different classes of VKMs (Fig. 5C). Whereas the bAP amplitude increased heavily in VKMs where KA channels were eliminated, in VKMs where Na⁺ channels were removed, the bAP amplitude was drastically lower. In contrast, in VKMs involving the h, CaT, and KDR channels, the change in bAP amplitude hovered around 0% change, suggesting a minimal impact of these channels on bAP amplitude at 300 µm. Similarly, R_in (Fig. 5 D–F) increased in VKMs involving h and KA channels and changed minimally in VKMs involving the CaT, Na⁺, and KDR channels. Motivated by these well-defined demarcations and by the conformity of these results to experimental and theoretical results involving these channels and measurements (14, 17–20, 22, 26, 32), we asked whether we could use measurements from specific classes of VKMs to assess the relative importance of corresponding channels for different measurements at different locations.

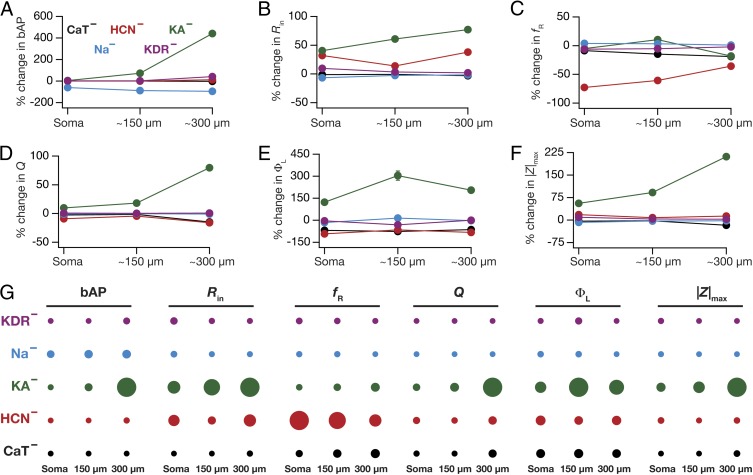
To do this, we quantified the statistics (mean ± SEM) of percentage changes (Fig. 5) in each of the 18 measurements obtained from the five different classes of VKMs (Fig. 6 A–F). From these plots, it was obvious that the quantitative contributions of different VGICs to any given measurement were differential and were also dependent on the location of the measurement. To visualize these differential contributions more effectively (cf. ref. 15), we computed the “contribution strength” of each VGIC to all 18 location-dependent measurements (Fig. 6G). Specifically, if 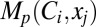represented the mean percentage change (Fig. 6 A–F) of measurement p (1 ≤ P ≤ 6) at location x_j (1 ≤ j ≤ 3) of VKMs derived by deleting channel C_i (1 ≤ i ≤ 5), then the contribution strength of a channel C_q to a given measurement p at a specific location x_r was computed as

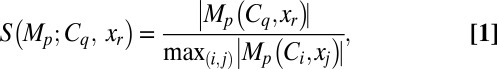where |.| represented the absolute value of the argument, and 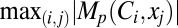depicted the maximum value of 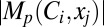spanning all locations from all classes of VKM. This procedure was repeated for all 6 measurements, and the contribution strengths corresponding to each (p, q, r) combination were depicted as circles such that 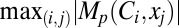and 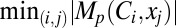were depicted by the largest and smallest diameter circles, respectively (Fig. 6G). In other words, the contribution strength of a VGIC to a specific measurement at a given location was linearly related to the diameter of the circles, and normalization of circle diameters was with reference to all values of M_p.

Fig. 6.

Virtual knockout of specific conductances reveals contrasting contributions of different conductances to individual physiological measurements. (A–F) Percentage changes (represented as mean ± SEM) at three different locations (soma, 150 µm, and 300 µm; Fig. 1A) corresponding to back-propagating action potential (bAP) amplitude (A), input resistance (R_in) (B), resonance frequency (f_R) (C), resonance strength (Q) (D), total inductive phase (Φ_L) (E), and maximum impedance amplitude (|Z|_max) (F) after removing a specific conductance from the population of valid models. For all panels, the plots for specific conductances are color coded as in the labels in A. (G) Quantification of the relative impact of different conductances on specific physiological measurements recorded at each of the three locations. The relative effect of each conductance on a given physiological measurement at each location is specified by the diameter of the circle against that combination. The largest and the smallest diameters were measurement specific and were assigned to the maximum and minimum absolute changes, respectively, of the measurement spanning all locations and conductances.

What inferences could we draw from the contribution strengths about the relative contributions of specific channels to different measurements and how did these inferences compare with existing experimental data? In answering this, we found that KA channels had the maximal impact on the bAP amplitude, with its contribution to dendritic bAP higher than the somatic action potential (Figs. 5 A–C and 6 A and G). This is expected because of the higher levels of the expression of KA channels in dendrites compared with the soma and the ability of KA channels to reduce AP amplitude (20, 32). Next, we found that knocking out h or KA channels increased R_in (Figs. 5 D–F and 6 B and G), with an increased influence in distal dendrites than at the soma (18, 21, 22, 33). Impedance properties (f_R, Q, and Φ_L) were critically dependent on h channels (Figs. 5 G–R and 6 C–G), where large changes in corresponding experimental measurements were observed upon blocking/knockout of these channels (18, 19, 33, 36). Thus, for cases where experimental data were available, our results were consistent with conclusions arrived through genetic deletions and/or pharmacological blockade of specific channels in hippocampal pyramidal neurons.

What testable predictions do these contribution strengths offer in cases where experimental data were not available? The prominent inferences were related to the role of the two dendritic inactivating channels (KA and CaT) in regulating impedance-related measurements. Specifically, we noted that KA channels exert a prominent influence on all measurements, with the contribution to measurements higher in distal dendrites compared with the contributions at the soma (Fig. 6). Whereas the roles of KA channels in regulating bAP amplitude and R_in are established (20, 21, 32), their roles in modulating impedance-related measurements are yet to be tested (14). With reference to these impedance-related measurements, the large window component of KA channels enables them to behave as leak channels in the subthreshold range, thereby providing specific predictions about their contributions (Figs. 5 G–R and 6 C–G) to these measurements (14). Next, the array of contribution strengths also predicted a critical role for the CaT channels in augmenting resonance-related properties mediated by h channels (14), especially at distal dendritic locations (Figs. 5 G–R and 6 C–G). Although the role of CaT channels in mediating resonance is established in other neuronal subtypes (37, 38), it is not known whether the higher density of dendritic CaT channels (23) contributes to theta-frequency resonance in distal dendrites of CA1 pyramidal neurons. Together, our results provide quantitative testable predictions elucidating a significant role for CaT and KA channels in impedance-related properties of CA1 pyramidal neuron dendrites. Finally, the ability of VKM-based contribution strengths to confirm existing results and provide testable predictions on the contributions of specific ion channels to various measurements establishes our virtual knockout methodology as a generalized technique for analyzing the relative impacts of specific parameters on physiological measurements.

Discussion

The maintenance of functional gradients across the dendritic arbor is critical for several aspects of neurophysiology, including signal integration, optimal tuning of neuronal responses, neural coding, synaptic plasticity, and normalization of several measurements across the dendritic arbor (2, 3, 5, 6, 39). Pyramidal neurons, despite the large baseline turnover of underlying channel proteins, retain an amazing regularity in the expression of these topographically continuous functional maps and have led to several outstanding questions that lack clear answers. How do neurons with complex dendritic arborization achieve such functional homeostasis? What mechanisms drive the localization and targeting of different channels to specific locations in the process of achieving such remarkable functional similarity across pyramidal neurons? How do neurons account for complex nonlinear spatio-kinetic interactions among ion channels expressed in different compartments while invoking specific mechanisms for channel targeting (4, 7, 8, 11, 17)?

Our results, involving global sensitivity analyses of six coexistent functional maps encoded by 32 different somatodendritic parameters, clearly demonstrate that channelostasis involving only individual VGICs or their pairs was expendable in the maintenance of overall homeostasis of several coexistent functional maps (Figs. 2–4). This implies that neural mechanisms involved in regulating topographical functional homeostasis of these maps need not maintain the density and properties of individual channels at specific values at specific locations. This presents an enormous opportunity for neurons to encode novel information or react to pathological insults through several nonunique combinations of channel plasticity, while still maintaining functional homeostasis. Further, the significance of this conclusion might be assessed by the observation that this is despite the constraints placed on individual channelostasis by (i) the necessity of the coexistence of six continuous maps on the same neuronal topograph (Figs. 2 and 3), (ii) the nonlinear spatio-kinetic interactions among VGICs at different locations, and (iii) the complex array of interdependencies between channels and measurements that govern these functional maps (Figs. 5 and 6). The requirements on the channel expression/trafficking machinery, instead, could be focused on maintaining the overall functional homeostasis through a collective channelostasis mechanism involving several ion channels. Under such a scenario, several downstream signaling pathways could recognize perturbations (that could arise during an encoding process or a pathophysiological insult) to the overall functional homeostasis of these maps by specific sensing mechanisms (say, local calcium levels at different somatodendritic locations). This, in turn, could trigger changes in different channels, depending on the specific perturbation to the homeostasis, thereby maintaining a collective channelostasis that is not overly reliant on individual ion channel densities or properties. Furthermore, in the absence of a regime where individual channels are severely constrained, such collective channelostasis should also translate to tremendous neuron-to-neuron variability in the local mRNA levels of different channel subunits across the neuronal dendritic arborization. Finally, as channelostasis of individual channel types is governed by different cell-autonomous and/or activity-driven signaling mechanisms, such a lack of individual channelostasis would imply neuron-to-neuron variability in the local concentrations of different downstream signaling enzymes and their gradients. Thus, our results on the lack of individual/paired channelostasis in the maintenance of topographically analogous, coexistent functional maps present specific predictions for the mechanisms that govern the trafficking, localization, and targeting of underlying ion channels. Future research could focus on experimentally testing these predictions through quantitative assessments of neuron-to-neuron variability in protein/mRNA levels (4, 7, 8, 40).

It is established that all functional maps are not mutually exclusive, owing to some cross-dependencies on the same channels (3, 18, 19). Furthermore, activity-dependent changes in synapses and in VGICs underlying some functional maps have shown to be governed by the same underlying signaling mechanisms (3, 41–45), imposing additional dependencies on the covariance among these functional maps. Finally, there is experimental evidence from several systems for activity-dependent and independent mechanisms of maintaining the coexpression of specific conductances (13, 15, 46–53). How do we reconcile these observations with the absence of strong pairwise correlations (Fig. 4) across parameters that underlie the coexistent functional maps (51)?

A potential explanation could be the presence of several location-dependent signaling cascades that differentially affect the different VGICs (45), leading to combinatorial possibilities of plasticity, which include those on space, enzyme type, and phosphorylation site. In conjunction with our results on the possibility of achieving functional homeostasis in the absence of individual channelostasis, this implies that the interdependencies of functional maps do not automatically impose correlations in channel expression. Finally, correlations in channel expression profiles across the somatodendritic trunks of pyramidal neurons, with emphasis on location-specific correlations, have not been experimentally determined. In this context, it is important that future experiments that assess targeting and localization of ion channels within complex dendrites should focus on the location dependencies and gradients of all signaling molecules and their collective impact on targeting and plasticity of specific VGICs (54, 55). Specifically, our experimental understanding on synergistic interdependence of various forms of plasticity and their cross-dependencies on specific signaling pathways and on levels of calcium (27, 42–45) should be expanded to the location dependence of all signaling molecules across the somatodendritic arbor. Additionally, computational approaches toward understanding channel localization and their impacts on topographic functional maps should incorporate these synergistic dependencies and the locus of different forms of plasticity (3, 18, 25, 27, 45). Such incorporation should be specific for a given neuronal subtype and should be in the form of precisely designed rules that account for the location and cross dependencies of plasticity in specific ion channels in the chosen subtype (56). Under such a scenario, the study of channelostasis and its relationship to functional homeostasis would encompass proteostasis as a whole, leading to a broad holistic approach toward specific targeting of ion channel subunits and maintenance of topographically constrained functional map homeostasis (1, 7, 51).

Methods

A reconstructed hippocampal CA1 pyramidal neuron (n123), obtained from Neuromorpho.org was used as the substrate for all simulations (Fig. 1A). Passive electrical parameters were set using a fit-based approach to match all measurements under consideration with their experimental counterparts (17–19, 22, 24, 26, 27). Specific membrane capacitance C_m was set at 1 µF/cm². Specific membrane resistivity, R_m, and intracellular resistivity, R_a, varied along the somato-apical trunk as functions of radial distance of the compartment from the soma, x (17, 18, 27),

where R_m-max = 145 kΩ.cm² and R_a-max = 110 Ω.cm were default values at the soma, and R_m-min = 125 kΩ.cm² and R_a-min = 10 Ω.cm were values assigned to the terminal end of the apical trunk (which was ∼425 µm distance from the soma for the reconstruction under consideration). The other default values were R_m-d = R_a-d = 320 µm, R_m-k = 40 µm, and R_a-k = 14 µm. The basal dendrites, the axonal compartments, and apical obliques had somatic R_m and R_a. All neuronal models were compartmentalized using the 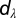rule (57) to ensure that each compartment was smaller than 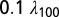, where 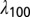was the space constant computed at 100 Hz. This led to 833 compartments in the base model and varied from 777 to 909 compartments across valid models.

Channel Kinetics and Distribution.

Our study included five types of conductance-based VGIC models: Na⁺, KA, KDR, CaT, and h channels. The kinetic schemes for Na⁺, KDR, and KA channels were adopted from ref. 26, the h channel was modeled as in ref. 22, and the CaT channel kinetics were taken from ref. 58. Reversal potentials for Na⁺, K⁺, and h channels were set at 55 mV, –90 mV, and –30 mV, respectively. The CaT current was modeled using the Goldman–Hodgkin–Katz formulation with the default values of external and internal Ca²⁺ concentrations set at 2 mM and 50 nM, respectively (14). Whereas Na and KDR conductances were uniformly distributed across the somatodendritic arbor, h, CaT, and KA channel conductances increased with increase in dendritic distance from the soma (20, 22, 23). The rise in intracellular calcium concentration consequent to current (I_Ca) through T channels and its decay were modeled as in ref. 14.

For Na and KDR channels, Y-g represented the uniformly distributed conductance density and Y-V_A depicted the half-maximal activation voltage for 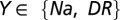, and Na-V_I symbolized half-maximal inactivation voltage of Na channels (Table S1). While assessing properties associated with action potential propagation, maximal conductance values of Na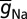⁺ (= Na-g = 12.5 mS/cm²) and KDR ( 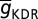= DR-g = 10 mS/cm²) channels in different compartments were uniformly set such that the action potential amplitude was around 100 mV across all compartments when the KA conductance was absent (20, 26). 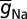in the axon initial segment was set fivefold higher compared with its somatic value (59). The rest of the axon was treated passively. To account for slow inactivation of dendritic Na⁺ channels, an additional inactivation gating variable was included in dendritic Na⁺ channels (26). KA conductance was set as a linearly increasing gradient as a function of radial distance from the soma, x (17, 20, 26):

The default value of the somatic 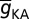, A-g_B, was 3.1 mS/cm², and A-F (= 5) quantified the slope of this linear gradient. To accommodate experimental observations on differences between the activation parameters of the KA channels in CA1 pyramidal cells (20), a proximal model (A_P) was used for compartments with radial distances less than 100 µm from the soma, beyond which point the distal A-type K⁺ conductance model (A_D) was used. A_P-V_A and A_D-V_A depicted the half-maximal activation voltages for proximal and distal KA channels, respectively. A-V_I represented the half-maximal inactivation voltage and A- 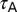depicted the activation time constant, common for both A_P and A_D (26).

The gradient of maximal h conductance (22) followed a sigmoidal dependence on the radial distance from the soma, x (17, 18, 27), to match impedance-based maps in the base model with appropriate experimental counterparts:

The default value of somatic 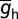, h-g_B, was 40 µS/cm²; somatodendritic fold increase of 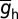, h-F was 20; half-maximal distance of 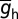, h-d was 370 µm; and the parameter quantifying the slope, h-k was 14 µm. The basal dendrites had somatic 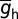(18). Along the somatoapical axis, the half-maximal activation voltage for h channels was –82 mV for x ≤ 100 µm, linearly varied from –82 mV to –90 mV for 100 µm ≤ x ≤ 300 µm, and was –90 mV for x > 300 µm (22). The CaT conductance gradient (23) was modeled as a sigmoidal increase with increasing radial distance from the soma, x:

The default value of somatic 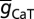, T-g_B was 55 µS/cm²; somatodendritic fold increase of 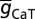, T-F was 25; half-maximal distance of 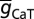, T-d was 370 µm, and the parameter quantifying the slope, T-k was 15 µm. The basal dendrites had somatic 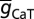. Apart from these, Y-V_A represented the half-maximal activation voltage for 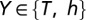, h-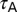 symbolized the h channel activation time constant, and T-V_I and T- 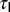depicted the half-maximal inactivation voltage and inactivation time constant for CaT channels, respectively. The default values provided for each of the parameters correspond to the base model and satisfy experimental constraints on the coexistence of the six functional maps along the same somato-apical trunk (Fig. 1 and Fig. S1).

Measurements.

To quantitatively measure the back propagation of action potentials into dendrites (20, 24), an action potential was initiated at the soma (1 nA current for 2 ms) and the amplitude of the bAP was measured at various locations along the somato-apical trunk (Fig. 1B). In cases where action potential initiation did not occur (say in the sodium channel virtual knockouts; Figs. 5 and 6), the maximal passive response was used as the substitute. Input resistance (R_in) was measured by injecting subthreshold current pulses of amplitudes spanning –50 pA to +50 pA, in steps of 10 pA, and recording the local voltage responses to these current pulses (Fig. 1C, Upper). The respective steady-state voltage responses at a given location were plotted against the corresponding current amplitude to obtain the V-I plot (Fig. 1C, Lower). The slope of a linear fit to this steady-state V-I plot was taken as the R_in for that location (Fig. 1C, Lower), and the procedure was repeated for all locations along the somato-apical trunk to construct the R_in functional map.

The subthreshold intrinsic response dynamics of the model to oscillatory inputs were characterized by injecting a chirp stimulus (14, 18, 19, 36): a sinusoidal current wave with constant amplitude (100 pA, peak to peak) with frequency linearly increasing from 0.1 Hz to 15 Hz in 15 s (Fig. 1D, Upper). The Fourier transform of the local voltage response (Fig. 1D, Lower) was divided by the Fourier transform of the chirp stimulus (Fig. 1D, Upper) to obtain the complex valued impedance Z(f), as a function of frequency f. The impedance amplitude profile |Z(f)| was computed as the magnitude of this impedance (Fig. 1E, Upper),

where Re(Z(f)) and Im(Z(f)) were the real and imaginary parts of the impedance |Z(f)|, respectively. The frequency at which |Z(f)| reached its maximum value was measured as the resonance frequency, f_R (Fig. 1E, Upper); |Z|_max denotes the maximum impedance amplitude, which by definition equals |Z(f_R)|. Resonance strength (Q) was measured as the ratio of the maximum impedance amplitude to the impedance amplitude at 0.5 Hz. Finally, the local impedance phase profile ϕ(f) was computed as (Fig. 1E, Lower)

Total inductive phase (Φ_L), which was defined as the area under the inductive part of ϕ(f) (Fig. 1E, Lower) was as follows (19):

All of the four local impedance-based measures were computed across the somato-apical trunk to construct the respective functional maps. Transfer impedance-associated measurements were quantified by injecting chirp stimulus at various locations along the somato-apical trunk and measuring the voltage response at the soma (28). The transfer impedance amplitude profile |Z_TR(f)| (Fig. S2C) and transfer impedance phase profile ϕ_TR(f) (Fig. S2C) were computed from the voltage response and chirp stimulus, similar to the respective local impedance profiles. The firing rate profile (f–I curve) of a model neuron was assessed by injecting step current pulses from 50 pA to 250 pA in steps of 50 pA at the soma for 1 s. The number of action potentials was counted for each current injection and plotted against the respective current amplitude to obtain the f–I curve (Fig. S2A).

All simulations were performed using the NEURON simulation environment (57) at –65 mV and 34 °C, with an integration time step of 25 µs. All analyses were performed using custom-built software written with IGOR Pro (Wavemetrics). Correlation analysis was done using the statistical computing package R (www.R-project.org).