Training-free atomistic prediction of nucleosome occupancy

Significance

Nucleosomes alter gene expression by preventing transcription factors from occupying binding sites along DNA. Conventional methods to predict nucleosome occupancy are trained on observed DNA sequence patterns. The method presented here uses physical principles and all-atom force fields to predict both nucleosome occupancy along genomic sequences as well as binding to known positioning sequences. Our method calculates the energy of both nucleosomal and linear DNA of the given sequence. Based on the DNA deformation energy, we accurately predict the in vitro occupancy profile observed experimentally for a 20,000-bp genomic region. DNA with all C bases methylated at the 5 position shows less variation of nucleosome binding: Strong binding is weakened and weak binding is strengthened compared with normal DNA.

Abstract

Nucleosomes alter gene expression by preventing transcription factors from occupying binding sites along DNA. DNA methylation can affect nucleosome positioning and so alter gene expression epigenetically (without changing DNA sequence). Conventional methods to predict nucleosome occupancy are trained on observed DNA sequence patterns or known DNA oligonucleotide structures. They are statistical and lack the physics needed to predict subtle epigenetic changes due to DNA methylation. The training-free method presented here uses physical principles and state-of-the-art all-atom force fields to predict both nucleosome occupancy along genomic sequences as well as binding to known positioning sequences. Our method calculates the energy of both nucleosomal and linear DNA of the given sequence. Based on the DNA deformation energy, we accurately predict the in vitro occupancy profile observed experimentally for a 20,000-bp genomic region as well as the experimental locations of nucleosomes along 13 well-established positioning sequence elements. DNA with all C bases methylated at the 5 position shows less variation of nucleosome binding: Strong binding is weakened and weak binding is strengthened compared with normal DNA. Methylation also alters the preference of nucleosomes for some positioning sequences but not others.

In cells, DNA molecules are stored in the form of chromatin that consists of repeating nucleosome units with superhelical DNA wrapped around a protein octamer core (1, 2). Neighboring nucleosomes are connected by extended straight stretches of DNA called the linker region. Given that certain transcription factors prefer to bind to naked DNA (3), a bound nucleosome may silence the genetic message of its DNA segment. Although the in vitro nucleosome occupancy is mainly governed by physical principles setting preferences for certain sequences, the exact placement of nucleosomes in vivo will also be influenced by higher order chromatin structure (3), chromatin remodeling (4), interaction with DNA-binding transcription factors (5), and epigenetic factors (6) such as histone modifications and DNA methylation (7). These subtle epigenetic changes (often referred to as chromatin marks) may provide a convenient way to manipulate genetic expression without altering the underlying genetic code. As a result, they have become a central focus of modern biomedical research. Here, we present a structure-based, in silico approach that captures how a DNA-based epigenetic mark, methylation, affects both the distribution of nucleosomes along genomic sequences and their preferred dyad location along known nucleosome-positioning sequences. The present work constitutes, to our knowledge, the first step toward computational structural epigenetics.

This central importance in transcriptional regulation inspired development of experimental methods to map nucleosome positions. The most commonly used approach employs micrococcal nuclease to cleave DNA along the linker regions so that nucleosome positions can be indirectly inferred from the centers of DNA sequence fragments (8). Based on earlier work using localized hydroxyl radicals (9), a direct chemical approach has been developed to map nucleosomes (10). The availability of these nucleosome maps spurred the development of computational methods that were traditionally trained on experimental data.

Early approaches depend on the sequences of the DNA and are based on experimentally observed binding patterns. The pioneering dinucleotide study of Trifonov and Sussman (11) was followed by the first comprehensive study of k-mers, sequence motifs k nucleotides in length (12). In fact, the guiding-dinucleotide model, which accounts for both periodicity and positional dependence, currently predicts single nucleosome positions most accurately (13). Other powerful knowledge-based approaches for predicting nucleosome organization (14) and single-nucleosome positioning (15) were developed using global and position-dependent preferences for k-mer sequences (14, 15). Interestingly, it has been reported (16) that much simpler measures, such as percentage of bases that were G or C (the GC content), could also be used to produce surprisingly accurate predictions of nucleosome occupancy.

The second type of knowledge-based method depends on DNA structure in addition to the sequence (17, 18). This approach was initiated by the pioneering work of Olson et al. (17) who investigated the geometry of stacks of two neighboring base-pair steps as observed in crystal structures. The variation of the geometrical parameters governing DNA bending provides an estimate of the bending energies associated with specific base-pair steps. For example, the approach followed by Xu and Olson (18) relies on knowledge-based dinucleotide step energies to calculate the bending energy of a sequence threaded on a nucleosomal DNA template. By the very insightful use of overlapping structural fragments, Lavery and coworkers introduced an all-atom resolution physics-based method for the high-throughput modeling of DNA–protein-binding sites (19, 20). This clever method divides the interface into a set of overlapping DNA fragments each associated with the protein fragments with which it interacts. This allows large interfaces to be examined in reasonable computer time. Application to the nucleosome (20) yielded the nucleosome-binding preferences for any DNA sequence. Comparison of results with experiments for eukaryotic transcription start sites was very encouraging (20).

Although sequence based methods (11–15) are predictive and cost-effective, they cannot directly account for any structural information, which is especially relevant if one is to distinguish identical sequence motifs with distinct epigenetic marks. Furthermore, current structure-based methods (17–20) either rely on statistical data from prior experiments (17, 18) and lack the information needed to capture epigenetic changes (e.g., methylation) or use fragments (19, 20) so that the physical system is not modeled as a whole. Thus, these methods cannot capture all aspects of the fine epigenetic effects that control biology.

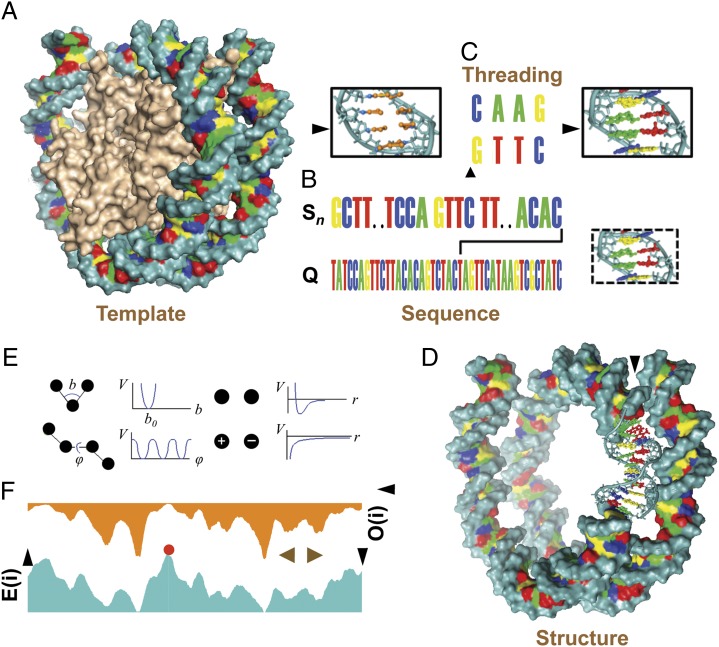
To break this reliance on known experimental data and adequately take epigenetic marks into account, we use a protocol that models nucleosomal DNA as an all-atom assembly. It involves threading a particular sequence on a template structure followed by conformational optimization (21, 22) guided by an all-atom energy function (23) with implicit solvent model (24). As such, our predicted nucleosome occupancies and dyad positions are not biased by assumptions beyond the conventional approximations associated with all-atom empirical force fields (23). Although we use an empirical molecular mechanics force field, our method can be used with any force field that can be computed efficiently and can be systematically improved in concert with our expanding physicochemical knowledge of basic atomic interactions. Our protocol is described in detail in Fig. 1 and Fig. S1.

Fig. 1.

Threading any DNA sequence onto a nucleosome-shaped DNA template. (A) Surface representation of superhelical DNA (backbone in cyan, A in green, C in blue, G in yellow, and T in red) wrapping around the histone core in the nucleosome structure (PDB ID code 1kx5). (B) The representative local sequence S_198,305, whose first nucleotide is at position n = 198,305 along the genomic sequence (denoted by Q) of yeast chromosome 14, is shown. To demonstrate the threading protocol (C) a tetranucleotide (4-nt), GTTC is chosen from the oligonucleotide, TCCAGTTCTT located at position 51 of the 147-nt local sequence S_198,305. GTTC in a 4-bp structure is shown in dashed box. (C) The two-step design protocol for the chosen tetranucleotide. First, the native sequence of the DNA nucleosome template is converted to a sequence of planes each defined by a root atom (light blue) and three pseudoatoms (orange). Second, the base planes are replaced with bases from the tetranucleotide sequence. As a result of the design protocol, the native (human) DNA is removed and the yeast sequence is added. (D) DNA accommodating the local sequences S_n. The DNA surface is omitted for the region 51–60 that includes the 10-nt oligonucleotide discussed in B. (E) Showing the all atom energy terms used in the calculation. (F) The nucleosome energy E(i) or related occupancy O(i), plotted as a function of the local sequence position (i). The red dot marks the energy at local sequence S_n. The size of a nucleosome is indicated by the brown arrowheads.

Using our ab initio method, we successfully predict the in vitro nucleosome occupancy profile along a well-studied (14) 20,000-bp region of genomic yeast sequence. We also predict the strong interaction of nucleosomes with 13 nucleosome-positioning sequences known to be high-affinity binders. Our calculations show that DNA methylation weakens the nucleosome-positioning signal suggesting a possible role of 5-methylated C (5Me-C) in chromatin structure. We expect this physical model to be able to capture further subtle structural changes due to base-methylation and hydroxy-methylation, which may be magnified in the context of chromatin.

Results and Discussion

Sensitive Sequence Dependence of Energy.

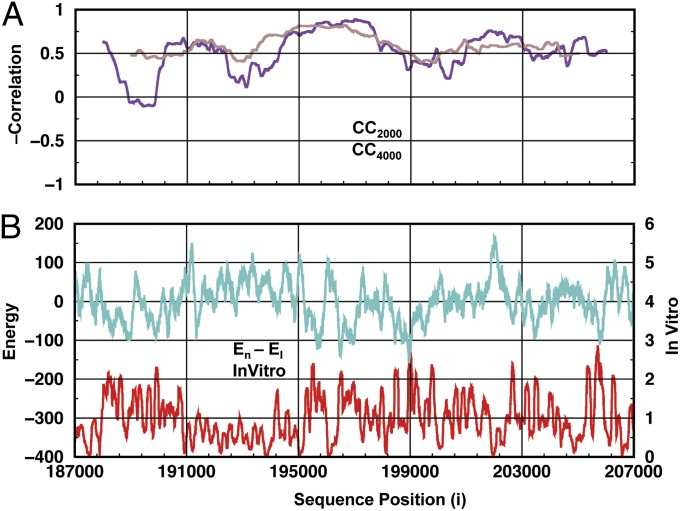
Our physics-based method is used with a template from a high-resolution crystal structure (25) to predict the nucleosome formation energy, E_n − E_l (where E_n is the energy of the particular sequence on DNA that is bent to fit the nucleosome and E_l is the energy of the same sequence on ideally straight B-DNA, termed “linear DNA”). E_l is used as reference energy to eliminate the dependence on trivial effects such as the number of hydrogen bonds made between the two strands. Fig. 2 compares our predicted energy with the in vitro experimental occupancy for sequence positions from 187,000 to 207,000 in yeast chromosome 14 (26, 27); it shows clear negative correlation between the two data sets: The in vitro nucleosome occupancy is higher at the sequence positions where the nucleosome formation energy is lower. Position-dependent correlations (Fig. 2A) show that the correlation is generally uniform along the sequence although there are regions with high correlation (195,000–199,000) and others with low correlation (187,000–191,000). These weakly correlated regions are narrow and are not detected with a 4,000-bp window. Fig. 2B depicts the in vitro experimental nucleosome occupancy and computed nucleosome formation energies. The overall correlation between the experimental and modeled data are −0.612. Fig. S2 shows the ab initio nucleosome occupancy profiles obtained when energies are converted to probabilities of occupancy using the Boltzmann formula (SI Materials and Methods).

Fig. 2.

Nucleosome formation energy and the in vitro occupancy profile for sequence positions from 187,000 to 207,000 with single-position increments in yeast chromosome 14. (A) The position-dependent negative correlation of the in vitro profile and nucleosome formation energy is shown using windows of 2,000 (violet) and 4,000 (brown) bp. The nucleosome formation energy is the difference between the energy of DNA bent as if on a nucleosome and a linear B-DNA (one type of right-handed DNA conformation) structure with the same sequence, i.e., (E_n − E_l). Calculations were performed using the AMBER99-bsc0 force field, an implicit electrostatic solvent description, and PDB 1kx5 and linear B-DNA templates. (B) The nucleosome formation energy (cyan) and experimental profile (red) plotted along the sequence. The overall correlation of the nucleosome formation energy and in vitro profile is −0.613.

The Effect of DNA Methylation.

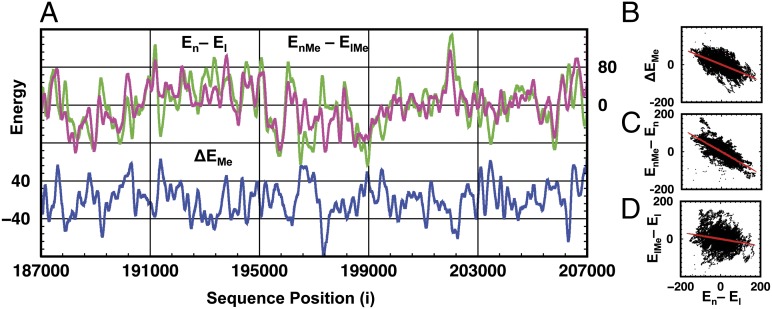
Although methylation does not occur in yeast, we aimed to study its enhanced physical effect. Therefore, we methylated all C bases of our studied sequence (used in Fig. 2) at the 5 position (5Me-C). At first sight, the energy values of nucleosome formation (E_nMe − E_lMe) (Fig. 3A) look very much like the corresponding energy values for normal DNA (E_n − E_l). Closer examination shows that whenever the nucleosome formation energy of normal DNA is particularly large or small, the energy of 5Me-C DNA is less extreme. Thus, methylation moderates the sequence dependence of the nucleosome formation energy. Quantitatively, this moderating effect is reflected by the smaller SD of the formation energies for the methylated sequence compared with those of the normal sequence (43.0 and 52.1 kcal/mol, respectively). These observations are further supported by Fig. 3B showing how the effect of methylation on the nucleosome formation energy, ΔE_Me defined as ΔE_Me = (E_nMe − E_lMe) − (E_n − E_l), is negatively correlated with (E_n − E_l) with a correlation coefficient of −0.584. Fig. 3 C and D plots the methylation energies for both linear and nucleosomal DNA and indicates that nucleosome methylation (E_nMe − E_n) and nucleosome formation energy (E_n − E_l) are strongly anticorrelated [correlation coefficient (CC) = −0.739], whereas the methylation energy change on the linear form (E_lMe − E_l) has only weak anticorrelation with (E_n − E_l) (CC = −0.196). From this we infer that the effect of methylation on the nucleosome formation energy arises from methylation of the nucleosomal form and not the linear form. Additional correlation plots are presented in Fig. S3.

Fig. 3.

Methylation changes nucleosome formation energy. (A) Nucleosome formation energies for both methylated (magenta) and unmethylated (green) DNA are shown as a function of sequence position. The change of nucleosome formation energy, caused by methylation, ΔE_Me = (E_nMe − E_lMe) − (E_n − E_l) is plotted (blue) to show its correlation with nucleosome formation energies (E_n − E_l) and (E_nMe − E_lMe) (green and magenta, respectively). (B) Plot of ΔE_Me against E_n − E_l has a CC of −0.584. (C) Methylation energy on the nucleosome (E_nMe − E_n) as a function of E_n − E_l also shows strong anticorrelation (CC = −0.739). (D) Weak anticorrelation (CC = −0.196) occurs between nucleosome formation energy E_n − E_l and methylation energy on linear DNA (E_lMe − E_l). For clarity, averages (<E>) are subtracted from all energy values so that E − <E> is used instead of E.

DNA methylation affects the static atomic structure of DNA in a manner that is predictable in that it is easy to add methyl groups to normal DNA. In addition to affecting properties of DNA such as the tendency for strand separation (28), and free energy of Z-DNA, a left-handed DNA form, formation (29), methylation should affect the sequence dependence of the nucleosome formation energy. Whereas recent contradictory investigations found that nucleosome positioning may enhance (30) or protect (31) DNA methylation patterning throughout the genome, the reverse problem, namely the effect of methylation on nucleosome occupancy has remained an open question.

We find that methylation moderates the sequence dependence of nucleosome positioning. This is supported by the intuitive argument that 5Me-C resembles the thymine base in that both have a methyl group at position 5 of the pyrimidine base, whereas this group is absent in C.

GC Content, in Vitro Occupancy, and Methylation.

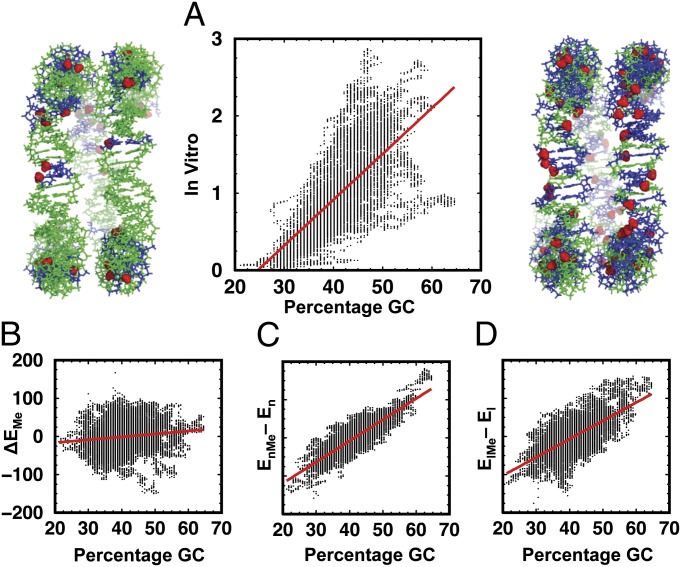
Why are all-atom force-field calculations able to predict the in vitro nucleosome occupancy almost as well as trained knowledge-based methods? It has been shown that the dominant factor contributing to nucleosome binding is simply the concentration of GC base pairs in the DNA stretch to which a nucleosome binds (16). Fig. 4A shows that the in vitro nucleosome occupancy of the DNA depends on the percentage GC with a correlation of 0.685 between the two quantities. Furthermore, the range of in vitro occupancies increases as a function of increasing GC content: at low GC content, there is weak nucleosome binding, whereas at high GC content, nucleosome occupancy can be moderate or high. Further related correlation plots are found in Fig. S4.

Fig. 4.

(A) The in vitro nucleosome occupancy of the region 187,000–207,000 studied here is plotted against percentage GC to show a strong correlation of 0.685. The images on the left and right show side views of superhelical turns of DNA template accommodating sequences with low (Left) and high (Right) percentage GC and all C bases methylated at the 5 positions (A and T nucleotides in green; G and C nucleotides in blue; and methyl groups on the 5Me-C bases shown in the red space-filling representation). (B) The weak correlation (CC = 0.132) between the methylation-related change in nucleosome formation energy (ΔE_Me) and the percentage GC, where ΔE_Me = (E_nMe − E_lMe) − (E_n − E_l) or equivalently (E_nMe − E_n) − (E_lMe − E_l), is shown. (C and D) Methylation energies for the DNA in nucleosome form (E_nMe − E_n) in C and the linear form (E_lMe − E_l) in D show strong correlations of 0.859 and 0.676 to percentage GC.

It is of note that the methylation-induced changes in nucleosome formation energy are not simply additive: When methylating all cytosines to 5Me-C, the magnitude of the methylation effect, ΔE_Me, has almost no correlation with the percentage GC, and hence the number of methyl groups added (Fig. 4B). Overall methylation affects both nucleosomal and linear DNA so that the energy differences (E_nMe − E_n) and (E_lMe − E_l) are both strongly correlated with percentage GC (Fig. 4 C and D) but their difference (ΔE_Me) is not. This may be explained by the complex interplay of factors such as certain sequence motifs, local variations in the nucleosome structure, and the methylation effect.

Nucleosome-Positioning Target Sequences.

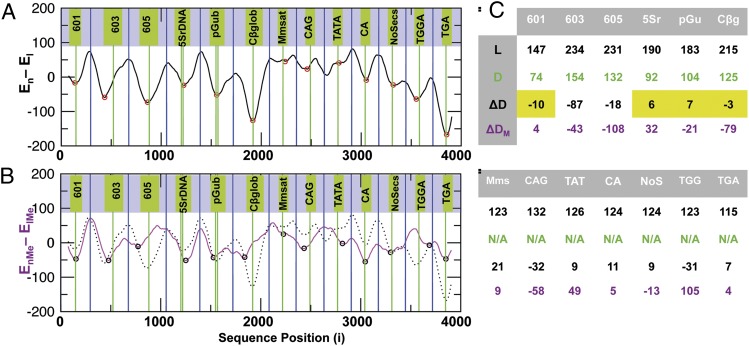
The concentration of GC base pairs influences nucleosome occupancy along long stretches of genomic sequences by virtue of the easier bending into the major and minor grooves. High GC content cannot explain the precise preferred location of nucleosomes along positioning target sequences that bind single nucleosomes precisely. We tested the ability of our computational protocol to predict single nucleosome positions on established target-positioning sequences taken from ref. 13. Fig. 5A presents the nucleosome formation energy calculated along a DNA sequence (Fig. S5), which consists of known nucleosome-positioning target sequences separated by a random sequence spacer. The results clearly show that our “training-free” method not only predicts the preferred binding to positioning target sequences but also often predicts the nucleosome dyad locations to be close to the minima on the nucleosome formation energy landscape. Fig. S6 shows that these results are reproducible with more detailed counterion models.

Fig. 5.

(A) Nucleosome-formation energies as a function of the position along a test sequence that is constructed by concatenating nucleosome-positioning target sequences separated by a random DNA sequence of 147 nt. The green vertical lines indicate known dyad locations where the nucleosome is expected to be centered. If the dyad location is not known, the green lines refer to the center nucleotide of the sequence. Blue lines indicate the center of the random sequence on our nucleosome template. Red circles mark minima of the computed energy. (B) The computed nucleosome formation energy for normal (black dotted line from A) and 5Me-C methylated (magenta) DNA are shown. Black circles mark energy minima or saddle points. (C) Four properties of the 13 established nucleosome-positioning sequences 601, 603, 605, 5Sr DNA, pGub, chicken β-globulin, mouse minor satellite, CAG, TATA, CA, NoSecs, TGGA, and TGA are shown. (Row 1) L is length or the number of nucleotides in the sequence. (Row 2) D is an experimentally verified dyad location (if available). (Row 3) ΔD is the difference between the dyad locations and the nearest energy minimum. Yellow shading highlights the accurate prediction of nucleosome positions (within 10 nt) for 4 of the 6 sequences with verified dyad locations. If dyad locations are not known, ΔD represents the difference between the location of the center nucleotide and the nearest energy minimum or saddle point. (Row 4) ΔD_M is the same as ΔD for methylated DNA.

Fig. 5C summarizes the accuracy with which our method predicts nucleosome positions (or equivalently the positions of the dyad axis). Overall, in 4 of 6 sequences, known nucleosome positions were predicted within 10-nt resolution. Unlike in the former coarse statistical predictions on the genomic scale (Fig. 3), here the base-pair level prediction accuracy is affected by using an initial template structure other than the crystal structure (25). In addition to moderating the extreme sequence dependence of the nucleosome formation energy, Fig. 5B shows that the methylation effect depends on sequence identity. Its impact ranges from having a weak effect (target sequence 601) to causing a complete switch in nucleosome-binding preference (target sequence chicken β-globulin).

Unlike the most accurate sequence knowledge based methods (13–15), our method is training-free as it does not exploit the use of any statistical data on either sequence or structural patterns that correlate with nucleosome positions. As such it can be applied to methylated DNA, for which statistical data are difficult to obtain. Therefore, our method can provide this missing link, the occupancy profile for modified DNA, on which knowledge-based methods (13, 14) can then be trained and used to study the genome-wide effect of DNA based epigenetics on nucleosome occupancy.

DNA Methylation and Transcriptional Regulation.

Our results suggest that methylation alters the thermodynamic stability of nucleosomes bound to a given sequence. By modulating the sequence dependence of DNA deformation energy, methylation could help unlock or lock certain DNA regions with particularly strong or weak nucleosome binding. Promoter regions, which are particularly rich in CpG islands (32), are sensitive targets of hypermethylation. According to our study, 5-methylation of these C bases would weaken the sequence dependence of nucleosome occupancy and facilitate nucleosome relocation along hypermethylated promoter regions by lowering the thermodynamic barrier. This could change the accessibility of transcription factor-binding sites and result in down-regulated gene expression. This mechanism can explain methylation-based silencing of tumor suppressor genes (33, 34). Thus, our finding can have implications for cancer cell genomes with methylated CpG islands (35). The effect of methylation in altering the preference of nucleosome binding to only certain positioning sequences suggests that methylation can have the role of a gene-selective activator in the transcriptional machinery.

Current Sequence-Based Methods.

Computationally cost-efficient alternatives for predicting genome-wide nucleosome occupancy are the knowledge-based methods dependent on observed sequence motifs (13–15). As they are trained on experimental statistical data, they are not able to predict something that has not been observed before, for example global methylation of C at position 5. They also require context as it may not be sufficient to consider only short motifs such as dinucleotides (11, 12). For example, nucleotides adjacent to the motifs may need to be taken into account. One may use a more detailed model by considering longer motifs (12, 14, 15), however longer motifs require more statistical data that is often not available. Sequence-based methods can, however, collect statistical information on any observed data including our computed occupancy profiles for normal and methylated DNA. Thus, fundamental methods such as the one presented here can be combined with various force fields (Fig. S7) to generate training data for faster sequence- or even structure-based methods (as discussed in Existing Structure-Based Methods).

Existing Structure-Based Methods.

The current structure knowledge-based approaches are based on the variation of 3D structures, which are described at the level of overlapping base pairs (17, 18). They assume that the variation is caused by environmental thermal energy so that it is described by a quadratic energy function, which is parameterized by the statistical variations seen in crystal structures. Unfortunately, there is never enough data to explore conformational variability properly and there is no data available for new situations such as epigenetic modifications. Some high-throughput physics-based approaches use overlapping fragments (19, 20). Given that fragment energies are short-range, these methods are not able to fully capture long-range interactions such as electrostatics, and the lack of this ability can lead to unexpected predictions (Fig. S8). The present energy calculations can be used to generate training sets for structural knowledge-based methods (17, 18). In this way, the expanding data on atomistic interactions derived from computed structures can be exploited to progressively improve the resolution of knowledge-based methods and also provide reliable information on the relative stability of nucleosome binding.

Sequence-Dependent DNA Bending Dominates.

The excellent agreement found here with the experimental nucleosome occupancy suggests that the variation in nucleosome formation energy mainly originates from the sequence dependence of the DNA deformation energy. The validity of our model is further supported by a pioneering computational study (performed with a similar physics based energy function), which revealed the importance of sequence dependent DNA flexibility and bending in protein–DNA recognition (36). We also find that for occupancy predictions (Fig. 3 and Fig. S2) an ideal DNA superhelix template (Fig. S7) gives similar results to the one we obtain with a template from the nucleosome crystal structure (25). Contact density calculations on the reconstructed nucleosome particle, which is composed of all histone proteins with added hydrogen atoms and our independently optimized nucleosomal DNA structures, showed that DNA–DNA contacts dominate (Fig. S9A), and are the only ones affected by methylation (Fig. S9 B–D). Fig. S10 showed that the methylation effect on the contact density is very similar to the effect of a new sequence that increases the number of contacts between adjacent bases within the same DNA strand. Thus, the interaction between the DNA and histone proteins likely has only a subtle modulating influence. These subtle effects are implicitly captured by our method in that our structural-optimization protocol does not alter the initial nucleosomal DNA crystal structure by more than 1.7 Å (Fig. S11) and conserves the minor groove width modulations and helical parameters (Fig. S12) found in the experimental structure (25). Overall, our finding implies that the “imprint” of the histone core, such as the sequence dependence of minor groove variations, will modulate the occupancy profile, which is more significantly influenced by the overall topology (geometry of the superhelix) of the nucleosomal DNA structure. Although this small modulation can be crucial when predicting nucleosome positioning at base-pair resolution, our results suggest that the GC percentage sets the overall energetic preferences for superhelix geometry.

Conclusion

Our physics-based training-free method is able to compute nucleosome occupancy profiles along genomic sequences. It does not rely on training data or fragment libraries and its use of all atoms allows it to evaluate the effect of a wide variety of DNA-based chromatin modifications such as 5-hydroxy-methyl-cytosine and 6-methyl adenosine. The fine-scale structural information that can be extracted from our computed occupancy profiles can augment statistical information used by existing sequence-based methods, which are fast enough to predict nucleosome organization in entire genomes. Our results also suggest how the GC content (GC percentage) provides a strong but coarse background signal for nucleosome positioning: This makes it challenging to capture further subtle effects. Unlike any other previous approaches, the atomistic nature of our technology holds the promise to provide a virtual microscope under which we hope to isolate some of the fine effects that control gene expression.

Materials and Methods

Mutating a Single Base on the DNA Template.

Central to our approach is threading nucleotide sequences onto a DNA structural template like that determined by X-ray crystallography (25) and deposited in the Protein Data Bank (PDB) (37). Here, we use two sets of sequence-independent reference atoms: “plane atoms” C2, C4, and C6 (following the International Union of Pure and Applied Chemistry naming convention), which are common to all nucleotides and determine the orientation of the base plane; and “root atoms,” comprising the N9 atom of A and G bases and the N1 atom of C and T bases, which connect the base to the sugar ring (Fig. 1). Given a template, T, and a sequence, S, our threading protocol proceeds as follows: (i) Delete all nonbackbone atoms in the template apart from the root and plane atoms. (ii) Build nucleotide type S(i) at template position T(i). Here, atom N1 or atom N9 of the new nucleotide replaces the root atom. Next, atom C2 and atom C6 for bases C and T or atom C4 and atom C8 for bases A and G are built so that C2 and C6 (for C and T) or C4 and C8 (for A and G) are in the same plane defined by the C2, C4, and C6 atoms of the local native base. All of the atoms in the base are built to satisfy the equilibrium bond lengths, bond angles, and torsion angles defined by the Assisted Model Building with Energy Refinement (AMBER)99-bsc0 force field (23).

Threading the Genomic Sequence onto the DNA Template.

Fig. 1 shows the template structure, which is the DNA superhelix from crystal structure in PDB ID code 1kx5 (25). Note, that our protocol allows the use of template structures, such as an ideal DNA superhelix (38). Fig. 1 also illustrates a target sequence, S that is taken as a continuous stretch of genomic sequence, Q; (here from the yeast database in ref. 26). The length of S always corresponds to the length of the superhelix in the template structure (147 bp). Given the DNA template, we build the 5′–3′ DNA strand with sequence S using the guide atoms (discussed in Mutating a Single Base on the DNA Template and Fig. 1) and then repeat the procedure with the complementary sequence for the other DNA strand. Note that the interaction between the DNA and the histone core is only implicitly incorporated into our prediction that starts with DNA bent by the nucleosome. This approximation is made both to reduce computer time and to avoid dependence on the less reliable DNA–protein interaction energy parameters and the structurally less well-defined histone tails.

Implementation and Software.

All optimization calculations and all-atom threading protocols have been implemented into the Methodologies for Optimization and Sampling in Computational Studies (MOSAICS) software package (39) and its associated scripts.