Viral Kinetics in Hepatitis C or Hepatitis C/Human Immunodeficiency Virus–Infected Patients

Abstract

Background & Aims

Kinetic modeling of hepatitis C virus (HCV) response to interferon (IFN)-based therapy provides insights into factors associated with treatment outcomes. HCV/human immunodeficiency virus (HIV)–co-infected patients show lower response rates vs. HCV-monoinfected patients. Reasons for this remain unclear. This study evaluated kinetic parameters and treatment responses in co-infected vs monoinfected patients.

Methods

Co-infected patients were randomized within a US multicenter trial (ACTG 5071) to receive pegylatedinterferon (PEG-IFN) alfa-2a + ribavirin vs. IFN alfa-2a + ribavirin. Monoinfected controls were matched prospectively for treatment, genotype, age, sex, race, and histology. Quantitative HCV-RNA testing was performed at hours 0, 6, 12, 24, 48, and 72; days 7, 10, 14, 28, and 56; and weeks 12, 24, 48, and 72.

Results

Twelve HCV/HIV–co-infected and 15 HCV-monoinfected patients underwent viral kinetic sampling. Among HIV-positive patients the mean CD4+ count was 325 cells/mm³. Seventy-five percent of patients were genotype 1. The HCV-RNA level was undetectable at 72 weeks in 25% and 40% of co-infected and monoinfected patients, respectively. Phase 1/2 declines, free virus clearance rate, and infected hepatocyte death rate were not affected by co-infection status but differed by treatment. Efficiency (∈) ≥ 90% at 60 hours was associated with viral clearance (P = .02). Modeling with pooled parameters suggests baseline viral load is a key factor in time to response in this cohort. Predicted clearance time increased by 28% in co-infected patients.

Conclusions

Co-infection status did not affect key kinetic parameters. Among kinetic parameters, efficiency was associated significantly with viral clearance. Co-infected patients may require longer treatment duration than monoinfected patients given their generally higher baseline viral loads.

Hepatitis C virus (HCV) infection has emerged as a major cause of morbidity and mortality among patients infected with human immunodeficiency virus (HIV) in the post–highly active antiretroviral therapy era. Despite this observation, treatment options for HCV in those with HIV infection have lagged behind developments and options for those infected with HCV alone. The reasons for this are complex and related to concerns regarding tolerability and efficacy of treatment response with interferon (IFN)-based therapies.¹

Mathematic modeling of treatment-associated perturbation of viral equilibrium initially was described in the context of antiretroviral therapies.² Variations of these techniques have been applied successfully to HCV infection to determine estimates of viral production, define phases of decline, and to predict treatment response. Biphasic and triphasic response models have been proposed to explain actual changes in HCV viral load after exposure to IFN and other agents.^3–5

There are limited data regarding HCV viral kinetics among those co-infected with HIV. In an effort to define kinetic parameters, evaluate response, and develop paradigms that might predict on-treatment and sustained response, we performed viral kinetic sampling at multiple early time points in a subset of co-infected patients enrolled in a US multicenter treatment trial. Monoinfected control subjects were matched prospectively to this co-infected subset to evaluate accurately the effect of HIV infection on response to IFN-based therapies.

Materials and Methods

Study Populations

ACTG 5071 is a multicenter US treatment trial evaluating safety and efficacy of IFN-based therapies in HCV/HIV–co-infected patients. Enrollment required evidence of active HCV and HIV infection, with a liver biopsy examination consistent with chronic HCV in IFN-naive patients. Patients with evidence of decompensated liver disease or other comorbid liver causes were excluded. Patients were randomized to receive either pegylated-interferon (PEG-IFN) alfa-2a (180 mcg once per week) + ribavirin (escalating to 1000 mg/day) or standard IFN alfa-2a (6 MU three times per week for 12 weeks, then 3 MU three times per week) + ribavirin (escalating to 1000 mg/day). Treatment was for 48 weeks. End-of-treatment response (ETR) was defined as HCV viral loads below the detectable limits of the assay at week 48. However, patients classified as virologic nonresponders at 24 weeks underwent liver biopsy examination. If histologic improvement (≥2 histologic activity points) was seen, patients were offered the option of completing 48 weeks of therapy. Otherwise, patients were censored as nonresponders. All patients were followed-up for 24 weeks after completion of treatment to evaluate sustained virologic response status, defined as nondetectable HCV viral load at week 72. Twenty-one sites participated in the main clinical trial. Of these, 5 sites offered enrollment into ACTG 5091s, a substudy of viral kinetics, which required intensive blood sampling during the first 2 weeks of treatment. Initial dosing of IFN was observed directly by study staff and ribavirin was initiated simultaneously. Samples were collected at times 0, 6, 12, 24, 48, and 72 hours, and at 7, 10, 14, 28, and 56 days after the initial dosing. Subsequent samples were collected at weeks 12, 24, 48, and 72 from start of therapy. Blood was collected in accordance with protocols for viral sampling, including separation from cells within 3 hours and freezing aliquots of plasma, which were stored at −70°C until tested in a central laboratory.

HCV-monoinfected controls were enrolled prospectively after identification of active patients in this viral kinetic study. Controls were IFN-naive patients from the University of Cincinnati Medical Center who were matched to patients by the following characteristics: (1) sex, (2) age ± 5 years, (3) race, (4) HCV genotype, and (5) presence or absence of cirrhosis. Controls were placed on the same treatment arm to which their HCV/HIV–co-infected match had been randomized. Patients were sampled and followed-up in an identical manner to the co-infected treatment cohort. All patients provided informed consent at time of entry into the AACTG and the studies were approved by the institutional review boards at each individual site.

HCV-RNA Quantification

The HCV-RNA level was evaluated by using the Cobas Amplicor HCV Monitor Assay (Roche Molecular Systems, Indianapolis, IN). This nucleic acid amplification polymerase chain reaction methodology has been evaluated previously in HCV/HIV–co-infected patients.⁶ The lower limit of detection is 600 IU/mL and the upper range is 500,000 IU/mL. Samples greater than the reporting range were diluted 1:100 in HCV-negative human plasma and retested to determine the actual viral titer.

Kinetic Modeling and Statistical Analysis

The biphasic model for HCV kinetics was applied to both the monoinfected and co-infected patients.³ This model is fit in 2 stages. For the first 48 hours of therapy the viral load at time t is described as follows:

$$V\left(t\right)=V_0[1-\epsilon +\epsilon \exp (-c(t-t_0)\left)\right]t>t_0$$ (1)

where viral decay begins at time t₀, V₀ is the viral load at time t₀, c is the rate of clearance of free virus per day (day⁻¹), and ∈ is the treatment efficiency in blocking viral production, with a range between 0 (no efficiency) and 1 (100% efficiency). The fitted parameters from equation 1, V₀, t₀, c, and ∈, are substituted in the following equation describing the viral load from days 0–14:

$$\begin{array}{cc}\hfill V\left(t\right)=V_0\left\{A\exp \right[-& {\lambda }_1(t-t_0)]\hfill \\ \hfill & +(1-A)\exp [-{\lambda }_2(t-t_0\left)\right]\}t>t_0,\hfill \end{array}$$ (2)

where

$$\begin{array}{cc}\hfill A=(c\epsilon & -{\lambda }_2)∕({\lambda }_1-{\lambda }_2),\hfill \\ \hfill & {\lambda }_{1,2}=1∕2\left\{\right(c+\delta )\pm {[{(c-\delta )}^2+4(1-\epsilon \left)c\delta \right]}^{1∕2}\}\hfill \end{array}$$ (3)

and δ is the infected cell death rate (day⁻¹). In this model, λ₁ represents the slope (in log-scale) of the first phase decline (day⁻¹) and λ₂ represents the second phase decline (day⁻¹). If the estimated parameter, λ₂, is not greater than 0, then the patient is predicted to never be completely free of virus (ie, V(t) > 0 for all t). In prior models, the first phase parameters were calculated between 24 and 48 hours. Because 3 patients in our study had their fifth viral load measurement taken at 52, 53, and 60 hours, extending the cut-off time of first phase parameter estimations to 60 hours allowed us to use data from more patients. Similarly, slightly better fits were obtained when the second phase parameter estimation was extended to 400 hours after initial treatment instead of 336 hours (14 days). One patient missed the 14-day collection and had a measurement taken on day 22. In 2 cases, using viral load measurements taken at days 28 and 56 improved the model fit significantly; otherwise, extending phase II parameter estimation to 1400 hours did not improve the results. The lower bound set for viral load was 600 IU/mL because that was the limit of detection of the assay. Bounds on estimated parameters were set within plausible limits: 0 < c < 10/hour (0 < c < 240/day), t₀ ≥ 2.0 hours, and ∈ ≤ .997 to provide for better convergence of the numeric procedures. Bootstrapping of viral load data (number of repetitions = 199) was used to generate 95% confidence intervals for the estimated parameters for each patient.

A linear regression also was fit for each patient in which the natural logarithm of the viral load was the dependent variable and time in hours was the independent variable. Previous work has shown that the relationship may not be linear, especially in the early stages of treatment (eg, as suggested by the biphasic kinetic model).^3,7,8 Thus, a robust linear regression model was fit to the data for the first 14 days of treatment. The robust model is resistant to outliers but nevertheless is able to capture the long-term linear trend. The particular method used is the least median of squares regression procedure. Unlike least squares, which minimizes the sum of the squared residuals, least median of squares fits the parameters of the straight line that minimizes the median of the squared residuals.⁹ Although least median of squares is able to fit more complex models (eg, a cubic function in time), there often was insufficient data to fit any more parameters than the 2 required for a straight line (slope and intercept). The nonlinear regression models were run in SAS version 8.0 (SAS Institute, Cary, NC). Two algorithms (Marquardt and Newton-Raphson) were used. With both methods, convergence criteria are met when the change in the gradient between iterations is smaller than 1.0e-5.

Summary statistics are expressed as either mean ± SD or median (range). Group comparisons of treatment response or model parameters were made using the Fisher exact test, McNemar exact test, Student t test (with the Satterthwaite correction to degrees of freedom for unequal variances), the Mann–Whitney U test, Spearman rank correlation, or linear and logistic regression models as best fit the data. A 2-sided hypothesis with α ≤ .05 was considered statistically significant in all cases.

Results

Study Population

Twenty-seven patients provided informed consent and agreed to participate in the viral kinetic substudy. These included 12 HCV/HIV–co-infected patients and 15 HCV-monoinfected matched controls. The controls were matched prospectively using the criteria listed earlier, and single or double matches were found for 10 HCV/HIV–co-infected patients. Matches could not be identified for 2 co-infected patients; their data were not used in paired analysis. Group demographics are shown in Table 1. No significant demographic differences were found between treatment groups with the exception of alanine transaminase levels, which were significantly higher in the monoinfected control group at baseline (P = .04). This difference was no longer evident by week 12. In 70% of the matched pairs, the HCV viral load was higher in the co-infected patient than in the monoinfected control. Six co-infected and 2 monoinfected patients discontinued treatment before week 48: 6 at week 24 (nonresponse and per protocol), and 2 at week 2 (1 monoinfected, 1 co-infected, both owing to treatment intolerance). Two co-infected and 5 monoinfected patients were nonresponders at week 24, who showed histologic improvement and chose to continue with treatment. Of the 13 patients treated with PEG IFN, 7 (54%) achieved ETR, of whom 5 achieved sustained virologic response (SVR). Of those who achieved SVR, only 2 were co-infected. Of those treated with standard IFN (n = 14), 5 (36%) achieved ETR and 4 of these had a sustained response. One of these was co-infected. Individual patient characteristics, including genotype, race, baseline HCV viral load, and response to treatment are shown in Table 2.

Table 1.

Patient Group Demographics

	Co-infected patients	Monoinfected patients	P valuea
N	12 (44.4%)	15 (55.5%)
Age	46.1 (range, 38–60)	46.9 (range, 39–55)	NS
Sex
Men	10	14	NS
Women	2	1
Race
Caucasian	6	7	NS
African American	6	8
HCV genotype
1b	9 (75.0%)	13 (86.7%)	NS
2b	3 (25.0%)	2 (13.3%)
Median HCV log10	6.75 (range, 4.9–7.5)	5.87 (range, 4.9–7.2)	.16
Viral load at baseline (lU/mL)	6.57 ± .71	6.19 ± .70
Cirrhosis (n, %)	1 (8.3%)	1 (6.7%)	NS
Treatment randomization
PEG IFN	5	8	NS
Standard	7	7
Mean baseline ALT levels (lU/mL)	58 (range, 18–127)	100 (range, 46–229)	.04
Mean CD4+ count (cells/mm3)	325 (range, 175–855)	N/A

NOTE. N = number of patients in each subset.

NS, not specified.

^aP values determined by Mann–Whitney U test or χ² test.

^bGenotype 1 includes 1, 1a, and 1b.

Table 2.

Individual Patient Characteristics and Outcomes

IDa	Treatment	Genotypeb	Race	Predicted Oc	Baseline HCVd	ETR	SVR
013698De	S	2b	W	28	7.30	N	N
013703Je	P	1a	W	65	6.84	Y	N
013713Ie	S	1a	B	76	6.88	N	N
044516Le	S	1a	HB	3650	6.61	N	N
044519Fe	S	2b	HW	24	7.47	Y	Y
044522H	P	1a	HB	NE	6.75	N	N
240108G	P	2b	W	NE	4.85	Y	Y
240366A	S	1a	W	NE	6.70	N	N
242425De	P	1a	B	232	6.75	N	N
242611H	S	1a	B	NE	6.80	N	N
242872H	P	1b	B	NE	6.21	Y	Y
243265Ce	S	1b	W	82	5.68	N	N
C01	P	1a	W	NE	6.75	Y	N
C02e	P	2b	W	3650	5.78	Y	Y
C03e	S	1a	B	54	5.29	Y	Y
C04	P	1	B	NE	5.76	N	N
C05e	S	2b	W	32	6.94	Y	Y
C06e	P	1a	B	663	5.89	N	N
C07e	S	1a	W	19	5.91	Y	Y
C08e	S	1a	W	274	5.84	N	N
C09e	P	1a	B	3650	5.58	N	N
C10e	P	1a	B	507	6.68	N	N
C11e	P	1a	B	11	4.90	Y	Y
C12e	S	1a	W	36	6.62	Y	N
C13	S	1a	B	NE	6.67	N	N
C14	S	1a	B	NE	7.11	N	N
C15e	P	1a	W	137	7.17	Y	Y

S, standard IFN + ribavirin; W, non-Hispanic white; N, no; P, PEG-IFN + ribavirin; Y, yes; B, non-Hispanic black; HB, Hispanic black; HW, Hispanic white; NE, not estimable.

^aHCV/HIV co-infected patients (n = 13) are identified by 6 digits + 1 letter. HCV monoinfected controls (n = 15) are identified by “C” + 2 digits.

^bHCV genotype determined by line probe assay (LiPA, Bayer Corporation, Tarrytown, NY).

^cDays to viral clearance as predicted by the mathematic model. Patients with inestimable or unreliable parameter estimates were not included in this analysis. Patients with estimated days to clearance greater than 9999 days were censored to 3650 days.

^dBaseline HCV viral load (log₁₀ IU/mL).

^eRegression model converged.

Model Fit

By using the mathematic model of Neumann et al³ as described earlier, kinetic parameters were calculated first using the Marquardt algorithm. The resulting point estimates for several patients did not lie well within the bounds of the 95% confidence interval, indicating poor model fit, and several other patients did not have model convergence. We therefore reprogrammed the model using the Newton-Raphson algorithm, with much improved results. Convergence was achieved in 18 of 27 patients (11 monoinfected and 7 co-infected). Key parameters and 95% confidence intervals for all 18 patients are shown in Table 3.

Table 3.

Point Estimates and 95% Confidence Intervals for Patients With Model Convergence as Calculated by the Method of Neumann et al

IDa	Treatment	V0b	t0c	cd	ε e	δ f	λ 1 g	λ 2 h
013698D	S	7.30 (6.87–7.5)	9.00 (8.30–9.02)	47.77 (41.54–49.0)	.76 (.15–.94)	.44 (.04–2.59)	47.88 (41.84–49.76)	.33 (.029–.50)
013703J	P	6.86 (.73–7.34)	12.04 (2.00–14.99)	3.93 (2.33–37.14)	.93 (.78–.98)	.11 (.02–.25)	3.94 (2.32–37.18)	.10 (.019–.20)
013713I	S	6.92 (6.74–7.26)	11.39 (2–13.70)	22.67 (1.47–240)	.55 (.071–.89)	.21 (.007–19.20)	22.76 (1.77–240.23)	.12 (0–.16)
044516L	S	6.60 (5.95–6.76)	7.64 (2.96–12.00)	100.76 (0–240)	0 (0–.74)	19.20 (.08–19.20)	119.96 (19.20–259.2)	0 (0–.14)
044519F	S	7.47 (6.97–7.50)	6.45 (2.00–13.99)	9.48 (3.99–48.45)	.99 (.98–.997)	.25 (.07–.35)	9.49 (3.99–48.45)	.25 (.075–.34)
242425D	P	6.74 (6.56–6.81)	2.00 (2.00–13.71)	2.19 (1.81–4.43)	.86 (.76–.89)	.036 (.009–.07)	2.20 (1.81–4.44)	.031 (.008–.53)
243265C	S	5.58 (5.47–5.74)	11.66 (2.00–14.01)	28.65 (1.97–240)	.76 (.36–.88)	.082 (.010–.37)	28.67 (1.98–240.23)	.062 (.008–.14)
240108G	P	5.14 (3.96–6.32)	2.00 (2.00–2.00)	5.76 (0–13.1)	.997 (.98–1)	N/A	5.74 (0–13.0)	N/A
C02	P	5.80 (5.13–5.87)	7.33 (4.05–12.38)	112.9 (12.78–240)	0 (0–.61)	19.20 (.01–19.20)	132.10 (18.41–259.20)	0 (0–.091)
C03	S	5.27 (4.99–5.78)	12.24 (2–14.17)	36.26 (2.06–138.70)	.81 (0–.97)	.096 (.0084–19.20)	36.28 (2.07–138.78)	.078 (0–.14)
C05	S	6.39 (5.96–6.94)	10.95 (2.00–13.57)	31.61 (2.31–142.37)	.90 (.67–.99)	.21 (.022–.42)	31.63 (2.35–142.39)	.19 (.022–.31)
C06	P	5.88 (5.77–5.96)	7.85 (6.20–12.45)	98.96 (29.71–196.05)	.10 (0–.33)	.10 (.004–19.20)	99.06 (29.74–201.20)	.011 (0–.032)
C07	S	5.90 (5.57–6.36)	11.36 (2.00–14.79)	33.20 (3.94–47.67)	.98 (.94–.997)	.19 (.018–.29)	33.20 (3.94–47.67)	.18 (.018–.28)
C08	S	5.82 (5.74–5.94)	11.26 (3.87–13.03)	29.49 (1.98–71.12)	.53 (.36–.68)	.043 (.0017–.15)	29.50 (1.99–71.18)	.023 (.0011–.058)
C09	P	5.65 (5.56–5.71)	5.97 (2.00–7.65)	163.60 (99.03–240)	0 (0–.20)	19.20 (.0084–19.20)	182.80 (103.28–257.73)	0 (0–.022)
C10	P	6.67 (6.63–6.78)	9.84 (2–10.81)	14.84 (0.94–194.23)	.51 (.34–.67)	.032 (.012–.071)	14.86 (.95–194.31)	.016 (.0075–.024)
C11	P	4.96 (4.85–5.04)	11.96 (7.17–13.33)	4.39 (3.06–5.64)	.99 (.98–.994)	.066 (.0043–.097)	4.39 (3.06–5.64)	.065 (.0043–.095)
C12	S	6.59 (6.39–7.25)	9.38 (2.00–10.53)	38.79 (2.85–132.18)	.94 (.87–.99)	.18 (.037–.27)	38.80 (2.86–132.19)	.017 (.036–.24)
C15	P	7.03 (6.90–7.36)	12.01 (8.32–14.40)	9.26 (3.72–61.24)	.93 (.87–.97)	.056 (.0051–.14)	9.27 (3.73–61.24)	9.052 (.0048–.13)

NOTE. The 95% confidence interval, calculated from a bootstrap with 199 repetitions, is shown in parentheses below the fitted point estimate.

S, standard IFN alfa2a + ribavirin; P, PEG-IFN alfa2a + ribavirin; N/A, not applicable.

Data from Neumann et al.³

^aHCV/HIV-co-infected patients are listed first with 6 digits and a letter. HCV-monoinfected controls are identified by “C” + 2 digits.

^bViral load (log IU/mL) at time t₀.

^cDelay (hours) between start of treatment and onset of action.

^dClearance rate of free virus (per day).

^ePercent (%) efficacy of treatment at blocking viral production.

^fDeath rate of infected hepatocytes (per day); not applicable for 240108G owing to rapid clearance (<1day).

^gSlope of first phase decline per day (log scale), calculated through first 60 hours of viral load measurements.

^hSlope of second phase decline per day (log scale), calculated through first 400 hours of viral load measurements with the exception of C03 and C10. These patients had significant improvement of model fit with utilization of viral load measurements taken at days 28 and 56, and this information is included in the second-phase parameter estimates. Not applicable for 240108G owing to rapid clearance (<1 day).

Individual Patient Results

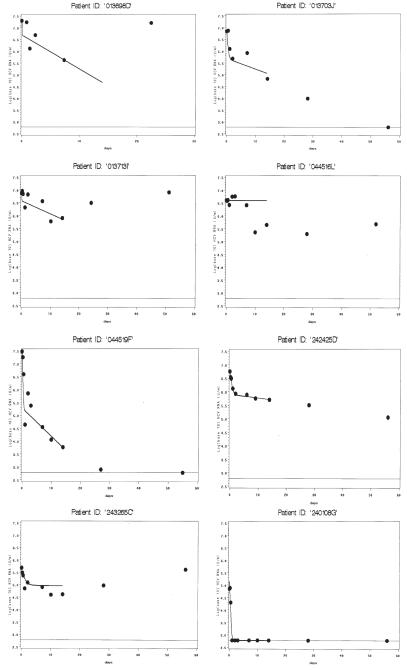
Individual model fits plotted with actual viral load measurements are shown in Figures 1–4. The graphs are classified by infection status and model convergence. Regarding co-infected patients with model convergence (Figure 1), 3 patients (013703J, 044519F, and 242425D) all exhibited models that appeared to correspond well to observed values, suggesting that the parameter estimates were highly reliable. One co-infected patient (240108G) showed very early viral clearance (1 day), and was fit to a single-phase model because no estimation of a phase 2 decline could be obtained. This patient was included in the graphs of model convergence and analyses of ∈, c, and λ₁, but not δ or λ₂. Other patients (013698D, 013713I, 044516L, and 243265C) showed early viral decline followed by rebound. Although the algorithm converged in these patients, the parameter estimates should be interpreted with caution. Patient 013698D had missed a viral load measurement at hour 6. This patient’s estimates were deemed unreliable despite convergence, and were not used in parameter comparisons. Patient 044516L also had very poor fit and was not used in parameter comparisons. However, the other 2 patients have fits that are plausible for their patterns of viral decline during the period of analysis, and their data were used in subsequent analyses.

Figure 1.

Panel of model fit and observed viral loads over time for HCV/HIV co-infected patients with convergence. Viral load (log₁₀ IU/mL) is shown on the y-axis. Days are shown on the x-axis. Dots represent observed values, solid line represents model fits. Fitted values are shown through the time points used in the model for each individual patient. (14 days for patients in this panel). The lower limit of assay detection is represented by the thin solid line at log₁₀(600) IU/mL.

Figure 4.

HCV-monoinfected patients without model convergence. Viral load (log 10 IU/mL) is shown on y-axis. Days are shown on the x-axis. Only observed values are shown. The lower limit of assay detection is represented by the thin solid line at log10(600) IU/mL.

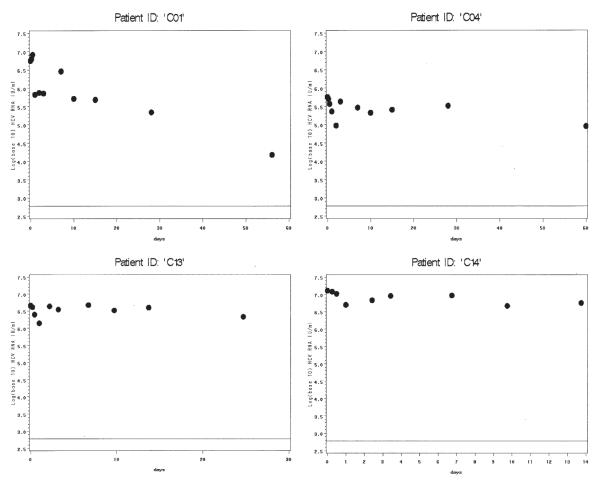
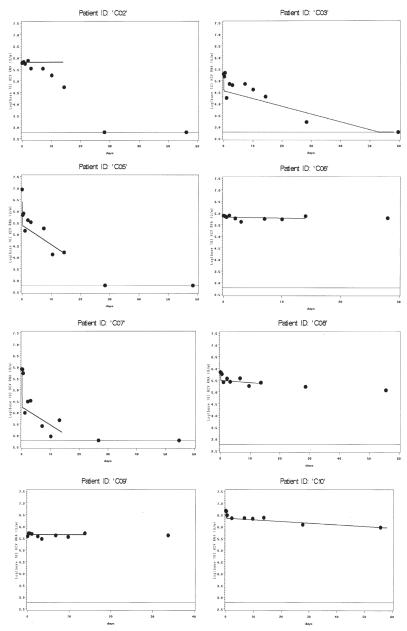
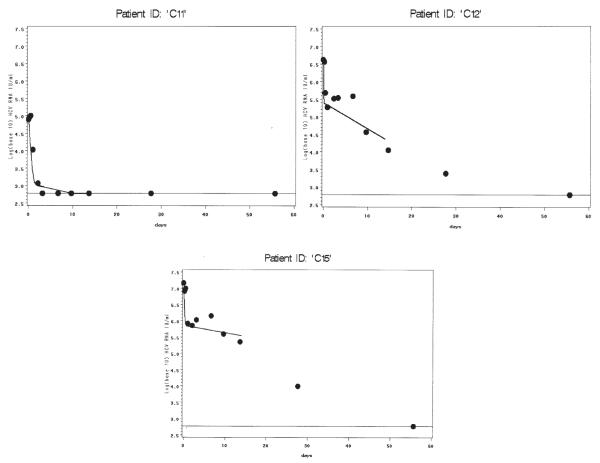
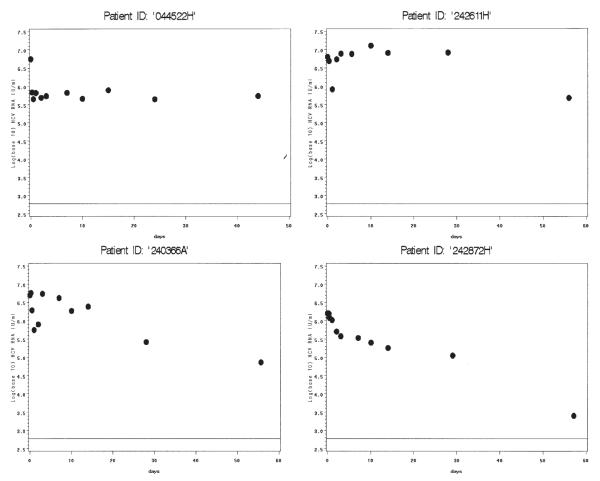
Among monoinfected patients with model convergence (Figure 2), most had strong model fits, including patients with viral decline (C05, C07, C11, C12, C15) and without (C06, C08, C09). Although patient C02 achieved algorithm convergence, this patient’s fit describes the data poorly after the first 5 days. This patient also had missed a viral load measurement at hour 6. Models for C03 and C10 only converged when data from days 28 and 56 were added to the model, but the ensuing fits are convincing. Four patients in each group did not achieve model convergence (Figure 3, co-infected, and Figure 4, monoinfected). These patients generally had strong initial rebound, rendering phase 1 algorithm convergence unattainable with the current model. One patient (242872H), despite fairly consistent viral load decline, did not achieve model convergence even after adding data from 28 and 56 days. The reason for this is unclear; this was the only patient without obvious rebound whose data did not generate reasonable parameter estimates.

Figure 2.

Panel of model fit and observed viral loads over time for HCV monoinfected patients with convergence. Viral load (log 10 IU/mL) is shown on the y-axis. Days are shown on the x-axis. Dots represent observed values, solid line represents model fits. Fitted values are shown through the time points used in the model for each individual patient. For patients C03 and C10, using data from days 28 and 56 allowed much improved parameter estimation. The lower limit of assay detection is represented by the thin solid line at log10(600) IU/mL.

Figure 3.

HCV/HIV co-infected patients without model convergence. Viral load (log 10 IU/mL) is shown on the y-axis. Days are shown on the x-axis. Only observed values are shown. The lower limit of assay detection is represented by the thin solid line at log10(600) IU/mL.

Viral Production and Half-Life

HCV viral production was estimated using methods described previously.³ Briefly, the clearance rate was determined by multiplying the HCV clearance parameter (c) by the baseline HCV-RNA viral load and extracellular fluid volume factor, which is estimated to be 13,360 mL/70 kg, multiplied by the actual pretreatment body weight in kilograms. The overall median production rate for patients with reliably estimable clearance rates was 5.32e+10 (range, 2.47e+08–6.77e+11) IU/mL. The median HCV production rate in monoinfected patients was 5.11e+10 (range, 2.47e+08–2.55e+11) IU/mL. The median rate in all co-infected patients was 1.08e+11 (range, 7.08e+09–6.77e+11) IU/mL. This difference did not reach statistical significance (P = .29).

The viral half-life was calculated as described previously.³ Only patients whose clearance parameters were able to be estimated reliably were used in this analysis. The mean HCV viral half-life was 2.63 hours (95% confidence interval, 1.28–3.99 h), with no significant differences between co-infected vs. monoinfected patients.

Parameter Comparisons

Four key comparisons with respect to treatment and co-infection status were performed. First, we evaluated the HCV kinetics of treatment response in all patients stratified by treatment intervention. Pooled analysis using reliable parameter estimates in both patient groups (Table 4) revealed that the median ∈ in patients treated with PEG was 89.6% (range, 0%–99.7%). The median ∈ for patients treated with standard IFN was 85.4% (range, 53.2%–99.4%). The median first phase decline (λ₁) in the PEG-IFN group was 12.1/day (range, 2.2–182.8/day) vs. 30.6/day (range, 9.5–38.8/day) in the standard IFN group. Analysis of the second phase decline (λ₂) in this subset of patients yielded median values of .03/day (range, 0–.10) and .14/day (range, .02–.25) for PEG and standard treatments, respectively. There were no other significant differences observed in kinetic parameters between treatment groups. Comparison of other estimated parameters by treatment for all patients with model convergence is shown in Table 4.

Table 4.

Comparison of Kinetic Parameters by Treatment Group

	% ε (Efficiency of treatment in first 60 hours)		c (Rate of clearance of free virus per day)		δ (Death rate of infected hepatocytes per day)		λ1 (Slope of phase 1 viral decline)		λ2 (Slope of phase 2 viral decline)
Treatmenta	Mean ± SE	Median (range)	Mean ± SE	Median (range)	Mean ± SE	Median (range)	Mean ± SE	Median (range)	Mean ± SE	Median (range)
PEG IFN + r	66.5 ± 41.0	89.6 (0–99.7)	37.9 ± 60.3	7.5 (2.2–163.6)	2.80 ± 7.23	0.07 (.03-19.2)	56.8 ± 72.5	12.1 (2.20–182.8)	.040 ±.037	.031 (.0–.10)
(n = 8)
Co-infected	93.1 ± 6.84	93.4 (86.0–99.7)	3.95 ± 1.78	3.93 (2.19–5.74)	.07 ± .05	.07 (.04–.11)	48.0 ± 77.8	3.93 (2.20–137.8)	.068 ±.052	.068 (.031–.10)
(n = 3)
Monoinfected	50.6 ± 45.6	50.6 (0–98.8)	58.2 ± 70.6	14.8 (4.39–163.6)	3.89 ± 8.56	.06 (.03–19.2)	62.1 ± 77.9	14.9 (4.39–182.8)	.029 ±.028	.016 (.0–.065)
(n = 5)
P value	.18		.056		NS		NS		NS
Standard IFN +	80.8 ± 18.2	85.4 (53.2–99.4)	28.8 ± 9.2	30.5 (9.5–38.8)	.16 ± .07	.18 (.04–.25)	28.8 ± 9.2	30.6 (9.5–38.8)	.13 ±.077	.14 (.023–.25)
r (n = 8)
Co-infected	76.8 ± 22.1	75.8 (55.2–99.4)	20.3 ± 9.81	22.7 (9.48–28.6)	.18 ± .09	.21 (.08–.25)	27.2 ± 15.9	27.7 (9.49–47.9)	.14 ±.097	.12 (.062–.25)
(n = 3)
Monoinfected	83.1 ± 17.9	90.2 (53.2–97.9)	33.9 ± 3.70	33.2 (29.5–38.8)	.14 ± .07	.18 (.04–.21)	33.9 ± 3.70	33.2 (29.5–38.8)	.13 ±.075	.17 (.023–.19)
(n = 5)
P value	NS		.025		NS		.025 (Mann–Whitney U test)		NS
Pooled	NS		.12		.093		.045		.009
analysis: P
value for
differences
between
treatment
groups

NOTE. Fifteen patients with converging regression models, estimable 95% confidence intervals, and reasonable model fits were included in this analysis. Patients excluded from the analysis were 013698D and C02 (both missing 6-hour viral load measurements), and 044516L (clearly a poor fit despite convergence). Patient 240108G was not included in analysis of second phase response owing to rapid clearance (<1 day).

P values ≤ .25 are reported. The Mann–Whitney U test was used in all statistical comparisons.

NS, not specified.

^aPEG IFN + r, PEG-IFN alfa-2a + ribavirin; Standard IFN + r, standard IFN alfa-2a + ribavirin.

Within the treatment group analysis, we conducted 3 subanalyses. First, we excluded patients with obvious rebound and without viral decline (013713I, C06, C08, C09, and C10), as has been performed previously.¹⁰ The second subanalysis excluded non–genotype 1 patients, and the third subanalysis excluded African-American patients. Results are shown in Table 5. In general, the trends seen in the overall treatment-based parameter comparisons held true in the subanalyses. The efficacy parameter was numerically greater in PEG-treated patients in all cases, whereas clearance, death rate, and phase 2 slope appeared greater in the patients treated with standard IFN.

Table 5.

Comparison of Kinetic Parameters by Treatment Group Subanalysis

Patient group	Treatment group	% εa Median (range)	c/dayb Median (range)	δ/dayc Median (range)	λ1/dayd Median (range)	λ2/daye Median (range)
Without reboundersf	PEG IFN + r (n = 5, 3 co-infected)	93.5(86.0–99.7)	4.39(2.2–9.3)	.061 (.036–.11)	4.39(2.2–137.8)	.059 (.03–.10)
	Standard IFN + r (n = 6, 2 co- infected)	92.0(75.8–99.4)	32.4 (9.5–38.8)	.18 (.082–.25)	32.4 (9.5–38.8)	.18 (.06–.25)
P valueg		NS	.006	.033	.10	.055
Genotype 1 only	PEG IFN + r (n = 7, 2 co- infected)	86.0 (0–98.8)	9.26 (2.20–163.6)	.066 (.032–19.2)	9.3 (2.2–182.8)	.031 (0–.10)
	Standard IFN + r (n = 6, 2 co- infected)	78.2 (53.2–97.9)	31.3 (22.7–38.8)	.14 (.04–.21)	31.4 (22.8–38.8)	.097 (.23–.18)
P valueg		NS	.20	NS	.20	.045
Without African-  Americans	PEG IFN + r (n = 3, 2 co-infected)	93.5 (93.2–99.7)	5.74 (3.93–9.26)	.084 (.045–.11)	9.27 (3.93–137.8)	.078 (.052–.10)
	Standard IFN + r (n = 6, 2 co- infected)	92.0 (53.2–99.4)	30.5 (9.5–38.8)	.18 (.04–.25)	30.6 (9.5–38.8)	.18 (.023–.25)
P valueg		NS	.02	NS	.12	.12

NOTE. Patient groups represent subanalyses of the patients in Table 4.

PEG IFN + r, PEG-IFN alfa-2a + ribavirin; Standard IFN + r, standard IFN alfa-2a + ribavirin; NS, not specified.

^aPercent (%) efficacy of treatment at blocking viral production.

^bClearance rate of free virus (per day).

^cDeath rate of infected hepatocytes (per day); not applicable for 240108G owing to rapid clearance (<1 day).

^dSlope of first phase decline per day (log scale), calculated through first 60 hours of viral load measurements.

^eSlope of second phase decline per day (log scale), calculated through first 400 hours of viral load measurements with the exception of C03 and C10.

^fGroup without rebounders excluded patients 0137131, C06, C08, C09, and C10, retaining patients with patterns of viral decay.

^gP values ≤.25 are reported. The Mann–Whitney U test was used for all statistical comparisons.

Second, we evaluated the HCV viral kinetics for co-infected vs monoinfected patients. When stratified by infection status, and including patients with model convergence, pooled analysis with both treatment arms revealed a median ∈ of 89.7% (range, 55.3%–99.7%) and 85.4% (range, 0%–98.8%) for co-infected and monoinfected patients, respectively. Analysis of the phase 2 decline in these patients yielded median λ₂ slopes of .104/day (range, 0–.25/day) for co-infected patients and .06 (range, 0–.19) for monoinfected patients. Median clearance rates were 7.61/day (range, 4.39–163.6/day) and 32.4/day (range, 2.2–28.7) in the co-infected and monoinfected groups, respectively (P = .02). There were no significant differences between groups regarding the phase 1 response or the infected cell death rate. Because of the small numbers of patients with reliable parameter estimates, matched analysis was not possible. Subanalyses were performed as described earlier. In all cases, when rebounder, non–genotype 1, and African-American patients were removed, the clearance rates became higher in the monoinfected patients than in the co-infected patients (P = .06). No other substantive changes were detected.

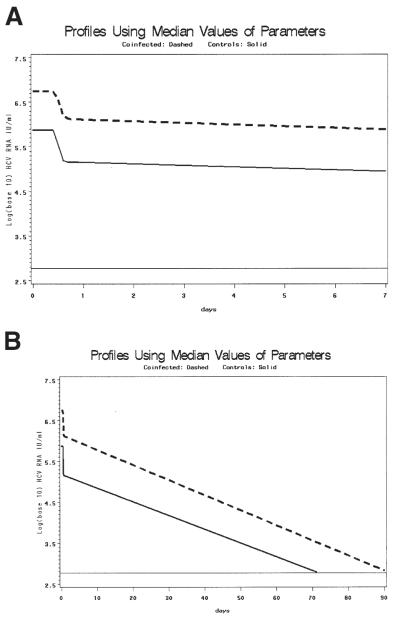
Because no difference was observed between co-infected and monoinfected patients in terms of ∈ or λ₂ slope using pooled analysis, we speculated that baseline viral load would affect treatment outcome significantly. To evaluate the effect of baseline viral load on treatment outcome further, a model of time to clearance was derived from the median parameter estimates from the pooled data. Median V₀, treatment efficacy, clearance, infected cell death rate, and delay in viral decline from reliable estimates of genotype 1 co-infected and monoinfected patients were used to predict time to clearance (HCV RNA <600 IU/mL) in co-infected vs. monoinfected patient pools. The estimated V₀ was 6.86 log₁₀ IU/mL for co-infected and 5.88 log₁₀ IU/mL for monoinfected patients. T₀ was 11.39 vs 11.26 hours for co-infected and monoinfected, respectively; c was 33.20 and 22.67/day, respectively; δ was .11 and .10/day, respectively; and ∈ was .76 and .81, respectively. These parameters were used to calculate λ₁ and λ₂ and the resulting pooled model fits. The results of this model are shown in Figure 5. Assuming no rebound, the patients in both groups are predicted to clear within 90 days, with the co-infected patients taking approximately 20 days longer to clear.

Figure 5.

(A, B) Graphs using median kinetic parameters from genotype 1 patients to show delayed clearance in co-infected patients: all parameters (∈, c, δ, V₀, t₀) were calculated from the median pooled values of the study population for whom the model converged and who had viral clearance. The estimated V₀ was 6.86 log₁₀ IU/mL for co-infected and 5.88 log₁₀ IU/mL for monoinfected patients. T₀ was 11.39 vs. 11.26 hours for co-infected and monoinfected patients, respectively; c was 33.20 and 22.67/day, respectively; δ was .11 and .10/day, respectively; and ∈ was .76 and .81, respectively. These parameters were used to calculate λ₁ and λ₂ and the resulting pooled model fits. Solid line represents co-infected patients, dashed line represents monoinfected patients. The lower limit of assay detection is represented by the thin solid line at log₁₀(600) IU/mL. (A) Early viral clearance (through 7 days). (B) Extension of model estimation through clearance (90 days). There is an approximately 20-day differential for predicted time to clearance between co-infected and monoinfected patients.

Third, we examined predicted time to clearance vs that observed for each of the 3 models described earlier in the Materials and Methods section. Patients who never cleared were assigned a days-to-clearance value larger than the maximum observed or predicted values so that the Spearman correlation coefficient would assign ties to these values—specifically, 3650 days. Predicted days-to-clearance by the biphasic model described by Neumann et al³ was correlated with observed days-to-clearance for the subset of reliable estimates. The Spearman test yielded a statistically meaningful correlation (ρ = .68, P = .0018). The weighted least squares and least median of squares models, also described earlier, yielded similar results.

Finally, we evaluated viral kinetic parameters to determine which single or group parameters were most predictive of ETR response or SVR. From an intent-to-treat analysis, 4 of 12 (33%) co-infected patients and 8 of 15 (53%) monoinfected patients showed ETR at week 48. Three of 12 (25%) co-infected patients achieved SVR compared with 6 of 15 (40%) monoinfected patients. When treatment was considered, 7 of 13 (54%) of the PEG group achieved ETR vs. 5 of 14 (36%) of the standard treatment group, and 5 of 13 (38%) of the PEG group achieved SVR vs. 4 of 14 (29%) of the standard group. None of these differences achieved statistical significance, likely because of the small sample sizes. Three of the 5 patients with genotype 2 rapidly cleared virus independent of co-infection or treatment status. One genotype 2 patient dropped out of the study at day 14, and the other genotype 2 patient cleared virus at day 56.

Among patients with algorithm convergence, 2 patients with ∈ < .90 achieved ETR and SVR. One of these, C02, had a missing 6-hour data point and therefore unreliable parameter estimates, despite model convergence. The other patient, C03, had ∈ = .81 with substantial rebound around day 7 before eventual clearance. Two patients had ∈ > .90 and subsequent ETR, but not SVR. One of these, co-infected patient 013703J, was treated with standard IFN, and the other, C12, was treated with PEG IFN. Both were genotype 1. Ninety percent treatment efficacy yields a decrease in HCV viral load of at least .5 log IU/mL within the first 48 hours of treatment (median decrease for ∈ ≥ 90% was 1.3 log₁₀ IU/mL). Although the number of patients with reliable parameter estimates was too small for multivariable logistic regression, patients with ETR had larger phase 2 slopes than those without ETR (.137 vs. .031, P = .08), and the same trend held for SVR (.13 vs. .062, P = .19). The only parameter to show a strong or significant correlation with either ETR or SVR was ∈ (ρ= .69, P = .001 for ETR; ρ= .55, P = .021 for SVR).

Discussion

Mathematic modeling of viral kinetics has proven to be a powerful tool in our understanding of viral replication and treatment intervention. When applied to HIV infection, the use of viral kinetic modeling dramatically altered our perception about the biology of the virus, its natural history, and the likelihood of cure with existing antiretroviral agents. Similarly, HCV infection is also amenable to modeling, albeit with somewhat different mathematic constructs that reflect differences in pathobiology and therapeutic agents. Models first used to describe the use of IFN in HCV-infected patients revealed very high levels of replication and at least a 2-phase response curve.^3,5,11 Others argued that HCV viral clearance with IFN-based therapy can be approximated better by using a 3-phase model.¹² However, the ideal unifying model has not been identified yet, as evidenced by the proportion of patients whose responses are not predicted using existing constructs.

The study of HCV in the context of HIV infection has particular relevance in the realm of clinical medicine and as a window to our understanding of variable response to treatment in patients with varying degrees of immune dysfunction. This study evaluated prospectively HCV viral kinetics in both HIV–co-infected patients and HCV-monoinfected controls. Previous studies of IFN-based therapies in co-infected patients strongly suggest a diminished treatment response both during and after completion of treatment compared with responses in HCV-monoinfected patients. Even with the use of PEG IFNs, this disparity in virologic response rates persists. The reasons for this diminished response are unclear, although plausible explanations may include high HCV viral load, impaired response of IFN-mediated antiviral pathways, or immunologic dysfunction characterized by delayed clearance of infected hepatocytes. Viral kinetic modeling permits evaluation of these factors.

Multivariate models of treatment response in HCV-monoinfected patients suggest that genotype is the most important factor in treatment response.^13,14 Although only 5 patients in this study had non-1 genotype, 3 patients showed rapid viral clearance after initiation of either standard IFN (n = 2) or PEG-IFN alfa-2a (n = 1) and 1 treated with PEG IFN cleared in 56 days. The last genotype non-1 patient did not complete the study. Among monoinfected patients, HCV viral load generally is regarded as the second major predictor of treatment response.¹⁴ High viral load has been defined arbitrarily as greater than 2 million copies/mL or greater than approximately 800,000 IU/mL. By using these criteria, many studies have shown that HCV/HIV–co-infected patients are much more likely than monoinfected counterparts to have higher serum viral titers.^6,15,16 This observation may represent increased viral production in co-infected patients or, alternatively, a decreased HCV clearance. Torriani et al¹⁷ described a prolonged HCV virion half-life among co-infected patients compared with historical controls—about 7 hours compared with 2–4 hours. This observation, however, may represent an artifact of small sample size or the lack of a prospectively matched control population. Our data showed that HCV virion half-life was not affected by HIV status.

Early (phase 1) response to treatment is determined by the calculation of ∈, or treatment efficiency, which is postulated to represent the level of inhibition of viral production in infected hepatocytes. Our findings suggest that PEG IFN can be more effective than standard IFN in achieving an early decrease in HCV viral production. However, the lack of response in 3 African Americans treated with PEG limited the ability to detect a significant difference. Interestingly, HIV status was not a factor in phase 1 response, suggesting that IFN response pathways are intact in co-infected patients. However, it must be noted that increased viral load may play an important role in overall response, and that when all patients in the study were considered, the median baseline viral load of co-infected patients was 6.75 log IU/mL vs. 5.87 for monoinfected patients. The fitted models in Figure 5 clearly show a delay in clearance associated with the higher viral load that often is observed in co-infected patients, despite the similarities in median parameter estimates between the 2 groups. When the statistically comparable median parameters from the co-infected and monoinfected patient groups are used to predict time to clearance, the co-infected patient takes approximately 28% longer to clear virus than the monoinfected patient, suggesting that the delay in clearance is caused by the higher viral titer. Larger studies in kinetic modeling would be required to validate this hypothesis.

Phase 2 response has been attributed to immunologically mediated clearance of infected hepatocytes,¹⁸ although there is little scientific evidence to support this concept. Again, we found no difference between monoinfected and co-infected patients with regard to the phase 2 decline, leading to the conclusion that infected-cell clearance also was similar between groups. Even among case-control pairs with CD4+ less than 500 cell/mm³, differences in the λ₂ parameter were not observed. Although other investigators have suggested that the phase 2 decline is the best parameter predictor of SVR,^7,19 our data were not supportive of this conclusion. In general, monoinfected patients had phase 2 parameters that were more reflective of their observed viral decay compared with co-infected patients, perhaps owing to the late viral rebound seen in 4 of the co-infected patients with model fits (Figure 1). This does not appear to be the case in monoinfected patients (Figure 2); most patients either had little initial response to the drug, or eventually cleared. Moreover, ∈ was the only parameter that was correlated with either ETR or SVR. Overall, our data suggest that ∈, rather than in second-phase slope, accounts more reliably for the observed outcomes. This is consistent with previous observations of the association between ∈ and treatment response.^17,20,21 It should be noted that among African-American patients, a factor known to affect outcomes,²⁰ 4 had ∈ < .8. Of these, 1 was co-infected and treated with standard IFN, and the other 3 were monoinfected and treated with PEG. However, 3 other African-American patients, 2 co-infected and treated with PEG IFN, 2 monoinfected and treated with standard, and 2 monoinfected and treated with PEG, had relatively high ∈ values (.86, .081, and .098, the latter 2 achieving SVR). It also is noteworthy that one of the 2 patients with ETR and SVR without estimable parameters, 242872H, was also African American and was treated with PEG. All 8 patients were genotype 1, yet 3 of the 8 were able to achieve SVR. This suggests that race, although important, is not the only factor determining response to IFN-based treatment. Although ETR rates for co-infected patients were similar to those for monoinfected patients, SVR was decreased in the co-infected cohort. The reasons for this finding remain unclear.

Even for monoinfected patients, there is disagreement regarding the nature of second-phase decline and how this slope can best be modeled to predict SVR. It has been proposed that this decline describes the rate of viral eradication without cell death, and that it needs to incorporate a function for host-specific immune responses to be more accurately predictive.²² Some investigators have attempted to model the effect of differential immune responses with a third phase of viral decline,¹⁹ some by incorporating an inflation factor for an increasing rate of infected cell death.¹² However, our data did not reveal a third phase of viral decline; patients either cleared quickly, necessitating the fit of a single-phase model, or fit a biphasic model with gradual clearance, or never cleared (phase 2 slope of 0), although it is possible that more frequent viral load measurements taken after 2 weeks of treatment may have reflected a changing rate of decline. Moreover, the current model does not allow for the possibility of viral production from an extrahepatic reservoir. There is evidence that HCV may replicate in macrophages and lymphocytes,^23–27 as well as in extrahepatic tissues,²⁸ however, the impact of such a reservoir on viral kinetics is unknown. The quantity of replication is likely small relative to hepatic viral production, but selection of a treatment-resistant variant from such a reservoir could contribute to viral rebound and to altered production and clearance rates over time. Analysis of quasispecies change in different compartments would be required to determine if this model should incorporate the possibility of multiple viral compartments with varying degrees of production and infectivity.

There are limitations to this study that should be noted. First, although the study design controlled for patient characteristics known to affect response to treatment such as genotype, age, and race by matching co-infected and monoinfected patients, reliable parameter estimates were not able to be obtained for several matched pairs. This necessitated the use of subanalyses to observe treatment effects without confounding factors. Second, at the time of study initiation, induction dosing of standard IFN commonly was used. It is possible that the variability in timing of administration of standard IFN, combined with its short half-life, contributed to the observed phase 1 results; however, analysis of the actual times of sample collection revealed that only 1 patient (C12) sample was collected at a time point that would have a high likelihood of impacting viral kinetics owing to the receipt of the second dose of IFN (6 mIU). Before that, the patient had >1 log decline within the first 12 hours; therefore, we think the ∈ of .94 is not unreasonable, and it is unlikely that phase 1 results were affected significantly. It also is possible that the high induction dosing of standard IFN (6 MU tiw for 12 weeks) contributed to a somewhat higher efficacy than has been observed elsewhere.¹⁰ A similar effect was observed with high doses (10–15 mIU) of IFN-alfa 2b during initial HCV kinetics research.³ However, it is noteworthy that many of the observed rebounds in patients treated with PEG IFN (013703J, 243265C, 044519F, C01, C15) occurred between days 4 and 7, and several standard IFN–treated patients (044516L, 240366A, 242611H, C12, C13) had very early rebound, suggesting that pharmacokinetics may have played a role in early treatment effect. Models have been described that allow for variation in drug kinetics and efficacy²⁹; however, drug concentration levels were not measured in this study, so this type of analysis could not be conducted. Third, viral kinetic analysis is a time-, cost-, and sample-intensive process. Parameter estimation could have been reliable for a greater proportion of patients had it been possible to sample more frequently in the first 48 hours.

In conclusion, viral kinetic modeling indicates that PEG IFN is superior to standard IFN in achieving both on-treatment and sustained viral response, and that this finding can be attributed to improved phase 1 efficacy of viral inhibition and possibly to phase 2 decline in monoinfected patients. It also is possible that the pegylation allows IFN to exert constant pressure on the virus, preventing phases of rebound. Substantive differences between co-infected and monoinfected patients in terms of phase 1 and phase 2 responses were not observed. However, higher viral loads at initiation of therapy may play an important role in treatment outcomes among co-infected patients. These data suggest that longer treatment duration may be necessary to achieve sustained viral clearance of HCV.

Abbreviations used in this paper

ETR

end-of-treatment response

HIV

human immunodeficiency virus

IFN

interferon

PEG

pegylated

SVR

sustained virologic response