Biophysical Underpinnings of the Repeat Length Dependence of Polyglutamine Amyloid Formation

Background: The molecular basis for the repeat length dependence of disease risk in polyglutamine diseases is not known.

Results: We show here a nonlinear dependence of aggregation propensity versus polyglutamine repeat length that qualitatively mirrors how age of onset depends on repeat length.

Conclusion: This provides further support for a role for aggregation in these diseases.

Significance: This lends support to therapeutic strategies targeting aggregation.

Abstract

There are now 10 expanded CAG repeat diseases in which both disease risk and age of onset are strongly dependent on the repeat length of the polyglutamine (polyQ) sequence in the disease protein. Large, polyQ-rich inclusions in patient brains and in cell and animal models are consistent with the involvement of polyQ aggregation in the disease mechanism. This possibility is reinforced by studies showing strong repeat length dependence to the aggregation process, qualitatively mirroring the repeat length dependence of disease risk. Our understanding of the underlying biophysical principles that mediate the repeat length dependence of aggregation, however, is far from complete. A previous study of simple polyQ peptides showed that N*, the size of the critical nucleus that controls onset of aggregation, decreases from unfavorable tetramer to favorable monomer over the range Q₂₃ to Q₂₆. These data, however, do not explain why, for all peptides exhibiting N* ∼ 1, spontaneous aggregation rates continue to increase with increasing repeat length. Here we describe a novel kinetics analyses that maps out the nonlinear dependence with repeat length of a nucleation efficiency term that is likely related to aspects of nucleus structure. This trend accounts for why nucleus size increases to tetrameric at repeat lengths of Q₂₃ or below. Intriguingly, both aggregation and age of onset trend with repeat length in similar ways, exhibiting large changes per added Gln at low repeat lengths and small changes per added Gln at relatively long repeat lengths. Fibril stability also increases with repeat length in a nonlinear fashion.

Introduction

There are a large number of triplet repeat expansion diseases in abnormal human biology (1). Some pathogenic triplet expansions occur in noncoding DNA segments, whereas others occur in coding regions. One fascinating subset of the latter grouping are the 10 known expanded CAG repeat diseases that are associated with expansions of a polyglutamine (polyQ)² sequence in a disease protein (2). These maladies, which include Huntington disease (3, 4), are progressive neurological disorders often presenting with movement or psychiatric symptoms (2). The boundaries between benign and pathogenic polyQ repeat lengths vary for different diseases from about 20 to about 45, with pathological thresholds in the range of 30–40 in most cases (2). In each disease, inheritance of a CAG repeat only slightly longer than the threshold confers a dramatic increase in disease risk. Above this characteristic threshold, age of onset decreases as repeat length increases according to a nonlinear trend featuring relatively large decreases in age of onset for repeat lengths just above the threshold, and much smaller decreases with each added CAG repeat at much longer repeat lengths (5, 6). Furthermore, age of onset and severity of symptoms actually decrease, in a mouse model of Huntington disease, at a very long polyQ repeat length (7). One possible explanation for these nonlinear trends in age of onset is an attenuation in the efficiency of formation of the toxic species at longer repeat lengths. Although the molecular mechanisms by which polyQ tract expansion triggers disease onset remain undefined (8–15), it seems reasonable to expect that, whatever the underlying molecular events that trigger the early cellular events in disease onset, these events should exhibit their own characteristic repeat length dependence.

One proposed family of molecular mechanisms is associated with the tendency of polyQ chains to aggregate into amyloid fibrils or other assemblies (16–18). Neuronal inclusions staining for polyQ have been identified in autopsy material in all 10 of the known expanded polyQ diseases, and polyQ aggregates are also a recurring feature of cell and animal models of polyQ diseases (2, 19, 20). Although evidence has been presented that the very large inclusions visible by light microscopy are more protective than toxic (21), it is very likely that expanded polyQ-producing cells harbor a variety of much smaller aggregates that are invisible to such techniques (22). For example, small oligomers and amyloid fibrils have been identified in studies of polyQ protein aggregation in vitro (23–26), oligomeric forms of unknown molecular structure can be detected in cells (27, 28) and in extracts of animal models (29), and isolated amyloid fibrils have been imaged in a cell culture model by super-resolution fluorescence microscopy (30). Importantly, polyQ aggregation both in vitro (31) and in cell (32) and animal (33) models exhibits a repeat length dependence that mirrors remarkably well the repeat length dependence of disease and age of onset.

Few studies have been reported examining the repeat length dependence of polyQ spontaneous amyloid formation and its underlying basis. One challenge in designing such studies is the fact that disease-associated polyQ sequences are always situated in the interior portions of the disease proteins (2), and, at least in some cases, the flanking sequences to the polyQ can have enormous impacts on their aggregation tendencies and mechanisms (25, 34). Nonetheless, the repeat length dependence of aggregation rate of polyQ sequences appears to be fundamental, manifesting not only in simple polyQ peptides with only a few solubilizing charged flanking residues (31) but also in the disease protein context (25). Given that polyQ is the common feature of all expanded polyQ disease proteins, it seems appropriate to first examine the structural basis for the repeat length effect in the isolated polyQ sequence.

Recently, we reported that one strong correlation with polyQ repeat length is the nucleus size, or critical nucleus, N*, for aggregation (35). We found that sequences containing Q₂₃ or lower require a tetrameric nucleus (i.e. N* = 4) for initiation of amyloid growth, whereas sequences of Q₂₆ or above require formation of a monomeric nucleus (N* = 1) that is presumed to be some specific, highly unfavorable folding state (35, 36). Because aggregation via a monomeric nucleus is much more efficient, sequences of Q₂₆ or higher exhibit much faster spontaneous aggregation as compared with Q₂₃ or shorter polyQ at similar concentrations (35). This dramatic change in nucleus size does not fully account for the repeat length dependence of aggregation, however. In particular, whereas all repeat lengths of Q₂₆ or above initiate aggregation via a monomeric nucleus (35), previous studies suggest that aggregation rates continue to increase as repeat lengths increase above Q₂₆ (31, 33, 37). Furthermore, the underlying explanation for why a change in nucleus size occurs precisely in the Q₂₃–Q₂₆ repeat length regime remains a complete mystery. Finally, it is worth considering that whereas repeat length clearly influences the kinetics of aggregation, there may also be a role for repeat length differences in aggregate stability in defining whether aggregates of particular polyQ repeat lengths can actually accumulate under in vivo conditions.

Here we conduct a quantitative analysis of the nucleation kinetics of a series of simple polyQ peptides with respect to polyQ repeat length, placing a special emphasis on a nucleation kinetics parameter not previously studied in a systematic way. We also investigate the dependence of fibril stability on repeat length. The results reveal clear patterns in both comparisons, suggesting that both may play a role in aggregation in vivo and hence perhaps in polyQ toxicity. The results also suggest a fundamental transition region for both properties in the Q₂₃ to Q₂₆ region, suggesting a common structural rationale.

EXPERIMENTAL PROCEDURES

All peptides were acquired crude from the Small Scale Synthesis facility at the Keck Biotechnology Resource Laboratory of Yale University. Peptides were purified and disaggregated, and reactions were prepared at 37 °C and monitored by HPLC as described (38, 39). Dissociation reactions to determine ΔG_elong were performed by diluting end stage aggregation reactions with PBS and following dissociation upon incubation at 37 °C by HPLC (38). Nucleation kinetics analysis of the HPLC/sedimentation aggregation kinetics data was performed as described (38, 39). N* values were calculated by subtracting 2 from the slope of the log-log plot of rate versus concentration (40). To obtain y-intercept values (log[0.5 k₊²K_N*]) of the log-log plots for the data analysis described here, experimental data were extrapolated by applying the closest integer slope (i.e. 3 for N* = 1, etc.).

RESULTS

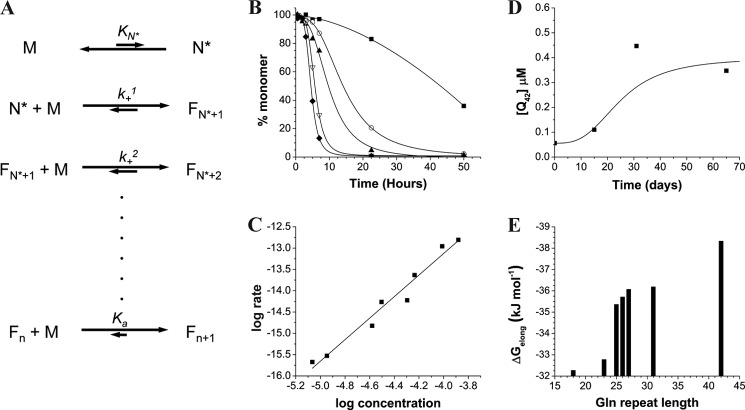
Based on their multimeric nature, aggregation rates typically exhibit a dependence on starting concentration, and details of this dependence can provide important information on the mechanisms of how reactions are initiated (“nucleation”) (41) and how aggregates, once established, are propagated (“elongation”) (42). Sigmoidal time courses are typically observed for nucleated growth polymerization reactions such as those undergone by simple polyQ peptides (41). A general mechanism for this type of process is shown in Fig. 1A. The slow onset of aggregation, often referred to as a lag time, reflects the operation of a high energy barrier to the organization of an aggregation nucleus (Fig. 1A, N*). As is typical for aggregation dominated by primary nucleation (41), lag phases for early polyglutamine aggregation kinetics tend to exhibit rather gradual onsets of aggregation; this is in contrast to the abrupt onset of aggregation observed in cases of secondary nucleation (41, 43). Once initiated, aggregation reactions proceed until monomer is essentially depleted and a position of equilibrium (Fig. 1A, last line) is reached (44).

FIGURE 1.

Analysis of nucleated growth polymerization of K₂Q₄₂K₂ amyloid formation. A, nucleated growth polymerization mechanism (41) where M is the monomer ensemble, N* is the critical nucleus, F species are growing fibrils, K_N* is the equilibrium constant for nucleus formation, k₊ values are macroscopic elongation rate constants for the nucleus and nascent fibril, and K_a is the association constant for fibril elongation. B, aggregation kinetics monitored by HPLC sedimentation assay at starting concentrations 131 μm (♦), 97.4 μm (▿), 58.1 μm (▴), 31.3 μm (○), and 8.6 μm (■). C, log-log plot of initial aggregation rates versus initial concentrations. D, determination of C_r value by monitoring dissociation of monomer from amyloid fibrils to an equilibrium concentration of monomer. E, ΔG_elong values, derived from measured C_r values, versus polyQ repeat length.

Incubation at 37 °C of freshly disaggregated (see ”Experimental Procedures“) K₂Q₄₂K₂ in PBS leads to a time-dependent loss of monomer from solution that exhibits this kind of typical sigmoidal aggregation kinetics curve (Fig. 1B). Incubation at lower starting concentrations leads to similar sigmoidal time courses featuring longer lag times (Fig. 1B). All the peptides in this study exhibited analogous concentration-dependent, sigmoidal aggregation time courses. All of the aggregated products appear to be homogeneous, amyloid-like structures by electron microscopy (not shown).

Critical parameters of the nucleation mechanism can be extracted from the concentration-dependent kinetics data using the mathematical approach of Ferrone and co-workers (see “Experimental Procedures”) (40, 41) based on a thermodynamic model of aggregation nucleation (Fig. 1A). The culmination of this analysis is a log-log plot of initial aggregation rate with respect to starting concentration. The slope of the log-log plot is related to the critical nucleus N*, which is the number of molecules required to form the nucleus. The y-intercept of the plot is related to the efficiency with which this critical nucleus promotes aggregation initiation, based on underlying parameters for the equilibrium constant for nucleus formation (K_N*) and the rate constants for elongation of the nucleus and growing fibril (k₊) (Fig. 1A).

The log-log plot for K₂Q₄₂K₂ is shown in Fig. 1C. The parameters extracted for K₂Q₄₂K₂, as well as for other simple polyQ peptides, are summarized in Table 1. The table shows that the N* values for aggregation of all peptides examined tend to be fractional values lying in the vicinity of 1, consistent with a monomeric nucleus. Similar values have been obtained previously for simple polyQ peptides with repeat lengths of Q₂₆ or higher (35, 36, 40, 45–47). Although it is possible that genuine fractional values for N* might reflect subtleties of the nucleation mechanism (48), it is important to note that the precision of the log-log plots, even when they include up to 10 data points, is moderate. Thus, although our typical experimental scatterplots can reliably distinguish between N* = 1 and N* = 2, they cannot reliably distinguish between an N* of 1.0 and fractional values hovering around N* = 1 (35). Table 1 also shows the y-intercept values from the log-log plots. More positive values of the y-intercept are associated with greater efficiency of conversion of the critical nucleus into propagating fibrils. Thus, larger K_N* values favor the transient formation of nuclei in equilibrium with the monomer ensemble, and larger k₊ values favor more efficient conversion of these nuclei into growing fibrils that, once formed, are energetically unlikely to completely dissociate (Fig. 1A). Table 1 shows that for simple polyQ peptides with N* values in the range of 1, y-intercept values become more positive as repeat length increases.

TABLE 1.

Parameters for polyglutamine nucleation and elongation

All data are from this work, unless otherwise indicated.

Repeat lengtha	N*	log (0.5 k+2KN*)b	Cr
			μm
18	3.7c	NDd	3.6c
23	3.9c	NDd	3.0c
25	NDd	NDd	1.1c
26	1.0	−3.15	1.0
26	0.9c	−3.33	NDd
27	1.2	−3.62	0.8
27	0.9c	−3.08	NDd
29	0.8	−2.48	NDd
30	0.7	−2.80	NDd
31	1.0	−1.87	0.8
34	1.0	−1.68	NDd
37	0.9	−2.10	NDd
42	0.5	−0.92	0.3
47	0.9e	−0.22	NDd

^a All peptides are of general structure K₂Q_nK₂.

^b Listed only for peptides with N* ∼ 1.

^c From reference (35).

^d Not determined.

^e From reference (36).

Although the concentration of monomer when fibril formation reaches equilibrium (Fig. 1A, last line) is often only a very small percentage of the starting concentration, the final concentration is not zero and is actually highly significant. If the number of fibrils, and hence their molar concentration, is static as equilibrium is approached (Fig. 1A, last line), and if the free energy change for elongation is essentially independent of fibril length, then the concentration of monomers at equilibrium, C_r, is equivalent to the average fibril dissociation constant, K_d (44). The inverse is therefore K_a (Fig. 1A, last line), which has an associated free energy of elongation, ΔG_elong (44). Thus, the lower the C_r value, the farther the equilibrium position is to the right, and the more resistant the fibrils are to dissociation. The derived ΔG_elong can be remarkably robust, for example by giving information on the energetic costs of mutations for amyloid formation that are in very good agreement with the energetic costs of folding for the same mutations in a β-sheet of a globular protein (49). The most robust way to determine the C_r is by monitoring the dissociation of freshly made fibrils; a typical determination by this method is shown for K₂Q₄₂K₂ in Fig. 1D. In contrast to amyloid fibrils of Aβ₄₀, which dissociate to equilibrium within 1 day in PBS at 37 °C (44), K₂Q₄₂K₂ and other polyQ fibrils take weeks to dissociate to equilibrium (Fig. 1D). It should be noted that although the best fit of the data in Fig. 1D is a sigmoidal curve, confidence is not high that this is a realistic representation of dissociation kinetics, which would require substantially more data points to determine. On the other hand, confidence in the plateau values (the C_r) of such plots is high because they generally match extremely well with the plateau values in the fibril association direction (44, 50). The C_r values for the polyQ peptides examined in this study are shown in Table 1. The values tend to lie in the low μm range, similar to those found for Aβ₄₀ (44, 50). Such C_r values are associated with ΔG_elong values of −32.2 to −38.3 kJ/mol. It can be seen from Table 1 that C_r values tend to decrease, and amyloid fibril stability tends to increase, as polyQ repeat length increases.

DISCUSSION

Our data (Table 1) show that there is a general improvement in nucleation efficiency (the k₊²K_N* term) as well as amyloid fibril stability (the C_r term) as polyQ repeat length increases. Beyond these general trends lie some subtleties that are worth exploring. For example, graphical representation of the C_r data (Fig. 1E) shows a nonlinearity to the increase in fibril stability with increasing repeat length. Between Q₁₈ and Q₂₃, ΔG_elong changes by only 0.1 kJ/mol per residue, and between Q₂₅ and Q₄₂, the average change is about 0.17 kJ/mol per residue. However, between Q₂₃ and Q₂₅, ΔG_elong changes by about 1.3 kJ/mol per residue. This represents a dramatic increase in fibril stability over a very short polyQ repeat length range, suggesting an underlying structural cause. Interestingly, recent vibrational CD and hydrogen exchange studies also suggest dramatic changes in polyQ amyloid structure as polyQ repeat length increases over a similarly narrow range (51).

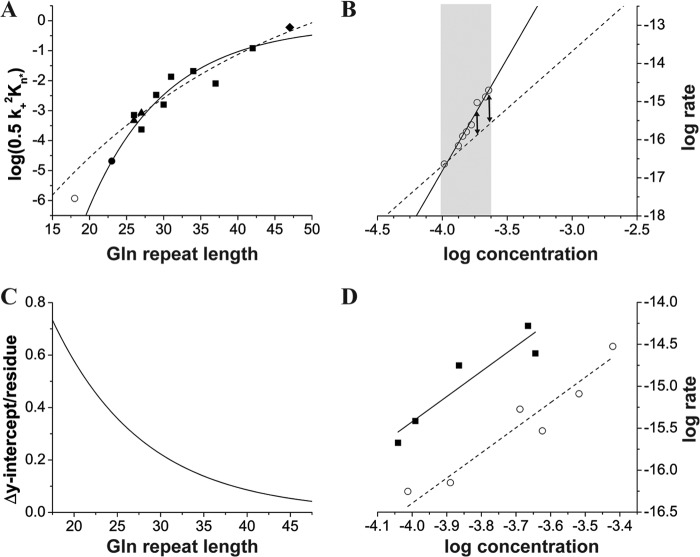
A qualitatively similar discontinuity was observed in the Q₂₆ range for the trend of nucleation efficiency with repeat length, and we explored the basis of this nonlinearity in some detail. Fig. 2A shows a plot of log(0.5 k₊²K_N*), the y-intercept of the log-log plots, with respect to polyQ repeat length. The experimental data points from nucleation kinetics performed in this work (■), in addition to previously reported analyses (35, 36) of other peptides in the series K₂Q_nK₂ (▴,♦), show a nonlinear dependence of log(0.5 k₊²K_N*) with repeat length (Fig. 2A, dashed line). In the low repeat length range, log(0.5 k₊²K_N*) changes relatively steeply with repeat length, whereas at longer repeat lengths there is a more shallow dependence. The trend suggests that as repeat length is successively reduced from Q₃₁ to Q₂₆, the structures involved in the formation and elongation of the nucleus become increasingly sensitive to each loss of a Gln residue. This in turn suggests a possible explanation for the mysterious change in nucleation mechanism that occurs in the Q₂₃–Q₂₆ range. Perhaps the nucleation mechanism changes at low polyQ repeat length because the N* = 1 mechanism becomes so energetically unfavorable, as capsulized in the y-intercept value, that it is effectively outcompeted by the N* = 4 mechanism.

FIGURE 2.

Analysis of repeat length dependence of polyQ peptides aggregating by an N* = 1 mechanism. A, scatterplot of log(0.5 k₊²K_N*), the y-intercept of log-log plots, versus repeat length for peptides in the series K₂Q_nK₂ of various polyQ repeat length. Data shown are from this study (■) or from references (35) (▴) and (36) (♦). Also shown are points representing the maximum possible values for the y axis for K₂Q₂₃K₂ (●) and K₂Q₁₈K₂ (○) peptides aggregating via an N* = 1 mechanism (see ”Discussion“ and panel B of this figure). The lines represent exponential fits to different sets of data points: dashed (■,▴,♦); solid (■,▴,♦,●). B, log-log plot estimating the maximal possible value for the y-intercept for a K₂Q₂₃K₂ peptide aggregating via an N* = 1 mechanism. Concentration-dependent aggregation data (○) are from Ref. 35. The solid line is the best fit straight line to these data, giving a slope of 5.9 and an N* of 4.0, as described (35). The dashed line is a theoretical line of slope = 3.0 drawn through the lowest experimental data point and extrapolated to the y axis. See ”Discussion“ for details. C, transformation of the panel A fit line showing how the y-intercept value changes with polyQ repeat length at different polyQ repeat lengths. D, experimental initial aggregation rates at different starting concentrations for the peptides K₂Q₉pGQ₉K₂ (○) and K₂Q₁₀pGQ₁₀K₂ (■), where p = d-Pro. The best fit straight lines give N* values of 0.81 and 0.98, respectively. Data were therefore fit to straight lines of slope 3.0, and the lines were extrapolated to the y axis to give intercepts of −4.39 and −3.42, respectively. This gives a difference in y-intercepts of 0.98.

One way to rigorously test this hypothesis would be to obtain experimental data for short polyQ peptides under conditions favoring the N* = 1 mechanism, so that additional data points could be added to Fig. 2A. This is not practical, however, given the clear preference for the N* = 4 mechanism with these short polyQ peptides. We therefore devised an alternative strategy in which we (a) assumed the hypothesis to be correct, (b) determined an approximate y-intercept for a K₂Q₂₃K₂ peptide based on this assumption, (c) included this estimated data point in a fit of the experimental y-intercept data, and (d) used independently obtained experimental data to test the accuracy of the resulting trend line in the low repeat length regime of the fit. [It is important to note that the y-intercept values for K₂Q₂₃K₂ aggregating by either an N* = 1 or an N* = 4 mechanism will be different because of the difference in the value of K_N* expected for the two mechanisms; thus, one cannot use the y-intercept for the N* = 4 mechanism in the proposed analysis.]

Our approach is to inquire what the highest y-intercept value might be for an N* = 1 mechanism for K₂Q₂₃K₂ such that it would still be cleanly outcompeted by the N* = 4 mechanism and hence not observed experimentally. This was done using the graphical analysis shown in Fig. 2B. This figure shows the standard log-log plot of aggregation rates versus starting concentration with the data points (○) previously described for K₂Q₂₃K₂ (35). These data points fall in the experimentally accessible part of concentration space shown by the gray shading; aggregation rates for poorly aggregating K₂Q₂₃K₂ peptides at concentrations outside of this range are extremely difficult to measure accurately. The solid line shows the fit to the experimental data leading to the previous determination (35) that N* = 4 under these conditions. The dashed line shows the hypothetical log-log fit, with a slope of 3 corresponding to N* = 1, extrapolated to the y axis. The dashed line is drawn so that any data points on this line would represent slower aggregation rates than those experimentally observed (arrows). This indicates that an N* = 1 mechanism for K₂Q₂₃K₂ might be observable were it not for the relative efficiency, in the experimental concentration range, of the N* = 4 mechanism. The y-intercept of the dashed line, −4.68, is thus the highest possible y-intercept for an N* = 1 mechanism for K₂Q₂₃K₂ such that it would still not be experimentally observed due to the competing N* = 4 mechanism. We believe that the actual y-intercept value must be reasonably close to this y-intercept upper limit because N* is systematically increasing from 1 to 4 as repeat length shrinks from Q₂₆ to Q₂₃ (35).

The addition of this upper limit estimate for K₂Q₂₃K₂ (●) to Fig. 2A shows that it qualitatively continues the general trend of the experimental data (■,▴,♦). These data, plus the K₂Q₂₃K₂ estimate, yield a good fit to an exponential equation that emphasizes the nonlinear relationship in the data (Fig. 2A, solid line). Interestingly, when a graphical analysis (not shown) of previously obtained (35) K₂Q₁₈K₂ data is conducted in analogy to that shown in Fig. 2B, it yields an upper limit (○) y-intercept that falls well above the Fig. 2A solid trend line. This is consistent with the hypothesis that although the N* = 1 and N* = 4 mechanisms are of comparable efficiency in the Q₂₄–Q₂₅ repeat length range, as repeat lengths decrease further in this concentration range, the N* = 1 mechanism becomes increasingly unfavorable and hence the N* = 4 mechanism becomes increasingly favored.

The ever increasing challenge of kick-starting amyloid growth via a monomeric nucleation mechanism as polyQ repeat lengths become shorter is shown in Fig. 2C, which is a transform of the Fig. 2A solid line fit. It shows that the y-intercept value is predicted to change by only about 0.07 for each added or subtracted Gln residue in the Q₄₃ range, but is predicted to change by about 0.7, or 10 times as much, in the Q₁₆ range. Although the Δy/residue values predicted for polyQ in the Q₂₆–Q₄₇ range are based on experiment, the Δy/residue values in the Q₂₀ range cannot be experimentally tested directly for simple polyQ peptides in this concentration range because the N* = 1 mechanism is not competitive with the N* = 4 mechanism under such conditions. However, it is possible to devise an experimental test for the reasonableness of the Fig. 2A fit and the resulting Fig. 2C trend by constructing short polyQ analogs constrained, through introduction of β-hairpin-inducing mutations (52), to aggregate via an N* = 1 mechanism. The log-log plots of two such peptides are shown in Fig. 2D. As expected, although both peptides aggregate via N* values in the range of 1, the longer peptide, K₂Q₁₀pGQ₁₀K₂ (a nominal Q₂₂ peptide counting the central d-Pro and Gly residues), aggregates significantly faster than the shorter peptide, K₂Q₉pGQ₉K₂ (a nominal Q₂₀ peptide). This is because K₂Q₁₀pGQ₁₀K₂ has a more favorable y-intercept, which was found to be 0.98 higher than the corresponding value for K₂Q₉pGQ₉K₂. This corresponds to a Δy/residue value of 0.49, which is in very good agreement with the Δy/residue value of 0.53 predicted for polyQ in the Q₂₁ range based on the curve in Fig. 2C. We believe that this agreement supports our underlying hypothesis and the methods used to test it.

We interpret the results shown in Fig. 2 as being consistent with the hypothesis that aggregation via a monomeric nucleus becomes increasingly less competitive as polyQ repeat length decreases until, in the K₂Q₂₃K₂ range, it becomes so unfavorable that it is out-competed by an alternative nucleation mechanism involving a tetrameric nucleus. This happens, despite the added constraint of diffusional entropy in assembling a tetrameric nucleus, because of the high inefficiency associated with productive nucleation via a monomeric nucleus. This high inefficiency at low polyQ repeat length might be due to a highly unfavorable K_N*, highly unfavorable k₊ values, or both (Fig. 1A). We think it is most likely that the solid trend line in Fig. 2A is primarily due to the impact of repeat length on the folding equilibrium constant for the monomeric nucleus, K_N*. Steep dependence of the folding free energy on polyQ repeat length might be expected, for example, if the monomeric nucleus for polyQ aggregation is a highly unfavorable β-hairpin, as has been suggested (35, 45, 52). Although detailed repeat length-dependent calculations are needed, our results are consistent with preliminary computational studies of polyQ folding and self-association (53, 54).

The graphical analysis shown in Fig. 2B also suggests that at starting concentrations lower than about 100 μm, the monomeric nucleation pathway will become more favorable than the tetrameric nucleation pathway for a K₂Q₂₃K₂ peptide. However, although this prediction may be quantitatively correct, the point is that aggregation by both mechanisms is so unfavorable for short polyQ sequences at such low concentrations as to be unobservable.

Together, our results provide new details for how polyQ repeat length influences the likelihood that amyloid aggregates will emerge and accumulate. Decreases in polyQ repeat length below Q₂₆ affect the energetics of fibril formation especially dramatically. First, low polyQ repeat lengths destabilize the structures required for aggregation nucleation to such an extent that the monomeric nucleation mechanism that is operative at higher polyQ repeat lengths becomes poorly competitive. Second, lower repeat lengths lead to a dramatic reduction in fibril stability so that it becomes reasonable to consider that the poor thermodynamic stabilities of amyloid fibrils of short polyQs may well be responsible for the lack of amyloid accumulation by such sequences in cells and animals.

In contrast to the dramatic effects operating at the low end of the repeat length range examined here, we find very modest systematic increases in nucleation efficiency and fibril stability as repeat lengths increase above the Q₃₀ range. Although we were not able to examine the very long repeat lengths found in some patients, the curvature in Fig. 2C suggests that the Δy/residue parameter will continue to get smaller and smaller as repeat lengths increase for polyQ sequences with higher repeats than those studied here. Such results could provide a mechanistic explanation for the significant curvature found in correlations of age of onset versus CAG repeat length in several CAG repeat expansion diseases, such that in patients with very high repeat lengths the average decrease in age of onset for each added CAG is substantially smaller than the corresponding value for lower repeat lengths (5, 6).