Chloride and Salicylate Influence Prestin-dependent Specific Membrane Capacitance

Background: The SLC26a5 outer hair cell motor drives electromechanical behavior of this sensory/effector cell.

Results: A kinetic model fits the combined effects of salicylate and chloride on prestin-associated membrane capacitance.

Conclusion: Data support a theory whereby prestin differentially changes area state upon binding of chloride and salicylate.

Significance: The model of prestin activity points to the molecular underpinnings of electromotility in outer hair cells.

Abstract

The outer hair cell is electromotile, its membrane motor identified as the protein SLC26a5 (prestin). An area motor model, based on two-state Boltzmann statistics, was developed about two decades ago and derives from the observation that outer hair cell surface area is voltage-dependent. Indeed, aside from the nonlinear capacitance imparted by the voltage sensor charge movement of prestin, linear capacitance (C_lin) also displays voltage dependence as motors move between expanded and compact states. Naturally, motor surface area changes alter membrane capacitance. Unit linear motor capacitance fluctuation (δC_sa) is on the order of 140 zeptofarads. A recent three-state model of prestin provides an alternative view, suggesting that voltage-dependent linear capacitance changes are not real but only apparent because the two component Boltzmann functions shift their midpoint voltages (V_h) in opposite directions during treatment with salicylate, a known competitor of required chloride binding. We show here using manipulations of nonlinear capacitance with both salicylate and chloride that an enhanced area motor model, including augmented δC_sa by salicylate, can accurately account for our novel findings. We also show that although the three-state model implicitly avoids measuring voltage-dependent motor capacitance, it registers δC_sa effects as a byproduct of its assessment of C_lin, which increases during salicylate treatment as motors are locked in the expanded state. The area motor model, in contrast, captures the characteristics of the voltage dependence of δC_sa, leading to a better understanding of prestin.

Introduction

The piezoelectric-like motor molecule SLC26a5 (prestin) underlies the ability of OHC² to enhance hearing (1–3). This boost in performance is driven by a voltage-dependent mechanical response, termed somatic electromotility (4–6). Associated with the mechanical response is a bell-shaped nonlinear capacitance (NLC), which results from the voltage sensor activity of the motor (7, 8). Long before the molecular identification of the motor, two-state Boltzmann models of the motor incorporating state-dependent surface areas were developed (9–12). These were founded on experimental evidence that surface area in the OHC is voltage-dependent (13). In support of these models, we measured changes in specific membrane capacitance that corresponded to the distribution of motors, evidencing an increase in linear capacitance as more motors were driven into the expanded state by hyperpolarization (14). Membrane capacitance necessarily depends on membrane surface area and/or associated changes in membrane thickness. A derived equation based on that observation, termed the two-state C_sa model equation, is far superior in fitting NLC data than is a simple two-state one. Recently, Homma and Dallos (15) proposed a three-state Boltzmann model that rivals the two-state C_sa model in the data-fitting precision of salicylate-treated OHCs, but that additionally challenges the existence of a voltage-dependent area change accompanying the conformational transitions of prestin. Here we provide further evidence that an area motor model better describes the biophysical behavior of the motor. Through modeling, we show how salicylate competition with chloride may result in state-dependent modification of specific membrane capacitance.

EXPERIMENTAL PROCEDURES

The methods for single hair cell recordings were the same as described previously in detail (16). Hartley albino guinea pigs were sacrificed with halothane. Temporal bones were excised, and the top three turns of the cochleae were dissected for enzyme treatment (0.5 mg/ml dispase I, 10–12 min). Individual outer hair cells were isolated by gentle trituration. Isolated single outer hair cells were then studied under whole cell voltage clamp and were held at 0 mV to eliminate the electrical drive for chloride across the lateral membrane. A custom made Y-tube perfusion system was used to deliver experimental solutions to isolated OHCs. The base extracellular solution contained, in mm, 140 NaCl, 2 CaSO₄, 1.2 MgSO₄ and 10 Hepes. Chloride concentration was adjusted from 1 to 140 mm by substituting chloride with gluconate. Final solutions were adjusted to ∼300 mosm with d-glucose and adjusted to pH 7.2–7.3 with NaOH. Pipette solutions (same as extracellular solution except with the addition of 10 mm EGTA) contained chloride ranging from 1 to 140 mm. The extracellular perfusion solution (1–140 mm chloride) also contained graded concentrations of salicylate (1 μm to 10 mm).

Nonlinear capacitance was measured using a continuous high resolution (2.56-ms sampling) two-sine stimulus protocol (10-mV peak at both 390.6 Hz and 781.2 Hz) superimposed onto a voltage ramp from −150 to +140 mV at a clock sample period of 10 μs (17, 18). Capacitance data were fit to the first derivative of a two-state Boltzmann function with an additional component describing the changes in specific membrane capacitance generated by motor state transitions (14). This equation is termed the two-state C_sa model equation.

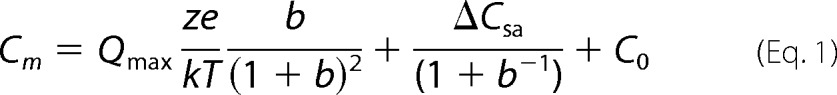where

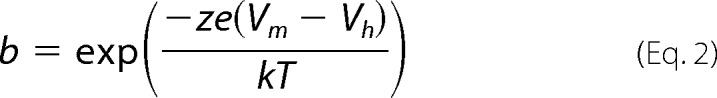Q_max is the maximum nonlinear charge moved, V_h is voltage at peak capacitance or equivalently, at half-maximum charge transfer, V_m is membrane potential, z is valence, e is electron charge, k is Boltzmann's constant, and T is absolute temperature. C₀ is defined as the capacitance of the membrane when all motors are in their compact state, the minimum membrane capacitance; ΔC_sa is the maximum increase in capacitance that occurs when all motors change from compact to expanded state, each motor contributing a unit response of δC_sa. Voltage-dependent NLC was calculated from estimates of Q_max, namely NLC = Q_max/(4kT/ze). The number of motors is: N = Q_max/ze.

Alternatively, NLC was fit with the three-state model equation, possessing two sets of Boltzmann parameters (z₁, V_h1, z₂, V_h2, N = N₁ + N₂) of Homma and Dallos (15).

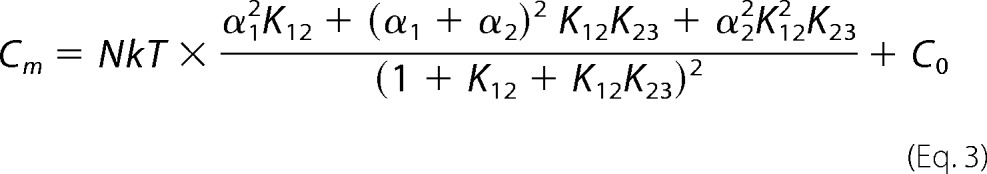where

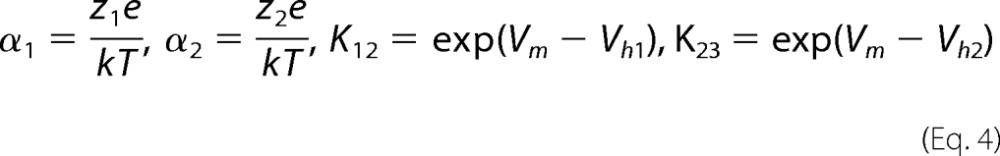Fits and plots were made in SigmaPlot. Data points from published plots were extracted using Plot Digitizer version 2.0 (University of South Alabama).

A kinetic model describing prestin activity, which we used previously to explain chloride-dependent coupling between prestin charge movement and electromotility (19) and the effects of thermal jumps on prestin voltage dependence (20), was extended to provide competitive binding of salicylate to the chloride binding site of the protein. The model was assessed using MATLAB Simulink in conjunction with jClamp. The new model, which includes a stretched exponential transition that accounts for stretched exponential behavior of NLC (21) and accurately reproduces magnitude and phase behavior of the electromotility frequency response,³ is presented below with the new salicylate binding component.

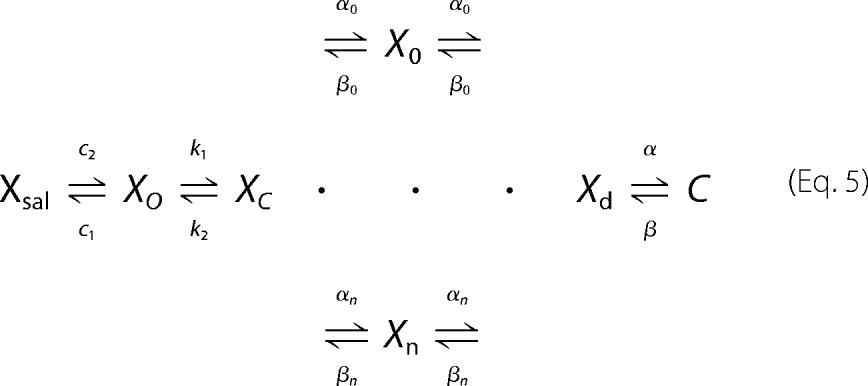X_sal state is bound by salicylate. X_o state is unbound by anion. X_c state is bound by chloride, but intrinsic voltage sensor charge is not responsive to the membrane electric field. A slow, multiexponential conformational transition to X_d state via X_n states enables voltage sensing within the electric field. Depolarization moves positive sensor charge outward, simultaneously resulting in compact state C, which corresponds to cell contraction. The differential equations are

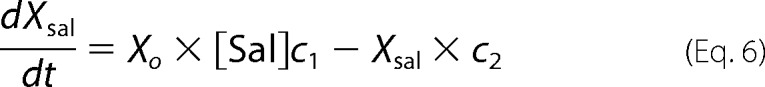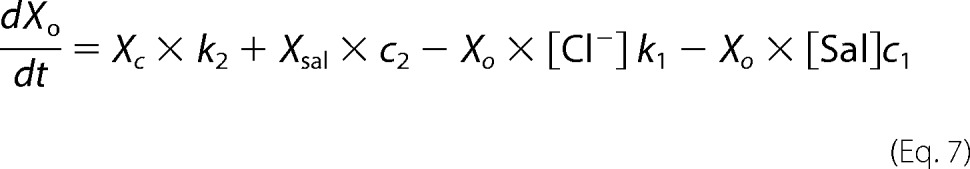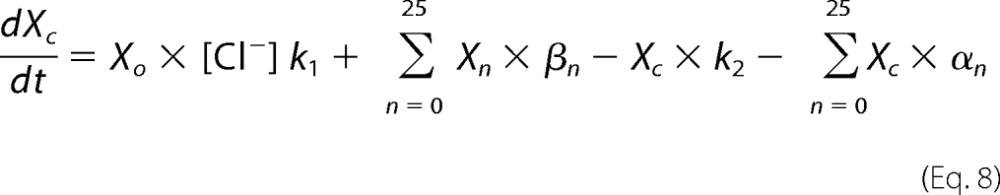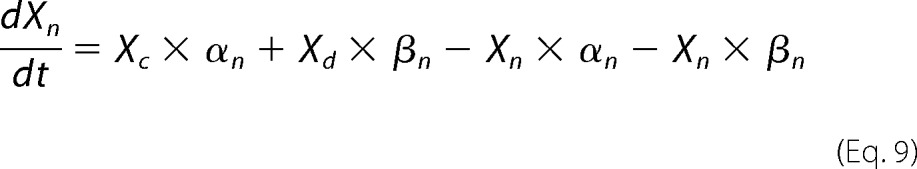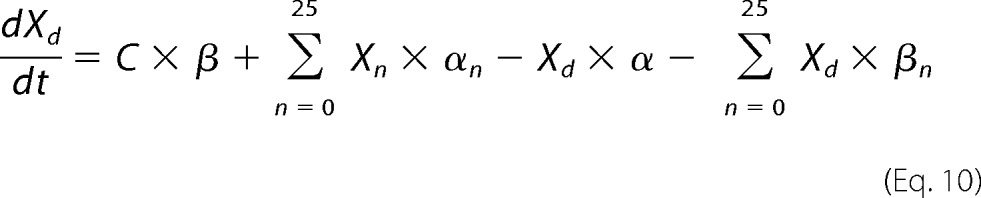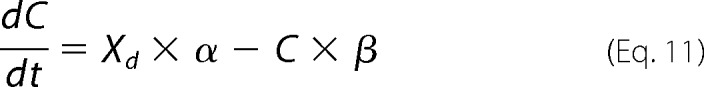where α_n = A × (exp(−n))^w, w = 0.6, A = 2.5 × 10⁴ for N = 0.25, β_n = α_n, k₁ = 1.5 × 10⁵, k₂ = k₁ × Clk_d, Clk_d = 0.012, c₁ = 3 × 10⁸, c₂ = c₁ × Salk_d, Salk_d = 30 × 10⁻⁷, α = 1.3 × 10⁶ × exp((z × F × V_m/(2 × R × T))), β = 7.7 × 10⁴ × exp((−z × F × V_m/(2 × R × T))), z = 0.7, nPres = 25 × 10⁶, or in the case of Fig. 5, N determined from fits to the biophysical data. The equivalence of α_n and β_n transition rates assures detailed balance of the reaction scheme (22).

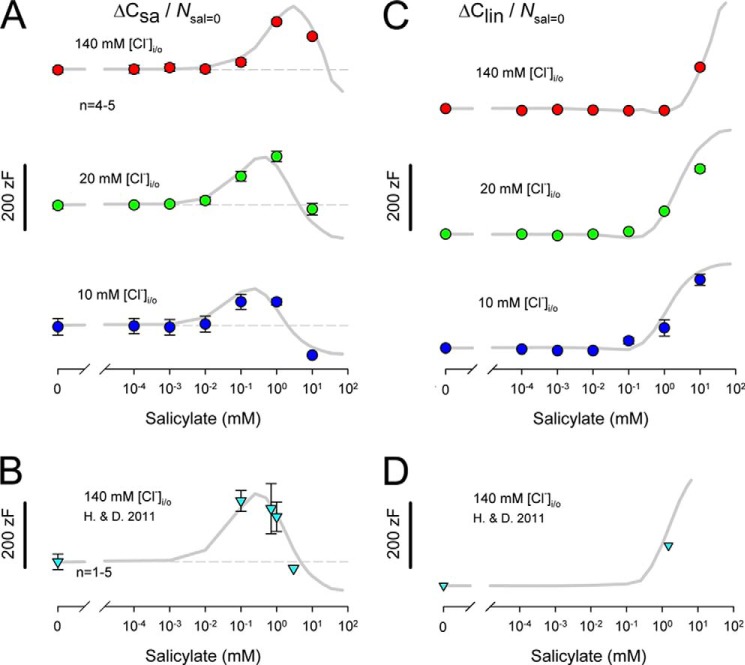
FIGURE 5.

Chloride and salicylate dependence of specific membrane capacitance. ΔC_sa is normalized by dividing by N (Q_max/ze) at 0 salicylate conditions. A, dashed lines show initial ΔC_sa for each chloride condition in the absence of salicylate: upper panel, 140 mm chloride, 141 zF; middle panel, 20 mm chloride, 110 zF; lower panel, 10 mm chloride, 88 zF. Note that in each case ΔC_sa is stable until a particular concentration of salicylate induces an increase in ΔC_sa followed by a decrease. The onset of salicylate effects is chloride-dependent, arising at lower salicylate levels as chloride is reduced. The meno presto model, which incorporates prestin-dependent changes in C_m arising from changes in motor surface area/membrane thickness, follows this pattern. B, data from Homma and Dallos (15) (H. & D. 2011); see their supplemental Fig. S3A (140 mm [chlorine] internal). The dashed line shows an initial ΔC_sa of 96 zF. A similar pattern of ΔC_sa change is observed when salicylate concentration is changed. Both the salicylate K_d and the ΔC_sa scaling factor for salicylate bound motors required adjustment to fit their data and are related to the higher salicylate sensitivity of mouse prestin (see “Results” for details). C, Clin also depends on the interaction between salicylate and chloride, showing a leftward shift along the salicylate concentration axis as chloride is reduced. The area motor model (gray lines) recapitulates this behavior. D, Homma and Dallos (15) Clin data are well described by the area motor model (see “Results”).

jClamp provides an automation link to MATLAB, which allows voltage stimuli to be delivered to and current responses to be obtained from Simulink models. Thus, biophysical and model data are analyzed exactly the same. Solutions were obtained with the ode45 (Dormand-Prince) solver at a fixed absolute tolerance of 10⁻⁶. The meno presto model was interfaced to jClamp via a model of the patch clamp amplifier and OHC. The linear component of the patch-cell model was composed of R_s in series with a parallel combination of R_m and C_lin. Given the above meno presto model parameters, model results were obtained with patch clamp parameters of R_s = 6.1 megohms, R_m = 275 megaohms, and C₀ = 23 pF. To reiterate, the exact same voltage stimuli and exact same analysis of model data were performed as with the biophysical data. Model responses were allowed to reach steady state prior to ramp perturbations.

RESULTS

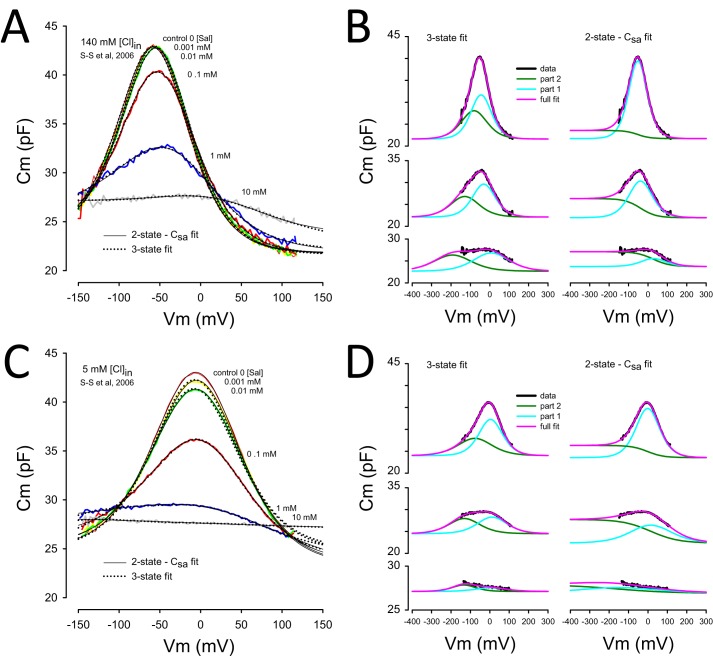
We previously showed that the effectiveness of salicylate inhibition of NLC is chloride-dependent (3). Fig. 1A shows NLC traces of an OHC with 140 mm intracellular chloride. Increasing concentrations (0.001, 0.01, 0.1, 1, 10 mm) of salicylate reduce the magnitude of NLC and shift its voltage dependence in the depolarizing direction. The traces were fit to the two-state C_sa model equation (Equation 1) and the three-state model equation (Equation 3) (see “Experimental Procedures”). Note that each fit is indistinguishable without statistical analysis. In fact, Homma and Dallos (15) found that Equation 1 gave a 4× better fit. Nevertheless, it is not the quality of the fit that is of concern here; it is the underlying mechanism. In Fig. 1B, the 0.1, 1, and 10 mm traces are replotted with the subcomponents of the two equations shown. In the left panels, two independent Boltzmann functions underlie the full fit. In the right panels, a single Boltzmann function and a coupled sigmoidal function, sharing the same V_h and number of motors, contribute to the full fit. Within the data region, each fit is quite reasonable. However, whereas the two-state C_sa fit shows an increasing membrane surface area/reduced membrane thickness, reflected in C_m, as the motors redistribute to the extended state, the three-state fit indicates no such changes. Similar results are found when intracellular chloride is set to 5 mm (Fig. 1, C and D). Note, however, that with reduced chloride there is a different dose-dependent effect of salicylate on ΔC_sa as compared with the 140 mm chloride condition. As with the 140 mm chloride data, the three-state model shows no differences in linear capacitance at voltage polarity extremes. A more telling evaluation of the two models is shown in Fig. 2, where both equations are used to fit the data of Santos-Sacchi and Navarrete (14) who utilized extreme voltages of ±200 mV to measure NLC. Those fits indicate that one Boltzmann component of the three-state model may actually serve as a surrogate for the sigmoidal component of the two-state C_sa model equation. Below we evaluate the interaction of salicylate and chloride effects on prestin to explore the appropriateness of the two models.

FIGURE 1.

Model-dependent differences in salicylate effects on the NLC of prestin. Contributions of area fluctuations in prestin differ with the three-state model of Homma and Dallos (15) or the two-state C_sa model of Santos-Sacchi and Navarrete (14). A, data from Fig. 1B of Santos-Sacchi et al. (3) (S-S et al, 2006) showing effects of different salicylate concentrations on NLC at an intracellular chloride level of 140 mm. Each trace was fit with both models, each providing near equivalent fit quality. B, details of fits by each model for the 0.1, 1, and 10 mm salicylate conditions, top, middle, and bottom panels, respectively. Each model is composed of two components, labeled part 1 and part 2. Essentially, the sum of each component produces the full fit. Although the two-state model gives an offset in C_m at hyperpolarized levels, the three-state model does not. C, data from Fig. 1A of Santos-Sacchi et al. (3) with an intracellular chloride level of 5 mm showing an enhanced effect of salicylate. As above, fits of both models were made, both showing good correspondence. Some small differences are noted at depolarized levels. D, fit components of both models. Again, an offset in C_m arises at hyperpolarized levels for the two-state model, but not the three-state model. Note that for each chloride condition, the offset in C_m (ΔC_sa) increases and then decreases with increasing chloride concentration.

FIGURE 2.

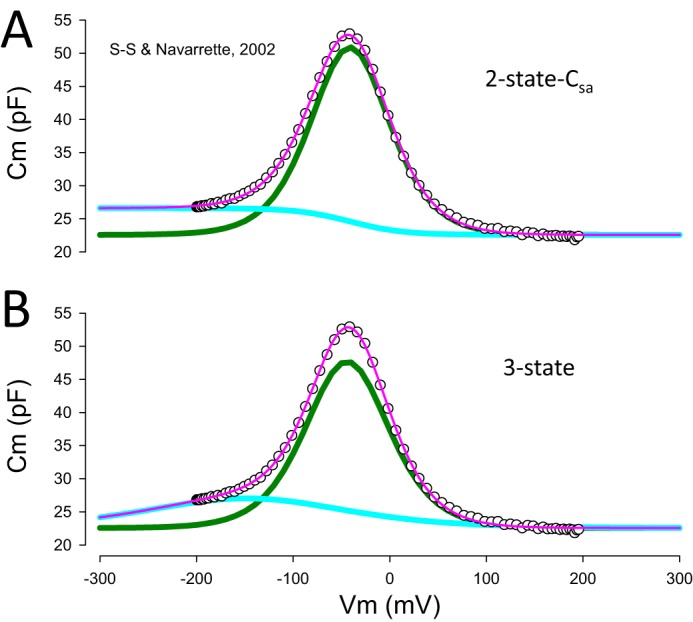
Two-state C_sa and three-state fits of NLC determined over a very wide voltage range. A, two-state C_sa fit, showing underlying components. B, three-state fit with underlying components. Note that the unconstrained fit of the three-state equation found one component V_h that effectively placed a sigmoidal-like C_m function at the hyperpolarized extreme, mimicking the two-state C_sa model's constrained fit of its single V_h. Data are from Santos-Sacchi and Navarrete (14) (S-S. & Navarrete, 2002).

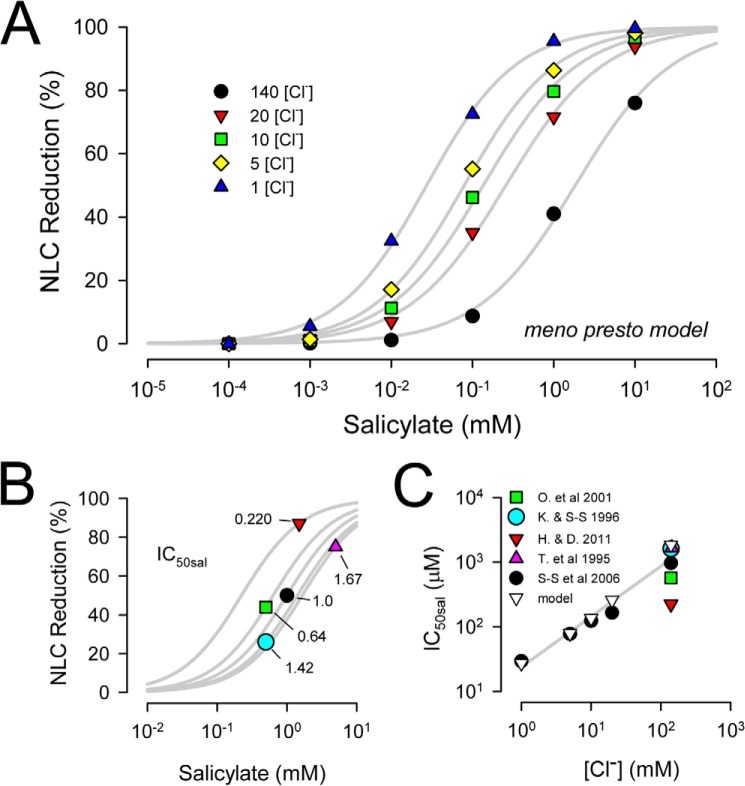
To help understand the effects of salicylate, we extended a kinetic model of prestin we are currently working on, termed the meno presto model because it includes a slow, stretched exponential intermediate transition between chloride binding and the voltage-enabled state (Fig. 3). We have used this model previously to explain chloride-dependent uncoupling between prestin charge movement and electromotility (19) and the effects of thermal jumps on prestin voltage dependence (20). Because we will use this model to evaluate the interaction of salicylate and chloride on ΔC_sa, we first confirm its ability to reproduce known chloride-dependent salicylate effects on NLC (3). Fig. 4A shows the model results illustrating that the IC_50sal reduces when intracellular chloride is reduced. Five publications report on salicylate effects on NLC (all reporting at least the 140 mm chloride condition), and from those we estimate IC_50sal by fitting Hill functions with the coefficient n set to 1 (Fig. 4B), as experimentally determined (23). Three values arise from studies on guinea pigs (3, 23, 24), being 1.67, 1, and 1.42 mm; a value of 0.64 mm comes from rat prestin-transfected cells (25), and a value of 0.22 mm comes from mouse OHCs (15). These values are plotted in Fig. 4C along with the extended measures of IC_50sal reported in Santos-Sacchi et al. (3). The model IC_50sal data (open white triangles) from Fig. 4A shows chloride dependence similar to our previous biophysical data (filled black circles) (3), indicating that our model may be useful in characterizing any chloride-dependent behavior of ΔC_sa.

FIGURE 3.

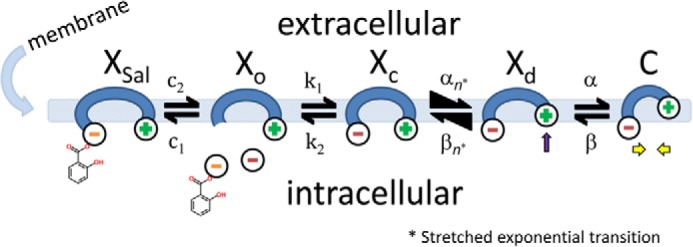
Extension of the stretched kinetic model of prestin activity to provide salicylate competition with chloride. X_sal state is bound by salicylate. X_o state is unbound by anion. X_c state is bound by chloride, but intrinsic voltage sensor charge is not responsive to membrane electric field. Slow, multiexponential conformational transition to X_d state via X_n states enables voltage sensing of electric field. The α_n and β_n transitions are multiexponential (see “Experimental Procedures”). Depolarization moves positive sensor charge outward, simultaneously resulting in compact state C, which corresponds to cell contraction. Equivalence of α_n and β_n transition rate constants assures detailed balance of the reaction scheme.

FIGURE 4.

Model results of salicylate effect on NLC correspond to biophysical data. A, model predicts chloride dependence of salicylate effects, showing that reduced IC_50sal as chloride is lowered, as determined experimentally by Santos-Sacchi et al. (3) (see their Fig. 2). B, comparison of IC_50sal from different studies. Because only one study fully evaluated the chloride dependence of IC_50sal, IC_50sal was estimated by fitting a Hill function through the single data points obtained at 140 mm chloride with the Hill slope, n, fixed at 1, as experimentally determined (3). Biophysical data points were from guinea pig OHCs (Tunstall et al. (24), extracted from their Fig. 5C; Kakehata and Santos-Sacchi ((24)), extracted from their Fig. 1C; Santos-Sacchi et al. (3), extracted from their Fig. 2); rat prestin transfected HEK cells (Oliver et al. (25), extracted from their Fig. 5b); and mouse OHCs (Homma and Dallos (15), extracted from their Fig. 2). C, comparison between model and biophysical data shows that the model recapitulates biophysical data. Straight line fit is through model points. Legend: O. et al 2001, Oliver et al. (25); K. & S-S 1996, Kakehata and Santos-Sacchi ((24)); H. & D. 2001, Homma and Dallos (15); T. et al 1995, Tunstall et al. (24); S-S et al, 2006, Santos-Sacchi et al. (3).

Homma and Dallos (15) uncovered behavior of ΔC_sa that they believed was incompatible with our two-state C_sa area motor model (see their Fig. 2H). They found that ΔC_sa increases with salicylate concentration before it decreases. Because we determined that the conformational switch of the motor from compact to expanded state results in a 130 zF/motor (δC_sa) increase in C_m (23), they reasoned that as salicylate removed motors from the active pool there should only be a decrease in ΔC_sa with increasing salicylate concentration. This reasoning disregards our published observation that salicylate increases ΔC_sa above that measured in its absence. Thus, we contend that when salicylate binds to a motor, either its surface area is greater than an unbound expanded motor and/or the membrane thickness is reduced when bound. We and others have shown that salicylate in the absence of prestin has no measurable effects on membrane capacitance (23, 24). Homma and Dallos (15) also show this. Clearly, then, the salicylate effect results from interaction with prestin. Fig. 5A shows the effects of salicylate with 140 mm intracellular chloride on ΔC_sa. The data have been normalized by motor number, N, in the absence of salicylate for comparisons (ΔC_sa/N_sal=0). A non-monotonic increase followed by a decrease is similar to the Homma and Dallos data (15). At this chloride concentration, in the absence of salicylate, a unit δC_sa per motor is calculated to be 141 zF, similar to our previous estimates (14). In our model, to account for the salicylate dose-response function, each salicylate-bound motor unit δC_sa had to be factored by 1.9 (solid line), in line with our previous observations (14). We also observed similar behavior when chloride levels were reduced; however, the salicylate dose-response function shifted leftward along the concentration axis with reduced chloride. With a fixed unit δC_sa scale factor of 1.9 for salicylate-bound motors, the model response also shifted when chloride was reduced, and exhibited appropriate response magnitude.

We previously showed that the effects of externally applied salicylate (1 mm) on NLC required about 60 s to reach steady state (23). Because Homma and Dallos (15) used a 1-min perfusion to change salicylate from 0 to 1.5 mm, during which time they evaluated NLC, steady state effects were only achieved before and after perfusion. For this reason, we evaluate the data from their supplemental Fig. S3A (140 mm chloride, intracellular) where salicylate concentration was set definitively. Interestingly, those data (Fig. 5B) required that the salicylate K_d (Salk_d) or equivalently the rate constant c₂ of our model be reduced by an order of magnitude, in line with their more sensitive estimated IC_50sal (Fig. 4B). Additionally, the δC_sa scale factor had to be increased to 3. It must be emphasized that the Salk_d and Clk_d in our model do not necessarily correspond in magnitude to IC₅₀ values of NLC effects that we and others have measured, because through our experiments on NLC we neither inspect these directly, nor should IC₅₀ values necessarily agree with K_d values in other than a simple two-state system. The utilized k_d values, however, produce IC₅₀ values for NLC that are consistent with our experimental observations.

Finally, we investigated the behavior of C_lin. For the two-state C_sa model equation, C_lin is the linear capacitance, which is the minimum capacitance at extreme depolarized voltages where all motors are in the compact state. For the three-state model equation, C_lin is equivalently the capacitance at either hyperpolarized or depolarized extremes. Similar to Homma and Dallos (15), we find a monotonic increase in C_lin in our data when fit with the two-state C_sa equation (Fig. 5C). It reaches an asymptote when ΔC_sa vanishes, that is, when salicylate binds to all motors and locks them in the expanded state. Thus, C_lin tells about the state residence of motors, just as ΔC_sa does; the measures are reciprocal. Importantly, just as ΔC_sa is dependent on the interaction of salicylate and chloride (Fig. 5A), so too is C_lin (Fig. 5C). In Fig. 5D, we plot C_lin that arises from three-state fits of our model data that explicitly incorporate motor-generated δC_sa. As expected, and in agreement with Homma and Dallos (15), C_lin rises monotonically to an asymptote, until all motors are in the salicylate-bound extended state. Unfortunately, Homma and Dallos (15) only report on salicylate effects on C_lin using a 1-min perfusion of extracellular salicylate, so we cannot unequivocally determine intermediate concentrations of salicylate from their data (see their Fig. 2C) except at the onset of perfusion (zero salicylate) and at the steady state end of perfusion (1.5 mm salicylate). Thus, we only plot those two points, and they lie on our model prediction curve. Thus, although the three-state model cannot identify the voltage-dependent nature of prestin-associated capacitance change, it nevertheless reports on it as C_lin.

DISCUSSION

The area motor model of OHC motor activity was based on biophysical evidence that OHC surface area increases upon hyperpolarization (13). Given the constraints of a cylindrically shaped cell and a constant cytoplasmic volume, alterations in surface area result in cell length changes that correspond to measured characteristics of OHC electromotility (9, 11). Although various models of OHC electromechanical activity have arisen, including electro-osmosis (26, 27) and membrane flexo-electricity (28), several arguments against them have been made (29–31), chief among them the identification of the voltage-dependent motor protein prestin (1). Considering the vast number of prestin motors embedded in the OHC lateral membrane, whose membrane residence contributes markedly to OHC surface area (32, 33), unit area changes, ranging from 0.4 to 8 nm² (9, 11, 12, 34, 35), will have substantial effects on membrane surface area. Linear membrane capacitance is expected to change when either membrane surface area or associated changes in membrane thickness occur.

Recently, Homma and Dallos (15) have developed a three-state model of prestin activity, which challenges those earlier area motor models. In their model, no changes occur in linear capacitance at extreme hyperpolarizations or depolarizations despite very nice fits of NLC data within a restricted voltage range. In contrast, fits with the two-state C_sa model equation (14) predict that linear capacitance increases when motors redistribute into the expanded state, reaching an asymptote, ΔC_sa, at extreme hyperpolarizations where all motors reside in the expanded state. There are two reasons why Homma and Dallos (15) championed their new model over the area model, despite a better fit by the latter model. First, they observed that when fitting with the two-state C_sa model equation there is a non-monotonic change in ΔC_sa as salicylate concentration rises, an increase followed by a decrease. It was assumed that salicylate simply removes motors from the active pool, and thus motor contribution to area changes should monotonically decrease. However, we previously showed that salicylate increases ΔC_sa above that measured in its absence (14), implying that salicylate-bound motors are augmented in surface area and/or decrease membrane thickness. To be sure, we and others have shown that salicylate in the absence of prestin has no measurable effects on membrane capacitance (15, 23, 24). Consequently, when we use our new meno presto model incorporating salicylate effects on the motor, we satisfactorily fit the non-monotonic ΔC_sa behavior caused by salicylate. Furthermore, we show that this non-monotonic biophysical behavior varies with chloride level, with the model capable of describing the chloride dependence. Curiously, the three-state model accurately identifies a biophysical change in linear capacitance that is salicylate-dependent, which is precisely expected of that model should surface area increase due to increasing residence of prestin in the expanded state. Thus, although that model is built to ignore the voltage-dependent surface area changes due to prestin, it unavoidably detects that surface area change as a voltage-independent one.

The other reason why Homma and Dallos (15) favor their three-state model is that the coupling between sensor charge movement and electromotility is not tight, with zero charge extrapolations giving non-zero mechanical responses, regardless of the model equation. We previously observed uncoupling between sensor charge and electromotility (23, 36, 37). Indeed, we had shown that salicylate even at 10 mm, whereas nearly abolishing NLC, had much less of an effect on electromotility (23). Recently, we determined that the discrepancy between charge movement, measured with the dual sine admittance approach (17, 18) (also coded into jClamp), and electromotility is chloride-dependent (19), and thus, considering its competition with chloride, salicylate-dependent. Furthermore, we showed that a model incorporating slow intermediate kinetics between chloride binding and a two-state Boltzmann process substantially predicted disparities between sensor charge and electromotility (19). The meno presto model presented here, which integrates characteristics of the two-state C_sa model, possesses this capability as well. It should be noted that the three-state model, as is, can neither reproduce this result nor generate stretched exponential kinetics that is evident in OHC NLC (18, 21, 39) and prestin-transfected cell NLC (40). The meno presto model exhibits stretched exponential kinetics in capacitance measures similar to biophysical observations. One other point should be mentioned about the three-state model. Although the two-state C_sa model derives from biophysical evidence showing voltage-dependent surface area changes, the rationale for two independent Boltzmann processes in the three-state model is curiously lacking a rationale, other than its ability to fit NLC data within a restricted voltage region. In this regard, it is not at all clear why the V_h of each Boltzmann process should shift in an opposite direction during salicylate treatment (15). Even if salicylate could charge screen the membrane (41), voltage-dependent processes should shift in the same direction. The mechanism whereby the three-state model works is especially clear in the absence of salicylate when extended voltage ranges are used to measure NLC as in Fig. 2. One underlying Boltzmann process is simply shifted such that it mimics the sigmoidal nature of ΔC_sa generation that is revealed by the two-state C_sa model.

Interestingly, inspection of the literature on salicylate inhibition of prestin shows that mouse prestin appears more susceptible to inhibition than guinea pig prestin, with the guinea pig IC_50sal being ∼1–1.5 mm and mouse IC_50sal being ∼0.2 mm. Consequently, our new meno presto model was able to fit the mouse data of Homma and Dallos (15) by the reducing the forward rate constant, c₂ (see “Experimental Procedures”), by an order of magnitude. Although homology is high between the two species, perhaps some key residue differences could account for this. Alternatively, chloride and/or salicylate concentration may differ within the minute space between plasma membrane and subsurface cisternae among species. This femtoliter compartment is exactly where interactions between anions and prestin occur. Thus, it may be interesting to compare salicylate sensitivity among OHCs from a wide range of species.

In summary, we find that an area motor model, such as our meno presto model, accurately accounts for interactions between salicylate and chloride on the OHC motor, and that models that do not explicitly incorporate a motor-dependent area change will nevertheless detect one as an increase in linear capacitance. To be sure, it is crucial that a model be appropriate to understand the elementary nature of a voltage-dependent molecule (38).