Skip to main content
PMC home page
Genome Research logoLink to Genome Research
letter
. 2003 Jun;13(6a):1158–1168. doi: 10.1101/gr.466303

The Pattern of Polymorphism on Human Chromosome 21

Hideki Innan 1,1,2, Badri Padhukasahasram 1, Magnus Nordborg 1
PMCID: PMC403644  PMID: 12799351

Abstract

Polymorphism data from 20 partially resequenced copies of human chromosome 21—more than 20,000 polymorphic sites—were analyzed. The allele-frequency distribution shows no deviation from the simplest population genetic model with a constant population size (although we show that our analysis has no power to detect population growth). The average rate of recombination per site is estimated to be roughly one-half of the rate of mutation per site, again in agreement with simple model predictions. However, sliding-window analyses of the amount of polymorphism and the extent of linkage disequilibrium (LD) show significant deviations from standard models. This could be due to the history of selection or demographic change, but it is impossible to draw strong conclusions without much better knowledge of variation in the relationship between genetic and physical distance along the chromosome.

There are essentially two reasons for studying the pattern of genetic polymorphism in population samples. The first is to identify polymorphisms that have important phenotypic effects. The pattern of polymorphism is important when searching for alleles that are statistically associated with phenotypic differences, either because they are directly causative, or because they are in linkage disequilibrium (LD) with variants (at other sites) that are directly causative.

The second reason, which is also the focus of this paper, is interest in the evolutionary process that gave rise to the pattern of polymorphism. One may be interested in forces that influence all loci, such as migration, mutation, and recombination, or one may be interested in the history of selection on a particular locus. Many years of research in population genetics (empirical as well as theoretical) have led to a sophisticated mathematical theory for this type of analysis (for review, see Li 1997; Kreitman 2000; Nordborg 2001; Stephens 2001). Arguably the most fundamental insight that has emerged from this work is that in order to overcome the enormous variance that is due to random history and estimate evolutionary parameters accurately, data from surprisingly large numbers of loci are needed. Indeed, it can be said (with only slight exaggeration), that theory has typically told us that in order to answer the questions of interest, more data are required than is feasible to collect.

This situation is about to change. As a result of rapid advances in genotyping technology (primarily due to the enormous efforts devoted to finding polymorphisms associated with human diseases), polymorphism data on a genomic scale will soon become common. The most spectacular example to date is provided by Patil et al. (2001), who partially resequenced 20 copies of human chromosome 21. Although their data are in many ways unsuitable for evolutionary genetics (see below), this is to a significant extent compensated for by quantity: over 21,000 polymorphic sites, with enough recombination to ensure that most sites are effectively independent.

In the present study, we analyzed the data of Patil et al. (2001), focusing in particular on the overall fit of the data to standard models. We also discuss the possibility of finding footprints of selection in genomic polymorphism data.

RESULTS

We analyzed 21,840 SNPs from a 28-Mb region on the long arm of human chromosome 21 (Patil et al. 2001). This region comprises 80% of the whole chromosome, and does not include centromeric or telomeric sequence. The single nucleotide polymorphisms (SNPs) were obtained by resequencing (using chips) 20 independent copies of chromosome from a worldwide sample. The SNPs were thus not ascertained in any way, which avoids the serious biases that characterize most SNP data sets. However, other problems are associated with these data. First, roughly one-third of the 28-Mb region was not surveyed because of experimental failure, or because it contained repetitive sequences. The exact lengths and positions of these missing regions were not available to us. Second, there is a high rate of missing data (for particular chromosomes) in regions that were surveyed. Third, singleton variants (i.e., variants present only in one of the 20 chromosomes) could not be reliably determined, and were therefore removed from the data. One consequence of these problems is that we were unable to estimate polymorphism levels directly; instead we relied on estimates provided by D. Hinds at Perlegen Sciences. For more information about the data, see the Methods section.

Allele-Frequency Distribution

One of the simplest characteristics of genetic polymorphism data is the distribution of allele frequencies. In the present data, there are two alleles at each polymorphic site, and we do not know which allele is ancestral and which is derived. Thus, it makes sense to describe the data in terms of the frequency of the rarer allele at each locus (or an arbitrarily chosen allele, in case of even frequencies). Because we have data from 20 chromosomes, this frequency is a number between 1 and 10; however, because singleton data are not available, we have frequencies between 2 and 10. We will consider distribution of these frequencies, that is, what fraction of the SNPs fall in each of the classes 2,..., 10.

What should we expect this distribution to look like? The allele-frequency distribution can be calculated for a number of population genetics models. Of relevance here (and for DNA sequence polymorphism data in general) is the so-called infinite-sites model, which assumes that the per-site mutation rate is sufficiently low that all polymorphisms within a species are due to unique mutations. Thus there should never be more than two different bases segregating at site. This model is likely to be a reasonable approximation for the data: Patil et al. (2001) found 339 sites (out of a total of over 24,000 sites) that may have had three or more alleles (and excluded them from the data).

The top panel of Figure 1 shows the distribution of allele frequencies in the data of Patil et al. (2001) together with the distribution we would expect to see in a standard neutral model with constant population size and no population structure. The fit is very good. This may seem surprising, given that the human population has clearly not been constant. The allele-frequency distribution is expected to reflect demographic history. For example, population growth will typically tend to increase the frequency of loci with one rare and one common allele, whereas many forms of population subdivision will tend to increase the frequency of loci with both alleles at intermediate frequencies.

Figure 1.

Figure 1

Open in a new tab

Histogram of allele frequencies. The upper panel shows the observed distribution together with the distribution expected in a standard neutral model with constant population size. The lower panel shows the distribution expected with a constant population size, together with the distributions expected under three scenarios of exponential growth from an ancient constant size of 104 to a modern size of 109.The three scenarios make different assumptions about when growth started: 1000, 5000, or 10,000 generations ago. The histogram is based on the 2148 SNPs for which all 20 chromosomes were genotyped.

Previous human studies have given a decidedly mixed picture, with some data sets (mainly sequencing surveys of nuclear loci) showing an excess of intermediate-frequency alleles, whereas others (mitochondrial and Y chromosome data, and nuclear microsatellites) show an excess of rare alleles (Harpending and Rogers 2000; Wall and Przeworski 2000). Possible reasons for these contradictory results included differences in sampling and ascertainment (which makes it difficult to compare studies), and small sample sizes (in the sense of number of loci, which makes it possible for the differences to be due to chance alone).

In comparison with previous studies, the present data contain an enormous number of loci, and the fit observed in Figure 1 is therefore not likely to be an accident. The data do fit a model that assumes a constant population size, even though human populations plainly have undergone dramatic growth, at least in recent times. This paradox is resolved by noting that all singleton alleles have been eliminated from the data. The frequency of an allele is related to its age: More frequent alleles are likely to be older. The rarest allele that can be observed in the data of Patil et al. (2001) has a frequency of 2/20, which implies a population frequency of 10%. Such alleles are likely to be much older than any of the recent growth scenarios that have been discussed in the literature (Kimura and Ohta 1973; Griffiths and Tavaré 1998). In a sample of size 20, recent growth would mostly affect the relative frequency of the singleton class. Indeed, as is shown in the bottom panel in Figure 1, we should not expect to be able to see the traces of any growth that took place during the last 200,000 years in the data of Patil et al. (2001), at least not in the allele-frequency distribution.

However disappointing this may be, the fit observed in Figure 1 is nonetheless interesting, because it suggests that the part of the frequency distribution that reflects deeper human history is reasonably well approximated by a constant population size model. Because it is unlikely that ancient hominids lived in a single random-mating population, this finding is likely to reflect the remarkable robustness of the standard population genetics model to deviations from its assumptions (Nordborg 2001).

Average LD

The results in Figure 1 suggest that a simple population genetics model may fit the data. The simplest model for DNA sequence polymorphism is the infinite-sites mutation/recombination model (e.g., Nordborg 2001). The model has two parameters: the per-site mutation rate, θ, and the per-site recombination rate, ρ. Recombination is assumed to occur just like mutation: uniformly over the chromosome, and with low probability per site per generation. Available data are consistent with both assumptions: The relationship between physical and genetic distance appears to be roughly constant across the chromosome, and the total length is 55 cM or 34 Mb, leading to a per-site per-generation probability of recombination of r = 55/100/34 = 1.6 × 10-8 (Hattori et al. 2000). The per-site per-generation mutation probability, u, can be estimated using the amount of sequence divergence between species, and is typically found to be of order 10-9 in mammals (Li 1997). Both rates are scaled using a scaling constant often known as the “effective population size”, Ne, so that θ = 4Neu and ρ = 4Ner (e.g., Nordborg 2001).

It should be noted that it is not necessary for θ and ρ to be constant over the genome for the model to be a good approximation: It suffices that their averages over windows long enough to have been subject to mutation or recombination are constant. For example, it is completely unreasonable to assume that the selectively neutral mutation rate is the same for all sites; however, two human sequences differ by less than one mutation every kb, and it makes considerably more sense to assume that the rate is constant over windows of a few kb. We will discuss the spatial pattern in detail later; here we focus on average properties over large windows.

θ can readily be estimated using summaries of variation data, such as the number of segregating sites (Watterson 1975) or the nucleotide diversity (Tajima 1983). Patil et al. (2001) estimated that θ = 0.0007–0.0008 (depending on the estimator used), in agreement with other studies. This is expected given that θ can be reasonably well estimated even with smaller data sets. It is much more difficult to estimate ρ using data from single regions (Przeworski et al. 2000; Wall 2000). Given the size of the present data set, we used a very simple approach based on the rate of decay of LD. Pairwise LD is expected to decay as a function of distance at a rate that is determined by ρ, but the variance is enormous, making it very difficult to estimate ρ this way (Chakravarti et al. 1986; Weir and Hill 1986; Pritchard and Przeworski 2001; Nordborg and Tavaré 2002). However, because the present data set is so large, the method works here. Figure 2 shows the decay of average D′ (a measure of LD; Lewontin 1964) as a function of distance. Curve-fitting of the theoretical distribution indicates that ρ = 0.00042. This value is in agreement with previous estimates (Przeworski et al. 2000; Pritchard and Przeworski 2001).

Figure 2.

Figure 2

Open in a new tab

Average pairwise LD as a function of distance between loci. Distances have been binned, and each point represents the average of a very large number of nonindependent comparisons.

Note that θ/ρ = u/r under the infinite sites model. If θ and ρ are similar in magnitude (as the present data indicate), then so must u and r. Because r ≈ 10-8 (see above), so must u. This is somewhat higher than estimates from phylogenetic methods (Li 1997). We also note that these estimates imply Ne ≈ 6600, which is somewhat lower (about twofold) than previous estimates (Przeworski et al. 2000). A plausible explanation for this is that LD is inflated by admixture in the sample used by Patil et al. (2001).

Chromosomal Variation In Diversity Levels

A standard method in population genetics is to look at the level of sequence variability in sliding windows along the chromosome (i.e., a moving average). The main motivation for doing this is that “positive” selection on a particular site can leave a footprint in the pattern of variation surrounding the site (for review, see Kreitman 2000; Nordborg 2001). For example, whenever directional selection causes a favorable allele to go to fixation, variation in the surrounding chromosomal region will be decreased (a so-called “selective sweep”). Conversely, if some form of balancing selection maintains ancient alleles in the population, the local level of variability may be increased (causing a “peak of polymorphism”, such as is observed in the MHC; see Gaudieri et al. 2000). Note that these effects are in addition to the effect of different levels of constraint (“negative” selection) in different regions.

Detecting selection at the molecular level has long been a central problem in population genetics, and a variety of statistical “tests of selection” exist (Kreitman 2000). The canonical approach is to compute a summary statistic of the data, and compare its value to the distribution under a neutral null model. A serious drawback of this approach is that the neutral null model may be rejected for reasons other than selection: Demographic history and population structure can cause deviations similar to those expected under selection (Nordborg 2001).

Given genomic polymorphism data, a much better approach is to compare different regions. Demographic history and population structure affect all loci in the same way: Selection, by definition, acts on particular loci. Thus, the search for footprints of selection becomes a search for statistical outliers.

The width of the regions in which variability is reduced due to a selective sweep depends on how quickly the sweep occurred: Stronger selection will cause faster sweeps that affect a greater chromosomal region (Kaplan et al. 1989). Searching for regions of reduced variability in the data of Patil et al. (2001) is problematic because of the large amount of missing data: A region could have few SNPs simply because it was not surveyed. We overcome this problem by restricting our attention to very large windows of 500 kb. The variability in the number of surveyed sites between windows of this size is insignificant (see Methods).

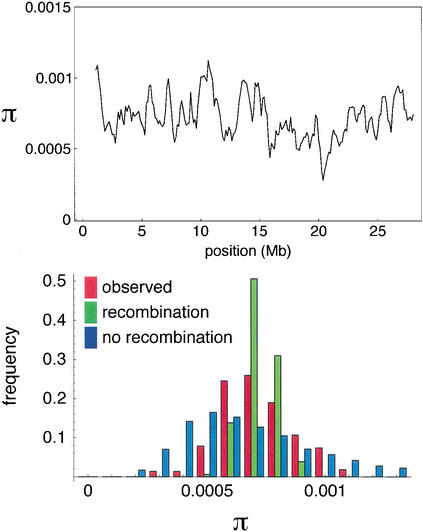
The upper panel of Figure 3 shows the moving average nucleotide diversity using windows of 500 kb. A strikingly large dip (π = 2.8 × 10-4) is observed between positions 20375 kb and 20875 kb, a region which contains approximately ten genes (Hattori et al. 2000). This dip is significantly different from what would be expected under the standard infinite-sites model with parameters estimated from the data: We did not observe as low a value even once in 5000 independently simulated 500-kb regions. It is tempting to conclude that the dip reflects a selective sweep, but this is not warranted, because the deviation from the standard model turns out to be genome-wide. As shown in the lower panel of Figure 3, the variance of π among windows is much greater than expected given the estimated rate of recombination. This phenomenon could be due to genome-wide selection, or demographic factors, but it could also reflect heterogeneity in the rate of recombination. Under the infinite-sites mutation/recombination model, the variance of π is a decreasing function of ρ (Hudson 1983; Pluzhnikov and Donnelly 1996). The reason for this is that the pattern of polymorphism at a site depends strongly on the genealogical history of that site: for example, the deeper the ancestry, the greater the probability of the site being polymorphic. Recombination makes the genealogical histories of different sites increasingly independent of each other; the more recombination in a region, the more different trees are sampled. Our estimate of the recombination rate for a 500-kb region is 210, which is sufficiently high to make the contribution of the variance in the underlying genealogical trees to the variance in π almost irrelevant. However, if some of the windows have much lower rates of recombination, the variance between windows would be much greater. As we shall see below, the pattern of LD is consistent with this explanation.

Figure 3.

Figure 3

Open in a new tab

The upper plot shows a moving average of nucleotide diversity, using nonoverlapping windows of size 500 kb. The bottom panel shows a histogram of these (nonindependent) windows, together with two sets of 5000 independently simulated windows. Both sets used the estimated θ = 7.2 × 10-4, but one used the estimated ρ = 4.2 × 10-4 whereas the other assumed no recombination within windows.

We also looked for regions of increased variation that might suggest a history of balancing selection. The peaks of polymorphism associated with balancing selection are expected to be quite narrow (Andolfatto and Nordborg 1998; Nordborg and Innan 2003). We investigated the distribution of π using 1-kb windows. Because of the large amount of missing data, the distribution is heavily skewed toward small values (data not shown). However, we also found several windows in which π is more than 10 times bigger than the genomic average. The haplotype pattern for one of these windows is shown in Figure 4. In this 1-kb region, there are 12 common SNPs, 11 of which are in perfect LD; there are two major haplotypes with frequencies 7/19 and 12/19. The average number of nucleotide differences between the two haplotypes is at least 11.4 (singletons and missing data might increase this value); the neutral expectation given an estimated θ of 7.6×10-4 is 1.7 (Innan and Tajima 1997). This value is consistent with a simple symmetrical balancing selection model with Nes = 5, where s is the selection coefficient (Innan and Tajima 1999). Given the estimated Ne, this would translate into a 0.1% advantage for heterozygotes.

Figure 4.

Figure 4

Open in a new tab

The pattern of 12 common SNPs between 17043 kb and 17044 kb. Green “C” and black “R” represent common and rare alleles at each SNP, respectively. Empty columns are due to missing data. The numbers give the position on the chromosome.

However, although such patterns are suggestive of balancing selection, the statistical evidence is not convincing. In fact, we cannot even reject a standard neutral model: Although the high level of polymorphism is indeed highly unlikely, it must be kept in mind that the data have 28,000 windows of size 1 kb. When multiple comparisons are taken into account, we find that we would expect to find a larger number of extreme peaks than was found. This problem is general; many evolutionary phenomena of interest will not be detectable in genomic screens. Independent evidence is essential. In the case of the pattern in Figure 4, there is no predicted gene in or in the immediate vicinity of the region.

Chromosomal Variation in LD

There is currently tremendous interest in the pattern of LD in humans (for review, see Ardlie et al. 2002; Nordborg and Tavaré 2002). Indeed, the pattern of LD was the major focus for Patil et al. (2001), who discovered large blocks of limited haplotype diversity. We have focused on another aspect of LD, namely the pattern of decay of pairwise measures of association. Figures 5, 6, 7 show how |r|, the absolute value of the correlation coefficient, decays as a function of distance. The figures reveal a remarkable heterogeneity in the extent of LD. In most regions, LD decays within 10 or perhaps 20 kb, but there are many regions of much more extensive LD. In particular, there are several regions where extremely high levels of LD persist more than 200 kb. A closer look at these regions reveals striking patterns of polymorphism.

Figure 5.

Figure 5

Open in a new tab

The pattern of LD along chromosome 21.The color of each point represents the absolute value of r, the correlation coefficient between SNPs (with respect to haplotype) at a pair of loci. The position of one of the loci is given (in kb) on the x-axis; the position of the second is given relative to that of the first (again in kb) on the y-axis. Thus, each vertical slice shows the pattern of LD in a 400-kb window around a particular SNP locus. The four panels show the pattern for the first 9 Mb; the remainder of the chromosome is shown in Figures 6 and 7.

Figure 6.

Figure 6

Open in a new tab

The pattern of LD along chromosome 21.The figure is the continuation of Figure 5.

Figure 7.

Figure 7

Open in a new tab

The pattern of LD along chromosome 21.The figure is the continuation of Figure 6.

The most extensive region of high LD is seen around 26 Mb. The pattern of polymorphism in this region is shown in Figure 8. Note that 15 of the 20 chromosomes appear to share an identical haplotype between 26089 and 26141 kb; this haplotype contains 22 SNPs and is 52 kb long. The average number of pairwise differences between the two main haplotypes is about 19.65, which is much smaller than the neutral expectation of 78.9 (Innan and Tajima 1997, but note that missing data may explain this difference). The pattern is suggestive of ongoing directional selection increasing the frequency of the majority haplotype (cf. Hudson et al. 1994).

Figure 8.

Figure 8

Open in a new tab

The haplotype pattern of 58 common SNPs between 26076 and 26180 kb. All (nonsingleton) SNPs are shown, except for seven where more than six chromosomes were undetermined. Approximately 34% of this region was masked by RepeatMasker because of repetitive elements, and was therefore not surveyed. The notation is the same as in Figure 4.

A second remarkable region is found around 17.4 Mb. In this region, there are two haplotypes (present at frequencies 7/19 and 12/19—data are missing for one chromosome) with almost no variation within each haplotype (Fig. 9). The haplotypes are more than 100 kb long. The average number of pairwise differences between the two haplotypes is 91.5, which is smaller than neutral expectation (172). This pattern is not directly suggestive of any simple selective scenario.

Figure 9.

Figure 9

Open in a new tab

The pattern of 58 nonsingleton SNPs between 17366 and 17461 Kb. Thirty-six SNPs with more than six missing chromosomes are not shown. Approximately 25% of this region was masked before sequencing. The notation is the same as in Figure 4.

Although selection can create heterogeneity in LD, it is by no means the only explanation. Actual variation in the underlying recombination rate (the relationship between genetic and physical distance) as well as various demographic scenarios have been proposed as explanations for variations in the distribution in LD (for review, see Pritchard and Przeworski 2001; Ardlie et al. 2002; Nordborg and Tavaré 2002). However, it is also necessary to consider chance alone. It is important to realize that LD is expected to be extremely variable even under the simplest population genetic model; low LD between a pair of loci does not necessarily mean that much recombination has occurred between the loci, and even if it did, this would not mean that there would be much recombination if history were repeated (Nordborg and Tavaré 2002).

To explore whether the observed pattern of LD requires an explanation other than chance, we simulated many large (2-Mb) regions using the infinite-sites model with the recombination and mutation parameters estimated above. An example is shown in Figure 10. These simulations showed without question that the pattern of LD observed in the data of Patil et al. (2001) is not compatible with the infinite-sites model and the estimated parameters. LD is indeed variable under this model, but it always decays within 20 kb or so, whereas LD in the data sometimes extends over 200 kb. This observation mirrors other observations that LD in humans often seems to be more extensive than predicted by models (Kruglyak 1999; Pritchard and Przeworski 2001; Ardlie et al. 2002). The main discrepancy lies in the heterogeneity of LD; for most of the chromosome, the pattern of LD appears to fit the model reasonably well.

Figure 10.

Figure 10

Open in a new tab

Simulations showing the expected pattern of LD under various scenarios. The upper panel was generated using parameters (θ and ρ) estimated from the data. The second panel used the same parameters, but assumed an exponentially growing population. The third panel used parameters estimated from the data, but added population subdivision. The fourth panel used the same value of θ, but decreased the recombination rate by a factor of ten. The figure should be compared with Figures 5, 6, 7.

Could demographic scenarios explain the data? We noted above that the human population is known to have undergone recent exponential growth. However, because it happened recently, this is expected to have only a slight affect on LD (Nordborg and Tavaré 2002). In any case, exponential growth is expected to decrease rather than increase LD (Slatkin 1994; Pritchard and Przeworski 2001). Our simulations support these conclusions: In models that involve growth, LD is even less likely to be as extensive as observed (Fig. 10). In contrast, population subdivision can increase LD. We simulated a simple two-deme model, and found that LD could easily be made as extensive as observed (Fig. 10), but that population subdivision of this type would have left a trace in the allele-frequency distribution. Thus, simple population subdivision does not appear to explain the data either. However, we note that it is usually possible to find some demographic model that explains any population genetic data (Felsenstein 1982).

Finally we investigated the effect of varying the recombination rate. The lower panel in Figure 10 shows the results of a simulation with a tenfold lower rate of recombination than estimated. The pattern of LD in this figure is superficially quite similar to that observed in the data. In particular, there are extensive blocks of LD separated by regions of low LD. Note that this pattern does not reflect hot- and cold-spots of recombination; the rate of recombination is uniform across all of the panels in Figure 10. Chance alone can create blocks of extensive LD, but not in chromosomal regions that have average levels of recombination.

DISCUSSION

Our main conclusion is that the simple infinite-sites model of recombination and mutation cannot explain the pattern of polymorphism observed on chromosome 21 by Patil et al. (2001). In particular, there is too much heterogeneity in LD and in the level of polymorphism along the chromosome. There are many factors that could contribute to this, demographic history and natural selection being among the more interesting ones. However, we have found that something as simple as variation in the relationship between genetic and physical distance along the chromosome could explain much of the pattern. In regions of low recombination, the pattern of polymorphism will be strongly affected by the randomness in the underlying gene genealogies, whereas in regions of normal recombination, this matters less. Low recombination can cause heterogeneity in the extent of LD as well as in the amount of polymorphism. This does not mean that other phenomena, such as selection or demographic history, do not affect the chromosomal pattern of variation, but it does imply that we need to have much better knowledge about recombination rates in humans before it becomes possible to draw meaningful conclusions about these phenomena. The recently published “Iceland map” (Kong et al. 2002) represents a considerable improvement, but it is still not detailed nearly enough. We note that the population frequency of recombination can be affected by polymorphism for inversions as well as by chromosomal properties.

Several recent studies have investigated the pattern of LD on human chromosomes. For chromosome 21, Wang et al. (2002) also found that the data of Patil et al. (2001) are inconsistent with uniform recombination. For chromosome 22, Dawson et al. (2002) did not investigate fit to any particular model, but found that that LD was more extensive in the regions of significantly reduced recombination that exist on this chromosome. Phillips et al. (2003) looked at chromosome 19 and also reanalyzed the data of Dawson et al. (2002), and found that the data fit a model of uniform recombination with the exception of a few extreme regions. The data for chromosomes 19 and 22 are in the form of ascertained SNPs, and are therefore not suitable for some of the analyses in the present paper.

A second conclusion concerns the problems we are likely to face as we start searching for traces of selection in genomic polymorphism data (e.g., Akey et al. 2002). Although such data can serve as a “genomic control” for population structure, so that traces of selection may be distinguished from the background (analogously to what has been proposed for association mapping; see Bacanu et al. 2000; Pritchard et al. 2000), the problem of multiple comparisons is very serious. The human genome contains over 106 windows of size 1 kb, and a selective process that only affects a small region may well be drowned out by the noise of neutrality. The situation is better when looking for phenomena that would affect larger regions, such as strong selective sweeps. When doing association mapping, false positives can be eliminated by testing for linkage in pedigrees or crosses (Ewens and Spielman 1995), but how do we test for false positives when looking for traces of selection?

METHODS

The chromosome 21 data of Patil et al. (2001) are based on the reference sequence by Hattori et al. (2000). The largest part of chromosome 21 is the q arm, which consists of about 34 Mb. The q arm reference sequence consists of four contigs (NT-002836, NT-001035, NT-003545, and NT-002835) with three gaps. For 32,397,439 bp of this arm, Patil et al. (2001) resequenced 20 copies, representing African, Asian, and Caucasian chromosomes. The chromosome sample is from a publicly available panel, and the ethnicity of each chromosome is not identified.

Patil et al. (2001) found 35,989 SNPs in a 21,676,868-bp region after masking 33% of the sequence as repetitive; 11,603 of the SNPs were singletons (sites where a minor nucleotide was present only once in the sample), and 339 may have had three or more alleles. The remaining 24,046 SNPs had two polymorphic nucleotides with a minor nucleotide present more than once in the sample. These 24,046 SNPs are publicly available at http://www.perlegen.com/haplotype, and have also been submitted to NCBI's SNP database. The data consist of the 20 haplotypes defined by these 24,046 SNPs. Note that there are many missing data in the data set. On average, data for 3.9 chromosomes are missing per site.

The analyses in the present study used the 21,840 SNPs on the longest contig, NT-002836, which covers most of the q arm (28 Mb). We did not use SNPs on the other three contigs because they are relatively short and there are gaps between them.

Allele-Frequency Distribution

In a standard neutral model (no geographic structure, constant population size, etc.), the probability that the derived allele occurs at frequency j in a sample of size n is proportional to 1/j. Therefore, the expected frequency of SNP loci with minor allele frequency j/n is given by 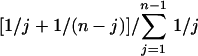Inline graphic. Figure 1 shows this distribution (normalized to take the missing singletons into account) for the 2148 SNPs where all 20 chromosomes were typed, together with theoretical expectations obtained from standard coalescent simulations. The model of exponential growth assumed that the ancestral population size was constant at 104 and started growing exponentially to the current population size of 5 × 109 somewhere between 1000 and 10,000 generations ago.

Estimating the Recombination Rate

Linkage disequilibrium is expected to decay as a function of distance due to recombination. We investigated the decay of |D|′ (Lewontin 1964). Each dot in Figure 2 represents the average of |D|′ for all pairwise values at the given distance ±500 bp.

The expectation of |D|′ as a function of the recombination rate per bp, ρ, was estimated using two-locus, two-allele Monte Carlo simulation to be |D|′ ≈ 4.4/(ρ d + 0.94) + 0.53, where d is the distance in bp. By fitting this curve to the observed distribution using least-squares, ρ was estimated to be 4.2 × 10-4.

We use D′ because its expectation does not depend strongly on sample size. Because so many data points are missing, other pairwise measures of LD would be less suitable. For example, the expectation of r2 contains a term that is proportional to the inverse of the sample size.

Distribution of the Mutation Rate

The distribution of θ was investigated by sliding 500-kb windows at intervals of 125 kb. Because of the large (and unknown) amount of missing data, we were not able to estimate θ from the data in Patil et al. (2001). Instead, θ in each window was estimated using a table kindly provided by D. Hinds at Perlegen Sciences, and publicly available at http://www.perlegen.com/haplotype/tables (as well as www.genome.org). The table consists of estimates of θ and the number of tiled sites for 3621 blocks (average length 7.7 kb) identified by Patil et al. (2001). For each 500-kb window, we calculated the average of the estimates of θ of the blocks in the window weighted by the numbers of tiled sites. This method works well when the window size is much larger than the block sizes.

A coalescent simulation was conducted to investigate the distribution of π in 500-kb windows. We assumed the estimated parameter values θ = 7.2 × 10-4 and ρ = 4.2 × 10-4, and calculated π for each replication. The total value of the mutation rate for each window was lowered by 1/3 to compensate for the 1/3 of the genome that was not surveyed due to masking of repetitive elements. There was little variation in the amount of missing data between windows of this size. The distribution of π from 10,000 independent simulated windows is shown in Figure 3.

Pattern of LD Across the Chromosome

The pattern of LD across the chromosome was investigated using the 16,498 SNPs for which the minor allele was present more than twice in the sample. For each SNP, |r| was calculated with every other SNP within 200 kb. The pattern of LD was also investigated using coalescent simulations as described above.

Acknowledgments

We are very grateful to Perlegen Sciences, and in particular D. Hinds, for the data. We also thank P. Calabrese, P. Donnelly, M. Przeworski, N. Rosenberg, M. Slatkin, and S. Tavaré for discussions and/or comments on the manuscript.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.466303

Footnotes

[Supplemental material is available online at www.genome.org.]

References

  1. Akey, J.M., Zhang, G., Zhang, K., Jin, L., and Shriver, M.D. 2002. Interrogating a high-density SNP map for signatures of natural selection. Genome Res. 12: 1805–1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Andolfatto, P. and Nordborg, M. 1998. The effect of gene conversion on intralocus associations. Genetics 148: 1397–1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ardlie, K.G., Kruglyak, L., and Seielstad, M. 2002. Patterns of linkage disequilibrium in the human genome. Nature Rev. Genet. 3: 299–309. [DOI] [PubMed] [Google Scholar]
  4. Bacanu, S.-A., Devlin, B., and Roeder, K. 2000. The power of genomic control. Am. J. Hum. Genet. 66: 1933–1944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chakravarti, A., Buetow, K.H., Antonarakis, S.E., Waber, P.G., Boehm, C.D., and Kazazian, H.H. 1986. Nonuniform recombination within the human β-globin gene cluster: A reply to B.S. Weir and W.G. Hill. Am. J. Hum. Genet. 38: 779–781. [PMC free article] [PubMed] [Google Scholar]
  6. Dawson, E., Abecasis, G.R., Bumpstead, S., Chen, Y., Hunt, S., Beare, D.M., Pabial, J., Dibling, T., Tinsley, E., Kirby, S., et al. 2002. A first-generation linkage disequilibrium map of human chromosome 22. Nature 418: 544–548. [DOI] [PubMed] [Google Scholar]
  7. Ewens, W.J. and Spielman, R.S. 1995. The transmission/disequilibrium test: History, subdivision, and admixture. Am. J. Hum. Genet. 57: 455–464. [PMC free article] [PubMed] [Google Scholar]
  8. Felsenstein, J. 1982. How can we infer geography and history from gene frequencies. J. Theor. Biol. 96: 9–20. [DOI] [PubMed] [Google Scholar]
  9. Gaudieri, S., Dawkins, R.L., Habara, K., Kulski, J.K., and Gojobori, T. 2000. SNP profile within the human major histocompatibility complex reveals an extreme and interrupted level of nucleotide diversity. Genome Res. 10: 1579–1586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Griffiths, R.C. and Tavaré, S. 1998. The age of a mutant in a general coalescent tree. Stochastic Models 14: 273–295. [Google Scholar]
  11. Harpending, H.C. and Rogers, A.R. 2000. Genetic perspectives on human origins and differentiation. Annu. Rev. Genomics Hum. Genet. 1: 361–385. [DOI] [PubMed] [Google Scholar]
  12. Hattori, M., Fujiyama, A., Taylor, T.D., Watanabe, H., Yada, T., Park, H.-S., Toyoda, A., Ishii, K., Totoki, Y., Choi, D.-K., et al. 2000. The DNA sequence of human chromosome 21. Nature 405: 311–319. [DOI] [PubMed] [Google Scholar]
  13. Hudson, R.R. 1983. Properties of a neutral allele model with intragenic recombination. Theor. Pop. Biol. 23: 183–201. [DOI] [PubMed] [Google Scholar]
  14. Hudson, R.R., Bailey, K., Skarecky, D., Kwiatowski, J., and Ayala, F.J. 1994. Evidence for positive selection in the superoxide dismutase (Sod) region of Drosophila melanogaster. Genetics 136: 1329–1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Innan, H. and Tajima, F. 1997. The amounts of nucleotide variation within and between allelic classes and the reconstruction of the common ancestral sequence in a population. Genetics 147: 1431–1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Innan, H. and Tajima, F. 1999. The effect of selection on the amounts of nucleotide variation within and between allelic classes. Genet. Res. 73: 15–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kaplan, N.L., Hudson, R.R., and Langley, C.H. 1989. The “hitch-hiking” effect revisited. Genetics 123: 887–899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kimura, M. and Ohta, T. 1973. The age of a neutral mutant persisting in a finite population. Genetics 75: 199–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kong, A., Gudbjartsson, D.F., Sainz, J., Jonsdottir, G.M., Gudjonsson, S.A., Richardsson, B., Sigurdardottir, S., Barnard, J., Hallbeck, B., Masson, G., et al. 2002. A high-resolution recombination map of the human genome. Nat. Genet. 31: 241–247. [DOI] [PubMed] [Google Scholar]
  20. Kreitman, M. 2000. Methods to detect selection in populations with applications to the human. Annu. Rev. Genomics Hum. Genet. 1: 539–559. [DOI] [PubMed] [Google Scholar]
  21. Kruglyak, L. 1999. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat. Genet. 22: 139–144. [DOI] [PubMed] [Google Scholar]
  22. Lewontin, R.C. 1964. The interaction of selection and linkage. I. General considerations; heterotic models. Genetics 49: 49–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Li, W.-H. 1997. Molecular evolution, Chapter 9. Sinauer Associates, Inc., Sunderland, MA.
  24. Nordborg, M. 2001. Coalescent theory. In Handbook of Statistical Genetics (eds. D.J. Balding, M.J. Bishop, and C. Cannings), pp. 179–212. J. Wiley, Chichester, UK.
  25. Nordborg, M. and Innan, H. 2003. The genealogy of sequences containing multiple sites subject to strong selection in a subdivided population. Genetics 163: 1201–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Nordborg, M. and Tavaré, S. 2002. Linkage disequilibrium: What history has to tell us. Trends Genet. 18: 83–90. [DOI] [PubMed] [Google Scholar]
  27. Patil, N., Berno, A.J., Hinds, D.A., Barrett, W.A., Doshi, J.M., Hacker, C.R., Kautzer, C.R., Lee, D.H., Marjoribanks, C., McDonough, D.P., et al. 2001. Blocks of limited haplotype diversity revealed by high-resolution scanning of human chromosome 21. Science 294: 1719–1723. [DOI] [PubMed] [Google Scholar]
  28. Phillips, M.S., Lawrence, R., Sachidanandam, R., Morris, A.P., Balding, D.J., Donaldson, M.A., Studebaker, J.F., Ankener, W.M., Alfisi, S.V., Kuo, F.-S., et al. 2003. Chromosome-wide distribution of haplotype blocks and the role of recombination hot spots. Nat. Genet. 33: 382–387. [DOI] [PubMed] [Google Scholar]
  29. Pluzhnikov, A. and Donnelly, P. 1996. Optimal sequencing strategies for surveying molecular genetic diversity. Genetics 144: 1247–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Pritchard, J.K. and Przeworski, M. 2001. Linkage disequilibrium in humans: Models and data. Am. J. Hum. Genet. 69: 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Pritchard, J.K., Stephens, M., Rosenberg, N.A., and Donnelly, P. 2000. Association mapping in structured populations. Am. J. Hum. Genet. 67: 170–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Przeworski, M., Hudson, R.R., and Di Rienzo, A. 2000. Adjusting the focus on human variation. Trends Genet. 16: 296–302. [DOI] [PubMed] [Google Scholar]
  33. Slatkin, M. 1994. Linkage disequilibrium in growing and stable populations. Genetics 137: 331–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Stephens, M. 2001. Inference under the coalescent. In Handbook of Statistical Genetics (eds. D.J. Balding, M.J. Bishop, and C. Cannings), pp. 213–238. J. Wiley, Chichester, UK.
  35. Tajima, F. 1983. Evolutionary relationship of DNA sequences in finite populations. Genetics 105: 437–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wall, J.D. 2000. A comparison of estimators of the population recombination rate. Mol. Biol. Evol. 17: 156–163. [DOI] [PubMed] [Google Scholar]
  37. Wall, J.D. and Przeworski, M. 2000. When did the human population size start increasing? Genetics 155: 1865–1874. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Wang, N., Akey, J.M., Zhang, K., Chakraborty, R., and Jin, L. 2002. Distribution of recombination crossovers and the origin of haplotype blocks: The interplay of population history, recombination, and mutation. Am. J. Hum. Genet. 71: 1227–1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Watterson, G.A. 1975. On the number of segregating sites in genetical models without recombination. Theor. Pop. Biol. 7: 256–276. [DOI] [PubMed] [Google Scholar]
  40. Weir, B.S. and Hill, W.G. 1986. Nonuniform recombination within the human β-globin gene cluster. Am. J. Hum. Genet. 38: 776–778. [PMC free article] [PubMed] [Google Scholar]

WEB SITE REFERENCES

  1. http://www.perlegen.com/haplotype; Perlegen Sciences homepage.

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES