Attentive Scanning Behavior Drives One-Trial Potentiation of Hippocampal Place Fields

Abstract

The hippocampus is thought to play a critical role in episodic memory by incorporating the sensory input of an experience onto a spatial framework embodied by place cells. Although the formation and stability of place fields requires exploration, the interaction between discrete exploratory behaviors and the specific, immediate, and persistent modifications of neural representations required by episodic memory has not been established. We recorded place cells in rats and found that increased neural activity during exploratory head-scanning behaviors predicted the formation and potentiation of place fields on the next pass through that location, regardless of environmental familiarity and across multiple testing days. These results strongly suggest that, during the attentive behaviors that punctuate exploration, place cell activity mediates the one-trial encoding of ongoing experiences necessary for episodic memory.

Through exploration, animals (including humans) create cognitive representations of their environments by incorporating sensory information about the external world onto an internally generated spatial framework^1–3, which resides in medial temporal lobe structures that are critical for declarative memory^4–6. The natural exploratory behavior of rats provides an ideal opportunity to investigate the specific relationship between attention to external sensory input and the updating of hippocampal memory representations. During exploration, rats and other animals intersperse periods of forward movement with pauses⁷, during which they often perform lateral head-scanning movements^8,9. These pauses are nonrandom, temporally structured, and sensitive to environmental features^10,11. It has been suggested that head scanning reflects investigation of environmental features^12,13 and that the pauses represent an animal’s active management of information gathered during exploration¹⁴.

Because head scanning tends to be intermittent and spatially inhomogeneous, it is difficult to obtain sufficient sampling to determine if and how this behavior may alter the firing properties of place cells. This sampling problem is especially problematic in open-field foraging tasks that are often used to study the spatial firing of place cells, head direction cells, and grid cells¹⁵. In other tasks, animals are often trained to run ballistic, stereotyped trajectories between fixed goal locations along narrow tracks. These types of tasks minimize the occurrence of scanning behavior, except at the goal sites, where any changes in place-field activity may be confounded with effects of reward. Furthermore, because place cells lose their spatial specificity during nonexploratory pauses¹, many place-field studies employ a velocity filter that removes most of the pauses and associated head-scanning behavior from analysis.

In the present study, we analyzed place-cell data from sessions in which rats moved along a circular track in search of irregularly placed rewards^16–18. This task resulted in large numbers of head scans that were analyzed with respect to the relationship between neural firing during head scanning and subsequent modifications of the cognitive map. We show that increased neural activity during this discrete, investigatory behavior is strongly associated with the abrupt formation or potentiation of place fields at the location of the scan. These new or potentiated place fields may serve as a memory index^19,20 that encodes the information obtained during the scan onto the hippocampal representation of the environment. This phenomenon provides a potential mechanism for the “automatic recording of attended experience”²¹ that is thought to characterize the hippocampal contribution to declarative memory.

Results

Head-scanning events

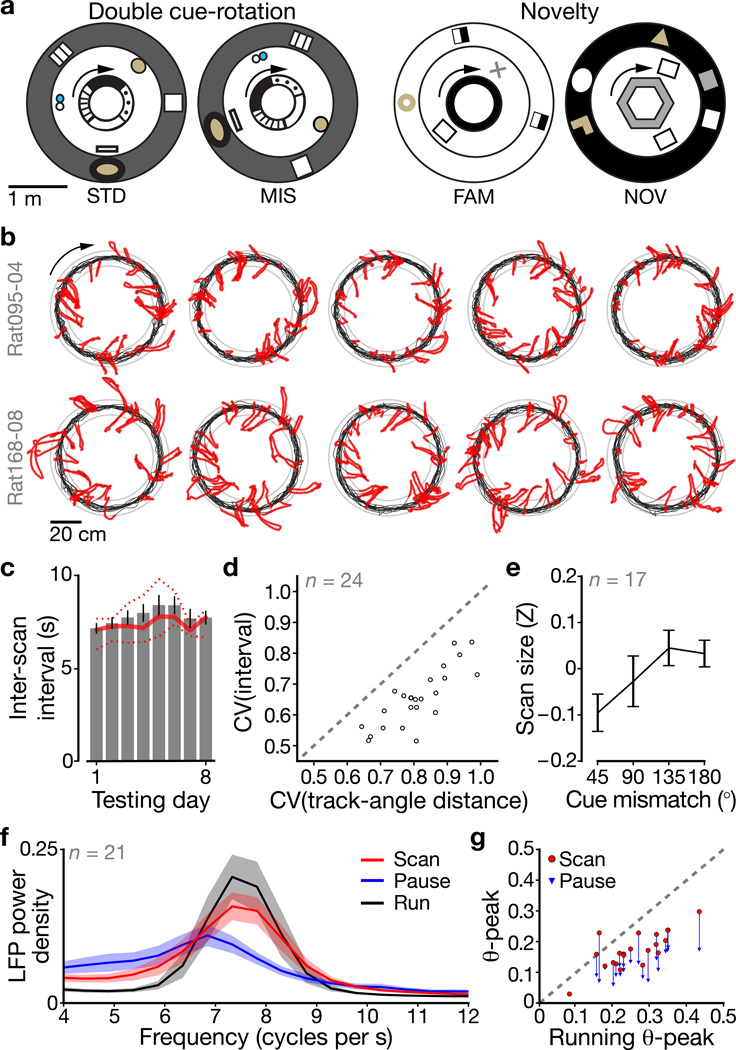
We quantitatively isolated head-scan events during pauses in running (Methods and Supplementary Fig. 1) while rats ran ~15 clockwise (CW) laps for food reward on closed-loop tracks in either double cue-rotation^16,17 (DR; 20 rats) or novelty¹⁸ (10 rats) experiments. DR experiments interleaved standard (STD) and local/global cue-mismatch (MIS) configurations (Fig. 1a, left); novelty experiments interleaved familiar (FAM) and novel-room (NOV) sessions (Fig. 1a, right). Scans occurred at all track positions and were directed across the track interior or outward to the global cues (Fig. 1b and Supplementary Fig. 2). Scan-event durations were ~2 s (n = 24 rats with potentiation events (see below), 2.2 ± 0.61 s, mean ± s.d.) and inter-scan intervals ranged 5–12 s (7.4 ± 1.5 s). There was no change in inter-scan intervals across testing days (two-tailed least-squares linear regression, R = 0.513, P = 0.193; Fig. 1c). Time elapsed since the previous scan was a better predictor of the next scan than distance traveled since the previous scan (n = 24 rats with potentiation events; two-tailed paired-difference t-test, t(46) = −14.0, P = 3.24×10⁻¹⁸; Fig. 1d).

Figure 1. Rats make exploratory scanning movements during pauses on closed-loop tracks.

a, Top-down schematics of the recording room during the DR (left) and novelty (right) experiments. Animals were trained to run CW (arrows) laps around tracks surrounded by distinct distal cues. Outer ring: curtains; inner ring: textured (left) or solid-colored (right) track. b, For two example DR datasets, scan events (red) are highlighted on full-session trajectories (black). Scan events were detected by analyzing lateral head motion during pauses in forward locomotion. Gray rings: track edges. c, Inter-scan interval across testing days (mean ± s.e.m.; days 1–8: n = 17, 16, 18, 20, 11, 11, 10, and 10 rats with datasets for the given day). Solid/dotted lines: median/inter-quartile range. d, Coefficients of variation (CV) show that inter-scan variability was lower when measured in time intervals (ordinate) compared to track-angle distances (abscissa). e, Total radial scan size (Z-scored within rat) varies with cue-mismatch angle (mean ± s.e.m., n = 17 DR rats with potentiation events). f, LFP theta-band power spectra (n = 21 CA1 rats, mean ± 95% c.i.) for running (black), scanning (red), and non-scanning pauses (blue). g, Within-rat spectral peaks for running (abscissa), scanning (red, ordinate), and non-scanning pauses (blue, ordinate). A line connects the scanning and non-scanning pause values for each rat, showing the consistent decrease for pauses across rats.

Is scanning in the present experiment related to active sensory acquisition, in accordance with the behavioral literature^8–14 on scanning during natural exploration? First, we hypothesized that greater mismatch angles would elicit larger scans, because the rat would search farther for the global landmarks predicted by the local cues at the rat’s current location. During initial presentations of each MIS angle, scan size increased with mismatch until leveling off between the two largest angles (n = 17 DR rats with potentiation events; two-tailed Friedman test, χ²(3,64) = 8.08, P = 0.0443; Fig. 1e). Second, we hypothesized that the theta rhythm, which is present during exploratory behavior⁸, would be prominent during scans. LFP power spectra (n = 21 rats with CA1 tetrodes; Fig. 1f) during scanning and running had prominent modes occurring around ~7.5 cycles/s, whereas non-scanning pauses demonstrated weaker (and lower-frequency, possibly Type II) theta. Comparing theta power modes across rats (Fig. 1g), theta power was weaker during scanning than forward running (n = 21 rats; two-tailed paired-difference t-test, t(40) = −7.34, P = 6.26×10⁻⁹), but stronger during scans than non-scanning pauses (t(40) = 6.68, P = 5.17×10⁻⁸). The reduction in theta power during scanning compared to running is likely due to the known relationship between theta power (as well as interneuron firing rate) and speed of movement^8,22 (Supplementary Fig. 3). These results suggest that head scanning is an active, exploratory behavior.

Place-field potentiation events

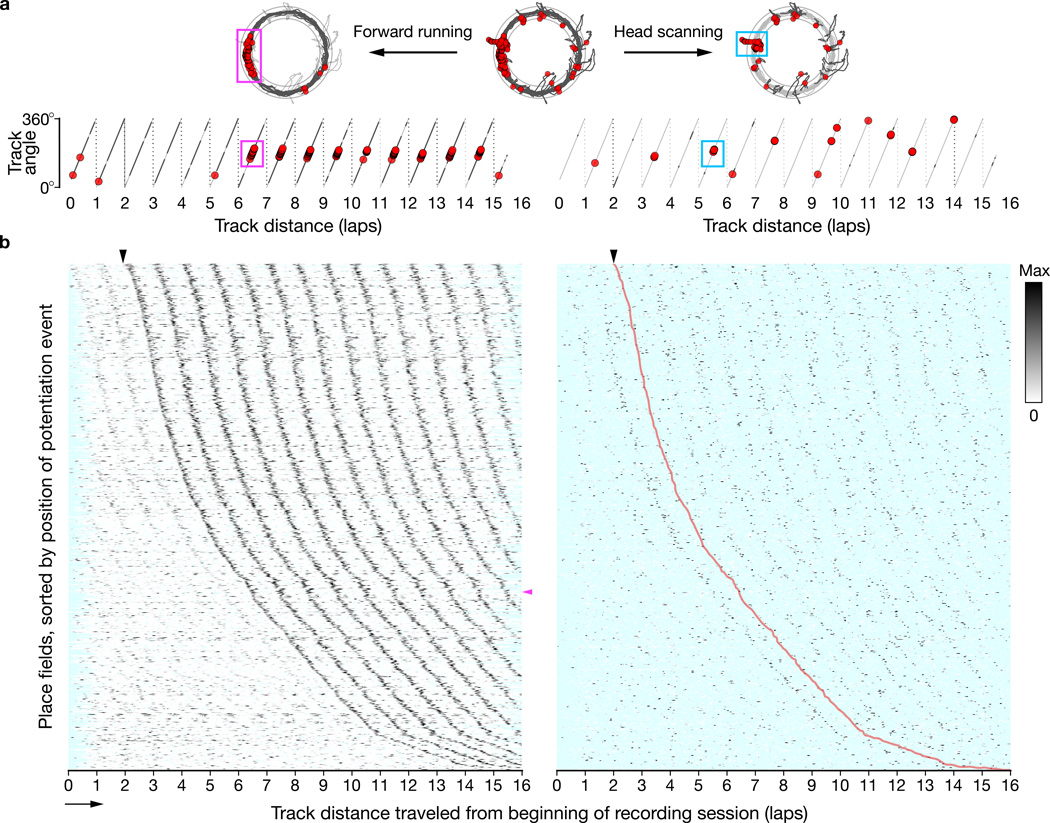
Although many place cells are active in their place fields from the animal’s first entry into that location, a fraction of cells are initially silent and develop a place field, often abruptly, over time^23–25. An example is shown in Figure 2a. The top center panel shows the firing of the cell, with a strong place field at the west position, for 15 laps of running in the DR task. The top left panel shows spikes that occurred only during periods of forward movement (dark gray lines). To show the cell’s firing across laps, we plot the cell’s spikes on the track angle of the animal’s position on each lap of the session (Fig. 2a, bottom left). For the first 6 laps, the cell was mostly silent. On lap 7 (magenta box), the place field abruptly appeared, and it persisted through the rest of the session.

Figure 2. Hippocampal place fields can strengthen abruptly following colocalized scan firing.

a, We divided trajectory and place-cell spiking data (top, center) into forward running (top, left) and head scanning (top, right) behaviors. Running and scanning data were analyzed across laps (bottom) to reveal mid-session potentiation events (magenta box) and scan activity (cyan box, encompassing scan firing one lap prior to the potentiation event). Light gray: full trajectory; dark gray: running (left) or scanning (right) behaviors; red circles: spikes. b, Linearized firing-rate maps across laps of 789 place-field potentiation events recorded from 24 rats, sorted by the track distance of the event’s first spike. (left) Periodic ridges in forward-running activity reflect repeated traversals of place fields. The leftmost dark ridge (black arrowhead: earliest possible event detection) comprises the potentiation-event traversals. (right) The firing-rate maps constructed from scanning data reveal a ridge of activity one lap preceding the potentiation ridge (replicated as a trace (red) from the left panel). Cyan: unsampled bins; magenta arrowhead: potentiation event example (a); arrow: running direction.

To find place-field potentiation events systematically, we analyzed a lap-by-lap dot-product measure of place-field strength. We used a threshold-based algorithm to detect abrupt, >50% increases in field strength relative to preceding laps that persisted across subsequent laps (Methods and Supplementary Fig. 4). We found 789 potentiation events across 5,510 place fields (~14.3%; Supplementary Table 1) from 24/28 rats. Linearized firing-rate maps across laps for all potentiation events are shown in the left part of Figure 2b. The abscissa of the maps is the distance traveled by the animal around the track since the start of the recording session: each tick mark represents one 360° cycle of travel around the track. The place fields are sorted on the ordinate by the track position of the first spike of the potentiation event. Thus the periodic ridges of activity represent place-field traversals for each lap (the magenta arrowhead indicates the example cell in Fig. 2a). The ridge starting at the black arrowhead (top) represents the abrupt increase in firing corresponding to the mid-session potentiation events for all cells. Potentiation includes both onset events, in which there is no previous field activity, and strengthening events, in which a previously existing field becomes stronger (as indicated by weaker ridges to the left of the potentiation ridge). Place-field potentiation events occurred uniformly across the entire track and in all experimental sessions, although they were more prevalent in novel and mismatch sessions (Supplementary Fig. 5).

Is there a relationship between the potentiation of place fields and the firing of cells during scanning behaviors? The right side of Figure 2a shows the firing of the example cell during head-scan events (dark gray lines). The right side of Figure 2b shows firing-rate maps from head scanning that correspond to the potentiation-event maps on the left. (Most bins are unsampled (cyan) because scans are discrete and sparsely distributed in space.) The place-field potentiation ridge from forward-running behavior (left) is reproduced as a red line on the scan-firing-rate maps (right, arrowhead). This comparison of scan firing with field potentiation demonstrates the main finding of the current report: the first strong ridge of activity during head scanning appears one lap prior to the place-field potentiation ridge (red line). In other words, scan firing predicts the formation or strengthening of the place field at that location on the next lap. The ridges on subsequent laps (to the right of the red line) indicate firing during head-scan events that occurred when the rat was in the newly potentiated place field.

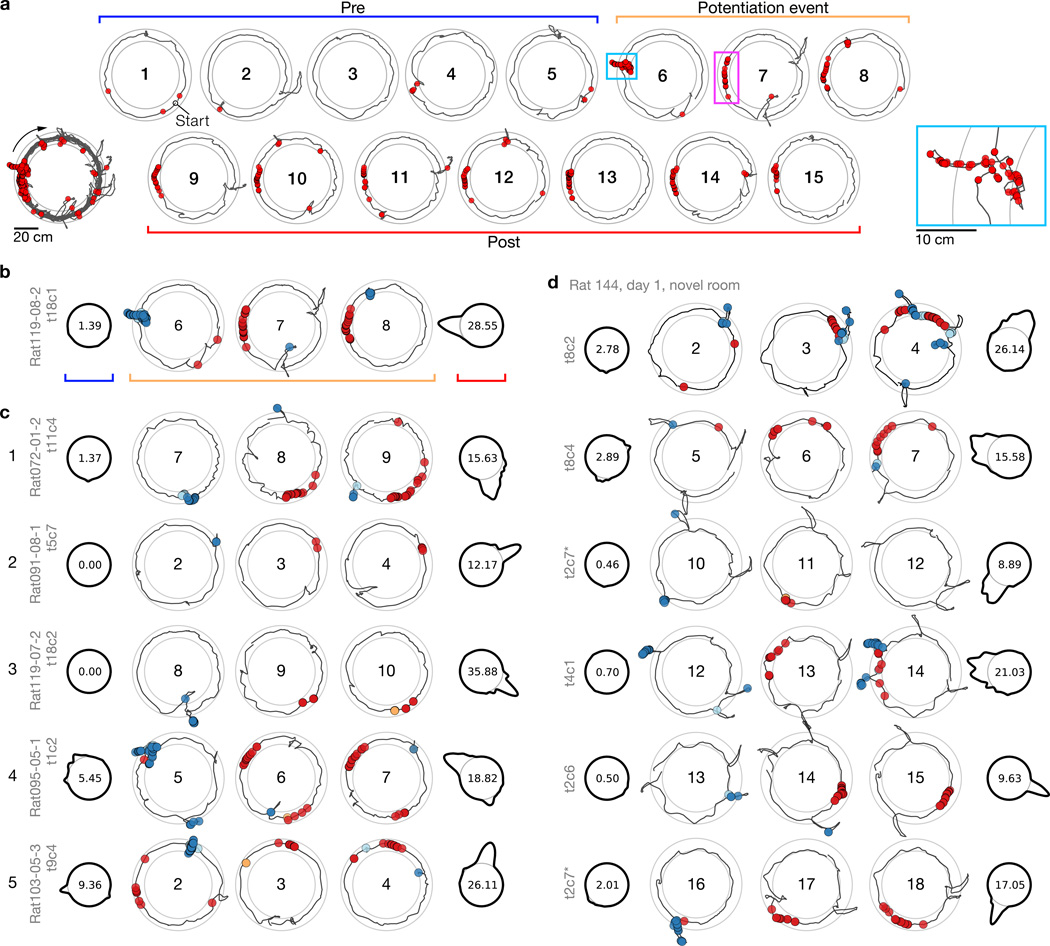
Examples of the scan–potentiation effect

The illustration in Figure 2b shows the relationship between head-scan firing and place-field potentiation at the population level. To demonstrate the phenomenon further, Figure 3 illustrates several examples of single place cells (see also Supplementary Fig. 6). Figure 3a shows the example cell from Figure 2a, with each lap presented individually. On laps 1–5, the cell was mostly silent, but it fired a strong burst during a head-scan event on lap 6 (cyan box, inset). On lap 7, the new place field appeared at the exact location of the head scan on the prior lap. Figure 3b presents a more compressed display of this potentiation event. The laps prior to the head scan (‘Pre’, blue bracket) are shown as a polar plot of firing rate as a function of track angle, with the base circle of the plot corresponding to 0 spikes/s; the peak firing-rate is displayed in the interior of the base circle. The lack of a strong peak on the first polar plot shows that the cell did not fire strongly in the first 5 laps. The ‘Potentiation event’ laps (orange bracket) show spike–trajectory plots centered on the potentiation event, with scan firing (blue circles) on lap 6 and place-field firing (red circles) on laps 7 and 8. Finally, the ‘Post’ polar map shows the potentiated place field for the remaining 7 laps. Examples from different rats (Fig. 3c) demonstrate the variability of the effect. Cell 1 fired during a low-amplitude scan on lap 7, followed by a robust place field on lap 8, which persisted throughout the session. Cell 2 fired a brief burst during a scan on lap 2 and developed a place field at that location on the next lap. Cell 3 had no field before firing during a large, bidirectional scan on lap 8, followed by the appearance of a place field on lap 9. Cell 4 fired during two separate scans on lap 5, and formed two place fields on lap 6 that persisted until the end of the session. Finally, cell 5 had a field at the west on the first 2 laps, before firing robustly during a scan at north-northeast. On lap 3, the cell fired at the location of the scan and the original place field was silenced.

Figure 3. Examples of the scan-related potentiation of place fields.

a, The place field from Figure 2a (lower-left inset) displayed by individual laps. Spiking during a large head scan (cyan box, lower-right inset) precedes a potentiation event at the same track position (magenta box). For further examples, laps are divided into three groups: prior to scan–potentiation (‘Pre’), 3 laps centered on the potentiation event lap, and following scan–potentiation (‘Post’). b, Display scheme for examples illustrated with the field from (a). In the Pre (blue bracket) and Post (red bracket) polar plots, track-angle position is represented as a circle (thin line) and the forward-running firing rate for a given location across the represented laps is proportional to the deviation of the thick line from the base (center: peak rate). Trajectory plots of the potentiation event (orange bracket; center: lap number) show behavior-coded spikes: scan (blue), peri-scan (cyan), pause (orange), and forward running (red). c, Examples from 5 rats in the DR experiment. d, A simultaneous ensemble of place cells recorded during initial exposure to the novel room, sorted by event lap. One of the cells (asterisk; ‘t2c7’) forms a new field on lap 11 (line 3), which further potentiates on lap 17 after a second scan event (line 6).

For most recording sessions, it is possible that potentiated fields were remapped or reactivated place fields that were learned previously. However, place cells in the novelty experiment underwent global remapping¹⁸; thus recordings from the first novel-room session allow examination of de novo place fields. Simultaneously recorded place cells (Fig. 3d and Supplementary Fig. 7) demonstrate new fields forming at different times within the session, each preceded on the prior lap by a colocalized scan with spiking activity.

Predictive analysis across potentiation events

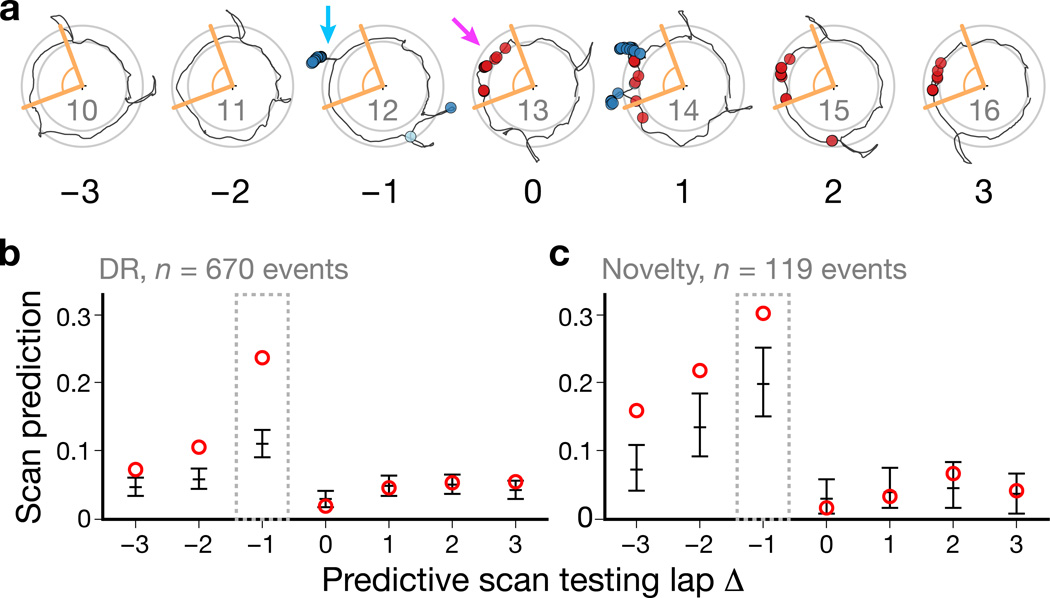
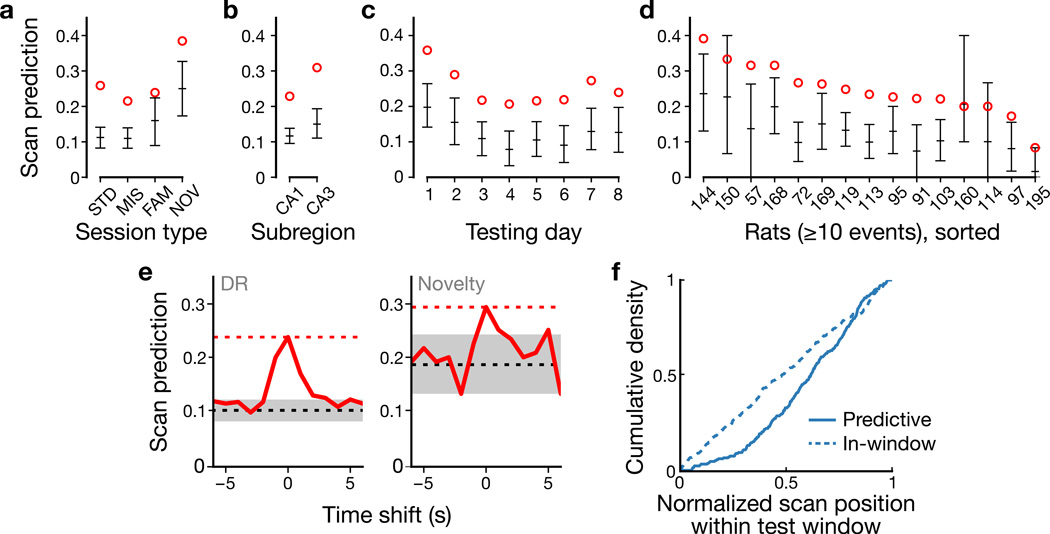
To quantify the prevalence of the scan–potentiation effect, we devised a predictive test based on a track-angle window around the potentiation event. The track-angle window was defined for each place field as a window that encompassed all of the spikes of the potentiation event, with a 10° buffer at each end and with a minimum size of 60° (Fig. 4a, lap Δ = 0; Methods and Supplementary Fig. 8a–d). For a range of laps relative to the potentiation event, we determined whether a scan occurred within the test window and, if so, whether the cell fired at a greater rate during the scan than expected based on a bootstrap distribution of firing during forward movement within the test window (Supplementary Fig. 8e–f). In Figure 4a, laps Δ = −1 and Δ = 1 each had scans that occurred in the test window. On lap Δ = −1, the cell fired more than expected during the scan; thus this scan would be considered a predictive scan. Because the place field had already formed by lap Δ = 1, the firing during the scan at the west position on lap Δ = 1 did not exceed the expected firing rate. However, the cell did fire at a higher-than-expected rate during a second scan at the northwest on lap Δ = 1, which would be considered a predictive scan. We calculated a Scan Prediction Index (SPI) for each lap as the fraction of potentiation events that had at least one predictive scan on that lap. The SPI was highest for the lap immediately preceding potentiation (Δ = −1) in both experiments (Fig. 4b–c).

Figure 4. Predictive analysis of the scan–potentiation relationship.

Scan Prediction Index values were computed across potentiation events for a range of scan testing laps relative to each event. a, Track-angle windows (orange) around a potentiation event (magenta arrow) were used to test whether an active scan (e.g., cyan arrow) was predictive for that event. b–c, SPIs across scan testing laps for the DR (b) and novelty (c) experiments. The highest values of the index occurred for the lap immediately preceding the potentiation event (lap Δ = –1). Scan firing on subsequent laps was within the expected values based on the place-field activity of the cell. Circles: observed; error bars: chance levels, mean ± empirical 95% c.i. derived from simulations (Supplementary Fig. 9).

To determine statistical significance of the observed SPIs, we modeled the chance level of predictiveness by randomizing distributions of scan timing and resampling scan spike counts from the observed spike train to generate expected distributions of SPIs (Methods and Supplementary Fig. 9). SPIs for the post-potentiation laps (Δ = 0…3) fell within the expected 95% confidence interval (c.i.; Fig. 4b–c, error bars), indicating that these baseline distributions captured the expected level of predictive scan firing on the null hypothesis that scan-related firing primarily reflects place-field activity. For the DR experiment (Fig. 4b), the SPI was well above the c.i. for lap Δ = −1 and fell dramatically for earlier laps (although still above baseline), indicating that the scan–potentiation effect is highly specific to the lap immediately preceding the potentiation event. (SPIs above baseline for the laps preceding lap Δ = −1 are primarily due to margin effects in detecting which lap actually contained the potentiation event in more ambiguous cases.) The drop-off for earlier laps was not as dramatic for the novelty experiment, which also produced higher pre-potentiation baselines (Fig. 4c). The higher baselines may be due to more frequent (DR: n = 17 rats with potentiation events, 0.13 ± 0.022 scans/s, mean ± s.d.; novelty: n = 9, 0.16 ± 0.016 scans/s; two-tailed Welch’s t-test, t(21) = 3.91, P = 0.000804) and more complex (cf. Supplementary Fig. 2) scanning compared to the DR experiments.

SPIs for the lap that preceded potentiation (Δ = −1) were significant across experimental variables and animals (Fig. 5). Regardless of session type, hippocampal subregion (CA1 vs. CA3), or testing day, SPIs were significantly above baseline (Fig. 5a–c and Supplementary Fig. 10). For rats with at least 10 potentiation events (15/24 rats; Fig. 5d), 14/15 SPIs were greater than the expected value (two-tailed binomial test, P_0.5 = 0.000977) and 11 were significantly predictive (P_0.025 = 2.97×10⁻¹⁵). To test sensitivity to scan timing, we computed SPIs while shifting the observed scan train forward and backward in time. Time-shifted SPIs (Fig. 5e) decreased from the observed value (red dashed line) for 1 s shifts and fell within baseline (gray region) within 1–4 s. Thus the observed SPIs reflect sub-second temporal alignment between scanning behavior and spiking. Notably, predictive scans were spatially biased (two-tailed Pearson’s χ²(29) = 65.0, P = 0.000143) toward the CW end of the test window (i.e., corresponding to the trailing edge of the subsequent place-field traversal), whereas nonpredictive scans within the window were spatially unbiased (χ²(29) = 25.5, P = 0.650; Fig. 5f and Methods). Thus scan firing predicts strong potentiation (Supplementary Fig. 10e) of a field leading up to the scan’s location (e.g., cells 1, 3, and 5 in Fig. 3c), reminiscent of the role of asymmetry in theories of hippocampal sequence encoding and prediction^26–28.

Figure 5. Predictive analysis of colocalized scans on the lap prior to potentiation.

a–d, SPIs of prior lap (Δ = −1 in Fig. 4b–c) for session type (a), subregion (b), day (c), and rat (d). Event counts for each category are provided in Supplementary Table 1. e, SPIs for time-shifted scans (solid red) in DR (left) and novelty (right) experiments. Dashed lines: observed (red) and chance levels (black/gray: mean ± empirical 95% c.i.) from Figure 4. f, Predictive scans (solid line; n = 214 scans) were spatially biased toward the CW (trailing) end of the test window, whereas nonpredictive within-window (dashed line; n = 264) scans were uniformly distributed.

Receiver operating characteristic analysis across scans

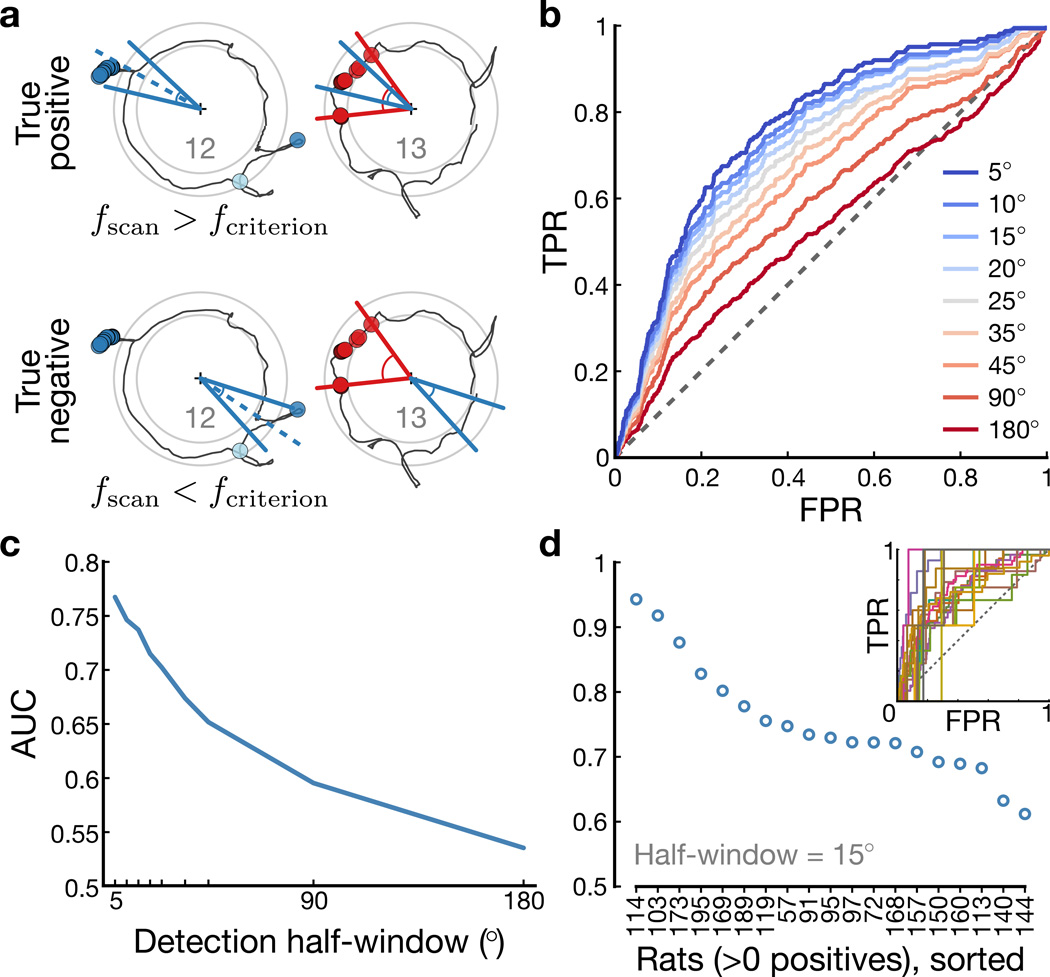
The SPI analysis demonstrated a significant correlation of scan firing relative to place-field potentiation, but it is not a causal analysis (the measure of scan firing depended on bounds determined by a future event) nor diagnostic (the absence of potentiation is not well-defined, preventing the evaluation of predictive specificity). It is important to analyze the data based on a forward prediction; that is, if a cell fires more than expected during a scan event, does this predict place-field potentiation on the next lap? Because a large majority of scans were not associated with any neural firing (in part because we only sampled a small fraction of the hippocampal cell population), we first had to narrow the dataset by identifying scans of interest in which neural activity was relatively strong. For every scan and place cell recorded concurrently (excluding scans from the first lap and last 3 laps of a session), we determined whether firing during the scan was greater than expected based on the prior history of firing at the scan location (Methods). A total of 33,723 scan–cell pairs (out of 129,218) passed this threshold. For these pairs, we tested whether a track-angle window centered on the scan’s position overlapped with the spatial extent of a potentiation event for that cell on the next lap.

Scans were classified as positive or negative predictors based on a scan-firing-rate threshold criterion (Fig. 6a, left side) and the outcome of the prediction was whether there was scan–potentiation overlap (Fig. 6a, right side). We computed receiver operating characteristic (ROC) curves by varying the scan-firing threshold to demonstrate the trade-off between the true-positive rate [TPR = true positives / (true positives + false negatives)] and false-positive rate [FPR = false positives / (false positives + true negatives)] for various sizes of the track-angle window on the next lap (Fig. 6b and Methods). The ROC curve with the widest test window (red) was close to the nondiscrimination (dashed) line, indicating near-chance level performance. Thus, higher-than-expected scan firing at a specific location was not diagnostic of whether a place field would potentiate at an arbitrary location on the track on the next lap. As the test window narrowed, however, the ROC curves (orange–blue) moved increasingly away from the nondiscrimination line, demonstrating the spatial specificity of the relationship between scan firing and subsequent field potentiation. The increased performance for narrow test windows is summarized as the area under the ROC curve (AUC; Fig. 6c), which reached a maximum of ~0.75 with a test window of ±5°. The AUC for individual rats (Fig. 6d) demonstrated significant performance above chance level (n = 19 rats with positive outcomes; AUC = 0.752 ± 0.0859, mean ± s.d.; one-tailed t-test, t(18) = 12.8, P = 8.86×10⁻¹¹) with all 19 rats having AUC > 0.5 with ±15° test windows. This result demonstrates that strong place-cell spiking during attentive head-scanning is a critical factor in abrupt place-field potentiation and emphasizes the precise, spatial specificity of the phenomenon.

Figure 6. ROC analysis of scan-firing-rate as a predictor of potentiation.

Across scan–cell pairs, we computed an index of scan firing relative to expected place-like firing (Methods). ROC curves for scan-firing-rate criteria were generated across scan–cell pairs with higher-than-expected firing. A true positive occurred when a cell fired above a specified threshold during a scan and a place field was potentiated on the next lap at that same location; a true negative occurred when the cell did not fire above the threshold and no place field was potentiated; a false positive occurred when the cell fired above threshold on a scan but no place field subsequently potentiated; and a false negative occurred when the cell fired below threshold on a scan but a place field subsequently potentiated anyway. a, Illustration of testing scans (blue) for predicting a subsequent potentiation event (red) of the corresponding place cell. b, ROC curves for a range of half-window sizes (red: wide; blue: narrow) for scan-firing-rate predictions of potentiation events. c, AUC across varying window sizes shows that smaller, more specific windows produce stronger discrimination. d, AUC for n = 19 rats with at least one potentiation event within the test window of a scan (i.e., at least one positive outcome). Inset: individual ROC curves; dashed line: chance performance.

Discussion

The present study demonstrated a novel relationship between a discrete, investigatory behavior (head scanning) and the sudden onset or potentiation of a place field the very next time the rat visited the location where the behavior occurred. Animals perform head scans during pauses in exploration to actively investigate their environments^9–11, presumably binding sensory information available at that location to the animal’s cognitive representation of its current location^12–14 (rearing, which is another discrete investigatory behavior, was not analyzed in the present study, as the rats rarely performed this behavior in our task). The one-trial nature of the potentiation of place fields related to head scanning is consistent with the putative role of the hippocampus in supporting episodic memory. The specific, local, and robust alterations to the hippocampal map may reflect the types of changes required for the hippocampus to serve the indexing role that is at the core of current theories of hippocampal memory function^19,20,29,30.

Several decades of place field studies have shown that, in a familiar environment under familiar behavioral conditions, place fields in rats are mostly stable³¹, with only subtle changes such as the size or shape of place fields^27,32,33 or population-level representations that can change gradually as a function of time or experience^34–37. The long-term stability in familiar environments³¹ raised the question of how the system is able to encode the items and events of experience to form an episodic memory in a stable environment. Leutgeb and colleagues³⁸ proposed that hippocampal “rate remapping” was a mechanism to encode episodic information about the content of an experience onto a stable spatial map. In this form of remapping, the locations of place fields remain stable, but the firing rates of the cells within their fields varies. Leutgeb and colleagues³⁸ hypothesized that the variations in firing rate may encode information about the animal’s experiences within that framework. Different experiences in the same location may be encoded by the same set of cells that have place fields at that location, with the distinct experiences being encoded by differences in the ensemble firing-rate vector. Dual hippocampal coding of spatial and nonspatial information has been shown by a number of experiments^3,39–42 that have proposed that this dual encoding may be related to the proposed role of the hippocampus in context-specific, episodic memory. However, none of these studies showed explicit, one-trial formation of place fields that is consistent with rapid updating of a stable map as the result of a discrete episode. In the present study, the potentiation of place fields was a local phenomenon that was not accompanied by global changes to place fields away from the scan location; thus, scan activity did not result in global remapping. Rate-remapping changes can include individual cells changing from a silent cell to an active cell. Thus, the one-trial potentiation of place fields coordinated by scanning behavior is a robust demonstration of the incorporation of information about attended external stimuli onto the hippocampal spatial framework, providing strong support for current theories of its role in episodic memory formation^1,5,21,43.

A number of studies have shown local changes to the place field map as the result of environmental or task manipulations, and it is useful to compare those results with the phenomenon described here. Frank and colleagues²⁵ and Hill²³ demonstrated the abrupt onset of place fields as rats explore a completely novel environment. We observed reduced interneuron firing as scans were initiated, which is consistent with velocity modulation and also with reports³⁴ of interneuron suppression as new place fields develop in a novel location. However, none of these studies related the place field onset to an explicit behavior of the rat at the location of the place field. Furthermore, our results show that the scan-related place field formation occurred even in familiar environments. O’Keefe described “misplace cells”¹ that fire when an animal encounters an object at an unexpected location or fails to experience an expected reward. Other experiments have shown how place-field responses can be affected locally by objects, barriers, or odors in a given location, or how place fields can change over time^32,36,37. However, in some of these experiments the changes were gradual, or the time course of the change was not investigated, making it unclear whether the local remapping was indicative of an immediate, episodic updating of the map.

The present results showed that head-scanning behavior was accompanied by theta rhythm, consistent with the interpretation that this is an active, exploratory behavior of the rat. It will be of interest in future analyses to determine whether there are other correlates in the LFP that are important for the scan behavior. Sharp-wave/ripples are associated primarily with sleep or quiet wakefulness accompanied by the large irregular activity state⁴⁴, but these events can also be detected during active behavior⁴⁵. Any role they may play in the scan–potentiation phenomenon is likely to be complex, and inspection of the examples shows that the neural spiking during a scan event does not always occur within the brief temporal constraints of a ripple burst. Nonetheless, this topic deserves further exploration.

Johnson and Redish⁴⁶ studied the hippocampal population code during periods when the animal pauses at a choice point at a T-junction, sometimes moving its head back and forth as it made its decision. During these pauses, the hippocampal population code for position sweeps alternately down the two choice arms, as if the animal were testing hypotheses about which arm to choose (“vicarious trial-and-error”). Although there were no choice points in the current experiment, and the Johnson and Redish study did not report local changes to the place fields related to the animal’s pauses, it would be of interest in the future to determine if there is any relationship between these two phenomena.

Although the present study does not directly address whether the field potentiation is associated with an explicit memory, the phenomenon is consistent with current thinking on the role of the hippocampus in supporting episodic memory. Morris and Frey²¹ have suggested that the function of the hippocampus is the “automatic recording of attended experience.” Information about the external world, including nonspatial information, is thought to be transmitted to the hippocampus via the lateral entorhinal cortex^5,6,47,48 (LEC). One potential mechanism for the scan–potentiation effect is that the LEC drives the hippocampal firing during the scan events. Heterosynaptic long-term potentiation between the lateral and medial perforant path inputs onto the place cells may strengthen the input from the medial entorhinal cortex (MEC) onto that place cell, such that the next time the animal visits that location, the cell fires in a robust place field driven by the spatially selective MEC inputs. This notion is consistent with prior reports that have shown a relationship between electrical stimulation of the hippocampus and the formation of new place fields^49,50. Feedback connections from the hippocampus to the neocortex via the deep entorhinal layers may allow the new place cells to serve as an index to the memory^19,20,30 of the input that drove the cell during the scanning event. Although this idea is speculative, the demonstration of scan-related place-field potentiation shows that the hippocampal map can indeed be updated in a robust, local, one-trial manner correlated to a discrete behavior, and this phenomenon may serve as a valuable model for the neural mechanisms that allow the hippocampus to record ongoing experience.

Online Methods

Data collection

Previously collected and published data^16–18 were combined and reanalyzed for the investigations reported here. Detailed descriptions of data collection methods for the DR⁵¹ and novelty¹⁸ experiments have been reported elsewhere. The two experiments presented in this study were within-subject designs, which precluded the need for group randomization or investigator blinding. We did not use statistical power analysis to estimate sample size requirements as there were no adequate a priori effect-size estimates available for the phenomenon studied here. We collected data from several series of experiments amounting to an atypically large sample relative to other studies in the field. All animal procedures were approved by the Institutional Animal Care and Use Committee of the University of Texas Health Science Center at Houston and conformed with NIH guidelines.

Subjects and surgery

Adult male Long-Evans rats were maintained at 80–90% of their ad libitum weights with free access to water. The rats were housed individually on a 12/12 hr light/dark schedule and experiments were performed during the dark phase of the cycle. For surgical implantation of the recording devices, animals were anesthetized with an initial dose of 60 mg/kg ketamine and 8 mg/kg xylazine, followed by isoflurane inhalation to effect. Microdrive arrays consisting of 14–20 tetrodes were then centered over the right dorsal hippocampus. Tetrodes were constructed from 4 0.0005-inch nichrome wires that were twisted together and gold-plated to obtain 200–500 kΩ impedance measured at 1 kHz or 0.0007-inch unplated platinum-iridium wires (~500 kΩ impedance). For post-operative analgesia, rats were administered ketoprofen subcutaneously (5 mg/kg) or 1 cc of oral acetaminophen (Children’s Tylenol liquid suspension, 160 mg). Analgesia was provided as needed the following day by a second injection of ketoprofen or by access to diluted acetaminophen in drinking water.

Recording electronics

After recovery from surgery, tetrodes were slowly advanced across several days until reaching the hippocampal CA1 or CA3 layers. Neural signals passed through head-stage amplifiers and were then filtered (0.6–6 kHz) and digitized (32 kHz) by a data acquisition system (Neuralynx, Bozeman, MT) before being stored on computer. The head-stage had a circular array of light-emitting diodes (LEDs). The output of a camera mounted on the ceiling was captured by a video frame grabber at 30 or 60 Hz. For every frame, head position was computed as the center-of-mass (COM) of all pixels containing light from the circular LED array.

Single-unit isolation

Offline single-unit isolation was primarily based on relative spike amplitudes of the signals recorded simultaneously across the four different wires of the tetrode. Unit isolation was subjectively categorized on a scale of 1 (very good) to 4 (marginal), based on the overlap of points in the multidimensional waveform parameter space. This classification of unit isolation was performed independently of the firing properties of the cells. Cells judged as marginally isolated were excluded from analysis.

Histology

After completing the experiments, marker lesions were made by passing current through a subset of tetrodes 24 h before transcardial perfusion with 4% formalin. The brains were kept in 30% sucrose formalin solution until being frozen, sectioned at 40 μm, and stained with cresyl violet. Recording locations were assigned by identifying the tetrode tracks across sections and matching them against the known configuration of tetrodes in the recording array. Finally, depth reconstruction of the tetrode tracks was performed for each recording session to identify the brain region in which the cells were recorded at that depth.

Double cue-rotation protocol

Rats were trained to run CW on a circular track (76 cm outer diameter, 10 cm width) to collect chocolate rewards placed at random locations on the track. Whenever the rat turned around and moved counter-clockwise (CCW), its progress was stopped by blocking its path with a paper folder. Grooming behavior was discouraged by the use of a hand-held clicker that was activated whenever the rat began to groom. By the time of recording experiments, grooming and turning around occurred infrequently. The track was composed of four textured surfaces that served as local cues, each covering a quadrant of the ring: a gray rubber mat with a pebbled surface, brown medium-grit sandpaper, beige carpet pad material, and gray duct tape with white tape stripes. The track was placed in a circular, curtained environment (2.7 m diameter) in which six distinct objects were present either on the floor or on the curtain as distal cues. During testing, the rat was placed on the track at a random starting point and allowed to run for 15 laps around the track. Each day of recording consisted of five sessions, with three STD sessions interleaved with two MIS sessions. STD sessions maintained the local and distal cue configuration as it was during training. In MIS sessions, the track and room-based objects were rotated CCW and CW, respectively, to achieve total cue mismatches of 45, 90, 135, or 180° between local and distal cues.

Novelty protocol

Recording rooms were cylindrical (2.7 m diameter) with the outer perimeter defined by curtains extending from floor to ceiling. A circular or hexagonal track was placed on a platform in the center of the room. Room A was set up with a gray, hexagonal track (40 cm hexagon sides, 10 cm track width) with black curtains and a variety of distal cues arranged around the room. In CCW order from the East track-position, the cues were a gray rectangular poster, a triangular piece of cardboard, a box on the floor, a circular white poster, an L-shaped piece of cardboard, another box on the floor, and a white rectangular poster. Room B was set up with a black, circular track (76 cm outer diameter, 10 cm track width) with white curtains and a different set of distal cues arranged around the room. In CCW order, the cues were a coat rack on the floor, a square black-and-white poster, a donut-shaped piece of cardboard, a box on the floor, and another square black-and-white poster. The rooms were counterbalanced such that five rats were randomly assigned to experience room A as FAM and room B as NOV, and the other five rats experienced the reverse. In the familiar room, rats were trained to run CW as in the DR experiments. For each of four testing days, rats were transported in the open (without disorientation) into the FAM behavioral room, placed on the track at an arbitrary location, and allowed to run 15 laps. Rats then rested again before they were transported to the NOV room. After 15 laps, rats rested and then performed the last FAM session. Two rats were additionally trained and tested for four days in the DR experiment after completing the novelty protocol.

Position tracking

Head-position tracking data were collected from a series of experiments, leading to small differences in video-tracking configurations. To calibrate the position data, we first detected position errors caused by occlusion or other factors and fixed those tracking samples by linear interpolation of the valid samples surrounding the errors. The experimenter-recorded center-pixel coordinates were then subtracted to loosely zero-center the data. To precisely zero-center the data, we divided the data into 32 track-angle bins and computed the median radius of all positions in each bin. The center angle and median radius of each bin were projected back into Cartesian coordinates to create 32 perimeter vectors. The perimeter vectors were averaged to estimate the center-offset of the tracking data, which was then subtracted from the tracking data. To calibrate the scale of the position data, the data were normalized by the median radius of the trajectory and then scaled by the known circular mid-track radius 33 cm (hexagonal mid-track radius ranged 29.5–34.8 cm). To mitigate noise due to pixel aliasing, we filtered the data with a 4/8 sample boxcar window for the 30/60 Hz tracking data (a 133 ms smoothing kernel).

Scanning events

Head-scanning events were detected (Supplementary Fig. 1; see Appendix 2 for details) as deviations from running baseline distributions of lateral head motion during pauses (<10 °CW/s) and were required to have minimum duration (400 ms) and size (2.5 cm, measured as total radial extent). Peri-scan epochs were defined as periods up to 1.5 s or 7.5° before/after the start/end of a scan. Average inter-scan intervals across testing days (Fig. 1c) were calculated for each rat as recording time divided by number of scans on the given testing day. Coefficients of variation (CV) of inter-scan intervals and track-angle distances (Fig. 1d) were computed as the sample s.d. divided by the sample mean of the respective inter-scan measurements within each rat. CVs for intervals and distances were tested with t-tests of matched-pair differences. For statistical testing, we employed the significance level α=0.05 and two tails unless otherwise specified.

To test whether scan size (measured as total radial extent in cm) varied with the cue-mismatch angle, we analyzed scans that were unambiguously directional, either oriented inward across the track or outward to the perimeter of the room. We defined directional scans as those that moved at least 2.5 cm radially in one direction from the starting point of the scan. Normalizing scan size within-rat by Z-score controlled for between-rat variability in scan size. To test for statistical differences in scan size (Fig. 1e), we used the Friedman test to avoid assumptions of normality and equal variance and to account for repeated measurements of rats across mismatch angles.

To compare scan frequency between the two experiments, the scan event-rate for each rat was calculated as total number of scans divided by total recording time. The event rate was calculated separately for each experiment for the two rats that performed both experiments. To test for the statistical difference of event-rate means and allow for comparison of unequal-sized samples and avoid the assumption of equal variance, we used Welch’s t-test with effective degrees-of-freedom approximated with the Welch-Satterthwaite equation.

LFP theta analysis

One channel from every tetrode was used as the source for LFPs, which were constructed by filtering (1–475 Hz) the amplified neural signal and recording the data at 1 kHz. For each tetrode and dataset (i.e., testing day), we computed relative theta power as the ratio of total theta-band (5–12 Hz) power to total power in the range 1–50 Hz. For each dataset with CA1 tetrodes, we analyzed the CA1 tetrode with the highest relative theta power. Across the sessions in each dataset, we collated the LFP data during forward running, scans, and non-scanning pauses (Appendix 2). We computed the behavioral power spectra (Welch’s average periodogram method over 2,048-sample, Hanning-windowed blocks with 50% overlap) and normalized by the total power in the LFP to construct power spectral density (PSD) functions. PSDs were averaged across all datasets for each animal with CA1 tetrodes. PSD errors were displayed (Fig. 1f) as 95% confidence intervals assuming normality. Theta peaks (maximum spectral density within theta band) were compared using Student’s t-tests of matched-pair differences to account for repeated measurements of rats across behaviors. To compute velocity-modulation curves and behavioral cross-correlations (Supplementary Fig. 3), instantaneous theta power and frequency signals were derived from the analytic signal computed from theta-filtered LFP signals and the Hilbert transform.

Place cells

Single-unit recordings from tetrodes unambiguously assigned to the hippocampal cornu ammonis layers were analyzed for place-cell responses by testing spike clusters in each recording session for several criteria. Putative pyramidal cells were selected by low average firing rates and high average spike widths. Units denoted interneurons by the experimenter were also excluded. The track-angle velocity of every spike was computed by linear interpolation of track-angle velocities at the start and end of the tracking frame containing the spike time. For each recording session, we filtered the spikes and track-angle occupancy by velocity-filtering (>10 °CW/s, or ~6 cm/s) and excluding scans, pauses, and off-track positions. We excluded units with <30 such spikes during the session. To ensure that temporally variable spatial responses were not excluded from analysis, we computed two measures of the mutual information between space and spiking: the spatially-binned spike information⁵² was thresholded at 1.0 bits/spike and the temporally-binned positional information⁵³ was peak-thresholded at 0.4 bits. If either measure was above threshold and statistically significant at P < 0.01, then the unit was included as a place cell for analysis. See Appendix 1 for details.

Place field analysis

Place fields were constructed from forward-running activity, defined as track-angle velocity >10 °CW/s excluding scans, peri-scan epochs, pauses, and off-track positions. To compute place field firing-rate maps, spike counts were divided by occupancy durations for the forward-running activity in each track-angle bin. Unwrapped linearized firing-rate maps have 30° bins (Fig. 2b and Supplementary Fig. 5c). Polar maps (Fig. 3 and Supplementary Fig. 6) and wrapped linear maps (Supplementary Fig. 5a–b) have 7.5° bins. Firing-rate vectors were smoothed with a gaussian kernel with s.d. set to bin width; smoothing was circular for wrapped and polar track-angle maps. Individual place fields were isolated using a floor threshold set to 12.5% of the unit’s maximum firing rate. Peaks greater than the floor threshold and >1.5 spikes/s were traced in both directions until hitting two subthreshold bins and any overlapping fields were merged. The track-angle width was measured across the above-threshold bins of the field and putative place fields <30° or >180° wide were discarded. Linearized maps were normalized to respective peak firing rates for display.

Field potentiation events

To find potentiation events (Supplementary Fig. 4; see Appendix 3 for details), we isolated individual place fields (as above) and computed dot-products of the activity on each lap (7.5° bins) with the whole-session place field. We tested each lap of every place field for stable >50% potentiation using two thresholds: a baseline maximum threshold tested the preceding (minimum 2, up to 5) laps for weaker field activity, and a follow-up minimum threshold tested whether the potentiation persisted through the following (minimum 3, up to 5) laps. To test for statistical differences in prevalence (Supplementary Fig. 5d–g), we used the Friedman test to avoid assumptions of normality and equal variance and to account for repeated measurements of rats across sessions.

Scan Prediction Index analysis

See detailed descriptions of scan predictiveness testing (Supplementary Fig. 8) in Appendix 4 and the SPI analysis (Supplementary Fig. 9) in Appendix 5. The predictive scan testing window is the track-angle window defined by bounds that are at least 30° from the COM and 10° from the positions of the first and last spikes of the potentiation event traversal (Supplementary Fig. 8a–d). Expected firing rates were computed by bootstrapping (1,000 samples) the forward-running activity in the time interval corresponding to the test window; within-window scan activity >97.5% of bootstraps was considered to be predictive (Supplementary Fig. 8e–f). SPI baselines were generated using a Monte Carlo randomization and resampling process (Supplementary Fig. 9): the timing of scans from other sessions in the event dataset were jittered 10 times (up to ±10 s) and pooled together, scan spike-counts were sampled from the event spike-train, scan predictiveness was tested as described above, then the observed number of scans were sampled from the randomized scan pool multiple times (5,000 samples for every SPI data point). Time-shifted SPI values were constructed as described above for randomized scans, except that the start times of scans within the potentiation event session were shifted incrementally from the actual start times. SPIs for each time-shift offset were computed based on the corresponding time-shifted scan train. For the analysis, scans were shifted from −6 to +6 s in increments of 1 s, such that the 0 s time-shift replicates the observed SPI.

To examine spatial bias of predictive and nonpredictive scans, we divided the set of scans within the predictive testing window of any potentiation event into those that scored as predictive for the event and those that did not. The testing windows were normalized such that the CCW and CW edges were mapped to 0 and 1, respectively, and each within-window scan was assigned a normalized position within its respective window. We statistically tested for spatial bias of within-window scan position by dividing the normalized window into 30 spatial bins (averaging ~8 scans per bin) and testing goodness-of-fit to the uniform distribution with Pearson’s χ²-test.

ROC analysis

We computed a scan-firing index S that compares scan firing with expected place-like firing for concurrently recorded scans and place cells (see Appendix 6 for details). This index ranges from −1 to +1 such that positive non-zero values indicate higher-than-expected scan firing, where the expectation is based on the spatial distribution of place-cell spiking in the same session as the scan but before the scan occurred. For various half-window sizes and across scan–cell pairs, we tested whether any potentiation event for the cell overlapped with a track-angle window centered at the position of the scan on the lap following the scan (Fig. 6a). To quantify scan activity as a predictor of potentiation, we constructed ROC curves across scan-firing-rate criteria (i.e., firing rate > criterion indicates a positive prediction) for scan–cell pairs with higher-than-expected scan firing (i.e., S > 0). The AUC for each ROC curve was computed by trapezoidal integration. Statistical significance of scan–potentiation was tested with a one-tailed Student’s t-test of within-rat AUCs (for 15° half-windows) against the null hypothesis of nondiscrimination. The test was one-tailed because the reverse prediction was not a sensible alternative hypothesis given the results of the SPI analysis.

Appendix 1: Spatial information criteria for place cell selection

To quantify the spatial selectivity of place cells, we computed measures of the mutual information between animal location and spiking activity using 1-dimensional spike count and occupancy distributions across track angle. The measurement of track-angle selectivity is improved by integrating activity across the radial axis (i.e., the axis along the absolute center of the track and the position of the animal at any given tracking sample). We used two different measures of spatial information. The measurement of the spatial information content of spikes introduced⁵² by Skaggs et al (1993) is a classic measure, but it was developed for 2-dimensional firing-rate maps and we found that, in our 1-dimensional rate maps, it often produced both false-positive errors (e.g., at the low information thresholds that are commonly used) and false-negative errors (e.g., when there was more than one subfield or the fields changed over the course of the session). The measure of positional information introduced⁵³ by Olypher et al (2003) uses spike-count distributions across temporal bins, which helps to detect spatial responses that were false negatives under the Skaggs measure. Thus to ensure that we included responses with multiple place fields or that changed over the course of the session, we combined the results of both measures. For the spiking activity within each recording session (see Methods/Place cells), we constructed spatial distributions (for both measures) across 48 track-angle bins (7.5° bin width) and temporal distributions (for the Olypher measure) across 100 ms bins. First, we computed the spatial information content of spikes⁵²

$$I_{\text{spike}}=\sum _{i=1}^{48}{p}_i\frac{r_i}{\overline{r}}{\text{log}}_2(\frac{r_i}{\overline{r}})$$ (1)

where p_i is the occupancy probability and r_i is the average firing rate, respectively, of track-angle bin i, and r̄ is the average firing rate across the session. Second, we computed the positional information⁵³

$$I_{\mathrm{p}\mathrm{o}\mathrm{s}}(x_i)=\sum _{k\ge 0}{P}_{k|x_i}{\text{log}}_2\left(\frac{P_{k|x_i}}{P_k}\right)$$ (2)

where k is the spike count within a time bin, P_k is the overall probability of k spikes, and P_k|xi is the conditional probability of k spikes occurring within track-angle bin i. Positional information thus measures location-specific information of spiking around the track.

We computed the statistical significance of both measures using an unbiased spike shifting procedure. Time-shifting is typically used to generate control distributions of spatial information by simply subtracting shift points from the observed spike train. In open-field environments or more complex tasks with highly variable trajectories across the recording session, this procedure is sufficient to temporally decouple the spike train from the animal’s position while preserving the temporal structure of the spike train as much as possible. However, in this study rats were trained to run in one direction continuously around closed-loop tracks, which resulted in comparatively regularized trajectories across laps in many recording sessions. Thus simple shifts of the observed spike train more easily produced spurious alignments of spikes with a particular location on the track, leading to false-negative errors. To preserve the structure of spike timing while reducing the likelihood of such spurious alignments, we took the additional step of first inverting the spike train such that a spike at the start of the session would be moved to the end of the session and vice versa. Shift points were then set at 0.5 s intervals from 15 s after the start to 15 s before the end of the session. For every shift point, the shift is subtracted from the spike train and any spikes shifted before the start of the session are wrapped around the end of the session. The resulting p-value was calculated as the fraction of shifted spike trains that yielded an information value greater than observed. We included a place-cell spike train for analysis if either I_spike > 1.0 bits/spike or max_i(I_pos(x_i)) > 0.4 bits with the respective information measure significant at P < 0.01. These information thresholds were judged by visual inspection of the data by experienced observers to minimize false-positive and false-negative errors. The resulting place-cell responses within each session were then searched for place-field potentiation events (below).

Appendix 2: Quantitative detection of head-scanning behavioral events

The detection of scanning events consists of three steps: head-motion quantities are derived from position tracking; trajectory processing finds putative scanning samples; and event processing determines the final set of scan events. We derived four quantities (Supplementary Fig. 1a) from the (x, y) position-tracking data to characterize forward and lateral motion:

$$\alpha =(180°/\pi )(2\pi -\mathrm{a}\text{tan}2(y,x)),\dot{\alpha }=\Delta \alpha /\Delta t,\overline{r}=\sqrt{x^2+y^2}-r_{\text{track}},\text{and}\stackrel{\dot{-}}{r}=\Delta \overline{r}/\Delta t$$ (3)

where atan2(y, x) is the function mapping Cartesian coordinates (x, y) to radian angles {0,2π}, α and α̇ are the track-angle (° CW) and track-angle velocity (° CW/s), r̄ and $\stackrel{\dot{-}}{r}$ are the track-centered radius and radial velocity, Δα is the frame-to-frame circular track-angle difference, Δt is the frame duration, and r_track = 33 cm is the radius of the circular track mid-line. These quantities are computed for every tracking sample in the trajectory of a session and analyzed in parallel with the (x, y) positional data.

To find putative scanning samples, we iterate across all trajectory samples from the start to the end of the session (Supplementary Fig. 1b). For each sample, we first determine whether it is a running sample by testing that it is both on track (|r̄| < 5 cm) and running forward (α̇ ≥ 10 °CW/s). If it is a running sample, the lateral head-movement data (r̄ and $\stackrel{\dot{-}}{r}$) are added to corresponding running buffers (r̄_buffer and ${\stackrel{\dot{-}}{r}}_{\text{buffer}}$) that store the most recent 4 s of data. If it is not a running sample, then we determine whether it is a putative scanning sample by testing

$$\left|\overline{r}\right|>5cm,$$ (4)

$$\overline{r}\notin {\mathrm{I}\mathrm{Q}\mathrm{R}}^{*}({\overline{r}}_{\text{buffer}}),\text{or}$$ (5)

$$\stackrel{\dot{-}}{r}\notin {\mathrm{I}\mathrm{Q}\mathrm{R}}^{*}({\stackrel{\dot{-}}{r}}_{\text{buffer}})$$ (6)

where Eqn. 4 indicates the sample is off track, and Eqns. 5 and 6 indicate the sample has a radius or radial velocity outside of expected values. The expected lateral head movement is based on the buffer data, and the function IQR^*(·) maps a buffer distribution to the interval {u − Δ/2, u + Δ/2} where {l, u} is the buffer’s inter-quartile range (IQR) and Δ = u − l. That is, this interval is centered on the buffer IQR but has twice the width, which was determined by inspecting the data to maximize the sensitivity of scan detection while minimizing false positives. If any of the inequalities in Eqns. 4–6 are satisfied, then the current sample is marked as a putative scanning sample.

Finally, we process the array of putative scanning samples to find scan events. Contiguous blocks of scan samples become putative events. For each event, we ensure that the event at least starts and ends on the track by tracing samples from the middle of the event in both directions until the trajectory reaches the edge of the track. Based on observation of the behavior, scans consist of sweeping the head away and then back to the approximate starting position of the scan on the track. To ensure the sweep back to the track is fully detected, we extended the end of the event as long as the trajectory continued to approach the start position of the scan. After both event extension procedures, we merged together any overlapping events or adjacent events with <400 ms gap. We discarded any events where the track angle between the start and end points was >45°, the duration was <400 ms, or the total radial extent was <2.5 cm. Timestamps for the remaining scan events were then recorded for subsequent analysis. For every scan, we also determined ‘peri-scan’ epochs by finding the periods before/after the start/end of the scan event up to 1.5 s or 7.5° track-angle distance away from the scan. Peri-scan activity was excluded from forward-running activity and is colored distinctly from scan and forward-running spikes in example spike plots.

Additionally, we detected non-scanning pause events, which were incorporated into the behavioral filtering that determined forward-running activity. Intuitively, these events are episodes when the animal is neither moving forward nor making lateral head movements that would qualify as a scan event. Putative pause samples were detected as on-track position frames, excluding scan events and peri-scan epochs, that satisfy

$$\sqrt{{\left(\frac{s}{5\mathrm{c}\mathrm{m}/s}\right)}^2+{\left(\frac{\dot{\alpha }}{10°/s}\right)}^2}<1$$ (7)

where α̇ is the track-angle velocity (Eqn. 3) and s is the trajectory path speed

$$s=\frac{\sqrt{\Delta x^2-\Delta y^2}}{\Delta t}$$ (8)

where Δx and Δy are frame-to-frame differences in (x, y) position. Contiguous blocks of pause samples were merged across <200 ms gaps. Pause events <400 ms duration were discarded and the remaining events were recorded.

Appendix 3: Quantitative detection of place-field potentiation events

We defined ‘forward-running activity’ for both spiking and behavior as periods of track-angle velocity >10 °CW/s excluding scan events, peri-scan epochs, pause events, and off-track positions. (See Appendix 2 above for details about behavioral events.) For a given place-cell response, we computed the whole-session firing-rate map (48 bins, 7.5° bin width, 7.5° gaussian kernel s.d. for circular smoothing) for forward-running activity. We isolated individual fields as contiguous blocks of track-angle bins (Methods/Place field analysis). For each field, we computed the circular center-of-mass (COM) based on the firing rates across its track-angle bins and recalculated the time bounds of each lap in the session based on new laps starting at the track angle opposite from the field COM. These lap boundaries ensured that place-field traversals would be contiguous and fully contained within each lap. Firing-rate maps for each lap were then computed and compared to the whole-session map using a normalized dot product

$$C_{jm}=\frac{{\Sigma }_{i\in x_j}{R}_i^m{S}_i}{{\Sigma }_{i\in X_j}{S_i}^2}$$ (9)

where X_j is the set of track-angle bins in field j, $R_i^m$ is the firing rate in bin i on lap m, and S_i is the whole-session firing rate in bin i. Note that the dot product in Eqn. 9 is normalized by the whole-session response and not the per-lap response. This normalization means that C_jm is not a correlation, but a measure of the magnitude of the lap response relative to the whole-session response. It is thus sensitive to both changes in spatial position of the spikes as well as firing rate. For each lap in the session, we determined the sets of baseline laps and follow-up laps to test. Baseline laps are the preceding 5 laps, down to a minimum of 2 laps if the test lap is close to the start of the session. Follow-up laps are the following 5 laps, down to a minimum of 2 laps if the test lap is close to the end of the session. A lap is not tested for potentiation events if it has less than 2 baseline or 2 follow-up laps; thus, the earliest potentiation event detected was on lap 3 and the latest was on the third lap before the end of the session. We calculated two thresholds relative to C_jm to test field j for potentiation on lap m (Supplementary Fig. 4). The baseline maximum threshold

$${\theta }_{\mathrm{p}\mathrm{r}\mathrm{e}}^m=C_{jm}-(0.5+m/N)C_{\text{potentiation}}$$ (10)

is adjusted by the number of laps into the session, where N is the number of laps and C_potentiation = 50% is the nominal amount of relative potentiation that we want to detect. The lap adjustment corrects for whole-session averaging (S, Eqn. 9) over changing place fields: early laps should have lower relative potentiation requirements than late laps (Supplementary Fig. 4a). The follow-up minimum threshold

$${\theta }_{\text{post}}^m=C_{jm}-C_{\text{tol}}(C_{jm}-\underset{b\in B}{\text{max}}{C}_{jb})$$ (11)

is based on the actual magnitude of the putative potentiation event, where B is the set of baseline laps and C_tol = 30% is a tolerance parameter allowing follow-up laps to be somewhat weaker than the potentiation event. The lap is then tested by checking that the baseline laps satisfy

$$\underset{b\in B}{\text{max}}{C}_{jb}<{\theta }_{\mathrm{p}\mathrm{r}\mathrm{e}}^m$$ (12)

and that at least 3 of the follow-up laps satisfy

$$C_{jf}\ge {\theta }_{\text{post}}^m,f\in F$$ (13)

where F is the set of follow-up laps. Application of these thresholds is illustrated in Supplementary Figure 4b. Multiple potentiation events were allowed for the same field, but a subsequent potentiation event must occur at least 4 laps after the preceding event. Once these requirements were met, we isolated the spikes constituting the place-field traversal for the event lap. Any event consisting of a single spike was discarded. Finally, the event was recorded along with the track-angle positions of the first and last spikes and the COM of the potentiation traversal.

To show that place fields can also weaken abruptly, we searched for sudden reductions in field strength (‘weakening’ events) by reversing the dot-product vector of field strength across laps before testing laps with the above algorithm. The minimum number of baseline laps was increased to 3 to prevent the spurious detection of weakening based on incomplete final laps in the trajectory. Due to the inherent uncertainty in marking the location of the absence of activity (in the case of active place fields that weaken to the point of becoming silenced), we delimited weakening events as the bounds of the last active traversal prior to the weakening event. Thus the track-unwrapped firing-rate maps in Supplementary Figure 5c are sorted by the position of the first spike of the last active traversal before the place field became weaker or deactivated.

Appendix 4: Testing for predictive place-cell activity during scans

The predictive scan testing window (Supplementary Fig. 8a–d) is defined for all place-field potentiation events as an absolute track-angle window. It is constructed as the union of a ‘minimum’ window

$$\{{\varphi }_{\mathrm{C}\mathrm{O}\mathrm{M}}+30°\mathrm{C}\mathrm{C}\mathrm{W},{\varphi }_{\mathrm{C}\mathrm{O}\mathrm{M}}+30°\mathrm{C}\mathrm{W}\}$$ (14)

and a ‘maximum’ window

$$\{{\varphi }_{\text{start}}+10°\mathrm{C}\mathrm{C}\mathrm{W},{\varphi }_{\text{end}}+10°\mathrm{C}\mathrm{W}\}$$ (15)

where ϕ_start, ϕ_COM, and ϕ_end are the track-angle positions of the potentiation event start, COM, and end, respectively. The minimum window is typically in effect for small event traversals (i.e., for place fields <60° wide), and the maximum window becomes effective for larger traversals. Our motivation was to adaptively delimit the field traversal while allowing for reasonable margins on both sides. The margin parameters that we chose are minimal while still helping to reduce false-negative errors in detection of the scan–potentiation effect. While the test window may be applied to the activity of any lap relative to the event, the analysis primarily targets the lap immediately preceding the event lap. Using unwrapped track angles, we apply the test window by moving it 360° CCW from the event lap to the preceding lap.

Two criteria are applied to the window on the test lap: first, there must be at least one scan with a starting track-angle position within the window; second, at least one of those scans must contain significantly more spiking activity than could be expected by contemporary place-field firing. That is, we examine whether there was more firing during the scan than what would be expected if there was a place-field traversal within the test window and the scan firing reflected nothing more than place-field activity. If any within-window scans are found, we construct a bootstrap distribution of place-field firing rates for the time interval corresponding to the trajectory that traverses the test window. Because complicated trajectories mean that multiple time intervals could possibly map onto the test window, we chose the time interval that starts at the latest crossing of the leading (CCW) edge and ends at the earliest crossing of the trailing (CW) edge of the test window. The procedure for testing scan activity is illustrated in Supplementary Figure 8e–f. The test interval is divided evenly into 20 ms bins, and we select all bins where both edges occur during forward-running activity. We then compute 1,000 bootstrap samples by resampling with replacement the interval with spike counts from the forward-running bins. For each bootstrap sample, we compute the firing rate as the total number of spikes divided by the total duration of the forward-running bins. The mean and empirical 95% confidence interval $\{r_l^{bs},r_u^{bs}\}$ of the bootstrapped firing-rate distribution are recorded. For each scan in the test window, we test whether

$$k_{\text{scan}}>r_u^{bs}\Delta t_{\text{scan}}$$ (16)

where k_scan is the scan spike count, Δt_scan is the scan duration, and $r_u^{bs}$ is the upper bound of the bootstrap firing-rate confidence interval. Any scan that passes is marked as a predictive scan for the corresponding potentiation event, and the potentiation event is marked as successfully predicted by scan activity.

Appendix 5: Scan Prediction Index and generation of control distributions

The Scan Prediction Index (SPI) was computed as the ‘positive predictive value’ (as defined by the statistics and diagnostic testing literature) of the scan–potentiation of place fields. For any given subset of the place-field potentiation events in our dataset, we calculated the SPI as the fraction

$$\mathrm{S}\mathrm{P}\mathrm{I}=\frac{\text{number of scan-predicted potentiation events}}{\text{number of potentiation events}}$$ (17)

To construct a baseline model of the expected value of the SPI and compute the uncertainty around the expected value (Supplementary Fig. 9), we started with the null hypothesis that scanning is no different than forward-running exploratory behavior such that any spikes during a scan would have occurred even if the animal had not been engaged in scanning behavior at that moment. In other words, the null hypothesis to be tested is that the apparent relationship between above-expected firing during a scan (measured as in Appendix 4) and subsequent place-field potentiation is no more than would be expected by the chance coincidence of unrelated cell firing and scanning behavior. We tested this null hypothesis with a Monte Carlo randomization and resampling procedure.

Typically, to randomize behavior relative to a spike train, the timing of the observed behavior would be temporally shifted by random offsets. Such randomization would preserve the temporal structure of the behavioral events (outside of the discontinuity at session boundaries) but discard any temporal dependence of scan event-rate and duration on the time elapsed within the recording session. By visual inspection of the behavior and scanning data, however, we observed that many rats scanned noticeably more frequently during the first few laps of a recording session than throughout the remainder of the session. For such temporally heterogeneous sessions, a baseline model based on temporal shifts would average across those differences, creating a bias to undershoot early and overshoot late potentiation events leading to false positive and negative errors, respectively. To preserve the temporal dependence of scanning behavior, we created randomized scans for each potentiation event by aggregating scans from all other sessions in the same dataset (e.g., for a potentiation event in session 4 of a double rotation (DR) experiment, scans were collected from sessions 1, 2, 3, and 5; Supplementary Fig. 9a) into a pool to be randomly sampled. Each different-session scan is added to the pool 10 times with random temporal jitter from U{−10,10} s to increase the short-term randomness but preserve the overall temporal distribution of scanning within a session for the given rat on the given testing day (Supplementary Fig. 9b). The 10 s maximum jitter was chosen as half the duration of a typical lap run; thus the jitter ranges up to approximately one-half lap in either direction, which largely preserves the lap order of scans while distributing the interpolated position of the randomized scans around the track. We found that the additional randomization provided by temporal jitter produced higher-quality SPI estimates for datasets with low overall rates of scanning. While the start time of the scan within the session is jittered, the randomized scans maintained their original duration so that the distribution of scan durations is preserved. To preclude the sampling of irrelevant scan times, randomized scans that extend beyond the duration of the event session were excluded from the pool.

For each randomized scan, we assigned the spike count corresponding to the number of spikes that occurred within the scan interval (i.e., starting at the randomized scan starting time and lasting for the original scan duration) in the observed spike train that produced the potentiation event (Supplementary Fig. 9c). Randomized scans were allowed to overlap the time intervals corresponding to observed scans and thus their spike counts could include spikes that occurred during observed scans. To assign positions to randomized scans, we used the start time of each scan to interpolate its unwrapped track-position within the event session. With a position and a spike count, the randomized scans were tested for predictiveness of the place-field potentiation event as described above in Appendix 4. The results of predictive testing for the randomized scan pool of an example potentiation event are illustrated as a row of boxes in Supplementary Figure 9d, where the orange boxes are the subset of randomized scans that passed the predictive scan test. We randomly sampled scans from the scan pool by choosing without replacement the same number of scans as the event session (blue outlines). If we consider an example event (Supplementary Fig. 9d), one particular sample may choose only nonpredictive scans; this would be a nonpredictive sample. However, if we again randomly sample the randomized scan pool, one of our selections may be a predictive scan (orange box with blue outline); this event would be considered randomly predicted by this particular sample, which would contribute positively to the expected SPI. We extended this sampling process to all place-field potentiation events (or a particular subset of events), the respective scan pools of the events, and a large number of samples; this is represented by the 3-dimensional matrix illustrated in Supplementary Figure 9e, for which the 2-dimensional front face represents a single random sample of the scan pools across events. Any event that selected (blue outlines) at least one predictive scan (orange boxes) was considered to be randomly predicted (red boxes) for this sample. We calculated the fraction of randomly predicted events across all potentiation events as the SPI (Eqn. 17) for the sample. To generate a distribution of expected SPIs under the null hypothesis that scanning and potentiation events were unrelated, we repeated this sampling procedure 5,000 times for every SPI data point (Figs. 4b–c and 5a–e and Supplementary Fig. 10a–d). The mean and empirical 95% confidence intervals (i.e., the 2.5 and 97.5 percentiles of the expected SPI distribution; Supplementary Fig. 9e, right) were then recorded for comparison with the observed SPI. We consider the observed value to be statistically significant if it is greater than the upper bound of the expected SPI confidence interval (Supplementary Fig. 9e, right).

It is critical to validate this baseline model by verifying that it does not tend to under- or over-represent the expected scan predictiveness. Since the scan–potentiation hypothesis is that scan activity precedes field potentiation, we would not expect the potentiation lap itself or the following laps to demonstrate significant scan predictiveness. This was a primary motivation for examining the SPIs across a range of laps both preceding and following the potentiation events (Fig. 4). For both experiments, as described in the main text, statistical significance of the scan–potentiation effect was achieved only for the preceding laps whereas the post-potentiation laps (including the potentiation event lap) yielded observed SPIs within the expected confidence intervals. We would further expect that observed post-potentiation SPIs would not show any systematic bias relative to the expected SPIs. Considering the 4 post-potentiation laps (predictive scan testing laps Δ = 0…3) for both experiments, 4/8 laps have lower than expected SPIs and 4 are greater than expected which is consistent with unbiased random fluctuation around the expected values (two-tailed binomial test, P_0.5 = 1.0). Furthermore, while focusing on time-shifted SPIs of short duration (~1 s; Fig. 5e) demonstrates the timing sensitivity of the observed values, time shifts of longer duration (~5 s) provide additional validation for the expected SPIs by showing convergence to the randomized baseline. These findings provide strong validation that our randomized baseline model of expected scan predictiveness is appropriate for comparison with the observed effect.

Appendix 6: Receiver operating characteristic analysis of scan–potentiation

The Scan Prediction Index analysis described above tests each potentiation event for predictive scan firing on the previous lap. This approach examined the necessity of scan firing for the occurrence of sudden place-field potentiation and allowed for the generation of highly-specific control distributions of scan predictiveness. However, this approach has two primary blind spots. First, because the analysis was oriented around the future outcome of scan firing (i.e., potentiation), the predictiveness of scan firing and the SPIs per se were not causal. Second, because of the difficulty of reasonably determining when a potentiation event did not happen, the analysis does not describe negative predictive power or specificity of the scan–potentiation relationship (i.e., whether lower levels of scan firing are predicted by the absence of subsequent potentiation). Thus, we devised a complementary analysis oriented around the hypothesized causative mechanism of scan–potentiation (i.e., higher-than-expected scan firing). This approach involved only the firing rate computed for a particular place cell during a scan and an expectation of scan-firing constructed from the history of the cell’s activity prior to the scan (Appendix 6.2). Setting a firing-rate criterion allowed for determination of positive (scan firing > criterion) and negative (scan firing < criterion) predictions of subsequent potentiation. The performance of scan-firing-rate as a predictor of potentiation was quantified by computing receiver operating characteristic (ROC) curves (Fig. 6; see below and Methods/ROC analysis).

Scans occurring within pre-existing place fields tend to reflect the place cell’s spatial activity. The spatial modulation of scan firing is demonstrated by the appearance of periodic ridges in the scan-firing-rate maps (Fig. 2b, right). For this reason, the scan–potentiation hypothesis is conditioned on higher-than-expected scan firing. In the SPI analysis, this expectation was derived from the forward-running activity within the temporal limits of the hit window that contained the scan being tested (Supplementary Fig. 8 and Appendix 4). For the ROC analysis, the hit window is not defined, because we are identifying scans before any subsequent place-field potentiation is investigated. Thus, we computed an index of scan firing relative to the historical spatial distribution of activity. For the historical spatial distribution of a cell, we created a 2-dimensional histogram with track location along one dimension and spike count along the other. For each 100 ms interval in the session that occurred before the start of the scan and while the animal was moving, we incremented the count of the histogram bin corresponding to the rat’s location (x_i) and the number of spikes (k_i) in that interval. We created a similar histogram of all 100 ms intervals spanning the time interval of the scan itself. For each location on the track (x_i) that had at least 1 sample in each of the historical and scan histograms, we created cumulative distribution functions of historical and scan spike counts for that location and determined the largest difference between the two functions. The scan-firing index was calculated as the sum of these differences across locations, weighted by the occupancy time of the scan trajectory at each location. Intuitively, this index produced a positive value if the scan firing was more than expected given the historical firing of the cell and a negative value if the scan firing was less than expected by the historical firing. Note that we do not use any statistical tests on this index; its purpose is to select the scans that will enter the ROC analysis (i.e., those with a positive scan-firing index).

To compute the scan-firing index, we divided the session into 100 ms temporal bins associated with a spike count (k), track angle (x), and path speed (v). For every pair of concurrently recorded scans and place cells, we computed

$$S=\sum _x{W}_{x_i}{D}_k(P_{x_i}^{\text{history}},P_{x_i}^{\text{scan}})$$ (18)

as a weighted sum across track-angle bins (W_xi) of differences between the historical and scan spike-count distributions $P_{x_i}^{*}$ at that location, where the difference is given by

$$D_k(P,Q)=(F_P-F_Q)({\text{arg max}}_k|F_P(k)-F_Q(k)|)$$ (19)

and F_X is the empirical cumulative distribution function for probability distribution X. Note that D_k (P, Q) amounts to a signed, discrete variation of the Kolmogorov-Smirnov D-statistic, such that positive differences in Eqn. 18 indicate a right-shift of the scan spike-counts to higher values than expected. The historical distribution P^history was constructed from time-bin samples prior to the start of peri-scan activity for which v > 4 cm/s. The scan distribution P^scan was constructed from all time bins between the start and end of the scan. The weights for each track-angle bin W_xi were proportional to the occupancy time in each bin

$$W_{x_i}=N_{x_i}/N$$ (20)

where N_xi is the number of time-bin samples in the scan spike-count distribution of track-angle bin x_i and N is the total number of scan samples. Track-angle bins with either no scan samples or no historical samples were treated as 0 in Eqn. 18.

To compute ROC curves (Methods/ROC analysis), we chose scan–cell pairs with S > 0 and for which the scan occurred after the first and before the thrid-to-last laps of the session (cf. the required baseline and follow-up laps for the detection of potentiation events; Appendix 3). We used a sliding threshold across scan-firing-rate (indicating prediction) and the presence of a subsequent potentiation event (indicating outcome) to compute the evaluation metrics (i.e., true-positive rate and false-positive rate) for each point of the ROC curve. We computed separate ROC curves for various test-window sizes for searching for field-potentiation events on the subsequent lap. Areas under the ROC curves were computed for each animal and statistical significance was determined using a t-test.