Rhythmic Cortical Neurons Increase their Oscillations and Sculpt Basal Ganglia Signaling During Motor Learning

Abstract

The function and modulation of neural circuits underlying motor skill may involve rhythmic oscillations (Feller, 1999; Marder and Goaillard, 2006; Churchland et al., 2012). In the proposed pattern generator for birdsong, the cortical nucleus HVC, the frequency and power of oscillatory bursting during singing increases with development (Crandall et al., 2007; Day et al., 2009). We examined the maturation of cellular activity patterns that underlie these changes. Single unit ensemble recording combined with antidromic identification (Day et al., 2011) was used to study network development in anesthetized zebra finches. Autocovariance quantified oscillations within single units. A subset of neurons oscillated in the theta/alpha/mu/beta range (8–20 Hz), with greater power in adults compared to juveniles. Across the network, the normalized oscillatory power in the 8–20 Hz range was greater in adults than juveniles. In addition, the correlated activity between rhythmic neuron pairs increased with development. We next examined the functional impact of the oscillators on the output neurons of HVC. We found that the firing of oscillatory neurons negatively correlated with the activity of cortico-basal ganglia neurons (HVC_Xs), which project to Area X (the song basal ganglia). If groups of oscillators work together to tonically inhibit and precisely control the spike timing of adult HVC_Xs with coordinated release from inhibition, then the activity of HVC_Xs in juveniles should be decreased relative to adults due to uncorrelated, tonic inhibition. Consistent with this hypothesis, HVC_Xs had lower activity in juveniles. These data reveal network changes that shape cortical-to-basal ganglia signaling during motor learning.

INTRODUCTION

Neural encoding of complex learned motor skills is poorly understood. The best-characterized motor systems are rhythmic and, in these systems, network oscillations play key roles in motor control (Kiehn and Kjaerulff, 1998; Marder and Bucher, 2007; Koch et al., 2011). Network oscillations are also implicated in arrhythmic behaviors, such as reaching (Churchland et al., 2012). What guides the assembly of oscillatory networks (e.g., local or global rules; Prinz et al., 2004) is not well understood.

The classes of cortical neurons and their synaptic interactions are well characterized, particularly in the hippocampus and neocortex (Klausberberger et al., 2003; Buzsaki et al., 2004; Somogyi, 2004; Spruston, 2008; Cardin et al., 2009; Kullmann, 2011). In general, local interneurons sculpt and coordinate the activity of principal neurons that project to more distant targets (Buzsaki and Chrobak, 1995; Cobb et al., 1995; Koos and Tepper, 1999; Royer et al., 2012). However, current understanding of the cellular players in motor control and how specific neuronal sub-types interact to produce and modulate oscillatory activity remains incomplete.

Adult zebra finches produce a highly stereotyped, rhythmic song that is learned during a critical period (Thorpe, 1958; Konishi, 1965; Marler, 1970). Singing is controlled by anatomically distinct brain areas (Nottebohm et al., 1976; Reiner et al., 2004). The cortical song nucleus HVC (HVC is the proper name) drives the production of learned song and appears to be a pattern generator (Nottebohm et al., 1976; Simpson and Vicario, 1990; Vu et al., 1994; Ashmore et al., 2005; Solis and Perkel, 2005; Aronov et al., 2008; Long and Fee, 2008; Aronov and Fee, 2012). Consistent with a role of rhythmic oscillations in song motor control, HVC network oscillation frequency and power during singing increase with song development (Crandall et al., 2007; Day et al., 2009).

In the current study, we investigated the cellular mechanisms underlying maturation of oscillations by comparing HVC activity in juveniles and adults. Four-tetrode recordings were made in the HVCs of anesthetized finches. Replay activity in the song system during anesthesia and sleep resembles that which occurs during singing (Dave et al., 1998; Schmidt and Konishi, 1998; Dave and Margoliash, 2000). We examined oscillations within and between single neurons that were recorded simultaneously. Principal neurons that project to either the cortical motor Robust Nucleus of the Arcopallium (HVC_RAs) or to the song basal ganglia (Farries and Perkel, 2002), Area X (HVC_Xs), were identified in the context of the network using antidromic stimulation. We found a rhythmic population of neurons that had an inverse firing relationship with the cortico-basal ganglia HVC_Xs. The oscillatory power and coordinated firing of the rhythmic neurons and the spiking activity of the HVC_Xs was developmentally regulated during the period of song learning.

MATERIALS AND METHODS

Animals and Surgical Procedures

Juvenile and adult zebra finches (Taeniopygia guttata) were reared in our laboratory. Birds were housed under a 14:10-h light:dark cycle and were given food and water ad libitum. The University of Minnesota Institutional Animal Care and Use Committee approved all procedures. Surgical and recording methods were as previously described (Day et al., 2011). Tetrode recordings were obtained from 21 male zebra finches: juveniles were 45–66 days old (n = 9 finches, 12 recording sessions), adults were >138 days old (n = 12 finches, 18 sessions).

All animals were deprived of food and water for a minimum of 1 h before an initial intramuscular injection of 20% urethane (5 μL g^–1). Two additional subdoses (not exceeding 30 μL dose^–1) were given at 30- to 45-min intervals. The bird was placed in a stereotaxic apparatus (Herb Adams Engineering) and lidocaine (1%, Xylocaine) was injected under the scalp. After resection of the scalp, craniotomies were made over HVC, Area X, and RA.

Bipolar stimulating electrodes were constructed from 200 μm Teflon-coated tungsten rods (A-M Systems, Sequim, WA) and cemented into place with dental acrylic within Area X at a depth of 3.7–4.2 mm. A reference electrode (125 μm bare silver wire) was cemented in place ~3.5 mm anterior and 4 mm lateral of the lambda arterial sinus. A threaded headpost was cemented to the bird's skull. After this preparatory surgery, the animal was moved into a sound-attenuating chamber (Industrial Acoustics Company, New York) on an air table (TMC, Peabody, MA). Once the animal was secured by the headpost, a bipolar stimulating electrode (FHC, Bowdoin, ME) (300–500 kΩ impedance) was inserted into RA.

Voltage Recording and Electrical Stimulation

Ensembles of single units in HVC were recorded extracellularly in 10–15 min recording sessions with a 4-tetrode array (A4×1; Neuronexus Technologies, Ann Arbor, MI) that was amplified by a 16-channel headstage preamplifier (10×) that connected to a Model 3600 16-channel amplifier (A-M Systems). Tetrodes were linearly distributed within HVC and positioned relative to the midsagittal sinus in the rostralcaudal plane (parallel to the sinus) with a spacing of 150 μm. Tetrodes with a recording site area of 312 μm² were used (0.5–2.0 MΩ impedance). Signals were amplified (1000×), filtered (1 or 300–10,000 Hz), and acquired at 22.05 kHz (PCI 6251; National Instruments, Austin, TX) under the control of custom written Matlab (Mathworks, Natick, MA) software. Activity in HVC was collected on 15-channels; the 4th recording site on one tetrode (#4) was not recorded to enable collection of chamber sound events on our analog-to-digital PCI card, which was limited to 16 channels.

Current stimulation (20–400 μA) was delivered by a stimulus isolation unit triggered by a Master 8 (AMPI, Jerusalem, Israel) to the efferent targets of HVC: Area X and RA. Only one target was stimulated at a time. Single, monophasic pulses of 200 μs duration were delivered at a rate of 0.5 Hz. Stimulation intensity was gradually increased until reliable antidromic spikes with few failures were observed in HVC.

Antidromic collision tests were executed in a subset of experiments to further confirm the antidromicity of the stimulation and to rule out the possibility of intervening synapses. For spike collisions, a two-window discriminator (FHC) was used to identify specific spontaneous spikes and selectively trigger stimulation within 1.5 ms.

Spike Feature Clustering

Spikes from multiple units on the same tetrode were sorted using automatic clustering of waveform features in 9–12 dimensions, depending on the number of recorded channels (tetrode 4 had only 3 channels due to use of the 4th channel for sound), followed by manual checking of each cluster. The 22-point (~1-ms) spike waveforms were used for clustering if they crossed a relatively low, predetermined threshold (median + 4 × standard deviation (STD); calculated independently on each channel for each recording session). Our conservative threshold included numerous “noise” events and clusters, which were subsequently rejected during manual cluster checking. Having a low threshold decreases the possibility of excluding part of a cluster. For each channel, features of thresholded waveforms were calculated (MClust, A.D. Redish) and subjected to unsupervised clustering with a Gaussian mixture model with unconstrained covariance matrices (KlustaKwik; K. Harris, Rutgers, http://klustakwik.sourceforge.net) to obtain a maximum of 30 initial “preclusters” using a classification expectation-maximization (CEM) algorithm. KlustaKwik allows for a variable number of clusters, penalized by the Akaike Information Criterion (AIC). The initial preclusters identified by KlustaKwik were manually checked and occasionally combined or split, using MClust 3.5 (A.D. Redish; http://redishlab.neuroscience.umn.edu/MClust/MClust.html) in the Matlab environment. Clustering was performed either on a Dell PC or blade server with a 64-bit processor.

Cluster quality was assessed using four criteria to ensure that sorted spikes accurately reflected single units. Clusters that did not pass all criteria were discarded. The four criteria for cluster quality were: (1) L-ratio score < 0.1; (2) isolation distance >16; (3) <1% violations of a 1-ms refractory period (Hirabayashi et al., 2013); and (4) visual separation of the cluster from “noise” and other clusters on at least 2 (of 12) dimensions. The L-ratio is a measure of the compactness of a cluster, whereas isolation distance quantifies how well a cluster separates from other clusters (Harris et al., 2000; Schmitzer-Torbert et al., 2005; Jackson et al., 2006). For spike waveform display and spike width analysis, a matrix of 64-point waveforms was created with the same indices as the 22-point waveform matrix that was used for clustering.

Developmental Neurobiology

Identification of Clustered Antidromic Single Units

All clusters used for further analysis, including those identified by antidromic stimulation, met the four criteria described above. Antidromic spikes coclustered with a subset of spontaneous spikes. Spontaneous spikes that triggered spike collisions also coclustered with antidromic spikes. The coclustering of spontaneous spikes with anti-dromic and/or collided spikes enabled the identification of spontaneous events as those of a principal neuron. Precise spike times relative to stimulation enabled the identification of fixed latency spikes and the determination of antidromic latency and its variability. Antidromic latency was defined as the mean time from stimulation to the peak of the action potential for at least 10 stimuli. Latency variability was defined as the STD of the latencies. The latency variability cut-off for identification of unit as a principal neuron was set at <125 μs. To exclude driving effects of stimulation as a mechanism of increased coherency, all spikes that were collected during and 100 ms after stimulation were excluded from analyses of waveform properties and network interactions. Spike width was calculated based on the duration of the positive peak of the action potential waveform at 25% of its maximum (Rauske et al., 2003).

Analyses of Spike Trains

The entire recording between antidromic stimulation epochs (excluding a 100-ms post-stimulus buffer) was used for spike width and spike train measurements. Spike rate for each single unit was defined as the total number of spikes divided by the total time in seconds. Interspike intervals (ISIs) were the time differences between successive spikes. The 95th percentile ISI is a robust measure of the maximal ISI. Burst durations were calculated with a maximum ISI of 10 ms to consider sequential spikes as part of the same burst. Sequential single spikes that had greater than 10 ms between them were each scored a burst duration of 0 ms.

Analyses of Oscillations

The entire recording between antidromic stimulation epochs (excluding a 100-ms post-stimulus buffer) was used for cross-covariance and coherency calculations. The binning window for spike trains was 1 ms. Cross-covariance was used to measure oscillatory activity between neurons

$$C_{A-B}\left(m\right)-E\left\{(A_{n+w}-{\mu }_A){(B_n-{\mu }_B)}^{\ast }\right\}$$

where C_A-B(m) is the cross-covariance of two spike trains in the time domain. A and B are the spike train vectors. E is the expected value operator. μ_A and μ_B are the mean values.*indicates the complex conjugate. Autocovariance is the cross-covariance when the spike trains are identical and from the same single unit. Cross- and autocovariances were calculated using a Matlab built-in function (xcov.m). The amplitude spectra of the covariances were calculated using fast Fourier transform (fft.m).

$${\gamma }_{A-B}\left(\omega \right)=\frac{C_{A-B}\left(\omega \right)}{\sqrt{C_{A-A}\left(\omega \right)•C_{B-B}}\left(\omega \right)}$$

Cross-covariance was used for this study because it is sensitive to oscillations. However, for comparison of the spike trains of HVC_Xs versus oscillatory neurons, we were most interested in fast functional (potentially synaptic) interactions, which are better measured with coherency (Rosenberg et al., 1989; Kimpo et al., 2003). Coherency was calculated as described (Rosenberg et al., 1989; Kimpo et al., 2003) with custom-written Matlab code. Coherency is the cross-covariance of the two spike trains normalized by the autocovariances of both (Rosenberg et al., 1989; Kimpo et al., 2003). Coherency was computed in the frequency domain where C_A-B(ω) is the cross-covariance of the two spike trains in the frequency domain and C_X-X(ω) is the autocovariance. For further analysis and plotting, γ_A-Bω was transformed into the time domain (Kimpo et al., 2003). Coherency reflects the relative probability of one neuron firing, given that the other has fired at time t = 0. Coherency values are unitless and range between –1 and 1. A large, positive coherency value at time –5 ms, for example, would indicate that every time one unit fired, the other was highly likely to fire 5 ms earlier. Same tetrode data are contaminated by overlapping waveforms at t = 0 ms for all spike train relationship measures. The jackknife STD was obtained using custom Matlab code (D. Q. Nykamp and T. A. Nick) that calculated the coherency 100 times, each time with a recording segment of 1% length thrown out. The STD was then computed from the resulting 100 coherency vectors. Significant negative coherency was defined as less than 3× jackknife STD.

Statistics

All measures of central tendency and dispersal are shown as median with interquartile range (IQR). The nonparametric Wilcoxon rank sum test was used to compare unmatched data. Significance was defined as a α = 0.05.

RESULTS

Recording Oscillations in the HVC Network

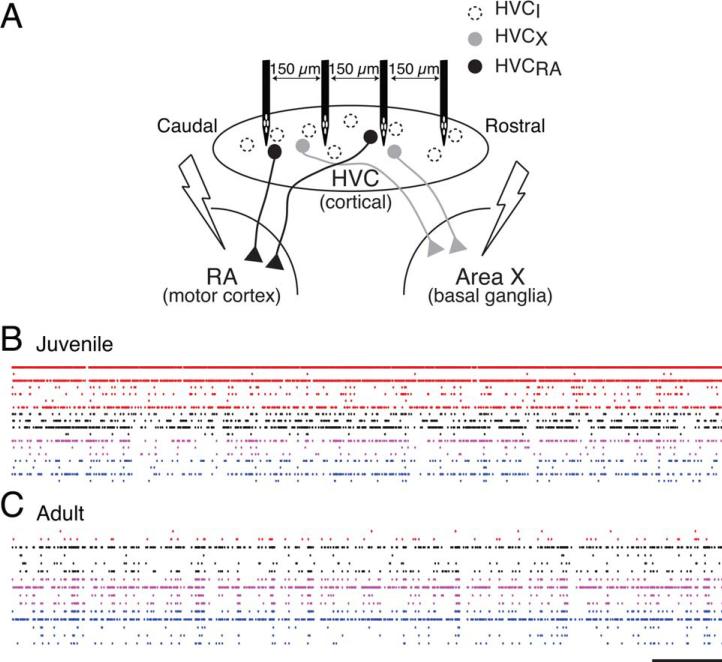
The development of oscillatory activity was examined in the HVC network using a four-tetrode recording array combined with antidromic identification of principal neurons (Fig. 1; Day et al., 2011). With this configuration, multiple single units can be sampled along 450 μm of the rostral-caudal axis of HVC [Fig.1(B,C)]. Consistent with previous population-level findings in the chronically recorded sleeping finch (Crandall et al., 2007), the HVC activity patterns of the juvenile (with plastic song) were subjectively and obviously different from the adult (with stable song). The most striking difference was in synchronous bursts that tended to be extended and involve a greater percentage of the network in the adult (Burst duration, Juv (229): median 6.24 ms, IQR [5.14– 7.49] ms; Adult (227): 6.60 ms, [5.57–8.16] ms; p < 0.007, Wilcoxon Rank Sum). In these same recordings, we also recently found that spike train coherency of HVC neuron pairs increases with development (Day et al., 2013), which indicates increased population synchrony with development.

Figure 1.

The recording configuration enabled the monitoring of multiple units across HVC. (A) The diagram shows the recording and stimulation configuration. HVC was recorded with a linear 4-tetrode array. Bipolar stimulating electrodes were placed in song nuclei RA and Area X to drive antidromic spikes (Day et al., 2011). (B,C) Multiple neurons in juveniles and adults were recorded, respectively. Single-unit spike trains are shown caudal-to-rostral, with the records from the same tetrode shown in the same color. Scale bar: 1 s. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

A Subset of HVC Neurons Oscillate

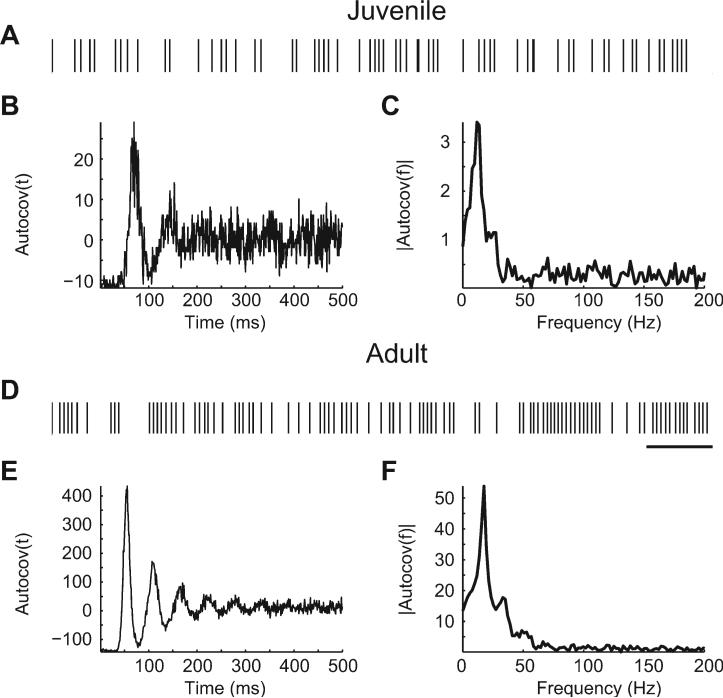
Neuronal synchrony and extended patterns of activity that are not peripherally driven are thought to arise from network oscillations (Engel et al., 2001). To assess oscillatory activity, the amplitude spectrum of the spike train autocovariance was calculated for each single unit in juveniles and adults. A subset of recorded neurons had oscillations that were readily apparent in the autocovariance. Example spike trains, autocovariances, and amplitude spectra are shown in Figure 2. Juvenile oscillatory neurons tended to have brief periods of firing with a relatively stable ISI intermingled with highly variable ISIs [Fig. 2(A)]. In contrast, adult oscillators fired for longer periods with a relatively fixed ISI [Fig. 2(D)]. These spike train patterns were reflected in the autocovariance in the time domain [Fig. 2(B,E)], which had multiple, regularly spaced peaks and valleys, and in the amplitude spectra of the autocovariances [Fig. 2(C,F)], which had peaks in the range 8–20 Hz. This frequency range includes theta (θ), alpha (α), mu (μ) and low beta (β) ranges. The definition of these ranges varies with animal (including human) and brain area. In the interest of brevity and not any functional interpretation, we will refer to this oscillation range (8–20 Hz) as “α” in this manuscript.

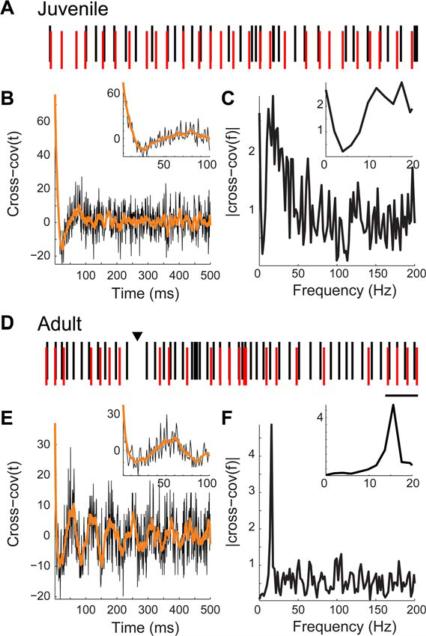
Figure 2.

A subset of HVC neurons were oscillatory, as revealed by autocovariance. Example spike trains (A,D), autocovariances (B,E), and amplitude spectra of the autocovariances (C,F) are shown for a juvenile and an adult HVC neuron. (A,D) The spike train of the juvenile neuron, A, reveals a variable pattern interspersed with short bursts of rhythmic activity. In contrast, the adult neuron, D, rhythmically fires over longer time spans. Scale bar: 1 s. (B,E) The autocovariance reflects the probability of firing, given that the same cell fired at time t = 0 ms. The autocovariances have multiple peaks of high covariance separated by time windows of negative covariance. This indicates that neurons were likely to fire in a stereotyped pattern, with spikes likely to occur in specific temporal relationships. (C,F) The amplitude spectra peaked in the alpha range for these neurons (11.72 and 17.58 Hz, respectively). This indicates that these neurons tended to fire rhythmically with a stereotyped ISI of 50–100 ms between spikes (85-ms and 57-ms ISI, respectively).

Adult Neurons and Networks Have More Oscillatory Power in the 8–20 Hz Range

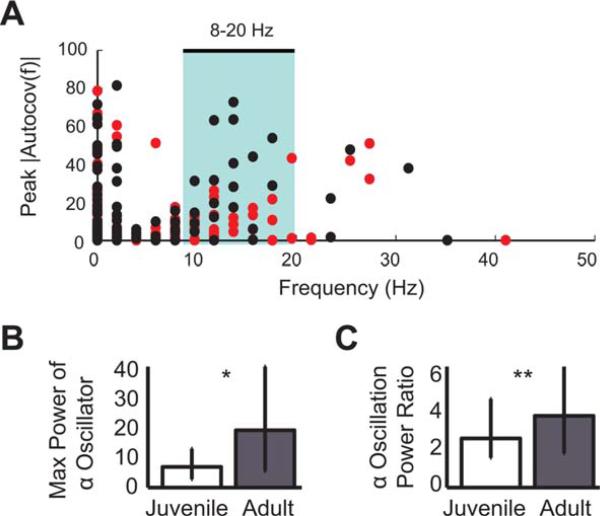
To obtain a view of the oscillatory activity of the HVC population, we plotted the frequency of the peak autocovariance versus the power of that peak for each single unit [Fig. 3(A)]. In the range 8–20 Hz, there were 11 (of 227) adult neurons that had a higher peak at a given frequency than any juvenile neuron. The maximum power of α-oscillators (that had their peak power 8–20 Hz) was significantly and substantially (276%) greater in adults relative to juveniles [Fig. 3(B)]. To assess the network effects of the increasing rhythmicity of the α-oscillator neurons, the relative α power was compared across all other HVC neurons (that did not have an 8–20 Hz autoco-variance peak) by taking a power ratio (median power 8–20 Hz/median power 0–200 Hz). This value was also significantly and substantially (173%) greater in adults than juveniles [Fig. 3(C)].

Figure 3.

Oscillatory activity in the 8–20 Hz range was greater in adults than juveniles. (A) A scatter plot of autocovariance peak frequency versus power at the peak frequency. A subset of adult neurons (black) had higher power in the frequency range 8–20 Hz (θ/α/μ/β range, highlighted by cyan box) than any juvenile neurons (red). (B) The maximum power of autocovariance of α-oscillator neurons that had peak power 8–20 Hz was significantly greater in adults (Ns = 28, 21; *p < 0.012). (C) Power ratios (median power 8–20 Hz/median power 0– 200 Hz) for all other neurons were significantly greater in adults, indicating that oscillatory power in the a range disproportionately increases across the HVC network during development (Ns = 194, 206; **p < 0.0023). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

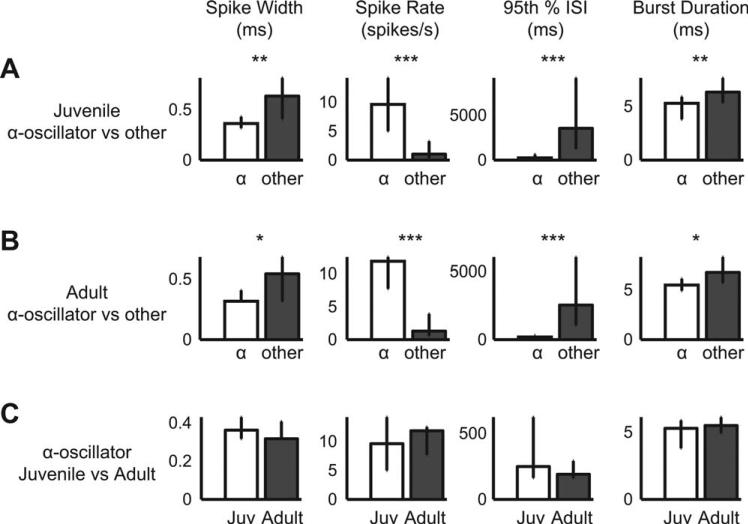
Activities of α-oscillator Neurons Differ from the Rest of the HVC Population and do not Change with Development

Neurons identified as α-oscillators were compared to the rest of the HVC population. In both juveniles [Fig. 4(A)] and adults [Fig. 4(B)], α-oscillators compared to the rest of the population had narrower action potentials, higher spike rates, lower 95th percentile ISIs (a robust assessment of maximal ISI), and shorter high-frequency bursts. Narrower spike widths and higher spike rates are characteristic of interneurons (Mooney, 2000; Rauske et al., 2003). The low 95th percentile ISI measure indicates that these α-oscillator neurons were never quiescent for very long. The shorter high-frequency burst measure indicates that the α-oscillators tend to fire only briefly at high frequencies (≥100 Hz).

Figure 4.

Waveforms and spike trains of α-oscillator neurons were distinct from the rest of the HVC neuronal population, but not developmentally regulated. (A) Juvenile α-oscillators had narrow spike widths, high spike rates, low 95th percentile interspike intervals, and short burst durations relative to the rest of the HVC neuron population (Ns = 24, 205; maximum ISI for a burst was 10 ms). Each column presents the same waveform or spike train parameter for A–C. For A–C: *p < 0.008; **p < 0.0002; ***p < 6 × 10²⁹. (B) Relative to other neurons, adult α-oscillators were similar to those of the juvenile in terms of spike widths, firing rate, maximal ISI, and burst duration (Ns = 18, 209). (C) Juvenile and adult α-oscillators were not significantly different with regard to measured spike width and spike train parameters (Ns = 24, 18).

In contrast to oscillation power, which increased with development (Fig. 3), spike width and spike train parameters of α-oscillators did not differ between juveniles and adults [Fig. 4(C)]. This indicates that the observed change in oscillation power cannot be attributed to changes in these measures, but rather results from a redistribution of ongoing activity such that ISIs become more stereotyped overall and more invariant in longer spiking sequences: The activity of the α-oscillators becomes more rhythmic with song development.

Pairs of α-oscillator Neurons Become More Correlated During Development

To test if α-oscillator neurons play a role in HVC-wide network synchrony, we measured the correlated activity of pairs of α-oscillators using cross-covariance. If a network of α-oscillators coordinate or transmit network synchronous oscillations, then their oscillations must be correlated. Example spike train pairs, cross-covariances, and amplitude spectra are shown in Figure 5. The α-oscillator neurons in these examples were 300 μm apart. From the juvenile [Fig. 5(A–C)], the best example of α-oscillation in the cross-covariance that we observed shows weak and variable relationships between spike trains. In the cross-covariance [Fig. 5(B)], there is a relatively high peak indicative of synchrony, then a decrease indicative of decreased probability of firing, but the oscillation quickly dies out. In contrast, the adult α-oscillator pair [Fig. 5(D–F)] had relatively reliable spike timing relationships that were reflected in the cross-covariance, which had multiple peaks [Fig. 5(E)]. The amplitude spectrum of the cross-covariance revealed a strong peak in the α range [Fig. 5(F)], indicating that the adult α-oscillator pair fires together in a coordinated pattern in the range 8–20 Hz.

Figure 5.

Relationships of spike trains of pairs of α-oscillator neurons in a juvenile and an adult. (A,D) Pairs of spike trains are shown for two neurons from the same recording with autocovariance peaks 8–20 Hz. The neurons were 300 μm apart. For visual clarity, the spike rasters are vertically offset and the more caudal neuron is shown in black and the rostral, in red. In the adult image, a >100 ms window where neither cell fired is indicated with an arrowhead. Scale bar: 200 ms. (B,E) Cross-covariance of two oscillatory neurons in a juvenile, B, and an adult, E. The cross-covariance here reflects the probability of the caudal neuron firing, given that the rostral neuron fired at t = 0 ms. The low frequency components are highlighted by smoothing with a 10-ms window (orange). The insets show data on an expanded time scale. (C, F) Amplitude spectra of the cross-covariances reveal peaks in oscillatory activity in the 8–20 Hz range. The insets show data on an expanded frequency scale. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Pairs of Mature α-oscillator Neurons are Significantly More Correlated with Each Other and Other Neurons

The correlated activity of α-oscillator pairs was quantified by taking the peak power of the amplitude spectrum of the cross-covariance [Fig. 6(A)]. Adult pairs were significantly more correlated. Next, the impact of α-oscillator activity on other neurons was addressed by comparing the correlated activity of α-oscillator neurons with all other neurons in the HVC population. The α-oscillation power ratio was significantly greater in adults. This indicates that α-oscillator neurons functionally interact with the broader HVC population in adults, but not or less so in juveniles.

Figure 6.

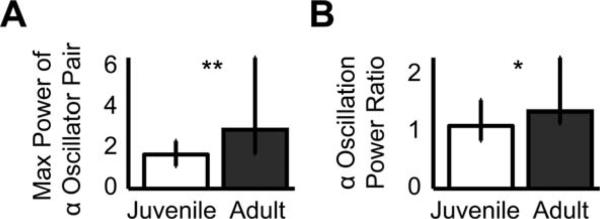
Spike trains of oscillatory neurons were more correlated in adults than in juveniles. (A) The maximum cross-covariance power of pairs of α-oscillator neurons that had peak power 8–20 Hz was significantly greater in adults (Ns = 74, 34 pairs; **p < 9 × 10^–5). (B) Power ratios (median power 8–20 Hz/median power 0–200 Hz) for all pairs that contained exactly one α-oscillator were also significantly greater in adults (Ns = 84, 42; *p < 0.0003).

α-Oscillator Neurons Functionally and Tonically Inhibit HVC_Xs

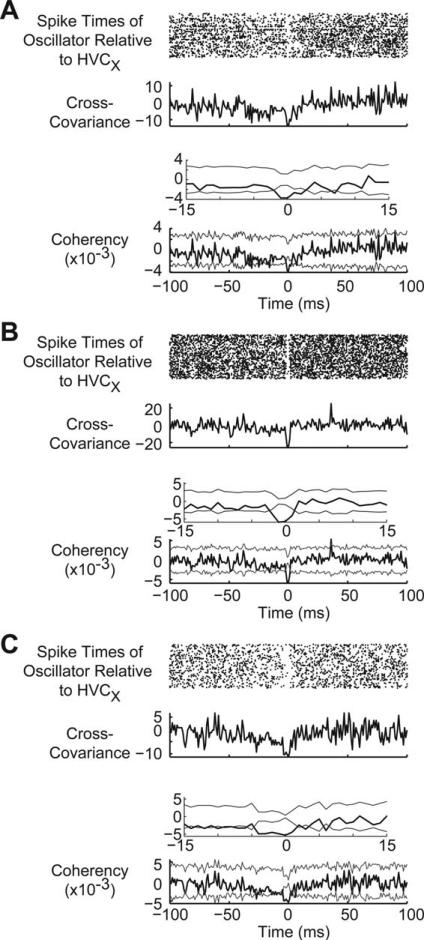
Do α-oscillator neurons affect the output of HVC? To answer this question, we examined the spike train relationships of α-oscillator neurons with HVC principal neurons: HVC_Xs and HVC_RAs. We were able to obtain a small number of recordings that contained both an antidromically identified HVC_X neuron and an α-oscillator neuron (N sessions, Juvenile: 9; Adult: 10). We rarely saw HVC_RAs and α-oscillators in the same recording session (N sessions, Juvenile: 2; Adult: 1), possibly due to the differential anatomical distribution of HVC_RAs (Wild et al., 2005) and, perhaps, the α-oscillators. Alternatively, RA stimulation necessary for antidromic identification may alter HVC rhythmicity. Previous work that has found only a little evidence of inhibition of HVC_RAs (Mooney, 2000; Mooney and Prather, 2005), so there may be no reliable relationship between the activities of α-oscillator neurons and HVC_RAs. In contrast, we found three adult oscillator-HVC_X pairs and all three pairs showed the same pattern: α-oscillators were reliably silent at least 2 ms prior to the firing of HVC_Xs [Fig. 7(A–C)]. Both members of each pair were always on the same tetrode, indicating that the strongest (and most detectable) functional interactions between α-oscillators and HVC_Xs are highly localized. We did not see a similar pattern in any of the juvenile pairs.

Figure 7.

Adult oscillatory neurons appear to tonically inhibit Area X-projecting HVC neurons and control their firing through release from inhibition. Neurons were identified as α-oscillators based on peak autocovariances in the range 8–20 Hz. (A–C) Each panel shows a dot raster (top), cross-covariance (middle), and coherency (bottom) spike train relationships between an α-oscillator and HVC_X. All data in each panel are temporally aligned. Data in A–C are from three different adult animals. The top panel shows the spike times of the α-oscillators relative to the spike of an HVC_X that fired at time t = 0 ms. Note the ≥4 ms gap in activity that surrounds time t = 0 ms, which suggests that these neurons released the HVC_X from inhibition, allowing it to fire. Because each of these pairs was recorded on the same tetrode, the measure at exactly t = 0 cannot be trusted, due to overlapping waveforms. The bottom panel shows the coherency and thin gray error traces that indicate 3× jackknife STD. The insets show data on an expanded time scale near zero. Note the dip below the error, indicating signifi-cant negative coherency, at time zero. Bin size for the dot rasters and cross-covariance/coherency calculations was 1 ms.

The Activity of HVC_Xs is Developmentally Regulated

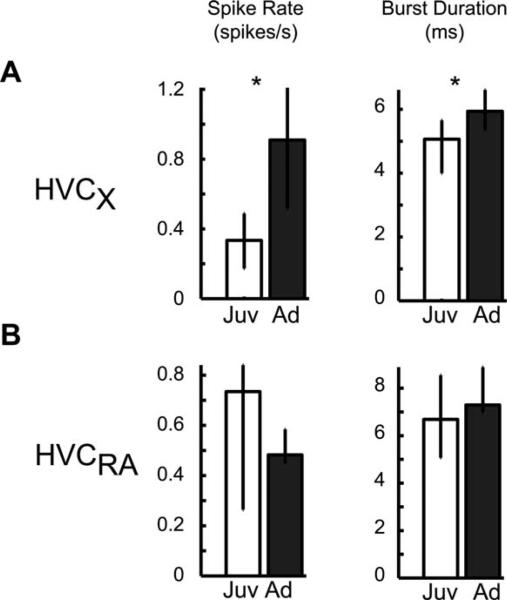
Our finding that adult α-oscillator neurons were silent before the firing of HVC_Xs (Fig. 7) indicates that α-oscillators functionally inhibit HVC_Xs. This suggests that α-oscillators sculpt HVC_X firing times through coordinated release from inhibition. The juvenile data, which indicate no such relationship, could result either from a lack of functional inhibition from α-oscillators or, alternatively, from disorganized inhibition from multiple α-oscillators (which becomes increasingly organized as the animal matures, Figs. 5 and 6). If the former hypothesis is correct (and other factors affecting HVC_X activity, such as extrinsic inputs and intrinsic excitability, are relatively constant), then HVC_Xs should show more activity in the juvenile. Alternatively, if the lack of an oscillator-HVC_X relationship in juveniles results from disorganized inhibition from multiple α-oscillators, then HVC_Xs should show less activity in the juvenile. Consistent with the latter hypothesis, we found that spike rates and burst durations of HVC_Xs were significantly lower in the juvenile compared to the adult [Fig. 8(A)]. The activity of the other population of HVC principal neurons, HVC_RAs, did not significantly change and showed opposite trends in spike rate with development [Fig. 8(B)].

Figure 8.

Area X-projecting neurons become more active with development. (A) Consistent with a role of oscillatory neurons in the development of song, spiking activity of their target neurons (HVC_Xs) changes with development (Ns = 13, 16; *p < 0.03): Spike rate and burst duration increased (max ISI 10-ms within the burst). (B) The activity of the other population of HVC principal neurons (HVC_RAs) was not developmentally modulated based on the measured spike train parameters (Ns = 6, 6).

DISCUSSION

A Subclass of HVC Neurons Oscillate and the Power of the Oscillation is Developmentally Regulated

With developmental song learning, the oscillatory bursting activity of the HVC population during singing increases (Crandall et al., 2007; Day et al., 2009). Correspondingly, there are cellular and network oscillations within HVC that increase with developmental song learning: We found that spiking of a subtype of HVC neuron oscillates in the 8–20 Hz range and the power of the oscillation increases with development. At the network level, the correlation of spiking activity in pairs of α-oscillatory neurons increased with development.

Network Oscillations are Important for Function in the Mammalian Brain

Rhythmic oscillations, which are measured in local field potential recordings and the activity of single neurons, shape the firing of principal neurons (Llinas et al., 1991; Klausberberger et al., 2003; Sirota et al., 2008; Burgess and O’Keefe, 2011; Buzs aki and Wang, 2012). Fundamental cortical processes, such as attention, memory, and sensory processing, are regulated by rhythmic oscillations (Benchenane et al., 2011). The role of rhythmic activity in cortical motor control is less clear, but recent evidence highlights the role of oscillations even in arrhythmic behaviors, such as reaching (Churchland et al., 2012). The importance of the HVC oscillations that we describe here is not known. Song is a rhythmic behavior and HVC appears to be its pattern generator (Nottebohm et al., 1976; Simpson and Vicario, 1990; Vu et al., 1994; Ashmore et al., 2005; Solis and Perkel, 2005; Aronov et al., 2008; Long and Fee, 2008). Thus, these oscillations may serve, most simply, to provide a timing cue for the production of learned vocalizations. They may, alternatively or in addition, have roles in the regulation of song plasticity and motor learning (Day et al., 2008, 2009).

Developmental Modulation of Network Oscillations Present yet Another Similarity Between Avian and Mammalian Brains

The finding that rhythmic oscillations are developmentally regulated during the critical period for sensorimotor learning identifies the song system as a good model for studying the mechanisms of oscillations and their role in cortical processing in the context of behavior. Previous work has shown that brain oscillations in humans and other mammals are developmentally regulated (Gramsbergen, 1976; Clarke et al., 2001; Marshall et al., 2002) and that aberrations in brain oscillations correlate with neural disease (Cantor et al., 1986; Stroganova et al., 2007; Uhlhaas and Singer, 2010). Notably, neural oscillations may have a role in speech processing (Giraud and Poeppel, 2012), which, like birdsong, is a learned vocalization (Marler, 1970; Doupe and Kuhl, 1999; Bolhuis et al., 2010). We have previously found cellular and molecular similarities between the forebrain song system and mammalian brain systems that have a critical period in their development: prolonged bursting of some neurons (Fagiolini and Hensch, 2000; Crandall et al., 2007) and developmental regulation of parvalbumin and extracellular matrix perineuronal nets (Hockfield and McKay, 1983; Hensch, 2005; Balmer et al., 2009). It will be interesting to determine whether α-oscillator neurons express parvalbumin or perineuronal nets and if their activity is affected by perineuronal net perturbation, as in mammalian neurons (Dityatev and Schachner, 2006; Dityatev et al., 2007). Understanding the interactions of extracellular matrix, interneurons, and oscillations in the tractable birdsong behavioral model may illuminate the roles of all three in neural plasticity and, potentially, human disease.

Mature α-Oscillator Neurons Resemble Rhythmic Neurons in Mammalian Brain

Certain neurons in the mammalian brain oscillate in the range that we report (8–20 Hz). The theta rhythm generated in the hippocampus (allocortex) appears to result from the interactions of principal neurons and interneurons in the stratum radiatum (Goutagny et al., 2009). Interneurons in the stratum oriens of the hippocampus, oriens-lacunosum moleculare (O-LM) neurons, phase-lock to theta-modulated inputs (Kispersky et al., 2012), and fire in the lower range of the oscillatory neurons described here. O-LM cells may specialize in the transmission and amplification of theta rhythms (Kispersky et al., 2012) and form an anatomical framework for the transmission of theta in the longitudinal axis of the hippocampus (Gloveli et al., 2005). Pyramidal cells of neocortical layer 5 can oscillate within the theta/ alpha range (5–12 Hz; Silva et al., 1991). Mu rhythm (15–25 Hz) suppression may be necessary for the firing of mirror neurons, which belong to a subclass of pyramidal neurons discovered in layer 5 that appear to link perception of an action with the action itself (Hari et al., 1998; Rizzolatti and Craighero, 2004; Arnstein et al., 2011). The suppression of mu rhythm is often used as a metric for mirror neuron activity (Pineda, 2005; Nystr€om et al., 2010). These facts are interesting in light of our data that show that the proposed song mirror neurons, the HVC_Xs (Prather et al., 2008), fire during suppression of mu-range oscillators.

The origin of at least some mammalian oscillations, including neocortical gamma, is not clear. They may be produced solely by interneurons or the interactions of interneurons and principal neurons (Tiesinga and Sejnowski, 2009). We do not know the generator of the 8–20 Hz rhythm detected in the α-oscillatory neurons, which could come from intrinsic and/or extrinsic sources. However, stimulating HVC resets the song (Vu et al., 1994) and cooling results in the slowing of song (Long and Fee, 2008), both indicative of an intrinsic pattern generator. It will be interesting to determine whether α-oscillator neurons, similar to hippocampal O-LM neurons (Gloveli et al., 2005), provide an anatomical structure for theta/alpha transmission and thus define a functional axis within the HVC pattern generator (Nottebohm et al., 1982; Stauffer et al., 2012; Day et al., 2013).

Potential Functional Roles of the Oscillations

Low frequency (theta/alpha/mu/beta) oscillations, such as we describe here, are thought to be important for the transmission of neural information long-distances between brain areas during top-down processing, whereas higher frequency (high beta/gamma) oscillations are thought to reflect local information processing (von Stein and Sarnthein, 2000). In the adult finch, HVC may effectively transmit to downstream areas and thus drive learned song because of the development of low frequency oscillations. In contrast, HVC does not appear to be important for unlearned juvenile vocalizations, since animals can produce unlearned and rambling sounds when HVC is completely ablated (Simpson and Vicario, 1990; Aronov et al., 2008). As song matures, HVC is then free to “try out” various network activity patterns and transmit them during unstructured rambling. Because HVC receives convergent inputs from several auditory areas (Mello et al., 1998; Coleman and Mooney, 2002; Cardin et al., 2004; Coleman et al., 2007; Bauer et al., 2008), it is well positioned to reinforce (or discard) these patterns or to forward the information to downstream areas that ultimately feed back to HVC through midbrain dopaminergic circuits or other pathways (Hamaguchi and Mooney, 2012).

HVC Oscillatory Neurons Functionally Inhibit Cortico-Basal Ganglia Neurons

The observed changes in the oscillation power and coordination of rhythmic neurons directly impacted the output of the HVC circuit: HVC_X cortico-basal ganglia neurons were functionally inhibited by the rhythmic α-oscillator neurons. Consistent with an increase in the coordination of inhibition and release of inhibition, HVC_Xs increased their activity levels with development. In addition to changes in coordinated inhibition, other factors that may affect the development of HVC_X activity include the expression patterns of voltage-gated ion channels and extrinsic inputs. The current study does not address these factors. Instead, it shows developmental regulation of spike rates and coordinated activation of neurons that functionally inhibit HVC_Xs.

We have previously found that activation of the adult, but not juvenile, HVC is rostrocaudally ordered, such that projection neurons fire preferentially with fast-spiking presumed interneurons that are rostral to them. In addition, projection neurons appear to fire in order from rostral to caudal (Day et al., 2013). The results of this previous study are consistent with traveling waves of inhibition within HVC that are led by projection neurons that fire at the leading edge. How would a traveling wave of inhibition lead to the activation of projection neurons? The data in the current study indicate that HVC_Xs fire during decreases in inhibition. In addition, previous brain slice studies have shown post-inhibitory rebound excitation in HVC_Xs (Dutar et al., 1998). All of these data, combined with our current finding of developmental regulation of functionally inhibitory neurons, suggest a coordinated disinhibition model of cortico-basal ganglia signaling: In the juvenile, oscillatory inter-neurons are uncoordinated, subjecting HVC_Xs to continuous, weak inhibition. As oscillatory interneurons mature, they fire more regularly and in a coordinated manner, such that HVC_Xs are more effectively inhibited and disinhibited during discrete time windows. During disinhibited windows, HVC_Xs rebound from inhibition and fire. In the adult, waves of inhibition may inhibit the oscillatory interneurons, thus precisely coordinating the activation of HVC_Xs in a spatiotemporal map.

What would be the impact of precise coordination of cortico-basal ganglia signaling in the song system? We have previously found that patterned bursting activity in HVC predicts song variability millisecond-by-millisecond in chronically recorded, singing juvenile and adult finches (Day et al., 2008, 2009). On the basis of these data, we proposed that HVC limits song plasticity by entraining the activity of the Anterior Forebrain Pathway (AFP) with coordinated bursts (Day et al., 2008, 2009). This model was further supported by a recent study that found that lesions of the basal ganglia target nucleus of HVC within the AFP (Area X) perturbed patterned bursting in the AFP cortical nucleus and blocked auditory modulation of song (Kojima et al., 2013).

We found that cortico-basal ganglia signaling increases with development. What is the general function of cortico-basal ganglia signaling? Previous work has shown that HVC_Xs have the same activity patterns whether they are hearing or producing (with no auditory feedback) a song (Prather et al., 2008), thus suggesting that these cells are mirror neurons (Hilliard and White, 2009; Fogassi, 2011) and that they function to provide a motor signal that can be compared to auditory feedback in order to perceive and sculpt the learned vocalization. Our current data indicate that these neurons provide weaker signals to the basal ganglia in juveniles. If a weak signal is interpreted by efferent areas as a “mistake” or an indication to continue production of variable songs, then song plasticity may be permitted or enhanced through previously described pathways (Bottjer et al., 1984; Kao et al., 2005; Olveczky et al., 2005; Kao and Brainard, 2006). Whether the proposed motor signal for auditory feedback comparison (Prather et al., 2008) is interpreted based on the performance of an entire song motif (~1 sec) or smaller time segment, is not known. However, previous work suggests that song is learned in relatively short duration segments (smaller than a song syllable; Ravbar et al., 2012) and HVC regulates plasticity millisecond-by-millisecond (Day et al., 2008). Short duration learned fragments would be outlasted by prolonged bursts within the HVC network that we have previously described (Crandall et al., 2007). Thus, sensory feedback from a song fragment could act directly on elements of the network that produced the fragment, shape the coordinated activity of inhibitors and/or disinhibitors of HVC_Xs, and thereby control cortico-basal ganglia signaling.