Can Molecular Dynamics and QM/MM Solve the Penicillin Binding Protein Protonation Puzzle?

Abstract

Benzylpenicillin, a member of the β-lactam antibiotic class, has been widely used to combat bacterial infections since 1947. The general mechanism is well-known: a serine protease enzyme (i.e., DD-peptidase) forms a long lasting intermediate with the lactam ring of the antibiotic known as acylation, effectively preventing biosynthesis of the bacterial cell wall. Despite this overall mechanistic understanding, many details of binding and catalysis are unclear. Specifically, there is ongoing debate about active site protonation states and the role of general acids/bases in the reaction. Herein, a unique combination of MD simulations, QM/MM minimizations, and QM/MM orbital analyses is combined with systematic variation of active site residue protonation states. Critical interactions that maximize the stability of the bound inhibitor are examined and used as metrics. This approach was validated by examining cefoxitin interactions in the CTX-M β-lactamase from E. coli and compared to an ultra high-resolution (0.88 Å) crystal structure. Upon confirming the approach used, an investigation of the preacylated Streptomyces R61 active site with bound benzylpenicillin was performed, varying the protonation states of His298 and Lys65. We concluded that protonated His298 and deprotonated Lys65 are most likely to exist in the R61 active site.

Introduction

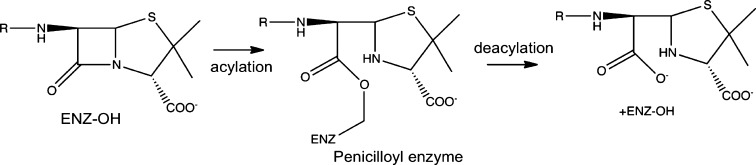
In response to environmental factors, bacteria have been developing small molecule resistance strategies for millions of years.¹ Recently, drug resistance reached pandemic status while antibiotic development has slowed substantially.²⁻¹⁰ Penicillins, the first antibiotics, and cephalosporins (β-lactams) are the most commonly used antibiotics.^11,12 The general mechanism of action for β-lactam antibiotics is covalent bond formation with an active site residue of d-alanyl-d-alanine carboxy-peptidase/transpeptidase enzymes (DD-peptidases), also known as penicillin-binding proteins (PBPs). Upon formation of the acyl-enzyme intermediate (i.e., acylation, Figure 1), the biosynthesis of the peptidoglycan bacterial cell wall is inhibited, ultimately resulting in bacterial cell death.¹²⁻¹⁵ A deacylation step can occur; however, for PBPs this process is very slow.

Figure 1.

The acylation and deacylation reactions are shown for a generalized β-lactam antibiotic and a serine protease type enzyme. For the current work, the ENZ–OH is Ser62 in R61, and the β-lactam is benzylpenicillin.

Here, we focus on the DD-peptidase from Streptomyces sp. R61 (hereafter named R61), a PBP in the low molecular mass B (LMMB) class.^16,17 A definitive characterization of the acylation mechanism at the atomic level has not been achieved for penicillin binding proteins. A major hurdle has been the lack of knowledge concerning the protonation states in the preacylated enzyme–substrate complex. This is a challenging problem due to the need for accurate descriptions of protein flexibility, solvation effects, active site polarity, protein–ligand interactions, and more. Specifically, there is uncertainty about the general acid and base for both the acylation and deacylation reactions. In a review of DD-peptidases by Pratt,¹⁸ he discusses their mechanistic complexity, which is a consequence of ambiguous protonation states. He proposes that Lys65 acts as the general acid when protonated; however if the acylation and deacylation mechanisms are symmetrical, then the lysine most likely exists as a general base. If Lys65 is the general base, then Tyr159 acts like the general acid. The uncertainty of the situation is indicated by Pratt: “It is possible, however, given the positions of these residues, that they might exchange roles or, in a deletion mutant, either one could, less effectively perhaps, carry out both roles.” His speculation in this recent review illustrates the necessity for a deeper understanding of the active site’s physiochemical properties.

Friesner and co-workers¹⁹ addressed the protonation state question for the deacylation step. They employed quantum mechanical/molecular mechanical (QM/MM) methodology to better understand the difference between Enterobacter cloacae P99 cephalosporinase, a class C β-lactamase, and R61. They examined several possibilities involving three residues, Tyr159, Lys65, and His298, and determined the most likely R61 deacylation configuration to be protonated Tyr159, deprotonated Lys65, and protonated His298. These conclusions were drawn based on the lowest reaction barrier that was catalytically competent; however, full active site reorganization based on protonation state changes was not taken into account. It is unclear how much this would have affected their results.

Other PBPs have also been investigated via computational methods. Mobashery and co-workers²⁰ examined PBP 5 with an acetyl d-Ala-d-Ala bound substrate using a combination of molecular dynamics (MD) simulations and ONIOM, a QM/MM-like method. MD simulations resulted in three different conformers: the PBP 5 Michaelis complex, the acyl-enzyme, and the tetrahedral species resulting from water addition to the acyl-enzyme. Their calculations reveal that Lys47 acts as a general base for the proton abstraction from Ser44 in the serine acylation step. Another goal of this work was to determine the role of surrounding residues that do not directly contact the substrate, namely Lys213. However, ultimately characterization of this residue was not possible, further confirming the challenges associated with identifying the role of key active site residues that are not directly involved with the reaction.

DD-peptidases and β-lactamases are both considered serine-protease type enzymes that form acyl-enzyme intermediates with β-lactam derivatives.^21,22 β-lactamases, enzymes that evolved to compete with DD-peptidases, are also known to quickly hydrolyze the β-lactam ring, rendering it useless.²³⁻²⁶ There has been a great debate whether the active site lysine in β-lactamases is protonated²⁷⁻³³ or deprotonated,^32,34,35 which coincides with the ambiguity associated with the acylation mechanism. Furthermore, studies have suggested that key β-lactamase active site residues (i.e., Lys73, Glu166) change their protonation state in the precovalent Michaelis complex upon ligand binding.^{30,33,34,36−38} Prior to the review by Pratt,¹⁸ Mobashery and co-workers³⁸ investigated the protonation states of active site residues for the class A β-lactamase TEM-1. They state their results are likely to hold true for PBPs; however given the differences between β-lactamase and DD-peptidase active sites, this statement warrants closer examination.¹ Further complicating the transferability of their conclusions is the fact that a β-lactam substrate was not bound in their study, which would potentially affect active site pK_a values and thus protonation states (vide supra).³⁸ Their investigation utilized pK_a perturbation, NMR, and MD simulations to determine the protonation states of Lys73 (analogous to Lys65 in R61) and Glu166; there is no residue analogous to Glu166 in R61. Tyr159 in R61 could act as the general acid functioning similar to Glu166 in TEM-1; however this has only been speculated¹⁸ and not confirmed.

Further examination of the acylation mechanism revealed that Glu166 abstracts a proton from Lys73, which would therefore exist in its natural base form and rule out the possibility of the carboxylate of the β-lactam derivative facilitating the reaction. Moreover, Mobashery and co-workers³⁸ state that it would be unsuitable for Glu166 and Lys73 to both be deprotonated according to molecular dynamics studies performed on TEM-1 that resulted in unstable trajectories as reported by Massova and Kollman.³⁹ Hence, for class A β-lactamases they conclude that only one of these residues is protonated; however, that residue could vary based upon the acylation mechanism. Their work agrees with previous reports²⁷⁻³² stating that the native state of Lys73 in class A β-lactamases is protonated. Alternatively, if Glu166 is protonated, the pK_a of the active site is perturbed, allowing Lys73 to be in its free base form in the preacylation step, aligning with other works.^32,34,35 Later in 2005, Mobashery and co-workers³⁶ examined the acylation mechanisms of TEM-1 with penicillanic acid bound in the active site. Similar to the PBP 5 investigation, this work was performed computationally. It was determined that the mechanism has “remarkable duality,” indicating that both pathways of Glu166 and Lys73 acting as the general base remain possible. Despite these results for β-lactamases, the absence of Glu166 in the R61 active site makes extrapolating from TEM-1 to R61 (a LMMB PBP) speculative and clearly worthy of independent study.

Herein, we use a novel, combined approach for protonation state prediction that employs MD simulations, QM/MM structural refinements, and QM/MM orbital analyses. This approach is first validated by examining cefoxitin interactions in CTX-M and comparing results to the high resolution (0.88 Å) crystal structure produced by Chen et al.⁴⁰ In that work, nearly all hydrogen atoms were identified in key residues including Ser70, Lys73, Ser130, Glu166, Lys234, and the catalytic water. This structure facilitated a detailed understanding of hydrogen bonding patterns and protonation states in the active site. Upon confirming the validity of this computational approach, it is systematically applied to predict the protonation states of active site residues Lys65 and His298 in the preacylated benzylpenicillin-R61 complex. Critical interactions that maximize the stability of enzyme–substrate complexes are identified. Protonation states are subsequently prioritized based upon orbital stabilities and active site electrostatic networks, which are monitored during extended MD simulations to ensure the stability of these key interactions.

Theoretical Methods

The cocrystallized structure of a bound cefoxitin (CFX) molecule to a CTX-M β-lactamase enzyme from E. coli (PDB ID: 1YMX)⁴¹ was used for the purposes of validating the proposed methodology. This is the same enzyme as published by Chen et al.⁴⁰ with a resolution of 0.88 Å (PDB ID: 2P74), to which our results were compared for validation. Initial processing of the 1YMX PDB structure was performed with www.charmming.org.⁴² The covalently bound β-lactam substrate had to be “back mutated” to the noncovalent preacylated form; the initial parameters and topology for the CFX ligand were derived using www.paramchem.org.⁴³ Two different protonation states were set up for the β-lactamase. The first state had Lys73 protonated while Glu166 was deprotonated. The second state, after proton transfer, had both Lys73 and Glu166 in their neutral forms. The remainder of the β-lactamase setup was the same as described below for the R61 protonation states following the initial processing.

The cocrystallized structure of benzylpenicillin covalently bound to DD-peptidase, Streptomyces R61 (PDB ID: 1PWC) was used throughout.⁴⁴ Initial processing of PDB coordinates was done with www.charmming.org.⁴² We manually back mutated the structure to the noncovalent preacylated form and obtained parameter and topology files for benzylpenicillin (PENG, Figure 2) via www.paramchem.org.⁴³ CHARMM⁴⁵ c37a1 was used to prepare the protein, add hydrogens, and assign protonation states of ionizable residues. The PATCh command was used to substitute the different protonation states for Lys65 and His298 (Table 1). Additionally, a disulfide bridge was patched between Cys291 and Cys344. The CHARMM22⁴⁶ and CHARMM36⁴⁷ generalized forced fields (C22 and CGenFF) were used in combination with the FLEXible parameter reader. An initial steepest decent minimization of 200 steps was performed on the system with the heavy atoms of the protein and PENG restrained with a 500 kcal mol^–1 Å^–2 force constant. The structure was solvated in a rhombic dodecahedron (RHDO) water box using TIP3P waters. Again, a partial steepest descent minimization (100 steps) was performed to allow the system to relax while keeping PENG restrained, again with a 500 kcal mol^–1 Å^–2 force constant. After solvation, an iterative Monte Carlo neutralization procedure was performed; water molecules were replaced by potassium or chloride ions at random to balance the system charge and yield a final salt concentration of 0.15 M. At each iteration, a short minimization (10 steps) was performed and compared to the previous steps. After 15 iterations, the lowest energy structure was retained and minimized using the adopted basis Newton–Raphson (ABNR) method to a gradient tolerance of 0.01 kcal mol^–1 Å^–1 without restraints. The full structure including all waters (crystal and noncrystal), ions, PENG, and protein was heated from 110.15 to 310.15 K (body temperature) over 50 ps. The heated system was then equilibrated at constant pressure (1 atm) and temperature (310.15 K) for 150 ps to ensure the system was in a stable conformation and at thermal equilibrium. For the 11 ns MD simulations, the domain decomposition (DOMDEC) parallelization package of CHARMM was used.⁴⁸ All water molecules and ions were removed that were more than 5 Å from the protein and ligand. The system was solvated in a cubic box and neutralized to 0.15 M with potassium and chloride ions. This was done to utilize the efficiency of the DOMDEC parallelization package that requires a cubic solvation box. Dynamic load balancing (DLB) was turned off for heating, which occurred from 110.15 to 310.15 K over 50 ps. Production runs were performed at constant pressure (1 atm) and temperature (310.15 K) for 11 ns.

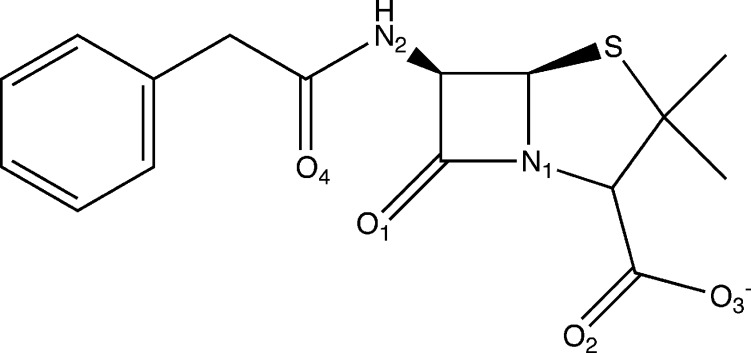
Figure 2.

The structure for benzylpenicillin, also known as penicillin G.

Table 1. Numbering Scheme for Each System and Its Respective Protonation State.

system	Lysine65	Histidine298 Nδ	Histidine298 Nε
I	protonated	protonated	protonated
II	protonated	protonated	deprotonated
III	protonated	deprotonated	protonated
IV	deprotonated	protonated	protonated
V	deprotonated	protonated	deprotonated
VI	deprotonated	deprotonated	protonated

Following the MD simulation, extensive RMSD and distance analysis was performed on the simulation results. A representative structure (based on distances) was chosen and minimized using QM/MM⁴⁹ until a 0.005 kcal mol^–1 Å^–1 rms gradient tolerance was achieved. PENG was treated quantum mechanically during this optimization at the B3LYP/6-31G* level of theory.⁵⁰⁻⁵² The remainder of the system was unrestrained and treated using the C22 force field.

QM/MM Natural Bond Orbital (NBO) analysis⁵³⁻⁵⁵ was performed on all systems to gain insight into orbital interactions. Link atom and residue selection details of the NBO calculations can be found in the Supporting Information. Computations were carried out with Q-Chem/CHARMM⁴⁵ + NBO, using CHARMM version c37a1, Q-Chem 4.0,⁵⁶ and NBO 5.0.^57,58 The NBO results listed can be compared to the water dimer O LP → H–O σ* interaction of 10.3 kcal mol^–1 to give a relatable depiction. Further, pK_a values were estimated using PROPKA,⁵⁹⁻⁶² a very fast empirical pK_a prediction tool for proteins and protein–ligand complexes. The pK_a of Lys65 was computed using the PROPKA version 3.1 Web interface for the crystal structure and protonation states I and IV.

Results and Discussion

Recently introduced by Yang and Cui,^54,55 QM/MM NBO has been used to gain insight into orbital interactions occurring in active sites.¹⁰⁰ The second-order perturbation theory analysis of the Fock matrix in the NBO basis is carried out to evaluate orbital stabilization/charge transfer. Combining this analysis with MD simulations and QM/MM structural refinement reveals significant insight into the multifarious active sites of β-lactamases and DD-peptidases. From the MD simulations, relevant average interaction distances (AVGD) are discussed.

Class A β-lactamase, CTX-M

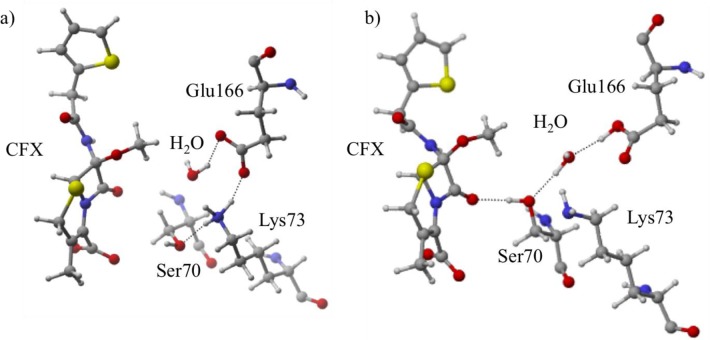
The aforementioned procedure is initially benchmarked against a high-resolution class A β-lactamase crystal structure, CTX-M. In the work by Chen et al.,⁴⁰ several conclusions were drawn that are herein confirmed using our current computational approach. During the acylation reaction, they state that both Lys73 and Glu166 are in their neutral form. We examined both protonation state combinations discussed,⁴⁰ Lys73:protonated//Glu166:deprotonated known as protonation state A and Lys73:deprotonated//Glu166:protonated protonation state B. Following initial equilibration and QM/MM minimization, NBO results indicated that state B has approximately two-thirds more orbital stabilization than state A, aligning with experimental findings (Figure 3).

Figure 3.

Active site variation in the CTX-M protein–CFX ligand system upon altering the protonation state. Protonation state A (a, left) provides less hydrogen bonding stabilization to CFX than B (b, right). Structural differences occur due to alternating protonation states of Glu166 and Lys73.

Approximately 20% of the total orbital stabilization for B is an interaction between the Thr235 side chain and the carboxylate of cefoxitin’s cepham ring (Table 2). This hydrogen bond only exists in the preferred protonation state (B). This is confirmed by analyzing the MD simulations; the AVGD for O(Thr235)···O(cefoxitin carboxylate) is 3.72 Å in B but is 4.82 Å in A. This Thr235 interaction is related to the relocation of Lys73 as a consequence of altering the Glu166 protonation state. In A, a strong hydrogen bond is formed between two charged residues, Lys73 and Glu166, as illustrated by the N···O QM/MM distance (QM/MM_N–O = 2.60 Å), which perturbs the location of surrounding residues to eliminate the hydrogen bond between Thr235 and cefoxitin. In contrast, state B adopts an alternative active site conformation due to the neutral forms of Lys73 and Glu166, i.e., eliminating the possible charge–charge stabilization that occurs in A. MD simulations confirm these findings and reveal that the AVGD_N–O (K73 – E166) is 1.80 Å shorter in state A compared to B.

Table 2. NBO Orbital Stabilization (from Perturbation Theory Contributions) Results for the Interactions between the β-Lactamase, CTX-M, and the CFX Ligand^a.

protonation state	residue	NBO analysis	percentage of total NBO orbital stabilization for the state
A	H2O	4.5	4%
A	H2O	1.4	1%
A	H2O	16.7	16%
A	H2O	9.3	9%
A	H2O	13.5	13%
A	H2O	21.9	22%
A	Asn104	3.5	4%
A	Ser237	19.9	20%
A	Ser237	10.9	11%
B	H2O	2.8	2%
B	H2O	26.9	17%
B	H2O	30.8	19%
B	H2O	11.7	7%
B	H2O	1.7	1%
B	H2O	1.2	1%
B	H2O	0.8	0%
B	H2O	1.4	1%
B	Ser70	14.9	9%
B	Thr235	11.7	21%
B	Lys234	0.5	0%
B	Ser237	25.2	16%
B	Ser237	6.1	4%
B	Gly238	1.9	1%

^aAll NBO values are in kcal mol^–1 (all interactions LP → σ*).

Additionally, Chen et al. comment on the dynamic relationship between the protonation state of Glu166 and the position of Lys73 and Ser130. They hypothesize that if state A is correct, then Glu166 and Lys73 will be closer in distance, while Lys73 will be farther from Ser130. Conversely, in B the opposite conformation would be adopted: Glu166 would be farther from Lys73 while Lys73 would be closer in proximity to Ser130. Our computational results confirm their hypotheses. As already highlighted, QM/MM results yield a Lys73–Glu166 distance (N···O) of 2.60 Å in state A while Lys73 and Ser130 (N···O) are 3.44 Å apart. The opposite pattern is observed from QM/MM state B results; Lys73 is closer to Ser130 (2.83 Å) and farther from Glu166 (3.84 Å). Again, analysis of the 11 ns MD simulations corroborates the QM/MM findings. The AVGD_N–O for K73–E166 is 0.30 Å shorter than K73–S130 in state A, whereas this AVGD_N–O is 1.03 Å longer in state B. Correctly reproducing experimental protonation states, active site reorganization, and bonding patterns for a β-lactamase with a bound β-lactam inhibitor allows us to proceed with confidence in our methodology.

R61 DD-Peptidase Active Site Reorganization via Molecular Dynamics

Six molecular dynamics simulations were performed, one for each of the varying protonation states of Lys65 and His298 (Table 1), which drastically alter the location of key active site residues in R61. Upon completing this step, six DD-peptidase/benzylpenicillin QM/MM minimizations were performed. There are three main functional groups of benzylpenicillin that act as hydrogen bond acceptors: the carbonyl group of the β-lactam ring (O₁), the carboxylate group (O₂ and O₃), and the carbonyl group of the benzylpenicillin tail (O₄). Additionally, an amide group (N₂), a hydrogen bond donor, serves as a fourth functional group (Figure 2). Several R61 active site residues participate heavily in the stabilization of benzylpenicillin; e.g., Arg285, Thr299, Thr301, Ser62, Lys65, and His298. For each protonation state, the total orbital stabilization is determined and each interaction reported as a percentage of the system’s total orbital stabilization. Hence, we determine which protonation states maximize functional group–residue interactions. Furthermore, 11 ns MD simulations are used to monitor key interactions identified from QM/MM minimized structures. From this, we predict the most likely protonation state for the bound benzylpenicillin–R61 complex.

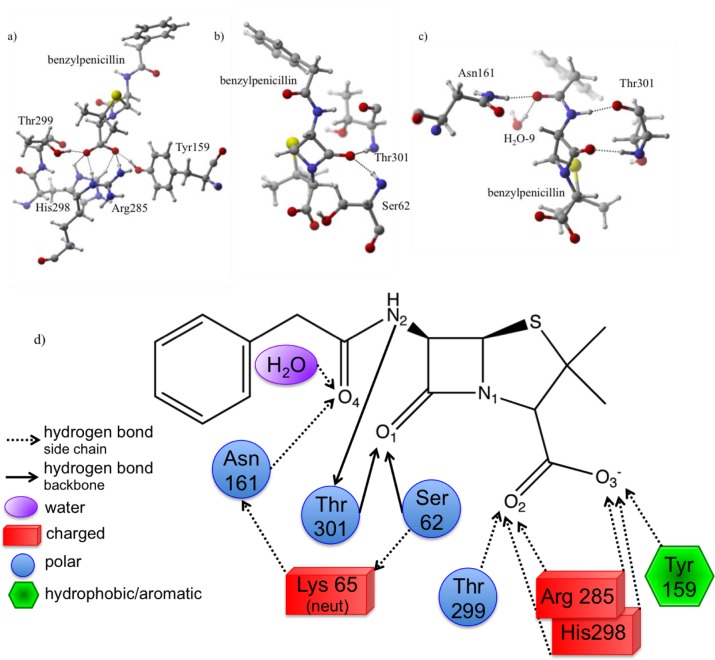
Protonation State I: Protonated Lys65–Protonated N_δ/Protonated N_ε His298

In this protonation state, the benzylpenicillin carboxylate group receives significant stabilization from several active site residues (Figure 4). The greatest contribution arises from Arg285, which forms two strong hydrogen bonds with O₂ and O₃. Analysis confirms the largest quantity of orbital stabilization (43%) arises from lone pairs (LP) on O₂ and O₃ donating into separate H–N antibonding (σ*) orbitals on Arg285. For these interactions, the H(Arg285)···O_x QM/MM_H–O is 1.65 and 1.62 Å for O₂ and O₃, respectively. MD simulations confirm the stability observed in QM/MM structures, an AVGD_H–O of 2.21 and 1.98 Å for O₂ and O₃.

Figure 4.

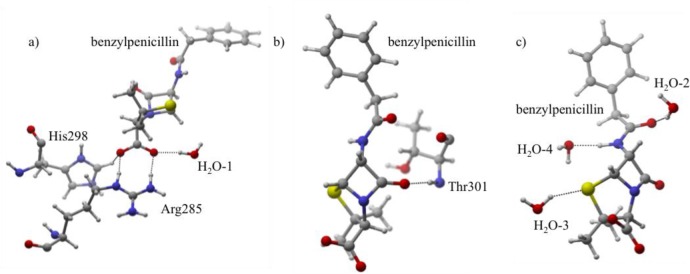
Protonation state I. (a) Hydrogen bonds are depicted between His298, Arg285, and H₂O-1 and the carboxylate group of benzylpenicillin. (b) The stabilizing hydrogen bond between O₁ and Thr301 is depicted. (c) Shows water molecules that stabilize O₄ (H₂O-2), the sulfur (H₂O-3), and the tail H–N₂ (H₂O-4).

Despite Arg285’s contribution in I, additional interactions significantly stabilize the carboxylate. 10% of I’s total orbital stabilization results from two interactions: an active site water (H₂O-1) donates a hydrogen bond to O₂ (QM/MM_H–O = 1.81 Å, Figure 4) and protonated His298 acts as an O₃ hydrogen bond donor (O₃ LP → H–N σ*, QM/MM_H–O = 1.96 Å). The interaction responsible for stabilizing the carbonyl group of the β-lactam ring exists between O₁ and the backbone amide of Thr301 accounting for 9% of the total orbital stabilization for this protonation state (O₁ LP → H–N σ* Thr301, QM/MM_H–O = 1.78 Å). Active site water molecules interacting with O₄ (QM/MM_H–O = 1.66 Å), the sulfur (QM/MM_H–S = 2.43 Å), and the tail amide (QM/MM_H–O = 1.79 Å) contribute another 34% of orbital stabilization to the active site ligand.

Protonation State II: Protonated Lys65–Protonated N_δ/Deprotonated N_ε His298

Similar to protonation state I, Arg285 provides the carboxylate group of benzylpenicillin with the most stabilization, 34% (Figure 5). Two strong hydrogen bonds between Arg285’s N–H groups and O₂ (QM/MM_H–O = 1.71 Å) and O₃ (QM/MM_H–O = 1.71 Å) are formed and governed by O_x (x = 2,3) LP → H–N σ* orbitals. MD simulations show the Arg285-O₂ hydrogen bond is more stable than Arg285-O₃, with an AVGD_H–O2 of 1.88 Å vs an AVGD_H–O3 of 3.29 Å. This indicates that that O₃ receives additional stabilization from other active site residues, evidenced by the non-Arg285 carboxylate orbital stabilization (an additional 43%). The largest contribution results from the hydroxyl side chain of Thr299 (27%) hydrogen bonding with O₃ (O₃ LP → H–O σ* Thr299, QM/MM_H–O = 1.61 Å), which is stable throughout the MD simulation (AVGD_H–O = 1.74 Å). Lys65 is protonated in this state; therefore the adjacent Ser62 seeks out an alternative hydrogen bond acceptor. A weak interaction is formed between the O₂ of benzylpenicillin and the serine side chain (QM/MM_H–O = 2.73 Å). The lone pairs of O₂ (QM/MM_H–O = 2.25 Å) and O₃ (QM/MM_H–O = 2.45 Å) are further stabilized by donating electron density into the antibonding orbitals of His298’s C_ε–H and N_δ–H (2%).

Figure 5.

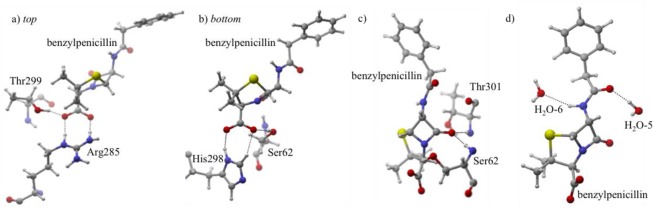
Protonation state II. (a,b) For visual clarity, the carboxylate hydrogen bonding interactions are separated between a and b. Labels top and bottom refer to the position of Arg285 relative to His298. (c) The carbonyl forms hydrogen bonds with Thr301 and Ser62. (d) The tail carbonyl and the tail H–N₂ group hydrogen bond to H₂O-5 and H₂O-6, respectively.

In addition to the side chain of Ser62 acting as a hydrogen bond donor to stabilize the carboxylate (13%); Ser62’s backbone amide forms a weak interaction with O₁ (2%, QM/MM_H–O = 1.90 Å). However, a larger contribution of stabilization occurs between the lone pair of O₁ and backbone H–N σ* orbital of Thr301 (8%, QM/MM_H–O = 1.79 Å). Additionally, active site waters predominantly stabilize both O₄ and H–N₂ in the benzylpenicillin tail, contributing 13% to the total orbital stabilization for II.

Protonation State III: Protonated Lys65–Deprotonated N_δ/Protonated N_ε His298

Several residues stabilize the carboxylate group (Figure 6) in this protonation state, but unlike the others, Arg285 does not play the most significant role. Only one Arg285 interaction exists in the QM/MM protein–ligand minimized structure (LP O₃ → H–N σ* Arg285, QM/MM_H–O = 3.18 Å) providing 9% of the total orbital stabilization for III; however, it is clear from MD simulations that O₂ also interacts with Arg285 (AVGD_H–O = 2.36 Å). Furthermore, Thr299 (QM/MM_H–O = 1.67 Å) and an active site water (H₂O-7, QM/MM_H–O = 1.74 Å) donate hydrogen bonds to O₃, resulting in 34% of the total orbital stabilization for III. An additional 38% is a result of Ser62 (QM/MM_H–O = 1.71 Å) and Tyr159 (QM/MM_H–O = 1.67 Å) combining to stabilize O₂.

Figure 6.

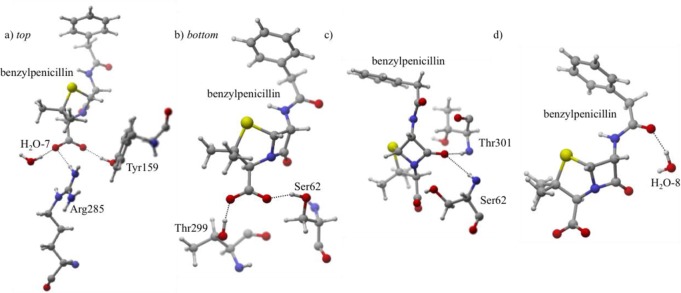
Protonation state III. (a,b) For visual clarity, the carboxylate hydrogen bonding interactions are separated between a and b. Labels top and bottom refer to the position of H₂O-7 relative to Thr299. (c) The carbonyl forms hydrogen bonds with Thr301 and Ser62. (d) H₂O-8 molecule stabilizes O₄.

The β-lactam carbonyl group shows a similar stabilization pattern to II. The backbone amides of Ser62 (QM/MM_H–O = 2.55 Å) and Thr301 (QM/MM_H–O = 1.81 Å) stabilize benzylpenicillin by accepting lone pair electron density from O₁ into their H–N σ* orbitals. The NBO analysis indicates that Thr301 is the predominant stabilizing residue (9%), whereas Ser62 makes only a small contribution (1%). This is confirmed by MD simulations that show the AVGD_H–O is 0.30 Å shorter between O₁ and Thr301 as compared to O₁–Ser62. Finally, in contrast to states I and II, III has only one interaction stabilizing the benzylpenicillin tail, an active site water (H₂O-8, QM/MM_H–O = 1.76 Å) accepting and O₄ lone pair electron density (9%, LP O₄ → H–O σ*).

Protonation State IV: Deprotonated Lys65–Protonated N_δ/Protonated N_ε His298

Protonation state IV (Figure 7) also has two strong hydrogen bonds between Arg285 and benzylpenicillin’s carboxylate group (28% of IV’s total orbital stabilization) with QM/MM_H–O of 1.74 and 1.72 Å for O₂ and O₃, respectively. These interactions are confirmed to be stable via MD simulations, AVGD_H–O = 1.89 and 2.68 Å for O₂ and O₃, respectively. Additional interactions exist between O₂ and Tyr159 (13% – LP O₂ → H–O σ* Tyr159, QM/MM_H–O = 2.62 Å) and O₃ and Thr299 (21% – LP O₃ → H–O σ* Thr299, QM/MM_H–O = 1.63 Å). His298 contributes a smaller carboxylate stabilizing contribution (2%). Similar to previously discussed protonation states, electron delocalization from the O₁ lone pair into backbone amide (Ser62, Thr301) σ* orbitals provides another 10% of the total stabilization.

Figure 7.

Protonation state IV. (a) The interactions are depicted between active site residues and the carboxylate of benzylpenicillin. Arg285 is above His298 in the orientation show. (b) The carbonyl forms hydrogen bonds with Thr301 and Ser62. (c) Asn161, Thr301, and H₂O-9 contribute to the stabilization of the benzylpenicillin tail. (d) A 2D view of the active site is shown with interactions for IV.

Unlike protonation states I, II, and III (all protonated Lys65 states), the benzylpenicillin tail in IV is stabilized by active site residues in addition to an active site water. Thr301’s backbone carbonyl donates lone pair density into the H–N₂ σ* orbital of benzylpenicillin (13%, QM/MM_H–O = 1.74 Å). Benzylpenicillin’s tail carbonyl has two interactions: an active site water (H₂O-9, LP O₄ → H–O σ*, QM/MM_H–O = 1.71 Å) and the Asn161 side chain (LP O₄ → H–N σ*, QM/MM_H–O = 2.88 Å), combining for an additional 13% of this protonation state’s total orbital stabilization.

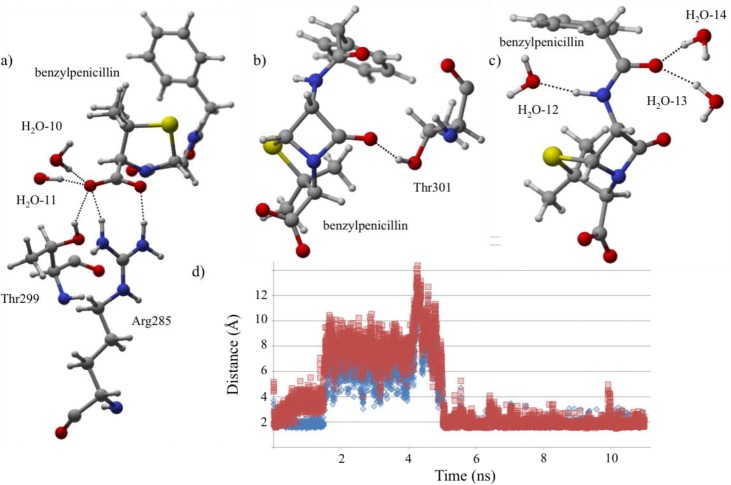
Protonation State V: Protonated Lys65–Protonated N_δ/Deprotonated N_ε His298

Protonation state V experiences less stabilization from active site residues than the previously discussed states. Despite the differences, Arg285 and Thr299 (Figure 8) continue to have a role in stabilizing benzylpenicillin. Arg285 donates hydrogen bonds to O₂ (7%, QM/MM_H–O = 1.73 Å) and O₃ (11%, QM/MM_H–O = 1.80 Å) in the QM/MM minimized structure. O₃ forms additional hydrogen bonds with Thr299 (2%, QM/MM_H–O = 2.33 Å) and active site water molecules (all interactions LP → σ*). Similar to protonation states I–IV, Thr301 donates a hydrogen bond to O₁ (11%, QM/MM_H–O = 1.77 Å). Furthermore, the benzylpenicillin tail (H–N₂, O₄) forms interactions with active site waters in the QM/MM minimized structure.

Figure 8.

Protonation state V. (a) The interactions are depicted between active site residues and the carboxylate of benzylpenicillin. (b) The carbonyl forms a hydrogen bond with Thr301. (c) The interactions shown stabilize O₄ and the H–N group of the benzylpenicillin tail. (d) The graph shows the distance measured between Arg285 and O₂(blue)/O₃(red).

V’s AVGDs and RMSFs show more deviation from the QM/MM structure compared to other states due to an artificial solvation barrier for 3 ns of the simulation. In particular, this is attributed to solvation eliminating (Figure 8d) the benzylpenicillin carboxylate···Arg285/Thr299 and carbonyl (O₁)···Thr301 hydrogen bonding, which occurs between 2 and 5 ns in the simulation. At 5 ns, the Arg285 and Thr299 interactions reform for the remainder of the 11 ns MD simulation, confirming that the QM/MM minimized structure is in the proper conformation. The fluctuation of these interactions suggests that less direct protein–ligand stabilization exists when compared to previously discussed states.

Protonation State VI: Deprotonated Lys65–Deprotonated N_δ/Protonated N_ε His298

Structure VI differs drastically from I–V (Figure 9). Instead of Arg285 providing the carboxylate group with the majority of its stabilization, it interacts with the carbonyl group (O₁) and imparts only 14% of the total orbital stabilization (Figure 9, QM/MM_H–O = 1.69 Å). Instead, a six-water cluster stabilizes the carboxylate group, where O₂ and O₃ each donate lone pair density into σ* H–O orbitals on three waters. This cluster provides 69% of VI’s total orbital stabilization. Similar to protonation states IV and V, O₄ is stabilized by both the Asn161 side chain (7%, QM/MM_H–O = 2.83 Å) and a water molecule (H₂O-16, 9%, QM/MM_H–O = 1.73 Å). Further, there is a small contribution from the sulfur donating lone pair electron density into the H–O σ* orbital of an active site water (H₂O-15). This protonation state drastically differs from I–V: it has fewer interactions with active site residues, and water molecules dominate its stabilization.

Figure 9.

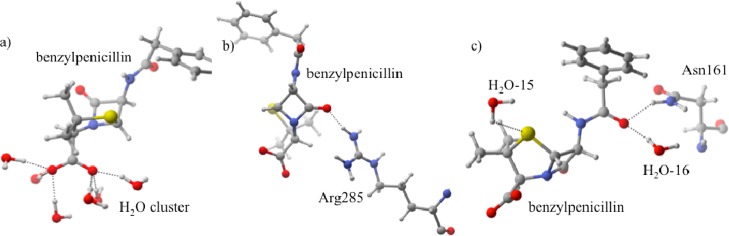
Protonation state VI. (a) The carboxylate group is stabilized by a six water cluster. (b) The β-lactam carbonyl forms a hydrogen bond with Arg285. (c) H₂O-15 and H₂O-16 stabilize the sulfur and O₄, respectively. Additional O₄ stabilization results from interaction with Asn161.

Carbonyl Stabilizing Interactions–O₁

The backbone H–N bond of Thr301 primarily stabilizes the O₁ atom of benzylpenicillin for all protonation states, except for VI (Table 3). In protonation state VI, significant electron donation exists from the O₁ lone pairs into the H–N σ* orbital of the Arg285 side chain. This is dissimilar from all other protonation states where Arg285 engages in hydrogen bonding with the carboxylate group. For states I–V, O₁ is stabilized by the backbone of Thr301. Additionally, II, III, and IV are further stabilized by O₁ donating lone pair electron density into Ser62’s backbone H–N σ* orbital. Despite these differences, the strength of the O₁ stabilization interactions is similar for protonation states I–V. Further discounting VI, the charge-neutral interaction between Arg285 and the carbonyl is expected to be significantly weaker than the salt bridge between Arg285 and the carboxylate that exists in the other protonation states.

Table 3. NBO Orbital Stabilization Results (from Perturbation Theory Contributions) for the Interactions between O₁ and All of Its Interacting Residues for Each Protonation State^a.

protonation state	residue	NBO analysis (kcal mol–1)	percentage of total NBO orbital stabilization for the state	AVG MD distanceb (Å)	QM/MM distance (Å)	RMSFb (Å)
I	Thr301	15.8	9%	2.81	1.78	1.38
II	Ser62	3.1	2%	3.10	1.90	0.51
II	Thr301	12.3	8%	2.01	1.79	0.38
III	Ser62	1.8	1%	3.24	2.55	1.11
III	Thr301	12.6	9%	2.94	1.81	1.39
IV	Ser62	7.3	4%	4.28	1.97	0.64
IV	Thr301	11.8	6%	3.07	1.77	0.91
V	Thr301	16.0	11%	5.81	1.77	1.29
VI	Arg285	26.6	14%	4.20	1.69	1.22

^aAll values are in kcal mol^–1 (all interactions LP → σ*).

^bNot reported for H₂O molecules due to fluctuation throughout MD simulation.

Carboxylate Stabilizing Interactions–O₂, O₃

Current NBO analysis hones in on the stabilizing charge transfer that occurs between active site residues/waters and benzylpenicillin. Until now, we have largely been comparing orbital interactions within the same protonation state. However, we can also use this information to gain a better understanding of how protonation states relate to each other. The water molecules interacting with VI’s carboxylate combine for significant orbital stabilization compared to the other states; however we can partially discount this due to the carboxylate’s solvent exposure. Specifically, this is attributed to the increased importance of charge–charge and dipole–dipole stabilization in the lower dielectric active site environment as compared to the more polarizable solvent.

The remaining protonation states all have strong interactions that make significant contributions to the overall stabilization of the carboxylate group (Table 4). II and IV have three hydrogen bonds for each O₂ and O₃, where III has two hydrogen bonds for O₂ and three for O₃. II, III, and IV all have different His298 protonation states, so further evidence is necessary to determine the most likely state. Here, I is added to our analysis. Despite I having fewer carboxylate contributions, the ones that exist are strong; therefore its inclusion is crucial to understanding the influence of varying Lys65’s protonation state (i.e., I vs IV). Strong interactions exist between Arg285 and both carboxylate oxygen atoms (O₂, O₃), with other contributions from an active site water (H₂O-1) and His298. This differs from II–VI where active site reorganization allows other residues (Ser62, Thr299, Tyr159) to compensate for orbital interactions conferred by Arg285, H₂O-1, and His298 in I.

Table 4. NBO Orbital Stabilization Results (from Perturbation Theory contributions) for the Interactions between O₂/O₃ and All of Its Interacting Residues for Each Protonation State^a.

protonation state	residue	oxygen interaction	NBO analysis (kcal mol–1)	percentage of total NBO orbital stabilization for the state	AVG MD distanceb (Å)	QM/MM distance (Å)	RMSFb (Å)
I	Arg285	O2	32.4	20%	2.21	1.65	0.83
I	H2O-1	O2	15.0	10%		1.81
I	Arg285	O3	38.7	23%	1.98	1.62	0.46
I	His298	O3	7.2	4%	2.75	1.96	0.65
II	Arg285	O2	24.8	16%	1.88	1.71	0.29
II	Ser62	O2	20.8	13%	3.84	2.73	1.07
II	His298	O2	3.8	2%	3.81	2.25	0.71
II	Arg285	O3	29.5	18%	3.29	1.70	0.67
II	His298	O3	1.3	1%	5.24	2.45	1.04
II	Thr299	O3	42.7	27%	1.74	1.61	0.15
III	Ser62	O2	28.8	20%	2.36	1.71	1.32
III	Tyr159	O2	26.7	18%	1.84	1.67	0.59
III	Arg285	O2			2.36	2.21	0.50
III	Arg285	O3	12.8	9%	2.59	3.18	0.71
III	Thr299	O3	29.2	20%	2.04	1.67	0.78
III	H2O-7	O3	20.0	14%		1.74
IV	Arg285	O2	23.9	13%	1.89	1.74	0.23
IV	His298	O2	4.4	2%	2.86	2.18	0.83
IV	Tyr159	O2	24.6	13%	4.07	2.62	0.99
IV	Arg285	O3	28.3	15%	2.68	1.72	0.46
IV	His298	O3	0.9	<1%	3.28	2.55	0.63
IV	Thr299	O3	39.0	21%	3.70	1.63	1.00
V	Arg285	O2	9.4	7%	3.28	1.73	2.31
V	Arg285	O3	14.8	11%	4.08	1.80	2.91
V	Thr299	O3	2.34	2%	5.48	2.33	3.22
V	H2O-10	O3	25.6	18%		1.64
V	H2O-11	O3	24.0	17%		1.66
VI	H2O-molecule	O2	21.1	11%		1.71
VI	H2O-molecule	O2	22.4	12%		1.68
VI	H2O-molecule	O2	29.7	16%		1.64
VI	H2O-molecule	O3	10.6	5%		1.75
VI	H2O-molecule	O3	21.9	12%		1.70
VI	H2O-molecule	O3	24.1	13%		1.60

^aAll values are in kcal mol^–1 (all interactions LP → σ*).

^bNot reported for H₂O molecules due to fluctuation throughout the MD simulation.

Electrostatic Networks and His298

Although orbital effects allow us to rationalize many binding and stabilization interactions, the overall electrostatic network is also critical. The structural comparison of I and IV indicates that those states are likely to possess significant long-range electrostatic stabilization. Their commonality is protonated His298, which results in an extensive charge network stemming from both the N_δ and N_ε sites. The first network stemming from His298’s H–N_δ site forms a hydrogen bond with the backbone carbonyl of Thr299, which in turn induces an interaction between the backbone amide of Gly300 and Thr307’s backbone carbonyl. This is also observed in the MD simulations for states I, II, IV, and V (all protonated N_δ states) where the Thr299 carbonyl oxygen and His298 N_δ have an AVGD_N–O of 2.80, 2.91, 3.15, and 2.90 Å compared to III and VI that have an AVGD_N–O of 3.69 and 3.59 Å. In the second network (Figure 10), the proton attached to the N_ε (I, III, IV, VI) initiates a hydrogen bond to the Tyr280 hydroxyl oxygen, whereas in states II and V the deprotonated N_ε acts as a hydrogen bond acceptor from Tyr280’s hydroxyl group. For the protonated N_ε states, a secondary interaction forms between Tyr280 and His108, where His108 accepts a hydrogen bond from Tyr280 forming a very stable hydrogen bonding network. Again this network remains intact over the course of the MD simulations. In states I, III, IV, and VI, the Tyr280–His108 AVGD_{H–N;I,III,IV,VI} is 2.68 Å, while the deprotonated N_ε states (II, V) have an AVGD_H–N;II,V of 3.45 Å. For example, in II, the hydroxyl hydrogen on Tyr280 flips (w.r.t. I, IV) and hydrogen bonds to the deprotonated N_ε of His298. This change disrupts the His298-Tyr280-His108 network, leaving His108’s N_δ without a hydrogen bond donor.

Figure 10.

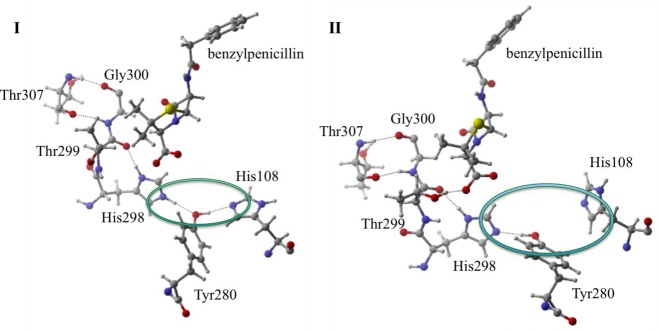
Charge network of His298-Tyr-280-His108 in I. In II, the charge network is eliminated due to active site rearrangement of varying the protonation state.

From this structural analysis, it is clear that protonated His298 results in the most extensive charge network for the R61 active site. Current results align with Friesner and co-workers’¹⁹ His298 protonation state prediction; however the previous prediction was made based upon the deacylation reaction energies with a relatively rigid active site. Herein, we incorporate complete ligand and active site flexibility, which allows us to corroborate previous results and gain greater insight into why His298 exists in its protonated form.

Determining the Lys65 Protonation State

Combining analyses from the previous sections, all states except for I and IV (protonated His298) can largely be eliminated as viable possibilities. The remaining difference between I and IV is that they possess protonated and deprotonated Lys65, respectively. Henceforth, we examine the hydrogen bond donors/acceptors not yet discussed. The biggest difference between these two states is the stabilization of O₄. Active site waters in I stabilize the O₄ carbonyl; however in IV, O₄ accepts a hydrogen bond (LP O₄ → side chain H–N σ*) from Asn161 (6%, QM/MM_H–O = 2.88 Å, Table 5).

Table 5. NBO Stabilizing Interactions (from Perturbation Theory Contributions) for Benzylpenicillin Atoms Excluding O₁, O₂, and O₃^a.

protonation state	residue	benzylpenicillin atom	NBO analysis (kcal mol–1)	percentage of total NBO orbital stabilization for the state	AVG MD distanceb (Å)	QM/MM distance (Å)	RMSFb (Å)
I	H2O-2	O4	25.3	15%		1.66
I	H2O-3	S1	8.3	5%		2.43
I	H2O-4	N2	24.1	14%		1.79
II	H2O-5	O4	16.9	10%		1.72
II	H2O-6	N2	5.2	3%		2.27
III	H2O-8	O4	13.4	9%		1.76
IV	Thr301	N2	24.3	13%	6.88	1.74	1.18
IV	Asn161	O4	10.8	6%	4.27	2.88	1.37
IV	H2O-9	O4	13.2	7%		1.71
V	H2O-12	N2	21.8	16%		1.68
V	H2O-13	O4	14.6	10%		2.92
V	H2O-14	O4	12.1	9%		2.34
VI	Asn161	O4	12.6	7%	3.15	2.83	1.54
VI	H2O-15	S1	1.7	1%		2.63
VI	H2O-16	O4	16.4	9%		1.73

^aAll values are in kcal mol^–1 (all interactions LP → σ*).

^bNot reported for H₂O molecules due to fluctuation throughout MD simulation.

Similar to the carboxylate group, this additional active site residue stabilization stems from the difference in protonation state. In IV, an extended hydrogen bonding network is formed as benzylpenicillin-Asn161-Asp114-Thr116 (Figure 11). This network does not exist for I because the protonation of Lys65 perturbs the active site such that the neighboring Asn161 moves farther (AVGD_H–O = 6.55 Å) from O₄, eliminating stabilization effects. This Asn161 movement opens the active site, allowing water to enter and preferentially stabilize O₄ and disrupt the active site network. This structural analysis indicates that deprotonated Lys65 contributes significantly to strengthening dipole–dipole interactions between benzylpenicillin and the R61 active site.

Figure 11.

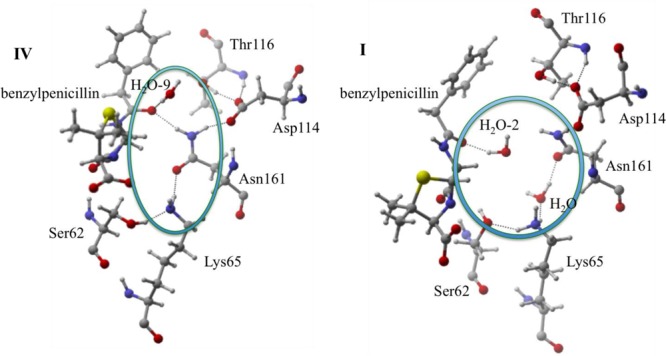
Benzylpenicillin-Asn161-Asp114-Thr116 charge network in IV. The same network is eliminated in I due to active site rearrangement.

It is essential to compare our discussed computational results to the experimental crystal structure⁴⁴ results. An additional analysis performed estimates the pK_a of Lys65 using the PROPKA Web interface, an empirical treatment of active site pK_a values. I and IV result in a pK_a of 6.48 and 6.69, respectively, which can be compared to the crystal structure’s predicted pK_a of 6.62. These results are extremely similar; hence, we cannot infer any additional conclusions from this analysis.

RMSDs for the protein backbone were computed between the crystal structure and the six QM/MM minimized states. All of the results fell within a narrow range of 0.64 Å (IV)–0.82 Å (V), further illustrating the necessity for the methods previously described. To gain a more detailed understanding of the most likely protonation state combinations, several RMSD analyses were performed comparing the crystal structure and the 11 ns trajectories for I and IV. This included comparisons between the protein backbone (RMSD: I = 1.47 Å, IV = 0.99 Å) and the heavy atoms of PENG and key active site residues (i.e., PENG, Arg285, Thr299, Gly300, Thr301, Ser62, Lys65, His298, Tyr159, Asn161; RMSD: I = 1.62 Å, IV = 1.61 Å). In these cases, the RMSD of IV is lower than that for I for the protein backbone; however, the region of the protein being focused on in the present work has nearly identical RMSDs for both states. Hence to determine the most likely protonation states, the detailed analysis presented above is warranted.

Assignment of Lys65 and His298 Protonation States

We determine I and IV have the most favorable electrostatic organization. The protonated His298 residue (I, IV) forms extensive hydrogen bond networks, which connect His108-Tyr280-His298(N_ε–H) and Thr307-Gly300-Thr299-His298(N_δ–H). However, a tail region hydrogen bonding pattern (O₄-Asn161-Asp114-Thr116) helps to stabilize IV and does not exist in state I. IV, which benefits from both aforementioned charge networks, can now be identified as having the most favorable electrostatic stabilization. IV also has the largest total orbital stabilization resulting from tightly bound interactions with Ser62, Thr301, Arg285, His298, Asn161, Tyr159, and Thr299.

Conclusions

Identification of protonation states has been particularly problematic for reactions with β-lactam antibiotics. Specifically, protonation state identification in DD-peptidases has directly contributed to confusion surrounding the acylation mechanism. Although numerous methods have been developed to tackle these challenging problems, no consensus exists on an all-encompassing technique. The current work describes a unique approach to predict active site protonation states and is validated against a well-studied β-lactamase enzyme with ultra high-resolution structural data.⁴⁰ The integration of MD simulations, QM/MM minimizations, and QM/MM orbital analysis provides a useful procedure for probing active site stabilization and predicting the most structurally and energetically favorable protonation state. Further, this approach should prove useful for differentiating side chain vs backbone stabilizing effects that can be targeted in rational drug design workflows. Using this combined approach, we identify the major orbital and electrostatic stabilization effects that govern the benzylpenicillin–R61 bound complex. From these results, we find that deprotonated Lys65 and protonated His298 yield the most favorable active site interactions and thus predict IV as the preacylation protonation state.

Supporting Information Available

QM/MM NBO setup details for peptidase and lactamase systems and a figure showing the placement and numbering of active site waters. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States