Dyadic Curve-of-Factors Model: An Introduction and Illustration of a Model for Longitudinal Non-Exchangeable Dyadic Data

Abstract

The analysis of longitudinal data collected from non-exchangeable dyads presents a challenge for applied researchers for various reasons. This paper introduces the Dyadic Curve-of-Factors Model (D-COFM) which extends the Curve-of-Factors Model (COFM) proposed by McArdle (1988) for use with non-exchangeable dyadic data. The D-COFM overcomes problems with modeling composite scores across time and instead permits examination of the growth in latent constructs over time. The D-COFM also appropriately models the interdependency among non-exchangeable dyads. Different parameterizations of the D-COFM are illustrated and discussed using a real dataset to aid applied researchers when analyzing dyadic longitudinal data.

The analysis of data collected from dyads across time may introduce a challenge to applied researchers. Dyad members may be either exchangeable or non-exchangeable. Exchangeable dyad members are those that cannot be differentiated by a certain variable (e.g., twins, coworkers, gay couples) whereas non-exchangeable dyad members are those that can be differentiated by a certain variable (e.g., husband and wife, parent and child, teacher and student) (see Kenny, Kashy, & Cook, 2006 for more information concerning dyadic data). Latent growth modeling (LGM) within the structural equation modeling (SEM) arena has become a popular method with which longitudinal data may be analyzed (Blozis, 2007a; Hancock & Choi, 2006). The LGM technique provides applied researchers with more modeling options and flexibility with which to evaluate individual growth across multiple measurement occasions. Fortunately, LGM may be extended to model the dependency among dyad members. Notwithstanding, little has been done to elucidate the extension of LGM methods to longitudinal data analysis within dyad populations. Hence, the purpose of this paper is twofold: (1) to extend the LGM method for use with longitudinal data for non-exchangeable dyads, and (2) to demonstrate the flexibility of possible parameterizations using the LGM method applied to a real longitudinal, non-exchangeable dyadic dataset.

Modeling Longitudinal Data Within a Single Population

Univariate Latent Growth Modeling

In the univariate latent growth model, also referred to as a first-order latent growth model, a single observed/manifest variable (e.g., reading score) measured on multiple occasions is a function of 1) an intercept factor which represents the standing of the individuals on the manifest variable at the temporal stage of development selected as a reference point (e.g., initial time of measurement), 2) a slope factor which represents differences in the individual’s trajectory of growth across time (e.g., linear growth), and 3) error which is associated with each manifest variable measured at multiple occasions, representing variance not explained by the latent growth model (Lawrence & Hancock, 1998).

A latent mean structure is commonly incorporated into a LGM in order to estimate means of the intercept and slope factors. This is accomplished by regressing the means on a constant value of one. A univariate, linear LGM across three equally spaced measurement occasions, centered at the initial measurement occasion, with a mean structure (represented with the triangle in which a value of one is included) is depicted in Figure 1. The univariate LGM has received considerable attention and, thus, will not be further described here (see Blozis, 2004; Lawrence & Hancock, 1998; McArdle, 1988; Singer & Willett, 2003; Willett & Sayer, 1994).

Figure 1.

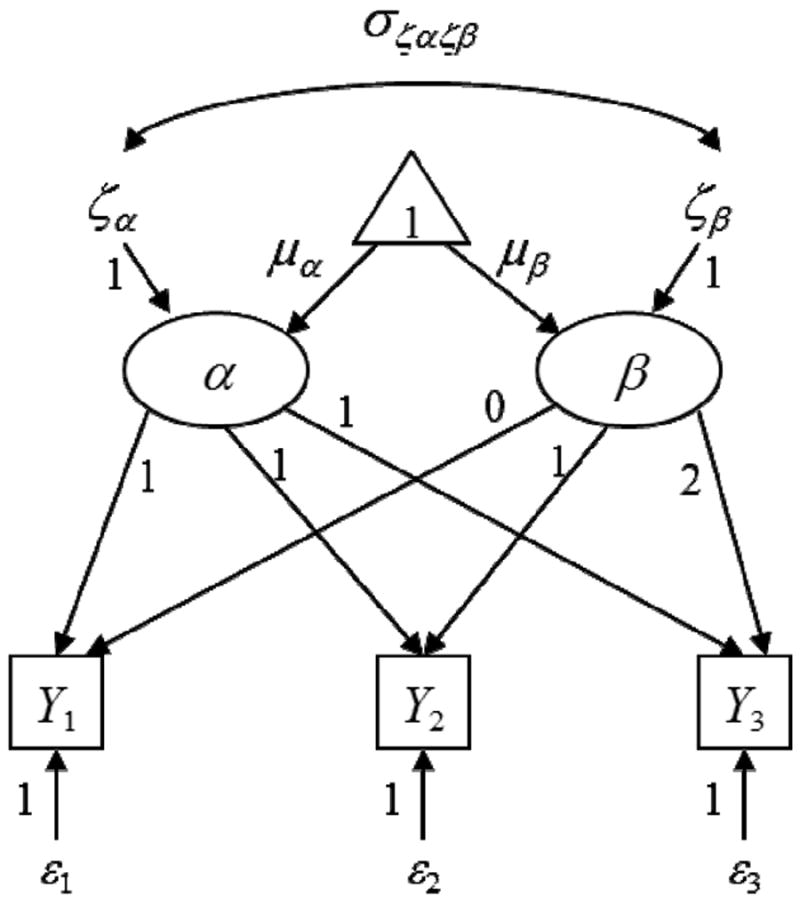
Univariate Linear Latent Growth Model for a Manifest Variable at Three Measurement Occasions Within a Single Population.

A first-order latent growth model is referred to as a univariate latent growth model in that only one manifest variable is modeled across measurement occasions. Researchers, however, may be interested in using more than one manifest variable to measure a latent construct (e.g., aggression, motivation). One option would then be to create a composite manifest variable in which the multiple measures of the factor of interest are aggregated, typically either by creating an average or a sum of the manifest variables. This composite variable would then be modeled across measurement occasions using the univariate LGM as in Figure 1.

It is important to note that when using composite scores in a univariate LGM, the growth trajectory of the latent factor of interest may be misrepresented under certain circumstances. When analyzing a univariate LGM, the variance in a composite variable is assumed to consist of common variance among the set of items used to create the composite score. However, the variance in a composite variable may also consist of each item’s error variance and specific (or “unique”) variance. It has been shown that biased parameter estimates are produced when measurement error in the items used to create a composite variable is not corrected (Fan, 2003) and that a composite variable will be comparable to the latent factor of interest only when the assumption of perfect reliability in the composite variable is met (Bollen & Lennox, 1991). In addition, factor loadings are assumed to be equal for each of the individual items of the latent construct.

Curve-of-Factors Model

The curve-of-factors model (COFM; McArdle, 1988), also referred to as a second-order or multivariate LGM, was introduced to address the problems noted involving the use of composite variables at each time point in the univariate LGM. The COFM extends the univariate LGM with the inclusion of multiple indicator variables of the latent factor of interest at each measurement occasion. Thus, it is possible to model each indicator’s unique error variance, factor loading on the construct of interest, and intercept. The COFM is a second-order factor model that combines a measurement model and a latent growth model (Blozis, 2007a; Hancock, Kuo, & Lawrence, 2001; Sayer & Cumsille, 2001). The first-order factors are the latent construct of interest at each time point. These factors are then modeled to load on the second-order latent growth factors which are, in this context, the intercept and slope factors. Figure 2 depicts a COFM of linear growth across T time points for a k-variable factor.

Figure 2.

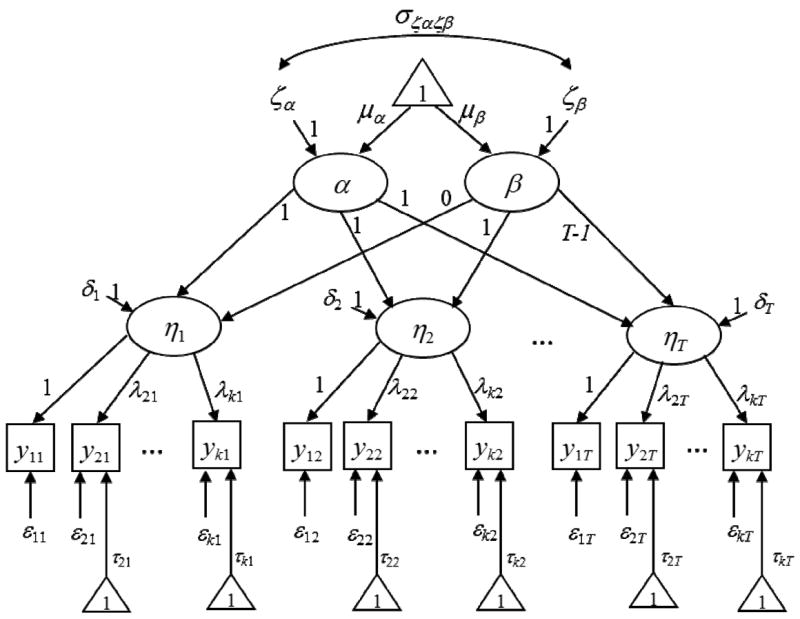
Curve-of-Factors Linear Latent Growth Model for Factors with k-Indicator Variables at T Measurement Occasions Within a Single Population.

The measurement portion of the model refers to the loadings of the indicator variables on the latent construct at each measurement occasion. The second-order factors (i.e., intercept and slope) provide the latent growth portion of the model used to describe the growth of the latent construct across time. Again, a mean structure is ordinarily incorporated into the COFM in order to estimate the intercept and slope factor means and is represented graphically as the triangle in which a value of one is contained in Figure 2¹. The COFM has also been reviewed considerably and, thus, will not be further elucidated here (see Blozis, 2007a; Hancock et al., 2001; McArdle, 1988; Sayer & Cumsille, 2001; Tisak & Meredith, 1990).

Longitudinal Measurement Invariance

When examining longitudinal growth, it is essential to determine whether the change in the construct of interest across measurement occasions is due to actual changes in the construct itself and not due to changes involving the measurement of the construct over time. Thus, an important assumption when examining longitudinal growth is that the measurement of the latent construct is invariant/equivalent across time (Meredith & Horn, 2001). In brief, measurement invariance/equivalence, in the longitudinal context, refers to the degree to which the relationships between indicator variables and the underlying latent constructs they measure are similar across measurement occasions.

Longitudinal invariance/equivalence may be assessed by constraining certain corresponding parameters at different measurement occasions to be equal. These equality constraints are commonly tested in a hierarchical manner in increasing order of invariance/equivalence strictness (Meredith, 1993). Borrowing from the nomenclature in the multiple-group comparison measurement invariance literature (Horn & McArdle, 1992; Meredith, 1993; Widaman & Reise, 1997), the more commonly assessed and/or discussed invariance levels, in an increasing order of stringency, include (1) metric or weak longitudinal invariance in which the corresponding factor loadings are equivalent across all measurement occasions (λ_k1 = λ_k2 = … =λ_kT); (2) scalar or strong longitudinal invariance in which the respective factor loadings and indicator variable intercepts (τ_k1 = τ_k2 = … =τ_kT) are equivalent across time; and (3) strict longitudinal invariance in which the corresponding factor loadings, indicator variable intercepts, and indicator variable error variances ( ${\sigma }_{{\epsilon }_{k1}}^2={\sigma }_{{\epsilon }_{k2}}^2=\dots ={\sigma }_{{\epsilon }_{\mathit{kT}}}^2$) are invariant across time. These levels of invariance are typically tested using a chi-square difference test, Δχ², between the baseline model without constraints and the model with equality constraints imposed corresponding to each particular invariance level being tested (see Blozis, 2007a; Ferrer, Balluerka, & Widaman, 2008; and Harring, 2009).

If longitudinal invariance/equivalence is not supported, the assessment of growth across time may not be meaningful given that growth may represent changes in the measurement of the latent constructs themselves rather than growth in the latent constructs of interest across measurement occasions. While finding support for the highest (strict) level of invariance would be ideal, it may be hard to achieve in practice. It has been argued that strict invariance is necessary to meaningfully compare factor means, covariances, and variances (Meredith, 1993). However, some researchers view residual variance constraints as too restrictive (Byrne, 1994) and contend that non-invariant residual variances only point toward reliability differences in the indicators (Little, 1997). Thus, it has been suggested that meeting the strong invariance assumption is sufficient to meaningfully interpret model parameters (Thompson & Green, 2006). It has been demonstrated that meaningful interpretations may be made even under partial measurement (metric/weak) and intercept (strong/scalar) invariance in the multiple-group literature (see Byrne, Shavelson, & Muthén, 1989). Nonetheless, Lubke and Dolan (2002) found that in certain situations, non-invariant residual variances can hinder the detection of mean differences elsewhere in the model. Regardless of the side that one takes in this debate, the constraints imposed within a model should ultimately complement the theoretical questions of interest (Bollen, 1989).

A related issue to measurement invariance concerns the selection of a reference indicator (RI) for the factor at each measurement occasion. It has been demonstrated that altering the choice of the RI under metric/weak measurement invariance alone may result in different outcomes with respect to growth parameters in COFMs whereas altering the choice of the RI under scalar/strong invariance will not change growth parameter outcomes (Ferrer et al., 2008; Stoel, van den Wittenboer, & Hox, 2004). Given these findings, it is important to establish, at a minimum, scalar/strong invariance of the item serving as the RI across measurement occasions.

Modeling Longitudinal Data Within a Dyad Population

In addition to being able to appropriately model items’ unique error variances, an added benefit of the COFM over the univariate LGM is that the COFM framework permits assessment of the degree of invariance across time that may be assumed. The benefits of the COFM for individuals within a single population should be extended to better assess growth for dyad members. The current study is designed to extend the use of the COFM for use with non-exchangeable dyads and to provide more specific details about the Dyadic COFM to facilitate its use and interpretation. The following section describes this model.

Dyadic Curve-of-Factors Model (D-COFM)

All of the benefits of using the COFM for a single population extend to its use in a non-exchangeable dyadic model. It is important to note that the D-COFM is not analyzed as a multiple-group model in which the data for each group are “stacked.” Instead, D-COFM data are organized similarly to the data used in a repeated-measures ANOVA in which each row of the dataset contains the measured responses for each non-exchangeable dyad (e.g., husband and wife, parent and child, teacher and student) with the columns containing information specific to each dyad member. Figure 3 depicts a D-COFM of linear growth across T time points for a k-variable factor.

Figure 3.

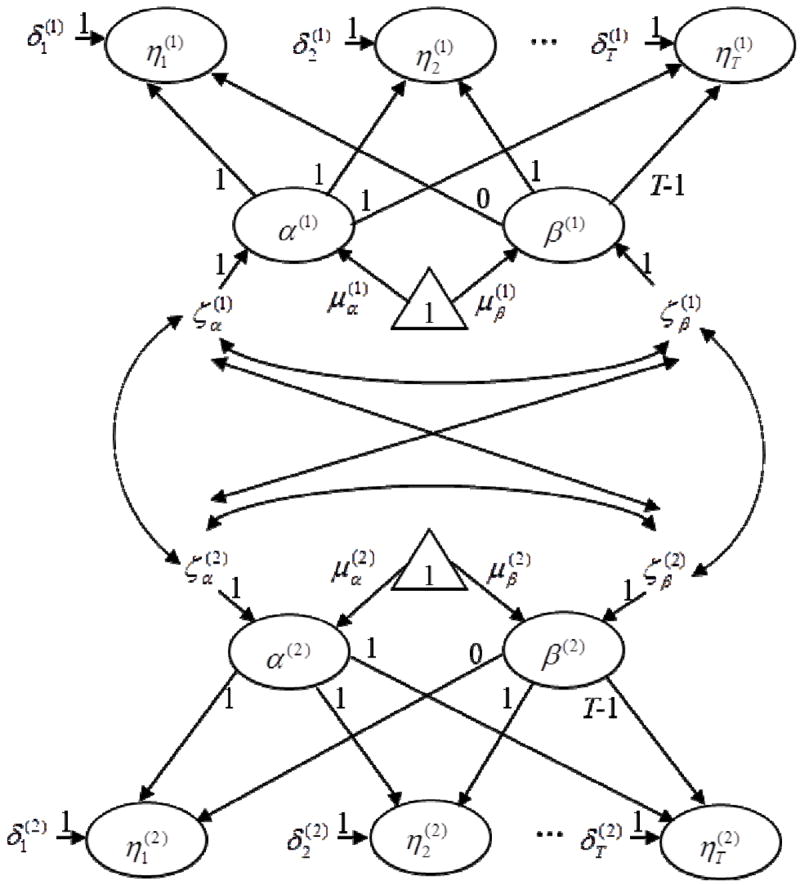
Dyadic Curve-of-Factors Linear Latent Growth Model for Factors with k-Indicator Variables at T Measurement Occasions.

Note. This model does not depict the measurement model and associated intercepts (see Figure 2 for those details). The “(1)” and “(2)” superscripts differentiate the two members of the non-exchangeable dyad.

Assume that k manifest variables, y_i1, y_i2, …, y_ik, measuring a single latent factor, η_i, are measured for each individual i in each non-exchangeable dyad member group m (where m = 1 or m = 2) on T different measurement occasions such that $y_i^{(m)}={[y_{i11}^{(m)},y_{i21}^{(m)},\dots ,y_{\mathit{ikT}}^{(m)}]}^{\prime }$ where t = 1, 2, …, T. If the same k indicator variables are measured at each time t, then q = k × T for each dyad member m. The measurement model with a mean structure incorporated is estimated for all individuals in each dyad member group simultaneously and is given as follows:

$${\mathbf{y}}_i^{(m)}={\mathbf{\tau }}^{(m)}+{\mathbf{\Lambda }}^{(m)}{\mathbf{\eta }}_i^{(m)}+{\mathbf{\epsilon }}_i^{(m)},$$ (1)

where ${\mathbf{y}}_i^{(m)}$ is a 2q × 1 vector containing raw scores on each indicator variable, y_i1, y_i2, …, y_ik, at each time, t, for individual i in each dyad member group, m; τ^(m) is a 2q × 1 vector containing means/intercepts for each indicator variable at each time, t, for each dyad member group, m; Λ^(m) is a 2q × T matrix containing first-order factor loadings associating each indicator variable, y_i1, y_i2, …, y_ik, with its latent construct, η_i, at each time, t, for each dyad member group, m; ${\mathbf{\eta }}_i^{(m)}$ is a 2T × 1 vector containing factor scores for each of the latent constructs at each time point, t, for each dyad member group, m; and ${\mathbf{\epsilon }}_i^{(m)}$ is a 2q × 1 vector containing normal, random errors for each indicator variable, y_i1, y_i2, …, y_ik, at each time, t, for each dyad member group, m.

Growth in the latent constructs, η_i, across time for each dyad member group may be modeled simultaneously and is given as:

$${\mathbf{\eta }}_i^{(m)}={\mathbf{\Gamma }}^{(m)}{\mathbf{\xi }}_i^{(m)}+{\mathbf{\delta }}_i^{(m)},$$ (2)

where ${\mathbf{\eta }}_i^{(m)}$ is a 2T × 1 vector containing factor scores for each of the first-order latent constructs at each time point, t, for each dyad member group, m; Γ^(m) is a 2T × p matrix containing second-order factor loadings reflecting the growth of the latent constructs for each dyad member group, m, where p represents the number of second-order (trajectory) factors; ${\mathbf{\xi }}_i^{(m)}$ is a 2p × 1 vector containing latent scores reflecting the type of growth modeled for each dyad member group, m; and ${\mathbf{\delta }}_i^{(m)}$ is a 2T × 1 vector containing disturbances associated with the first-order latent constructs, η_i, in each dyad member group, m. While several different parameterizations are feasible, one could hypothesize that ${\xi }_i^{(m)}={[{\alpha }_i^{(m)},{\beta }_i^{(m)}]}^{\prime }$, where ${\alpha }_i^{(m)}$ is the intercept representing the initial amount of the construct of interest for each dyad member group, m, and ${\beta }_i^{(m)}$ is the slope representing the linear rate of change in the construct of interest over time for each dyad member group, m. The first-order measurement model with a mean structure in Equation 1 and the first-order factor growth model in Equation 2 may be re-expressed jointly as follows:

$${\mathbf{y}}_i^{(m)}={\mathbf{\tau }}^{(m)}+{\mathbf{\Lambda }}^{(m)}\left({\mathbf{\Gamma }}^{(m)}{\mathbf{\xi }}_i^{(m)}+{\mathbf{\delta }}_i^{(m)}\right)+{\mathbf{\epsilon }}_i^{(m)},$$ (3)

where the second-order factor model in Equation 3, ${\mathbf{\Gamma }}^{(m)}{\mathbf{\xi }}_i^{(m)}+{\mathbf{\delta }}_i^{(m)}$, is substituted for the first-order factor in Equation 1, ${\mathbf{\eta }}_i^{(m)}$.

The latent means of the second-order intercept and slope factors are given by:

$${\mathbf{\xi }}_i^{(m)}={\mathbf{\mu }}^{(m)}+{\mathbf{\zeta }}_i^{(m)},$$ (4)

where ${\mathbf{\xi }}_i^{(m)}$ is a 2p × 1 vector containing intercept and slope parameters for individual i in each dyad member group, m; μ^(m) is a 2p × 1 vector containing latent means for the intercept, ${\mu }_a^{(m)}$, and the slope, ${\mu }_{\beta }^{(m)}$, for each dyad member group, m; and ${\mathbf{\zeta }}_i^{(m)}$ is a 2p × 1 vector containing the disturbances associated with the second-order intercept and slope constructs for each dyad member group, m.

The covariance matrix of raw scores on each indicator variable at each time for each dyad member group, ${\mathbf{y}}_i^{(m)}$, is given as:

$${\sum }_{\mathit{yy}}=\mathbf{\Lambda }(\mathbf{\Gamma \Phi }{\mathbf{\Gamma }}^{\prime }+\mathbf{\Psi }){\mathbf{\Lambda }}^{\prime }+{\mathbf{\Theta }}_{\mathbf{\epsilon }},$$ (5)

where Φ is a 2p × 2p covariance matrix for the second-order intercept and slope factors in each dyad member group; Ψ is a 2T × 2T covariance matrix for the first-order factors in each dyad member group; and Θ_ε is a 2q × 2q covariance matrix for the observed indicator variables’ residuals in each dyad member group.

The variances of the second-order intercept and slope factors are estimated via their disturbances in each dyad member group which appear along the main diagonal of Φ. Also, the covariances between intercept factors, between slope factors, and between intercept and slope factors within and across each dyad member group can be modeled via their disturbances which are the off-diagonal elements of Φ (see Appendix A for this parameterization of the covariance matrix Φ). The variances of the first-order factors in each dyad member group are estimated via their disturbances which are in the main diagonal of the covariance matrix for the first-order factors (ψ). The residual variances of the observed indicator variables appear along the main diagonal of Θ_ε. In addition, covariances between the residuals for the same items across measurement occasions within each dyad group could be modeled to represent that facets of the same latent construct tend to be correlated over time (Loehlin, 2004). Another possible parameterization of the D-COFM could include the covariances between the residuals of the same items across dyad member groups, also referred to as residual intraclass covariances (Olsen & Kenny, 2006).

As with the COFM illustrated in Figure 2, the D-COFM in Figure 3 is parameterized via the second-order slope factor loadings such that the intercept represents the initial amount of the latent construct and the linear growth of the construct across time is modeled within each dyad member group. Paralleling the possible parameterizations of the univariate LGM and the COFM, the second-order intercept factor in the D-COFM may represent the standing of the individuals in each dyad member group on the latent construct at other stages of development by selecting the final, middle, second, third, etc. measurement occasion as the reference point (Hancock & Lawrence, 2006). The intercept may also denote the average of the indicator variables across time (e.g., Stoolmiller, 1995) and various additional centering methods may be implemented (e.g., Blozis & Cho, 2008; Mehta & West, 2000). The growth trajectory may also be modeled as nonlinear using a variety of parameterizations (see Blozis, 2007b; Browne, 1993; Lawrence & Hancock, 1998; Stoolmiller, 1995; Stoolmiller, Duncan, Bank, & Patterson, 1993).

All of the same constraints that must be imposed in the COFM remain for the D-COFM. More specifically, the loading of the same variable at each time point is set to one and serves as the reference indicator (RI) for each of the first-order latent factors within and across dyad member groups. Given that the expected value of the manifest variables is dependent upon the intercepts, the manifest variables’ intercepts within each dyad group are estimated, which is achieved by regressing the manifest variable indicators on a vector of ones. The manifest variable serving as the RI for each first-order factor, however, has intercept values set to zero at each time point to ensure model identification. Also, model identification problems will be encountered if participants are not measured at a minimum of three measurement occasions with a minimum of three observed variables at each measurement occasion. Similar to the univariate LGM and the COFM, time-invariant or time-varying predictors may be introduced if individual variability has been detected in the intercept and slope factors within each dyad member group. Further, correlations among the residuals of the manifest variables may be modeled across time within and across each dyad member group².

Dyadic Measurement Invariance

When examining non-exchangeable dyads’ longitudinal growth, it is not only of interest to determine whether the change in the construct of interest across measurement occasions is due to actual changes in the construct itself, but it is also of interest to determine whether the change in the construct of interest across measurement occasions is similar for each dyad member group. Measurement invariance/equivalence, in the dyad-group context, refers to the degree to which the relationships between indicator variables and the underlying latent constructs they measure are similar across dyad groups. Dyadic measurement invariance may be assessed by constraining certain parameters to be equal across dyad member groups. Again, these equality constraints would typically be tested using a hierarchy of increasing invariance strictness via the Δχ² test statistic (Bollen, 1989).

For instance, metric/weak dyadic invariance would indicate that that the corresponding factor loadings are equivalent across dyad member groups (e.g., for item k at time t: ${\lambda }_{\mathit{kt}}^{(\mathit{1})}={\lambda }_{\mathit{kt}}^{(\mathit{2})}$). Once metric/weak dyadic invariance is supported, researchers could then test whether scalar/strong dyadic invariance holds which would require that the corresponding factor loadings as well as indicator variable intercepts (e.g., ${\tau }_{\mathit{kt}}^{(\mathit{1})}={\tau }_{\mathit{kt}}^{(\mathit{2})}$) are equivalent across dyad member groups. If model fit drops significantly upon addition of the intercept constraints, this would indicate that one dyad member group (e.g., wives) may have consistently scored at a different level (i.e., either higher or lower) on the manifest indicator variables as compared with the other dyad member group (e.g., husbands). On the other hand, if scalar/strong longitudinal invariance is supported, researchers could continue to test for strict dyadic invariance which would require that the corresponding factor loadings, indicator variable intercepts, and indicator variable error variances (e.g., ${\sigma }_{{\epsilon }_{\mathit{kt}}^{(\mathit{1})}}^2={\sigma }_{{\epsilon }_{\mathit{kt}}^{(\mathit{2})}}^2$) are equivalent across dyad member groups. If support is found for strict invariance, this would signify that the indicator variables are measuring the latent construct with similar variability among individuals across dyad groups.

Similar to issues concerning the selection of the reference indicator (RI) in the COFM, the selection of the RI in dyad-group models also has model interpretation implications. For instance, it has been demonstrated that selecting a RI with non-invariant factor loadings across groups in a multiple-group comparison can result in inaccurate results with respect to detecting invariance elsewhere in the model (Johnson, Meade, & DuVernet, 2009). As such, the item selected to serve as the RI, at a minimum, should be invariant across dyad member groups with respect to the relevant unstandardized factor loading. Moreover, if a mean structure is incorporated into the dyad-group context, the item selected as the RI should be invariant with respect to its intercept across dyad member groups in addition to the invariance of its unstandardized factor loading in order to satisfy strong/scalar invariance.

In addition to permitting the assessment of invariance across dyad members for measures at a certain point in time, the D-COFM would also allow examination of invariance across time to answer important questions concerning the similarities and differences between dyad member groups. The following section will describe an application of various parameterizations of the D-COFM to a real longitudinal dyadic dataset. These parameterizations will follow the invariance/equivalence hierarchy within the longitudinal context as well as within the dyadic-group context. It must be noted that this model will be applied to non-exchangeable dyadic data. The application of these techniques to exchangeable dyadic data requires satisfying further assumptions (see Kenny et al., 2006 and Olsen & Kenny, 2006 for more detailed information).

EXAMPLES

Data from the National Longitudinal Study of Adolescent Health (Add Health) were used to illustrate different parameterizations of the D-COFM using male and female full siblings’ responses to items on the Center for Epidemiologic Studies Depression Scale (CES-D; Radloff, 1977). Overall model fit was assessed using global fit indices, including the CFI, TLI, RMSEA, and SRMR. Relative model fit among models was assessed using the chi-square difference test, Δχ², and information criteria, including the AIC, BIC, and sample size adjusted BIC (aBIC)³.

Dataset

Participants

Add Health is a nationally representative longitudinal study of adolescents in the United States who were in grades 7-12 during the 1994-1995 academic year. Data on the Add Health cohort have been collected in four waves⁴ through 2009 and contain information on various subject areas, including participants’ physical, psychological, economic, and social well-being. Participants for the current study consisted of 541 male and female full sibling pairs who participated in the Add Health study. Ages of the participants at Wave 1 data collection ranged from 12 to 20 years with a mean of 16 years (SD = 1.66). Only one full sibling pair per household was included in the current study.

As is common with longitudinal studies, there was some attrition over the four waves of data collection. At time 1, there were 540 male siblings and 541 female siblings. By time 4, the number of valid responses to items was 443 for males and 460 for females. It is unknown, without further examination, whether these missing data patterns are missing at random (MAR) or not missing at random (NMAR). Nonetheless, given that the use of these data was solely to illustrate the D-COFM, data were assumed to be MAR. As such, full information maximum likelihood (FIML) was implemented in Mplus version 5.2 to handle missing data. Broader substantive generalizations from the results should therefore not be made.

Measure

Responses to a subset of the items from the Center for Epidemiologic Studies Depression Scale (CES-D; Radloff, 1977) were used as the observed variables. The original CES-D scale consists of 20 items measured on a four-point Likert scale ranging from 0 to 3 (0 = Rarely or None of the Time; 1 = Some or a Little of the Time; 2 = Occasionally or a Moderate Amount of Time; and 3 = Most or All of the Time). Only nine of the original 20 items were asked of participants during each of the four Add Health interview waves. A series of factor analyses were conducted to extract a subset of the nine items⁵ that measured a single factor across the four time points for brothers and sisters. This resulted in a subset of four items (items 1, 3, 5, and 6 from the original CES-D scale; see Table 1).

Table 1.

Center for Epidemiologic Studies Depression Scale (CES-D) Items Selected to Measure Depression for the D-COFM Illustrations

Item Number	Item
1.	I was bothered by things that usually don’t bother me
3.	I felt that I could not shake off the blues even with help from my family or friends.
5.	I had trouble keeping my mind on what I was doing.
6.	I felt depressed.

Note. Participants were given the following instructions when responding: “How often was each of these things true during the past week?”

Analysis and Results

A sequence of parameterizations of the D-COFM was performed and is subsequently described (see Table 2 for model descriptions). Prior to applying the D-COFM, a search for an appropriate reference indicator (RI) was conducted. Similar to the strategies recommended by Byrne et al. (1989), Rensvold and Cheung (2001), and Yoon and Millsap (2007), item 3 was found to satisfy strict invariance across time and across dyad member groups through a series of invariance tests using all possible RI options.

Table 2.

Description of D-COFM Models Estimated

Estimating Model	Model Description
ULGM	Unconditional Unconstrained D-COFM with Linear Growth Modeled
FMIM	Linear D-COFM with Full Factor Loading Constraints Across Time and Dyad Groups
FSIM	Linear D-COFM with Full Factor Loading and Item Intercept Constraints Across Time and Dyad Groups
PSIM	Linear D-COFM with Full Factor Loading and Partial Item Intercept Constraints Across Time and Dyad Groups
FRIM	Linear D-COFM with Full Factor Loading, Partial Item Intercept, and Full Residual Variance Constraints Across Time and Dyad Groups
PRIM	Linear D-COFM with Full Factor Loading, Partial Item Intercept, and Partial Residual Variance Constraints Across Time and Dyad Groups
IMCM	PRIM with Intercept Factor Means Constrained Across Dyad Groups
SMCM	PRIM with Slope Factor Means Constrained Across Dyad Groups
ISCCM	PRIM with Covariance Between Intercept and Slope Factors Constrained Across Dyad Groups
IVCM	PRIM with Intercept Factor Variances Constrained Across Dyad Groups
SVCM	PRIM with Slope Factor Variances Constrained Across Dyad Groups
CD-COFM	PRIM with Age as Predictor of Corresponding Dyad Member’s Intercept and Slope Factors

Individual plots and averages of the four items at each of the four time points were graphed for brothers and sisters to examine whether it was feasible to model a linear trajectory across time. A general linear pattern in the plots was found. Given that measurement occasions were unequally spaced, the slope factor loadings were set to 0, 2, 7, and 13 at times 1, 2, 3, and 4, respectively, to match the timing of measurement occasions⁴. In addition, the intercept was modeled to represent the initial amount of the depression construct.

As mentioned previously, several constraints are incorporated into the basic COFM for identification purposes, including setting the intercept of the RI (item 3) to zero for each factor and time point. In addition to the constraints, all estimated models included several covariances that were freely estimated in the D-COFM. Residuals for corresponding items across measurement occasions within each dyad group were allowed to covary given that the specific aspects of a construct of interest may be correlated over time (see, e.g., Loehlin, 2004). All covariances among the second-order growth factors both within and across dyad members were also estimated (see Figure 3).

Unconditional Unconstrained Linear Growth Model (ULGM)

For the first illustration, the unconditional, unconstrained D-COFM with linear growth was analyzed in which none of the items’ factor loadings, intercepts, or residual variances (with the exception of the RI) were constrained to be equivalent across time and/or across dyads. The unconstrained linear growth model fit the data well (ULGM; see Table 3 for model fit information). Second-order factor (growth trajectory) parameter estimates are presented in Table 4 and the second-order factor covariances with corresponding correlations are presented in Table 5 for the first set of models estimated. The intercept factor mean for brothers $({\widehat{\mathrm{\mu }}}_{\alpha }^{(B)}=.334)$ and for sisters $({\widehat{\mathrm{\mu }}}_{\alpha }^{(S)}=.482)$ was significantly greater than zero. There was significant variability in the initial measurement of depression among brothers $({\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(B)}}^2=.069)$ and among sisters $({\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(S)}}^2=.182)$. The slope factor mean for brothers $({\widehat{\mu }}_{\beta }^{(B)}=-.007)$ and sisters $({\widehat{\mu }}_{\beta }^{(S)}=-.008)$ indicated a significant decrease in linear growth across time in the depression construct. Thus, there tended to be a linear decline (on average) in depression across measurement occasions for both brothers and sisters. There was no significant variability in the declining rates of depression among the brothers $({\widehat{\sigma }}_{{\zeta }_{{\beta }_i}^{(B)}}^2=.001)$, whereas there was significant variability in the declining rates of depression among the sisters $({\widehat{\sigma }}_{{\zeta }_{{\beta }_i}^{(S)}}^2=.001)$.

Table 3.

Global Fit Indices and Information Criteria for the D-COFM Models Estimated

		Global Fit Indices and Information Criteria
Estimating Modela	df	χ2	CFI	TLI	RMSEA (90% CI)	SRMR	AIC	BIC	aBIC
ULGM	410	530.506*	.972	.966	.023 (.017, .029)	.043	30027.496	30671.786	30195.630
FMIM	431	564.914*	.969	.964	.024 (.018, .029)	.047	30036.789	30590.879	30181.385
FSIM	452	696.073*	.943	.937	.032 (.027, .036)	.050	30136.060	30599.949	30257.117
PSIM	446	586.644*	.967	.963	.024 (.018, .029)	.047	30028.660	30518.321	30156.442
FRIM	474	762.395*	.932	.929	.034 (.029, .038)	.056	30232.495	30601.888	30328.892
PRIM	469	622.618*	.964	.962	.025 (.019, .030)	.051	30050.962	30441.832	30152.964
IMCM	470	634.221*	.961	.959	.025 (.020, .030)	.052	30063.460	30450.033	30164.340
SMCM	470	622.996*	.964	.962	.025 (.019, .030)	.051	30049.071	30435.645	30149.952
ISCCM	470	627.918*	.963	.961	.025 (.019, .030)	.052	30055.012	30441.586	30155.893
IVCM	470	634.553*	.961	.959	.025 (.020, .030)	.053	30062.359	30448.933	30163.239
SVCM	470	622.029*	.964	.962	.024 (.019, .029)	.051	30049.173	30435.747	30150.054
CD-COFM	530	691.508*	.963	.961	.024 (.018, .029)	.051	33088.470	33513.701	33199.438

Note.

^aSee Table 2 for a description of models estimated.

^*p < .05. Italicized values denote the smallest information criteria values among the first six comparison models estimated.

Table 4.

Unstandardized Parameter Estimates of Second-Order Factor Means and Factor Variances for the First Six D-COFM Models Estimated

	Factor Means				Factor Variances
Estimating Modela	${\widehat{\mathrm{\mu }}}_{\alpha }^{(B)}$	${\widehat{\mathrm{\mu }}}_{\alpha }^{(S)}$	${\widehat{\mathrm{\mu }}}_{\beta }^{(B)}$	${\widehat{\mathrm{\mu }}}_{\beta }^{(S)}$	${\widehat{\sigma }}_{{\varsigma }_{{\alpha }_i}^{(B)}}^2$	${\widehat{\sigma }}_{{\varsigma }_{{\alpha }_i}^{(S)}}^2$	${\widehat{\sigma }}_{{\varsigma }_{{\beta }_i}^{(B)}}^2$	${\widehat{\sigma }}_{{\varsigma }_{{\beta }_i}^{(S)}}^2$
ULGM	.334*	.482*	-.007*	-.008*	.069*	.182*	.001	.001*
FMIM	.334*	.482*	-.007*	-.008*	.073*	.176*	.001	.001*
FSIM	.330*	.491*	-.006*	-.009*	.073*	.175*	.001	.001*
PSIM	.343*	.464*	-.007*	-.006*	.073*	.176*	.001	.001*
FRIM	.345*	.467*	-.007*	-.006*	.075*	.185*	.001	.001*
PRIM	.342*	.463*	-.007*	-.006*	.074*	.179*	.001	.001*

Note. α = intercept factor; β = slope factor; B = brother; S = sister.

^*p < .05.

^aSee Table 2 for a description of models estimated.

Table 5.

Parameter Estimates of Second-Order Factor Covariances and Corresponding Correlations Within and Across Dyad Member Groups for the First Six D-COFM Models Estimated

Estimating Modela	Factor Covariances and Corresponding Correlations
	${\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\beta }_i}^{(B)}}$	$r_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\beta }_i}^{(B)}}$	${\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(S)}{\zeta }_{{\beta }_i}^{(S)}}$	$r_{{\zeta }_{{\alpha }_i}^{(S)}{\zeta }_{{\beta }_i}^{(S)}}$	${\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\alpha }_i}^{(S)}}$	$r_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\alpha }_i}^{(S)}}$	${\widehat{\sigma }}_{{\zeta }_{{\beta }_i}^{(B)}{\zeta }_{{\beta }_i}^{(S)}}$	$r_{{\zeta }_{{\beta }_i}^{(B)}{\zeta }_{{\beta }_i}^{(S)}}$	${\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\beta }_i}^{(S)}}$	$r_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\beta }_i}^{(S)}}$	${\widehat{\sigma }}_{{\zeta }_{{\beta }_i}^{(B)}{\zeta }_{{\alpha }_i}^{(S)}}$	$r_{{\zeta }_{{\beta }_i}^{(B)}{\zeta }_{{\alpha }_i}^{(S)}}$
ULGM	-.001	-.134	-.008*	-.604	.039*	.347	< .001	-.187	< .001	-.036	-.002	-.146
FMIM	-.001	-.170	-.008*	-.616	.038*	.339	< .001	-.186	< .001	-.030	-.002	-.147
FSIM	-.001	-.168	-.007*	-.622	.038*	.340	< .001	-.189	< .001	-.032	-.002	-.150
PSIM	-.001	-.172	-.008*	-.617	.039*	.340	< .001	-.187	< .001	-.030	-.002	-.148
FRIM	-.001	-.173	-.008*	-.647	.040*	.337	< .001	-.215	< .001	-.016	-.002	-.150
PRIM	-.001	-.168	-.008*	-.620	.038*	.333	< .001	-.172	< .001	-.037	-.002	-.151

Note. α = intercept factor; β = slope factor; B = brother; S = sister.

^*p <.05.

^aSee Table 2 for a description of models estimated.

The brothers’ initial level of depression was not significantly related to their decreasing trajectory in depression $({\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\beta }_i}^{(B)}}=­.001)$ with a corresponding correlation $(r_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\beta }_i}^{(B)}})$ of −.134; however, the sisters’ initial level of depression was significantly and negatively related to their decreasing trajectory in depression $({\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(S)}{\zeta }_{{\beta }_i}^{(S)}}=­.008;r_{{\zeta }_{{\alpha }_i}^{(S)}{\zeta }_{{\beta }_i}^{(S)}}=­.604)$. Thus, sisters with low initial levels of depression tended to experience less decline in depression across measurement occasions as compared to sisters with high initial levels of depression who tended to experience greater decline in depression across measurement occasions. The covariance between brothers’ and sisters’ intercept factor disturbance variances was statistically significant $({\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\alpha }_i}^{(S)}}=.039)$. The positive relationship $(r_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\alpha }_i}^{(S)}}=.347)$ indicates that brothers with high initial levels of depression also tended to have sisters with high initial levels of depression. The covariance between brothers’ and sisters’ slope factor disturbance variances was not statistically significant $({\widehat{\sigma }}_{{\zeta }_{{\beta }_i}^{(B)}{\zeta }_{{\beta }_i}^{(S)}}<.001)$, indicating that the linear trajectory across time for brothers was unrelated to the linear trajectory across time for sisters $(r_{{\zeta }_{{\beta }_i}^{(B)}{\zeta }_{{\beta }_i}^{(S)}}=­.187)$. The covariance between the brothers’ intercept factor and the sisters’ slope factor was not statistically significant $({\widehat{\sigma }}_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\beta }_i}^{(S)}}<.001)$, indicating that the brothers’ initial level of depression was not statistically significantly related to the sisters’ decreasing trajectory in depression $(r_{{\zeta }_{{\alpha }_i}^{(B)}{\zeta }_{{\beta }_i}^{(S)}}=­.036)$. Further, there was no statistically significant relationship between the brothers’ declining rate in depression and the sisters’ initial level of depression $({\widehat{\sigma }}_{{\zeta }_{{\beta }_i}^{(B)}{\zeta }_{{\alpha }_i}^{(S)}}=­.002;r_{{\zeta }_{{\beta }_i}^{(B)}{\zeta }_{{\alpha }_i}^{(S)}}=­.146)$.

Longitudinal Dyadic Invariance Constraints

To mimic the sequential order of invariance testing within the longitudinal and multiple-group literature, metric/weak invariance was first tested across time and dyad member groups simultaneously. Subsequently, scalar/strong invariance was tested across time and dyad member groups simultaneously followed by testing for strict invariance across time and dyad member groups simultaneously. While these invariance levels were tested simultaneously, one could test these consecutively (i.e., longitudinally followed by dyadic invariance or vice-versa).

Full Metric Invariance Model (FMIM)

Corresponding indicators’ factor loading constraints were first imposed on the linear D-COFM across measurement occasions and across dyad member groups to assess whether metric/weak longitudinal and dyadic invariance was supported. The full metric invariance model (FMIM) fit the data adequately (see Table 3). Because MLR estimation was implemented, chi-square difference testing must be corrected appropriately using the Satorra-Bentler scaled Δχ² test ( $\mathrm{\Delta }{\chi }_{\mathit{SB}}^2$; Satorra & Bentler, 2001). The $\mathrm{\Delta }{\chi }_{\mathit{SB}}^2$ test between the unconstrained linear growth model and the constrained factor loading model was not statistically significant ( $\mathrm{\Delta }{\chi }_{\mathit{SB}}^2=32.11$, Δdf = 21, p > .05), supporting the less parameterized metric invariance model and thus providing evidence that the relationship between corresponding items and depression factors were similar across time and dyad member groups (see Tables 4 and 5 for the second-order parameter estimates of interest with these particular constraints imposed).

Full Strong Invariance Model (FSIM)

Corresponding indicators’ intercepts were then constrained across measurement occasions and across dyad member groups to examine whether scalar/strong longitudinal and dyadic invariance was supported. The full strong invariance model (FSIM) fit the data fairly well (see Table 3 for model fit information and Tables 4 and 5 for parameter estimates). Nonetheless, the $\mathrm{\Delta }{\mathrm{\chi }}_{\mathit{SB}}^2$ test between the constrained factor loading model and the constrained item intercept model was statistically significant ( $\mathrm{\Delta }{\mathrm{\chi }}_{\mathit{SB}}^2=127.724$, Δdf = 21, p < .05). Modification indices were examined to help pinpoint which item intercepts might be non-invariant across time and/or dyad member groups. Each item intercept associated with the largest modification index was freely estimated in sequential order until the $\mathrm{\Delta }{\mathrm{\chi }}_{\mathit{SB}}^2$ test between the FMIM and the current partial strong invariance model (PSIM) was no longer statistically significant.

Partial Strong Invariance Model (PSIM)

Six item intercept constraints were released, resulting in the final partial strong invariance model (PSIM; see Table 3 for model fit information and Tables 4 and 5 for parameter estimates for this model). It was found, for instance, that the intercept for item six was higher at the first measurement occasion for the sisters than the same item’s intercepts at all four measurement occasions for the brothers. Also, the intercept of item six was higher at the first measurement occasion than the same item’s intercepts at the remaining three measurement occasions for the sisters. Accordingly, the sisters “felt more depressed” at the first measurement occasion than the brothers did at all four measurement occasions. In addition, the sisters “felt more depressed” at the first measurement occasion than they did at the succeeding three measurement occasions. It is important to note that the non-invariant intercepts indicate that some source other than the factor is influencing mean differences. Thus, latent mean differences are not only due to the influence of the factor, but also due to differences in the intercepts.

Again, while there is debate among researchers with respect to the level of intercept invariance when making meaningful conclusions, we continue with model-fitting for illustrative purposes. Applied researchers should endeavor to make sense of potential non-invariance and assess whether the non-invariance invalidates use of the relevant indicator.

Full Residual Invariance Model (FRIM)

To test for strict longitudinal and dyadic invariance, corresponding item residual variances were constrained to be equal across measurement occasions and across dyad member groups. The full residual invariance model (FRIM) fit the data fairly well (see Table 3 for model fit information). However, the $\mathrm{\Delta }{\mathrm{\chi }}_{\mathit{SB}}^2$ test between the partial scalar/strong invariance model (PSIM) and the fully constrained residual variance model was statistically significant ( $\mathrm{\Delta }{\mathrm{\chi }}_{\mathit{SB}}^2=99.084$, Δdf = 28, p < .05). Each item error variance associated with the largest modification index was freely estimated in successive order until the $\mathrm{\Delta }{\mathrm{\chi }}_{\mathit{SB}}^2$ test between the PSIM and the current model was no longer statistically significant (see Tables 4 and 5 for the second-order parameter estimates of interest with these particular constraints imposed).

Partial Residual Invariance Model (PRIM)

Five item residual variance constraints were released, resulting in a partial residual invariance model (PRIM; see Table 3 for model fit information). It was found, for example, that the residual variance associated with item 1 at the second measurement occasion for sisters was larger than it was for the brothers at all measurement occasions and for the sisters at the remaining measurement occasions. This could suggest overall variability in depression across time and across dyad member groups.

Thus, the sequential testing of longitudinal dyadic invariance resulted in selection of the PRIM. Parameter estimates of interest in the final model (PRIM) were not too dissimilar from those in the ULGM (see Tables 4 and 5). The Mplus code for the PRIM is included in Appendix B.

Additional Tests of Interest

Researchers may be interested in whether there are statistically significant differences between certain parameters estimated for the brothers and the sisters. More specifically, one may test whether there are significant differences between intercept factor means, slope factor means, the covariance between the intercept and slope factor disturbances, the intercept factor disturbance variance, and the slope factor disturbance variance for the brothers and the sisters. These were tested individually by running the PRIM with an additional constraint of interest included (e.g., intercept factor mean constraints across dyad groups) and subsequently conducting the $\mathrm{\Delta }{\mathrm{\chi }}_{\mathit{SB}}^2$ test between the PRIM and the newly constrained model. A statistically significant $\mathrm{\Delta }{\mathrm{\chi }}_{\mathit{SB}}^2$ test would indicate a significant difference between the brothers’ and sisters’ parameter estimates of interest (e.g., intercept factor mean). Second-order (growth trajectory) parameter estimates are not presented for this set of models because the estimates for these same parameters when they are freely estimated are already provided in Tables 4 and 5.

All of the models with these constraints of interest fit the data well (see Table 3). The model comparison tests indicated that there was a statistically significant difference between the brothers’ and the sisters’ intercept factor means. The sisters, on average, demonstrated a significantly higher level of depression than did the brothers during the initial measurement occasion in the 1994-1995 school year (see Table 4). There was a statistically significant difference between the brothers’ and sisters’ intercept and slope factor disturbance covariances. More specifically, a moderately strong negative and statistically significant relationship between initial levels of depression and their linear rate of decline in depression across time was demonstrated among the sisters whereas there was no significant relationship demonstrated among the brothers (see Table 5). There was also a significant difference between the brothers’ and sisters’ intercept factor disturbance variances, indicating more variability among the sisters’ initial levels of depression than among the brothers (see Table 4). There was no statistically significant difference between brothers’ and sisters’ slope means or between the variability in linear rates of decline in depression across measurement occasions for the brothers and sisters (see Table 4). Hence, brothers’ and sisters’ rate of linear growth (decline) in depression across measurement occasions could be assumed equivalent and the variability in growth rates was comparable for the dyad members.

Conditional D-COFM (CD-COFM)

The models examined thus far have been unconditional models in which no predictor variables were included. Researchers may want to include predictor variables to examine how well they may explain the variability in the intercept and slope factors. To illustrate this, the age of the brothers and the sisters at the initial measurement occasion during the 1994-1995 academic year was hypothesized to have a direct effect on the respective dyad member’s intercept and slope factors and were included in the PRIM as a predictor variable. The conditional model fit the data adequately (see Table 3). However, only the age of the brothers at the initial measurement occasion statistically significantly predicted their initial amount of depression. Every one year increase in age resulted in a .042 increase in initial level of depression among the brothers and every one standard deviation increase in age resulted in a .258 standard deviation increase in initial level of depression among the brothers. There still remained a significant amount of unexplained variance in the brothers’ and sisters’ intercepts as well as in the sisters’ slope after including age as a predictor.

Discussion

The purpose of this paper was to provide various illustrations of and demonstrate the flexibility of the D-COFM with data for non-exchangeable dyads in longitudinal studies. Longitudinal and dyadic invariance tests when implementing the D-COFM were illustrated using items selected from the Center for Epidemiologic Studies Depression Scale (CES-D; Radloff, 1977) from the Add Health dataset to represent depression in male and female full siblings across four measurement occasions. These illustrations resulted in the PRIM, in which full metric/weak invariance, partial scalar/strong invariance, and partial residual invariance was exhibited longitudinally and across dyad groups.

Overall, all of the D-COFM models tested fit the data well (see Table 3) and the estimates for the first six unconditional models with sequential invariance constraints did not change substantially (see Tables 4 and 5). Given that model fit information differences among the models were negligible, the information criteria were examined to select from among the set of models which would cross-validate best in subsequent samples. The least constrained and, thus, more parameterized model (ULGM) resulted in the smallest AIC value (italicized in Table 3) among the models testing invariance across time and dyad member groups up through the PRIM. This is not unexpected given that the AIC has a propensity to select more parameterized models (Bozdogan, 1987; Browne & Cudeck, 1989). In contrast, the partial residual invariance model (PRIM) resulted in the smallest BIC and aBIC values (italicized in Table 4), suggesting support for the pattern of time and dyad member invariance reflected in this model’s parameterization. Again, the PRIM was the model with full metric/weak invariance and with intercepts and error variances found only to meet assumptions of partial invariance across time and across dyad groups. There is still a lack of consensus about the meaningful interpretation of parameter estimates under partial invariance (Byrne et al., 1989; Meredith, 1993) and, thus, further research is warranted with respect to the validity of interpretations made under partial invariance situations.

For comparison purposes, an unconditional model and a conditional model including age as a predictor were estimated in which composite scores at each measurement occasion were used to evaluate possible differences from the D-COFM illustrations. The fit of the unconditional models were adequate, although they did not demonstrate better fit than their D-COFM counterparts⁶. The composite models yielded similar patterns of results as their D-COFM counterparts; however, they cannot be used to investigate the patterns and degree of measurement non-invariance. Consequently, some of the potentially important theoretical differences among dyad member groups across time would be unnoticed. Invariance tests are restricted with the use of composite variables and assume, at the very least, that measurement invariance is satisfied. In addition, composites assume perfect reliability among the manifest variables used to create the composite which is difficult to achieve in applied settings. Lastly, the use of composite scores without a correction for measurement error can bias the growth trajectory’s parameter estimates (Fan, 2003).

As with all applications of statistical techniques, the appropriate assumptions should be examined and satisfied. For instance, attrition occurred in the Add Health study, rendering missing CES-D data for the D-COFM illustrations. Data were assumed missing at random (MAR), however, the validity of this assumption is unclear. Assuming that data are MAR when missing data patterns are in fact not random can compromise the validity of the results. Thus, researchers are encouraged to discern whether missing data are due to some phenomena related to the research question under investigation to better ensure the soundness of the findings from the data. It is again emphasized that the dataset and models investigated in the current study were used solely to demonstrate the D-COFM and not for the reader to make broader substantive generalizations based on the specifics of the analyses conducted.

Upon graphical observation of the data, it was determined that the growth rates tended to be linear. Also, a model fit comparison between a linear model and one with an unspecified functional form supported the fit of the linear model⁷ which was then assumed in all ensuing D-COFM model illustrations. It is important that researchers examine the growth trajectories individually as well as aggregately in order to appropriately model growth and render more valid conclusions. If data do demonstrate a non-linear pattern, it could be modeled in various ways as previously highlighted.

The intervals between each of the four measurement waves were unequal and were modeled as such using the slope factor loading values. Treatment of measurement occasions as fixed versus varying does have some implications. For instance, the age of the siblings varied at all measurement occasions. Age at the first measurement occasion was included as a predictor in the conditional D-COFM, however, various centering strategies may be implemented to accommodate this age heterogeneity as well as other types of heterogeneity found in the timing of measurement waves (see, e.g., Blozis & Cho, 2008 and Mehta & West, 2000).

It is important to note again that the constraints illustrated and discussed are appropriate for longitudinal, non-exchangeable dyadic data. When working with longitudinal, exchangeable dyadic data, however, additional invariance constraints are necessary and model fit along with comparisons are not as straightforward. Briefly, because the members of a dyad are exchangeable, meaning that they are unable to be differentiated with respect to a particular characteristic (e.g., gender), researchers randomly assign members of a dyad to either dyad member group, m. Additional parameterizations include covariances among the corresponding item residuals across dyad member groups (intraclass covariances) which may then be constrained to be equal across measurement occasions. Finally, model fit and comparisons may be conducted using adjusted fit indices due to the random assignment to exchangeable dyad member groups (see Kenny et al., 2006 and Olsen & Kenny, 2006 for more information). Future research should examine the impact of various parameterizations and invariance constraints on the interpretation of parameters of interest for exchangeable dyads.

In conclusion, the D-COFM extends the COFM which was recommended as an extension of the univariate LGM in order to overcome problems inherent when modeling composite scores across measurement occasions without meeting the necessary assumptions. The D-COFM will not only allow longitudinal invariance testing, but will allow dyadic member group invariance testing while appropriately modeling the dependence among non-exchangeable dyads. Researchers may be able to model linear or nonlinear growth across time as well as examine the standing of individuals on the latent construct at other stages of developmental interest. The influence of predictors, observed and/or latent, at the individual- and/or dyad-level may also be investigated. In addition, researchers can assess differences in the mean intercept and mean slope values (as well as additional parameters) across non-exchangeable dyad groups. In conclusion, it is hoped that the illustrations of the D-COFM provided in this paper will help applied researchers when analyzing dyadic longitudinal data.

Appendix A

The D-COFM Parameterization in the Second-Order Factor Covariance Matrix (Φ)

The parameterization in the D-COFM, as demonstrated in Figure 3, looks like the following in the covariance matrix for the second-order intercept and slope factors:

$$\mathbf{\Phi }=\left[\begin{array}{cccc}{\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{1})}}^2& {\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{1})}{\zeta }_{{\beta }_i}^{(\mathit{1})}}& {\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{1})}{\zeta }_{{\alpha }_i}^{(\mathit{2})}}& {\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{1})}{\zeta }_{{\beta }_i}^{(\mathit{2})}}\\ {\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{1})}{\zeta }_{{\alpha }_i}^{(\mathit{1})}}& {\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{1})}}^2& {\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{1})}{\zeta }_{{\alpha }_i}^{(\mathit{2})}}& {\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{1})}{\zeta }_{{\beta }_i}^{(\mathit{2})}}\\ {\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{2})}{\zeta }_{{\alpha }_i}^{(\mathit{1})}}& {\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{2})}{\zeta }_{{\beta }_i}^{(\mathit{1})}}& {\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{2})}}^2& {\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{2})}{\zeta }_{{\beta }_i}^{(\mathit{2})}}\\ {\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{2})}{\zeta }_{{\alpha }_i}^{(\mathit{1})}}& {\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{2})}{\zeta }_{{\beta }_i}^{(\mathit{1})}}& {\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{2})}{\zeta }_{{\alpha }_i}^{(\mathit{2})}}& {\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{2})}}^2\end{array}\right],$$

where ${\sigma }_{{\zeta }_{{\alpha }_i}^{(m)}}^2$ and ${\sigma }_{{\zeta }_{{\beta }_i}^{(m)}}^2$ are the variances of the intercept and slope factor disturbances, respectively, for each dyad member group (m = 1 or m = 2); ${\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{1})}{\zeta }_{{\alpha }_i}^{(\mathit{1})}}$ and ${\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{2})}{\zeta }_{{\alpha }_i}^{(\mathit{2})}}$ are the covariances between the intercept and slope factor disturbances within each dyad member group; ${\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{2})}{\zeta }_{{\alpha }_i}^{(\mathit{1})}}$ and ${\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{2})}{\zeta }_{{\beta }_i}^{(\mathit{1})}}$ are the covariances between the intercept and slope factors’ disturbances across each dyad member group, respectively; ${\sigma }_{{\zeta }_{{\beta }_i}^{(\mathit{2})}{\zeta }_{{\alpha }_i}^{(\mathit{1})}}$ is the covariance between the intercept factor disturbance in dyad member group one and the slope factor disturbance in dyad member group two; and ${\sigma }_{{\zeta }_{{\alpha }_i}^{(\mathit{2})}{\zeta }_{{\beta }_i}^{(\mathit{1})}}$ is the covariance between the intercept factor disturbance in dyad member group two and the slope factor disturbance in dyad member group one.

Appendix B

Mplus Code for the PRIM

TITLE: D-COFM with Full Factor Loading, Partial Item Intercept, and Partial Residual Variance Invariance
DATA:	File is C:\Documents and Settings\Dyadic SEM\Dyad.txt;
VARIABLE:	Names are Pairid	Aid1 B1I1-B1I9 B2I1-B2I9 B3I1-B3I9 B4I1-B4I9
		Aid2 S1I1-S1I9 S2I1-S2I9 S3I1-S3I9 S4I1-S4I9;
	Usevariables are	B1I1 B1I3 B1I5 B1I6 B2I1 B2I3 B2I5 B2I6 B3I1 B3I3 B3I5 B3I6 B4I1 B4I3 B4I5 B4I6
		S1I1 S1I3 S1I5 S1I6 S2I1 S2I3 S2I5 S2I6 S3I1 S3I3 S3I5 S3I6 S4I1 S4I3 S4I5 S4I6;
	Missing are (999);
ANALYSIS:	Estimator = MLR;
MODEL:	!!First-order Factors (B1-B4) for the Brothers with Factor Loading Constraints !!Across Time and with Corresponding Loadings for Sisters
	B1 by B1I1*(1)    B1I3@1    B1I5 (2)    B1I6 (3);
	B2 by B2I1*(1)    B2I3@1    B2I5 (2)    B2I6 (3);
	B3 by B3I1*(1)    B3I3@1    B3I5 (2)    B3I6 (3);
	B4 by B4I1*(1)    B4I3@1    B4I5 (2)    B4I6 (3);
	!!First-order Factors (S1-S4) for the Sisters with Factor Loading Constraints !!Across Time and with Corresponding Loadings for Brothers
	S1 by S1I1*(1)    S1I3@1    S1I5 (2)    S1I6 (3);
	S2 by S2I1*(1)    S2I3@1    S2I5 (2)    S2I6 (3);
	S3 by S3I1*(1)    S3I3@1    S3I5 (2)    S3I6 (3);
	S4 by S4I1*(1)    S4I3@1    S4I5 (2)    S4I6 (3);
	!!Intercept and Slope Factors for Brothers (I1 and S1, respectively) I1 S1 ∣ B1@0 B2@1 B3@7 B4@13;
	!!Intercept and Slope Factors for Sisters (I2 and S2, respectively) I2 S2 ∣ S1@0 S2@1 S3@7 S4@13;
!!Have to Constrain Intercept for Reference Indicator to Zero for Model Identification !!For both Brothers and Sisters [B1I3@0 B2I3@0 B3I3@0 B4I3@0]; [S1I3@0 S2I3@0 S3I3@0 S4I3@0];
!!Item Intercept Constraints Across Time and Dyad Members [B3I1 B4I1] (4); [B2I5 B4I5] (5); [B1I6 B2I6 B3I6 B4I6] (6);
[S1I1 S2I1 S3I1 S4I1] (4); [S1I5 S2I5 S4I5] (5); [S2I6 S3I6 S4I6] (6);
!!Non-invariant Item Intercepts Freely Estimated [S1I6 S3I5 B2I1 B3I5 B1I1 B1I5];
!!Estimate Intercept and Slope Factor Means for Brothers and Sisters [I1* I2*];  !!Later Constrained to be Equal to Test for Significant Difference [S1* S2*];  !!Later Constrained to be Equal to Test for Significant Difference
!!Estimate Intercept and Slope Factor Variances I1* I2*;  !!Later Constrained to be Equal to Test for Significant Difference S1* S2*;  !!Later Constrained to be Equal to Test for Significant Difference
!!Covariances Between Intercept and Slope Factor Disturbances !!for Brothers and for Sisters !!Later Constrained to be Equal to Test for Significant Difference I1 with S1; I2 with S2;
!!Covariances Between Dyad Intercept and Between Dyad Slope Factor Disturbances I1 with I2; S1 with S2;
!!Covariances Between Intercept and Slope Factor Disturbances Across Dyad Members I1 with S2; I2 with S1;
!!Covariances Among Same Item Residuals Across Time Within Dyad Member Group B1I1 with B2I1 B3I1 B4I1; B2I1 with B3I1 B4I1; B3I1 with B4I1;
B1I3 with B2I3 B3I3 B4I3; B2I3 with B3I3 B4I3; B3I3 with B4I3;
B1I5 with B2I5 B3I5 B4I5; B2I5 with B3I5 B4I5; B3I5 with B4I5;
B1I6 with B2I6 B3I6 B4I6; B2I6 with B3I6 B4I6; B3I6 with B4I6;
S1I1 with S2I1 S3I1 S4I1; S2I1 with S3I1 S4I1; S3I1 with S4I1;
S1I3 with S2I3 S3I3 S4I3; S2I3 with S3I3 S4I3; S3I3 with S4I3;
S1I5 with S2I5 S3I5 S4I5; S2I5 with S3I5 S4I5; S3I5 with S4I5;
S1I6 with S2I6 S3I6 S4I6; S2I6 with S3I6 S4I6; S3I6 with S4I6;
!!Item Residual Variance Constraints Across Time and Dyad Members B1I1 B2I1 B3I1 B4I1 (7); S1I1   S3I1 S4I1 (7);
B2I3 B3I3 B4I3 (8);      S3I3 S4I3 (8);
B1I5 B2I5 B3I5 B4I5 (9); S1I5 S2I5   S4I5 (9);
B1I6 B2I6 B3I6 B4I6 (10); S1I6 S2I6 S3I6 S4I6 (10);
!!Non-invariant Item Residual Variances Freely Estimated S2I1 S2I3 B1I3 S1I3 S3I5;