Annotating Large Genomes With Exact Word Matches

Abstract

We have developed a tool for rapidly determining the number of exact matches of any word within large, internally repetitive genomes or sets of genomes. Thus we can readily annotate any sequence, including the entire human genome, with the counts of its constituent words. We create a Burrows-Wheeler transform of the genome, which together with auxiliary data structures facilitating counting, can reside in about one gigabyte of RAM. Our original interest was motivated by oligonucleotide probe design, and we describe a general protocol for defining unique hybridization probes. But our method also has applications for the analysis of genome structure and assembly. We demonstrate the identification of chromosome-specific repeats, and outline a general procedure for finding undiscovered repeats. We also illustrate the changing contents of the human genome assemblies by comparing the annotations built from different genome freezes.

Any genome can be conceptualized as a string of letters. Every word composed of those letters has a certain number of exact matches within the genome, its word count. Knowledge of word count is useful for probe design, discovery of repeat elements, genome annotation, and mathematical modeling of genome evolution. The tools available for sequence homology analysis, such as BLAST and FASTA (Pearson and Lipman 1988; Altschul et al. 1990) were not designed for this purpose, and are unnecessarily cumbersome. We therefore sought a new tool for finding the word counts for words of arbitrary length in any given genome.

Our interest in this problem has its origins in microarray hybridization analysis. We have developed methods using oligonucleotide probes for detecting gene copy number changes in mutant and normal genomes (Lucito et al. 2003). We require our probes to be highly unique in the genome. Our approach, like that others have taken, is to count the exact matches of probe substrings, or words, to the rest of the genome (Li and Stormo 2001). When such words have lengths below 16, this task can be accomplished using a simple tabulation of words and their counts. When the word length exceeds 15, such directly addressable structures become impractical. More robust data structures, such as the suffix array and suffix tree, could easily provide us with optimal or nearly optimal theoretical time bounds for word count determinations. However, in practice, these too proved to be impractical solutions for the case of the human genome for reasons that we will detail. We solved this problem by applying and building upon a Burrows-Wheeler transform of the entire human genome sequence.

The tool we created is capable of rapidly annotating any sequence, even the entire genome, with the counts of its constituent words. We quickly realized that this method has other applications beyond probe design. In this article we describe our algorithm, provide some implementation details, and then discuss the relationships between our implementation and preexisting tools and data structures. Lastly, we illustrate some applications to the analysis of genome structure and assembly.

METHODS

Fundamentals

To determine word counts rapidly, we sought to minimize the number of computations per word and to eliminate time-consuming disk access operations. We achieve this by creating a data structure that we can efficiently query and that can also reside entirely in random access memory (RAM). Our solution depends upon the Burrows-Wheeler transform, a method used to create a reversible permutation of a string of text that tends to be more compressible than the original text (Burrows and Wheeler 1994). It is also strongly related to the suffix array data structure (Manber and Myers 1993) in ways that will be made apparent.

First, given a genome G of length K, we create a new string G$ of length K+1 by appending a “$” to the end of that genome. (We assume a single strand, reading left to right.) We then generate all K+1 “suffixes” of G$, where the suffixes are the substrings that start at every position and proceed to the end. We next associate with each suffix the letter preceding it. In the case of the suffix that starts at the first position, we associate the new $ character and assume that “$” has the lowest lexicographical value in the genome alphabet. The string of antecedent letters, in the lexicographical order of their suffixes, is the Burrows-Wheeler transform of the G$ string, which we refer to as the “B-W string” or the “BWT”.

For example, if the genome were simply “CAT”, our G$ string would be “CAT$”. Then the suffixes of the genome in sorted order would be: “$”, “AT$”, “CAT$”, and “T$”. The Burrows-Wheeler transform of this particular G$ would be the letters that “precede” each of those suffixes taken in the same order, specifically “TC$A”. In practice, the sort operation is performed on the integer offsets, or pointers, into the original string based on the suffix that starts at that position. To continue the example, the list of pointers taken in the order of the sorted suffixes would be [3,1,0,2]. This list of pointers is in fact the suffix array for the string “CAT$”.

We could use the suffix array to compute word counts using a binary search (Manber and Myers 1993). However, the suffix array for the human genome, at approximately 12 gigabytes (3 billion, 4-byte integers), is too large to fit in RAM for any of our machines. We would also need access to the entire genome in order to perform such a binary search, adding another 3 gigabytes uncompressed. On the other hand, the B-W string is alone sufficient to determine word counts. Recall that it is no larger than the original genome and, like any other string of characters, it can be compressed using any of a variety of text compression techniques. Furthermore, in our implementation, all but a negligibly small portion of the compressed form can remain so throughout execution. Together with auxiliary data structures that enable the B-W string to be rapidly queried, the entire structure for the human genome can be compressed into a little over 1 gigabyte of RAM.

The Basic Algorithm

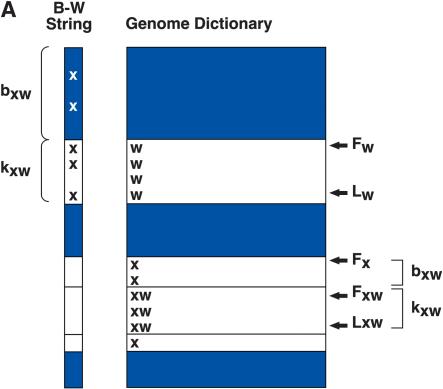
Heuristically, the B-W string can be viewed as a navigational tool for a “virtual” Genome Dictionary, an alphabetical listing of all the suffixes of the human genome. Suppose we wish to know whether a substring occurs in the genome, and if so, in how many copies. Let us first consider the case where the substring is a single character, X. We can view all the occurrences of X in the Genome Dictionary as a block where F_X and L_X are the indices of its first and last occurrence, respectively. The size of this block, k_X = L_X − F_X + 1, is the number of occurrences of X, and is readily determined by counting the number of occurrences of X from the beginning to the end of the B-W string.

In order to consider the case for longer words, we first need to determine F_X, L_X, and k_X for each character X of the genome alphabet. The sizes of each block, the k_X's, are easily determined by counting the instances of X in the B-W string. F_X is one plus the sum of the sizes of all antecedent blocks beginning with V, where V is any character occurring lexicographically before X. L_X is one less than the sum of k_X and F_X. We store the F_X and L_X for each letter X in an auxiliary data structure called “alphabounds”.

We can now proceed inductively to find the count for a word Z. Suppose W is a suffix of Z, W exists in the genome, and we know the indices F_W and L_W of its block in the Genome Dictionary (Fig. 1A). To continue the induction we need to know whether XW exists as a substring, where X is the character preceding W in Z, and we need to know the indices of the XW block, F_XW and L_XW, in the Genome Dictionary.

Figure 1.

Our algorithm for rapidly determining the exact word counts in a large string for any length word. (A) Graphically defines the variables and data structures used in the algorithm. (B) A pseudocode representation of the algorithm itself.

If and only if X occurs in the B-W string between F_W and L_W, then XW exists as a substring of the genome (Fig. 1A). Furthermore, the number of X's in the “W block” of the B-W string, k_XW, is the copy number of the substring XW in the genome. Finally, the indices of XW are easily computed, namely:

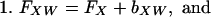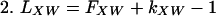where b_XW is the number of words beginning with X in the Genome Dictionary that occur before XW. Recall that F_X has been determined for each character X of the alphabet. b_XW can be determined by counting the number of X's that occur before the W block of the B-W string (Fig. 1A).

We reiterate this procedure, lengthening the suffix one character at a time, stopping if the suffix does not exist in the Genome Dictionary. If the suffix W encompasses the entire word Z, k_W is the number of occurrences of Z in the genomic string. An outline of this procedure in pseudocode is displayed in Figure 1B.

The basic algorithm transforms a pattern matching problem into a counting problem. Counting thus becomes the rate-limiting step, and therefore we facilitate it in ways described below.

Preprocessing and Database Construction

To count exact matches of words our method requires only the B-W string, but to build the string we still need to create a suffix array for the genome. Although the suffix array is not needed to determine word frequency, and is much too large to be held in RAM, it should be retained on disk, because it can also be used to find the coordinates of matches.

Building a suffix array can be reduced to a “sort in-place” operation. For a string of the size of the genome, we implemented a parallel radix sort using a 16-node cluster. The genome was divided into 100 equal-size substrings, each overlapping by seven nucleotides. The offsets into the genome (i.e., the “genome” coordinate) within each substring were then assigned to one of 5⁷ “prefix” bins according to the 7-mer at each offset. (The genome alphabet was A, C, G, T, and N.) The offsets within each prefix bin were then sorted based on the sequence following the 7-mer prefix, creating the suffix array.

For the human genome, we made a special case for N's. The human sequence contains about 6^*10⁸ N's, mainly in large blocks ranging from 200 kb to 30 Mb in length. The presence of these long blocks increased sort time by a factor of 10, so we decided not to sort coordinates with 7-mer prefixes containing N's. As long as the constituencies of blocks bounded by prefixes containing N's are correct, their internal order is irrelevant for determining counts of N-free words. Thus, all queries with sequences containing no N's are still valid. We refer to this variant as the “N-incomplete” Burrows-Wheeler transform.

The first character preceding each offset, taken in the order of the sorted offsets, constitutes the B-W string. The B-W string is still three gigabytes, too large for our workstations. To compress the string further, we used a simple dictionary-based compression scheme, where one of 125 distinct single byte codes represents one of each of the 5³ possible three-letter substrings. We chose this compression scheme, even though greater compression can be achieved, because it has a constant compression ratio, 3:1, and allows us to count characters, for the most part, without decompressing.

In the pseudocode for our counting algorithm, all steps are rapid “look-ups” or simple computations except for steps 7 and 9 (Fig. 1B). These steps involve counting the B-W string over potentially large blocks of characters. In order to speed counting, we created an auxiliary data structure, the “K-interval counts”, where K is an integer multiple of the compression ratio, by precounting on the B-W string. We determine the cumulative counts for each character and record them for every K^th position. To carry out counting steps, therefore, we need only count the particular character in the string from the relevant position to the nearest position that is a multiple of K. The number of characters that needs to be counted in any step is thus no more than K/2. In our implementation we set K equal to 300 characters, or, equivalently, 100 compressed bytes.

We have also experimented with the notion of subintervals of size K^ within each interval K. At every K^^th position within each K-interval, we record how many instances of each character we have seen since the beginning of the encompassing interval. If we limit the size of K to be <2⁸, for example, then the counts for each letter at every K-interval can be recorded using a single byte. This allows us to increase the “density” of the counting index by a factor of K/K^ while increasing the space requirements for the K-interval counts by a factor of only [(K/K^)/4]. We have implemented a variant of our data structure that utilizes this hierarchical indexing scheme. Depending on the choices of K and K^, we have seen a three- to fivefold increase in query execution speed while maintaining a memory requirement of less than two gigabytes for the human genome. Full details of this variant are provided at our Web site (http://mer-engine.cshl.edu).

To further speed the counting process we introduce a final data structure, the “dictionary-counts”. Recall our simple 3:1 compression scheme, where bytes 0 through 124 decompress to “AAA” through “TTT” respectively. The dictionary-counts structure is a small two-dimensional array that can be thought of as a matrix with 125 rows and five columns. Each row corresponds to one of the compression dictionary entries, and each column corresponds to each letter of the genome alphabet, A through T. Let us assume, for instance, that we are in the process of determining the number of A's in step 9 of Figure 1B. Using the K-interval counts structure described above, we can “jump” to within at most 50 bytes of our current F_w in a single look-up. Let us also assume that this F_w is pointing to the third “T” in a compressed “ATT” which is in turn at the 49th byte of the interval. For each of the 48 preceding bytes, we simply use the byte as the row number in our dictionary-counts array and the letter of interest, “A”, as our column “number”. At those coordinates we will find the number of times that the letter “A” appears in that compressed byte. Therefore we must perform 48 look-ups in this small directly addressable table. Finally, we must decompress the 49th byte with another simple table look-up, and examine the first two letters “AT”. The dictionary-counts may seem like a minor component. However, when it is combined with the K-interval counts structure, the act of counting any number of characters requires only K/6 +1 table look-ups, plus two character comparisons in the worst case. In actuality this structure requires approximately 65 kilobytes of memory. It is also the data structure used for the majority of all computations in any single iteration of our algorithm.

We refer to the joint data structures and search protocols as the “mer search engine” or simply the “mer-engine”.

Validation for the Human Genome

The most rigorous way to validate all the data structures and protocols we have just described is to perform a reverse transform. Starting with the position in the B-W string corresponding to the last character of a genome, and using the protocols and data structures just described, one should be able to reconstruct that genome sequence. However, the N-incomplete transform of the human genome is not a proper Burrows-Wheeler transform string, and hence the full genomic string cannot be reconstructed from it.

Therefore to validate our human mer search engine, we picked at random a million words of varying lengths, from three to 1000 characters. We determined the word count and coordinates of each by scanning the genome text. We compared the word counts with those returned by the “mer search engine”, and in each instance there was complete concordance. We also referred to the suffix array to obtain coordinates, and they agreed perfectly as well.

Performance for Genomes

The time complexity of a query for a particular word is linearly proportionate to the length of the word and to the size of K for the K-interval counts. We have tested our implementation on a Dell PowerEdge 1650 with dual 1GHz Pentium III processors and 4GB of physical memory running Linux. Importing a human chromosome from disk, annotating with counts of all overlapping words of length 24 (for both sense and antisense), and writing the results to disk takes an average of 1 min per megabase. This hardware configuration is now over 2 yrs old, and we expect significantly faster execution times on machines purchased today. Furthermore, we expect that our “dictionary-counts” data structure, requiring a mere 65 kilobytes, will take advantage of the so-called Level 1 cache of present day CPU architectures. These statistics do not take into account the addition of the subintervals of size k. We have experienced reductions in time requirements of up to fivefold through this simple modification. The disadvantage of this variant is the additional space requirement of roughly 750 MB.

The time required for the preprocessing stage is dominated by the construction of the suffix array. This operation requires a sort of all of the cyclical permutations of the genome. Therefore the time complexity of the preprocessing stage in its entirety reduces to O(n lg n) where n is the size of the genome. For this process we make use of every node in our cluster, with a total execution time of approximately 6 h for a single assembly of the human genome.

Although there are a variety of ways for enhancing performance, the operating times both for preprocessing and annotation are reasonable with our current implementation.

Relation to Existing Tools

In the context of genome research, we are inclined to view our algorithm as a companion to methods or tools built around approximate homology searching such as BLAST and BLAT. In general we found that in pursuits such as repeat discovery and in particular probe design, our method reduces greater than 98% of the work to a simple and rapid “scan” operation; namely that of word-count annotation. The final analysis is then performed using a low-stringency approximate homology search on a vastly reduced set of “candidate” entities. In our probe design protocol described below, greater than 99% of our candidates already satisfied our full requirements prior to this final analysis. In this same sense, and rather appropriately, both of the approximate homology-based tools mentioned here use exact matches as their first-pass criteria before performing a more rigorous sequence alignment. It is feasible that our data structure could act as an alternative exact-matching “core” for variants of these tools.

We find that approximate homology tools alone are insufficient and impractical in such pursuits when performed at the whole-genome or multiple-genome scales. BLAST in particular, we find, tends to greatly multiply the amount of data that must be processed. For instance, when attempting to design unique probes within a large subset of the repeat-rich human genome, many of the candidate regions will have homology among themselves as well as within the entire genome. The resulting output contains the cross-products of these homologies. Furthermore, the best local alignments are reported, not all alignments. The output is therefore inadequate as an estimate of possible cross-hybridization in microarray experiments. BLAT, on the other hand, sacrifices completeness for speed; it cannot find matches for sequences that have a number of occurrences above a predetermined cutoff. Neither of these tools can readily yield a statistic that can be used as a measure of predicted cross-hybridization, such as an aggregate of counts for all constituent 15-mers.

REPuter (Kurtz and Schleiermacher 1999) is an existing program which can be used for repeat analysis and discovery as well as finding areas of uniqueness. It relies on exact pattern matching algorithms used for the traversal of its underlying data structure, which is a suffix tree. This program is a complete software solution for genome research in that it enables one to perform exhaustive repeat analysis, detection of unique substrings, and approximate alignments with statistics, all within a graphical user environment (Kurtz et al. 2001). Its usefulness in the context of the entire human genome and beyond, however, is limited due to tremendous memory requirements necessitated by the reliance on a suffix tree. We provide further detail of this issue in the following section.

Relation to Existing Data Structures

Our data structure could be described as a compressed index into a suffix array. The query process is essentially an attempt at a partial reverse Burrows-Wheeler transform of the query word within the context of the genome. A necessary component of this query process is a set of pointers into the suffix array, namely F_w and L_w, which is carried through each iteration. In this way, the algorithm is an alternative to performing a binary search using the entire suffix array along with the entire genome. It is this freedom from the need to refer to coordinates of suffixes during search that allows us to achieve our tremendous space reduction. If there is further interest in retrieving the coordinates of every exact match, then the suffix array can be accessed as it normally would be; either from disk or active memory depending on available resources. It is worth noting, however, that there is a simple extension to our query algorithm that enables the retrieval of coordinates for all matches using only a small subset of the entire suffix array. Because our primary interest lies in the word count determinations alone, we refer the interested reader to our Web site for a full description of this extension (http://merengine.cshl.edu). In all comparisons made in this section, we assume this exclusive interest in word count queries within genomes.

A binary search through a suffix array can determine the count c of a word of length p within a genome of length n in O(p lg n) time while requiring O(n lg n) + O(n) bits of storage (Manber and Myers 1993). In practice, the suffix array for the human genome of length n > 2³¹ requires a total of 5n bytes of storage; 4n bytes are required for the suffix array itself plus n bytes for the original string, all of which must be referenced throughout a search. If the hardware in use does not have sufficient RAM, then the search procedure is dominated by disk I/O operations. Disk retrievals are slower than active memory retrievals by many orders of magnitude. Our algorithm can perform a similar word count query in O(pK) time requiring O[(n/K) lg n] + O(n) bits of storage. In practice, our data structures for the human genome require (n/3 + {20 [n/(K/3)]}) bytes of storage where K is the size of the intervals in our K-interval counts structure. Herein lies the versatility of the mer-engine: K can be increased or decreased depending upon the requirements and available resources. If RAM is scarce then K can be increased by Q, resulting in a linear decrease in space requirements and similar increase in execution times, both proportional to Q.

Another data structure that is commonly used for exact pattern matching is the suffix tree. We refer the reader to Gusfield (1997) for a detailed description of suffix trees and the many possible variations on their construction and use in problems of exact and approximate pattern matching. A suffix tree requires O(n lg n) + O(n) bits of storage and O(p) time to perform a word count for any word of length p which occurs c times within a genome of length n. Unfortunately these expressions, particularly the space requirement, do not translate directly to expected performance in modern computer architectures. Recall that the program REPuter uses a suffix tree as its underlying data structure (Kurtz and Schleiermacher 1999). The authors of that program present a method for reducing the space requirements of a suffix tree (Kurtz 1999), which is used by the REPuter program (Kurtz et al. 2001). However, REPuter is said to still require 12.5n bytes of storage for a suffix tree of a genome of length n (Kurtz and Schleiermacher 1999). This requirement is several times larger than the complete memory requirements of a suffix array. It is likely to be prohibitively large for all but the most expensive hardware platforms when applied to the entire human genome.

An “opportunistic data structure” based on the Burrows-Wheeler transform has been described (Ferragina and Manzini 2000) and is referred to as the “FM-Index”. The core search algorithm for the FM-Index is nearly identical to the one described in our pseudocode and is used to perform word count queries. Through a very clever compression and indexing scheme, the FM-Index achieves space requirement bounds of O[(n / lg n) lg lg n] bits of storage while being capable of performing word count queries in O(p) time for any word of length p within a genome of length n. This is true given the authors' assumption that their variable for the “bucket size” is assigned the value of lg n. We'll refer to this parameter hereafter as b. This variable plays a role similar to that of our variable K in that it subdivides the transform string for better index performance. Note that for K > (lg ²n / lg lg n) our implementation requires less space. If one increases the value for b beyond lg n, particularly in the case where n ≥ 2³², they run the risk of dramatically increasing the space requirements for the FM-Index. More specifically, the structure referred to by the authors as “S” has space requirements bounded by the term b2^{b^}, where b^ is the maximum size of any one of the (n / b) compressed buckets and has an upper bound of c lg n where c < 1. This means that the actual space requirements are dependent upon local properties of the transform string. Our space requirements are dependent only upon K and n (the alphabet size for genomes is negligibly small; however, it is a factor in practical space requirements for both the mer-engine and the FM-Index). If one decides to reduce b to avoid this risk, then our space requirement advantage increases.

The O(p) time complexity for the FM-Index derives from the fact that within any iteration of the search procedure, where one iteration is performed for each of the p characters of the query word, counting is accomplished via look-ups within at least seven directly addressable data structures. Each of these look-ups requires constant theoretical time, so their combined time requirement reduces to O(1). Recall the mer-engine variant in which subintervals of size K^, where K^ < K and K < 2⁸ are introduced. Assume, for example, we choose values of K = 240 and K^ = 15. Then this mer-engine variant would require four table look-ups plus two character comparisons for each iteration of the search algorithm in the worst case. We believe this practical worst-case very nearly approximates a theoretical time complexity of O(p) and has space requirements of roughly 60% of the original genome size n, including the compressed transform string, regardless of n. Furthermore, the last four steps of each iteration are isolated to accessing a structure that requires only 65 kilobytes of memory, again, regardless of n.

We could not locate any performance data for the implementation of the FM-Index referenced above. However, word count query performance for the Escherichia coli genome FM-Index has been analyzed for an implementation variant (Ferragina and Manzini 2001). The mer-engine for the human genome performs word count queries for words between eight and 15 nucleotides in length ∼150 times faster than the E. coli implementation described therein. This does not take into account the speed-up that we observe with the introduction of subintervals to our K-interval counts structure. We believe this discrepancy may be accounted for by any combination of the following: difference in CPU clock speed, the fact that not all “buckets” remain in active memory for the duration of the test, and the requirement, in this particular variant, of complete decompression of buckets prior to the final counting stage. The authors Ferragina and Manzini (2001) do not mention any specific application of the FM-Index to genome research.

Alternative algorithms and data structures based on the Burrows-Wheeler transform have been defined (Miller 1996; Sadakane 1999). One algorithm relies heavily upon an additional “transformation matrix” which maps a character's position in the sorted list of all characters to its new position in the transform string (Miller 1996). The challenge with this strategy is finding a succinct way to store this transformation matrix, which starts out at exactly the same size as the suffix array for the same string. The other algorithm is simply a compressed form of a suffix array, which is entirely decompressed before performing a search (Sadakane 1999).

Availability

Our code for executing the Burrows-Wheeler transform is highly platform-dependent. That is to say, it was optimized for our particular cluster configuration and will likely require revision for general use. However, this code will be made available upon request, and all the information required for building the BWT is provided in the text above. To accommodate readers who wish to perform mer analyses without having to perform the Burrows-Wheeler transform, several preprocessed mer-engines are available. We have placed the BWT of the genomic strings for S. pombe, C. elegans, and Fugu rubripes, as well as the N-incomplete BWT of the June 2002 assembly of the genomic string for human chromosome 1 and the entire genome, and their auxiliary data structures, on our public Web site (http://mer-engine.cshl.edu) for downloading. Additionally, we have supplied C++ code that enables mer frequency queries from any of these strings residing either on disk or in RAM, and have provided the Perl code for visualizing the resulting C++ output (Fig. 2).

Figure 2.

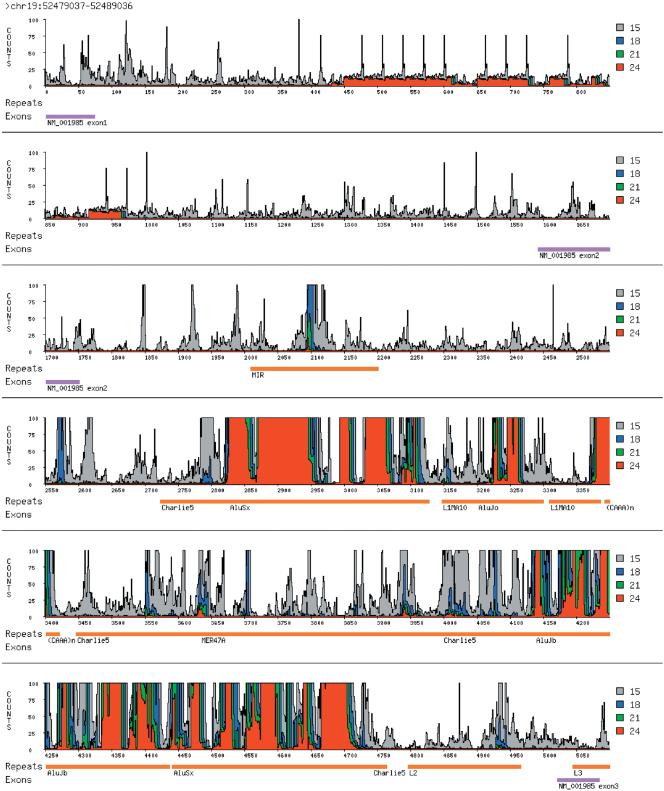
Word count terrain from a 5-kb region on chromosome 19. The coordinates of this region in the June 2002 assembly of the human genome are at the top. Along the x-axis is the relative position of a given word within the region; along the y-axis is the absolute word count, with counts for different lengths drawn in different colors, according to the legend. Word counts are capped at 100. Underneath the terrain, repeats detected by RepeatMasker are annotated in orange. Exons from the RefSeq data set are indicated in purple. In this case, the word counts are derived from the June 2002 assembly of the entire human genome.

RESULTS AND DISCUSSION

Annotating Sequences With Word Counts

Using the above tools, any region of the genome can be readily annotated with its constituent mer frequencies. We have depicted annotations of a 5-kb region of chromosome 19 as a histogram in Figure 2, using four mer lengths, 15, 18, 21, and 24 bases. We call such annotations “terrains”. For each coordinate and each word length, we determined the count of the succeeding word of the given length, in both the sense and antisense directions. We then plotted these counts on the y-axis, with each pixel on the x-axis corresponding to a coordinate. The heights of counts exceeding 100 are truncated, and each word length is color-coded (see Fig. 2 legend).

This region was picked somewhat arbitrarily, but it illustrates some major themes. We have taken repeat and exon annotations of this region from the human genome browser at UCSC (Karolchik et al. 2003) and aligned them to our terrain. There is significant discordance between annotated repeats and high terrain. We note that several regions annotated as repeats by the UCSC browser in fact have very low word counts, even with 15-mers. This is not unexpected, as our method is based on exact matches, and some repeats are very ancient and highly diverged. The relatively unique regions within repeats may nevertheless be useful for probe design, and the exact count method readily finds such regions.

To us, one of the most striking features of the terrain is the presence of narrow spikes in 15-mer counts. This is a virtually universal property of all regions of the human sequence we have examined, including coding exons. To develop a better understanding of this phenomenon, we decided to examine what the word count annotation of this region would look like if the genome were instead a randomly generated sequence, but with the same size and dinucleotide frequency distribution as the human genome. The terrain is still rough, but there are very few spikes. We hypothesize that these spikes result from the accidental coincidence of 15-mers in ordinary sequence with 15-mers present in high-copy-number repeats. Such high-copy-number sequences are not as frequently found in a random genome.

Computations on Subsets of the Genome

We also encounter regions of high terrain that are not annotated as repeats by RepeatMasker (http://ftp.genome.washington.edu/RM/RepeatMasker.html). RepBase (Jurka 2001), the database of repeats used by RepeatMasker, does not include region-specific or chromosome-specific repeats. With our method, such repeats are easy to find because exact match counting can form the basis for a set algebra of the genome. In particular, we can make transform strings from subsets of the genome and examine the partition of words between these sets. Here we illustrate the use of this concept to find chromosome-specific repeats.

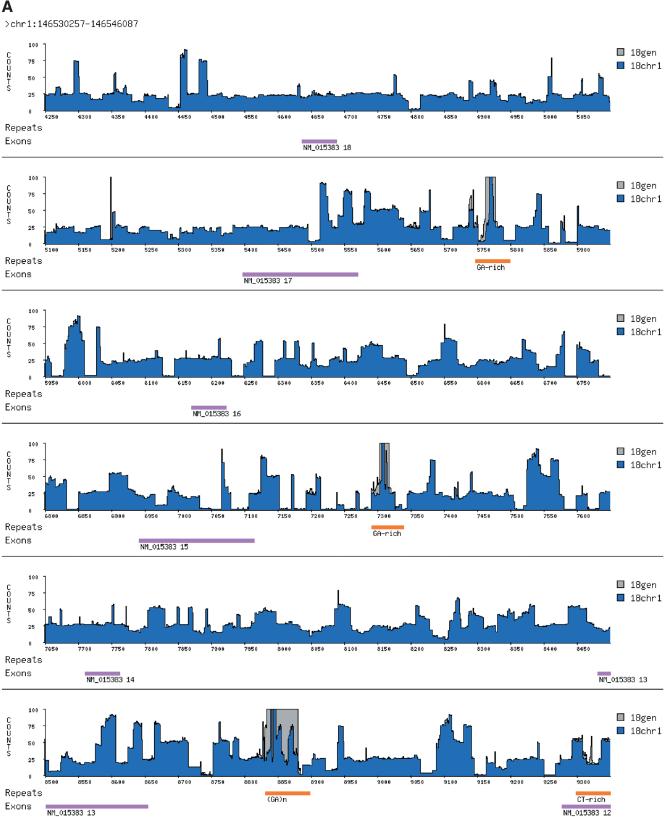
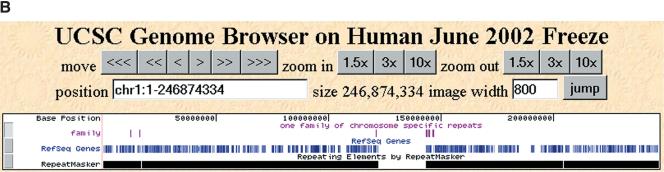
We made a transform string from chromosome 1 and annotated it with the word counts from itself and from the entire genome. We then looked for contiguous regions of chromosome 1, at least 100 bp in length, with high 18-mer counts in which the exact matches were found to derive mainly from chromosome 1. We readily found such regions, ranging in length from 100 bp to 35 kb. Focusing on one such region, we observed that its mer terrain was nearly a step function, composed of shorter sequences each with a signature modal frequency and length. We collected all of the chromosome-specific regions containing one of these signature regions and quickly identified a family of chromosome 1-specific sequences. Figure 3A illustrates the mer terrain for a portion of one of these family members; Figure 3B portrays the location of its recurrences on chromosome 1. At least one instance of this repeat has been annotated as overlapping a RefSeq gene (accession no. NM_015383), with many exons that together encode a large predicted protein sequence having low homology to myosin.

Figure 3.

A chromosome 1-specific region. (A) This region was selected in the following way: 18-mers were identified whose chromosome 1 counts were ≥90% of their whole genome counts. These 18-mers were strung together to create “chromosome-specific repeats” as long as the space between them was less than 100 bp. At the top of the figure are the coordinates of this region in the June 2002 assembly. Along the x-axis is the relative position of a given 18-mer within these coordinates. Along the y-axis is the absolute word count, with whole-genome counts drawn in gray and chromosome 1 counts in blue. Word counts are truncated at 100. Underneath the terrain, repeats detected by RepeatMasker are annotated in orange. Highlighted in purple are RefSeq exons that overlap this region from RefSeq gene NM_015383. (B) The chromosome-wide distribution of this family of chromosome-specific repeats, as viewed in the UCSC Genome Browser. The entire length of chromosome 1 is shown, with the purple “family” track indicating recurrences of this repeat. Below the family track are tracks that indicate both the positions of RefSeq genes and RepeatMasker annotations along chromosome 1.

This is the first such repeat that we have investigated in any depth, and we expect to find other examples that merit attention. The same process by which we identify chromosome-specific repeats can be applied to finding repetitive DNA throughout the genome that is not recognized by RepeatMasker or other programs. One merely creates a mer-engine from the subsets of repeat sequences recognized by any pre-existing repeat analysis software of choice, and compares annotations from the whole genome mer-engine and the known repeat mer-engine to find unknown repeats.

Probe Design

Probes are generally useful for their ability to hybridize specifically to complementary DNA, and therefore one of the primary objectives in probe design is to minimize cross-hybridization. Some investigators have used repeat masking to exclude repeat regions from consideration for probe design. As we have described above, this is not a perfect solution, in that it does not protect the investigator from all regions that are repetitive, for example, chromosome-specific repeats, and it excludes “repetitive” regions that are quite unique in actuality.

Although the rules for hybridization between imperfectly matched sequences are not well understood, it is clearly sensible to avoid probes that have exact “small” matches to multiple regions of the genome. Using a directly addressable data structure, such as a hash table, it would be a simple matter to store and retrieve counts for words as large as 14-mers. We could then attempt to minimize aggregate exact 14-mer match counts, but for genomic probes we think this method is inadequate. First, it is unclear that exact matches of 14-mers have any effect on hybridization under normally stringent annealing conditions. Nor do 14-mer counts predict homology, let alone uniqueness in the genome. We have compared 16-mer counts to the geometric mean of counts from their constituent 14-mers, and we do not see a good correlation between the two for sequences that are essentially unique (data not shown).

We propose the following general protocol for probe design. First, choose the shortest length such that when the genome is annotated with mer-counts of exact matches of that length, sufficiently long stretches of uniqueness are found. Second, choose a shorter length such that exact matches of that length represent stable hybrids under the appropriate stringency conditions. Then, from the regions judged to be unique at the first length, choose probes that minimize the aggregate mer-counts of the second length. This protocol can be executed using the mer-engine tools we described in the previous section.

We followed this protocol in the accompanying article to select 70-mer probes from small BglII fragments (Lucito et al. 2003). We required uniqueness in the space of 21-mer counts, and then within these regions selected a 70-mer with the lowest sum of 15-mer counts, with a cut-off value of about 900. We added a few additional requirements, to eliminate runs of single nucleotides and severe base composition bias. Almost all probes picked by these protocols, and synthesized and printed on glass, in fact performed well under our microarray hybridization conditions.

We used BLAST to test whether probes picked by this protocol are indeed unique in the published genome sequence. We queried 30,000 such probes against the genome using the default parameters for MegaBLAST (filtration of simple sequence was turned off). More than 99% of our probes were unique over their entire length. However, for completeness, we suggest adding a final step to the probe design protocol, whereby all remaining candidates are subjected to a low-stringency approximate homology search against the genome in a best-first order.

Monitoring Genome Assemblage

As the human genome project progresses, new assemblies, based on freezes, are periodically released. We assume that each new assembly is an improvement upon the ones that came before. Because our probes derive from the December 2001 and April 2002 assemblies, downloaded from the UCSC Genome Browser, we have remapped the probe set to subsequent assemblies using BLAST and BLAT (Kent 2002). We also annotate them with the mer-engine built from each assembly because we have greater confidence in the hybridization ratios found for probes with stable copy number and map location.

An unexpected result of this process was that 1.2% of our probes vanished from the June 2002 assembly. That is to say that for 1.2% of our probes, all of their constituent 21-mers went from copy number one in their original assembly, to copy number zero in a subsequent assembly. Yet these probes behave as expected in our microarray experiments: They have good signal and hybridize to fragments with the restriction endonuclease profile predicted from their original assembly (Lucito et al. 2003).

Our surprise at this outcome prompted us to investigate the extent of this phenomenon on a larger scale. The mer-engine is the appropriate tool for this exploration. We decided to look for all unique sequences within a single chromosome within an assembly that were lost between that assembly and a subsequent one.

In particular, we annotated all of chromosome 10 from the December 2001 assembly with genomic 18-mer counts from both the original assembly and the June 2002 assembly. We observed a large number of n-to-m transitions in 18-mer counts, where “n-to-m transitions” refers to a mer that went from n copies in the original assembly to m copies in the subsequent assembly. Although we describe the 1-to-0 transitions in this report, we note that they represent a small percentage of all transitions. We call 18-mers with 1-to-0 transitions “orphans”. We stored the coordinates of runs of at least 13 consecutive orphans. We further clustered the orphans into “dropout fragments” as long as the gaps between them were not greater than 100 base pairs, and no more than 35% of the fragment length was composed of gaps.

We performed a homology search, using BLAST, to compare the dropout fragments with the vector database to eliminate any possible vector contaminants from our set. No homology to vector sequence was found. In total we found approximately 800 dropout fragments ranging from 30 bp to 21 kb in length, with a combined length of approximately 300 kb. Table 1 provides a list of the size distribution of the fragments.

Table 1.

Size Distribution of Fragments Lost Between Assemblies of Chromosome 10

Fragment length interval (bp)	Percentage of total	Length of largest fragment in interval (bp)	Percentage of interval remapped
30-100	54	99	21
101-200	8	199	29
201-400	15.5	400	16
401-800	15.5	797	14
801-1600	5.3	1507	20
1601-3200	0.5	3008	100
3201-6400	0.6	5789	100
6401-12800	0.5	12293	100
12800+	0.1	21104	100

The fragments included in this distribution were chosen in the following way: the December 2001 assembly of Chromosome 10 was annotated with 18-mer counts within the entire December 2001 assembly as well as within the June 2002 assembly. We stored the coordinates of runs of at least 13 consecutive 18-mers whose counts transitioned from 1 to 0 between assemblies. These 18-mers were further clustered into “dropout fragments” as long as the gaps between them were not greater than 100 bp, and no more than 35% of the fragment length was composed of gaps. A homology search using BLAST was performed to compare the dropout fragments with the vector database; no homology to vector sequence was found. Approximately 800 dropout fragments were found, ranging from 30 bp to 21 kb in length with a combined length of approximately 300 kb.

At the time of this writing, we were able to perform a remapping of the fragments to the April 2003 assembly, and the percentage of fragments that returned to the assembly are provided. Although some returned, we found that new orphans were also created (data not shown). The coordinates of the dropout fragments in the original December 2001 assembly are available on our Web site.

We assume that many of the dropout fragments are indeed human sequence: They behave that way in our hybridization experiments; they have no homology to vector sequences; and some are conserved in mice. Although there may be technical reasons explaining the dropout of some of these fragments, such as difficulty in assembly or poor-quality sequence, it is also likely that, due to insertion/deletion and order-of-sequence polymorphisms in humans, no fixed linear rendition of the genome is feasible. It may initially strain credulity that a 21-kb region can be polymorphic, but such large-sized events have been documented (Robledo et al. 2002), and the data from our accompanying paper strongly suggest that much larger copy number polymorphisms are commonplace in the human gene pool (Lucito et al. 2003).