The Balance of Driving Forces During Genome Evolution in Prokaryotes

Abstract

Genomes are shaped by evolutionary processes such as gene genesis, horizontal gene transfer (HGT), and gene loss. To quantify the relative contributions of these processes, we analyze the distribution of 12,762 protein families on a phylogenetic tree, derived from entire genomes of 41 Bacteria and 10 Archaea. We show that gene loss is the most important factor in shaping genome content, being up to three times more frequent than HGT, followed by gene genesis, which may contribute up to twice as many genes as HGT. We suggest that gene gain and gene loss in prokaryotes are balanced; thus, on average, prokaryotic genome size is kept constant. Despite the importance of HGT, our results indicate that the majority of protein families have only been transmitted by vertical inheritance. To test our method, we present a study of strain-specific genes of Helicobacter pylori, and demonstrate correct predictions of gene loss and HGT for at least 81% of validated cases. This approach indicates that it is possible to trace genome content history and quantify the factors that shape contemporary prokaryotic genomes.

The principal driving forces that shape prokaryotic genomes and influence gene content are gene genesis, horizontal gene transfer (HGT), and gene loss. Gene content was first thought to be affected by gene genesis, in particular, duplication and divergence of single genes (Ohno 1970) or even entire genomes (Zipkas and Riley 1975; Wolfe and Shields 1997). The contribution of horizontal gene transfer has later been recognized as another significant factor (Eisen 2000; Ochman et al. 2000). Recently, it was shown that many pathogens evolved by reductive evolution, involving excessive gene loss (Andersson and Andersson 1999; Cole et al. 2001; Mira et al. 2001). However, the relative contributions of each of these processes has remained unknown to date.

To quantify the evolutionary processes that shape genome content, we have used an approach that takes into account the presence or absence of a gene (or gene family) on a phylogenetic tree. Consistent gene presence in a clade indicates that the corresponding gene was present in the ancestor of that clade, whereas occasional absence of a gene might result from gene loss. Finally, fragmented distribution of a gene family across very distantly related species is indicative of horizontal gene transfer (HGT) events (Ragan 2001).

The decision as to whether the observed distribution pattern of a gene is the product of HGT or multiple gene loss requires the estimation of the likelihood of these events (Ochman and Jones 2000). Recently, a similar approach for the estimation of the relative contributions of these processes has been proposed, using groups of orthologous genes across 16 genomes (Snel et al. 2002). However, difficulties arise with large numbers of genes exhibiting a sporadic distribution, especially in the prokaryotic world (Ouzounis and Kyrpides 1996; Pellegrini et al. 1999). This problem has been previously bypassed by the exploration of a larger parameter space, thus limiting the scope of conclusions (Snel et al. 2002). In this study, we derive estimates for the relative frequency of events shaping prokaryotic genomes such as gene gain, gene loss, and HGT, using protein families, thus avoiding the additional difficulty of defining orthologs (Ouzounis 1999). We show that using these estimates, it is possible to distinguish between HGT and gene loss and quantify the major forces responsible for the evolution of individual genomes.

RESULTS

We attempt to explain the present phylogenetic distribution of 12,762 protein families from 51 entire genome sequences by minimizing the number of potential gene gain and loss events. We approach the problem using phylogenetic profiles (Pellegrini et al. 1999) derived from the TRIBES protein family database (Enright et al. 2002) and phylogenetic trees (see Methods). We have used GeneTRACE, an algorithm that allows the reconstruction of protein family history using trees and a parsimony-based analysis (Kunin and Ouzounis 2003). The phylogenetic trees used were obtained by 16S rRNA multiple alignments, gene content sharing, and, for validation, random shuffling (see Methods). Shuffling the tree eliminates any phylogenetic signal while keeping the same topology, which serves as a negative control for the genuine phylogenetic trees.

Parameter Optimization

Sporadic distribution of a protein family on a tree may be the result of either multiple gene loss or HGT (Snel et al. 2002). If the number of potential loss events is less than a certain threshold, the distribution is explained by gene loss. When the number of these events exceeds the threshold, an HGT event is inferred. This threshold is defined as the HGT penalty. The higher the HGT penalty, the more unlikely HGT becomes, for any given phylogenetic profile.

To develop a realistic model for protein phylogeny using gene gain and gene loss events, we first need to estimate their relative occurrence. The optimal HGT penalty, previously proposed to correspond to the “expected relative frequency” of HGT versus gene loss (Snel et al. 2002), should in fact correspond to the observed ratio between these events. In other words, if the HGT penalty is set to 2, it is expected that two gene losses per HGT event should be observed. This correspondence is required to provide the fit between the theoretical estimate of the frequency of these events (HGT penalty) and the ratio observed in the data.

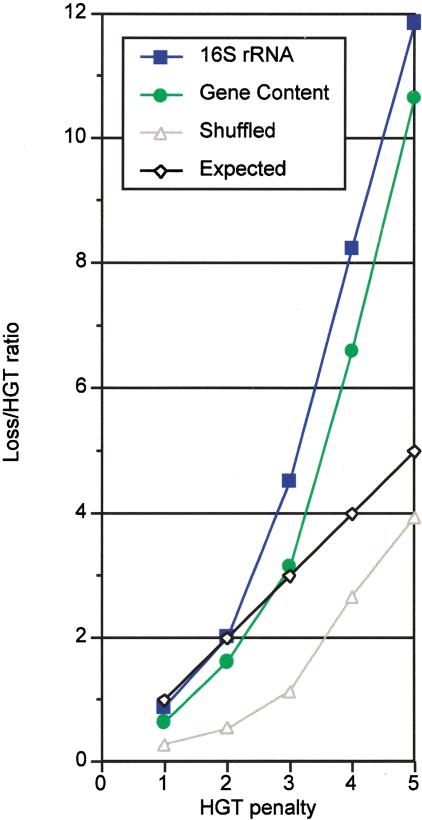
We experimented with HGT penalty values ranging between 1–5, counting all reported evolutionary events (Table 1). At low HGT penalty values (<2), gene loss is slightly overpredicted, whereas with higher HGT penalties (>3), gene loss predominates (Fig. 1). The shuffled tree overpredicts HGT at any tested threshold, because protein families are not meaningfully grouped on the tree. Interpolated curves of expected and observed ratio values for both 16S rRNA and gene content-derived trees intersect at HGT penalties between 2 and 3, indicating that the optimal HGT threshold is between these two values.

Table 1.

Numbers and Ratio of Events Reported on Different HGT Penalties

HGT penaltya	Loss eventsb	HGT eventsb	Families in HGTc
16S rRNA tree
1	9,342	10,468	5,274
2	14,847	7,374	4,286
3	21,304	4,702	3,263
4	26,307	3,191	2,504
5	29,365	2,474	2,071
Gene content tree
1	7,055	10,864	5,282
2	12,413	7,670	4,426
3	17,557	5,556	3,640
4	24,004	3,633	2,743
5	28,144	2,638	2,203
Shuffled tree
1	10,176	35,942	12,364
2	17,065	31,664	12,121
3	29,590	25,966	11,844
4	50,955	19,104	10,653
5	62,408	15,842	10,079

^aHGT penalty corresponds to the threshold value used

^bLoss and HGT events correspond to the number of events observed in the three trees

^cFamilies in HGT corresponds to the number of families predicted to be involved in HGT

Figure 1.

Comparison of observed and expected ratio of gene loss over HGT at various HGT penalties. The expected ratio implied by the model is shown in black (diamonds), and observed results are represented in blue (squares) for the 16S rRNA tree, green (circles) for the gene content tree, and gray (triangles) for the shuffled tree. The genuine trees are in agreement with the model (intersecting the expected linear curve) at HGT penalty values between 2 and 3. The shuffled tree overpredicts HGT at any tested HGT penalty value.

Stability of Average Prokaryotic Genome Size

To further estimate the relative occurrence of gene gain and loss, we assess average prokaryotic genome size stability. It has been proposed that genome size is subject to stabilizing selection (Mira et al. 2001). If the dominant force driving genome evolution was gene loss (Snel et al. 2002), it would result in ever-decreasing genome sizes. On the other hand, if genomes were shaped mainly by gene gain, namely, gene genesis (Wallace and Morowitz 1973) or HGT (Ochman et al. 2000), very large contemporary prokaryotic genomes would be produced (Mira et al. 2001). In practice, the sizes of most prokaryotic genomes occupy a narrow window of a few megabases (MB), between 0.6 and 8.6 MB (Moran 2002). This is in sharp contrast to the large variation of genome size in eukaryotes, where genome size varies more than 4 orders of magnitude, between 12 MB in Saccharomyces cerevisiae and 670,000 MB in Amoeba dubia (Cavalier-Smith 1985). The small variation of the prokaryotic genome size, combined with their more ancient origin, indicates that, averaged over all species, DNA gain and loss are two opposing factors being constantly balanced in prokaryotes. The ratio of genes per amount of DNA is remarkably constant in prokaryotes, averaging ∼1 kb per gene (Doolittle 2002). Thus, the stability of genome size implies stability of number of genes and balance between gene gain and loss as well.

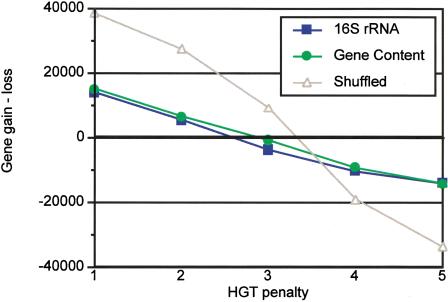
To identify the scenario with the most stable family content, we investigated the predicted balance between gene gain and loss on various HGT penalties (Fig. 2). On both 16S-rRNA- and gene-content-derived trees, gene gain prevails on HGT penalty lower than 2, and gene loss prevails on HGT penalties higher than 3, again indicating that the optimal threshold is between these two values (Fig. 2).

Figure 2.

The difference between gene gain and loss at various HGT penalties. The results for 16S rRNA, gene content, and shuffled trees are shown; represented as in Figure 1. The concordance of the two genuine (16S rRNA and gene content) trees is evident, contrasted to the shuffled tree. Genome stability (signified by zero difference, bold horizontal line) is achieved with HGT penalty values between 2 and 3.

Thus, two measures—correspondence of the expected and observed ratios between gene loss and HGT and the balance between gene loss and gene gain—indicate that an optimal threshold value for HGT penalty lies between 2 and 3. These values not only correspond to optimal parameters for this analysis, but may also reflect a genuine biological effect, indicating that gene loss is between two and three times more frequent than HGT. As gene genesis must compensate for the remainder of gene loss, we estimate that its contribution should be up to twofold the amount of HGT.

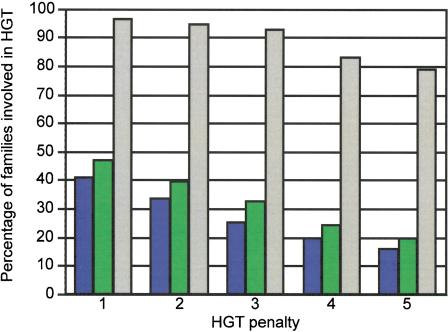
The fraction of families involved in HGT can be estimated, once the HGT penalty is known (Fig. 3). Although on the shuffled tree, most of the families are unrealistically indicated to be involved in HGT, the genuine trees (both 16S rRNA and gene content) imply that most protein families are gained exactly once and never transferred horizontally. We estimate that the fraction of protein families involved in horizontal transfer in the genomes under consideration is between 25% and 39% (Fig. 3).

Figure 3.

The fraction of families predicted to be involved in horizontal gene transfer at different HGT penalties. Percentages for the 16S rRNA tree are represented by blue bars, for the gene content tree by green bars, and for the shuffled tree by grey bars.

Evolution of Individual Species

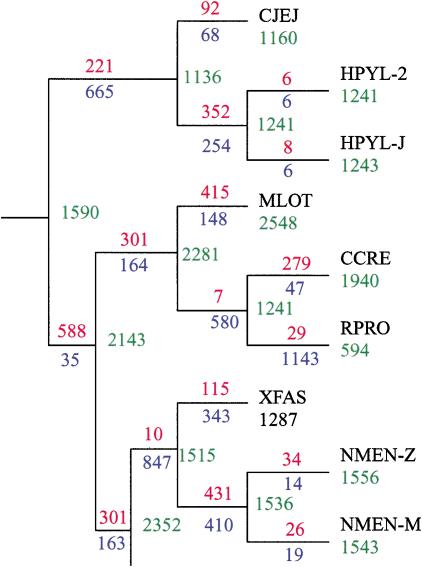
Although the average frequencies of HGT, gene genesis, and loss events may be estimated from a collection of genomes, individual species diverge from the average. Our analysis indicates that gene loss is extensive in smaller genomes, whereas large genomes tend to gain many protein families. Figure 4 illustrates the genomic history of a fraction of the 16S-derived phylogenetic tree, and the complete analysis for the 16S rRNA tree and the gene content tree are provided in the Supplemental Material, available at www.genome.org. Gene gain is observed virtually on all branches, except a few cases of intracellular parasites, such as Buchnera sp., Mycoplasma genitalium, and the strains of Chlamydia pneumoniae (data not shown). Our results also confirm previous suggestions that the Buchnera sp. genome represents one of the most stable genome sequences known to date (Andersson 2000), at least with regard to gene gain (Andersson and Andersson 1999). Gene loss is also observed on all branches, even on branches leading to species with the largest genomes, such as Mesorhizobium loti and Pseudomonas aeruginosa (Fig. 4). Persistent gene family loss in the case of larger genomes represents a remarkable trend, previously observed for orthologous genes (Snel et al. 2002). Finally, individual strains normally appear to gain and lose very few genes (Fig. 4).

Figure 4.

A segment of the 16S rRNA tree, with the predicted number for protein families at each node displayed (green), and the number of families gained (red) or lost (blue) for each branch. The genomes represented in this tree segment are: Campylobacter jejuni (CJEJ), Helicobacter pylori strains 26695 (HPYL-2) and J99 (HPYL-J), Mesorhizobium loti (MLOT), Caulobacter crescentus (CCRE), Rickettsia prowazekii (RPRO), Xyllela fastidiosa (XFAS), and Neisseria meningitidis strains Z2491 (NMEN-Z) and MC58 (NMEN-M). See text for discussion.

Evidently, the present set contains a multitude of pathogenic bacteria, and as such may not sufficiently represent the bacterial world. Yet obligatory parasitic bacteria were consistently reported to be derived by regressive evolution, and there is an overall agreement of the described evolutionary scenarios with present knowledge, indicating the robustness of our approach.

Model Validation With the Strain-Specific Genes of Helicobacter pylori

We aimed to confirm that our proposed model fits previous observations on established data. Generally, there are multiple methods that allow the detection of HGT events (Ragan 2001), although in practice no single method can establish such proposals. Instead, different methods point to likely cases, which must be corroborated independently (Eisen 2000). These approaches include the detection of anomalous nucleotide composition, highest sequence similarity to distantly related species, and discrepancies between sequence family and species trees. We compared the evolutionary model presented here, based on protein family distribution, to previously proposed independent approaches (Table 2).

Table 2.

Analysis of Strain-Specific Genes of Helicobacter pylori

Gene identifiera	Strain 26695 (HP**)	StrainbJ99 (Jhp**)	Verdictc	Tree analysisd	Nucleotide composition biase	Closest BLAST homologf	E-valueg
HP0315h		-	?	Undecided		Paracoccus alcaliphilus	5e-12
HP0342		-	?	Undecided	•	Streptococcus pneumoniae	6e-05
HP0435	+		✓	HGT	••	Arabidopsis thaliana	6e-07
HP0447	+		✓	HGT		Aquifex aeolicus	2e-21
HP0452	+		✓	HGT	••	Aquifex aeolicus	2e-21
HP0454	+		✓	HGT	••	Mus musculus	1e-12
HP0855		-	✓	Loss	•	Campylobacter jejuni	1e-130
HP1045		-	✓	Loss	••	Campylobacter jejuni	0.0
HP1193		-	✓	Loss	••	Yersinia pestis	2e-88
HP1334	+		✓	NAi	•	Neisseria meningitidis	5e-46
jhp0164	-		?	Undecided	•	Lactococcus lactis	5e-40
jhp0165		+	✓	NAi	•	Bacillus subtilis	5e-12
jhp0540	-		✓	Loss	•	Campylobacter jejuni	4e-25
jhp0928		+	✓	HGT		Rhizobium rhizogenes	1e-119
jhp0932		+	✓	NAi	•	Neisseria meningitidis	2e-50
jhp1297		+	✓	HGT	••	Mycoplasma pulmonis	2e-86

^aGene identifier

^bStrains 26695 and J99 display the gene gain (+) or loss (-) for the corresponding gene as predicted by GeneTRACE

^cVerdict represents that there is agreement (✓) with supporting evidence (13 cases) or the verdict is inconclusive (?) where it has not been possible to delineate the evolutionary history of the corresponding genes, because of very low sequence similarity relationships and lack of relevant information (3 cases)

^dTree analysis lists the most likely scenario using a phylogenetic tree of the corresponding family

^eNucleotide composition bias signifies highly (••) or moderately (•) anomalous nucleotide composition

^fClosest BLAST homolog lists the species name for the best BLAST hit in the nonredundant protein database

^gE-Value is also reported in the last column. The analysis is performed with an HGT penalty of 3

^hGene content tree suggests a gain

ⁱNonapplicable—no tree: insufficient sequence data

We have analyzed the genome of Helicobacter pylori, for strains J99 (Alm et al. 1999) and 26695 (Tomb et al. 1997). Previously, analysis of these strains identified 162 strain-specific genes (Janssen et al. 2001), of which only 27 have at least one homolog in another complete genome and were further considered. To establish anomalous nucleotide distributions, only proteins longer than 100 amino acid residues have been used (Garcia-Vallvé et al. 2000), reducing the number to 16 individual cases (Table 2).

The analysis of protein families containing strain-specific genes of the two H. pylori strains indicates that the presence of 13 of these genes can be attributed to either gene gain or gene loss (9 and 4, respectively). This result is also supported by detailed manual analysis, including the generation and boot-strapping of dendrograms (Table 2).

In virtually all cases (Table 2), there is total agreement between the gene content and 16S rRNA trees. An estimate of precision for the method would be 81% (13 out of 16 cases), with three undecided and no false positive cases. It is encouraging that in some cases, our predictions are better than anomalous nucleotide composition, for example, in the case of genes HP0447 and HP1045 (Table 2). Although the detection of closest homologs by BLAST (Altschul et al. 1997) does not necessarily reflect genuine evolutionary relationships within a family (Koski and Golding 2001), it is important to emphasize that it can support cases of HGT derived independently. In conclusion, our approach automatically generates scenarios for gene gain or loss highly consistent with detailed manual analyses.

DISCUSSION

We have attempted to quantify the major events during the evolution of gene families, namely, gene genesis, loss, and horizontal gene transfer (HGT). Evolutionary scenarios for individual protein families were generated, with gain and loss events reported. The relative frequencies of the events shaping genome content were estimated by two methods: the correspondence between the observed and expected ratio of gene loss and HGT and the assessment of the balance between gene gain and loss. Both methods indicate that loss is up to three-fold more frequent than HGT, and gene genesis contributes up to twofold as many genes as HGT.

Although our approach provides the very first attempt to estimate the ratio of processes shaping gene content, this type of analysis is dependent on the availability of genome sequences. It is possible that with wider representation of more species in the phylogenetic tree, some of the events presently interpreted as gene genesis in sparsely sampled clades may turn out to represent HGT events. Also, HGT from extinct clades may result in assignment of gene genesis, although this would require all the descendants of the clade generating the gene to be extinct. On the other hand, our analysis refers to protein families, rather than individual genes, and thus gene loss may be underestimated. A single gene genesis or HGT event introducing a member of a new family into a clade will be detected, whereas multiple gene loss events may be needed to eliminate all members of a multigene family. A future approach may quantify the processes discussed for individual genes, rather than protein families, as well as quantify the amount of gene duplication.

The number of families involved in horizontal transfer is estimated between 25% and 39% of the total number of families examined. Thus, although HGT can be considered as a significant factor that shapes prokaryotic genome sequences, it is remarkable that phylogenetic distributions of at least 60% of protein families can be explained merely by vertical inheritance. Although on average gene gain and loss were assumed to be balanced, it is evident that evolution of individual lineages might significantly deviate from this balance, consistent with present knowledge. A case study of strain-specific genes of H. pylori strains implies that the precision of the method is at least 81%. With a multitude of yeast, plant, and animal genomes becoming available, a similar analysis could reveal how the contribution of the processes shaping genome content differs in eukaryotes. This approach has the potential to provide insights into the emergence of complex cellular processes and potentially restore the complete gene content of ancestral species.

METHODS

Protein families were derived using an all-against-all clustering of complete genome sequences with the TRIBE-MCL algorithm (inflation value 2; Enright et al. 2002). This algorithm allows the rapid and fully automated clustering of large amounts of sequence similarity data derived from pairwise BLAST (Altschul et al. 1997) similarity scores with high quality (Enright et al. 2002). The families were derived for 10 archaeal and 41 publicly available bacterial species or strains (Bernal et al. 2001). Eukaryotes were not included.

To eliminate bias toward a particular type of phylogenetic tree, we have used two independently derived trees. First, the 16S rRNA tree, derived from multiple alignments of the 16S rRNA gene sequences (downloaded from the RDP; Maidak et al. 2001), and second, the gene content tree, derived from a distance table of gene content sharing using the method described in Snel et al. (1999). Trees were manually rooted on the branch between Archaea and Bacteria. To assess the performance of the method, we have compared the results observed on these trees against a shuffled tree. To obtain shuffled trees, the terminal nodes of the 16S rRNA tree were randomly permuted while the tree topology was preserved. In the case of the gene content tree, the genomes of Mycobacterium species were removed because of their inconsistent positions in the tree.

Phylogenetic profiles (Pellegrini et al. 1999) were generated for the presence and absence of a protein family in a genome. For the purposes of this study, all families considered contain proteins with representatives in at least two genomes, resulting in 12,762 protein families in the case of 16S rRNA and 11,145 for the gene content tree. The GeneTRACE algorithm used in this study is similar to the one used previously for groups of orthologous genes (Snel et al. 2002), independently developed for protein families (Kunin and Ouzounis 2003). The complete trees and list of studied species are available in the Supplemental Material.

The initial input for GeneTRACE consists of phylogenetic profiles of protein families and an evolutionary tree spanning all species involved. Inner nodes on this tree represent ancestral species. Two types of events are considered: protein family gain and loss; gene gain can be further classified as gene genesis or HGT. The algorithm consists of the following stages:

1. For each inner node, the minimal number of potential changes that are required to obtain the observed family distribution is calculated for both possible cases: gene family presence and absence at the node. Both gene acquisition and loss are penalized by a single point. The calculation proceeds from terminal nodes of the tree toward the root. For each parental node on the tree, the penalty is equal to the sum of the penalties of its daughter nodes. These penalties are transformed into assignments of family presence or absence at the node Z in any of the three following cases.

   1. If the descendants of the node Z exhibit a uniform pattern, either family presence or absence, the corresponding pattern is assigned to node Z.
   2. If the difference between the number of potential gains and losses is larger than a threshold value called the HGT penalty, and the family presence is observed on at least two daughter subtrees, family presence is assigned to node Z.
   3. If the difference between the number of potential gains and losses is smaller than a certain threshold value (set to 4 in all experiments reported here), family absence is assigned to node Z.
      In cases where none of the above criteria are satisfied, the decision for assignment of family presence or absence is delayed until the next stage.

2. To resolve these ambiguities, starting from the root of the tree, unassigned nodes inherit the parental assignment. The parent of the root is assumed not to contain any genes, thus delaying the first assignment to the first evidence of family presence.

This two-pass procedure is an improvement over the original approach suggested by Snel et al. (2002), which takes into account the general context of the subtree neighborhoods for ambiguous cases.