Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Jun 1.
Published in final edited form as: J Magn Reson. 2014 Mar 20;243:25–32. doi: 10.1016/j.jmr.2014.03.004

Finite-Pulse Radio Frequency Driven Recoupling with Phase Cycling for 2D 1H/1H Correlation at Ultrafast MAS Frequencies

Yusuke Nishiyama 1, Rongchun Zhang 2,3, Ayyalusamy Ramamoorthy 2,*
PMCID: PMC4037380  NIHMSID: NIHMS578835  PMID: 24713171

Abstract

The first-order recoupling sequence radio frequency driven dipolar recoupling (RFDR) is commonly used in single-quantum/single-quantum homonuclear correlation 2D experiments under magic angle spinning (MAS) to determine homonuclear proximities. From previously reported analysis of the use of XY-based super-cycling schemes to enhance the efficiency of the finite-pulse-RFDR (fp-RFDR) pulse sequence, XY814 phase cycling was found to provide the optimum performance for 2D correlation experiments on low-γ nuclei. In this study, we analyze the efficiency of different phase cycling schemes for proton-based fp-RFDR experiments. We demonstrate the advantages of using a short phase cycle, XY4, and its super-cycle XY414 that only recouples the zero-quantum homonuclear dipolar coupling, for the fp-RFDR sequence in 2D 1H/1H correlation experiments at ultrafast MAS frequencies. The dipolar recoupling efficiencies of XY4, XY414 and XY814 phase cycling schemes are compared based on results obtained from 2D 1H/1H correlation experiments, utilizing the fp-RFDR pulse sequence, on powder samples of U-13C,15N-L-alanine, N-acetyl-15N-L-valyl-15N-L-leucine, and glycine. Experimental results and spin dynamics simulations show that XY414 performs the best when a high RF power is used for the 180° pulse, whereas XY4 renders the best performance when a low RF power is used. The effects of RF field inhomogeneity and chemical shift offsets are also examined. Overall, our results suggest that a combination of fp-RFDR-XY414 employed in the recycle delay with a large RF-field to decrease the recycle delay, and fp-RFDR-XY4 in the mixing period with a moderate RF-field, is a robust and efficient method for 2D single-quantum/single-quantum 1H/1H correlation experiments at ultrafast MAS frequencies.

Keywords: Ultrafast MAS, Dipolar recoupling, RFDR, Proton Detection

Introduction

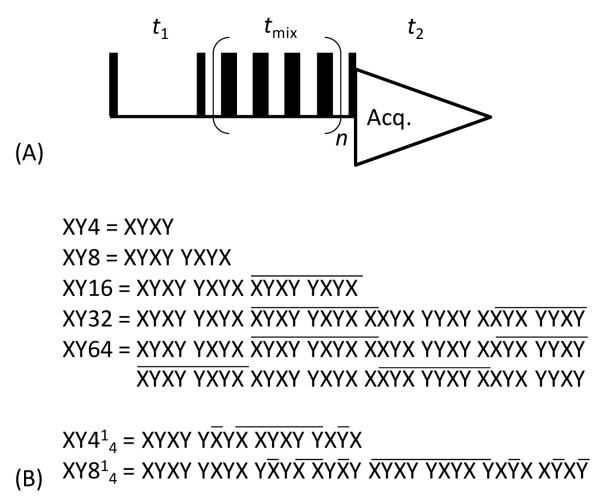
Atomic-resolution structural and dynamics information obtained using solid-state NMR experiments can provide piercing insights into the functional properties of a variety of biological molecules including membrane proteins, amyloid proteins and microcrystalline globular proteins [1-8]. In studies using magic angle spinning (MAS), recoupling RF pulse sequences are typically used to obtain homonuclear chemical shift correlation spectra of low-γ nuclei (mostly 13C) - enabling the assignment of resonances and interatomic distance measurement - from uniformly or non-selectively labeled proteins. One such recoupling sequence is the finite-pulse radio frequency-driven dipolar recoupling (fp-RFDR), which uses a single 180° pulse at the center of each rotor period [9, 10]. While the simple form of this sequence is easy to implement and attractive, its efficiency is lowered by the pulse imperfections such as resonance offset and RF field inhomogeneity, and the interferences from chemical shift anisotropy (CSA) and heteronuclear dipolar couplings[9, 11]. Previous studies have demonstrated the effectiveness of XY-based phase cycling to overcome the limitations of fp-RFDR. Among various phase cycling schemes reported in the literature (Figure 1), a recent study reported the best performance of fp-RFDR using XY814 phase cycling[12]. The idea behind XY-based phase cycling for the fp-RFDR pulse sequence can be explained by the symmetry based sequence [11, 13] and its super-cycle. Especially the XY814 phase cycling utilizes global super-cycling to suppress the second-order cross terms. While this phase cycling is well suited for studies on low-γ nuclei, it is not certain if this phase cycling would render similar performance for fp-RFDR experiments on protons. Its long cycle duration may not be desirable and therefore it is worthwhile to examine the efficiencies of different phase cycling schemes for proton-based fp-RFDR experiments.

Figure 1. Phase cycling schemes.

Figure 1

Open in a new tab

(A) 2D 1H/1H chemical shift correlation experiment using the zero-quantum dipolar recoupling sequence fp-RFDR. (B) A list of phase cycling schemes used for the fp-RFDR sequence in the present study.

1H based fp-RFDR experiments on solids are challenging, because of low spectral resolution due to unaveraged residual 1H-1H dipolar coupling interactions and relatively small span of chemical shift. However, recent studies have shown the benefits of using 2D 1H/1H fp-RFDR experiments on mobile solids, such as model membranes, to recover motionally averaged dipolar couplings among protons[14, 15]. In addition, the ability of fast MAS enabled the use of fp-RFDR sequence with high 1H spectral resolution [1, 3]. In this study, we demonstrate the use of 2D 1H/1H fp-RFDR experiments under ultrafast MAS condition and also report an examination on the efficiencies of different phase cycling schemes for the fp-RFDR sequence. The criteria for an optimum phase cycling in the fp-RFDR sequence is two-fold: (a) it should reduce the loss of total longitudinal magnetization during the RFDR mixing time enabling a better signal-to-noise ratio; (b) an efficient phase cycle should provide the maximum cross peak intensity in a 2D 1H/1H correlation spectrum. The cross peak intensity depends on the rate of magnetization exchange via the recoupled 1H-1H dipolar couplings, which is determined by the following two factors. One is the scaling factor of the recoupled 1H-1H dipolar interactions. In the fp-RFDR sequence, this is solely determined by the ratio of the 180° pulse length to the cycle time of sample spinning. The second factor is the loss of magnetization due to relaxation including the RF-field inhomogeneity, chemical shift offset, long-range dipolar couplings, RF-induced sample heating. These factors – particularly the second one - greatly affect the efficiency of the phase cycling used in fp-RFDR experiments.

In this study, we systematically evaluate the performances of various phase cycling schemes for the fp-RFDR sequence. Our results show that a short phase cycle, XY4 corresponding to the R44−1 symmetry, and its super-cycle XY414 are well suited for proton-based fp-RFDR experiments. The fp-RFDR using these phase cycling schemes renders zero-quantum homonuclear dipolar recoupling by suppressing all other interactions including CSA, heteronuclear dipolar and scalar couplings, and isotropic chemical shifts. Since the magnetization transfer during the mixing time of a first-order dipolar recoupling sequence is independent of the MAS frequency, the fp-RFDR based 2D chemical shift correlation experiments utilizing these phase cycling schemes have unique advantages in studying biological solids at very fast and ultra-fast MAS frequencies.

Experimental

All NMR experiments were performed on a 600 MHz JNM-ECA600II NMR spectrometer (JEOL RESONANCE Inc., Tokyo, Japan) equipped using a 0.75 mm ultrafast MAS probe. Powder samples of U-13C,15N-L-alanine and glycine were purchased from Isotec and were used without any modification. N-acetyl-15N-L-valyl-15N-L-leucine (NAVL) was prepared as explained elsewhere[16, 17]. Samples were packed in a 0.75 mm zirconia rotor and all experiments were performed at room temperature (ca. 24 °C). Experiments were performed to optimize the width of the 180° pulse so that the loss of net magnetization after fp-RFDR can be minimized. The 180° pulse width that gave the maximal signal intensity after fp-RFDR irradiation was used in the subsequent experiments reported in this study. The experimentally optimized 180° pulse width was 5 μs for 110 kHz RF-field strength, 2.7 μs for 231 kHz, and 1.3 μs for 467 kHz. It should be noted that these 180° pulse widths are longer than that calculated from the respective RF field strength, because of the transients at the rising and falling edges of the pulses. All other experimental conditions used in this study are given in figure captions.

Simulations

The spin dynamics simulations were performed using the SPINEVOLUTION software[18]. Three proton spins were considered in the simulations. Distance between any two protons was set at 0.16 nm. The simulations were performed at 80 and 92 kHz spinning speeds with a length of 2 μs for the 180° pulse. As results obtained with the two spinning speeds are similar, only data obtained from 92 kHz MAS are presented. Through simulations, we obtained the build-up of the magnetization transfer efficiency from one proton to another as a function of fp-RFDR mixing time. The RF field strength was deliberately misset to evaluate the effect of the RF field inhomogeneity.

Results and Discussion

In this study, we systematically investigate the efficiencies of different phase cycling schemes by employing them in the proton-based fp-RFDR pulse sequence (Figure 1) under ultrafast MAS conditions. Experimental results obtained from powder samples of U-13C,15N-L-alanine and NAVL are given, while those from glycine are not included as they support the results obtained from other compounds and do not provide additional new information. The simulations were performed at 80 and 92 kHz spinning speeds with a 180° pulse length of 2 μs as mentioned above. As results obtained with the two spinning speeds are similar, only data obtained from 92 kHz MAS are presented here.

Signal loss under RFDR

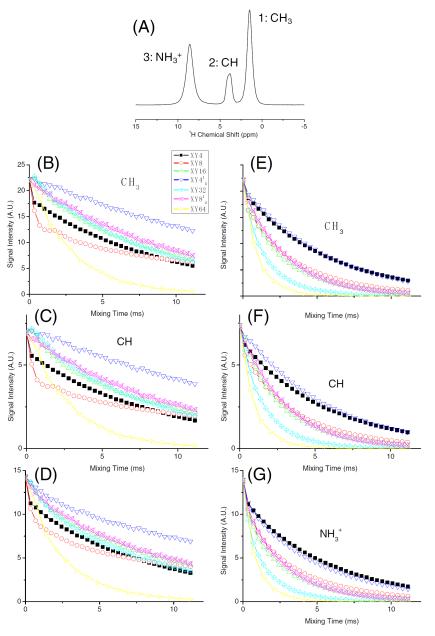
The ability of an fp-RFDR pulse sequence to retain the z-magnetization during the mixing time depends on the perfectness of the 180° pulse used to recouple 1H-1H dipolar couplings and the magnitude of the recoupled dipolar coupling. A detailed theoretical analysis of the fp-RFDR and related scaling of the recoupled 1H-1H dipolar couplings can be found elsewhere[11]. For example, the resonance offset and RF field inhomogeneity lower the efficiency of the 180° pulse while a long duration 180° pulse renders a fast magnetization exchange via the recouped 1H-1H dipolar coupling. Therefore, we measured the loss of z-magnetization for each phase cycle using the pulse sequence given in Figure 1 by keeping t1=0. 1D 1H spectra were recorded as a function of RFDR mixing time for each phase cycling (listed in Figure 1) at two different RF field strengths (467 and 110 kHz) on L-alanine at 92 kHz MAS. For a direct comparison of the performances of different phase cycling schemes employed in fp-RFDR, peak intensities measured as a function of mixing time are given in Figure 2. These experimental results suggest that the loss of magnetization during the fp-RFDR irradiation significantly depends on the phase cycling scheme as well as the RF-field strength used for the 180° pulses in fp-RFDR. The least signal loss was observed for XY414 at the highest RF field strength and for both XY4 and XY414 at the lowest RF power strength (criterion (a) mention in Introduction). For any given phase cycle, the loss of magnetization is lesser when a higher RF field is used as shown in Figure 2.

Figure 2. Loss of magnetization under RFDR.

Figure 2

Open in a new tab

(A) Proton MAS NMR spectrum of U-13C,15N-L-alanine powder sample obtained at 92 kHz MAS. (B-G) Peak intensities measured from 1D 1H NMR using the pulse sequence given in Figure 1A (for t1=0) as a function of fp-RFDR mixing time. Measurements were carried out using two different RF field strengths for the 180° pulse in the fp-RFDR sequence: 467 kHz (B, C and D) and 110 kHz (E, F and G).

Rate of magnetization transfer

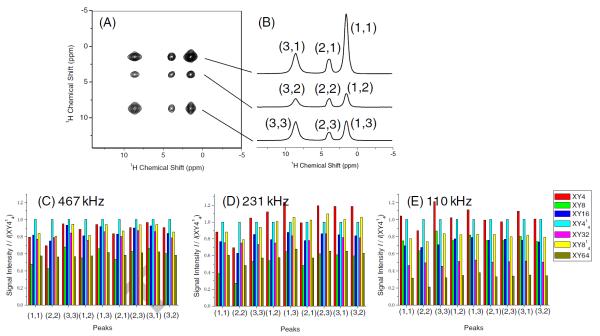
2D 1H/1H fp-RFDR experiments were carried out using different phase cycling schemes to compare their abilities to recover 1H-1H dipolar couplings and transfer magnetization between protons. A representative 2D 1H/1H fp-RFDR spectrum and 1D spectral slices are shown in Figure 3A and Figure 3B, respectively. Intensities of both diagonal and cross peaks were measured from 2D spectra and are compared in Figure 3(C-E) for three different RF field strengths (467, 231, and 110 kHz). The results presented in Figure 3(C-E) are useful to evaluate the tolerance of different phase cycling schemes against the relaxation effect during the fp-RFDR irradiation. The observed intensities of cross and diagonal peaks depend on the build-up rate of longitudinal magnetization exchange, relaxation of proton spins that results in a loss of net magnetization, and the length of the mixing time used in the fp-RFDR irradiation. For a given RF field strength, the same mixing time was used for all phase cycling schemes: 2.78 ms for 467 kHz, 1.39 ms for 231 kHz, and 1.39 ms for 110 kHz. As a result, the width of the 180° pulse is the same for a given mixing time, and therefore, the measured intensities of cross and diagonal peaks solely determined by the relaxation of protons; it should be noted that the build-up rate (that depends on the scaling factor of the recoupled 1H-1H interaction) is expected to be the same for all phase cycling schemes when the 180° pulse width is the same. Thus, we can evaluate the rate of relaxation from the cross and diagonal peak intensities at a chosen mixing time for each of the RF field strengths used in the study. Note that the intensities of cross and diagonal peaks obtained using different RF field strengths cannot be compared, because the scaling factors and mixing times are different for different RF field strengths. Data presented in Figure 3(C-E) revealed that the cross peak intensities from 2D spectra obtained using XY4, XY414 and XY814 are relatively higher than those obtained using other phase cycling schemes, although the best phase cycling depends on the RF-field strength used for the 180° pulses in the fp-RFDR pulse sequence. These results, in addition to the results given in Figure 2, suggest that XY4, XY414 and XY814 render better performances for proton-based fp-RFDR experiments. While the better performance of XY814 compared to other super-cycles is in excellent agreement with previous studies on low-γ nuclei, the better performances of the shortest phase cycle XY4 and of its super-cycle XY414 are a gratifying surprise. Therefore, to better understand their performances, these three schemes were selected for further examination as explained below.

Figure 3. 2D chemical shift correlation of protons using fp-RFDR.

Figure 3

Open in a new tab

(A) A representative 2D 1H/1H RFDR spectrum of L-alanine powder sample obtained at 92 kHz MAS. (B) Representative 1D spectral slices extracted from the 2D 1H/1H RFDR spectrum; proton resonances are labeled as 1 (CH3), 2 (CH) and 3 (NH3+); for example, the label (3,1) indicates the cross peak between NH3+ and CH3 resonances in the 2D RFDR spectrum, where CH3 is in the indirect dimension and NH3+ is in the direct dimension. (C-E) A comparison of the peak intensities measured from 2D 1H/1H fp-RFDR spectra obtained at RF field strengths of 467, 231, and 110 kHz with mixing times of 2.78, 1.39, and 1.39 ms, respectively, using different phase cycling schemes (given in Figure 1).

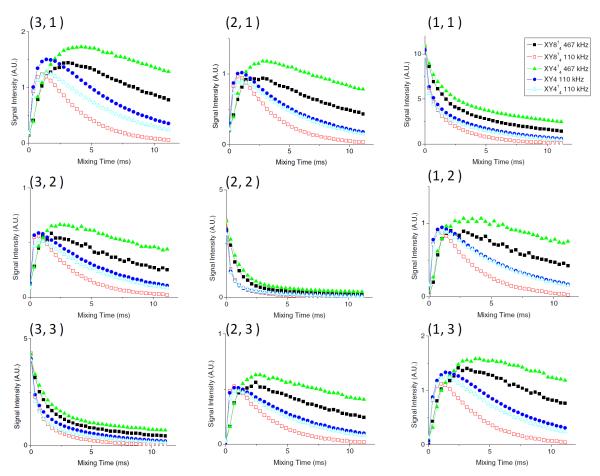
2D 1H/1H fp-RFDR spectra for various mixing times were measured using XY4, XY414 and XY814 phase cyclings (Figure 4). The intensities of both diagonal and cross peak were measured and plotted as a function of the fp-RFDR mixing time in Figure 4 for a direct comparison. These results indicate that the rates of initial build-up curves for the cross peaks mainly depend on the RF-field strength, and not on the phase cycling. This is because the initial build-up rate is dominated by the scaling factor of the recoupled 1H-1H dipolar interaction, which is solely determined by the duty factor of 180° pulses in fp-RFDR, i.e. the RF-field strength. Interestingly, the maximum cross peak intensities are higher for XY414 and XY4 than that for XY814, especially with the use of a high RF field. Indeed, the quicker decay in XY814, than in XY414 and XY4, reduces the maximum cross peak intensities. Based on these analyses, XY414 and XY4 are the best candidates when the applied RF field strength is very high or moderate, respectively. The higher build-up rate observed for the lower RF field strength (or a longer 180° pulse width) is in complete agreement with the previously reported theoretical analysis [11]. It is worth noting that the maximum cross-peak intensities are always obtained when the strongest RF field strength was used in fp-RFDR despite the slower build-up of magnetization transfer. This might be due to the reduced loss of magnetization from T2ρ during the 180° pulses of fp-RFDR when the RF field strength is high. The duty factor of RF-pulses during fp-RFDR at 92 kHz spinning speed is 12% for 467 kHz RF-field strength, but it is 46% for an RF-field strength of 110 kHz; the duration of a 180° pulse is shorter for a stronger RF field than that of a weaker RF field, and therefore the effect of T2ρ should be less when a stronger RF field is used. This shows that the XY414 phase cycling with a high RF field strength is preferable to achieve the best mixing of magnetization, if the sample allows a strong RF-irradiation and a long mixing time due to smaller scaling factors. If the sample is heat sensitive, XY4 phase cycling with a low RF-field strength should be used.

Figure 4. Efficiency of dipolar recoupling by fp-RFDR.

Figure 4

Open in a new tab

Variation of peak (both diagonal and cross) intensities on the fp-RFDR mixing time obtained using XY4, XY414 and XY814 phase cycles at the indicated RF field strengths. Peaks are labeled as described in Figure 3 caption.

Effects of RF field inhomogeneity and chemical shift offset

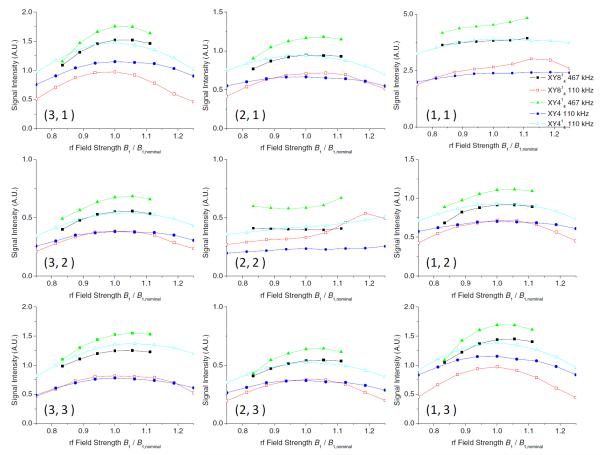
Since the efficiency of the 180° pulse depends on the RF field inhomogeneity and chemical shift offset frequency, the efficiency of the phase cycles against these effects were examined. 2D 1H/1H fp-RFDR experiments were performed on alanine for XY4, XY414 and XY814 phase cycles by deliberately missetting the RF field strength for the 180° pulse to determine the RF field inhomogeneity effect whereas the irradiation frequency of the 180° pulse was offset to measure the chemical shift offset effects. Peak intensities measured from these 2D spectra are given in Figure 5 and Figure 6. As shown in Figure 5, RF field inhomogeneity up to 15% has no significant effect on the performances of these phase cycles. Offset does not significantly affect the fp-RFDR performance when a high RF field strength was used for the 180° pulse, but it does so for a low RF field strength as shown in Figure 6. Spin dynamics simulations were carried out to evaluate the magnetization transfer efficiency by fp-RFDR as a function of RF field inhomogeneity and chemical shift offset. Simulated results are shown in Figure 7. Obviously, the XY414 exhibits a better performance against chemical shift offset. On the other hand, the tolerance against RF field inhomogeneity is similar for all three phase cycling schemes as shown in Figure 7. It should be mentioned that the intensity difference for the three phase cyclings is very small.

Figure 5. RF field inhomogeneity dependence of fp-RFDR.

Figure 5

Open in a new tab

Variation of peak (both diagonal and cross) intensities on the fp-RFDR RF field inhomogeneity obtained using XY4, XY414, and XY814 phase cycles at RF field strengths of 467 kHz and 110 kHz with mixing times of 2.78 ms and 1.39 ms, respectively. Peaks are labeled as described in Figure 3 caption.

Figure 6. Offset dependence of fp-RFDR.

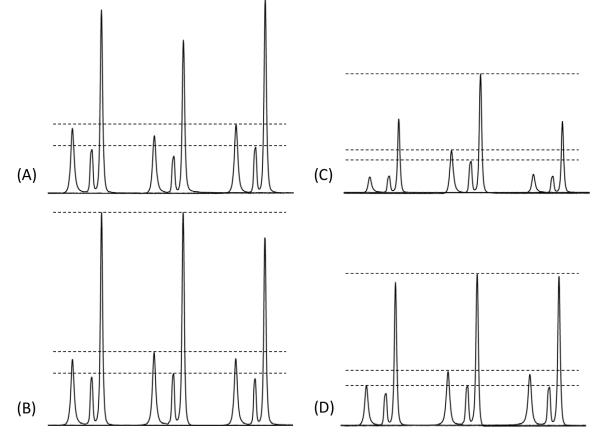
Figure 6

Open in a new tab

Chemical shift offset dependence of 2D 1H/1H fp-RFDR spectra of U-13C,15N-L-alanine powder sample obtained using XY814 (A,C) and XY414 (B, D) phase cycling schemes at RF field strengths of 467 kHz with a mixing time of 2.78 ms (A, B) and 110 kHz with a mixing time of 1.39 ms (C, D). Slices at the CH3 peak in the indirect dimensions were shown to display (3,1), (2,1), and (1,1) peaks. Sample spectra observed at three different offsets (−16.5, 5.5 and 25.5 ppm) (left to right) are shown. All spectra are presented on the same scale for a direct comparison.

Figure 7. Simulations of fp-RFDR efficiency.

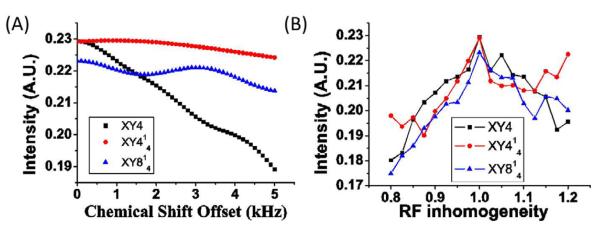
Figure 7

Open in a new tab

Effects of (a) chemical shift offset and (b) RF field inhomogeneity on fp-RFDR buildup intensity at a mixing time of 8 ms with different phase cyclings as indicated. The RF field strength was deliberately misset in order to evaluate the effect of RF field inhomogeneity, where the value on x-axis indicates the ratio of the applied RF field strength to the accurate RF field strength (i.e., 250kHz).

An efficient phase cycling scheme for proton-based RFDR experiments

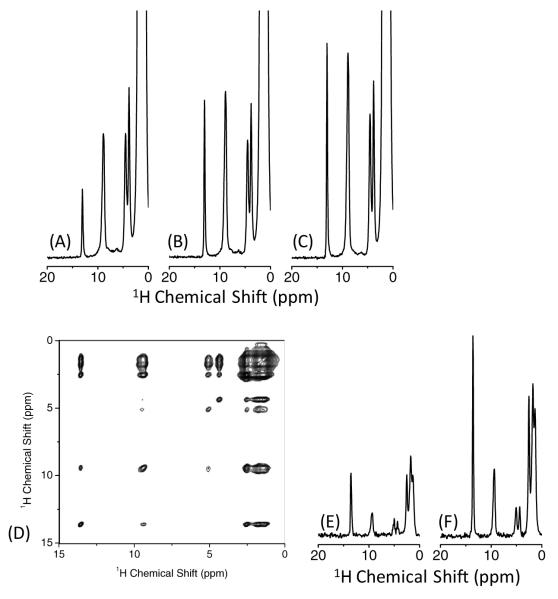
Our results in Figure 2 have demonstrated that the loss of signal intensity was the least for the XY414 phase cycle with the strongest RF field, while the results in Figure 4 demonstrated that the build-up rate is fastest when using a low RF power that provides a higher scaling factor for the 1H-1H dipolar coupling in fp-RFDR. We employed the fp-RFDR-XY414 phase cycling with a strong RF field during the recycle delay and fp-RFDR-XY4 phase cycling with a weak RF field during the mixing time in 2D 1H/1H correlation experiments. While the criterion for the first fp-RFDR is to avoid the loss of the total magnetization (see below), the second fp-RFDR should maximize the rate of magnetization exchange. Since fp-RFDR-XY414 rendered the minimum loss of net magnetization during RFDR irradiation, it is employed in the recycle delay. The main purpose of the fp-RFDR during the recycle delay is to shorten the repetition time. The fp-RFDR transfers the magnetization from 1H nuclei with a shorter T1 relaxation time to those with longer T1 relaxation time, allowing us to use a shorter recycle delay than the longest T1 relaxation time.[19] While the intensities of peaks in the resultant spectra cannot be used to obtain quantitative information, this approach is very useful to enhance the intensity of weak signals and to observe all peaks including cross peaks in multidimensional NMR spectra. This is successfully demonstrated on NAVL as discussed below. The T1 relaxation time of the carbonyl proton (~13 ppm) of NAVL is 8.3 s, which is significantly longer than the shortest T1 (1 s) of other protons in the molecule. When the repetition time of 2.2 s was used, the signal intensity of the carbonyl proton was partly suppressed due to rapid repetition (Figure 8A). On the other hand, the signal intensity is recovered if we apply fp-RFDR-XY814 with a stronger rf field during the recycle delay (Figure 8B). As demonstrated from our experimental results, the efficiency is further improved if we employ XY414 phase cycling, giving the maximum signal intensity (Figure 8C). The less loss of magnetization enables us to apply longer and larger number of RFDR trains, ensuring better magnetization transfer efficiency. Further improvement can be seen in 2D 1H/1H fp-RFDR experiments when the fp-RFDR-XY414 phase cycle during the recycle delay to shorten the spin-lattice relaxation time and XY4 with a weak RF field strength in the fp-RFDR mixing time. This combination provided better signal intensity than the fp-RFDR that utilized XY414 in the mixing period and without any fp-RFDR during the recycle delay as demonstrated in Figure 8 (D-F).

Figure 8. fp-RFDR for T1-reduction of protons.

Figure 8

Open in a new tab

Single pulse 1H NMR spectra of a powder sample of NAVL obtained at 100 kHz MAS without fp-RFDR (A), with fp-RFDR of XY814 (B), and with fp-RFDR of XY414 (C) during the recycle delay. 2D 1H/1H fp-RFDR correlation spectrum of NAVL (D) and slices (E and F) at the chemical shift frequency of the carbonyl proton (~13 ppm) along the direct dimensions observed with fp-RFDR-XY414 (E) and fp-RFDR-XY4 during the mixing time and with fp-RFDR- XY414 during the recycle delay (F). A relaxation delay of 2.2 s (A-C) and 2 s (D-F), and RF field strengths of 467 kHz during the repetition delay and 110 kHz during mixing time were used. Number of fp-RFDR cycles (3 for (B) and 6 for (C, D, F)) and duration of each fp-RFDR (1.92 ms for (B) and 6.4 ms for (C, D, F)) were optimized such that the carbonyl proton peak (~13) ppm is maximized.

Conclusions

In this study, we have reported an evaluation of different XY based phase cycling schemes for the fp-RFDR 1H/1H homonuclear recoupling sequence based on ultra-fast (at 80, 92 and 100 kHz) MAS experiments on powder samples of U-13C,15N-L-alanine, glycine and NAVL. We have demonstrated that the efficiency of a phase cycle for a proton-based fp-RFDR experiment is different from that for low-γ (for example 13C) nuclei. For proton-based RFDR experiments, an efficient phase cycle should avoid the loss of magnetization due to relaxation and interference from pulse imperfections, CSA and dipolar couplings. Among the phase cycling schemes examined in this study, our results show that a short phase cycle XY4 is well suited for proton-based fp-RFDR experiments at low RF power levels, whereas its super-cycle XY414 exhibits high efficiency when a high RF power is used. These relatively shorter duration phase cycles are preferred for 2D 1H/1H chemical shift correlation experiments under fast and ultra-fast MAS frequencies as they exhibit robustness to chemical shift offset, and also avoid the loss of magnetization due to relaxation. Our results further demonstrate that the performance of a short phase cycle XY4 is better than that of super-cycles XY8, XY16, XY32 and XY64 under all experimental conditions; XY8 was the most ineffective phase cycle while higher super-cycles like XY16 and XY32 are better. We believe that the short phase cycles reported in this study will be valuable for the measurement of 1H-1H distances to determine the three-dimensional structure of biomolecules in solid-state.

Highlights.

  • 2D 1H/1H RFDR experiments are demonstrated under ultrafast MAS conditions.

  • Performances of various XY-based phase cycling schemes are compared.

  • Results show that XY4 and its super-cycle XY414 render excellent performances.

  • The use of RFDR- XY414 shortens the recycle delay for faster data acquisition.

Acknowledgment

This research was supported by funds from NIH (GM084018 and GM095640 to A.R.) and JEOL Resonance Inc. (Tokyo, Japan). We would like to thank the JEOL Resonance scientists for help with the spectrometer and ultrafast MAS probe.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • [1].Zhou DH, Shah G, Mullen C, Sandoz D, Rienstra CM. Proton-Detected Solid-State NMR Spectroscopy of Natural-Abundance Peptide and Protein Pharmaceuticals. Angew. Chem. 2009;121:1279–1282. doi: 10.1002/anie.200801029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [2].Zhou DH, Shea JJ, Nieuwkoop AJ, Franks WT, Wylie BJ, Mullen C, Sandoz D, Rienstra CM. Solid-State Protein-Structure Determination with Proton-Detected Triple-Resonance 3D Magic-Angle-Spinning NMR Spectroscopy. Angew. Chem. Int. Edit. 2007;46:8380–8383. doi: 10.1002/anie.200702905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [3].Zhou DH, Shah G, Cormos M, Mullen C, Sandoz D, Rienstra CM. Proton-Detected Solid-State NMR Spectroscopy of Fully Protonated Proteins at 40 kHz Magic-Angle Spinning. J. Am. Chem. Soc. 2007;129:11791–11801. doi: 10.1021/ja073462m. [DOI] [PubMed] [Google Scholar]
  • [4].Linser R, Dasari M, Hiller M, Higman V, Fink U, Lopez del Amo J-M, Markovic S, Handel L, Kessler B, Schmieder P, Oesterhelt D, Oschkinat H, Reif B. Proton-Detected Solid-State NMR Spectroscopy of Fibrillar and Membrane Proteins. Angew. Chem. Int. Edit. 2011;50:4508–4512. doi: 10.1002/anie.201008244. [DOI] [PubMed] [Google Scholar]
  • [5].Linser R, Bardiaux B, Higman V, Fink U, Reif B. Structure Calculation from Unambiguous Long-Range Amide and Methyl 1H–1H Distance Restraints for a Microcrystalline Protein with MAS Solid-State NMR Spectroscopy. J. Am. Chem. Soc. 2011;133:5905–5912. doi: 10.1021/ja110222h. [DOI] [PubMed] [Google Scholar]
  • [6].Petkova AT, Ishii Y, Balbach JJ, Antzutkin ON, Leapman RD, Delaglio F, Tycko R. A structural model for Alzheimer’s β-amyloid fibrils based on experimental constraints from solid state NMR. Proc. Natl. Acad. Sci. 2002;99:16742–16747. doi: 10.1073/pnas.262663499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [7].Tycko R. Molecular structure of amyloid fibrils: insights from solid-state NMR. Q. Rev. Biophys. 2006;39:1–55. doi: 10.1017/S0033583506004173. [DOI] [PubMed] [Google Scholar]
  • [8].Parthasarathy S, Nishiyama Y, Ishii Y. Sensitivity and Resolution Enhanced Solid-State NMR for Paramagnetic Systems and Biomolecules under Very Fast Magic Angle Spinning. Acc. Chem. Res. 2013;46:2127–2135. doi: 10.1021/ar4000482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [9].Bennett AE, Rienstra CM, Griffiths JM, Zhen W, Lansbury PT, Griffin RG. Homonuclear radio frequency-driven recoupling in rotating solids. J. Chem. Phys. 1998;108:9463–9479. [Google Scholar]
  • [10].Bennett AE, Griffin RG, Ok JH, Vega S. Chemical shift correlation spectroscopy in rotating solids: Radio frequency driven dipolar recoupling and longitudinal exchange. J. Chem. Phys. 1992;96:8624–8627. [Google Scholar]
  • [11].Ishii Y. 13C–13C dipolar recoupling under very fast magic angle spinning in solid-state nuclear magnetic resonance: Applications to distance measurements, spectral assignments, and high-throughput secondary-structure determination. J. Chem. Phys. 2001;114:8473–8483. [Google Scholar]
  • [12].Shen M, Hu B, Lafon O, Trébosc J, Chen Q, Amoureux J-P. Broadband finite-pulse radio-frequency-driven recoupling (fp-RFDR) with (XY8)41 super-cycling for homo-nuclear correlations in very high magnetic fields at fast and ultra-fast MAS frequencies. J. Magn. Reson. 2012;223:107–119. doi: 10.1016/j.jmr.2012.07.013. [DOI] [PubMed] [Google Scholar]
  • [13].Levitt MH. In: Encyclopedia of Nuclear Magnetic Resonance. Grant DM, Harris RK, editors. Vol. 9. Wiley; Chichester, England: 2002. pp. 165–196. [Google Scholar]
  • [14].Aucoin D, Camenares D, Zhao X, Jung J, Sato T, Smith SO. High-resolution 1H MAS RFDR NMR of biological membranes. J. Magn. Reson. 2009;197:77–86. doi: 10.1016/j.jmr.2008.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [15].Ramamoorthy A, Xu J. 2D 1H/1H RFDR and NOESY NMR Experiments on a Membrane-Bound Antimicrobial Peptide Under Magic Angle Spinning. J. Phys. Chem. B. 2013;117:6693–6700. doi: 10.1021/jp4034003. [DOI] [PubMed] [Google Scholar]
  • [16].Wei Y, Ramamoorthy A. 2D 15N–15N isotropic chemical shift correlation established by 1H–1H dipolar coherence transfer in biological solids. Chem. Phys. Lett. 2001;342:312–316. [Google Scholar]
  • [17].Ramamoorthy A, Gierasch LM, Opella SJ. Four-Dimensional Solid-State NMR Experiment That Correlates the Chemical-Shift and Dipolar-Coupling Frequencies of Two Heteronuclei with the Exchange of Dilute-Spin Magnetization. (Series B).J. Magn. Reson. 1995;109:112–116. doi: 10.1006/jmrb.1995.1157. [DOI] [PubMed] [Google Scholar]
  • [18].Veshtort M, Griffin RG. SPINEVOLUTION: A powerful tool for the simulation of solid and liquid state NMR experiments. J. Magn. Reson. 2006;178:248–282. doi: 10.1016/j.jmr.2005.07.018. [DOI] [PubMed] [Google Scholar]
  • [19].Ye YQ, Malon M, Martineau C, Taulelle F, Nishiyama Y. Rapid measurement of multidimensional 1H solid-state NMR spectra at ultra-fast MAS frequencies. J. Magn. Reson. 2014;239:75–80. doi: 10.1016/j.jmr.2013.12.010. [DOI] [PubMed] [Google Scholar]

RESOURCES