Role of Myelin Plasticity in Oscillations and Synchrony of Neuronal Activity

Abstract

Conduction time is typically ignored in computational models of neural network function. Here we consider the effects of conduction delays on the synchrony of neuronal activity and neural oscillators, and evaluate the consequences of allowing conduction velocity (CV) to be regulated adaptively. We propose that CV variation, mediated by myelin, could provide an important mechanism of activity-dependent nervous system plasticity. Even small changes in CV, resulting from small changes in myelin thickness or nodal structure, could have profound effects on neuronal network function in terms of spike-time arrival, oscillation frequency, oscillator coupling, and propagation of brain waves. For example, a conduction delay of 5 ms could change interactions of two coupled oscillators at the upper end of the gamma frequency range (∼100 Hz) from constructive to destructive interference; delays smaller than 1 ms could change the phase by 30°, significantly affecting signal amplitude. Myelin plasticity, as another form of activity-dependent plasticity, is relevant not only to nervous system development but also to complex information processing tasks that involve coupling and synchrony among different brain rhythms. We use coupled oscillator models with time delays to explore the importance of adaptive time delays and adaptive synaptic strengths. The impairment of activity-dependent myelination and the loss of adaptive time delays may contribute to disorders where hyper- and hypo-synchrony of neuronal firing leads to dysfunction (e.g., dyslexia, schizophrenia, epilepsy).

Introduction

The functional and evolutionary significance of myelin is typically interpreted in terms of the increased conduction velocity (CV) it confers through the mechanism of saltatory conduction (Tasaki, 1939). However, faster is not always better, as many aspects of brain function require precise temporal relationships among the signals originating from distant brain areas and, thus, a proper distribution of the CVs. In the vertebrate nervous system, CVs range from a small fraction of a m/s to hundreds of m/s in different axons. The speed of conduction is largely dependent on the thickness of myelin, axon diameter, and the spacing and width of nodes of Ranvier. Glial cells form myelin and influence the spacing of nodes, and in the PNS at least, affect axon diameter as well (de Waegh et al., 1992; Garcia et al., 2003). In order to mediate proper spike-time arrival among axons of different lengths converging onto a common target, these axonal parameters are crucial to establish proper conduction delays. It is commonly assumed that the transmission speeds and delays are genetically specified and fixed at the developmental stage, and the changes in degree of myelination in an adult brain are only considered in cases of pathology (e.g., demyelination and dysmyelination). This view is changing, and there is growing evidence that neurotransmitters mediate communication between axons and myelinating glia (Kukley et al., 2007; Ziskin et al., 2007; Bakiri et al., 2009), and that myelination is a dynamical, activity-dependent process (Fields, 2010).

Two principal mechanisms for changing CV are altering axon diameter and myelination (in vertebrates), the latter being the most effective means of increasing the CV. Enlarging axon diameter only is much less effective because CV increases in proportion to the square root of the axon diameter in unmyelinated fibers (Tasaki, 2004), while it increases linearly with the diameter of myelinated axons (Hursh, 1939). Additionally, the enlargement of axon caliber is metabolically and anatomically less feasible as a means of activity-dependent regulation of conduction delays. There is ample evidence now that the functional activity and action potentials influence proper development of myelin sheaths (Fields, 2013 for review). For example, in the experiments with the development of barrel cortex in mice (Barrera et al., 2013) sensory deprivation (removal of whiskers on one side), while not changing the onset of myelination relative to the controls, does significantly decrease the amount of myelin ensheathing each axon in the barrel region. Several molecular mechanisms for activity-dependent regulation of myelination have been identified in vitro (Stevens et al., 1998, 2002; Ishibashi et al., 2006; Wake et al., 2011) and social isolation in mice alters myelination of prefrontal cortex (PFC) with behavioral consequences (Makinodan et al., 2012; Liu et al., 2012). Human brain imaging shows structural differences in white matter regions of the brain after learning (Zatorre et al., 2012).

The possibility that activity-dependent regulation of myelination could adaptively influence temporal relations, oscillations and synchrony in the interactions of distant brain regions, provides a novel and previously unexplored form of activity-dependent nervous system plasticity. Plasticity of conduction time delays in neural circuits might complement the well-studied plasticity of synaptic function. Plasticity of conduction delays would be most relevant for complex cognitive functions and consciousness, since the timing of signals is of great importance in neural processing of information across different time and length scales. At the small scale of neuronal cells, precise arrival of action potentials at the postsynaptic neuron is perhaps the most important factor in triggering a new action potential, since different spikes arriving only a few milliseconds apart will fail to integrate to cause sufficient depolarization. At the scale of the whole body, signals sent from brain to the peripheral nervous system need to preserve precise timing and phase relationships in order to ensure coordinated motion. For example, in the case of limb coordination (Haken et al., 1990; Schöner et al., 1990) the same phase relationship in the movement of different limbs is preserved for a particular type of gait, but can differ among different animal species or among different types of gaits within the same species. The importance of timing in perception is also evident at the system level. For example, auditory neurons preserve the temporal structure of tones by phase-locking their responses with the stimulus. Using information-theoretic measures it was found that the temporal precision of the auditory information coding is coarser than 1 ms, but finer than 5 ms (Kayser et al., 2010). Similar findings hold for visual (Victor and Purpura, 1996; Butts et al., 2007) and other temporal tasks (Nemenman et al., 2008), with the consensus that the required precision for spike arrival timing was on the order of few or several milliseconds. In some specialized circuits, at the system level, the timing constraints can be at the sub-millisecond range. A well-known example of such fine temporal detection is that of spatial localization of sound based on interaural time difference (ITD), where across many vertebrate species ITDs as small as 10 μs can be resolved. The precision that is required at cellular and axonal level to achieve such precision at the system level is largely dependent on the details of the detection mechanism. In one of the earliest explanations of how such spatial localization might occur, the Jeffress model (Jeffress, 1948), the existence of precisely arranged “delay lines” is posited, which through coincidence detection positionally code (place code) the ITDs. Evidence for the existence of such delay lines has been found in birds (Carr and Konishi, 1990; Cheng and Carr, 2007; Seidl et al., 2010; see Seidl, 2013 for review) but their existence in mammals is more controversial (Grothe et al., 2010). Presence of such coincidence detection circuitry suggests that the sub-millisecond precision needs to be maintained at the axonal level.

Considering such stringent requirements for precision, as well as general importance of timing in the interaction between different signals, it would appear that the plasticity mediated through glia and myelination, which can adaptively modulate the CV along the axons and thus the timing, would be highly beneficial for the vertebrate brains. In the majority of computational models of neural network function, temporal conduction delays are typically ignored or are held constant. In a simple network shown in Fig. 1a, traditional neuronal networks would only keep the information about the connectivity and the weights between the source neuron and the target neurons. A more elaborate approach would account for temporal delays, τ_i, however, these are usually treated as fixed. This is an incorrect assumption if the CV is allowed to change. Since the intrinsic activity in the mammalian brain is often oscillatory (Bullock, 1997), one would similarly have to account for changes in the phase difference, ϕ_i. While the importance of spike timing in excitable systems has already been recognized, the emphasis on the importance of temporal and phase delays in the context of brain oscillations is lacking. Brain rhythms of various frequencies have been associated with selective attention, arousal, sleep, information processing, sensory gating of information, memory formation, emotion, perception, and consciousness (Buzsáki, 2006; Ainsworth et al., 2012). Furthermore, entrainment and interactions between the oscillation generators in different brain regions are essential, e.g., the entrainment of neocortical neurons through phase locking to the hippocampal theta rhythm (Buzsáki, 2006; Burgess et al., 2007; Sirota et al., 2008).

Fig. 1.

(a) Connectivity and synaptic strength cannot fully describe the functioning of a system with time delays and variable propagation speeds. (b) Two neurons, S₁ and S₂, firing at times t₁ and t₂, are sending action potentials to a single target neuron along corresponding axons. The spikes propagate at different conduction speeds v₁ and v₂, according to x_i(t) = v_i(t – t_i), i = 1, 2, and hence arrive at potentially different times, t₁ + d₁/v₁ versus t₂ + d₂/v₂ unless v₁ and v₂ are matched to encode a particular time-locked pattern. (c) In recurrent thalamo-cortical resonance large-scale synchronized events between remote brain regions occur. The distances, d_i, from a given thalamic nuclei to different cortical areas can differ significantly, hence the task of synchronizing distant cortical areas requires the conduction delays to be adjusted.

The outline of this review is as follows. We first reiterate some basic notions behind the role of myelin plasticity in spike timing, since the oscillations in the brain are certainly a reflection of the underlying spike timing. We then focus on the role of myelin plasticity in synchrony and oscillations, first reviewing basic literature on their generative mechanisms and coupling between them. While the details of precise mechanisms that underlie the maintenance and interactions can be elucidated in some cases (Destexhe and Sejnowski, 2003), in most cases the details of such interactions are not known. Instead, we take a more general approach and review some basic models of coupled oscillators (CO) with delay encountered in physics literature. Through them we elaborate on the consequences that activity-dependent myelin plasticity, i.e., the adaptive propagation speed and time delays, can have on improved neural system function.

Spike Timing and Conduction Delays in Excitable Systems

For spiking activity to propagate in a feed-forward neuronal network, usually several spikes are needed to arrive within a narrow time window to cause sufficient depolarization and trigger an action potential at the postsynaptic cell. Hence, the temporal relationships and coincidences in neuronal firing are of great importance for efficient propagation of activity (for reviews see Kimura and Itami, 2009; Seidl, 2013). In general, the state dynamics of the excitable spiking systems is nonlinear and can be complex, however, characterization of the coincident firing in the observed point process is simple. For any pair of neurons, if the absolute time difference between their spikes, |t_i − t_j|, is repeatedly smaller than some prescribed tolerance level, δt, the pair are deemed coincident, i.e., synchronous. The same concept can be extended to a group of neurons, now dealing with all pairwise temporal differences. In both cases we ignore more complicated issues of declaring such spike-time simultaneity statistically significant, since here we aim to address a simpler point about the relationships among the CVs, spatial distances, and temporal coincidences.

For finite CVs and the inclusion of temporal delays, synchrony at one stage of feed-forward processing does not imply synchrony at the next stage. In a simple example shown in Fig. 1b, the two source neurons, S₁ and S₂, firing at times t₁ and t₂, are sending action potentials to a single target neuron along the corresponding axons, each with different conduction delays, τ₁ and τ₂. The condition that the two impulses arrive at the target simultaneously is now t₁ + τ₁ = t₂ + τ₂, which means that the activity is most likely to propagate farther if the spiking of neurons S₁ and S₂ are not synchronous but are time-locked at Δt = t₂ − t₁. Hence, the synchrony in the laboratory time frame is less important than the proper matching of spike-times and conduction delays—a concept termed “polychrony” (Izhikevich, 2006). A simulation study of polychronization in a network of spiking neurons with spike-time-dependent plasticity (STDP) showed that a particular sequence of firing will propagate through a network of spiking neurons with reproducible time-locked, but not synchronous, firing sequences with millisecond precision (Izhikevich, 2006). However, the time-locked sequences that can be encoded with STDP in such a network are predetermined by the distribution of conduction delays among neurons, which appears to be a limitation when trying to encode a particular sequence, or to involve a particular set of neurons.

A millisecond time lag synchrony has been observed not only among nearby neurons but also among distant brain areas (interareal synchrony), in which the conduction latencies can be tens of milliseconds. Some models predict that for a particular network topology in which the introduction of intermediary network of neurons, connecting two distant (with long conduction delay) groups of neurons can lead to precise synchronization despite the long delays (Vicente et al., 2008). However, in the light of biological evidence that we review here, we argue that a more efficient way for two populations of neurons to synchronize is to adjust the conduction delay itself by adjusting the CV. The conduction delay is determined by the distances that signals need to traverse along the axons, d_i, and the corresponding conduction velocities, v_i. In the case of thalamo-cortical circuits, as sketched in Fig. 1c, an activation of thalamic nuclei will lead to synchronized activations of cortical areas covering a wide range of distances with millisecond precision. As the position of a spike at a particular time, t, along a given axon is given simply by x_i(t) = v_i(t − t_i) (see Fig. 1b), the spike arrival time at the target, t = t_i + τ_i = t_i + d_i/v_i will vary greatly if the CVs are assigned independent of their distances. Thus, the heterogeneity in time arrivals would reflect the heterogeneity in distances, increased further by the heterogeneity of CVs, if CVs are independently distributed. If we assume that a typical conduction speed in the cortex is on the order of 1 m/s, then the same spread in axonal lengths expressed in mm, will translate into equivalent spread of arrival times in terms of milliseconds, and for slower speeds this spread will be even greater. It appears then that the only way a synchrony with millisecond precision can be achieved, irrespective of traveling distances, is if the CVs are also adjusted to yield constant latencies, τ_i = d_i/v_i across all regions. Evidence that this happens during development can be found in the work of Salami et al. (2003), in which they study the conduction delays between the ventrobasal nucleus (VB), intermediate white matter (WM) region, and cortical layer IV in developing mice. In their study, the field potential latencies were measured from layer IV in response to thalamic (VB) and WM stimulation. In newborn animals the latencies for VB were much longer than from WM, however after postnatal week 3 both latencies assumed small and nearly equal values (around 2 ms). More specifically, at an early developmental stage (P3–P4) the CV for VB–WM pathway was already twice that of WM-IV (0.23 ± 0.03 m/s versus 0.1 ± 0.01 m/s), but a week after the onset of myelination, the VB–WM CV increased 14-fold to 3.28 ± 0.11 m/s, while WM-IV CV increased only threefold to 0.33 ± 0.05 m/s. The result of such significantly different amounts of myelin deposited on these two different pathways, is that their latencies, which differed by more than 5 ms in newborn mice, were matched now to within less than 0.5 ms.

Such differential and highly heterogeneous degrees of myelination among different axons, resulting in closely matched temporal delays is not something that happens only during development, and the plasticity in CV is in fact needed to maintain proper temporal relationships throughout the adult life. There is growing evidence that myelination may remain an active dynamical process even in the adult brain (Berthold et al., 1983; Liu et al., 2012; Young et al., 2013), and hence, from a stochastic point of view, it would be difficult to maintain a fixed CV and precise timing unless it is adaptive in some manner. Assuming the axonal lengths to be fixed, the conduction delay is in inverse relationship with the CV, hence an f-fold increase/decrease in speed will result in f-fold decrease/increase in conduction delays. Myelination has a profound effect on reducing temporal delays as a result of the approximately 50-fold increase in CV. However, even small changes, as small as 10%, which could result from relatively subtle changes in myelin thickness or nodal morphology, could have substantial effects on temporal synchrony and oscillations in neuronal firing. The distribution of delays in the brain is highly heterogeneous, ranging e.g., in the cat brain from 2 ms to 40 ms, with a median delay of 13.5 ms (Swadlow and Waxman, 2012). This means that in majority of the axons the 10% change in CV will shift the conduction delays by more than a millisecond and up to 4 ms, enough to affect oscillations and timing of spike arrival. Alternatively, participation of neurons in a particular task changes over time, and hence the axonal distances among neurons performing any given task can change over time. The effect of such positional change will depend on the CV. For the slower axons, the CV can be as low as 0.1 m/s, which means that the involvement of a neuron 1 mm further along the path, would translate into a 10-ms mismatch in arrival time. However, the CVs can be as large as several m/s. A good rule of thumb, again, is that the changes in distances on the order of millimeters will produce changes in conduction delays on the order of milliseconds.

Conduction Delays in Oscillations and Synchrony

Oscillations and synchrony are deemed to be of fundamental importance in nervous system function (see reviews by Bullock, 1997; Buzsáki, 2006; Fries, 2009; Ainsworth et al., 2012). These dynamical aspects of electrical activity in the brain have been studied extensively, in particular the oscillations between different cortical regions, across the corpus callosum connecting the two cerebral hemispheres, between the hippocampus and PFC (Sirota et al., 2008), and between the thalamus and cortex. The binding of multimodal sensory input in object recognition and context in memory formation and retrieval, for example, are thought to require rapid reciprocal interactions between distant populations of neurons coupled by oscillatory activity into transient functional assemblies firing synchronously. In the extreme, highly synchronous activity during slow wave sleep and during seizure are associated with the loss of consciousness. Ultimately, it is the interaction among different oscillatory processes that is fundamental in both normal function and pathology. It has been long recognized that such coupling can be influenced by rapid changes in synaptic strength, but less is known about how changes in CVs and delays will affect synchrony. In engineering, the transmission times are of great importance for synchronizing and designing efficient information and transportation systems. In physics, the best-suited paradigm for studying synchronization is that of CO. It is in context of CO that one can demonstrate fundamental consequences that the time delays can have on the stability of complex systems. Below, we first review some basic literature on the relevance of oscillations (brain rhythms) for brain function, in particular focusing on the interactions and coupling between the oscillators in different parts of the brain.

Oscillations and their interactions in the brain

Coordination of electrical activity among large assemblies of widely distributed neurons provides context-dependent binding of neurons into functionally coherent assemblies and selective routing of signals. This appears to be achieved through the interaction of various rhythms and different frequencies. Coupled oscillations can entrain particular phase relationship between functionally cooperating groups of neurons and can be flexibly configured within anatomically fixed networks in many different brain regions (Buzsáki, 2006; Singer, 2009).

Oscillatory patterns of firing in local circuits are typically produced by inhibitory interneurons, which are coupled through short-latency electrical and chemical synapses. Over large distances, reciprocal coupling of the oscillatory networks requires a significant conduction time and any fluctuation in CV can be detrimental, since the temporal precision needed for the oscillatory coupling and phase-locking increases with oscillation frequency. One way to alleviate this problem is to have synchronization among remote neurons occur at lower oscillation frequencies than for synchronization of local clusters of neurons, which have a shorter conduction delay. In such a scheme, the local networks are associated with oscillations at gamma frequencies (30–100 Hz), while the long-range synchronization and phase-locking involves lower frequency bands comprising theta (4–7 Hz), alpha (8–12 Hz), and beta (13–30 Hz) frequencies (von Stein and Sarnthein, 2000). The usual justification for such organization is that the long-range interactions cannot support synchronization with very high temporal precision as a result of slow conduction times and large temporal delays. However, long-range synchronization with zero latency can occur at higher frequencies (>30 Hz) even with large conduction delays (Buschman and Miller, 2007), because the local high-frequency oscillations become nested in lower frequency long-range oscillations. Furthermore, the observed coupling requires that the high-frequency local neuronal oscillations act in synchronous and phase-locked manner with the slower long-range oscillations (Fries, 2005; Palva et al., 2005; Canolty et al., 2006; Fries et al., 2007; Jensen and Colgin, 2007).

Despite increased difficulty, such coherence of oscillations over large distances in the brain is of great functional importance. Anticipation of a particular stimulus or motor act is associated with amplitude modulation and phase locking of oscillatory activity in the beta and gamma frequencies in cortical areas processing the stimulus (Roelfsema et al., 1997; Schoffelen et al., 2005). Such anticipatory synchronization can extend across widely distributed networks of cortical areas. For a recent review of coupled neuronal oscillation in cognitive function see (Uhlhaas and Singer, 2012). This review emphasizes dysfunctional coupling of neuronal oscillations through large-scale networks in neuropsychiatric disorders such as schizophrenia. In the visual cortex, synchrony is often observed over large distances with an oscillatory pattern of spike discharges in the gamma frequency range (30–60 Hz). Synchrony across the midline with the visual field in the opposite hemisphere is mediated through the corpus callosum (Engel et al., 1991), and synchrony in visual cortical areas also occurs with the superior colliculus.

The PFC is involved in gating memory, attention and decision-making. Coactivation of prefrontal and hippocampal networks in oscillatory rhythms is critical for precise information flow in mnemonic and executive tasks (Brockmann et al., 2011). The hippocampal theta bursts driving the neonatal prefrontal oscillations by phase-locking requires action potential propagation through long-distance pathways connecting these two regions. The oscillatory coupling between PFC and hippocampus develops in early postnatal life, starting at P5 in rat, with low gamma-band (approximately 40 Hz) oscillations. By adjusting oscillation frequency and phase of anatomically connected neuronal assemblies, effective coupling between groups of neurons can be enhanced or inhibited, and the increased PFC/hippocampal coupling during development is paralleled by functional changes. Encoding, retention and retrieval of memory improve with age throughout infancy and late childhood (Richmond and Nelson, 2007). In simultaneous recording from PFC and hippocampus a particular mechanism of phase–amplitude coupling of theta and gamma oscillations has been observed, in which the phase of the theta oscillations biases the amplitude of the gamma oscillations (Buzsáki et al., 1983; Soltesz and Deschenes, 1993) and similar phase–amplitude interactions have been observed for other frequency bands (Kandel and Buzsáki, 1997; Canolty and Knight, 2010). Another form of coupling, and perhaps more important, since it might also underlie the phase–amplitude coupling, is the phase–phase coupling (Tass et al., 1998). Its advantages for coding and information transfer have been studied extensively (Gerstner et al., 1996; Varela et al., 2001; Fell and Axmacher, 2011), as well as its role in the interactions of hippocampal theta and different sub-bands of gamma rhythms (Belluscio et al., 2007).

Knowing the importance of the temporal delays in coupling and the difficulty in synchronizing distant brain areas, it is natural to assume that the myelin plasticity can play a critical role in resolving this problem. The developing brain offers some evidence that this indeed is the case. The postnatal development of coordinated oscillatory activity between PFC and hippocampus parallels the postnatal myelination of hippocampus. In humans myelination of hippocampus begins prenatally, but continues through childhood, based on histological analysis (Abraham et al. 2010), and extends into adulthood as evidenced by MRI (Giedd et al., 1996). The first axons to be myelinated in the hippocampal circuit are the large hippocampal pyramidal cells that project to their respective subcortical and cortical fields. Myelination of the alveus in the human hippocampus is active during the 3rd postnatal month, but the first oligodendroglial cells are not detected in the dentate gyrus until the 5th month of age. GABAergic neurons in the medial septum are putative pace-maker neurons that drive hippocampal network activity and they are myelinated, suggesting that “appropriate conduction velocity”, achieved as a result of the myelination, is required for adult-like function of septo-hippocampal circuitry (Abraham et al., 2010).

Mathematical Models of Oscillations and Synchrony

Instead of delving into precise mechanisms of oscillation generation and coupling, as well as biological details of adaptive myelination, in this section we review more general approaches in studying synchronization and oscillation phenomena. Many insights can be gleaned from studying features of general oscillators and their coupling, without specifying the details of their generative mechanisms or their interactions. For example, synchronization phenomena, such as Arnold tongues, frequency and phase entrainment, amplitude death, etc., are observed universally for many different types and classes of oscillators. We also focus on two prototypical models of phase and amplitude coupling, and review literature in which the effects of temporal delays in the interactions have been studied.

Oscillations and waves basics

In the general picture, what constitutes the oscillators can be very different; they can be simple harmonic systems, e.g., a simple electrical LC resonant circuit, or a complex limit-cycle attractor in a non-linear, chaotic system. Frequently, an oscillator is defined by a set of non-linear differential equations, in which the solutions are limit cycle attractors. They are stable closed loops in state space into which the system spirals after a sufficiently long time period (see Fig. 3a). There are numerous examples of well-studied simple and nonlinear oscillators, such as the van der Pol oscillator, Rössler oscillator, the Brusselator, etc., but what they all share in common is that the state of the system can be described efficiently in terms of the amplitude, the phase and a characteristic periodic function, h, i.e., z(t) = A(t)h(θ(t)). The period of h is 2π, since the true period of the oscillator, T, is absorbed under the phase, θ, which indicates at what stage of the cycle the oscillator is in. In the case of waves, the periodic motion is propagating in a given medium with speed, v_p, and the phase at position x, and time t can be can be written as θ(x, t) = ωt + kx + ϕ₀, where ω is the angular frequency, ω = 2π/T, (hereafter referred to as simply frequency, instead of the usual cyclic frequency f = 1/T), k is wavenumber, k = 2π/λ, λ = v_pT, being the wavelength, and ϕ₀ is the initial phase at x = 0 and t = 0. When two oscillators interact their local phases will play a prominent role in determining the outcome of the interaction, i.e., whether they interfere constructively or destructively. For the gamma oscillations, which have a range of frequencies between 40 and 100 Hz, the period itself ranges between 10 and 25 ms. The delays of half the period, i.e., in the range 5−12.5 ms, would change the interaction of two oscillators from constructive to destructive. Even though such timing might seem less stringent than in the case of spike-time, one needs to keep in mind that even changes in a delay of one millisecond would change the phase by 36° for 100-Hz oscillations; thus, still affecting the amplitude of the resulting signal significantly.

Fig. 3.

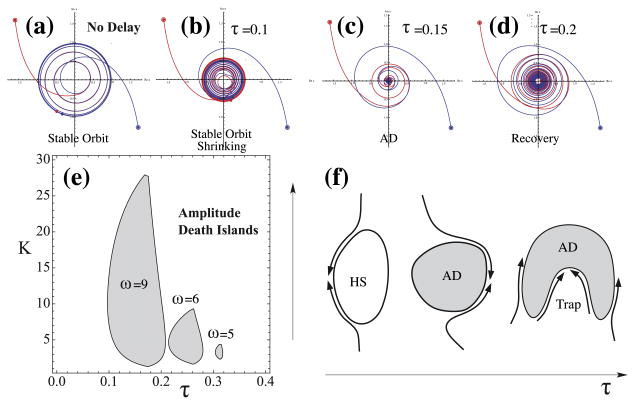
The dynamical state of coupled oscillators as a function of the coupling strength, K, and the time delay, τ. (a–d) Dynamics of two amplitude-coupled non-linear oscillators, as described by Eq. (6), for K = 5, ω₁ = 8, ω₂ = 9, and for different values of time lags as indicated. The trajectory of the two oscillators is depicted in a complex plane (containing the information about the amplitude and the phase) with red and blue lines respectively, where the circled dots indicate the starting positions, and plain blue and red dots indicate the positions at time t = 20. These positions end up in a large and stable limit cycle for zero time delay, for virtually any initial conditions as shown in (a). Increasing the time delay in the oscillator interactions leads to a decrease in amplitude (b), and for a range of values of delay it leads to amplitude death, i.e., at the origin of the complex plane, as shown in (c). Further increase of τ recovers the limit cycle, and start of the recovery is shown in (d). This behavior is summarized in (e) using (K,τ) state diagrams, which clearly shows the isolated regions of AD, the death islands, in which activity is quenched after a short period of time. This state diagram is calculated for coupled oscillators with matching frequencies, ω₁ = ω₂ = ω, and for three different values of ω, as indicated. (f) A sketch of how a dynamical system, in which K and τ can be changed adaptively and are functions of activity, can navigate itself away from the regions with hyper-synchronizability (HS), or amplitude AD regions. Depending on the shape of such regions and the type of dependence of the parameters K and τ on the activity, the system might still end up being trapped and unable to adapt further without entering the “death islands”.

CVs will also affect the spatial aspects of the interaction, since the wavelength will be proportional to the CV, and will have effect on the interference patterns of such waves (Burgess et al., 2007). As typical speeds in the brain are on the order of 1 m/s, this means that the typical wavelength of gamma oscillations will be on the order of few centimeters, smaller than the brain size in many vertebrate species. For slower CVs, the wavelength can be as small as a few millimeters. In typical neural network models the focus is on the connectivity between different neurons, but the spatiotemporal aspects of the interaction between them, induced by finite propagation speed of a signal are often ignored. In particular, the changes to CV in a developed adult brain are not accounted for. Just as with temporal issues, the change in CV of 10% would produce a 10% change in wavelength. If the distance between the brain regions is comparable or smaller than the wavelength, d ≤ λ, such a change will not produce a significant effect. But, as an example, if the distance is equal to 5λ, a 10% change will mean that the brain waves will interfere at a difference of λ/2, which will produce destructive interference. Thus, relatively small changes in conduction delays can have significant effects on the temporal and spatial aspects of neuronal oscillations. In some cases, a relatively small change in temporal delays can change constructive interference into destructive interference of such oscillations.

Coupled oscillator basics

The description of each individual oscillator, as well as simple harmonic interference between them is not where the true complexity of the oscillator systems lies, but rather at the interactions between them, which can affect the frequencies, and the phases of the individual oscillators. In such systems of interacting oscillators new collective dynamical modes can develop, and synchronization is one of them. Synchronization can manifest itself in different ways even in the case of precisely defined individual oscillators, where one can distinguish between the frequency locking and the phase locking synchrony. In the case of frequency locking, two oscillators with similar frequency will start oscillating at the same frequency, while for phase locking, two oscillators can have different frequencies but their phases can be locked if their characteristic frequencies satisfy nω₁ = mω₂, where n and m are integers. Ultimately, what leads to any type of synchronization is the interaction between the oscillators, and it is the nature of this coupling that will most strongly influence the dynamics of synchronization. In this chapter we transition away from reviewing biological evidence of the importance of the myelin plasticity on the brain function and toward model explorations. In particular, we address the concept of global myelin plasticity, i.e., that the myelination, and thus the conduction delays, dependent on the overall activity level in the axons can have important functional consequences on the stability of the system.

The notion of CO refers to a collection of self-sustained or limit cycle oscillators, each with their own natural frequency, ω_i, that are coupled to each other through some form of interaction. The magnitude of this interaction is determined by the coupling strength parameter(s). For a certain range of coupling strengths, and below a certain dispersion (spread) among the natural frequencies, a significant fraction of oscillators can assume a common frequency Ω and a fixed phase relationship, i.e., synchronize through both phase and frequency locking (entrainment). Christiaan Huygens was the first to report this phenomenon in his letters, as early as 1665. He studied the pendulum clocks, his own invention, and observed that two clocks hung on the same wooden beam would start oscillating at the same frequency. Huygens correctly concluded that this synchronization is the result of the clocks interacting through the wooden beam. Besides being entrained to the same frequency, the clocks were either in-phase (Δϕ = 0) or out-of-phase (Δϕ = π), an example of phase coupling.

Phase coupling

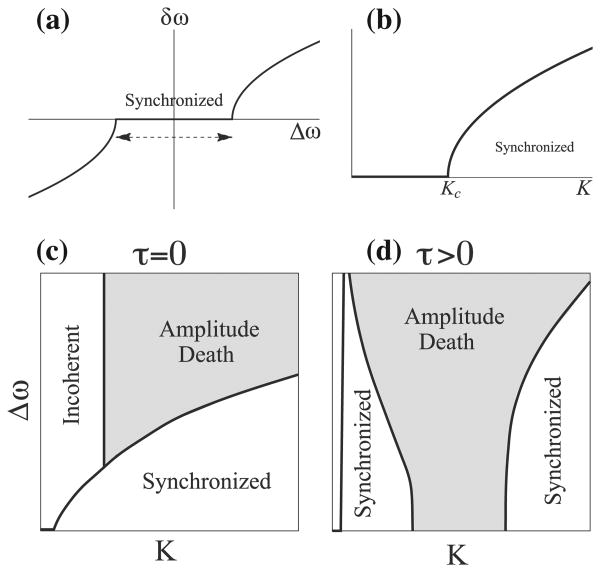
A prototypical model for phase coupling is the Kuramoto model (Kuramoto, 1975) (see Appendix A), in which each oscillator is represented by its phase, and the interaction between any two oscillators depends on their phase differences. In the simplest case there are two essential independent parameters, the coupling strength, K, and frequency mismatch, Δω, which is a measure of a spread among ω_i (e.g., in the case of two oscillators, Δω = |ω₁ − ω₂|), and the performance of the system is measured by the synchronization parameter, r, which takes values between 0 and 1, with 0 meaning total incoherence, and 1 meaning that all units are synchronized. The typical picture is sketched in Fig. 2a, b, suggesting that synchronization occurs only for a limited range of Δω and above some critical coupling strength, K_c. Outside those regions (“zones of entrainment”) the oscillator dynamics are incoherent. In many cases it is assumed that the interaction between the oscillators is “instantaneous,” and hence in the example of the pendulum clocks each is “aware” of the phase of the others. If one takes the finite propagation speed into account, and thus a time delay in their interaction, τ, the synchronization becomes a more difficult task, assuming that τ is not negligibly small compared to the period of the oscillations, or tuned precisely to be a multiple of the period of the natural oscillations. In studying the Kuramoto model with delays, Niebur et al. (1991) showed that the synchronized frequency Ω could now be modulated with either the coupling strength or the conduction delay. In the case of identical oscillators, ω_i = ω₀, Δω = 0, the lowest stable frequency, Ω_min, can be written as Ω_min ≈ ω₀/(1 + nKτ). This means that the presence of time delays enables the system to modulate the synchronization frequency with both, the coupling strength and the conduction delay.

Fig. 2.

The dynamical state of coupled oscillators as a function of the spread of natural frequencies of these oscillators, Δω, and the coupling strength, K. In the Kuramoto model synchronization occurs for (a) a sufficiently small mismatch Δω, as shown with zero frequency spread, δω, and for (b) a coupling strength that is larger than some critical value (assuming coupling is sufficiently large in (a), and the mismatch is not too large in (b)). A better way to depict dynamic regimes is to use state diagrams, which show more clearly what pair of values (K, Δω) will produce synchronization, or amplitude death for amplitude-coupled models. State diagrams for such a model are shown for (c) no time delays, and (d) when time delay is sufficiently large to affect the dynamics. Note that with the presence of time delay even the oscillators with identical frequencies (Δω = 0) can lead to AD for moderate coupling strength.

Amplitude coupling and amplitude death

States of the oscillators in Kuramoto model are described only by its phases, and it cannot explore other phenomena associated with the amplitude of the oscillators. In amplitude-coupled oscillator systems, particularly those in which there is a time delay for a large enough mismatch Δω, increasing the coupling strength further will, instead of synchronization, lead to oscillation quenching, known as oscillation death or amplitude death (AD), as sketched in a state diagram¹ in Fig. 2c (Aronson et al., 1990). The first observation of this phenomenon was also made more than a century ago in studies of sound by Lord Rayleigh, who reported cancellation of the sound of organ pipes when interacting with each other (Rayleigh, 1896). This phenomenon becomes even more important when one takes into account the time delays (Reddy et al., 1998), as can be gleaned by comparing the situation with no time delay (τ = 0, Fig. 2c), and with time delay (τ > 0, Fig. 2d). The three important dynamical domains, indicated in Fig. 2d are (1) synchronization, (2) amplitude death, and (3) incoherent behavior (drifting phase behavior). Hence, with the introduction of time delays, even a system with perfectly tuned oscillators (Δω = 0, i.e., ω₁ = ω₂) can come to a screeching halt. We implemented the same diffusive and linearly coupled oscillator model with time delay studied in Reddy et al. (1998), and motivated by work of Aronson et al. (1990). The model and its equations are described in Appendix B. In Fig. 3a–d, we show the dynamics of the system for a fixed amount of time in the complex plane. A complex number fully describes the state of an oscillator, since it contains both, its amplitude and phase (in the complex plane the amplitude is measured as the radial distance from the origin, while the phase is represented by the angle with the respect to the Real axis). The initial points of the dynamics are illustrated with circled dots for the system that has a stable limit cycle when there is no delay in the interaction (τ = 0). This means that for virtually any starting point, the system will eventually settle into its stable limit cycle that is dependent on the coupling strength, the values of the natural frequencies, and, of course, on the time delays in the interaction. Fig. 3b–d, show that by introducing time delay the nature of this limit cycle can change drastically. For τ = 0.1 (in dimensionless units of Eq. (6)) the system still exhibits a stable limit cycle but with much smaller amplitude and much slower convergence toward it. Most importantly, for a certain range of τ values, the origin becomes the attractor, which means that no matter where the system starts it will spiral in and experience amplitude death. While it is evident that τ = 0.15 is within such a region, the delay τ = 0.2 also lead to amplitude death but much slower, since it is right at the border of this range, and becomes evident only after for very long times. A better way to visualize the behavior of the system is to plot state diagrams in K–τ space. These plots show the appearance of isolated regions in which AD occurs—so called death islands. These regions depend on the average frequency, number of oscillators, and the type of oscillator used. As the number of oscillators in this model increases, the death islands become broader. In Appendix B, we show how these regions are calculated for this particular model of CO. In a realistic situation, however, a complex coupled oscillator system will likely be faced with a complicated landscape of such death traps. Thus, it will be highly beneficial for system performance if parameters τ and K are activity dependent. In this way the system can adaptively avoid death traps, or potential regions of hyper-activity, as sketched in Fig. 3f.

Discussion

At a system level, much of the activity in the brain is rhythmic and the interaction between different oscillators is critical for complex information processing. The effects of interactions between the oscillators depend on their frequencies, phases, amplitudes, as well as their propagation in the form of waves of neural activity, all of which are profoundly influenced by the conduction delays. This means that changes in myelination can also have strong effects on these oscillatory processes. Currently, the biological significance of myelin and demyelination are mainly interpreted in terms of conduction failure and spike-time arrival. Here, we emphasize that adaptive changes in myelination, i.e. myelin plasticity, could provide a cellular mechanism for modifying conduction delays to optimize rhythmic activity in the brain. Even small changes in CV resulting from subtle changes in myelination and nodal structure will have major effects on oscillatory phenomena, their interference and coupling. Ability to produce such adaptive changes in CV through myelin plasticity, would distinguish between the normal and abnormal nervous system function and development.

In the brain, the CV can be relatively slow so that delay times are comparable or greater than the needed temporal resolution for proper phase–phase and phase–amplitude interactions, and hence we cannot ignore its effects. When plasticity of CV becomes suboptimal, the deleterious effects of conduction delays on oscillatory activity in the brain could contribute to a wide range of dysfunction. Disruption in brain synchronization contributes to autism by destroying the coherence of brain rhythms and slowing overall cognitive processing speed (Welsh et al., 2005). Thalamocortical dysrhythmia is associated with schizophrenia, obsessive–compulsive disorder, and depressive disorder (Schulman et al., 2011), and the natural frequency of oscillations in the PFC are slower in individuals with schizophrenia (Ferrarelli et al., 2012). In a recent study, patients with schizophrenia could be discriminated from controls with 90% prediction accuracy by abnormal neural oscillation patterns (Xu et al., 2012) related to lexical processing (Xu et al., 2013). Dyslexic children have significantly decreased power of the 40-Hz gamma oscillation during processing of non-verbal sounds (Ucles et al., 2009). All of these examples demonstrate the importance of synchrony and oscillation in normal brain function.

A mechanism for changing CV in an activity-dependent manner seems necessary or at least advantageous to compensate for changes in axonal path length occurring during periods of growth and in response to changes in neuronal coupling as a result of changes in synaptic strength. Addressing the role of myelin plasticity in modifying the spike-time arrivals is an important topic, however, it also raises an important and difficult question as to how the local information of temporal mismatch influences oligodendrocytes further along the axons to coordinately modify the myelination. This important biological question is outside the scope of this work. Here, instead, we use models of phase and amplitude CO to argue that the myelin plasticity could provide an additional and powerful mechanism of nervous system plasticity that is complementing activity-dependent plasticity of synaptic transmission to produce stable interactions between different oscillators and hence is of great importance for the functional performance, learning, and overall dynamical stability.

To study general properties of CO we turn to the physics and dynamical systems literature. While many have studied the dynamics of CO, only a small fraction of those works treat the influence of the time-delayed interactions on collective oscillator behavior. In most studies a single delay parameter is considered, mainly because multiple delay times—one for each pair of oscillators—are difficult to analyze. We used two models which highlight the influence that time delay has on synchronization and quenching of the dynamics, and show how the delay can, together with coupling strength, modulate the frequency of synchronous oscillations, as well as how these interaction parameters, together with the description of a given non-linear oscillator, can be used to determine such properties. Since the coupling between the neurons changes, it is expected that any coupling between local oscillators will be adaptable as well. Commonly, in all the models of CO, the time delay, τ, and the coupling strength, K, were treated as control parameters determining the collective dynamics of the oscillators. Here, we suggest that treating both as adaptive is an efficient way for the system to avoid falling into “death traps”, which are inherent to the systems of CO with delayed interactions. For example, in Fig. 2d, we see that there are two synchronization regions, but the system will be trapped either inside the low-coupling strength domain, or alternatively, in the high-coupling strength region. Just changing K adaptively alone would not enable the system to switch between the two regimes. Therefore, it would appear advantageous to have more than one form of adaptation, beside coupling strengths, so that the system can navigate away from the regions of hyper-synchronization and hypo-activity as shown diagrammatically in Fig. 3f. Additionally, as indicated by the Eq. (5) for the Kuramoto model, K and τ play equivalent roles in modulating the synchronization frequency when they are entrained. This allows the system to modify the overall synaptic coupling, and still control the synchronization frequency independently.

Similar analysis that includes time delays has been done for other types of dynamics or oscillators. For example, in (Wirkus and Rand, 2002) the dynamics of the weakly coupled van der Pol oscillators in which the coupling terms have time delay, τ, produce different state diagrams. In general, the time delay not only increases the probability of the synchronized cluster state at small coupling strengths, but also causes the break-up of such clusters at large coupling strengths. This time-delay induced multi-stability is observed for different systems. The emphasis we are putting here is not on particular forms of synchronization, or the shape of the demarcation lines in the state diagrams, but the fact that a system in which the parameters are dependent on the activity can be tailored to prevent the collective dynamics for entering the regions of hyper-synchronization, or hyper-activity; or stabilize it against oscillation death, or hypo-activity. This raises some interesting clinical questions. Examples include schizophrenia and epilepsy, the former associated with hypo-activity, the latter with hyper-activity. At the same time, both are associated with the white matter abnormalities, hence, they could be the result of the brain not being able to balance and properly time activity in different cortical areas by adjusting delays, as described here. There is a diverse body of literature implicating abnormal white matter structure in a range of neuropsychiatric, neurological and developmental or learning disorders (Fields, 2008; Thomason and Thompson, 2011). For example, oligodendrocyte and myelin dysfunction have been identified as a primary cause of schizophrenia, rather than a secondary consequence of the illness or treatment (Takahashi et al., 2011). Bilateral white matter abnormalities are associated with temporal lobe epilepsy (Gross, 2011). Dysfunction of the normal left hemisphere language network implicates abnormal white matter development in dyslexia (Peterson and Pennington, 2012), and fractional anisotropy in white matter tracts in left temporo parietal and frontal areas differs from controls in people with dyslexia (Vandermosten et al., 2012).

For complex dynamical systems consisting of a set of interacting oscillators we argue that the effects of delays, caused by a finite CV, could have a profound effect on system function and collective dynamics. In particular, we showed that time delays can facilitate both synchronization and desynchronization, and when in the synchronization regime, can modulate synchronization frequency. We also show that time delays have a profound effect on the appearance and shape of the amplitude death domains, and having the adaptive time delays provides an efficient self-regulating mechanism for avoiding them. This further suggests that the myelin plasticity of CV is not only a possible form of nervous system plasticity, but may be necessary to maintain normal oscillatory activity in the developing and adult brain.

Abbreviations

CV

conduction velocity

CO

coupled oscillators

ITD

interaural time difference

PFC

prefrontal cortex

STDP

spike-time-dependent plasticity

VB

ventrobasal nucleus

WM

white matter

Appendix A. Kuramoto Model with Delay

The Kuramoto model (Kuramoto, 1975) is commonly used to study phase synchronization, in which the interaction between the corresponding oscillators is determined by the phases of the oscillators, ϕ_i, which also serve as the state variables. Here we write the general form, which includes arbitrary pair-wise time delays, τ_ij:

$$\frac{d{\varphi }_i}{dt}={\omega }_i+\sum _{j=1}^N{K}_{ij}sin({\varphi }_j(t-{\tau }_{ij})-{\varphi }_i(t))+{\xi }_i(t)$$ (1)

where ϕ_i is the phase of the ith oscillator, ω_i is its natural frequency, and K_ij is the interaction matrix. The sine function ensures that the in-phase and out-of-phase locked oscillators will be stable modes in which interaction ceases, but one can generalize this to any periodic coupling function, h. For periodic phenomena, the delay times can be adjusted to lead to complete destruction of coupling (ϕ_j(t − τ_ij) − ϕ_i(t) = 0), or, alternatively, to maximizing it when ϕ_j(t − τ_ij) − ϕ_i(t) = π/2. However, there is no clear prescription as to how the system that is capable of adjusting the timing would accomplish that in a realistic biological setting. Instead, we study global effects of timing using the mean field model in which all interactions are described by the average, mean-field coupling strength, K, and a single time delay parameter, τ, while the spread of ω_i is described by some distribution function, g(ω). In this case, the model for N oscillators can be simply written as,

$$\frac{d{\varphi }_i}{dt}={\omega }_i+\frac{K}{N}\sum _{j=1}^{N}sin({\varphi }_j(t-\tau )-{\varphi }_i(t))+{\xi }_i(t)$$ (2)

As a measure of synchrony in this model the amplitude of the average signal, r is used, which is determined using

$${re}^{i\psi }=\frac{1}{N}\sum _{k=1}^N{e}^{i{\psi }_k}$$ (3)

where ψ represents the average phase, and i is the imaginary unit. Kuramoto (Kuramoto, 1975) derived, in the absence of noise and for no time delay, that the critical coupling strength, K_c, below which r = 0, is

$$K_c=\frac{2}{\pi g(0)}$$ (4)

and that for a Lorentzian distribution g(ω) and K ⩾ K_c, the synchronization measure can be written as $r=\sqrt{1-K_c/K}$. The inclusion of time delay usually makes the synchronization harder to achieve, even though Yeung and Strogatz (1999) show that a perfect synchrony is possible in a system with a time delay. In (Niebur et al., 1991) a system with time delay is studied and it was shown that in the case of identical oscillators, ω_i = ω₀, Δω = 0, the synchronized frequency Ω satisfies the equation Ω = ω₀ − KN sin (Ωτ). This equation has multiple solutions and the lowest stable frequency is

$${\mathrm{\Omega }}_{min}\approx {\omega }_0/(1+nK\tau )$$ (5)

It was also shown that in the presence of even a minimal amount on noise, the system will settle into this state of smallest synchronous frequency. When there is no time delay, τ = 0, the dynamical system loses its ability to modulate the frequency, but when both K ≠ 0 and τ ≠ 0, the system will be able to adjust the synchronous frequency through the interaction parameters, without changing the constituent oscillator's properties. We deem this an important property for an adaptive complex system. If the delays are fixed then the system can adjust its frequency only by adjusting the coupling strengths, but this can be a limitation, since then the level of synchrony cannot be manipulated. For example, it has been found that the neuronal dynamics shows signatures of self-organized criticality (Beggs and Plenz, 2003), hence even in this case it might be desirable for the system to keep the coupling close to the critical value, in order to avoid overwhelming synchrony as encountered in epilepsy. This would then limit the ability to modulate the frequency, unless the temporal delays are also allowed to adjust adaptively.

Appendix B. Amplitude Response of Coupled Oscillators with Delay

In Reddy et al. (1998), motivated by works of Bar-Eli (1985) and Aronson et al. (1990), a generalized diffusively and linearly coupled oscillator model is studied as a function of time-delay. The model is well suited to study both the amplitude and the phase relationships among the CO with time delay and in the case of two CO can be written as

$$\begin{array}{l}\frac{{dZ}_1(t)}{dt}=(1+i{\omega }_1-|Z_1(t){|}^2)Z_1(t)+K(Z_2(t-\tau )-Z_1(t)),\\ \frac{{dZ}_2(t)}{dt}=(1+i{\omega }_2-|Z_2(t){|}^2)Z_2(t)+K(Z_1(t-\tau )-Z_2(t)),\end{array}$$ (6)

where Z₁(t) and Z₂(t) are complex numbers which describe both amplitudes and phases of two oscillators at time t. Note that if the system spends longer than τ time at point P_AD, defined as Z₁ = Z₂ = 0, it will remain in it forever. The stability of point P_AD will determine if the system is likely to gravitate toward such a point or be kicked out of it, if any amount of noise is introduced in the system. For a certain range of dynamical parameters (K, δω, τ) such a point will be stable, i.e., the dynamics of the system will likely lead to the amplitude death, and the range of parameters for which it happens will define the amplitude death regions (see Fig. 2c). It was found in (Aronson et al., 1990) for the case of no time delay τ = 0 and finite coupling strength, K ≠ 0, that the conditions for the existence of amplitude death regions in a δω–K state diagram are

$$K>1,\text{and}\delta \omega >2\sqrt{2k-1}$$ (7)

In Reddy et al. (1998), using linear stability analysis around point Z₁ = Z₂ = 0 it was found that AD regime is stable if

$$(1-K)\alpha =K^{2}sin(\alpha t\pm 2\overline{\omega }\tau )$$ (8)

where α is a function of K and δω as follows,

$$\alpha =\sqrt{\delta {\omega }^2-4{(1-K)}^2\pm 4\sqrt{K^4-{(1-K)}^2\delta {\omega }^2}}.$$ (9)

For τ = 0, this system naturally reduces to Eq. (7), while in the case of identical oscillators, ω₁ = ω₂ = ω, the equations for the amplitude death boundaries are as follows,

$$\tau =\frac{arccos(1-1/K)}{\omega -\sqrt{2K-1}}$$ (10)

and

$$\tau =\frac{\pi -arccos(1-1/K)}{\omega +\sqrt{2K-1}}$$ (11)

The region enclosed by these two curves corresponds to the death island regions depicted in Fig. 3e.