Coarse guidance by numerosity in visual search

Abstract

In five experiments, we examined whether the number of items can guide visual focal attention. Observers searched for the target area with the largest (or smallest) number of dots (squares in Experiment 4 and “checkerboards” in Experiment 5) among distractor areas with a smaller (or larger) number of dots. Results of Experiments 1 and 2 show that search efficiency is determined by target to distractor dot ratios. In searches where target items contained more dots than did distractor items, ratios over 1.5:1 yielded efficient search. Searches for targets where target items contained fewer dots than distractor items were harder. Here, ratios needed to be lower than 1:2 to yield efficient search. When the areas of the dots and of the squares containing them were fixed, as they were in Experiments 1 and 2, dot density and total dot area increased as dot number increased. Experiment 3 removed the density and area cues by allowing dot size and total dot area to vary. This produced a marked decline in search performance. Efficient search now required ratios of above 3:1 or below 1:3. By using more realistic and isoluminant stimuli, Experiments 4 and 5 show that guidance by numerosity is fragile. As is found with other features that guide focal attention (e.g., color, orientation, size), the numerosity differences that are able to guide attention by bottom-up signals are much coarser than the differences that can be detected in attended stimuli.

Introduction

Consider the problem of choosing one out of many raspberry bushes as a location to forage for food. All else being equal, one would want to select the bush bearing the largest number of fruits. As we look at an array of bushes, how well can our attention be guided to the best bush? Surely, a difference between 95 and 100 berries would not guide our choice, and, surely, the difference between 1 and 100 would guide. The goal of this article is to determine how effectively numerosity can guide the deployment of attention.

In the laboratory, the attributes of visual objects that can be employed to control the deployment of focal attention are studied using visual search tasks. Translating the raspberry example into the laboratory, searching for the most fruit-laden bush can be replaced with a search for the patch with the largest number of dots (target item) presented among patches with a smaller number of dots (distractor items). The total number of patches shown in the display is referred to as the set size. The slopes of the reaction times (RTs) × set size function reflect the cost of adding an item to the display. Searches that produce slopes near zero (i.e., increasing the number of distractor items produces no or little increase in RT) can be labeled as “efficient search” (Wolfe, 1994). Efficient search is one hallmark of an attribute that guides attention. The search is efficient because the presence of a unique guiding feature allows attention to be directed to the target item without multiple, random allocations of attention to other items that lack the feature (Wolfe, 1994).

It has repeatedly been demonstrated that target items that differ from distractors in one of a limited set of attributes will efficiently attract attention to their location. These guiding attributes include color, motion, orientation, and size (see Wolfe & Horowitz, 2004, for a more complete list). The differences between targets and distractors that will produce efficient search are not the same as the differences that we consciously perceive. First, efficient guidance requires larger differences than just noticeable perceptual differences (JNDs; Nagy & Sanchez, 1990). Second, those larger differences are not merely the JNDs multiplied by some factor. Guiding attributes have different properties than their perceived cousins. Guidance is more effective if the target is categorically unique (e.g., the only “steep” or the only “green” item; Wolfe, Friedman-Hill, Stewart & O’Connell 1992; Yokoi & Uchikawa, 2005). Moreover, differences that are perceptually equivalent can produce very different search results (Lindsey et al., 2010). Thus, the specific mechanisms of guidance for guiding attributes need to be determined empirically.

The list of guiding attributes includes uncontroversial ones such as color, motion, orientation and size (see above); other attributes (e.g., shininess or facial emotion) are less certain (see Wolfe & Horowitz, 2004, for a list). To restate the purpose of the present paper: Is numerosity capable of guiding focal attention?

Many studies using discrimination tasks have shown that small numbers in the range of about 1–4 are represented in a qualitatively different manner than larger numbers (Burgess & Barlow, 1983; Carey, 2001; Kaufman, Lord, Reese & Volkmann 1949; Trick & Pylyshyn, 1994; Xu & Spelke, 2000). Of course, larger numbers can be counted, but in a brief glimpse their numerosity must be estimated, while the numerosity of a smaller set can be directly ascertained (“subitizing”; Kaufman et al., 1949). In the present study, our aim is to investigate the guiding capabilities of larger numbers that fall in the estimation range.

While there do not seem to have been visual search experiments that directly study the guiding properties of numerosity outside of the subitizing range, relative numerosity has been studied using discrimination tasks. In a typical discrimination task, observers are briefly presented with patches of randomly arranged dots (see Fig. 1), and their task is to judge whether the two patches, presented simultaneously at different locations or sequentially at the same location, contain the same or different number(s) of dots; alternatively, observers might indicate which one of two patches (separated spatially or temporally) contained the larger or smaller number of dots (e.g., Barth, Kanwisher & Spelke 2003).

Fig. 1.

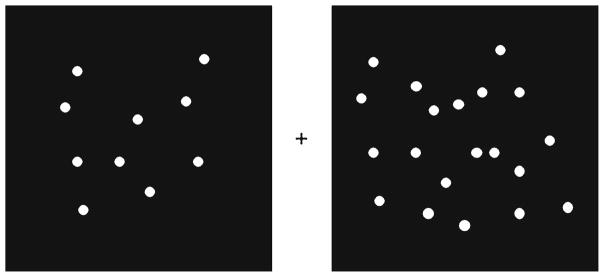
An example of a stimulus display that might be shown in a numerosity discrimination task

The results of discrimination tasks indicate that humans can represent numbers as mental magnitudes. However, these number representations are not accurate; rather, they show what is referred to as scalar variability. That is, the signal encoding the magnitude is noisy, “it varies from trial to trial, with the width of the signal distribution increasing in proportion to its mean” (Gallistel & Gelman, 2000, p. 59).

As might be expected from the ubiquity of Weber’s law, the ratio between the two stimuli seems to be the critical feature for successful numerosity discriminations. Discrimination tasks have shown that, when two patches are compared, the task gets harder as the number of dots gets larger (e.g., 8 dots vs. 9 dots is harder than 1 dot vs. 2 dots); this is the size effect. The task also gets harder when the difference between numerosities is smaller (e.g., 1 dot vs. 2 dots is harder than 1 dot vs. 9 dots); this is the distance effect (Cantlon & Brannon, 2006). This Weber law behavior was found in a number of numerical comparison tasks in human adults (e.g., Barth et al., 2003; Tokita & Ishiguchi, 2010), as well as in children (Xu, 2003; Xu & Spelke, 2000). It has been shown that adults can discriminate numbers that differ by at least a 7:8 ratio; that is, they can reliably discriminate patches with 7 dots versus 8 dots or 14 dots versus 16 dots (Barth et al., 2003; Halberda & Feigenson, 2008; Pietroski, Lidz, Hunter & Halberda 2009; van Oeffelen & Vos, 1982). For children, the ratio appears to be age dependent. For example, Xu, Spelke, and Goddard (2005; see also Lipton & Spelke, 2003, 2004; Xu, 2003; Xu & Spelke, 2000) have shown that, for infants 6 months of age, numerosity must differ by at least a ratio of 1:2 (e.g., 8 dots vs.16 dots) in order for discrimination to be accurate. For children 9 months of age, a ratio of 2:3 (e.g., 8 dots vs. 12 dots) is sufficient to permit accurate discrimination.

Two classes of proposals have been offered to describe the processes that might underlie the construction of our mental representation of quantity. The debate focuses on whether numerosity judgments are about number per se or whether judgments are derived from visual properties like density, area, distance between elements, and so forth. The finding that approximate numerosity judgments are strongly influenced by sensory properties of the stimulus seems to favor the account of derived numerosity. As an example, Durgin (1995, 2008) showed that density and regularity of the stimulus pattern affect numerosity judgments in human adults. Ross (2003) observed a somewhat different pattern of results: Density did not affect judgments, while the size of the dots did. Other authors (e.g., Allik, Tuulmets & Vos 1991; Burgess & Barlow, 1983; Burr & Ross, 2008; Krueger, 1972) have argued that numerosity perception is independent of such variables. They have argued that visual stimulation directly feeds into a numeric representation. In support of this view, Cantlon and Brannon (2006) showed that performance in a discrimination task was unaffected by density, surface area, and perimeter.

For present purposes, we do not need to take sides in this debate. However, it will be necessary to show how any claims about guidance by number are related to guidance by some other property, such as density. Intuition suggests that there must be some ratio of numerosity that will support efficient search for high-number targets among low-number distractors. On the basis of prior work with other attributes, it is likely that the ratio of high to low number required for efficient search will be greater than that required for discrimination. Furthermore, search based on numerosity might be “asymmetric.” That is, a ratio that permits efficient search for a high-numerosity target among low-numerosity distractors might not permit efficient search for a low-numerosity target among high-numerosity distractors. Such an asymmetry could arise if high numerosity was the feature, since Treisman has argued that it is often easier to find the presence of a feature than to detect its absence (Treisman & Gormican, 1988; Treisman & Souther, 1985). For example, in motion search, it is easier to find the only moving target than it is to find the only stationary target (Dick, Ullman & Sagi 1987; Royden, Wolfe & Klempen 2001). To anticipate our results, we find that numerosity can guide attention. The required ratios are larger than those for discrimination. The ratios get larger still when factors like density are controlled. Finally, while there is an asymmetry, it is possible to search efficiently for the lower numerosity target if the ratio is large enough.

There are a few studies that have involved visual search for some aspect of number. Numerosity was listed only as a “possible” attribute by Wolfe and Horowitz (2004), because the empirical evidence was limited at that time. One of the very few search studies that includes numerosity as an attribute defining the target was Experiment 3 in Treisman and Gormican (1988). In Treisman and Gormican’s study, observers had to search for a target defined by a pair of lines among single lines or vice versa. Search for a target defined by a pair of lines was efficient. Search for the single line among pairs was inefficient. The Treisman and Gormican study was limited to very small numbers, well within the subitizing range where observers might be expected to know immediately that this thing contained one item and that thing contained two (Sagi & Julesz 1985). In a different approach to the role of number in search in the subitizing range, Found and Müller (1996, Experiment 3) had observers decide whether there were three or four target items in displays containing a fixed number of 25 items. The target items were defined by color, by orientation, or on both the color and orientation dimensions. They found that RTs for three-item trials were longer than RTs for four-item trials. This might seem to be a rather unusual result. Normally “four” responses take longer than “three” responses in numerosity studies. However, Folk, Egeth, and Kwak (1988), having found a result similar to that in Found and Müller, proposed, quite reasonably, that the four-item responses involved less uncertainty than the three-item responses. If you find three, you might still find a fourth. If you find four, you know you are done. Regardless, Found and Müller’s Experiment 3 involved a response based on number, but not a search for number. Our experiments involve targets that are defined by their numerosity, not by another basic feature.

Experiment 1

Experiment 1 was designed to investigate whether numerosity guides attention and, if so, whether guidance follows the predictions of Weber’s law; that is, we test whether the efficiency of search performance is based on the target-to-distractor ratio or, alternatively, on the absolute difference of target and distractor number.

Method

Observers

Eight observers (6 female, 2 male) between 21 and 26 years of age (M = 23.4 years, SD = 1.7) were recruited from the participant pool of Fribourg University. Observers were paid at a rate of CHF 10 (approximately US$10), or they received course credit. All observers had normal or corrected-to-normal visual acuity and color vision. Observers were naïve as to the purposes of the experiment.

Apparatus and stimuli

Experiment 1 was run on a personal computer running the Windows XP professional operating system. Experiments were programmed in MATLAB 7.5.0 using Psychophysics Toolbox version 3.0.8 (Brainard, 1997; Pelli, 1997). Stimuli were presented on a 19-in. Philips Brilliance 202P7 cathode ray tube monitor. Viewing distance was about 80 cm.

Observers were presented with arrays of gray squares (RGB: 64, 64, 64) each subtending an area of 2.7° × 2.7° of visual angle. Each square contained 10, 20, or 30 circular dots with each dot subtending 0.2° × 0.2° of visual angle. Dots were all green (RGB: 0, 255, 0). For each “numerosity”, ten different dot configurations were created. The squares were presented on a gray background (RGB: 127, 127, 127). Three, 8, or 13 squares were positioned at random locations within a virtual grid of 4 × 4 cells. Square positions were randomly jittered relative to cell centers, with offsets in the range of 0.4° horizontally and vertically. On target-present trials, one of the squares (the target) contained either a larger or smaller number of dots, as compared with the other squares (the distractors); all distractor squares contained the same number of dots and had the same dot configuration (for a different approach, see Experiment 4). Within a block of trials, all targets had the same number of dots; the same was true for the distractors. Targets were presented on 50 % of the trials (target-present trials); on the remaining trials, all squares contained the same number of dots (target-absent trials).

Procedure

Observers were instructed to indicate, as rapidly and accurately as possible, whether a target was present or absent in the search array by pressing one of two designated keys on a standard keyboard. Each trial started with the presentation of an auditory warning signal (a beep of 100-ms duration) followed, after a delay of 100 ms, by the simultaneous onset of all the search items. The search array remained visible until the observer responded. At the end of each trial, participants were given feedback on whether the response was correct or not.

There were six conditions, corresponding to the six possible combinations of dot number in target and distractor squares: 10-dot target/30-dot distractors, as well as 10/20, 20/30, 30/10, 20/10, and 30/20. Data were analyzed in a 2 × 3 factorial design with the between-subjects factors of target-to-distractor polarity (i.e., was the target defined by a larger or smaller number of dots than the distractors) and target-to-distractor ratio (0.33 [10:30, 30:10], 0.50 [10:20, 20:10], 0.67 [30:20, 20:30]). For purposes of statistical analysis, ratios were calculated by dividing the smaller number of dots by the larger number of dots, irrespective of whether target or distractor squares contained the relatively larger (smaller) dot number. We will call this the absolute ratio. In Tables 1 and 2 and Figs. 2, 4, and 9, for the sake of clarity, we use ratios calculated by dividing target dot number by distractor dot number. This produces ratios less than and greater than 1.0—specifically, 0.33 (10:30), 0.50 (10:20), 0.67 (20:30), 1.50 (30:20), 2.00 (20:10), 3.00 (30:10). We will refer to this as the ratio. In each condition, participants completed 25 practice trials, followed by 300 experimental trials. The sequence of conditions was counterbalanced across observers. The total duration of the experiment was about 40 min.

Table 1.

Slopes (milliseconds/item) and errors (percentages) for Experiments 1–3 and each target-to-distractor ratio

Experiment	Slopes in ms/item (SE)					Errors (%)
	1 (n = 8)	2 (n = 10): Small set	2 (n = 10): Large set	3 Dot (n = 10)	3 Array (n = 10)	1 (n = 8)	2 (n = 10): Small set	2 (n = 10): Large set	3 Dot (n = 10)	3 Array (n = 10)
Ratio
0.33	3.7 (0.5)			4.0 (1.2)	6.3 (1.3)	7.7 (1.3)			8.8 (1.6)	14.4 (2.0)
0.50	7.0 (1.0)	9.9 (1.0)		24.7 (2.2)	30.7 (4.6)	12.0 (2.2)	5.5 (1.7)		13.3 (2.1)	14.3 (1.7)
0.67	9.6 (2.7)	21.7 (3.3)	13.2 (2.2)	28.2 (2.1)	28.1 (3.5)	21.2 (4.2)	10.1 (1.3)	11.6 (2.8)	27.8 (3.4)	29.9 (2.7)
0.75		29.2 (7.9)					22.5 (3.6)
0.80			31.3 (11.0)					26.6 (4.4)
0.83			34.8 (10.0)					30.5 (4.5)
1.20			23.0 (5.2)					27.8 (4.0)
1.25			25.2 (7.4)					27.0 (3.4)
1.33		14.7 (3.8)					19.0 (2.6)
1.50	11.7 (2.6)	10.3 (1.5)	4.6 (1.9)	32.7 (2.8)	34.0 (4.3)	9.4 (1.8)	15.5 (2.8)	7.3 (1.8)	16.6 (2.3)	19.8 (1.7)
2.00	2.3 (0.9)	7.0 (1.4)		10.8 (2.8)	8.8 (2.3)	9.3 (1.5)	4.9 (1.6)		15.5 (1.2)	16.8 (1.9)
3.00	0.3 (0.3)			2.5 (0.6)	1.1 (0.5)	6.8 (0.8)			8.3 (1.4)	7.8 (1.0)

Table 2.

Pearson correlations between reaction times and normalized target ranks for square area, total dot area, and density

Set Size	Ratio	Square area			Total dot area			Density
		Correl.	Sig.	N	Correl.	Sig.	N	Correl.	Sig.	N
6	0.33	.319	n.s.	16	.552	n.s.	16	−.039	n.s.	16
6	0.50	.521	n.s.	16	.759	n.s.	16	.148	n.s.	16
6	0.67	.133	n.s.	16	.583	n.s.	16	.731	n.s.	16
6	1.50	−.928	p < .01	16	−.376	n.s.	16	.110	n.s.	16
6	2.00	−.956	p < .01	16	−.804	n.s.	16	−.746	n.s.	16
6	3.00	−.998	p < .01	16	−.738	n.s.	16	.733	n.s.	16
12	0.33	−.312	n.s.	16	−.321	n.s.	16	.032	n.s.	16
12	0.50	−.254	n.s.	16	.172	n.s.	16	.327	n.s.	16
12	0.67	.192	n.s.	16	−.315	n.s.	16	−.210	n.s.	16
12	1.50	−.767	p < .01	16	−.415	n.s.	16	−.609	p < .05	16
12	2.00	−.861	p < .01	16	−.276	n.s.	16	.395	n.s.	16
12	3.00	−.883	p < .01	16	.156	n.s.	16	.014	n.s.	16

Note. No Bonferroni corrections were applied.

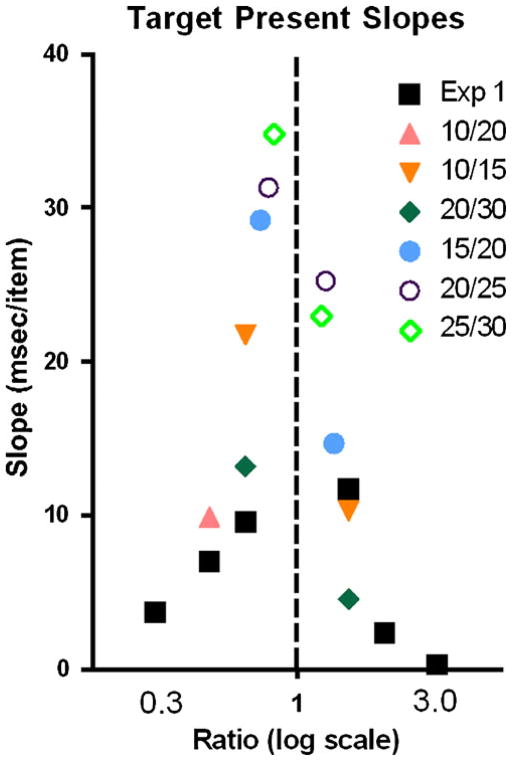
Fig. 2.

Slopes of reaction time × set size functions as a function of the ratio of target-to-distractor numerosity (plotted on a log scale). Black squares show results for the 6 conditions of Experiment 1. Colored shapes show the 12 conditions of Experiment 2. Legend gives the target and distractor numerosity. For points to the left of a ratio of 1.0, the smaller number represents the target numerosity. For points to the right, the larger number represents target numerosity

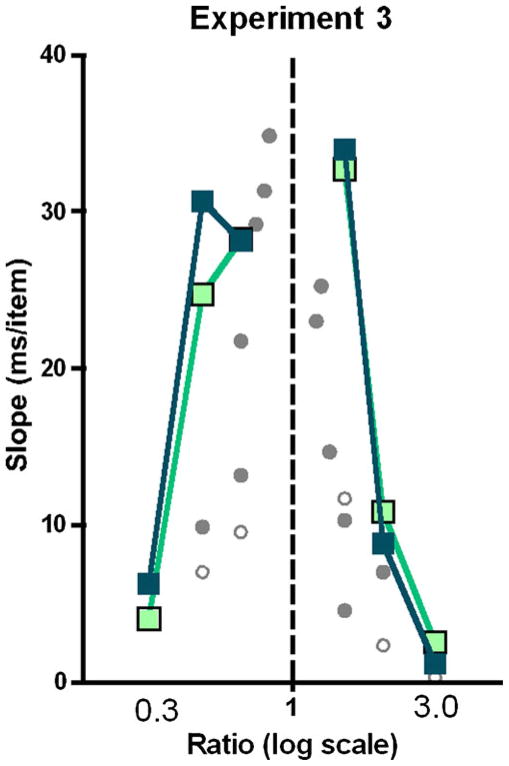
Fig. 4.

Colored squares show the data from Experiment 3 (light/open symbols = variable dot size conditions, dark = variable array size). Gray dots replot the slopes of Experiments 1 (open circles) and 2 (filled circles). Note that some conditions that produced efficient search in Experiments 1 and 2 become inefficient once cues like density are made useless

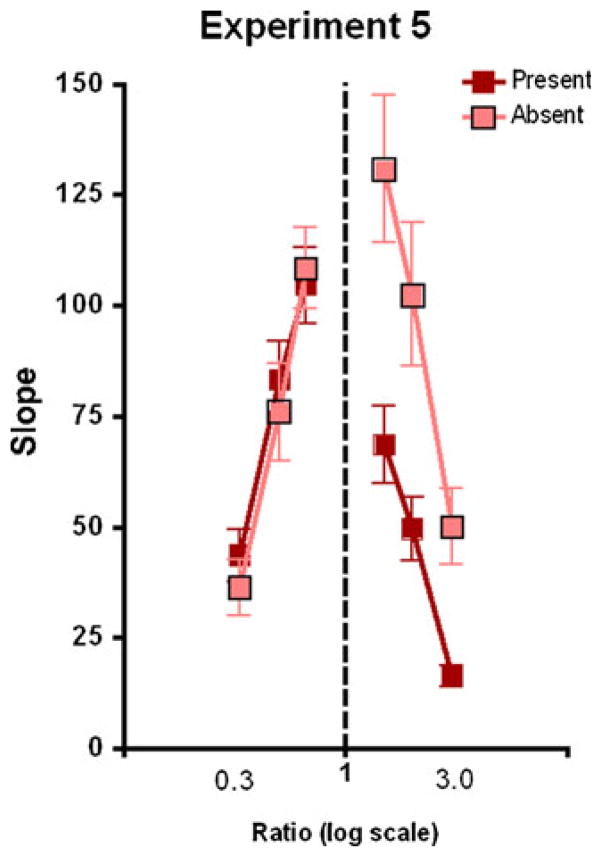
Fig. 9.

Colored squares show the data for Experiment 5 (light/open symbols = target-absent trials, dark = target-present trials)

Results

Responses that were incorrect and RTs that were below 200 or above 2,000 ms were excluded. A total of 8.52 % (incorrect = 8.47 %, too short/long = 0.05 %) of the trials were removed from analysis. For each observer and each condition, the slopes of the RT × set size function of target-present trial RTs were calculated.

Slope analysis

Figure 2 (see also Table 1) shows mean slopes for Experiments 1 and 2. Black squares show Experiment 1 as a function of ratio for the six experimental conditions. All these searches were relatively efficient, with efficiency increasing as the absolute ratio [or log(ratio)]¹ deviated more markedly from 1.0. If the results were based on the absolute difference in dot number, then 10/20, 20/30, 30/20, and 20/10 conditions—with their 10-dot differences—should all produce similar efficiencies. This does not appear to be the case. A 2 (polarity) × 3 (absolute ratio) repeated measures analysis of variance (ANOVA) was performed on the slope data. The ANOVA revealed a linear trend of absolute ratio, F(1, 7) = 17.65, p < .01, η² = .716, indicating that search becomes more efficient as the absolute ratio moves further from 1.0. The main effect of polarity, F(1, 7) = 4.96, p = .061, η² = .415, was not significant, indicating that there is no difference between search for targets defined as the larger or smaller number of dots. The interaction between polarity and absolute ratio, F(1, 7) = 4.35, p = .075, η² = .384, was not statistically significant.

Error rates

Error rates are given in Table 1. Though error rates seem to be quite high, they are comparable with the error rates of others studies (see Tokita & Ishiguchi, 2010). Error rates were subjected to a 2 (polarity) × 3 (absolute ratio) repeated measures ANOVA. The results reveal the linear trend for absolute ratio, F(1, 7) = 12.33, p < .05, η² = .638, to be significant. Here, the main effect of polarity is also significant, F(1, 7) = 8.60, p < .05, η² = .551, as is the interaction between polarity and absolute ratio, F(1, 7) = 34.82, p < .01, η² = .833. That is, more errors were made with smaller ratios and when the target was the item with the smaller number of dots.

Discussion

The results of Experiment 1 show that numerosity is able to guide attention efficiently, provided that the ratio is sufficiently different from 1.0.

Search efficiency seems to be systematically related to ratio, rather than to the absolute difference in dot number. This is more clearly seen in Experiment 2, where the range of ratios is extended.

Experiment 2

Experiment 2 was designed to test whether target-to-distractor ratio exclusively controls guidance (strict Weber’s law) or whether there is an effect of absolute number of target and distractor dots (size effect) or the relative numerical distance between target and distractor dots (distance effect). To assess the size effect, two sets of stimuli were used in Experiment 2 differing in the absolute number of the dots (i.e., 10/15 as compared with 20/30). Additionally, a different range of ratios (to put the distance effect to test) was used while the range (10–30) of dot numbers used was the same as in Experiment 1.

Method

Observers

Ten observers (all female) between 19 and 22 years of age (M = 20.7 years, SD = 1.1) were tested. All met the same requirements as in Experiment 1.

Stimuli and procedure

The experimental setup of Experiment 2 was the same as that in Experiment 1, with the following changes. There were 12 conditions: 10-dot target/20-dot distractor, 10 dots among 15 dots, 15 dots among 20 dots, 20 dots among 30 dots, 20 dots among 25 dots, 25 dots among 30 dots, and the reverse conditions. The 12 conditions can be organized into a 2 × 2 × 3 factorial design with the within-subjects factors of absolute size of the set (small, numbers 10–20; large, numbers 20–30), polarity (target square is the one with the larger or smaller number of dots), and absolute ratio (0.50, 0.67, 0.75 or 0.67, 0.80, 0.83). Although there are two ratios of 0.67, they differed in the way they were generated (10-dot target/15-dot distractors or 20-dot target/30-dot distractors, respectively). The sequence of presentation of sets and of the conditions within sets was counterbalanced between observers.

Results

Trials with responses that were incorrect and those with RTs that were below 200 or above 4,500 ms were excluded (for further details, see Experiment 1), leading to the removal of a total 11.33 % (incorrect = 11.26 %, too fast/slow = 0.07 %) of the trials.

Slope data

Experiment 1 demonstrated that search efficiency increases with larger target:distractor ratios. Comparing 10/15 with 20/30 (with identical ratios) and vice versa allows us to test whether the absolute number of target and distractor dots could also have affected search efficiency, in the sense that observers take longer to detect the target in larger set sizes. However, paired-samples t-tests showed that slopes do not increase with set size when the ratio is held constant [comparing 10/15 with 20/30, t(9) = 1.91, p = .089]. At a ratio of 1.5:1, if anything, participants were faster for larger set sizes [comparing 15/10 with 30/20, t(9) = 3.13, p < .025 (Bonferroni corrected)].

Experiment 1 showed only a marginal effect of polarity. In Experiment 2, a 2 (polarity) × 6 (absolute ratio) repeated measures ANOVA showed a significant main effect of polarity, F(1, 9) = 9.11, p < .05, η² = .503. The effect of polarity can also nicely be seen in Fig. 2. For each pair of points (10/20 vs. 20/10, etc.), the data point is higher to the left of the vertical line that represents parity between target-to-distractor ratios. Search for a target with fewer dots than the distractors produces less efficient search than does search for a target with a greater number of dots than the distractors.

Finally, Experiment 2 was designed to further examine the effect of ratio on the slope of the set size×RT function. To assess this, a linear mixed model investigated the effect on the slope of the ratio variable (as a fixed effect). Since repeated measurements are made on each observer (the response variable of each observer is measured at various ratios), we assume that error terms within an observer are correlated. The residual error covariance was taken into account into the model by including a block diagonal matrix, where each block was a first-order autoregressive covariance matrix. The correlation parameter was relatively large (.371), and the p-value of the Wald test was less than .001. Thus, ignoring these correlations could lead to incorrect results. The test of the fixed effect showed that ratio has a significant effect on slopes, t(65.089 Satterthwaite approximation) = 3.924, p < .001.

Error data

Error rates were analyzed in the same way as the slopes. Similar to the slopes, error rates do not increase with set size [comparison of 10/15 with 20/30: t(9) = 0.40, p = .696], and again, if anything, participants made fewer errors on trials with larger set sizes [comparison of 15/10 with 30/20: t(9) = 3.55, p < .025 (Bonferroni-corrected)]. In contrast to the slope data, a 2 (polarity) × 6 (ratio) repeated measures ANOVA did not show a significant main effect of polarity, F (1, 9) = 1.03, p = .337, η² = .103. Finally, ratio significantly affected error rates, t(74.877) = 6.386, p < .001 (the correlation parameter [value = .078] was also significant; the p-value of the Wald test is less than .001).

Discussion

As in Experiment 1, search efficiency (i.e., slopes of the set size × RT function) in Experiment 2 is determined by the proportions of target and distractor numbers. Furthermore, the absolute number of dots did not affect slopes. The absence of an effect of absolute number has been reported by others for discrimination tasks (Barth et al., 2003; Tokita & Ishiguchi, 2010). In our search tasks, when ratios were held constant, slopes tended to decrease as the total number of dots became larger. As was mentioned in the introduction, a comparable effect was observed by Barth et al. in a discrimination task. On the basis of these results, we would agree with Barth et al. that number estimations are not derived from an iterative counting-like process, because such an iterative mechanism would presumably require more time to enumerate larger sets.

Experiment 3

In Experiments 1 and 2, the dots and the squares were of fixed size; consequently, numerosity covaried with perceptual factors like density, interitem distance, and area covered by dots. Experiment 3 makes these factors unreliable guides to the target.

Method

Observers

Ten observers (6 female, 4 male) between the ages of 20 and 26 years (M = 22.8 years, SD = 2.3) were tested, meeting the same requirements as in the previous experiments.

Stimuli and procedure

In Experiment 3, the experimental setup was the same as in Experiment 1, with the following changes. In order to control for “filled” area and density, two different dot sizes (0.1° × 0.1° and 0.2° × 0.2°) and area sizes (1.8° × 1.8° and 3.1° × 3.1°) were used. As an example, in an array, all dots could be all small, and half of the squares in the array small and half of them big (see Fig. 3d); the target square could either be the small or the big square. Figure 3 gives all the possible combinations of targets and distractors used in Experiment 3. The display types shown in Fig. 3 were randomly mixed within a block of trials. Set sizes of 4, 10, and 16 squares were used in order to create arrays with half of the squares containing small or big dots. Similarly, half of the squares were small or large.

Fig. 3.

Examples of displays presented in Experiment 3. a Search for a target with 30 dots among distractors with 20 dots; squares are all big, and dots are either small or big. b Search for a target with 10 dots among distractors with 30 dots; squares are either small or big, and all dots are big. c Search for a target with 10 dots among distractors with 30 dots; squares are all small, and dots are either small or big. d Example of nontarget display. Distractors all contain 30 dots; squares are either small or big, and all dots are small

Results and discussion

Trials with incorrect responses and RTs below 200 or above 4,000 ms were excluded, leading to the removal of 11.87 % (incorrect = 11.59 %, too fast/slow = 0.28 %) of the trials.

Figure 4 shows the slope of the RT × set size functions for Experiment 3 dependent on the ratio of target to distractor number. Dark lines and closed symbols show the data for variable array size conditions, and light lines with open symbols show the data for variable dot size conditions. The two conditions produce essentially the same result; a 2 (manipulation: variable dot or array size) × 2 (polarity) × 3 (absolute ratio) repeated measure ANOVA of slopes showed that the main effect of manipulation was not significant, F(1, 9) < 1, n.s. In both cases, search is efficient only when the target-to-distractor ratio is 3:1 or 1:3.

Figure 4 also shows the slopes of Experiments 1 and 2, replotted as gray dots. As can be seen in Fig. 4, slopes for Experiment 3 lie above slopes for comparable ratio conditions in Experiments 1. The difference is statistically reliable; an ANOVA with the within-subjects variables of polarity and absolute ratio and the between-subjects variable of experiment showed not only significant main effects of absolute ratio [linear trend: F(1, 16) = 145.281, p < .001, η² = .901] and experiment, F(1, 16) = 49.684, p < .001, η² = .756, but also a significant linear trend × experiment interaction, F(1, 16) = 38.982, p < .001, η² = .709. That is, the difference in slopes between Experiments 1 and 3 gets larger as the ratio becomes smaller.

The added difficulty of the Experiment 3 conditions suggests that cues like density may have helped to guide search in Experiments 1 and 2. Once those cues are eliminated, target:distractor ratios that were quite efficient (e.g., in the 2:1, 1:2 range) become markedly less efficient. On the other hand, it is also well-known that increased irrelevant variation can make search less efficient, and the displays in Experiment 3 are “noisier” than those in Experiments 1 and 2. In either interpretation, it is clear that performance is less efficient in Experiment 3 than in Experiments 1 and 2, and this indicates that numerosity is, at best, a rather fragile guiding feature.

As in the earlier experiments, a 2 (manipulation: variable dot or array size) × 2 (polarity) × 3 (absolute ratio) repeated measures ANOVA of slopes showed a significant effect of absolute ratio, F(1, 9) = 202.25, p < .001, η² = .975, and it remains easier to find a larger number among smaller ones than vice versa, F(1, 9) = 20.46, p < .01, η² = .694.

To summarize, the pattern of results of Experiment 3 is similar to that of Experiment 1, except that varying total filled area and/or dot density causes performance to decline. This result suggests that area and density may have provided some guidance in the previous Experiments 1 and 2. However, target-to-distractor ratios of 3:1 and 1:3 still yielded efficient search in Experiment 3, indicating an ability to use large differences in numerosity to guide the deployment of attention.

Experiment 4

Rather “simple” stimuli were used in Experiments 1–3: Gray squares containing irregularly spaced but nonoverlapping circular green dots. However, a look at the outside world shows that stimuli, like the raspberries of our initial example, can vary in size and color. Moreover, they might partially occlude each other. Nevertheless, we can still assess their numerosity. Experiment 4 tested whether guidance of attention by numerosity survives when the stimuli are squares of different size containing colored and overlapping items of different sizes.

Method

Observers

Sixteen observers (13 female, 3 male) between the age of 19 and 46 years (M=24.1 years, SD=6.9) were tested, meeting the same requirements as in the previous experiments.

Stimuli and procedure

Sample stimuli for Experiment 4 are shown in Fig. 5. The experimental setup was the same as in Experiment 1, with the following changes. Randomly colored squares (subtending between 0.1° and 0.2° visual angle in width and height) were presented in “larger” gray-colored (RGB: 50, 50, 50) squares (subtending between 1.3° and 2.7° visual angle in width and height; see Fig. 5). The larger squares (6 or 12; i.e., the set size) were presented on a greenish (RGB: 50, 150, 75) background (subtending 15.9° visual angle in width and height).

Fig. 5.

Example of the displays presented in Experiment 4

We additionally recorded the rank of the target stimulus for its square size, total dot area, or density for each search array. For example, if the target stimulus had the largest density, it would be ranked “1” for density. It might have other ranks for area or size if the target stimulus had the largest density it would be ranked “6” or “12,” depending on the set size of the search array.

Results and discussion

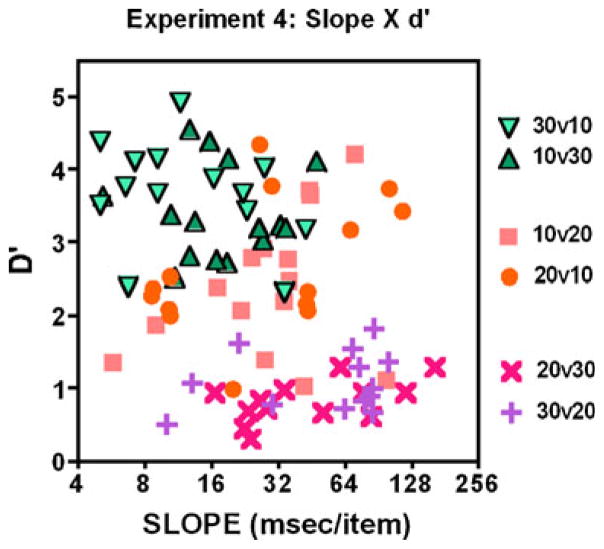
The very “noisy” stimuli used in Experiment 4 produced a wide range of RTs, RT × set size slopes, and error rates. RT analysis becomes questionable in the presence of large error rates. Accordingly, it is more useful to look at the joint pattern of search efficiency and errors. Thus, in Fig. 6, we plot the signal detection measure, d′, against the slope of the RT × set size function for each observer in each of the six conditions (slopes are plotted on a log scale only for graphical convenience).

Fig. 6.

Scatterplot of d′ × set size of the reaction time×set size function. Each data point represents the performance of one observer in one condition. The d′ values are based on corrected false alarm rates. If there were no false alarms for one observer in one condition, 0.5 false alarms were added. Slopes are plotted on a log axis only for convenience. One data point in the 30:10 condition is missing (slope = 0.8, d′ = 2.8)

Overall, while performance was worse in Experiment 4 than in the other experiments, the main pattern of results was similar. With a 3:1 ratio of target to distractor numerosity, performance was quite good, with observers showing high d′ and relatively low slopes. Certainly, a substantial subset of the observers could perform the 3:1 task with low error rates and a low slope. Performance was somewhat weaker in the 1:3 condition. After that, performance degraded dramatically. The 2:1 and 1:2 conditions show a strong speed–accuracy trade-off. Observers could do the task either quite efficiently or quite accurately, but not both. The 2:3 and 3:2 conditions were very hard (d′ hovers near 1.0) and generally inefficient.

The average slopes were 20.4 ms/item (10:30), 32.5 ms/item (10:20), 40.5 ms/item, (20:30), 52.8 ms/item (30:20), 39.1 ms/item (20:10), and 15.0 ms/item (30:10). The main trends apparent in the data are statistically reliable. A 2 (polarity) × 3 (absolute ratio) repeated measures ANOVA on d′ showed a significant linear trend for absolute ratio, F(1, 15) = 482.35, p < .001, η² = .970. Here, the main effect of polarity is also significant, F(1, 15) = 11.614, p < .01, η² = .436. However, the interaction between polarity and the linear trend of absolute ratio was not significant, F(1, 15) = 0.104, p = .751, η² = .007.

Could these results be driven by a variable other than numerosity? Might observers simply direct attention to the item with the largest (or smallest) square size, total dot area, or density? To assess this, we looked at the correlations between the (normalized) rank of the targets on each of these variables and RTs (see Table 2). Table 2 shows that most of the correlations were not significant. Square size was correlated with RT for conditions in which the target had higher numerosity than the distractors. Here, RTs were shorter when the square was bigger. Importantly, this was true for 3:1, 2:1, and 3:2 conditions, suggesting that the relatively good performance in 3:1 conditions is not due to a uniquely useful size cue in that condition.

Thus, overall, Experiment 4 replicates the pattern of findings from the previous experiments. However, the use of this more heterogeneous stimulus set makes search harder (Duncan & Humphreys, 1989). Now, only a subset of observers can use even a 3:1 ratio in numerosity to support efficient and accurate search.

Experiment 5

In the preceding experiments, luminance signals could still be informative. In the final experiment, we eliminated luminance information. An example of a search display for Experiment 5 is shown in Fig. 7. This is a set size of 4, large gray “items.” Numerosity is defined by the number of smaller, light and dark checkerboards, present within the item. Since the checkerboards were composed of an equal number of smaller squares of either 25 % (dark) or 75 % (light) gray and since the background color of an item was 50 % gray, the average luminance of each item was the same, regardless of numerosity condition. Additionally, as in Experiment 4, we controlled for the total area covered by the checkerboards (i.e., total checkerboard area was the same irrespective of whether the numerosity was 9, 18, or 27). Finally, by using checkerboards of different sizes, we prevented observers from being able to use checkerboard size as a search cue.

Fig. 7.

Example of the displays presented in Experiment 5

Method

Observers

Eleven observers (9 female, 2 male) between the age of 19 and 23 years (M = 20.4 years, SD = 1.2) were tested. They met the same requirements as in the previous experiments.

Stimuli and procedure

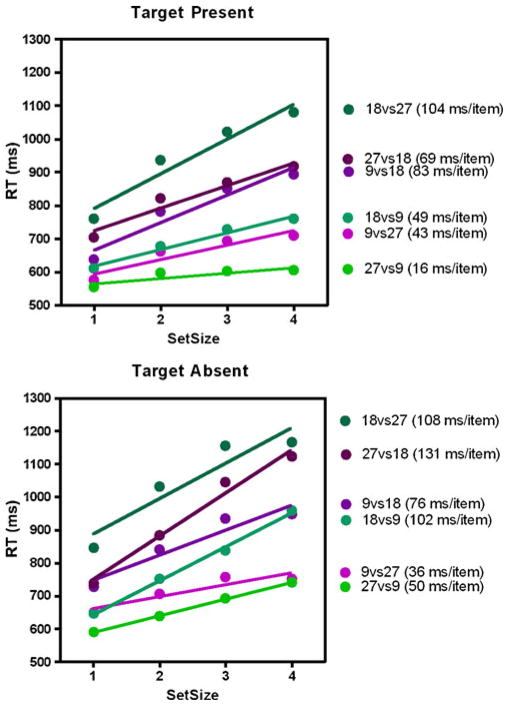
The experimental setup was the same as in Experiment 1, with the following changes. The number of large gray items was 1, 2, 3, or 4. The number of checkerboard elements within an item was 9, 18, or 27, producing ratios of 0.33 (9:27), 0.50 (9:18), 0.67 (18:27), 1.50 (27:18), 2.00 (18:9), and 3.00 (27:9). Checkerboard elements subtended between 0.1° and 0.5°. Gray background items subtended 3.2° visual angle in width and height; see Fig. 7). These were presented on a greenish background (RGB: 50, 150, 75) subtending 8.9° visual angle in width and height. Regardless of the numerosity, the total area covered by the checkerboard elements within an item was constrained to be 0.64, 0.81, or 1.0 deg².

Results and discussion

Overall, the performance of Experiment 5 was markedly worse than in the other experiments. Nevertheless, the main pattern of results was similar, with larger target-to-distractor ratios required to produce efficient search (see Figs. 8 and 9).

Fig. 8.

Reaction time (RT) × set size data for Experiment 5 (separately for target-present and target-absent trials)

The main trends apparent in the data were statistically reliable. A 2 (polarity) × 3 (absolute ratio) repeated measures ANOVA of slopes (ms/item) showed a significant linear trend for absolute ratio, F(1, 10) = 103.738, p < .001, η² = .912. Here, the main effect of polarity was also significant, F(1, 150) = 26.505, p < .001, η² = .726. However, the interaction between polarity and the linear trend of absolute ratio was not significant, F(1, 10) = 0.612, p = .452, η² = .058.

Additionally, with one exception (set size 2 and the 9 vs. 2 search condition: r = .998, p > .05), we did not find any significant density × set size correlations (all rs > .975, all ps > .142), indicating that density did not affect search performance.

Experiment 5 shows that, by the time the elements whose numerosity is to be assessed are isoluminant with the background, that numerosity can no longer guide search efficiently. In other situations, guidance survives with isoluminant stimuli. Thus, Cavanagh, Arguin, and Treisman (1990) found that search for a vertical item among horizontal remained efficient even when luminance information was removed. Orientation is a very strong guiding attribute. If we want to give numerosity status as a guiding attribute, it is a weaker attribute whose guiding power is disrupted by noise and, apparently, destroyed at isoluminance. Luminance might serve as a cue to number. More likely, isoluminant elements simply failed to support an effective assessment of number. In either case, the basic pattern of slopes, observed in Experiments 1–4, remains evident in Experiment 5. The efficiency of search is based on the ratio of numerosities. In Experiment 5, all of those efficiencies are in the inefficient range.

General discussion

The objective of the present study was to investigate whether attention can be guided to a target on the basis of its numerosity. Experiments 1 and 2 demonstrated that the efficiency of search was based on the target/distractor ratio (Weber’s law) and not on either the absolute number of dots or the simple difference between the numbers of target and distractor dots. Moreover, we observed a search asymmetry. Search for the smaller number among larger ones seems to be harder than search for the larger one among smaller ones. Experiment 3 disrupted cues on the basis of area or dot density. The same basic pattern of results was obtained, even though the task became more difficult. More dramatic disruptions of the stimuli in Experiments 4 and 5 preserve the pattern of results but render search inefficient, especially with the isoluminant stimuli of Experiment 5.

While the efficiency of numerosity search is based on the ratio of target and distractor numerosities, the ratios required for efficient search are much larger than simple numerosity JNDs. Halberda and Feigenson (2008), as an example, have shown that adults can reliably discriminate numerosities in a ratio of 7:8. As with other guiding attributes such as color and orientation, the representation of numerosity that can guide attention is much coarser than the perceptual threshold. Experiment 3 showed that, once visual factors like area and density are controlled for, a ratio of 3:1 seems to be adequate for good guidance. Experiment 4 shows that even those large ratios can barely support performance in the face of increased stimulus heterogeneity.

Although variation in total dot area and/or density made the attention-guiding signal less effective in Experiment 4, those variables did not drive performance, supporting the hypothesis that, even under these conditions, observers were still searching on the basis of numerosity. As was noted, there is a correlation between the overall target size and RTs in Experiment 4. Larger target items produce shorter RTs if you are looking for a more numerous target. It might be interesting to determine whether this represents a form of semantic priming. Looking for the target with the larger numerosity makes it more likely that attention will be guided to items that are simply larger. The correlation fails when the targets have the smaller numerosity.

Recent human neuroimaging studies have demonstrated that regions in the posterior parietal cortex (PPC)—specifically, the intraparietal sulcus (IPS) and the prefrontal cortex (PFC)—are engaged in the abstract representation of numbers (e.g., Castelli, Glaser & Butterworth 2006; Piazza, Pinel, Le Bihan & Dehaene 2007). In a similar vein, single-cell recordings in monkeys (Nieder, Freedman & Miller 2002; Nieder & Miller, 2004) have revealed homologous regions that contain neurons that are subject to Weber’s law. Activity in these numerosity-selective neurons is not affected by changes in the physical appearance (e.g., total dot area or density) of the display. Given that these two areas are functionally connected, it has been assumed (e.g., Nieder & Dahaene, 2009) that numerosity might first be encoded in PPC and then amplified and maintained in PFC to gain control over behavior. This suggests that, unlike other guiding attributes such as color, orientation, and so forth, which are encoded early on in the sensory pathway, numerosity may be a guiding property based on an abstract category at some distance from basic sensory features; two cars and two flowers have nothing in common, except that their set size is two.

Neuroimaging studies have shown that the IPS is not restricted to coding number. Number and size (Pinel, Piazza, Le Bihan & Dehaene 2004) and number and location (Zago et al., 2008) seem to overlap. In the monkey, Tudusciuc and Nieder (2007) have shown that 20 % of the neurons in the IPS encode numerosity, line length, or both. This could provide a different explanation for the correlation found between number and stimulus size, although it would not explain why this correlation does not arise when observers search for the smaller numerosity.

To summarize, we conclude that numerosity can guide the deployment of attention in visual search. Like other features, guidance by numerosity is based on a coarse representation of the underlying property. With attention, it is possible to perceive and act upon much more subtle differences in number. Moreover, unlike the stronger guiding features (e.g., color, size), numerosity is fragile, with performance faltering in the presence of even fairly modest stimulus noise.