The Comparison of Fluid Dynamics Parameters in an Andersen Cascade Impactor Equipped With and Without a Preseparator

Abstract

The fluid dynamic data in Andersen cascade impactor (ACI) are still lacking. Airflows and those affected parameters can be predicted in a preseparator and Andersen cascade impactor (ACI) by computational modeling. This study developed a validated computational fluid dynamic (CFD) model of an ACI and investigated the effects of the preseparator on the CFD parameters. Validation of the computational nozzle velocity for each of the stage 0 to stage 5 of the ACI stages was found to be within a 3.56% error. The flow field indicated that the preseparator accelerated the airflow velocity at the induction tube from 1.13 to 3.71 ± 0.09 m/s and 2.40 to 8.68 ± 0.16 m/s (at 28.3 and 60 L/min of flow rate, respectively). The preseparator produced a nozzle's wall shear stress ranged from 0.08 to 0.34 Pa on a collection plate, while the ex-preseparator spread wall shear from the plate's center was in a range of 0.11 to 0.37 Pa (at 28.3 L/min of flow rate). Moreover, the nozzle velocities increased along the distance from the middle of the collection plate to the periphery. The CFD explained the airflow of the preseparator equipped model by accelerating the airflow along the inlet port to maximize the trapping of desirable particles and the generation of a smooth wall shear stress at the collection plate to reduce the particle re-entrainment. While, the ex-preseparator generated an airflow that resulted in a higher wall shear stress occurring on the lower stages.

INTRODUCTION

USP 29, <601> on Aerosol, recommends using a cascade impactor for the evaluation of pharmaceutical aerosols, especially particle sizing, to replace microscopic examination. The reason that the cascade impactors are preferable over microscopy as the technique gives an aerodynamic parameter, which is relevant to pharmaceutical aerosols. During the time particles travel in the air, their diameters change from that of a visually observed diameter. According to Stokes law, the diameter of a particle during its suspension in the air is called its “aerodynamic diameter.” The goal of particle size distribution (PSD) measurement is to determine the output of aerosols emitted from the inhaler device, to mimic what is being introduced to the patient. If the PSD is distorted from reality during measurement then the procedure needs to be adjusted. At present, there are various kinds of instruments for determining aerodynamic particle diameters. An Andersen cascade impactor (ACI) is one commonly used device to characterize the particle size and predict the depositions of pharmaceutical aerosol particles [1]. This occurs through the impaction and retention of particles on the collection plate present at each stage of the impactor. Each stage of the ACI is composed of a number of nozzles that are specifically designed, precisely built, and arranged radially from the stages’ center. In fact, these nozzles gradually accelerate airstreams to a higher air velocity as the air flows through. The larger particles are retained on the earlier collection plates as the aerosols flow along the impactor. An aerodynamic diameter of the aerosol formulations can be determined for the particles collected on each plate. The operating airflow rate does affect the performance of the cascade impactor. A typical ACI operates at 28.3 L/min to evaluate particle sizes in a metered-dose inhaler (MDI). However, an ACI modified for a dry powder inhaler (DPI) operates at 60 L/min and is generally equipped with a preseparator to prevent overloading of the particles [1–3].

In general, the preseparator is an add-on part for the evaluation of dry power inhalers and is connected between the USP metal inlet and the cascade impactor stages. The aim of the add-on preseparator is to minimize the drug particle load that often occurs in the early stages of a cascade impactor. The preseparator is used to trap large particles and reduce the powder load over the lower stages, which may lead to nozzle obstruction and particle re-entrainment [4, 5]. Conventionally, a dry powder inhaler can be used at an airflow rate of from 28.3 to 90 L/min during an aerodynamic sizing experiment. Several studies have used a preseparator containing liquid or solvent to trap the powder that was overloaded before reaching the cascade impactor stage [6, 7].

Computational models are essential and are valuable tools for understanding and characterizing airflow patterns in any aerosol science. A computational fluid dynamic (CFD) model has been used as an aid for calculating and determining the particle size and the air flow from the ACIs to evaluate the performance of the impactor and other aerosol characteristics [5, 8–10]. Gulak et al. simply used a 2D single-nozzle model to determine if gravity affected the deposition of the particles in a computer simulation. In the case of a single-nozzle impactor operated at 28.3 L/min, there was a good agreement between the simulations with an experimental setup in models and gravity [8]. Sethuraman and Hickey employed a simple 2D preseparator model. They showed how the air velocity changed while the air was traveling along the preseparator using a computer simulation. Most particles were deposited under the inlet tube of the preseparator. Qualitative data can be achieved where low-velocity and high-pressure regions exist [9]. Vinchurkar et al. (2009) described the effects of the aerosol charge that increased the measured particle size distributions (deposition fraction on each stage) up to 30% and produced a reduced cutoff (d50) at each stage of up to 400%. The research work of multiple-jet models (whole stage cascade impactor) also produced clear flow patterns that were more useful when compared with a single jet design [5, 8].

There are many CFD parameters that can be used to describe airflow characteristics in the system. For example, CFD results (pressure and velocity profiles) have been used to identify cyclonic flow conditions in the devices attributes and to design two modifications of the Cyclohaler^TM [11]. A wall shear stress signifies axial components of the force that acts tangentially to the surface due to the skin friction and how it can be considered to affect the jet flow and the re-circulated flow in an airway. In the human extra-thoracic airway under steady inspiration, the length of the recirculation zones increased as the airflow rate was raised (an increase of the wall shear stress). There were minor separations and reattachments that occurred near the interface [12]. The wall shear stress was examined in the mouth–throat model and the lower respiratory tract; it showed that a higher wall shear stress was obtained in the mouth–throat model. It was observed that the airflow was split at the bifurcation and the high velocity zone was generated near the inner wall of the trachea [13].

The flow characteristics of the fluid have been shown to influence the particle deposition of the impinger. The cross flow had an effect on the impingement region towards the downstream direction. Then, a staggered nozzle arrangement showed deflections of the stagnation regions by a stronger collision of cross flow than for an in-line arrangement that can be expressed by a heat transfer parameter [14]. The wall shear stress or mass transfer parameter showed good agreement with the protein particle deposition from a radial impinging-jet cell [15]. However, there has been no detailed study of the airflow in the add-on preseparator compared with an ex-preseparator, the interactions among the nozzles, and the wall shear pattern on the collection plates based on the whole cascade impactor geometries. A clear understanding of the flow field dynamics inside the ACI can be obtained. This will be useful information for the evaluation of future developments of pharmaceutical aerosols.

For validation of the model, the computational results of the 3D velocities and flow through curve (FTC) data were demonstrated to be similar. The validation of the velocities and FTC was carried out to establish the predictive abilities of the CFD models [16]. Airflow velocities across a 200-mm cube were experimented with in a wind tunnel using a probe of laser Doppler anemometers. It was shown that these data provided good examples for computational validation of the development of CFD [17].

Therefore, many research works concerned with pharmaceutical aerosols have been performed with the ACI equipped with the preseparator to reduce particle over loading for the DPI formulations. However, the airflow effects and their phenomena needed to be fully investigated. For example, a three-dimension model could be described in more detail when compared with a two-dimension airflow in the add-on preseparator that should produce critical flow characteristics to reduce particle overloading along the ACI, and other CFD parameters that may be influenced by the preseparator in the ACI.

The aim of this study was to classify the flow field, airflow functions, and the effects of the preseparator and ex-preseparator in the ACI model, by drawing the geometries and mesh characteristics for the CFD study to simulate typical operational conditions.

The computational fluid flow patterns have been clarified and discussed. The simulations were performed at 28.3 and 60 L/min. The add-on preseparator was compared to the ACI without the preseparator in terms of the air streamline, flow velocity, and wall shear stress that can be linked to how does it work and its advantages. According to a previous study, the manufacturer’s data and experimental data were selected to validate the CFD model based on comparisons of the numerically predicted characteristics of the Andersen cascade impactor with a 28.3-L/min flow rate. This flow rate was expected to be of sufficient use in the simulation model to explore the characteristics of the airflow.

MATERIALS AND METHODS

Andersen Cascade Impactor Model

The Andersen cascade impactor consists of a USP metal inlet, stages 0 to stage 7, and a filter stage for traditional use at 28.3 L/min. The preseparator is the gateway to the eight collection stages and a filter stage [1]. Each ACI stage is composed of a number of nozzles, so the effect of any nozzle-to-nozzle interaction in each of the individual stages was therefore included in this research. Fluid parts were measured as discrete volumes together from the preseparator to the filter stage of the fluid part. Reducing the multipart geometric dimension to a more simple geometry minimized the complexity of the ACI model [5]. A perpendicular stage wall was introduced instead of a taper wall. The modified model provided a good and continuous mesh quality. The ANSYS Gambit program was employed to draw stage and plate geometries in order to create a computational geometry and mesh of the full cascade impactor. The ACI is composed of 11 parts (preseparator, stage 0 to 7, filter stage and base stage). The stage geometries were separately constructed from the stage’s body and continued with each nozzle, each nozzle was arranged by dividing the radius by the number of nozzles. Then a drawing of the collecting chambers with the collection plate was placed under each stage. The collection plates of stages 0, 1, and 2 each had a center hole with a 22.5-mm diameter and a 1.65-mm thickness. A half of the body part of the next stage was combined with an earlier stage for its continuity in a calculation. The number of nozzles and other simulated dimensional data of each stage were consistent with the values given in Table I. These data were obtained from the manufacturer and measured again using a digital vernier caliper. The geometrical models of stages 0, 1, 2, 3, 4, 5, 6, and 7 were individually built up for the whole dimensions of the ACI, preseparator as shown in Figs. 1 and 2. Finally, each stage was grouped as one continuous phase from the preseparator to the base stage. To balance the accuracy and computing resource, the mesh of each part was demonstrated using a mesh converged by an intensive grid converged study (using the preseparator and stage 0 model).

Table I.

Characteristics of the Mark II Andersen cascade impactor (ACI) based on the manufacturer's data

Stage	Number of nozzle	Radius (mm)	Length (mm)
0	96	1.275	4.1
1	96	0.94	4.1
2	400	0.457	1.5
3	400	0.3555	1.55
4	400	0.2665	1.55
5	400	0.1725	1.15
6	400	0.127	1.15
7	201	0.127	1.15

Fig. 1.

ACI geometry of each stage (0–7) plus the final filter

Fig. 2.

Mesh of each inlet types. (1) Preseparator. (2) Traditional USP metal inlet (cone)

Boundary and Initial Conditions

Air was drawn through a preseparator, into each stage and a nozzle (jet) or through a number of parallel nozzles (multi-jet). The mass flow inlet was assigned at an inlet boundary that was set in a traditional condition with a flow of 28.3 L/min. The jet flow went through the nozzle then bumped into the collection plate as the flows were forced to change direction by a 90° bend and passed through a small channel between the plate to the next stage. Furthermore, an outlet flow was used as the outlet boundary at the exit tube of the model. All surfaces were treated as being non-slip walls.

Governing Equation

A steady, incompressible, and isothermal system under standard laboratory conditions was considered for the flow in the preseparator and ACI. For a flow rate of 28.3 L/min, the maximum Reynolds number in the preseparator body was approximately 0.1057, and this indicated that laminar flow and Cunningham slip correction were incorporated in the simulation flow pattern in the cascade impactor. The conversion equations used in this study are shown below.

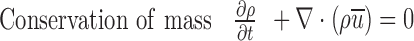1

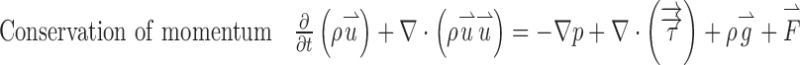2

Where 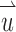is the velocity vector, p is the pressure, ρ is the fluid density, 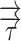is the stress, tensor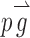, and and 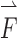are the gravitational body force and external body force, respectively.

Numerical Methods

In order to solve the governing mass and momentum conservation equations in considering the geometries, the Semi-Implicit Method for Pressure-linked Equation Corrected (SIMPLEC) algorithm of the CFD package Fluent 6 was employed. Laminar flow was used as a flow simulation. The default turbulence kinetic energy and dissipation rate of the outlet air were set as the outflow (constant equal to 1). For spatial discretization, the Green–Gauss node based, Pressure Staggering Option, and second-order upwind scheme were configured for gradient, pressure, and momentum discretization, respectively.

Model Validation of Flow Characteristic

To ensure that the flow pattern was correctly modeled, both an examination of both the iterative convergence and comparing it with experimental data were used to validate the computational model. First, the global mass and residual momentum were set as being lower than 3 orders of magnitude of the convergence of the flow field solution. Second, the predicted flow velocity at the nozzle of each stage was compared with the characteristics of the Mark II Andersen cascade impactor based on the manufacturer's data. The ACI comprising eight impaction stages, preseparator, and filter stage were used as a validating tool. Monodisperse silica spheres of size 4, 5, 7, and 10 μm (Phenomenex, UK) were used as a calibrant. The spheres (about 20 mg) were loaded into the in-house plastic device and run into the complete ACI set at flow rate of 60 L/min. After particle deposition had occurred, the deposited particles on the preseparator were carefully collected and weighed. The percent of particle deposition on the preseparator was compared between the experimental and computational data.

Fluid Flow Parameter Examination

The characteristics of the wall shear stress at the collection plate were obtained under two inlet conditions (traditional and add-on preseparator). The wall shear stress can be explained by Eq. 3, where μ is the dynamic viscosity, u is the flow velocity parallel to the wall, and y is the distance to the wall.

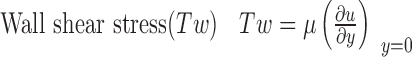3

To examine the fluid flow field in the full three-dimension preseparator, the velocity streamline, contour, and vector were set to determine the direction of the flow characteristics in the model of interest (preseparator and stage 0). Moreover, the velocity of each nozzle was characterized by its average volume velocity at the nozzle’s volume. The probe was used at a random position for determining the inlet velocity under the preseparator and ex-preseparator model.

Particle Tracking

The equation of particle motion was operated by using Runge–Kutta for the high order scheme and analytic for the low order scheme, where tracking scheme selection was set as automated. The maximum number of steps was 50,000 steps and the length factor was 5. A spherical shape was used for drag parameters. The particles initial position was located at the inlet part of each model and their initial velocities were set to zero. Brownian motion and Saffman life force were considered as the physical model. Accuracy control tolerance was set to 10⁵ and a maximum refinement was 20.

RESULTS AND DISCUSSION

Geometries and Mesh of the Andersen Cascade Impactor

The multi-compartment nature of an ACI is a major puzzle because of its complex geometrical information. The nozzle’s dimensions are 2,000-fold smaller than those of the stage’s body resulting in a quality of meshing [8]. The finite volumes for each part of the ACI and its Orthogonal Quality are presented in Table II. The model contained 4 to 11 million elements. The meshes’ quality was in the range of 0.127 to 0.269. Hence, the orthogonal quality ranges were acceptable [18].

Table II.

Number of finite volumes

Stage	Number of finite volume	Orthogonal quality
Preseparator and stage 0	4,935,053	1.80667e−01
Stage 1 and stage 2	11,483,290	2.65131e−01
Stage 3	7,891,939	2.69472e−01
Stage 4	9,746,739	2.65696e−01
Stage 5	9,580,427	2.21700e−01
Stage 6	7,530,427	1.26605e−01
Stage 7	5,700,052	2.43775e−01

Numerical Validation

The computational model was validated by convergence of the examined iteration and also the CFD results were compared to the experimental data. Therefore, the correlation was validated between the experimental and simulated. The airflow rate at 28.3 L/min was simulated for specific stages to compare with the manufacturer’s data. Based on the results (Table III), the numerically predicted average nozzle velocities were comparable to those of the manufacturer’s data. As described, these average nozzle values were based on the summation velocities of each frame of the nozzle divided by the number of frames at that particular stage. According to the manufacturer’s data [19], numerical predictions were all within an approximately 3.56% error for all stages except on stages 6 and 7. In these latter stages, the percentages of errors were within 8.10% of the manufacturer's data. The increase in the error of the predicted nozzle velocities at stages 6 and 7 can be explained by considering the expected numerical inaccuracies. This may be caused by the incremental errors of each stage that were introduced into the following stage. The significant increase in the solution complex was associated with the decrease of the nozzles’ size from 0.127 mm to 0.4 μm [9]. This would confirm the degree of accuracy of the airflow in the cascade impactor by our boundary conditions [5, 16].

Table III.

Numerical predictions of average nozzle velocities in meters per second compared with the manufacturer's data [5]

Stage no.	0	1	2	3	4	5	6	7
Predicted nozzle velocity	0.98	1.73	1.75	2.99	5.39	13.10	24.80	48.70
Manufacturers’ nozzle velocity	0.95	1.75	1.80	2.94	5.25	12.72	22.94	45.49
% Error for CFD vs. manufacturer	3.56	1.59	2.78	1.73	2.74	2.98	8.10	7.05

CFD computational fluid dynamic

Streamline Field Conditions of the Preseparator and Whole Cascade Impactor

The 3D streamline (Fig. 3(1)) shows that the streamlines of velocity start from the preseparator to the lower stages. In the preseparator, the flow direction is bent to the connection holes that pass the flow to stage 0. As the airflow is drawn through the connection holes, the bending zone of the airflow turns 360° from where it starts from the induction tube (A) straight to the middle plate (B) then turns 90° against the B plate. Then, a 90° turn was again made when the flow hit the preseparator wall. At this point, the magnitude of the air velocity decreased with the distance from the induction tube and was close to zero at the middle of the plate. This may increase the deposition on the preseparator wall of the larger aerosol particles. When the particle size was larger than 10 microns they lost their inertial force and were deposited on the preseparator plate and wall [9]. Finally, the streamline was bent sharply by about 180° because of the drawing force of the connection tube (C). By these processes, the impactor reduced the particles load on stage 0 (and lower stages) and improved the particle-sizing ability. In this 3D model, the airflow pattern in the preseparator showed some disagreement from the 2D model where the streamline was drawn directly to the connection tube (C) because of the limitations of the geometrical model’s dimensions [9]. From this flow pattern, the air velocity was accelerated near to the preseparator’s middle sheet (up to 3.71 ± 0.09 and 8.68 ± 0.16 m/s at the 28.3 and 60 L/min of flow rate, respectively) (Fig. 4). The streamline turned around the preseparator’s orifice and drove continuously to the preseparator’s outlet. Therefore, the preseparator inlet acted as a particle sizer in a similar way to what happens at the lower stage’s nozzle and where the B plate is the collection plate. The regions with more than a 90° bend produced the recirculation zone. The velocity profiles in the vertical portion of the ex-preseparator ACI seem to be less skewed than in the add-on preseparator ACI model (Fig. 5). The reduction in the velocity gradient was expected to cause an increase in the turbulent viscosity associated with the downstream propagation to the connection tube of the preseparator [20]. It means that those air recirculation zones were observed at the center of the preseparator, above the orifice, and it was predominant after exiting the orifice. These regions have a low velocity. The other large-sized particles were assumed to be trapped at stage 0. The streamline was observed to strike the collection plate of the preceding stage (stage 0), then flowed through the 180° bend and entered the connection section leading to the nozzle base. Moreover, the airflow was observed as the flow field was passing through the holes of the collection plates before further transitioning to the filter stage (Fig. 3(2)). Recirculation zones were predicted in the air streamline when reaching stage 0. This flow pattern induced the recirculation of the particles that was dependent on their diameter and disturbed the separation process taking place at the exit of the nozzle [9].

Fig. 3.

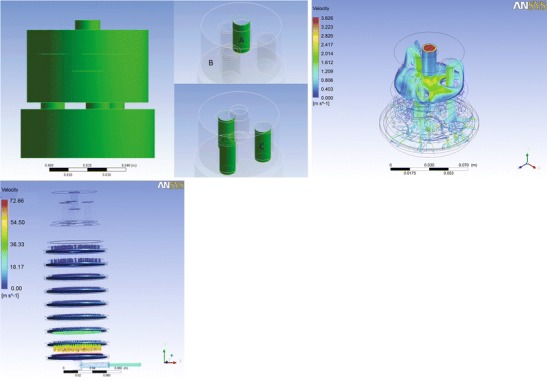
Streamlines and velocity profiles of the flow field in an Andersen cascade impactor. (1.1) Geometry of preseparator induction tube (A), middle plate (B), connection tube (C). (1.2) Velocity Streamlines. (2)Velocity profile of whole ACI simulation

Fig. 4.

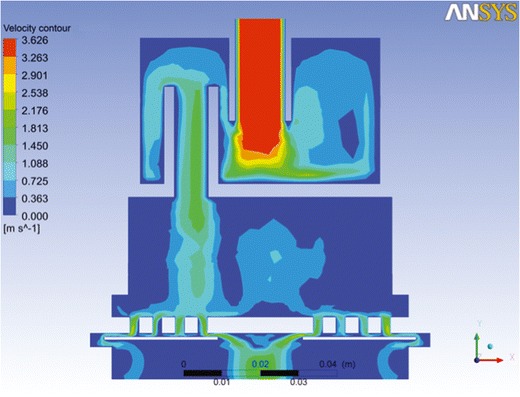
Velocity contour in the preseparator and stage 0

Fig. 5.

Velocity streamline of stage 0 under different inlet profiles. (1) Stage 0 under traditional induction port at 28.3 L/min. (2) Stage 0 under traditional induction port at 60 L/min. (3) Stage 0 under preseparator at 28.3 L/min. (4) Stage 0 under preseparator at 60 L/min

Velocity Inside the Preseparator and Whole Cascade Impactor

The velocity profile in Fig. 3(2) presents the velocity profile at each nozzle location of the eight stages. The velocity increased steadily from stage 0 to stage 7 and the difference in velocity between stage 0 and stage 7 is greater than 70%. The narrower the space through which the air travels the higher is the velocity [8]. When the nozzle velocity increases, it is able to accelerate the particle velocity, and this shows good agreement with the acceleration of the particles’ velocity [21]. The increased particle velocity increased the particle inertial force and promoted the impaction of the particles on the collection plate. It means that the small particles were more likely to deposit at the lower stage because of the increasing air particle acceleration produced by the narrower diameter of the nozzles.

The deposition of the aerosol particles can be described by the Stokes equation.

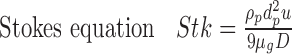4

Where ρ_p (kg m⁻³) is the particle density, d_p is the particle diameter, U is the fluid velocity, μ_g is the gas viscosity, and D is the nozzle’s diameter.

The streamline velocity of stage 0 showed a different clustering pattern for the high velocity where the streamline velocity was in the traditional induction port (Fig. 5(1)–5(2)) and exhibited a higher airflow velocity than that in the preseparator (Fig. 5(3)–5(4)) for both flow rates (28.3 and 60 L/min). These phenomena may be explained by the larger outlet cavity of the add-on preseparator ACI compared to the ex-preseparator ACI. The airflow velocity distributions were 0.390 ± 0.273 and 0.856 ± 0.600 m/s (at 28.3 and 60 L/min, respectively) for stage 0 following the preseparator. It is possible to generate a good re-entrainment of small particles that may reduce the number of small particles being trapped at the earlier cutoff size stage. At the point, it is not sufficient velocity to force large particle to be re-entrained. On the other hand, the ex-preseparator generated a higher airflow velocity (0.106 ± 0.191 and 1.010 ± 0.951 m/s at 28.3 and 60 L/min, respectively) that caused separation of the flow stream at the corner of the cone. Then, there is an annular region where a portion of the flow recirculation was created and resulted in a pressure loss in this region [6].

According to Fig. 6, the predicted numerical nozzle velocities were compared with each frame at stages 2 and 3; it showed that the nozzle velocities increased along the frame (from the center of the collection plate to the outer frame). Therefore, the center of the collection plate tended to trap the larger particles with a high population of the particles in comparison to within the stage. On the other hand, smaller particles (in the size range) were easily accelerated by the outer frame of the nozzles to deposit on the periphery of the collection plate. The smaller particles (outside the size range) were continuously moving and were further accelerated to the next stage of the ACI [10]. This assumption was supported by the particle acceleration in the air streamline (Stokes equation). Moreover, the 2D simulation showed a similar recirculation streamline pattern at the outer wall of each stage.

Fig. 6.

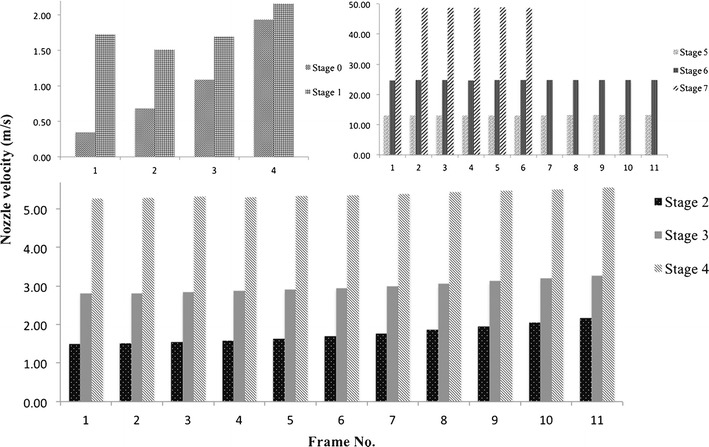
Numerical predicted nozzle velocities on each frame of each stage at 28.3 L/min

Wall Shear Stress on the Collection Plate (Impaction Plate)

These two models (preseparator and ex-preseparator) overcame the limitations of the previous model because the effect of the flow from the preseparator to the flow through the stages was clarified [8, 9]. According to Fig. 7, the wall shear stress on the collection plate was present on both the preseparator and the ex-preseparator. After the air flow from the three connection tubes of the preseparator, the three airflow streams reached stage 0 by passing through the nozzle that caused a spreading pattern of the wall shear stress grouping of “radius like” at the stage’s collection plate. While the spreading pattern was affected by the cone of the ex-preseparator that was continuously spread from the center of the collection plate. The increased velocity of air travels around the outer edges of the collection plates and affected a wall shear characteristic with a higher velocity nozzle area to cause a wider radius spread and a higher intensity of the wall shear. The wall shear stress on the collection plate ranged from 0.08 to 0.34 Pa (at 28.3 L/min of flow rate) under the preseparator produced air inlet, while the ex-preseparator wall shear stress presented in a range of 0.11 to 0.37 Pa (at 28.3 L/min of flow rate). In addition, the preseparator showed a reduction of the collection plate inlet when compared to that of the ex-preseparator inlet (Fig. 7).

Fig. 7.

The distribution and intensity of wall shear stress along the collection plate positions at 28.3 L/min. (1) Wall shear stress distribution under preseparator. (2) Wall shear stress intensity under preseparator. (3)Wall shear stress distribution under traditional induction port. (4) Wall shear stress intensity under traditional induction port

The wall shear stress represents the viscous energy loss within the flowing boundary layer and is related to the drag intensity in the fluid flow against the wall. At the stationary wall, the isothermal pressure was reduced in a moving fluid within an increment of length due to fluid friction (Fig. 8). By increasing the Reynolds number, it was possible to locate a wider stagnation region where the fluid flow velocity was proposed to be zero (it means that the flow direction was readily transformed). These wall shear stresses caused the “ring like” zone of high intensity wall shear stress around the stagnation region under each nozzle. Moreover, the detachment of particles and re-entrainment of the particles was also explained by the wall shear stress and that there was a critical value of the wall shear stress and the exposed time to react on those particles [22]. According to the wall shear stress equation, the intensity of the wall shear stress depended on the flow velocity, it meant that the preseparator could reduce the trapped particles to re-entrain back into the stream flow. Then, it might decrease the percentage wall loss of the impactor, due to the decreased air velocity and smoothed on the wall shear stress [7]. It was found that particle removal depended on the shear stress even when it was not a linear correlation, for which the particle removal phenomena needs to have a critical wall shear stress [23].

Fig. 8.

Schematic diagram of stagnation region and flow direction

Particle Collection Efficiency in the Preseparator

The particle collection efficiency was completely validated by the experimental data using monodisperse silica spheres. The trapped particles on the preseparator showed a good correlation between the experimental and simulation data (Table IV). The collection efficiency from the simulation data produced a sharper curve than that obtained from the experimental data (data not shown). In this study, trapped particles on stage 0 of the ACI without the preseparator was about two times higher than that of stage 0 of the add-on preseparator ACI. It was observed that most large particles (8 to 10 μm) were trapped on the preseparator. It can be explained that the air velocity near the wall of the impactor without the preseparator generated a higher airflow than with the preseparator resulting in higher particle deposition.

Table IV.

Percent collection efficiency of spherical silica particles on the preseparator by computational simulation and experimental (mean ± sd, n = 3) at an airflow rate of 60 L/min

Particle size (μm)	CFD	Experimental
4	7	9 ± 2
5	9	12 ± 3
7	43	50 ± 5
10	100	92 ± 6

CFD computational fluid dynamic

In conclusion, the current study has illustrated the utility of a CFD model to describe the airflow characteristics of the aerosol testing equipment. Results of this study can be used to achieve a better understanding of the principles associated with the airflow in the ex-preseparator ACI and the add-on preseparator ACI. According to the preseparator’s airflow, it indicated that the airstream traveled around the preseparator wall and traveled down to the next stage. Accelerating the air velocity of the preseparator inlet was proposed to persuade the larger particles to be trapped on the preseparator’s plate. However, the recirculation zone was clearly predicted in the preseparator and this may reduce particles loss on the wall. Moreover, the wall shear stress was reduced in the ACI equipped with a preseparator. The study proved that particle collection efficiency was different between the ACI with and without the preseparator. The preseparator can be used to reduce particle re-entrainment and minimize particles loading on the lower stages. Future applications of the developed ACI model include evaluating the effect of the drug particle size on the deposition and quantifying the effects of the aerosols on the performance of the impactor. Lastly, the CFD approach illustrated in this study can be used to design and develop the next generation of aerosol assessments.